A Comprehensive Performance Analysis of a 48-Watt Transformerless DC-DC Boost Converter Using a Proportional–Integral–Derivative Controller with Special Attention to Inductor Design and Components Reliability
Abstract
1. Introduction
- ❖
- A comprehensive performance analysis has been carried out for a 48-watt ( = 12 V, = 24 V, = 2 A, and = 100 kHz) transformerless DC-DC boost converter. The converter was designed and simulated with the help of a PID controller used for achieving precise regulation of the output voltage and ensuring a rapid response to disturbances through dynamic modeling. The PID controller is a feedback control system that adjusts the control input based on the error (the difference between the desired set-point and the measured process variable).
- ❖
- Further, to check the behavior of linear time-invariant systems and system stability, frequency response analyses were carried out using Bode plots at 100 kHz and 500 kHz frequencies.
- ❖
- Performance comparisons were made for uncompensated and compensated transformerless boost converters at 100 kHz and 500 kHz switching frequencies.
- ❖
- In this research paper, the converter’s performance analysis was carried out with special attention to inductor design and component reliability evaluation.
- ❖
- ❖
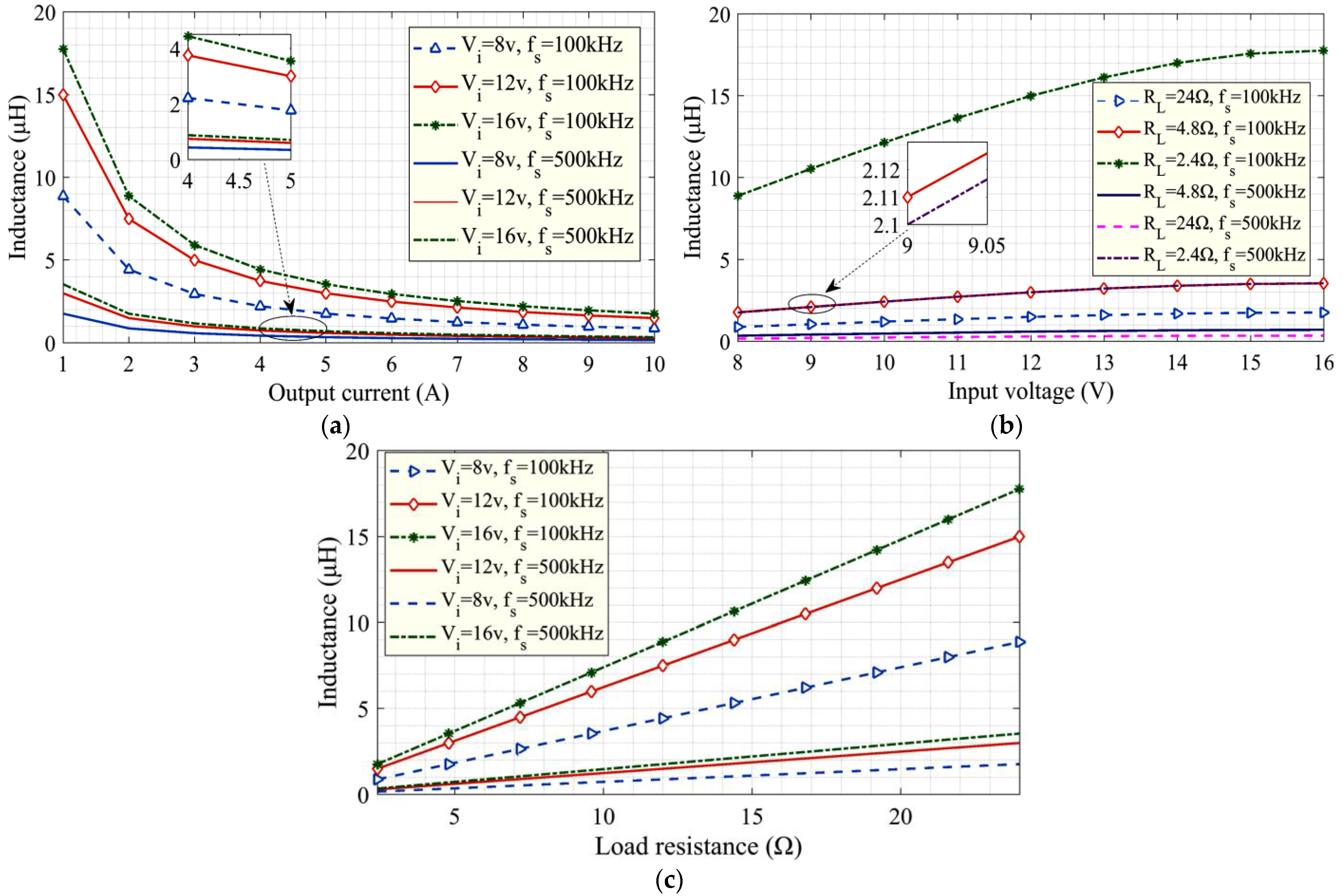
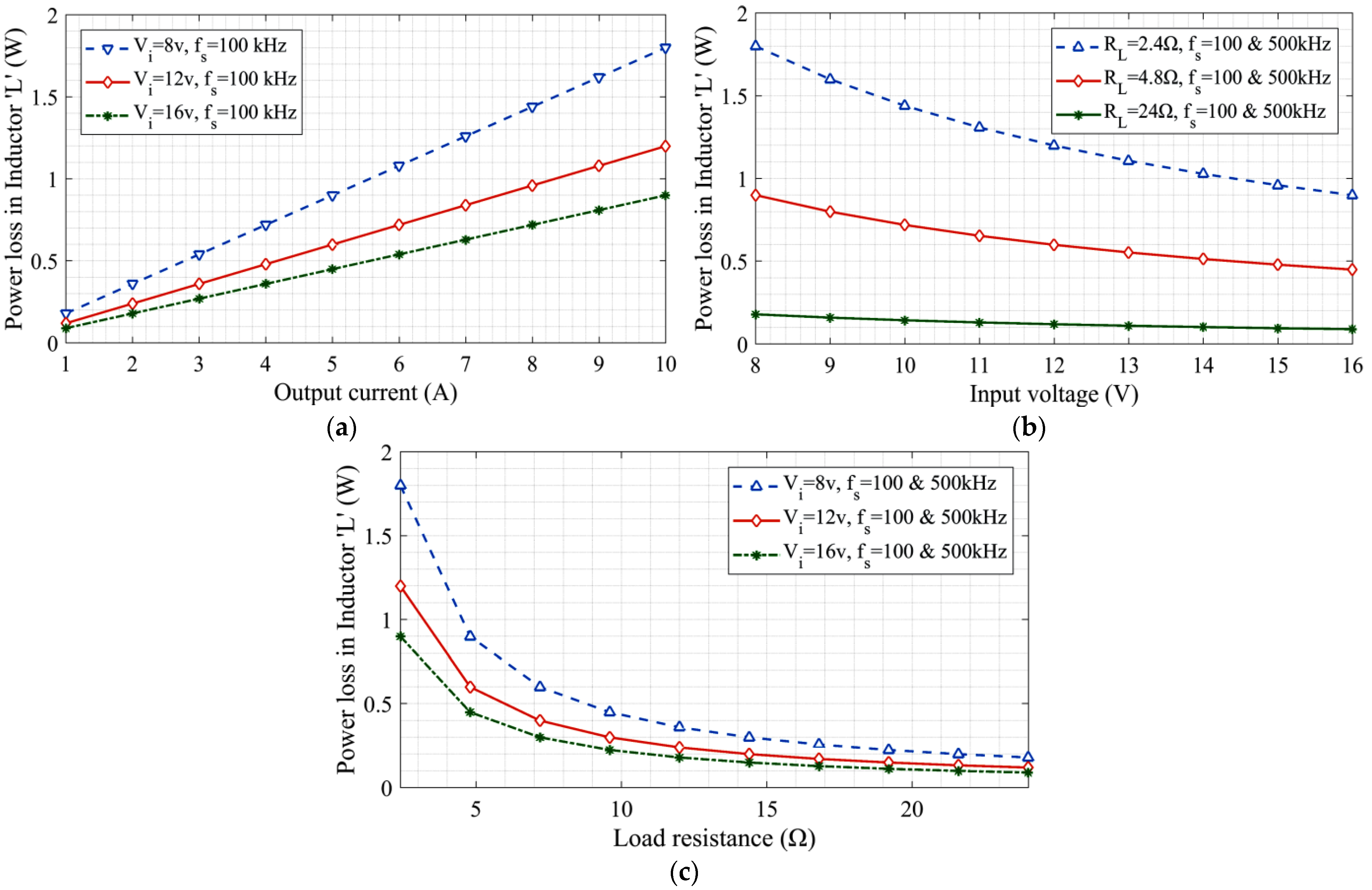
- Further, a performance investigation of the inductor “L” was carried out as a function of load current, supply voltage, and load resistance at 100 and 500 kHz frequencies.
- ❖
- Furthermore, considerable attention was directed towards analyzing the reliability and failure rates of active and passive components within a 48-watt transformerless DC-DC boost converter. These analyses offer valuable insights into the anticipated operational longevity and potential failure patterns of each component within a 48-Watt transformerless DC-DC boost converter. The evaluation of reliability contributes significantly to comprehending the component’s enduring performance.
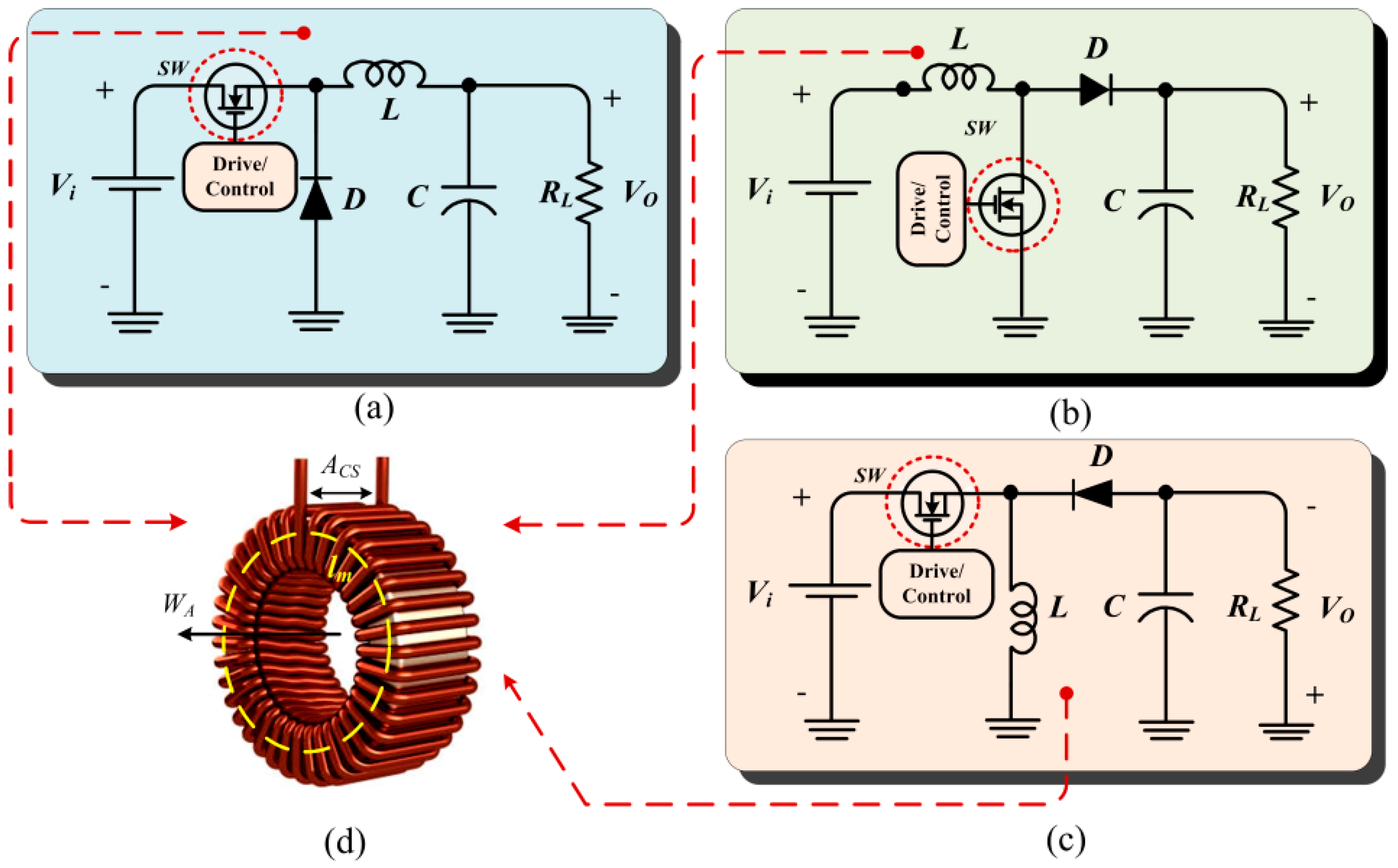
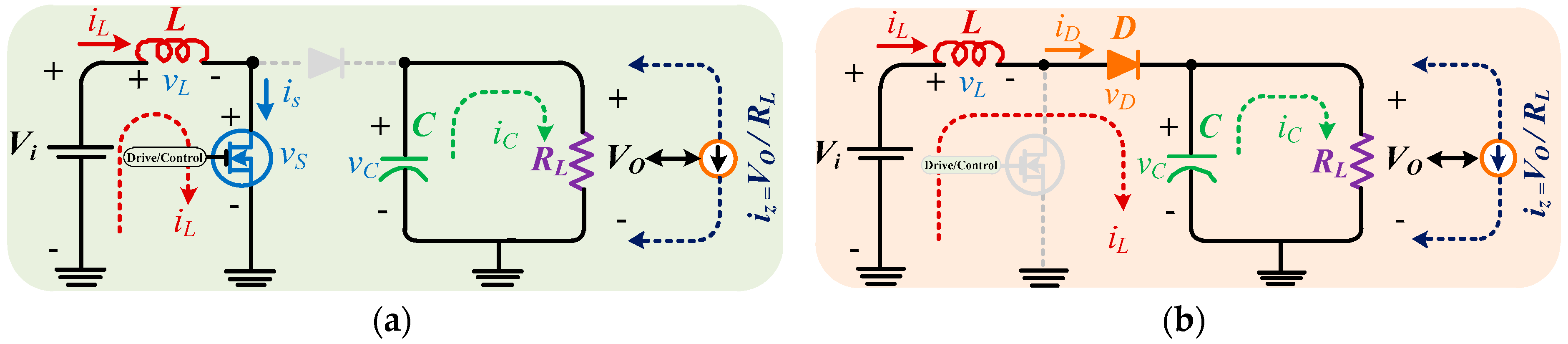
2. The Modeling of a Transformerless DC-DC Boost Converter
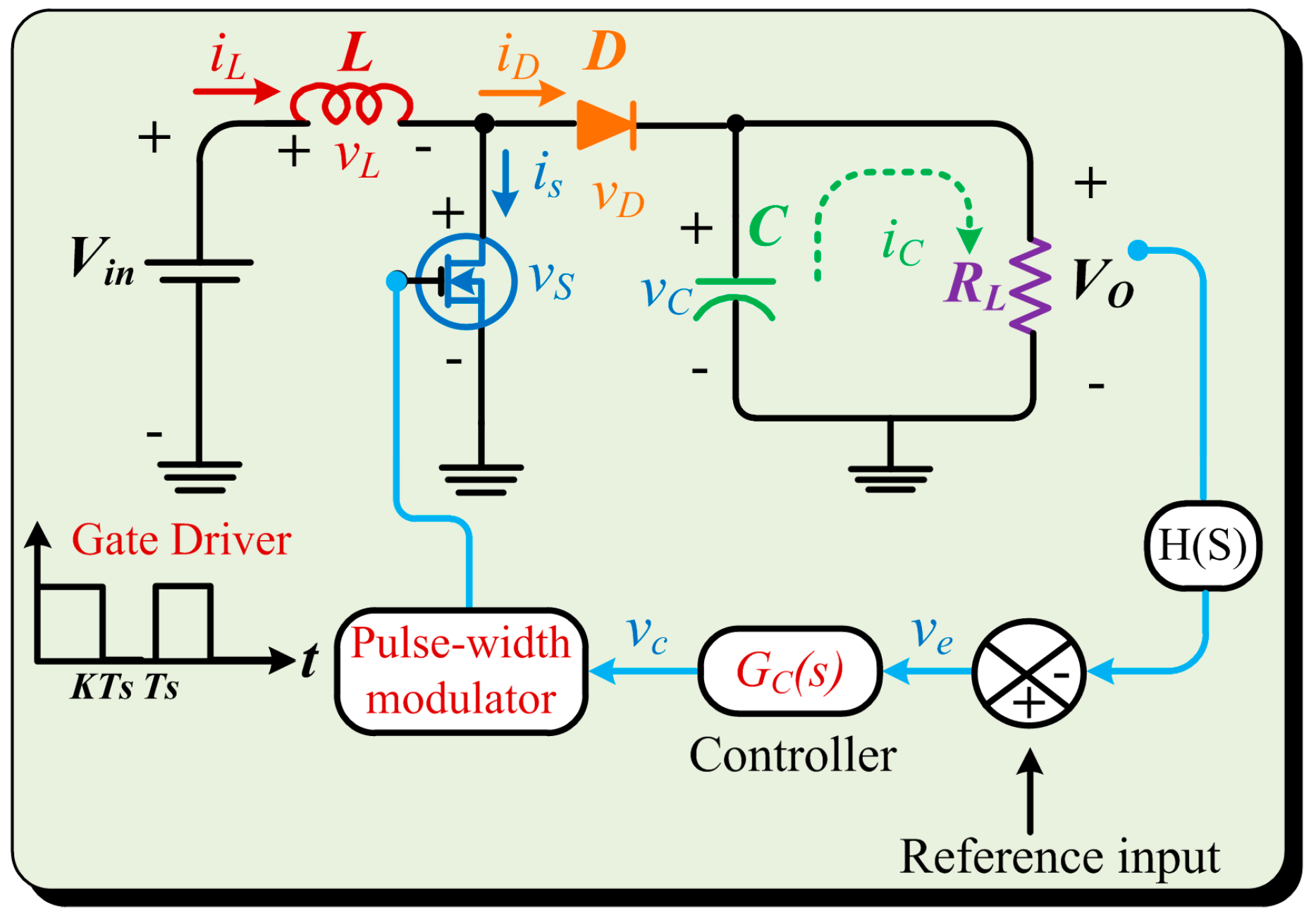
3. The Employed Control Technique
Proportional–Integral–Derivative (PID) Controller
- Proportional (P) term: The P-term generates a control output that is directly proportional to the current error, thereby determining an immediate corrective action based on the error’s magnitude. In boost converters, the P-term helps reduce steady-state errors by adjusting the duty cycle of the switches.
- Integral (I) term: The I-term integrates the error over time and applies corrective actions to eliminate prolonged steady-state errors. In boost converters, the I-term aids in removing offset voltage and ensuring tight regulation.
- Derivative (D) term: The D-term anticipates future errors by analyzing the rate of change of the error signal. It provides a control action to mitigate rapid changes, improving the converter’s transient response and stability.
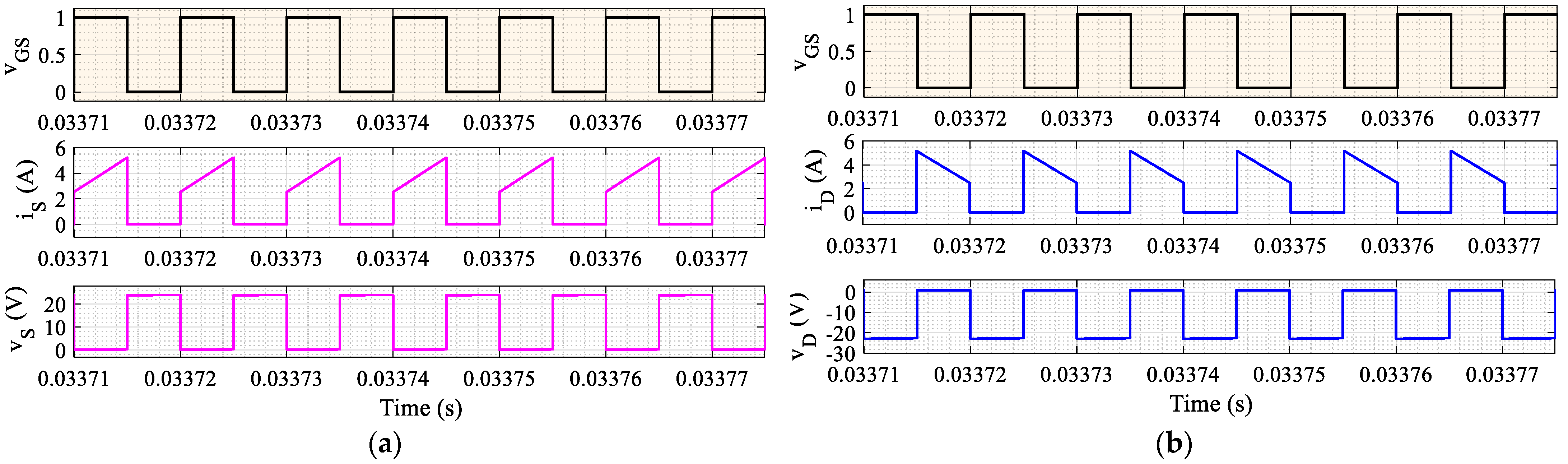
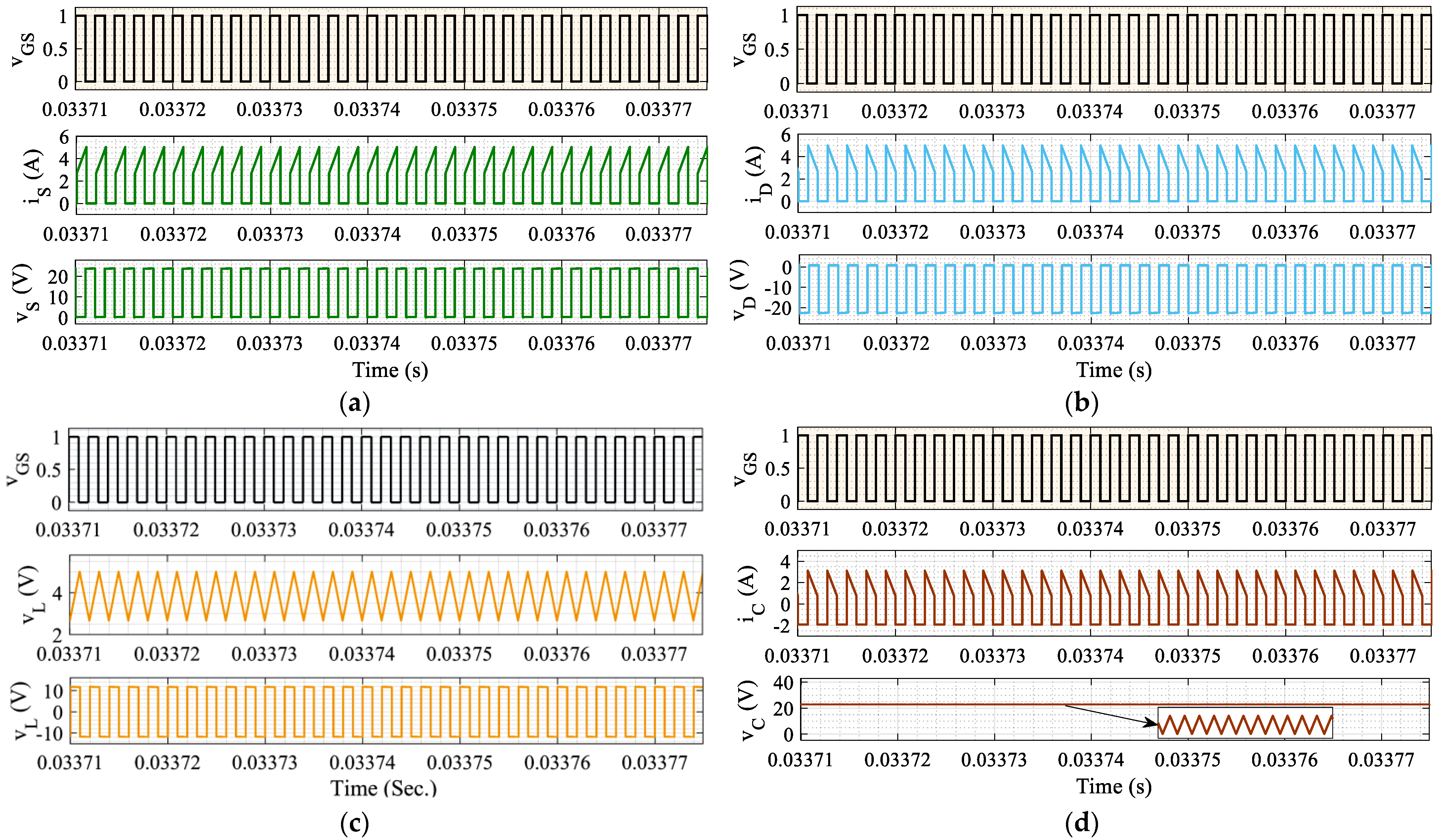
4. The Design of an Inductor in a 48-Watt Transformerless DC-DC Boost Converter
4.1. Factors Related to the Inductor Design
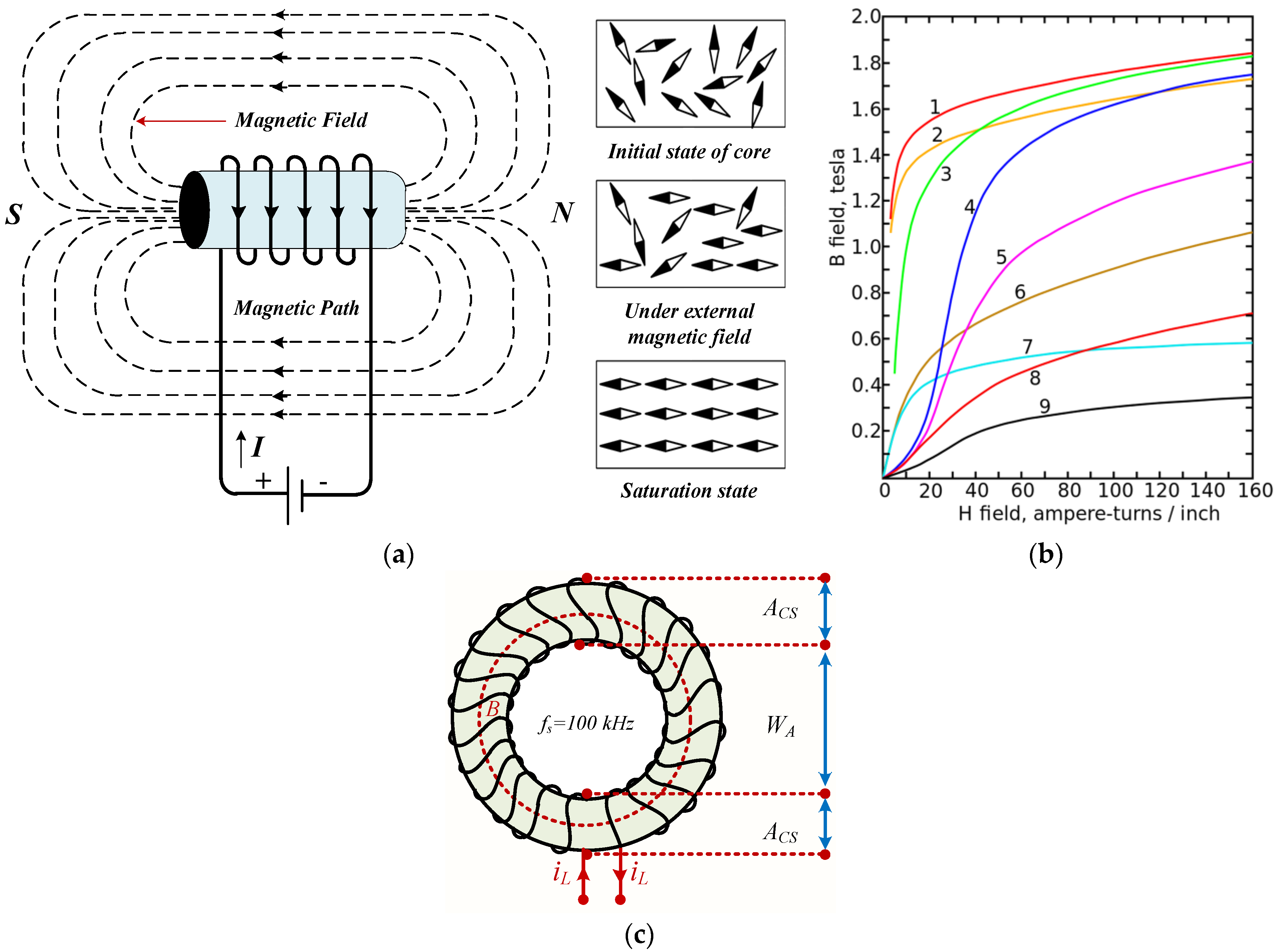
4.1.1. Magnetic Core Saturation: Reasons and Impact
4.1.2. The Selection of Core Material
4.1.3. Losses and Self-Heating
4.1.4. Ripple Currents in Inductors “L”
4.2. Evaluation of the Window Area ()
4.3. Evaluation of the Area Product ()
4.4. Assessment of Permeance ()
4.5. Assessment of the Number of Turns (N) and Wire Size (a)
5. Reliability and Its Associated Factors
5.1. Failure Rate
5.1.1. Instantaneous Failure Rate ()
5.1.2. Failure Rate in Time “”
5.2. MTTF
6. Evaluation of the Part Failure Rate of Active and Passive Elements in a 48-Watt Transformerless Boost Converter
6.1. Part Failure Rate of Inductor “L”
6.1.1. Base Failure Rate
6.1.2. Temperature Factor
6.1.3. Quality Factor
6.1.4. Environmental Factor
6.2. Part Failure Rate of the Switch (MOSFET)
6.3. Part Failure Rate of the Diode
6.4. Part Failure Rate of the Capacitor
6.5. Part Failure Rate of the Resistor
7. Results and Discussion
7.1. Analysis of the 48-Watt Transformerless DC-DC Boost Converter Using a PID Controller
7.2. Design and Analysis of Inductor “L” in a 48-Watt Transformerless DC-DC Boost Converter
Generalized Guidelines for Inductor Design in Transformerless DC-DC Converters
- Before going through the “Area Product Technique (APT)”, the ripple current and inductor value should be calculated according to the type of transformerless DC-DC converter topologies (using Equations (2) and (3) in the case of a boost converter).
- For designing an inductor, it is essential to obtain the mathematical information about the stored energy in the inductor .
- The crest factor ( should be evaluated according to the load current (as per the converter configuration and specifications) so that it can be used in the calculation of the area product ().
- For designing the inductor, the “window utilization factor (” can be considered as 0.6 for single-winding and 0.3 to 0.4 for multi-winding inductors.
- Further, the current density can be considered as .
- The flux density can be selected as 0.25, 1.5, and 1 for ferrite, amorphous, and CRNGO cores, respectively.
- From the datasheets [16], the core which has a higher area product than the evaluated values should be chosen in order to maintain the performance and safety margins (factors like saturation margin, temperature rise, core saturation, etc.).
- The evaluation of the number of turns and wire size can be accomplished through Equation (28). In this context, it is advisable to opt for a wire gauge with a cross-sectional area exceeding the calculated value using datasheets [16] in order to reduce the resistive losses and voltage drops, and for improving the long-term performance.
7.3. Analysis of Failure Rates and Reliability
Generalized Guidelines for the Analysis of Failure Rate and Reliability
- Before analyzing the failure rate and reliability of active and passive components, it is important to gather information about temperature levels. Generally, 25 °C is considered a common ambient temperature, but for office automation products, it can be considered to be 35 °C. For military and space use, it can further be considered to be more than 50 °C.
- The part failure rate should be evaluated only in “failure/106 h”.
- In failure rate analysis, the calculation of junction temperature is a crucial requirement. Sometimes. datasheets of power devices do not offer the junction-to-case thermal resistance (). Due to this, it becomes difficult to evaluate the junction temperature. In this case, the junction temperature can be calculated by considering the datasheets only with junction-to-ambient thermal resistance [.
- The base failure rate ( should be considered the same as provided in military handbooks without restricting the significant digits after the decimal point.
- The case temperature () should be calculated by taking into account the case-to-ambient thermal resistance and ambient temprature [.
- During the calculation of failure rates of inductors, the hot-spot temperature plays an important role and can be calculated as ‘’. Here, “” is the average change in temperature compared to the ambient temperature.
- It is advisable that researchers consider the selection of voltage stress “” in order to evaluate the stress factor mathematically. The voltage stress should be chosen as 0.054 (if ) and as (if 0.3 ). Here, “” is the ratio of the applied voltage to the rated voltage.
8. Conclusions
9. Technical Recommendations
9.1. Optimization of Inductor Design
9.2. Comparative Assessment with Other Controllers
9.3. Exploration of Higher Switching Frequencies
9.4. Implementation of Redundancy Strategies
9.5. Consideration of Environmental Factors
9.6. Expand Reliability Evaluation Using Weibull Analysis and Collaboration with Industries
10. Economical Considerations and Recommendations
10.1. Component Selection for Cost Efficiency
- During the component selection, focus should be given to both technical performance and economic feasibility.
- A thorough analysis of commercially available components can help to achieve a careful balance of performance and cost.
- According to the outcomes of this research, researchers are recommended to carefully choose components that balance the technical performance and economic feasibility.
- Researchers can use the obtained reliability data in identifying cost-effective alternatives that do not compromise the overall system performance.
- The investigation of various core materials for inductors, such as toroidal iron powder cores (T44-26 and T30-26), not only improves performance but also introduces the possibility of cost savings. Researchers can investigate alternative materials with higher saturation flux density, which balances the technical as well as cost considerations to ensure optimal resource utilization.
- Researchers can incorporate economic considerations into the component selection process. This involves conducting an in-depth assessment of commercially available alternatives, taking into account factors such as component costs, availability, and long-term reliability.
- With the help of the “Area Product Technique”, researchers can enhance their research work by not only enhancing the performance of the inductor but also minimizing the material costs.
10.2. Maintenance and Serving Strategies
- It is recommended that researchers implement a cost-effective maintenance protocol in order to minimize servicing costs. This may include preventive measures, maintenance procedures, and methods to improve the lifespan of critical components, such as the switching device (MOSFET).
- Researchers can use these reliability data to develop predictive and preventive maintenance protocols that meet the specific requirements of the identified components. The maintenance costs can be reduced by addressing potential failure points in advance, which results in a longer lifetime for the device, ultimately increasing the system’s reliability.
- Researchers can address potential issues in advance to reduce maintenance costs and increase reliability.
- To enhance the overall system reliability and reduce maintenance costs, researchers are encouraged to explore redundancy strategies for higher-failure-rate components like MOSFETs. This will further minimize the servicing costs of the converter.
10.3. Reliability Enhancement and the Total Cost of Ownership
- As the inductor exhibits exceptional reliability, efforts can be made to improve the reliability of other components, especially for the switching device. This can minimize the total costs of ownership over the device’s life cycle.
- Strategies for reliability enhancement.
- Researchers are recommended to focus on strategies that contribute to improving the reliability of specific components, particularly with lower failure rates. By selecting the critical components, the reliability of the entire system can be significantly improved by reducing the failure rate, which ultimately reduces the associated servicing costs.
- Researchers can conduct a comprehensive evaluation of servicing costs throughout the device’s life cycle, from initial manufacturing to ongoing operational and maintenance costs.
- Researchers can expand their findings by providing insights into the economic implications of reliability enhancements. By prioritizing reliability in design and maintenance strategies, researchers can offer a minimization in the total cost of ownership.
- Researchers can consider the use of cost-effective materials and design selections without reducing reliability. By optimizing the design for reliability, researchers can contribute to an economically sustainable approach that corresponds with the overall objective of reducing the total cost of ownership.
10.4. The Optimization of Design Parameters
- It is recommended that researchers consider the economic effects of design selections, especially related to the inductor.
- Evaluating the trade-offs between factors such as the core size, wire size, and number of turns can contribute to an economically optimized design.
10.5. Life Cycle Cost Analysis
- With the emerging power electronics technology, it is important to move beyond traditional cost assessments and adopt a holistic approach for life cycle cost analysis.
- Researchers can include a life cycle cost analysis to fully understand the economic implications of their power electronic devices.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abbas, F.A.; Abdul-Jabbar, T.A.A.; Obed, A.A.; Kersten, A.; Kuder, M.; Weyh, T. A Comprehensive Review and Analytical Comparison of Transformerless DC-DC Converters for Fuel Cell Applications. Energies 2023, 16, 3493. [Google Scholar] [CrossRef]
- Akhtar, M.F.; Raihan, S.R.S.; Rahim, N.A.; Akhtar, M.N.; Bakar, E.A. Recent Developments in DC-DC Converter Topologies for Light Electric Vehicle Charging: A Critical Review. Appl. Sci. 2023, 13, 1676. [Google Scholar] [CrossRef]
- Hossain, S.M.S.; Haque, M.A.; Islam, R.; Mohammed, O.A. A Review of Power Electronic Converters for Electric Aircrafts. In Proceedings of the 2023 Fourth International Symposium on 3D Power Electronics Integration and Manufacturing (3D-PEIM), Miami, FL, USA, 1–3 February 2023; pp. 1–8. [Google Scholar]
- Alavi, O.; Rajabloo, T.; De Ceuninck, W.; Daenen, M. Non-Isolated DC-DC Converters in Fuel Cell Applications: Thermal Analysis and Reliability Comparison. Appl. Sci. 2022, 12, 5026. [Google Scholar] [CrossRef]
- Williams, B.W. Basic DC-to-DC Converters. IEEE Trans. Power Electron. 2008, 23, 387–401. [Google Scholar] [CrossRef]
- Mollaee, H.; Ghamari, S.M.; Khavari, F. Self-tuning regulator adaptive controller design for DC-DC Boost converter with a novel robust improved identification method. IET Power Electron. 2022, 15, 1365–1379. [Google Scholar] [CrossRef]
- Guan, Y.; Cecati, C.; Alonso, J.M.; Zhang, Z. Review of High-Frequency High-Voltage-Conversion-Ratio DC–DC Converters. IEEE J. Emerg. Sel. Top. Ind. Electron. 2021, 2, 374–389. [Google Scholar] [CrossRef]
- Dahale, S.; Das, A.; Pindoriya, N.M.; Rajendran, S. An Overview of DC-DC Converter Topologies and Controls in DC Microgrid. In Proceedings of the 2017 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017; pp. 410–415. [Google Scholar]
- Musumeci, S. Energy Conversion Using Electronic Power Converters: Technologies and Applications. Energies 2023, 16, 3590. [Google Scholar] [CrossRef]
- Andrade, A.M.S.S.; Faistel, T.M.K.; Guisso, R.A.; Toebe, A. Hybrid High Voltage Gain Transformerless DC–DC Converter. IEEE Trans. Ind. Electron. 2021, 69, 2470–2479. [Google Scholar] [CrossRef]
- Rasheed, L.T. An optimal modified Elman-PID neural controller design for DC/DC Boost converter model. J. Eng. Sci. Technol. (JESTEC) 2023, 18, 880–901. [Google Scholar]
- Wang, L. PID Control System Design and Automatic Tuning Using MATLAB/Simulink; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Aseem, K.; Selva, K.S. Closed Loop Control of DC-DC Converters Using PID and FOPID Controllers. Int. J. Power Electron. Drive Syst. 2020, 11, 1323. [Google Scholar]
- Kobaku, T.; Jeyasenthil, R.; Sahoo, S.; Ramchand, R.; Dragicevic, T. Quantitative Feedback Design-Based Robust PID Control of Voltage Mode Controlled DC-DC S Converter. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 286–290. [Google Scholar] [CrossRef]
- Zaman, M.T.; Fu, X.; Challoo, R. State-Space Average Modeling Based PID Control for Three Novel Topologies of DC-DC Boost Converter. In Proceedings of the 2022 IEEE International Women in Engineering (WIE) Conference on Electrical and Computer Engineering (WIECON-ECE), Naya Raipur, India, 30–31 December 2022; pp. 115–120. [Google Scholar] [CrossRef]
- Mclyman, C.W.M.T. Transformer and Inductor Design Handbook; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Li, X.L.; Dong, Z.; Chi, K.T.; Lu, D.D.C. Single-Inductor Multi-Input Multi-Output DC–DC Converter with High Flexibility and Simple Control. IEEE Trans. Power Electron. 2020, 35, 13104–13114. [Google Scholar] [CrossRef]
- Calderon-Lopez, G.; Scoltock, J.; Wang, Y.; Laird, I.; Yuan, X.; Forsyth, A.J. Power-Dense Bi-Directional DC–DC Converters with High-Performance Inductors. IEEE Trans. Veh. Technol. 2019, 68, 11439–11448. [Google Scholar] [CrossRef]
- Cerda, C.; Rojas, F.; Pineda, C.; Pereda, J.; Diaz, M.; Salgado, J.; Droguett, G.; Valdés, D.; Gatica, G. Inductor Design for a High-Performance DC-DC Modular Multilevel Converter. In Proceedings of the 2019 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaiso, Chile, 13–27 November 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Liang, D.; Shin, H.-B. Coupled Inductor Design Method for 2-Phase Interleaved Boost Converters. J. Power Electron. 2019, 19, 344–352. [Google Scholar]
- Yu, X.; Su, J.; Lai, J.; Guo, S. Analytical Optimization of Nonsaturated Thermally Limited High-Frequency Transformer/Inductor Design Considering Discreteness of Design Variables. IEEE Trans. Power Electron. 2019, 35, 6231–6250. [Google Scholar] [CrossRef]
- Radmanesh, H.; Soltanpour, M.R.; Azizkandi, M.E. Design and Implementation of an Ultra-High Voltage DC-DC Converter Based on Coupled Inductor with Continuous Input Current for Clean Energy Applications. Int. J. Circuit Theory Appl. 2021, 49, 348–379. [Google Scholar] [CrossRef]
- Mojibi, M.; Radmehr, M. Reliability evaluation of buck converter based on thermal analysis. J. Microelectron. Electron. Compon. Mater. 2018, 48, 217–227. [Google Scholar]
- Nguyen, M.H.; Kwak, S. Enhance Reliability of Semiconductor Devices in Power Converters. Electronics 2020, 9, 2068. [Google Scholar] [CrossRef]
- Rahimpour, S.; Tarzamni, H.; Kurdkandi, N.V.; Husev, O.; Vinnikov, D.; Tahami, F. An Overview of Lifetime Management of Power Electronic Converters. IEEE Access 2022, 10, 109688–109711. [Google Scholar] [CrossRef]
- MIL-HDBK-217F. Military Handbook: Reliability Prediction of Electronic Equipment; Department of Defense: Arlington, VA, USA, 1995.
- Izci, D.; Hekimoğlu, B.; Ekinci, S. A new artificial ecosystem-based optimization integrated with Nelder-Mead method for PID controller design of buck converter. Alex. Eng. J. 2022, 61, 2030–2044. [Google Scholar] [CrossRef]
- Ekinci, S.; Hekimoğlu, B.; Kaya, S. Tuning of PID Controller for AVR System Using Salp Swarm Algorithm. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Ersalı, C.; Hekimoğlu, B. Nonlinear model and simulation of DC-DC Buck-Boost converter using switching flow-graph method. In Proceedings of the International Informatics Congress, Kunming, China, 17–19 February 2022; pp. 15–16. [Google Scholar]
- Scirè, D.; Lullo, G.; Vitale, G. Self-Heating Induced Instability of a Non-Linear Inductor in a SMPS: A Case Study. Renew. Energy Power Qual. J. 2023, 21, 656–661. [Google Scholar] [CrossRef]
- Scirè, D.; Vitale, G.; Ventimiglia, M.; Lullo, G. Non-linear inductors characterization in real operating conditions for power density optimization in SMPS. Energies 2021, 14, 3924. [Google Scholar] [CrossRef]
- Rozenshtein, V.; Friedman, A.; Wolfus, Y.; Kopansky, F.; Perel, E.; Yeshurun, Y.; Bar-Haim, Z.; Ron, Z.; Harel, E.; Pundak, N. Saturated cores FCL—A new approach. IEEE Trans. Appl. Supercond. 2007, 17, 1756–1759. [Google Scholar] [CrossRef]
- Yahaya, E.A. Magnetic core saturation. Int. J. Eng. Sci. Math. 2013, 2, 1–6. [Google Scholar]
- Zaidi, B.; Videt, A.; Idir, N. Optimization method of CM inductor volume taking into account the magnetic core saturation issues. IEEE Trans. Power Electron. 2018, 34, 4279–4291. [Google Scholar] [CrossRef]
- Cheng, T.; Lu DD, C.; Siwakoti, Y. Electro-thermal modeling of a Boost converter considering device self-heating. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 25–28 November 2019; pp. 1–6. [Google Scholar]








 ”: increasing, “
”: increasing, “ ”: decreasing).
”: decreasing).| Gains | Rise Time | Error | Settling Time | Overshoot |
|---|---|---|---|---|
| Kp |  |  | Minor Change |  |
| Ki |  |  |  |  |
| Kd | Minor Change | Minor Change |  |  |
| Performance Parameters | Uncompensated Condition | Compensated Condition | ||
|---|---|---|---|---|
| 100 kHz | 500 kHz | 100 kHz | 500 kHz | |
| Rise Time | 92.24 µs | 19.71 µs | 3.65 µs | 0.81 µs |
| Settling Time | 7.8 ms | 1.6 ms | 31.26 µs | 1.28 µs |
| Overshoot | 87.40% | 86.63% | 3.42% | 1.91% |
| Reference Tracking | No | No | Yes | Yes |
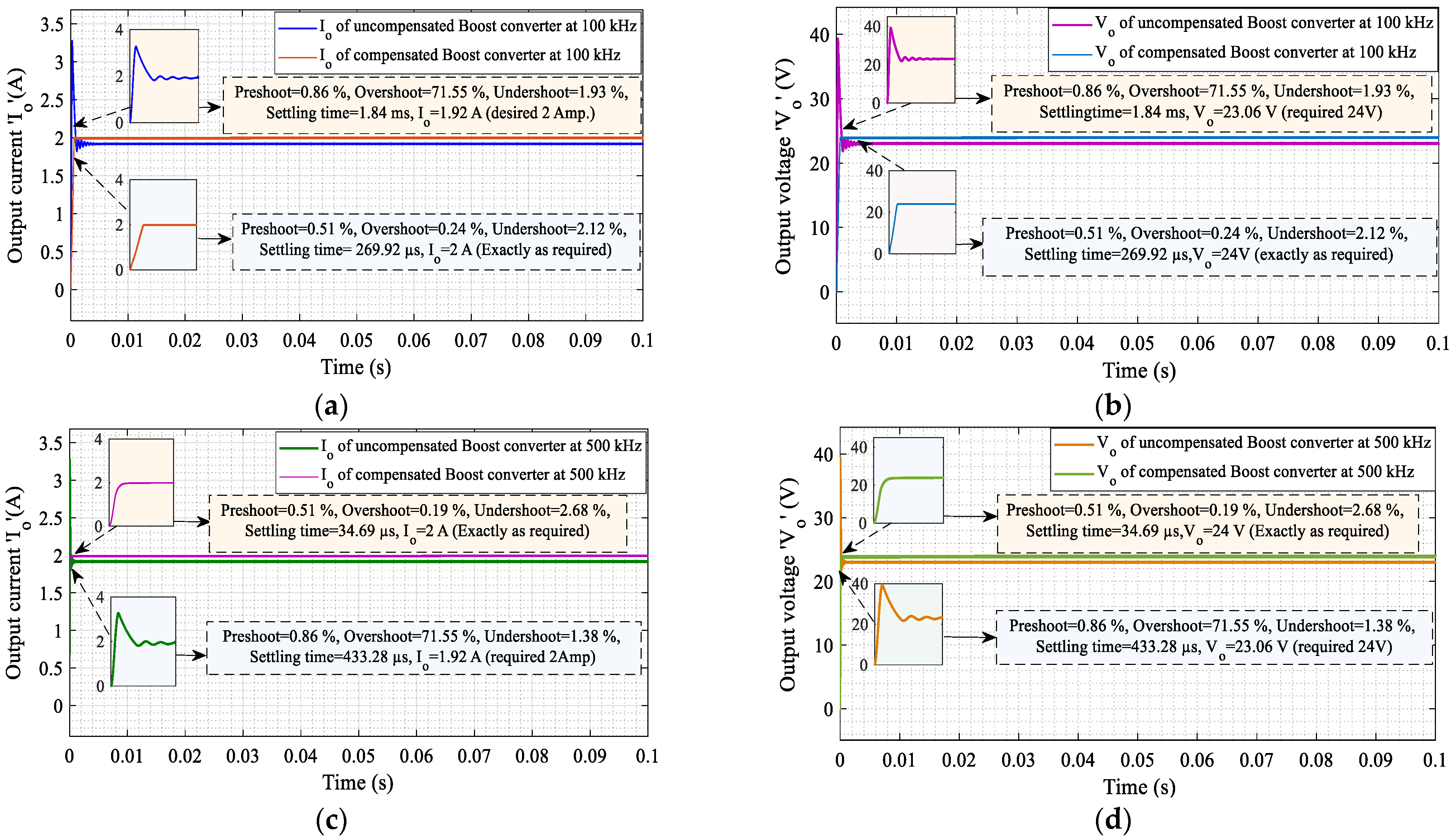
| Performance Parameters | Output Current Response (Io) | Output Voltage Response (Vo) | ||
|---|---|---|---|---|
| 100 kHz | 500 kHz | 100 kHz | 500 kHz | |
| Preshoot (without PID) | 0.86% | 0.86% | 0.86% | 0.862% |
| Overshoot (without PID) | 71.55% | 71.55% | 71.55% | 71.552% |
| Settling Time (without PID) | 1.84 ms | 433.28 µs | 1.84 ms | 433.280 µs |
| Undershoot (without PID) | 1.93% | 1.38% | 1.93% | 1.38% |
| Io and Vo (without PID) | 1.92 A | 1.919 A | 23.06 V | 23.05 V |
| Preshoot (with PID) | 0.51% | 0.51% | 0.51% | 0.51% |
| Overshoot (with PID) | 0.24% | 0.19% | 0.24% | 0.19% |
| Settling Time (with PID) | 269.92 µs | 34.69 µs | 269.92 µs | 34.69 µs |
| Undershoot (with PID) | 2.12% | 2.68% | 2.12% | 2.68% |
| Io and Vo (with PID) | 2 A | 2 A | 24 V | 24 V |
| Elements | (°C/W) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Switch (MOSFET) | 0.012 | 2.14 | 5.5 | 8 | 6 | NA | NA | NA | NA |
| Diode | 0.0030 | 2 | 5.5 | NA | 6 | 0.1078 | NA | 1 | NA |
| Inductor | 0.000030 | NA | 3 | NA | 6 | NA | NA | NA | NA |
| Capacitor | 0.00012 | NA | 3 | NA | 6 | NA | 1 | 2.7656 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jayaswal, K.; Palwalia, D.K.; Guerrero, J.M. A Comprehensive Performance Analysis of a 48-Watt Transformerless DC-DC Boost Converter Using a Proportional–Integral–Derivative Controller with Special Attention to Inductor Design and Components Reliability. Technologies 2024, 12, 18. https://doi.org/10.3390/technologies12020018
Jayaswal K, Palwalia DK, Guerrero JM. A Comprehensive Performance Analysis of a 48-Watt Transformerless DC-DC Boost Converter Using a Proportional–Integral–Derivative Controller with Special Attention to Inductor Design and Components Reliability. Technologies. 2024; 12(2):18. https://doi.org/10.3390/technologies12020018
Chicago/Turabian StyleJayaswal, Kuldeep, D. K. Palwalia, and Josep M. Guerrero. 2024. "A Comprehensive Performance Analysis of a 48-Watt Transformerless DC-DC Boost Converter Using a Proportional–Integral–Derivative Controller with Special Attention to Inductor Design and Components Reliability" Technologies 12, no. 2: 18. https://doi.org/10.3390/technologies12020018
APA StyleJayaswal, K., Palwalia, D. K., & Guerrero, J. M. (2024). A Comprehensive Performance Analysis of a 48-Watt Transformerless DC-DC Boost Converter Using a Proportional–Integral–Derivative Controller with Special Attention to Inductor Design and Components Reliability. Technologies, 12(2), 18. https://doi.org/10.3390/technologies12020018










