An Optimum Load Forecasting Strategy (OLFS) for Smart Grids Based on Artificial Intelligence
Abstract
1. Introduction
2. Related Work
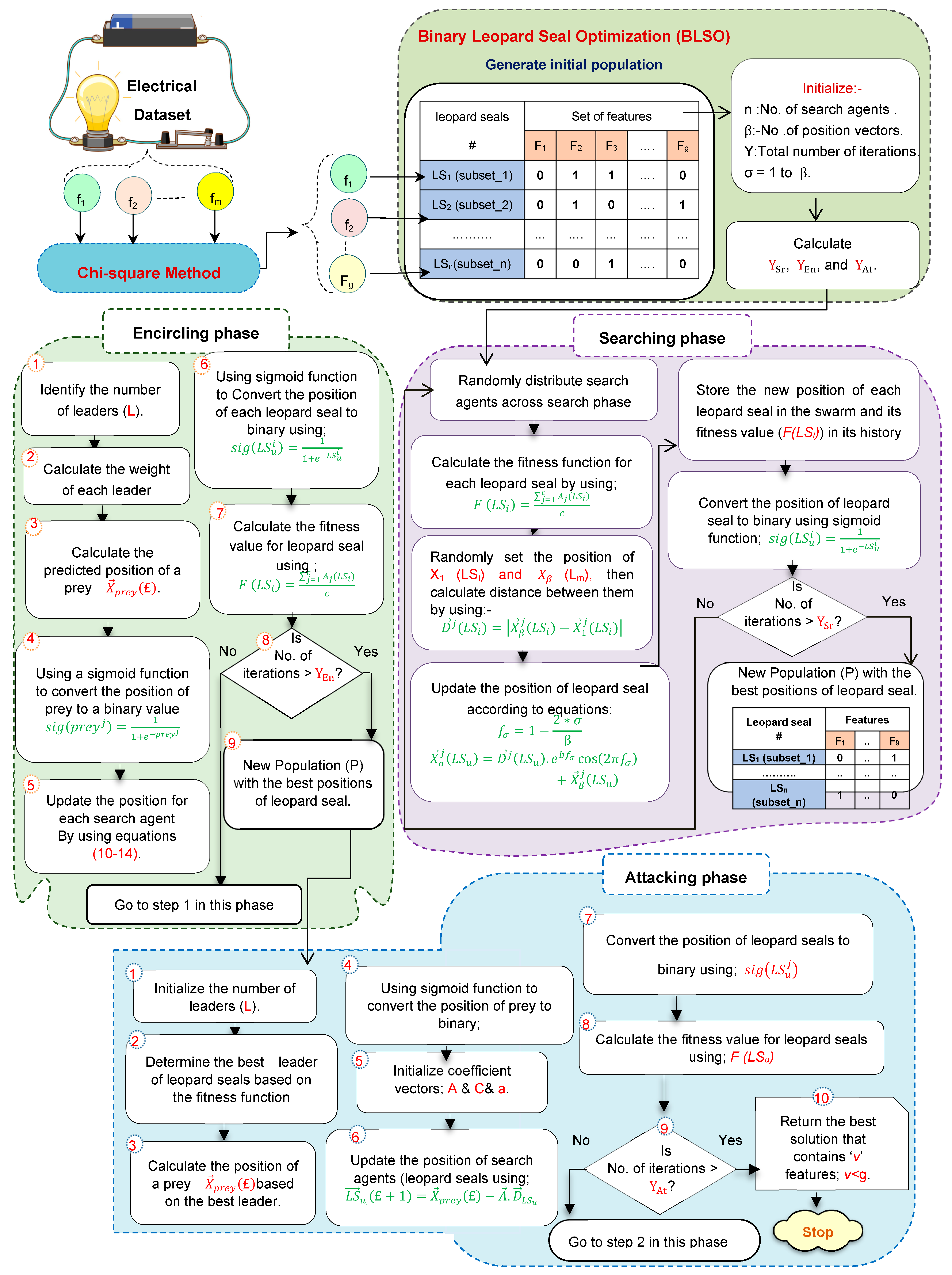
3. The Proposed Optimum Load Forecasting Strategy (OLFS)
3.1. The Advanced Leopard Seal Optimization (ALSO)
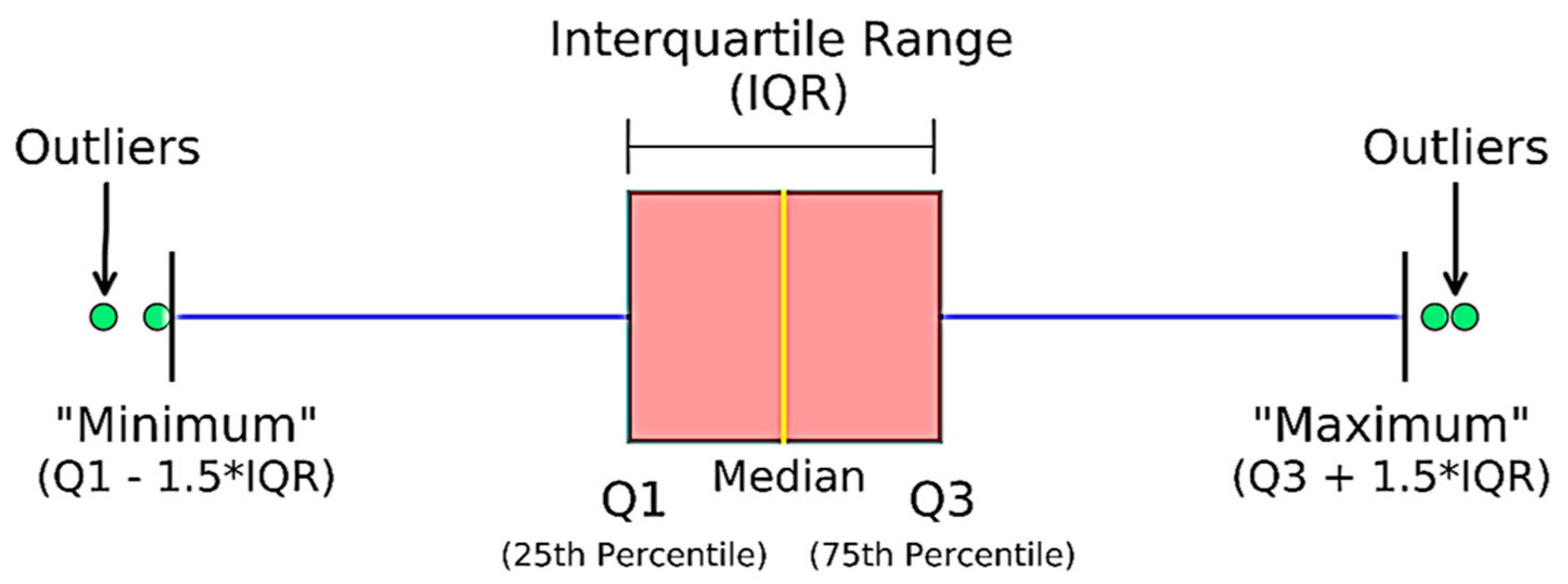
3.2. Interquartile Range (IQR) Method
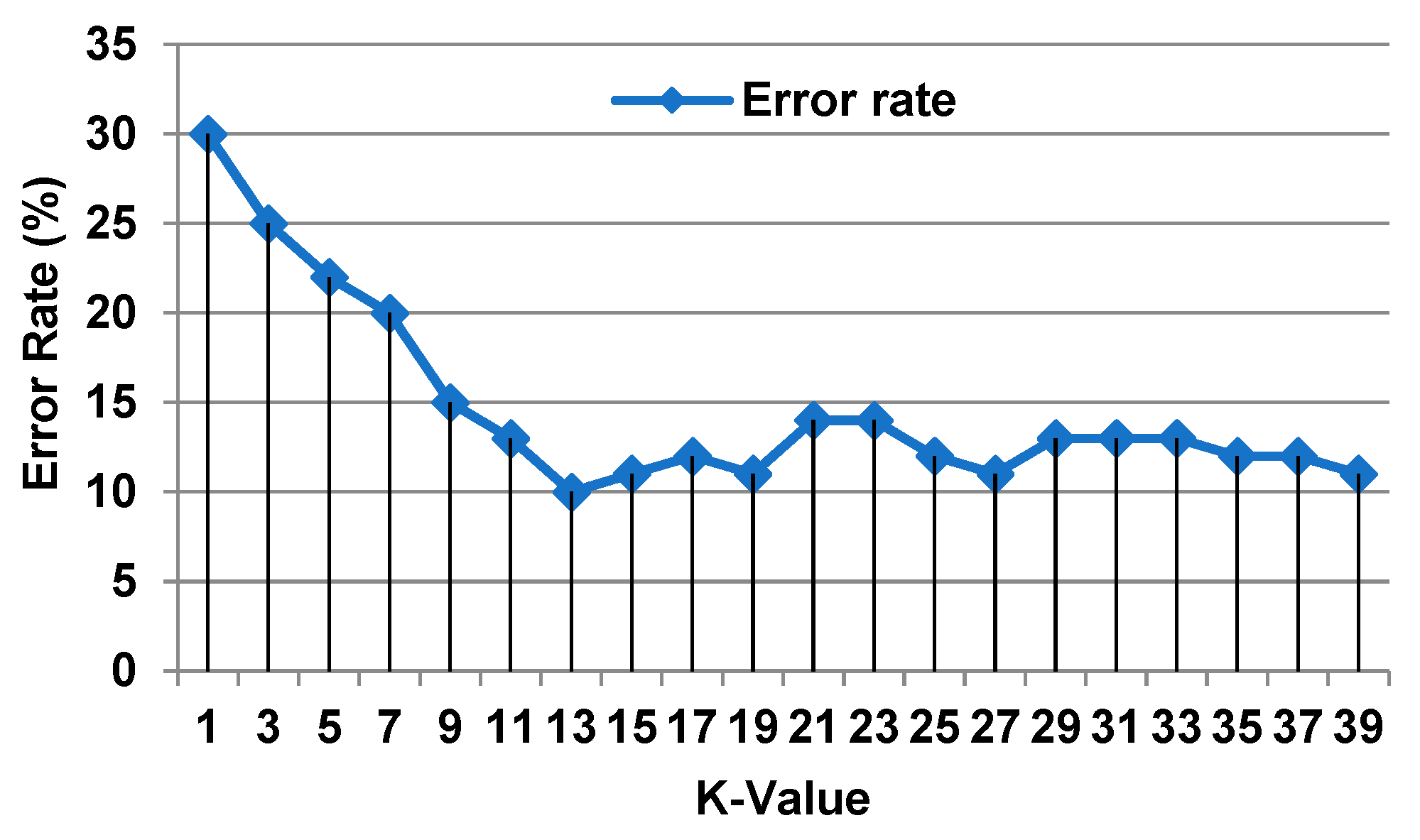
3.3. The Proposed Weighted K-Nearest Neighbor (WKNN) Algorithm
4. Experimental Results
4.1. Electricity Load Forecast Dataset Description
4.2. Testing the Proposed Optimum Load Forecasting Strategy (OLFS)
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abumohsen, M.; Owda, A.; Owda, M. Electrical Load Forecasting Using LSTM, GRU, and RNN Algorithms. Energies 2023, 16, 2283. [Google Scholar] [CrossRef]
- Gomez, W.; Wang, F.; Amogne, Z. Electricity Load and Price Forecasting Using a Hybrid Method Based Bidirectional Long Short-Term Memory with Attention Mechanism Model. Int. J. Energy Res. 2023, 2023, 1–18. [Google Scholar] [CrossRef]
- Tarmanini, C.; Sarma, N.; Gezegin, C.; Ozgonenel, O. Short term load forecasting based on ARIMA and ANN approaches. Energy Rep. 2023, 9, 550–557. [Google Scholar] [CrossRef]
- Rabie, A.H.; Ali, S.H.; Saleh, A.I.; Ali, H.A. A fog based load forecasting strategy based on multi-ensemble classification for smart grids. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 209–236. [Google Scholar] [CrossRef]
- Rabie, A.; Saleh, A.; Ali, H. Smart electrical grids based on cloud, IoT, and big data technologies: State of the art. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 9450–9478. [Google Scholar] [CrossRef]
- Saleh, A.I.; Rabie, A.H.; Abo-Al-Ez, K.M. A data mining based load forecasting strategy for smart electrical grids. Adv. Eng. Inform. 2016, 30, 422–448. [Google Scholar] [CrossRef]
- Tian, M.-W.; Alattas, K.; El-Sousy, F.; Alanazi, A.; Mohammadzadeh, A.; Tavoosi, J.; Mobayen, S.; Skruch, P. A New Short Term Electrical Load Forecasting by Type-2 Fuzzy Neural Networks. Energies 2022, 15, 3034. [Google Scholar] [CrossRef]
- Mounir, N.; Ouadi, H.; Jrhilifa, I. Short-term electric load forecasting using an EMD-BI-LSTM approach for smart grid energy management system. Energy Build. 2023, 288, 113022. [Google Scholar] [CrossRef]
- Lin, F.-J.; Chang, C.-F.; Huang, Y.-C.; Su, T.-M. A Deep Reinforcement Learning Method for Economic Power Dispatch of Microgrid in OPAL-RT Environment. Technologies 2023, 11, 96. [Google Scholar] [CrossRef]
- Alrashidi, A.; Qamar, A.M. Data-Driven Load Forecasting Using Machine Learning and Meteorological Data. Comput. Syst. Sci. Eng. 2022, 44, 1973–1988. [Google Scholar] [CrossRef]
- Khan, S. Short-Term Electricity Load Forecasting Using a New Intelligence-Based Application. Sustainability 2023, 15, 12311. [Google Scholar] [CrossRef]
- Cordeiro-Costas, M.; Villanueva, D.; Eguía-Oller, P.; Martínez-Comesaña, M.; Ramos, S. Load Forecasting with Machine Learning and Deep Learning Methods. Appl. Sci. 2023, 13, 7933. [Google Scholar] [CrossRef]
- Chodakowska, E.; Nazarko, J.; Nazarko, Ł. ARIMA Models in Electrical Load Forecasting and Their Robustness to Noise. Energies 2021, 14, 7952. [Google Scholar] [CrossRef]
- Wang, A.; Yu, Q.; Wang, J.; Yu, X.; Wang, Z.; Hu, Z. Electric Load Forecasting Based on Deep Ensemble Learning. Appl. Sci. 2023, 13, 9706. [Google Scholar] [CrossRef]
- Janane, F.Z.; Ouaderhman, T.; Chamlal, H. A filter feature selection for high-dimensional data. J. Algorithms Comput. Technol. 2023, 17, 17483026231184171. [Google Scholar] [CrossRef]
- Nicholas, P.; Tayaza, F.; Andreas, W.; Justin, M. A Review of Feature Selection Methods for Machine Learning-Based Disease Risk Prediction. Front. Bioinform. 2022, 2, 927312. [Google Scholar]
- Available online: https://www.kaggle.com/datasets/saurabhshahane/electricity-load-forecasting (accessed on 1 December 2023).



| Technique | Advantages | Disadvantages |
|---|---|---|
| Gated Recurrent Unit (GRU) [1] | GRU is an accurate method. |
|
| Hybrid Forecasting Model (HFM) [2] | HFM is suitable, reliable, and has a high performance. |
|
| Artificial Neural Network (ANN) [3] | ANN is an accurate method. |
|
| Support Vector Regression based on Radial Basis (SVR-RB) function [10] | SVR-RB provides high accuracy. | Outlier rejection method should be used before using prediction model to provide more accurate results. |
| Hybrid Prediction Technique (HPT) [11] | HPT provides accurate results. | HPT took a large amount of execution time to be implemented. |
| Long Short-Term Memory (LSTM) [12] | LSTM is an accurate method. |
|
| Auto-Regressive Integrated Moving Average (ARIMA) technique [13] | ARIMA provides accurate predictions after applying preprocessing phase. | ARIMA is affected by noise. |
| Deep Ensemble Learning (DEL) method [14] | DEL is an accurate model. | DEL takes a long execution time. |
| Classifier | Accuracy of Every Seal | The Best Seal | |
|---|---|---|---|
| LS1 | LS2 | ||
| C1 = SVM | 0.75 | 0.75 | LS2 |
| C2 = KNN | 0.9 | 0.8 | LS1 |
| C3 = NB | 0.7 | 0.9 | LS2 |
| Average accuracy | 0.767 | 0.816 | LS2 |
| Parameter | Description | Applied Value |
|---|---|---|
| b | A number that defines the movement shape of logarithmic spiral in the encircling phase | 3 |
| u | No. of alpha leopard seals | 7 |
| R | The maximum number of iterations | 100 |
| r | Random value that is needed in the sigmoid function | Random in [0, 1] |
| K | The number of nearest neighbors used in KNN method | 1 ≤ K ≤ 40 |
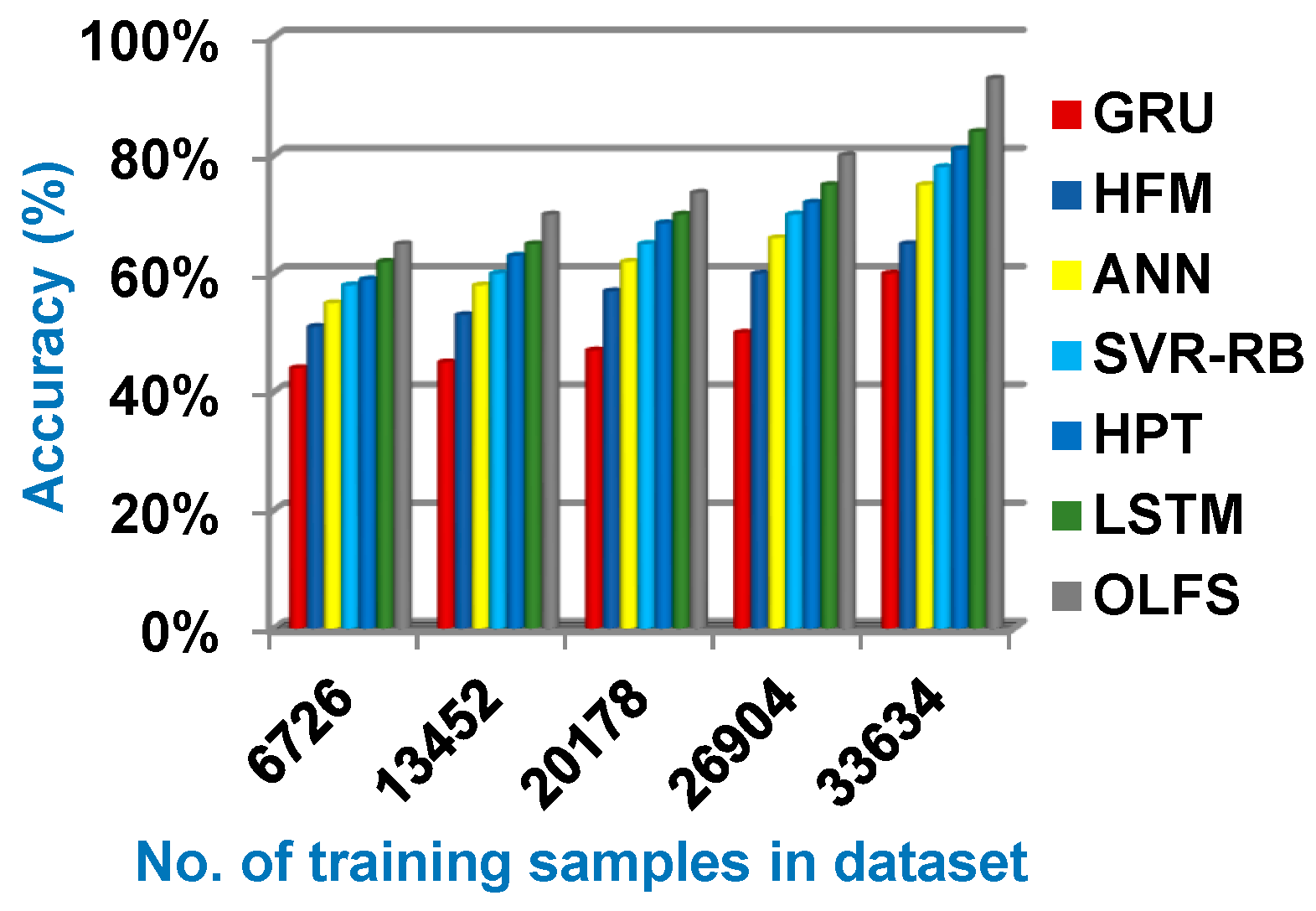
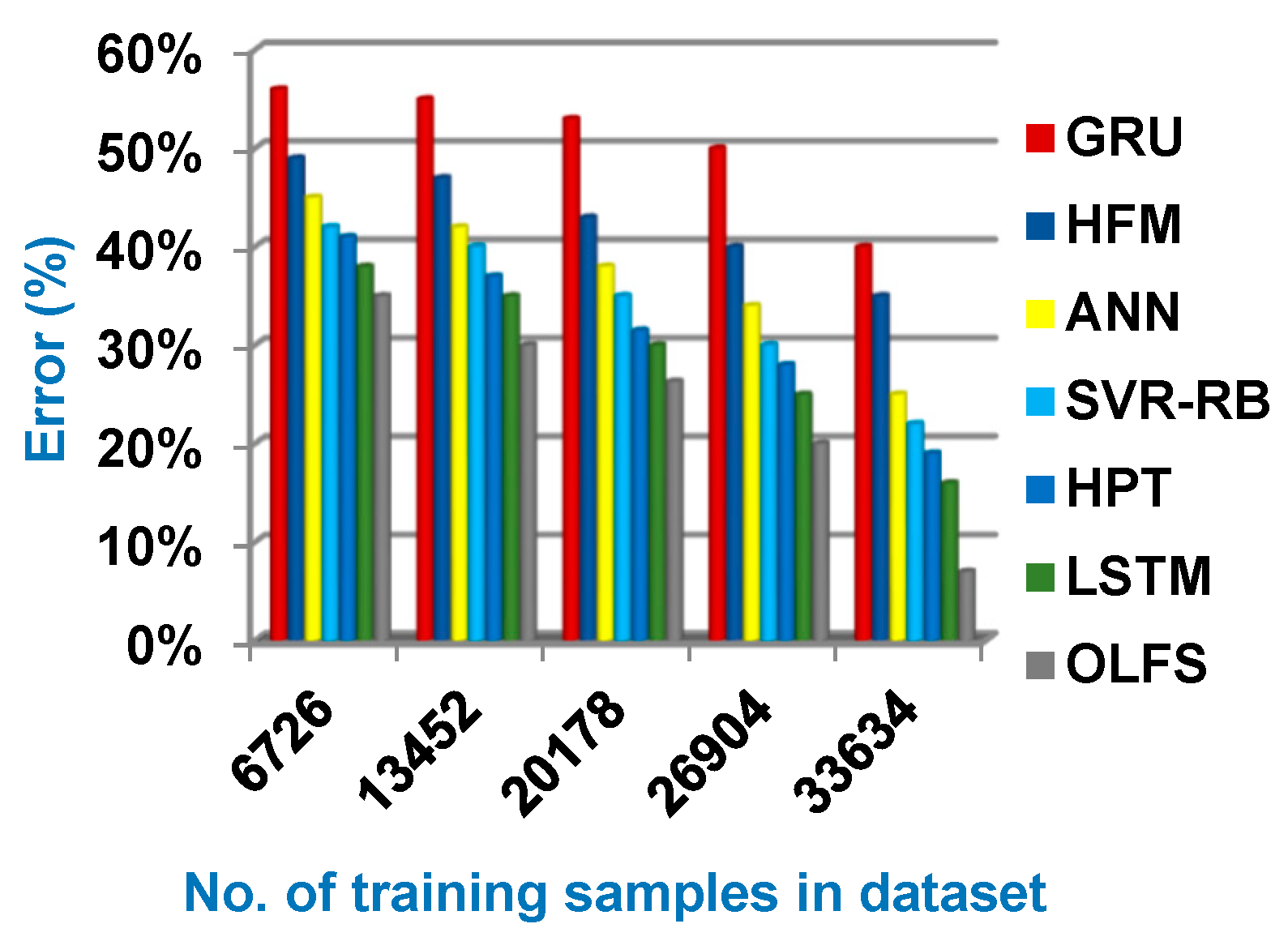
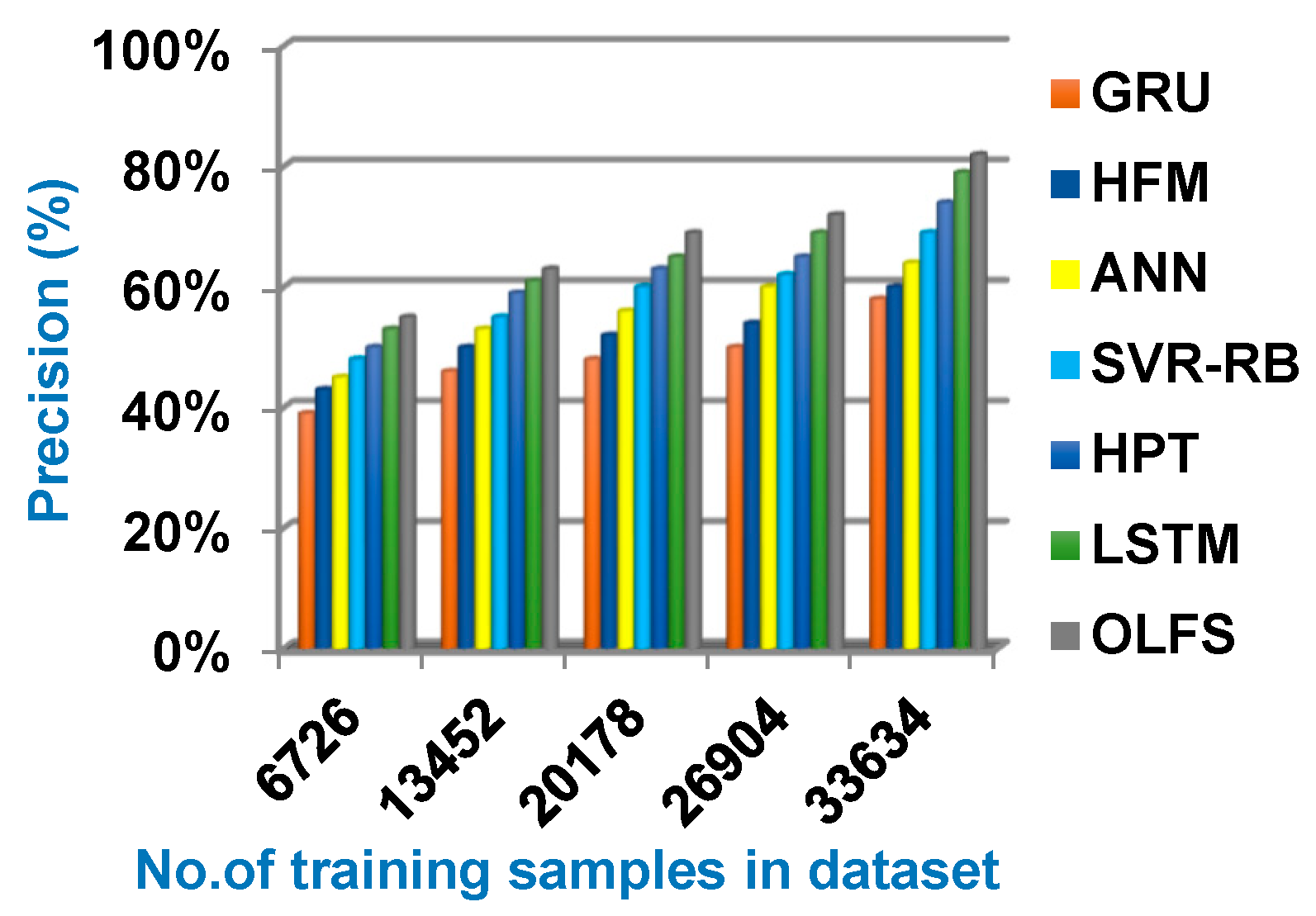
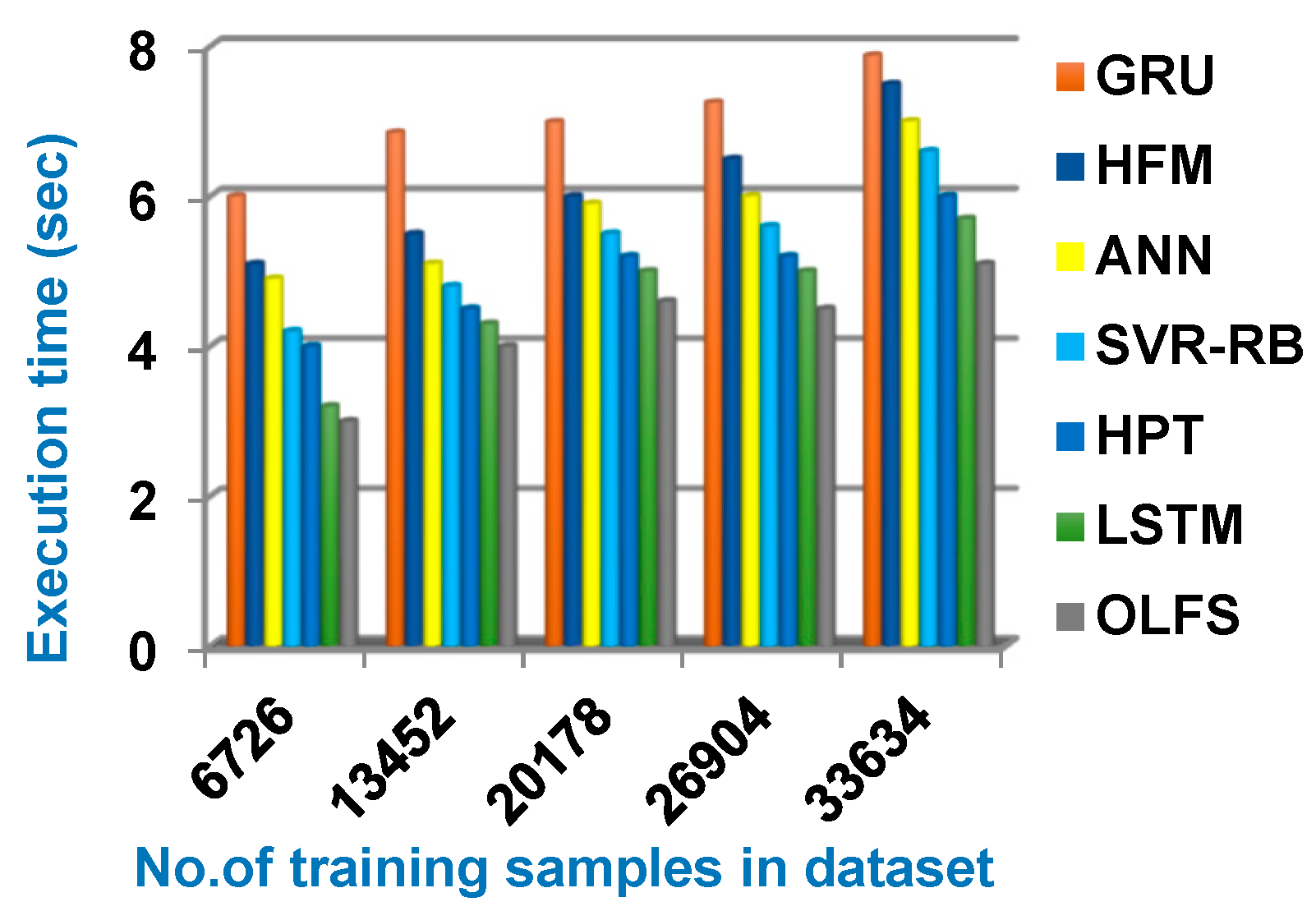
| Prediction Methods | GRU | HFM | ANN | SVR-RB | HPT | LSTM | OLFS |
|---|---|---|---|---|---|---|---|
| Accuracy (%) | 60 | 65 | 75 | 78 | 81 | 84 | 93 |
| Error (%) | 40 | 35 | 25 | 22 | 19 | 16 | 7 |
| Precision (%) | 58 | 60 | 64 | 69 | 74 | 79 | 82 |
| Recall (%) | 80 | 55 | 59 | 63 | 68 | 73 | 75 |
| Implementation time (s) | 7.88 | 7.5 | 7 | 6.6 | 6 | 5.7 | 5.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabie, A.H.; I. Saleh, A.; Elkhalik, S.H.A.; Takieldeen, A.E. An Optimum Load Forecasting Strategy (OLFS) for Smart Grids Based on Artificial Intelligence. Technologies 2024, 12, 19. https://doi.org/10.3390/technologies12020019
Rabie AH, I. Saleh A, Elkhalik SHA, Takieldeen AE. An Optimum Load Forecasting Strategy (OLFS) for Smart Grids Based on Artificial Intelligence. Technologies. 2024; 12(2):19. https://doi.org/10.3390/technologies12020019
Chicago/Turabian StyleRabie, Asmaa Hamdy, Ahmed I. Saleh, Said H. Abd Elkhalik, and Ali E. Takieldeen. 2024. "An Optimum Load Forecasting Strategy (OLFS) for Smart Grids Based on Artificial Intelligence" Technologies 12, no. 2: 19. https://doi.org/10.3390/technologies12020019
APA StyleRabie, A. H., I. Saleh, A., Elkhalik, S. H. A., & Takieldeen, A. E. (2024). An Optimum Load Forecasting Strategy (OLFS) for Smart Grids Based on Artificial Intelligence. Technologies, 12(2), 19. https://doi.org/10.3390/technologies12020019







