Real-Time Scheduling with Independent Evaluators: Explainable Multi-Agent Approach
Abstract
1. Introduction
- We devised a novel multi-agent environment to simulate resource allocation in the varying of the planning horizon within dynamic scheduling;
- We designed a sophisticated reward function with an adjustable level to attenuate the effects of human-driven events;
- We suggested a technique to refine the decision-making process during the sequential rescheduling phase with active human agents present;
- We established mapping between RL nomenclature and a BDI cognitive framework.
- We proposed Large Language Model (LLM)-based tools to elucidate the intricacies of cooperative–competitive game interactions between agents for a supervising human expert;
- We applied our findings to the task of allocating operating rooms (OR).
2. Related Works
3. Preliminary
3.1. Reinforcement Learning
3.2. Non-Stationary
3.3. Multi-Agent Actor–Critic Methods
4. Methods and Materials
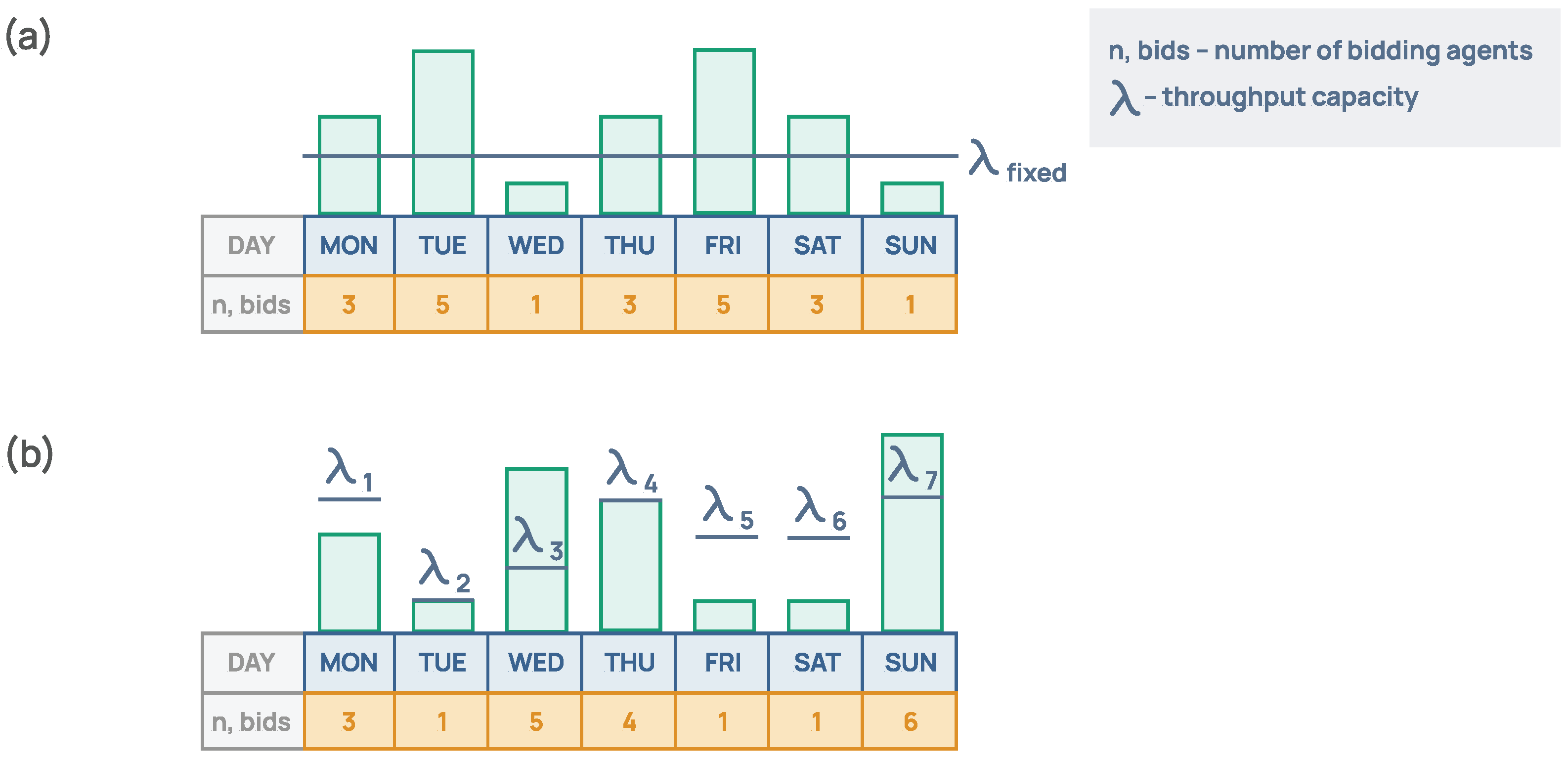
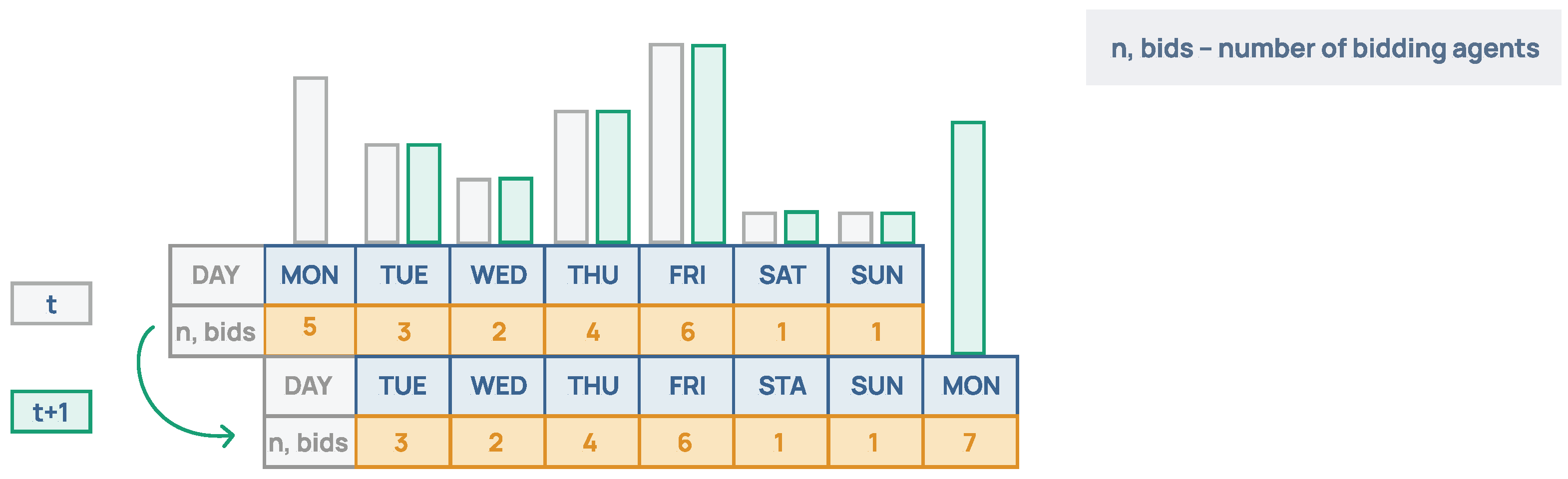
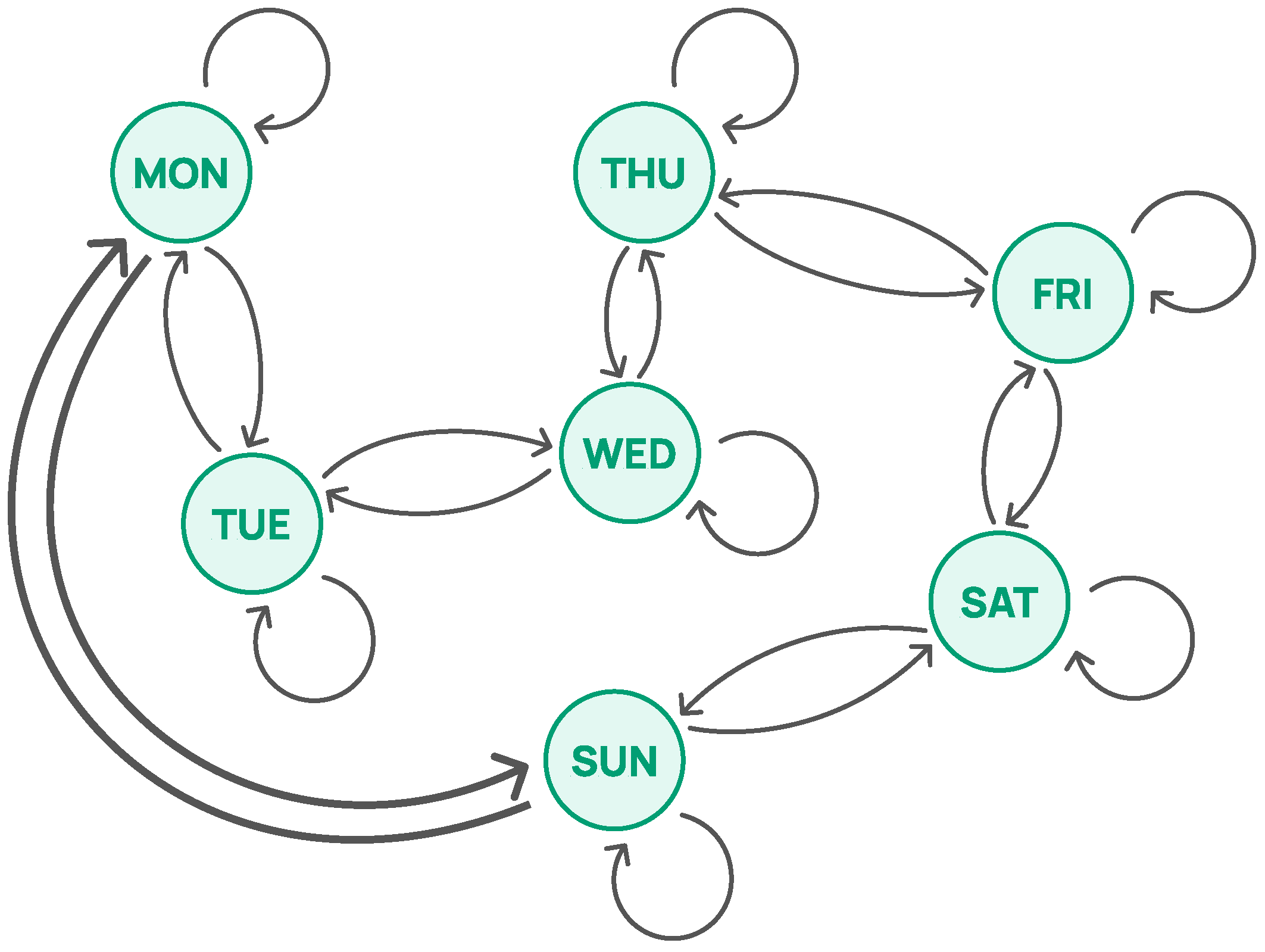
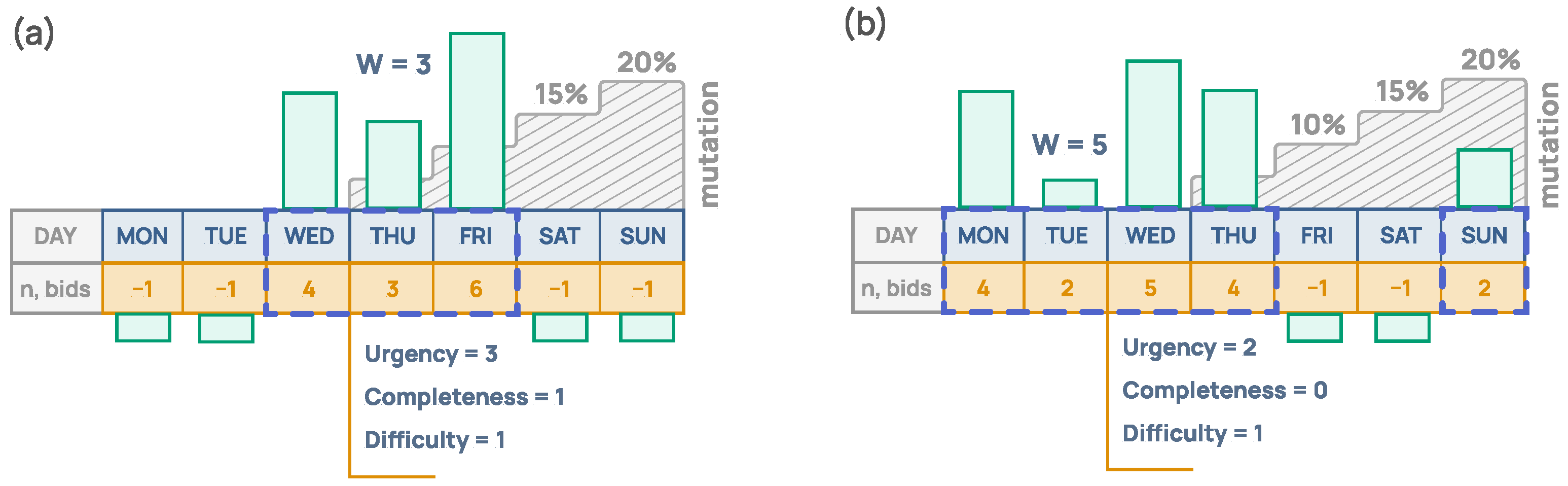
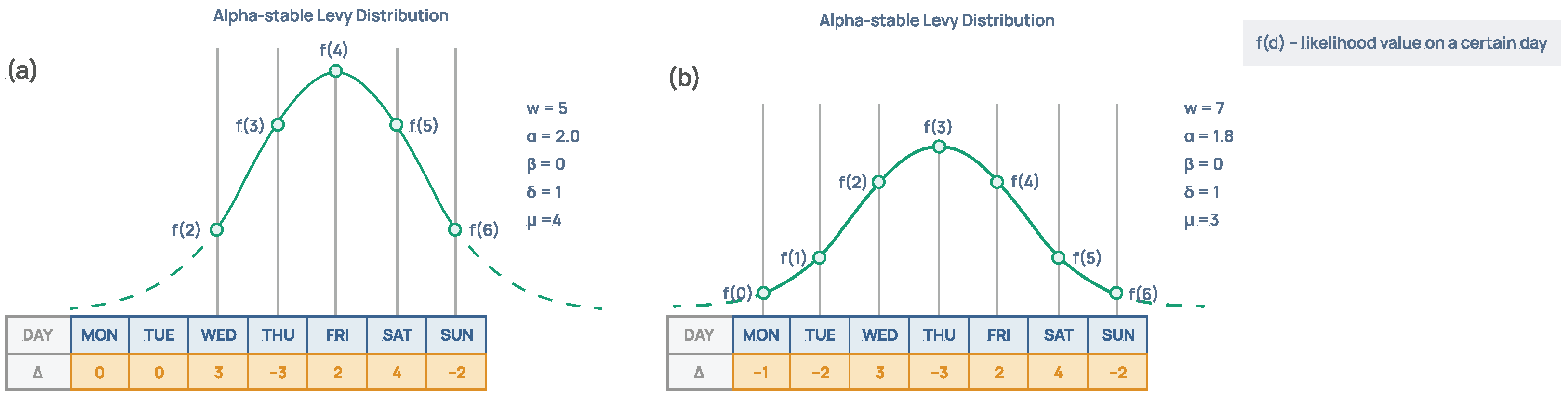
4.1. Environment Design
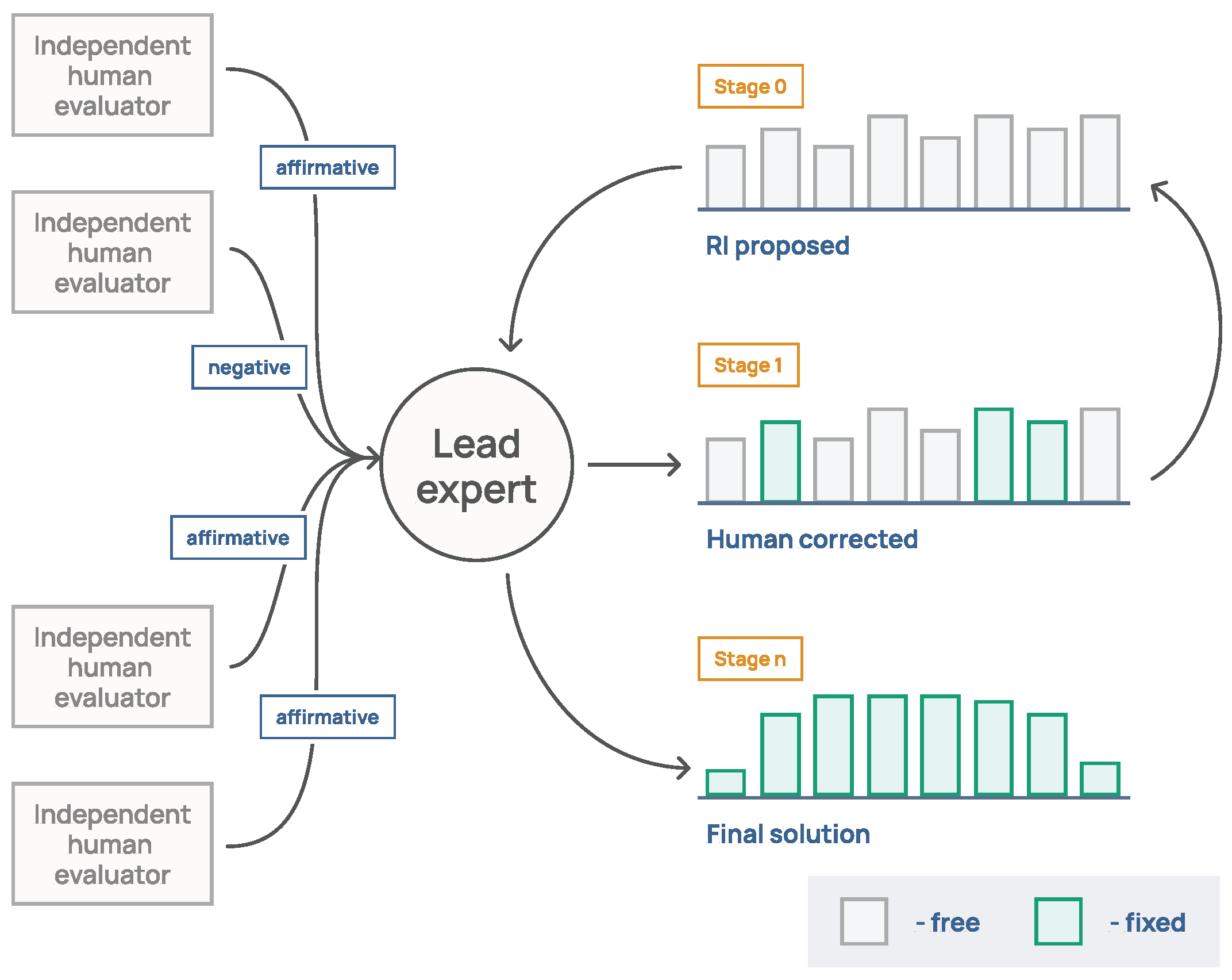
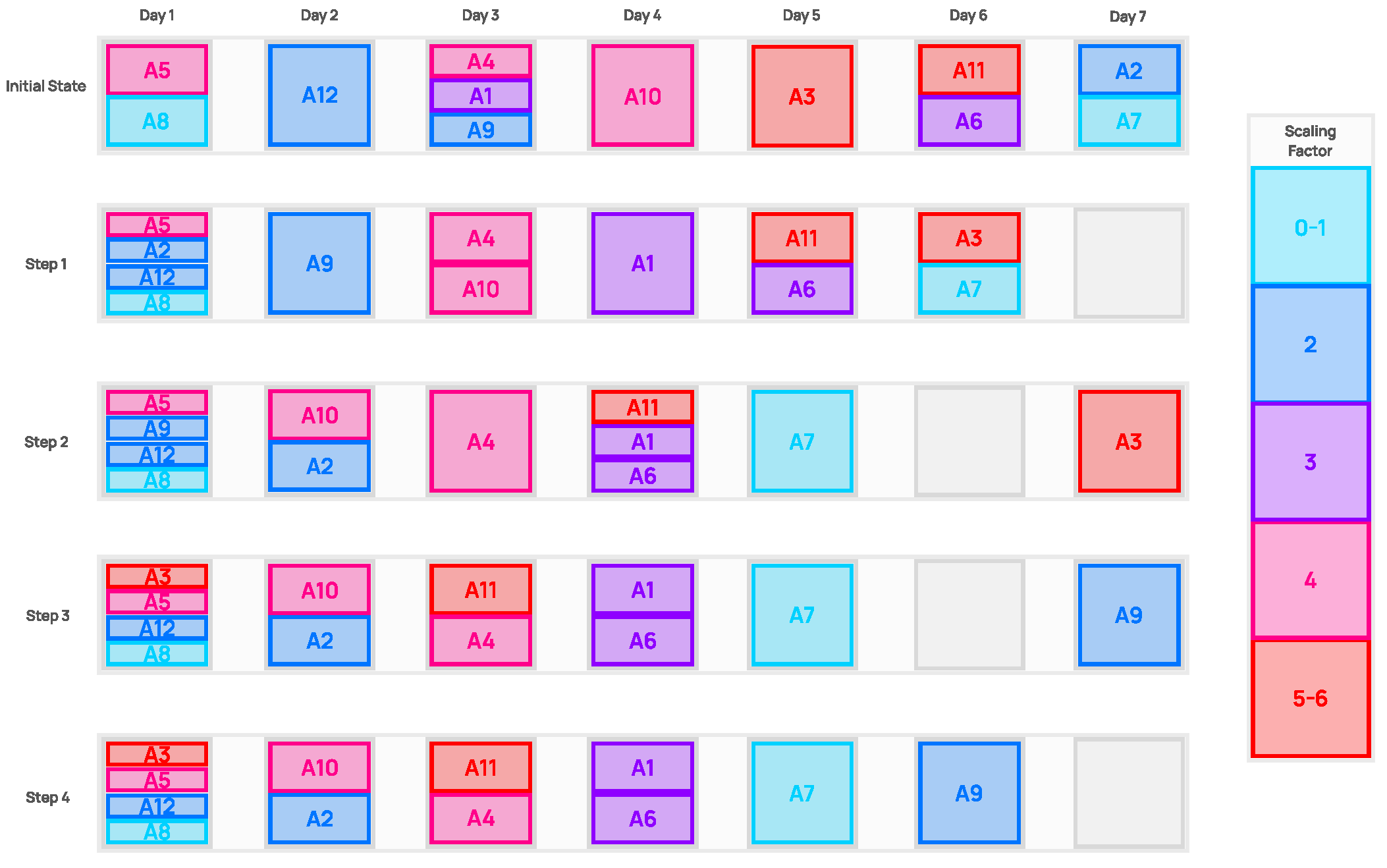
4.2. Rescheduling with Human Feedback
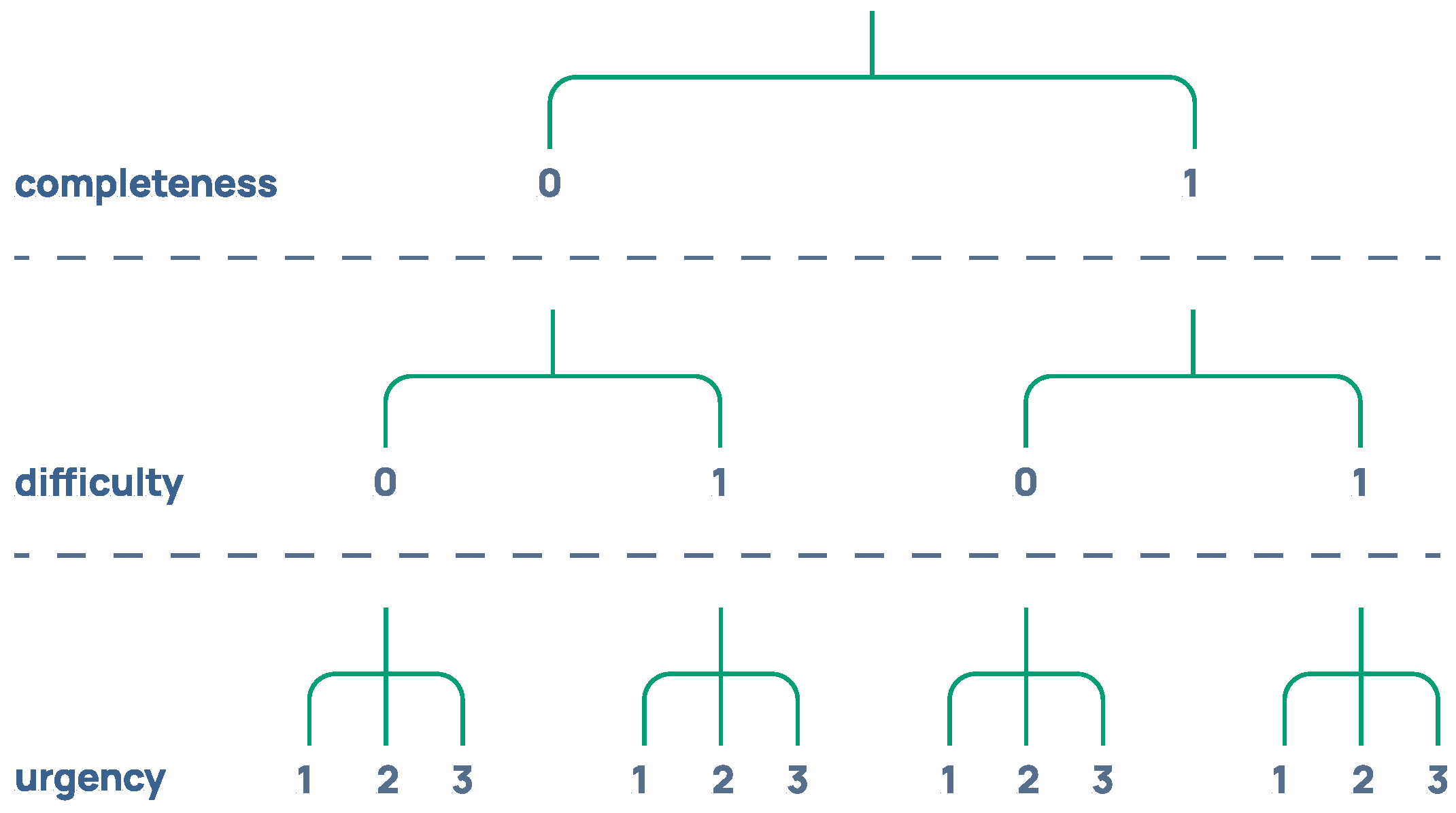
4.3. Evaluating the Schedule Quality
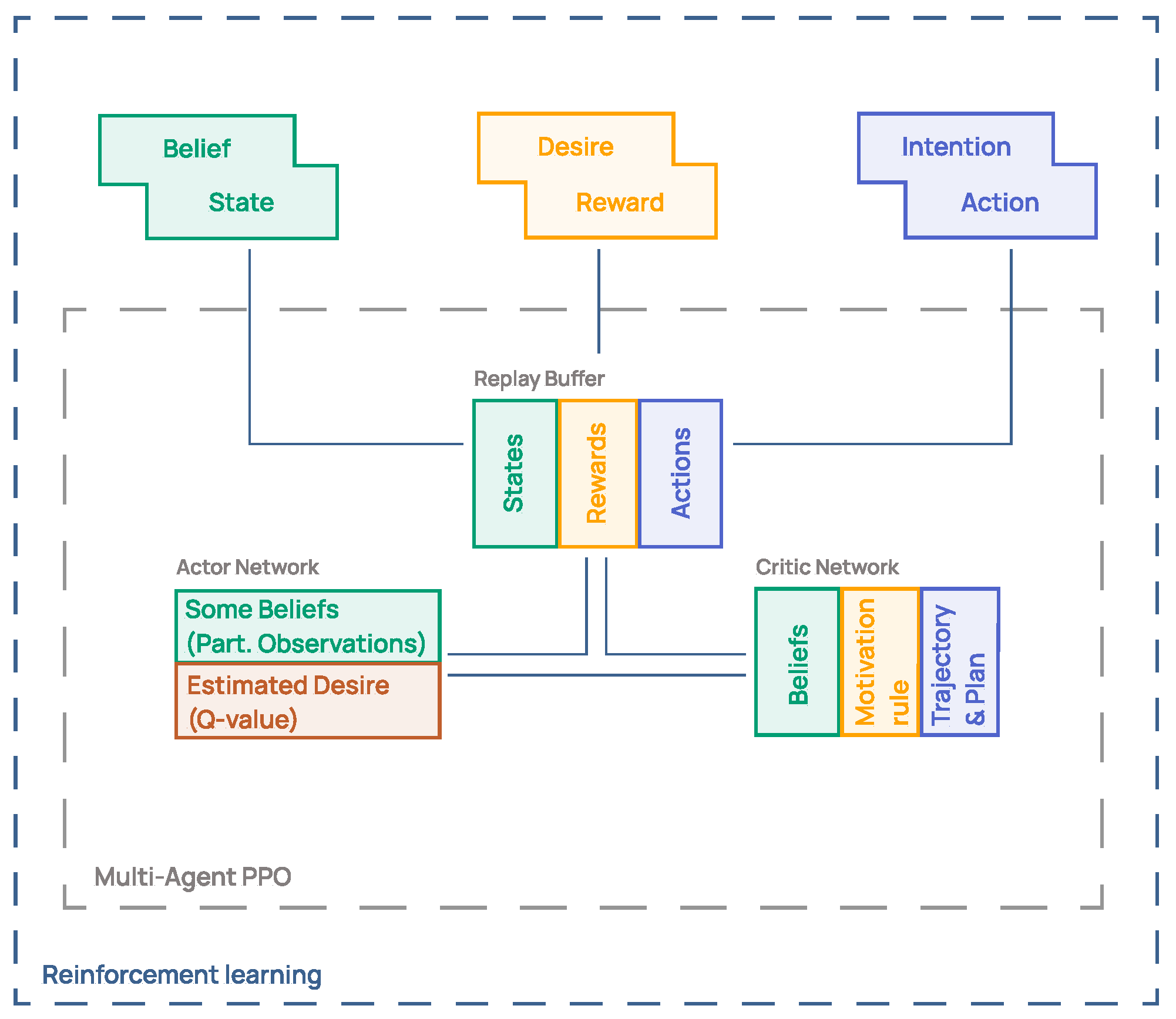
4.4. Mapping Between Belief–Desire–Intention Structure and Reinforcement Learning Terminology
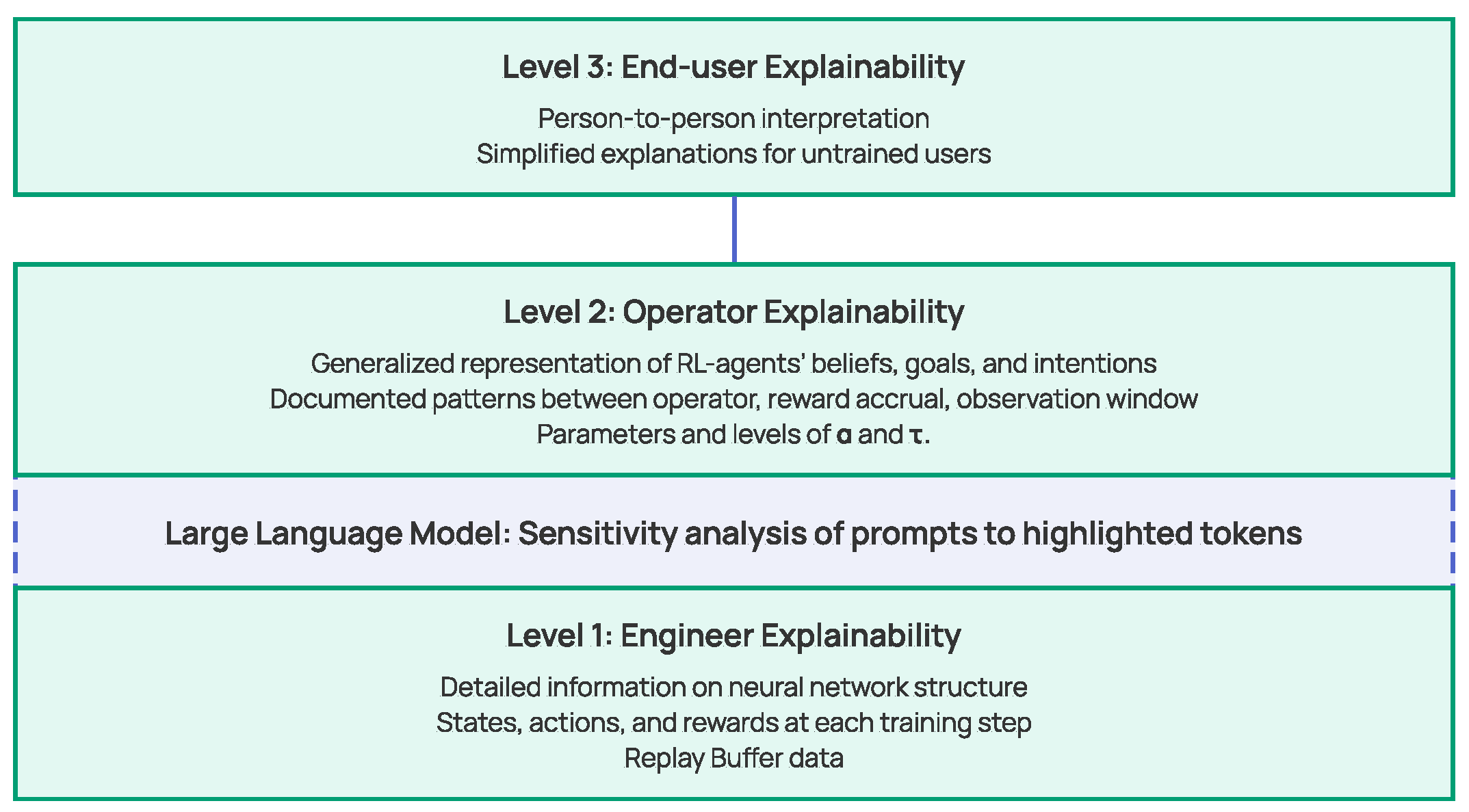
4.5. Multi-Level Explainability
4.6. Natural Language Bridging
4.7. Prompt Sensitivity Analysis
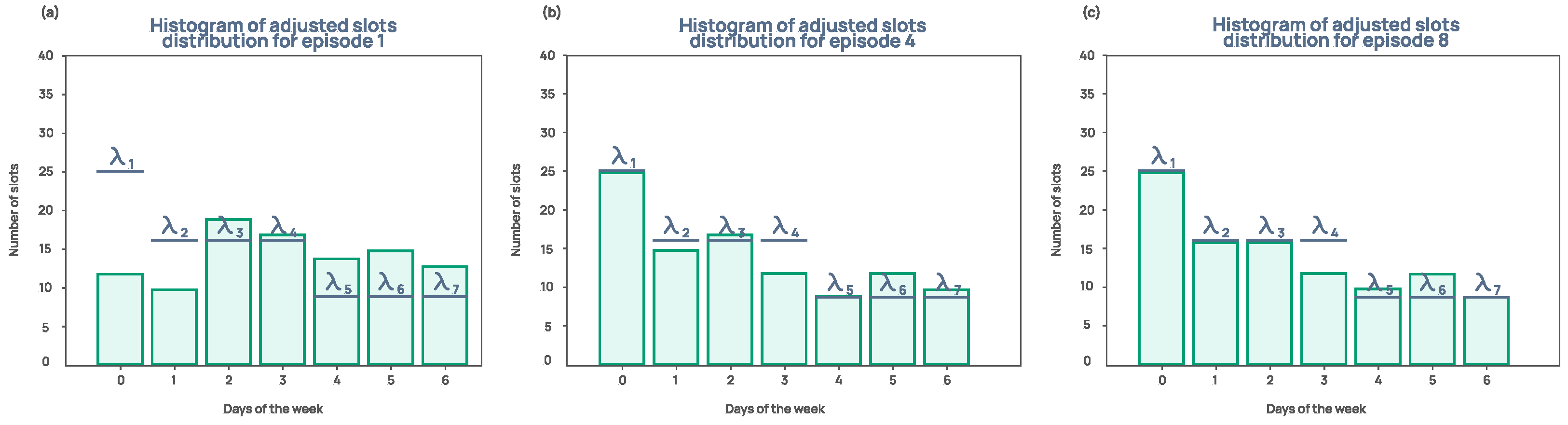
4.8. Experiment Design
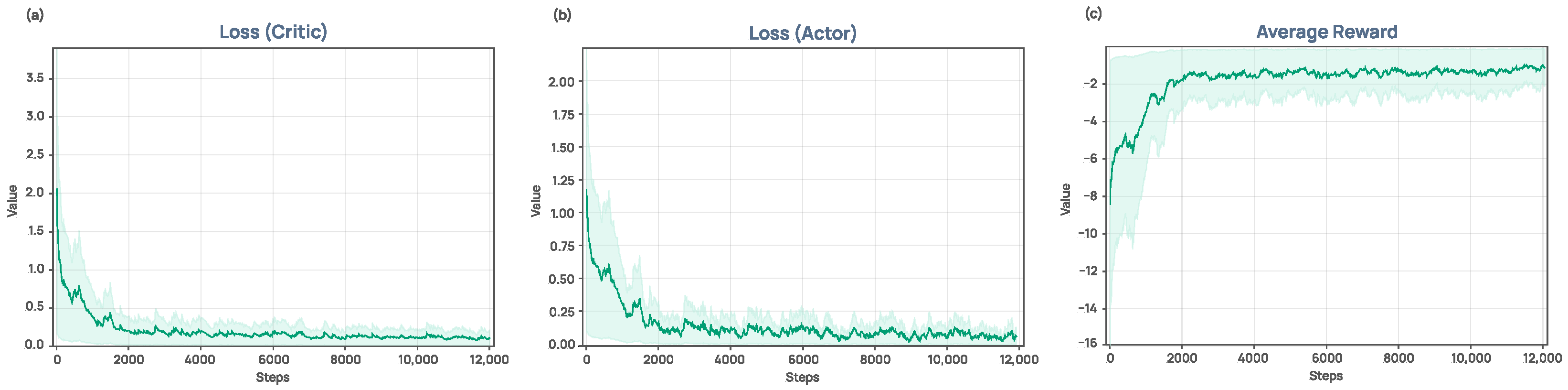
5. Results and Discussion
6. Limitations
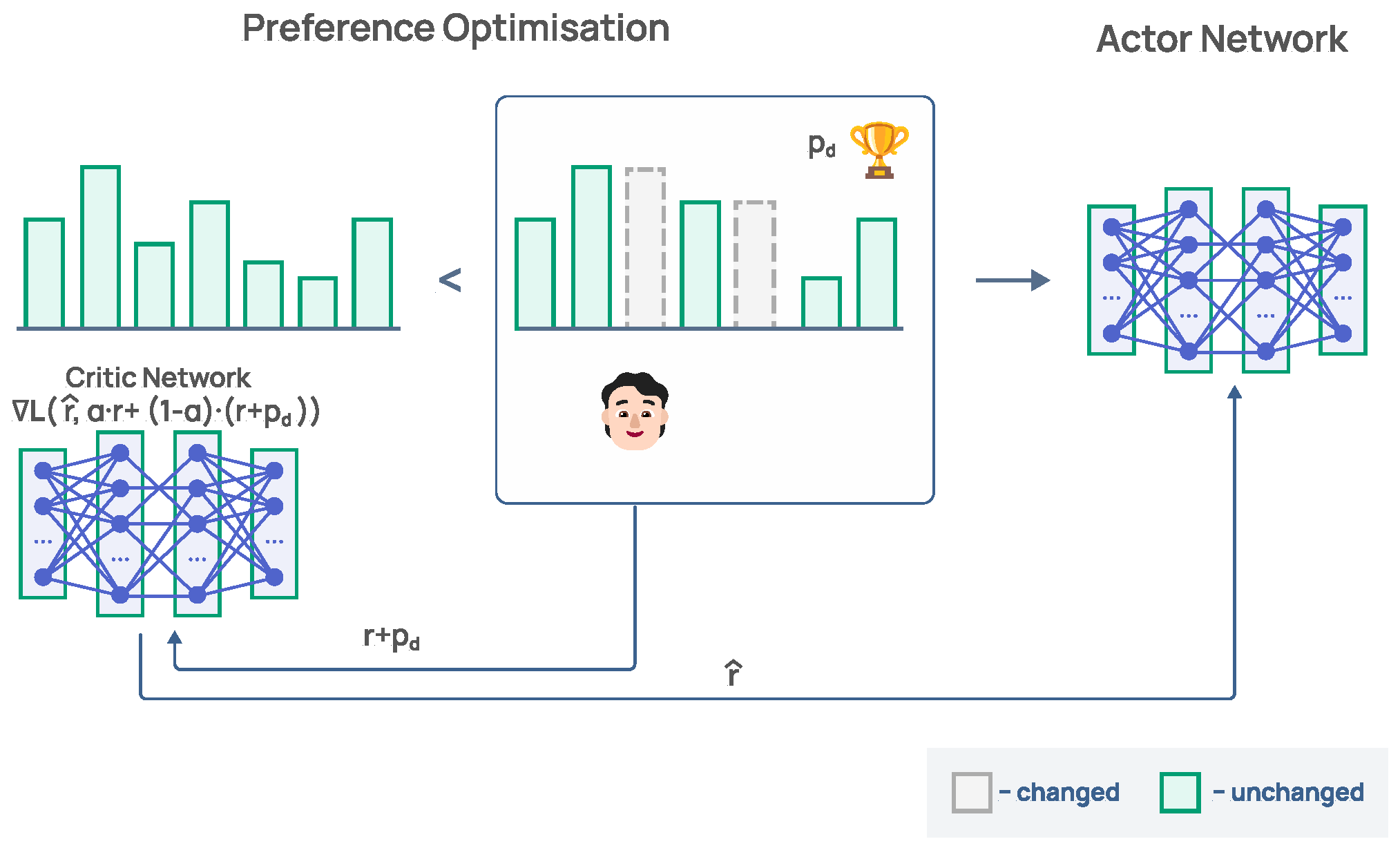
6.1. Direct Preference Optimization
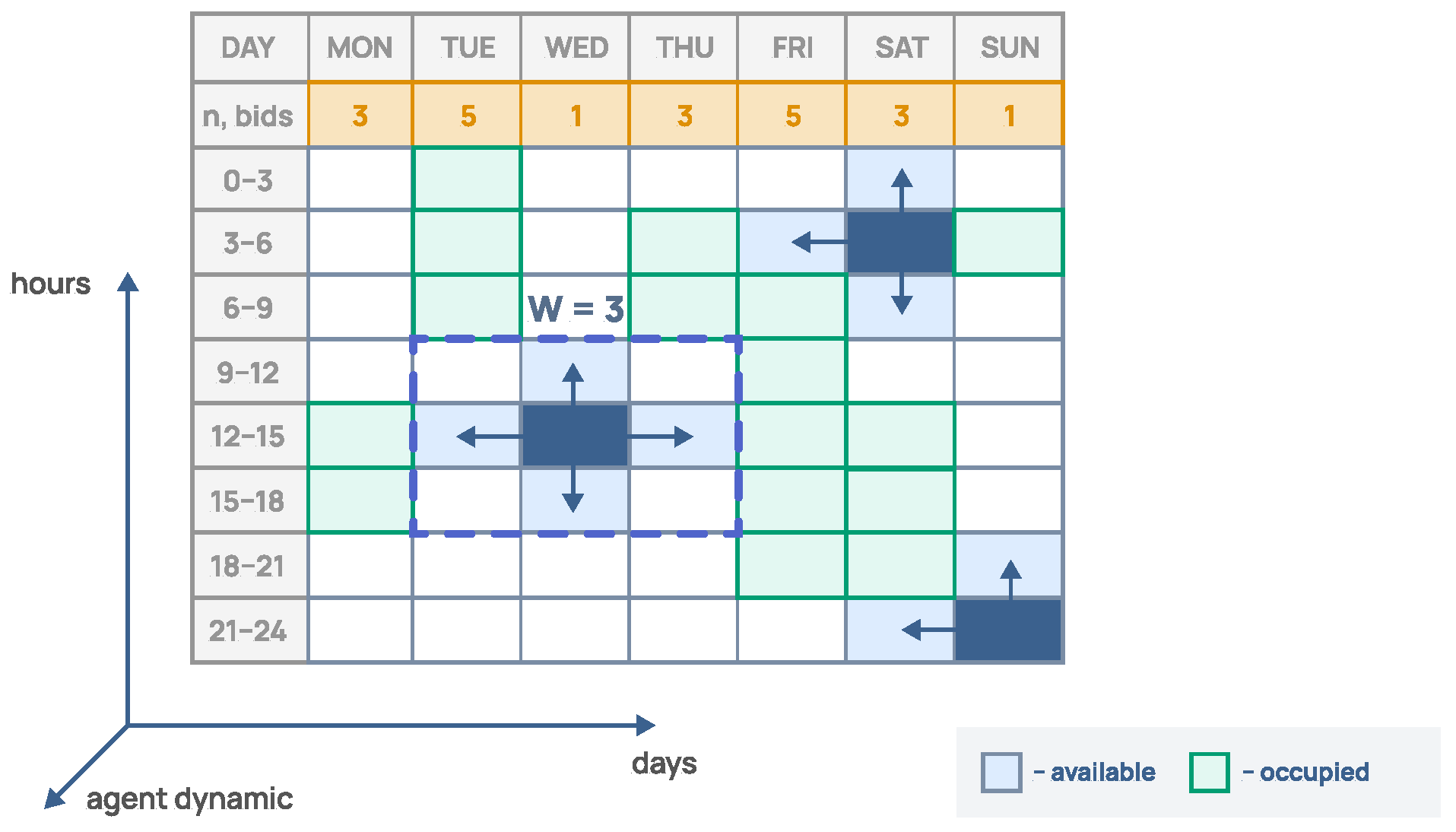
6.2. Day and Time Management
6.3. Linked Entities
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


Appendix B
Appendix B.1
Appendix B.2
Appendix B.3
Appendix B.4
Appendix B.5
Appendix C
Appendix C.1
Appendix C.2
Appendix C.3
Appendix D
Appendix D.1
Appendix D.2
Appendix D.3
Appendix D.4
Appendix D.5
References
- Zhang, J.; Ding, G.; Zou, Y.; Qin, S.; Fu, J. Review of job shop scheduling research and its new perspectives under Industry 4.0. J. Intell. Manuf. 2019, 30, 1809–1830. [Google Scholar] [CrossRef]
- Albrecht, S.V.; Christianos, F.; Schäfer, L. Multi-Agent Reinforcement Learning: Foundations and Modern Approaches; The MIT Press: Cambridge, MA, USA, 2024. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of PPO in cooperative multi-agent games. Adv. Neural Inf. Process. Syst. 2022, 35, 24611–24624. [Google Scholar]
- Retzlaff, C.O.; Das, S.; Wayllace, C.; Mousavi, P.; Afshari, M.; Yang, T.; Saranti, A.; Angerschmid, A.; Taylor, M.E.; Holzinger, A. Human-in-the-loop reinforcement learning: A survey and position on requirements, challenges, and opportunities. J. Artif. Intell. Res. 2024, 79, 359–415. [Google Scholar] [CrossRef]
- Christiano, P.F.; Leike, J.; Brown, T.; Martic, M.; Legg, S.; Amodei, D. Deep reinforcement learning from human preferences. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wu, X.; Xiao, L.; Sun, Y.; Zhang, J.; Ma, T.; He, L. A survey of human-in-the-loop for machine learning. Future Gener. Comput. Syst. 2022, 135, 364–381. [Google Scholar] [CrossRef]
- Muslimani, C.; Taylor, M.E. Leveraging Sub-Optimal Data for Human-in-the-Loop Reinforcement Learning. arXiv 2024, arXiv:2405.00746. [Google Scholar]
- Wu, J.; Huang, Z.; Hu, Z.; Lv, C. Toward human-in-the-loop AI: Enhancing deep reinforcement learning via real-time human guidance for autonomous driving. Engineering 2023, 21, 75–91. [Google Scholar] [CrossRef]
- Abdalkareem, Z.A.; Amir, A.; Al-Betar, M.A.; Ekhan, P.; Hammouri, A.I. Healthcare scheduling in optimization context: A review. Health Technol. 2021, 11, 445–469. [Google Scholar] [CrossRef] [PubMed]
- Almaneea, L.I.; Hosny, M.I. A two level hybrid bees algorithm for operating room scheduling problem. In Intelligent Computing: Proceedings of the 2018 Computing Conference; Springer International Publishing: Cham, Switzerland, 2019; Volume 1, pp. 272–290. [Google Scholar]
- Akbarzadeh, B.; Moslehi, G.; Reisi-Nafchi, M.; Maenhout, B. A diving heuristic for planning and scheduling surgical cases in the operating room department with nurse re-rostering. J. Sched. 2020, 23, 265–288. [Google Scholar] [CrossRef]
- Belkhamsa, M.; Jarboui, B.; Masmoudi, M. Two metaheuristics for solving no-wait operating room surgery scheduling problem under various resource constraints. Comput. Ind. Eng. 2018, 126, 494–506. [Google Scholar] [CrossRef]
- Molina-Pariente, J.M.; Hans, E.W.; Framinan, J.M. A stochastic approach for solving the operating room scheduling problem. Flex. Serv. Manuf. J. 2018, 30, 224–251. [Google Scholar] [CrossRef]
- Wong, A.; Bäck, T.; Kononova, A.V.; Plaat, A. Deep multiagent reinforcement learning: Challenges and directions. Artif. Intell. Rev. 2023, 56, 5023–5056. [Google Scholar] [CrossRef]
- Panzer, M.; Bender, B. Deep reinforcement learning in production systems: A systematic literature review. Int. J. Prod. Res. 2022, 60, 4316–4341. [Google Scholar] [CrossRef]
- Al-Hamadani, M.N.; Fadhel, M.A.; Alzubaidi, L.; Harangi, B. Reinforcement Learning Algorithms and Applications in Healthcare and Robotics: A Comprehensive and Systematic Review. Sensors 2024, 24, 2461. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Yang, Z.; Basar, T. Multi-Agent Reinforcement Learning: A Selective Overview of Theories and Algorithms. In Handbook of Reinforcement Learning and Control; Springer: Cham, Switzerland, 2021; pp. 321–384. [Google Scholar]
- Pu, Y.; Li, F.; Rahimifard, S. Multi-Agent Reinforcement Learning for Job Shop Scheduling in Dynamic Environments. Sustainability 2024, 16, 3234. [Google Scholar] [CrossRef]
- Wan, L.; Cui, X.; Zhao, H.; Li, C.; Wang, Z. An effective deep Actor-Critic reinforcement learning method for solving the flexible job shop scheduling problem. Neural Comput. Appl. 2024, 36, 11877–11899. [Google Scholar] [CrossRef]
- Mangalampalli, S.; Hashmi, S.S.; Gupta, A.; Karri, G.R.; Rajkumar, K.V.; Chakrabarti, T.; Chakrabarti, P.; Margala, M. Multi Objective Prioritized Workflow Scheduling Using Deep Reinforcement Based Learning in Cloud Computing. IEEE Access 2024, 12, 5373–5392. [Google Scholar] [CrossRef]
- Monaci, M.; Agasucci, V.; Grani, G. An actor-critic algorithm with policy gradients to solve the job shop scheduling problem using deep double recurrent agents. Eur. J. Oper. Res. 2024, 312, 910–926. [Google Scholar] [CrossRef]
- Amir, O.; Doshi-Velez, F.; Sarne, D. Summarizing agent strategies. Auton. Agents Multi-Agent Syst. 2019, 33, 628–644. [Google Scholar] [CrossRef]
- Lage, I.; Lifschitz, D.; Doshi-Velez, F.; Amir, O. Toward robust policy summarization. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems, Montreal, QC, Canada, 13–17 May 2019; pp. 2081–2083. [Google Scholar]
- Williams, S.; Crouch, R. Emergency department patient classification systems: A systematic review. Accid. Emerg. Nurs. 2006, 14, 160–170. [Google Scholar] [CrossRef]
- Mosqueira-Rey, E.; Hernández-Pereira, E.; Alonso-Ríos, D.; Bobes-Bascarán, J.; Fernández-Leal, Á. Human-in-the-loop machine learning: A state of the art. Artif. Intell. Rev. 2023, 56, 3005–3054. [Google Scholar] [CrossRef]
- Gómez-Carmona, O.; Casado-Mansilla, D.; López-de-Ipiña, D.; García-Zubia, J. Human-in-the-loop machine learning: Reconceptualizing the role of the user in interactive approaches. Internet Things 2024, 25, 101048. [Google Scholar] [CrossRef]
- Gombolay, M.; Jensen, R.; Stigile, J.; Son, S.H.; Shah, J. Apprenticeship scheduling: Learning to schedule from human experts. In Proceedings of the 25th International Joint Conference on Artificial Intelligence (IJCAI 2016), New York, NY, USA, 9–15 July 2016; pp. 1153–1160. [Google Scholar]
- Xue, W.; An, B.; Yan, S.; Xu, Z. Reinforcement Learning from Diverse Human Preferences. arXiv 2023, arXiv:2301.11774. [Google Scholar]
- Hejna, J.; Sadigh, D. Few-Shot Preference Learning for Human-in-the-Loop RL. In Proceedings of the 6th Conference on Robot Learning (CoRL 2022), Auckland, New Zealand, 14–18 December 2022. [Google Scholar]
- Liang, X.; Shu, K.; Lee, K.; Abbeel, P. Reward Uncertainty for Exploration in Preference-based Reinforcement Learning. arXiv 2022, arXiv:2205.12401. [Google Scholar]
- Ge, L.; Zhou, X.; Li, X. Designing Reward Functions Using Active Preference Learning for Reinforcement Learning in Autonomous Driving Navigation. Appl. Sci. 2024, 14, 4845. [Google Scholar] [CrossRef]
- Walsh, S.E.; Feigh, K.M. Differentiating ‘Human in the Loop’ Decision Process. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; pp. 3129–3133. [Google Scholar]
- Arakawa, R.; Kobayashi, S.; Unno, Y.; Tsuboi, Y.; Maeda, S.I. DQN-TAMER: Human-in-the-Loop Reinforcement Learning with Intractable Feedback. arXiv 2018, arXiv:1810.11748. [Google Scholar]
- Meng, X.L. Data Science and Engineering with Human in the Loop, Behind the Loop, and Above the Loop; Harvard Data Science Review: Boston, MA, USA, 2023; Volume 5. [Google Scholar]
- Varga, J.; Raidl, G.R.; Rönnberg, E.; Rodemann, T. Scheduling jobs using queries to interactively learn human availability times. Comput. Oper. Res. 2024, 167, 106648. [Google Scholar] [CrossRef]
- Barabási, A.L. The origin of bursts and heavy tails in human dynamics. Nature 2005, 435, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, A.; Oliveira, J.G.; Dezsö, Z.; Goh, K.I.; Kondor, I.; Barabási, A.L. Modeling bursts and heavy tails in human dynamics. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006, 73, 036127. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Wan, R.; Qi, Z.; Luo, S.; Shi, C. Robust offline reinforcement learning with heavy-tailed rewards. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 2–4 May 2024; pp. 541–549. [Google Scholar]
- Cayci, S.; Eryilmaz, A. Provably Robust Temporal Difference Learning for Heavy-Tailed Rewards. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2024; Volume 36. [Google Scholar]
- Lu, Y.; Xiang, Y.; Huang, Y.; Yu, B.; Weng, L.; Liu, J. Deep reinforcement learning based optimal scheduling of active distribution system considering distributed generation, energy storage and flexible load. Energy 2023, 271, 127087. [Google Scholar] [CrossRef]
- Rafailov, R.; Sharma, A.; Mitchell, E.; Manning, C.D.; Ermon, S.; Finn, C. Direct preference optimization: Your language model is secretly a reward model. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2024; Volume 36. [Google Scholar]
- An, G.; Lee, J.; Zuo, X.; Kosaka, N.; Kim, K.M.; Song, H.O. Direct preference-based policy optimization without reward modeling. Adv. Neural Inf. Process. Syst. 2023, 36, 70247–70266. [Google Scholar]
- Wells, L.; Bednarz, T. Explainable ai and reinforcement learning—A systematic review of current approaches and trends. Front. Artif. Intell. 2021, 4, 550030. [Google Scholar] [CrossRef] [PubMed]
- Wani, N.A.; Kumar, R.; Bedi, J.; Rida, I. Explainable Goal-driven Agents and Robots—A Comprehensive Review. ACM Comput. Surv. 2023, 55, 102472. [Google Scholar]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. (CSUR) 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Lundberg, S. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Anjomshoae, S.; Najjar, A.; Calvaresi, D.; Främling, K. Explainable agents and robots: Results from a systematic literature review. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems; International Foundation for Autonomous Agents and Multiagent Systems, Montreal, QC, Canada, 13–17 May 2019; pp. 1078–1088. [Google Scholar]
- Langley, P.; Meadows, B.; Sridharan, M.; Choi, D. Explainable agency for intelligent autonomous systems. In Proceedings of the 29th Innovative Applications of Artificial Intelligence Conference, San Francisco, CA, USA, 6–9 February 2017. [Google Scholar]
- Coroama, L.; Groza, A. Evaluation metrics in explainable artificial intelligence (XAI). In Proceedings of the International Conference on Advanced Research in Technologies, Information, Innovation and Sustainability, Santiago de Compostela, Spain, 12–15 September 2022; Springer Nature: Cham, Switzerland, 2022; pp. 401–413. [Google Scholar]
- Yan, E.; Burattini, S.; Hübner, J.F.; Ricci, A. Towards a Multi-Level Explainability Framework for Engineering and Understanding BDI Agent Systems. In Proceedings of the WOA2023: 24th Workshop From Objects to Agents, Rome, Italy, 6–8 November 2023. [Google Scholar]
- Alelaimat, A.; Ghose, A.; Dam, H.K. Mining and Validating Belief-Based Agent Explanations. In International Workshop on Explainable, Transparent Autonomous Agents and Multi-Agent Systems; Springer Nature: Cham, Switzerland, 2023; pp. 3–17. [Google Scholar]
- Dennis, L.A.; Oren, N. Explaining BDI agent behaviour through dialogue. Auton. Agent Multi-Agent Syst. 2022, 36, 29. [Google Scholar] [CrossRef]
- Cruz, F.; Dazeley, R.; Vamplew, P. Memory-based explainable reinforcement learning. In Proceedings of the AI 2019: Advances in Artificial Intelligence: 32nd Australasian Joint Conference, Adelaide, SA, Australia, 2–5 December 2019, Proceedings 32; Springer International Publishing: Cham, Switzerland, 2019; pp. 66–77. [Google Scholar]
- Sequeira, P.; Gervasio, M. Interestingness elements for explainable reinforcement learning: Understanding agents’ capabilities and limitations. Artif. Intell. 2019, 288, 103367. [Google Scholar] [CrossRef]
- Zhang, G.; Kashima, H. Learning state importance for preference-based reinforcement learning. Mach Learn 2024, 113, 1885–1901. [Google Scholar] [CrossRef]
- Bratman, M.E.; Israel, D.J.; Pollack, M.E. Plans and resource-bounded practical reasoning. Comput. Intell. 1988, 4, 349–355. [Google Scholar] [CrossRef]
- Ciatto, G.; Calegari, R.; Omicini, A.; Calvaresi, D. Towards XMAS: EXplainability through Multi-Agent Systems. CEUR Workshop Proc. 2019, 2502, 40–53. [Google Scholar]
- Georgeff, M.; Pell, B.; Pollack, M.; Tambe, M.; Wooldridge, M. The belief-desire-intention model of agency. In Proceedings of the Intelligent Agents V: Agents Theories, Architectures, and Languages: 5th International Workshop, ATAL’98, Paris, France, 4–7 July 1998, Proceedings 5; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–10. [Google Scholar]
- de Silva, L.; Meneguzzi, F.; Logan, B. BDI agent architectures: A survey. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, V. 7, Yokohama, Japan, 7–15 January 2021; pp. 4914–4921. [Google Scholar]
- Shu, T.; Xiong, C.; Socher, R. Hierarchical and Interpretable Skill Acquisition in Multi-task Reinforcement Learning. arXiv 2017, arXiv:1712.07294v1. [Google Scholar]
- Ehsan, U.; Tambwekar, P.; Chan, L.; Harrison, B.; Riedl, M.O. Automated rationale generation: A technique for explainable AI and its effects on human perceptions. In Proceedings of the 24th International Conference on Intelligent User Interfaces, Companion, Marina del Ray, CA, USA, 16–20 March 2019; pp. 263–274. [Google Scholar]
- Brown, T.B. Language Models are Few-Shot Learners. arXiv 2020, arXiv:2005.14165v4. [Google Scholar]
- Anderson, A.; Dodge, J.; Sadarangani, A.; Juozapaitis, Z.; Newman, E.; Irvine, J.; Chattopadhyay, S.; Fern, A.; Burnett, M. Explaining Reinforcement Learning to Mere Mortals: An Empirical Study. arXiv 2019, arXiv:1903.09708v2. [Google Scholar]
- Winikoff, M.; Sidorenko, G. Evaluating a Mechanism for Explaining BDI Agent Behaviour. In Proceedings of the Explainable and Transparent AI and Multi-Agent Systems: 5th International Workshop, EXTRAAMAS 2023, London, UK, 29 May 2023; pp. 18–37. [Google Scholar]
- Ahilan, S. A Succinct Summary of Reinforcement Learning. arXiv 2023, arXiv:2301.01379. [Google Scholar]
- Yu, Z.; Tao, Y.; Chen, L.; Sun, T.; Yang, H. B-Coder: Value-Based Deep Reinforcement Learning for Program Synthesis. arXiv 2023, arXiv:2310.03173. [Google Scholar]
- Li, W.; Wang, X.; Jin, B.; Sheng, J.; Zha, H. Dealing with non-stationarity in marl via trust-region decomposition. arXiv 2021, arXiv:2102.10616. [Google Scholar]
- Padakandla, S.; KJ, P.; Bhatnagar, S. Reinforcement learning algorithm for non-stationary environments. Appl. Intell. 2020, 50, 3590–3606. [Google Scholar] [CrossRef]
- Grondman, I.; Busoniu, L.; Lopes, G.A.; Babuska, R. A survey of Actor-Critic reinforcement learning: Standard and natural policy gradients. IEEE Trans. Syst. Man Cybern. Part (Appl. Rev.) 2012, 42, 1291–1307. [Google Scholar] [CrossRef]
- Dazeley, R.; Vamplew, P.; Foale, C.; Young, C.; Aryal, S.; Cruz, F. Levels of explainable artificial intelligence for human-aligned conversational explanations. Artif. Intell. 2021, 299, 103525. [Google Scholar] [CrossRef]
- Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Ichter, B.; Xia, F.; Chi, E.; Le, Q.V.; Zhou, D. Chain-of-thought prompting elicits reasoning in large language models. Adv. Neural Inf. Process. Syst. 2022, 35, 24824–24837. [Google Scholar]
- Wiseman, Y. Autonomous vehicles will spur moving budget from railroads to roads. Int. J. Intell. Unmanned Syst. 2024, 12, 19–31. [Google Scholar] [CrossRef]
- Seyedin, H.; Afshari, M.; Isfahani, P.; Hasanzadeh, E.; Radinmanesh, M.; Bahador, R.C. The main factors of supplier-induced demand in health care: A qualitative study. J. Educ. Health Promot. 2021, 10, 49. [Google Scholar] [CrossRef] [PubMed]
- Seyedin, H.; Afshari, M.; Isfahani, P.; Hasanzadeh, E.; Radinmanesh, M.; Bahador, R.C. Strategies for Reducing Induced Demand in Hospitals Affiliated with Iran University of Medical Sciences: A Qualitative Study. Evid. Based Health Policy Manag. Econ. 2022, 6, 273–284. [Google Scholar] [CrossRef]

| Algorithm | Metrics | Zero-Shot | Few-Shot Average (n = 10,000) |
|---|---|---|---|
| FIFO | 0.0 | 0.0 | |
| P, % | 0.0 | 0.0 | |
| , days | 2.0 | 2.22 | |
| , days | 2.0 | 2.25 | |
| MAPPO | 0.0025 | 0.0062 | |
| , % | 2.86 | 9.96 | |
| , days | 1.5 | 1.75 | |
| , days | 2.5 | 2.05 |
| Prompt | Concepts | Cosine Similarity | Jaccard Distance | Levenshtein Distance | |||
|---|---|---|---|---|---|---|---|
| Hard | Soft | Hard | Soft | Hard | Soft | ||
| Appendix B.1 | Intelligent agents | 0.3214 | 0.6237 | 0.3630 | 0.6207 | 0.3832 | 0.6771 |
| Reinforcement learning | 0.3361 | 0.6237 | 0.3143 | 0.6207 | 0.5689 | 0.6771 | |
| Simulation | 0.5473 | 0.5840 | 0.5333 | 0.5938 | 0.5689 | 0.6911 | |
| State transitions | 0.2748 | 0.8149 | 0.2647 | 0.8148 | 0.4192 | 0.7869 | |
| Resource optimization | 0.3641 | 0.3150 | 0.3429 | 0.3077 | 0.3643 | 0.4792 | |
| Appendix B.2 | Belief–desire–intention model | 0.2841 | 0.5722 | 0.3243 | 0.5000 | 0.3321 | 0.4542 |
| Agent beliefs | 0.4513 | 0.6708 | 0.4146 | 0.6111 | 0.5214 | 0.6044 | |
| Agent desires | 0.4885 | 0.8622 | 0.4103 | 0.8571 | 0.4786 | 0.9000 | |
| Agent intentions | 0.6294 | 0.6852 | 0.5455 | 0.7105 | 0.4643 | 0.8071 | |
| Planning horizon | 0.4138 | 0.5179 | 0.4000 | 0.4634 | 0.3643 | 0.5018 | |
| Appendix B.3 | Simulation | 0.2617 | 0.2369 | 0.2813 | 0.2727 | 0.3698 | 0.3708 |
| Reinforcement learning | 0.2826 | 0.2470 | 0.2500 | 0.2727 | 0.4688 | 0.4944 | |
| Beliefs | 0.5121 | 0.3298 | 0.4828 | 0.4138 | 0.5885 | 0.6461 | |
| Intentions | 0.2989 | 0.2462 | 0.3429 | 0.2432 | 0.5156 | 0.3539 | |
| Rewards | 0.3063 | 0.1858 | 0.3125 | 0.2105 | 0.5052 | 0.3708 | |
| Appendix B.4 | System logs | 0.5612 | 0.2060 | 0.4348 | 0.0893 | 0.6111 | 0.2310 |
| Log analysis | 0.2049 | 0.3584 | 0.0656 | 0.3043 | 0.1941 | 0.4196 | |
| Appendix B.5 | Belief–desire–intention model | 0.2950 | 0.7727 | 0.2237 | 0.6034 | 0.2978 | 0.5559 |
| Agent analysis | 0.9780 | 0.8950 | 0.9608 | 0.8113 | 0.9801 | 0.7224 | |
| Reasoning reconstruction | 0.3038 | 0.7133 | 0.1719 | 0.6071 | 0.3052 | 0.7093 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isakov, A.; Peregorodiev, D.; Tomilov, I.; Ye, C.; Gusarova, N.; Vatian, A.; Boukhanovsky, A. Real-Time Scheduling with Independent Evaluators: Explainable Multi-Agent Approach. Technologies 2024, 12, 259. https://doi.org/10.3390/technologies12120259
Isakov A, Peregorodiev D, Tomilov I, Ye C, Gusarova N, Vatian A, Boukhanovsky A. Real-Time Scheduling with Independent Evaluators: Explainable Multi-Agent Approach. Technologies. 2024; 12(12):259. https://doi.org/10.3390/technologies12120259
Chicago/Turabian StyleIsakov, Artem, Danil Peregorodiev, Ivan Tomilov, Chuyang Ye, Natalia Gusarova, Aleksandra Vatian, and Alexander Boukhanovsky. 2024. "Real-Time Scheduling with Independent Evaluators: Explainable Multi-Agent Approach" Technologies 12, no. 12: 259. https://doi.org/10.3390/technologies12120259
APA StyleIsakov, A., Peregorodiev, D., Tomilov, I., Ye, C., Gusarova, N., Vatian, A., & Boukhanovsky, A. (2024). Real-Time Scheduling with Independent Evaluators: Explainable Multi-Agent Approach. Technologies, 12(12), 259. https://doi.org/10.3390/technologies12120259








