Exploring Post-Quantum Cryptography: Review and Directions for the Transition Process

Abstract

As quantum computing advances, current cryptographic protocols are increasingly vulnerable to quantum attacks, particularly those based on Public Key Infrastructure (PKI) like RSA or Elliptic Curve Cryptography (ECC). This paper presents a comprehensive review of Post-Quantum Cryptography (PQC) as a solution to protect digital systems in the quantum era. We provide an in-depth analysis of various quantum-resistant cryptographic algorithms, including lattice-based, code-based, hash-based, isogeny-based, and multivariate approaches. The review highlights the National Institute of Standards and Technology (NIST) PQC standardization process, highlighting key algorithms, such as CRYSTALS–Kyber, CRYSTALS–Dilithium, Falcon, and SPHINCS+, and discusses the strengths, vulnerabilities, and implementation challenges of the leading algorithms. In addition, we explore transition strategies for organizations, emphasizing hybrid cryptography to ensure backward compatibility during migration. This study offers key insights into the future of cryptographic standards and the critical steps necessary to prepare for the transition from classical to quantum-resistant systems.

1. Introduction

Quantum computing connects the principles of quantum mechanics to process information in ways that classical computers cannot. Unlike classical computers, which use bits to represent either a 0 or a 1, quantum computers use quantum bits, or qubits, that can exist simultaneously in a superposition of both 0 and 1 states [1,2]. This property, combined with entanglement and interference, allows quantum computers to perform certain calculations exponentially faster than classical machines. While this technology is still in its developmental stages, its potential to revolutionize fields such as cryptography, optimization, and complex simulations is profound.

One of the most well-known quantum algorithms is Shor’s algorithm [3], which can factor large integers exponentially faster than the best classical algorithms. The significance of this lies in its ability to break widely used cryptographic systems, such as RSA [4] and Elliptic Curve Cryptography (ECC) [5,6], which rely on the difficulty of integer factorization and the discrete logarithm problem. A sufficiently advanced quantum computer running Shor’s algorithm could easily decrypt sensitive data encrypted with these classical methods, creating a serious threat to global data security. However, building scalable quantum computers capable of executing these algorithms reliably is still a major technical challenge [7].

Cryptography is essential for securing data and communications in the digital age. Classical cryptographic systems rely on mathematical problems that are hard for classical computers to solve, but the advent of quantum computing will change this landscape [8]. To prepare for this eventuality, researchers are focusing on two broad areas: Quantum Key Distribution (QKD) [9] and Post-Quantum Cryptography (PQC) [10]. These two approaches address the quantum threat from different perspectives, and understanding the distinction between them is crucial.

QKD leverages the principles of quantum mechanics to enable secure key exchange between parties. It does not rely on mathematical complexity for security but rather on the physical properties of quantum particles. If an eavesdropper tries to intercept the quantum key, their actions will inevitably disturb the quantum state, alerting the communicating parties to the presence of an intrusion [11]. QKD is already practical and has been implemented using current technology without the need for quantum computers. However, QKD is limited to key distribution and does not replace existing encryption systems used for securing communications.

In contrast, PQC refers to a set of cryptographic algorithms designed to be secure against quantum attacks. PQC aims to replace or enhance existing cryptographic methods to ensure long-term security, even in the presence of quantum computers. Unlike QKD, PQC does not rely on quantum mechanics but on mathematical problems that are believed to be resistant to quantum algorithms like Shor’s and Grover’s. These quantum-resistant algorithms are crucial for securing a broad range of applications, from digital signatures to data encryption and key exchange. While PQC algorithms are still being developed and standardized, they are expected to be the primary defense mechanism once quantum computers become powerful enough to break classical cryptography.

The field of PQC is an active area of research, with several promising quantum-resistant algorithms emerging. These include lattice-based, hash-based, code-based, and multivariate polynomial cryptographic schemes. Some of these algorithms offer resilience to quantum attacks because they are based on problems that quantum computers are not well-suited to solve efficiently. For instance, doubling the key size in symmetric algorithms can effectively mitigate the advantage quantum computers have using Grover’s algorithm.

The National Institute of Standards and Technology (NIST) has been leading the effort to standardize PQC algorithms. This ongoing process evaluates candidate algorithms based on their security, efficiency, and practicality for real-world implementation. The algorithms that survive this rigorous evaluation will form the backbone of future cryptographic standards, protecting data and communications in the post-quantum world. There have been numerous studies evaluating individual PQC algorithms and some surveys [12,13,14], but to the authors’ knowledge, there remains a significant gap in the literature in terms of providing a unified, comprehensive understanding of the various algorithmic approaches, such as lattice-based, code-based, multivariate, and isogeny-based cryptography, among others. This study addresses this gap by offering a comprehensive review of the most prominent PQC algorithms, focusing on their strengths, vulnerabilities, and implementation challenges, contextualizing their theoretical foundations and practical applications. In doing so, it not only compares the efficiency and security of these algorithms but also serves as a guide for stakeholders navigating the transition to post-quantum cryptographic solutions.

The algorithms included in our comparison have been selected based on several important factors that reflect their relevance to the field of PQC. First and foremost, all these algorithms were participants in the NIST PQC standardization process. Although some have since been eliminated or compromised, they initially represented strong candidates in the search for quantum-resistant cryptographic solutions. Their selection allows us to present a broad overview of the types of algorithms under consideration and the lessons learned from their evaluation. In addition, we also selected algorithms based on their diversity in approach, including lattice-based, hash-based, code-based, isogeny-based, braid-groups-based, and multivariate polynomial cryptographic schemes. This variety ensures that we cover a wide range of cryptographic techniques, helping to illustrate the trade-offs and design choices inherent in PQC. We believe it is important to include both successful and compromised algorithms in our analysis because it could help researchers not only understand the current state of PQC but also inform future efforts to develop secure cryptographic standards and not to make the same mistakes. We also examine the transition strategies for organizations looking to adopt PQC, particularly the role of hybrid cryptography in ensuring a smooth migration from classical to quantum-resistant systems.

The rest of the paper is structured as follows: Section 2 discusses the NIST standardization process, Section 3 explores the algorithms undergoing standardization, Section 4 provides a quantitative comparison and insights into future directions for PQC, and the paper concludes with a summary of key findings.

2. Post-Quantum Cryptography Standardization Process

In December 2016, NIST initiated a process to solicit, evaluate, and standardize quantum-resistant cryptographic algorithms that are secure against quantum and classical computers, and that are compatible with existing networks and communication protocols. At the time of writing this paper, the process is in its fourth round, where in each round some algorithms have been discarded and others have undergone further study. During the initial submission phase, NIST received a diverse set of 82 algorithms, but only 69 met the minimum acceptance criteria and submission requirements imposed by NIST. These submissions have spanned various cryptographic approaches, including but not limited to lattice-based, hash-based, and multivariate polynomial systems, aiming to address different aspects of quantum resistance, as shown in Figure 1.

From the initial 69 submissions, NIST conducted preliminary assessments to identify algorithms with the potential for quantum resistance based on their submitted security proofs and performance metrics, representing the the so-called first round. This round focused on eliminating proposals that clearly did not meet the stringent criteria set out for security against quantum computing threats or those that were impractical due to efficiency or complexity issues. The first round was concluded on 30 January 2019, with 43 algorithms eliminated and 26 progressing to the next round.

From January 2019 to July 2019, the selected second-round subset of algorithms were subjected to a more thorough evaluation. This included in-depth analyses of security under quantum attack scenarios, considerations of implementation complexities, and assessments of performance across various platforms. The goal was to refine the list by retaining only the candidates that demonstrated a balanced trade-off between security, efficiency, and practicality: 11 algorithms were eliminated and 15 progressed to the third round. The third round, from July 2020 to July 2022, scrutinized the finalists for higher security assurances and practical deployment capabilities. During this phase, NIST and the cryptographic community closely examined the finer details of each algorithm, such as side-channel resistance, adaptability to different hardware and software environments, and interoperability with existing protocols. Feedback from public and private sectors was crucial in identifying any overlooked vulnerabilities or performance issues. Only one public key encapsulation mechanism (KEM) was selected, CRYSTALS–Kyber, in addition to three digital signatures: CRYSTALS–Dilithium, which is recommended as the primary algorithm by NIST; Falcon, for applications that need smaller signatures than CRYSTALS–Dilithium; and SPHINCS, which is a slower and heavier algorithm than the CRYSTALS–Dilithium and Falcon algorithms, but is useful as a spare as it uses a different mathematical approach than the previous two algorithms. Finally, four of the alternative candidate KEM algorithms would advance to a fourth round of evaluation; these candidates would be evaluated for possible standardization at the end of the fourth round. On July 2022, NIST initiated the fourth round of its PQC standardization process, announcing the candidates under consideration. This round is currently active. Additionally, NIST plans to call for new proposals for public key digital signature algorithms to broaden its signature algorithm collection.

On 24 August 2023, NIST released drafts for three Federal Information Processing Standards (FIPS): FIPS 203 for the CRYSTALS–Kyber key-encapsulation mechanism, FIPS 204 for the CRYSTALS–Dilithium digital signature standard, and FIPS 205 for the SPHINCS+ stateless hash-based digital signature standard. These drafts were open for public review and comments until November 2023. After the review period, NIST finalized and formally adopted the standards based on the feedback received. NIST is also developing a new FIPS for the Falcon-derived digital signature algorithm, expected to be published in about a year.

3. Post-Quantum Cryptography Algorithms

In this section, we will explore in detail the algorithms that have been the subject of study and evaluation in the PQC standardization process carried out by NIST. Algorithms that have emerged as promising candidates for resisting quantum computing attacks will be examined, as well as relevant and associated algorithms that play a crucial role in the PQC landscape. From public keys to digital signature mechanisms, this section will provide a comprehensive overview of the most recent developments in the field of cryptographic security in a post-quantum environment.

3.1. Cryptography Background

Symmetric cryptography, also known as secret-key cryptography, uses a single key for both encryption and decryption. Well-known algorithms like Advanced Encryption Standard (AES) [15] and Triple Data Encryption Standard (3DES) are commonly used for protecting data. While symmetric algorithms are generally considered resistant to quantum attacks due to their efficiency and key sizes, Grover’s algorithm can reduce their security by approximately half. Therefore, increasing key sizes (e.g., from AES-128 to AES-256) is recommended to counter quantum threats. On the other hand, asymmetric cryptography, or public key cryptography, uses a pair of keys: a public key for encryption and a private key for decryption (or vice versa, depending on the specific algorithm employed) (Figure 2). RSA, DSA, and ECC are widely used asymmetric algorithms that rely on complex mathematical problems for security. However, algorithms like Shor’s algorithm make these cryptosystems vulnerable to quantum computers, as they can efficiently solve the factorization and discrete logarithm problems. As a result, the cryptographic community is shifting towards post-quantum alternatives to secure asymmetric encryption.

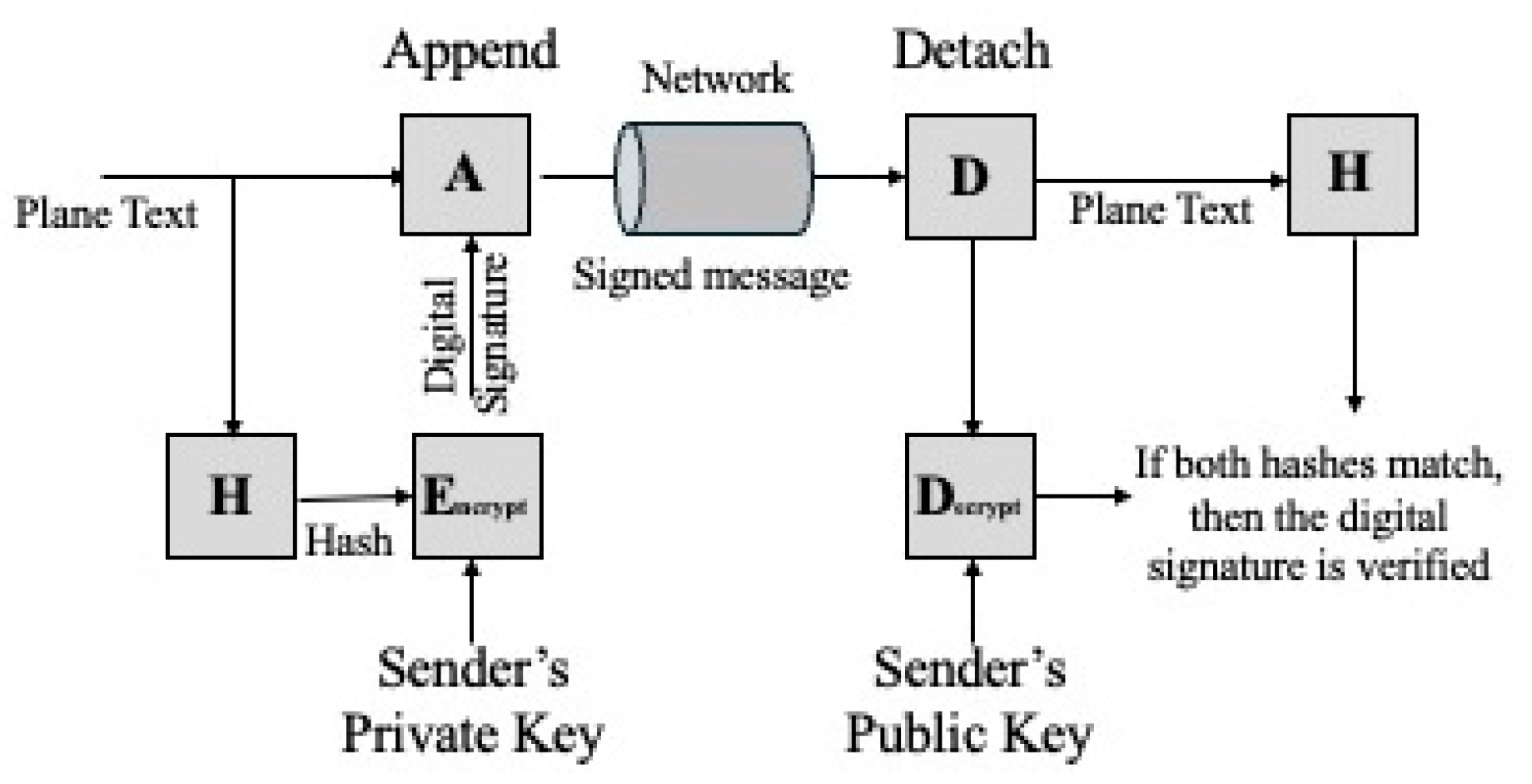
Digital signature and key exchange, also known as key establishment, are security processes that depend on asymmetric cryptography. Digital signatures are cryptographic techniques used to verify the authenticity and integrity of digital messages or documents. These signatures provide a mechanism to verify that a message originates from a verified source and has not been tampered with during transmission (Figure 3). Common digital signature algorithms include RSA, Digital Signature Algorithm (DSA), and Elliptic Curve DSA (ECDSA), with the last two standardized in [16], which rely on mathematical problems that are computationally difficult to solve, such as integer factorization and discrete logarithms. In the context of PQC, traditional digital signatures are vulnerable to quantum attacks, prompting the development of quantum-resistant signature schemes like CRYSTALS–Dilithium and FALCON. Next, key establishment refers to the process of securely exchanging cryptographic keys between parties to enable encrypted communication. It is a critical step to provide secure communication channels, especially over untrusted networks like the Internet. Traditional methods such as the Diffie–Hellman (DH) key exchange and Elliptic-Curve Diffie–Hellman (ECDH) [16] rely on the hardness of the discrete logarithm problem. However, these techniques are susceptible to being broken by quantum computers, necessitating the shift to post-quantum key establishment algorithms like Kyber and NTRU.

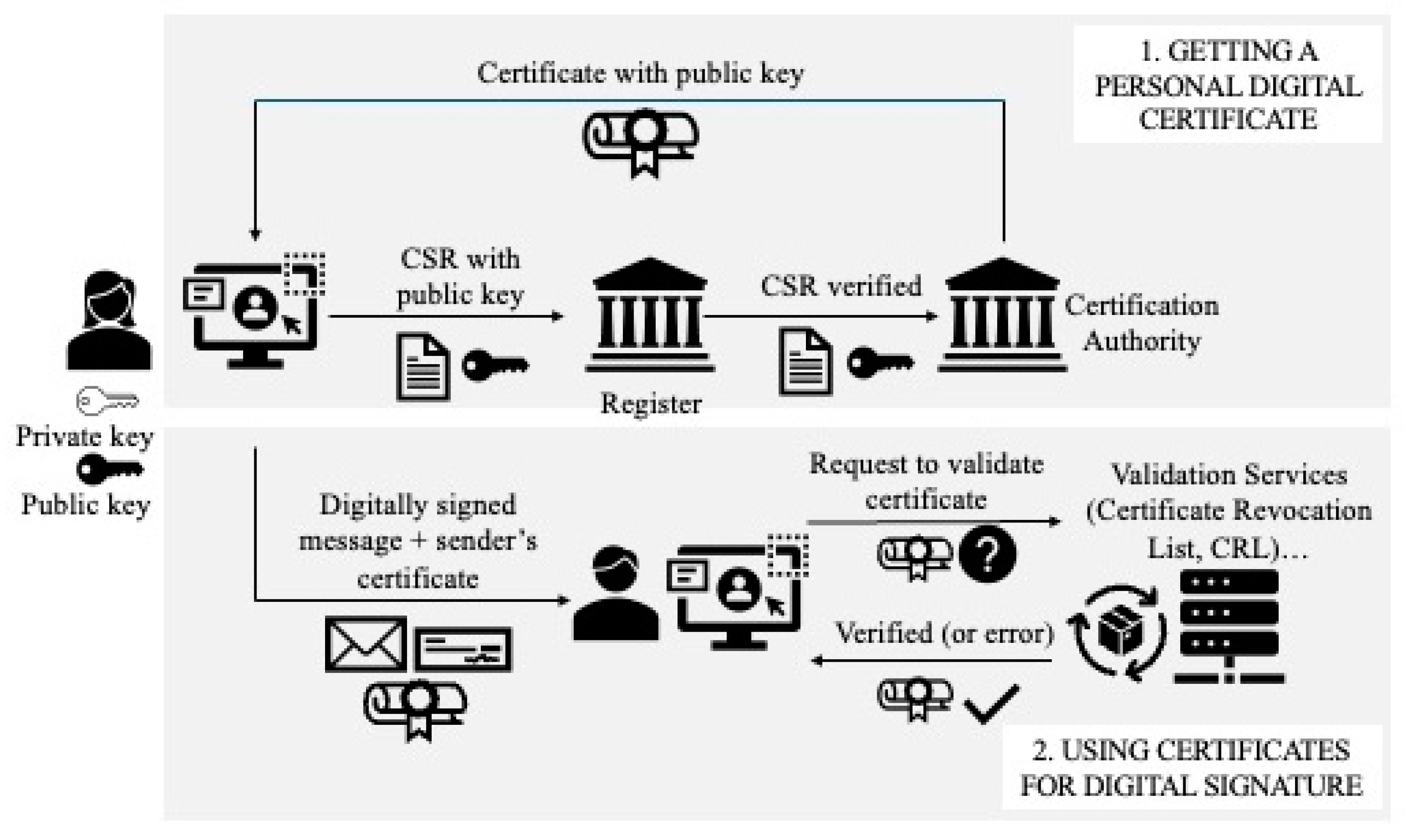
Public Key Infrastructure (PKI) is a framework that provides secure key management, distribution, and verification services for digital communication (Figure 4). It relies on asymmetric cryptography to establish trust and ensure secure data exchange between entities. PKI plays a fundamental role in enabling secure internet transactions, email encryption, and digital certificates. With the advent of quantum computing, the security of traditional PKI systems is at risk, prompting a need for post-quantum PKI solutions that can withstand quantum attacks while maintaining compatibility with existing infrastructure.

3.2. Code-Based Quantum-Resistant Algorithms

Code-based quantum-resistant algorithms refer to cryptographic systems that are based on error correction codes [15]. Some examples are the McEliece [17] and Niederreiter [18] encryption algorithms and the related Courtois, Finiasz and Sendrier signature scheme [19].

The McEliece cryptosystem is an asymmetric encryption algorithm that uses error-correcting codes to generate public keys from private arrays with purposefully injected errors. It was the forerunner scheme in using randomization in the encryption process, making use of linear codes and efficient algorithms for message decoding. Among its advantages is the speed of the encryption and decryption processes, comparable to that of the structured lattice key encapsulation mechanisms (KEM). McEliece consists of three methods: a probabilistic key generation algorithm that produces a public and private key, a probabilistic encryption algorithm, and a deterministic decryption algorithm. It has become a candidate for PQC because it is immune to attacks using Shor’s algorithm. The original algorithm uses binary Goppa codes [20], and one of its main drawbacks is the size of the public key, which is quite large (slowing key generation). In addition, the encrypted message is much longer than the plain text message with the corresponding increase in bandwidth use and the also rising likelihood of transmission errors. The original cryptosystem cannot be used for authentication or signature schemes because the encryption algorithm is not one-to-one and the algorithm is totally asymmetric. However, a signature scheme can be constructed based on the Niederreiter scheme, the dual variant of the McEliece scheme, whose main feature is a faster ciphering compared to McEliece keeping the same security level. The McEliece classic algorithm advanced to the fourth round of the NIST evaluation and was saved as an alternative key-setting algorithm. So, although the algorithm has not been selected to formally begin its standardization process, it is still being considered for future selection.

Bit Flipping Key Encapsulation (BIKE) is a code-based KEM that utilizes quasi-cyclic Moderate-Density Parity-Check (MDPC) codes, known for their decoding complexity, to offer quantum-resistant cryptographic security. It modernizes classic McEliece and Niederreiter systems with a bit-flipping algorithm to correct transmitted message errors iteratively. Its security stems from the challenging task of decoding these specific MDPC codes, allowing for smaller key sizes and balancing security with performance. BIKE’s adaptability to various platforms and its efficient encryption, decryption, and key generation processes make it suitable for widespread PQC applications, ensuring it remains effective in a future dominated by quantum computing. It moved to the fourth NIST round of evaluation, where it continues to be considered for future standardization.

Finally, Hamming Quasi-Cyclic (HQC) is a public key encryption method that utilizes the principles of error-correcting codes, specifically focusing on the Hamming codes in a quasi-cyclic format. The foundational idea behind HQC is to exploit the computational difficulty associated with decoding these Hamming quasi-cyclic codes without prior knowledge of the private key, a task that remains challenging for both classical and quantum computers. In the NIST standardization process, HQC has advanced to the fourth round as a code-based KEM. Specifically, it is an Indistinguishability under Adaptive Chosen-Ciphertext Attack (IND-CCA2) KEM variant of HQC-RMRS (the version using Reed-Muller concatenated with Reed-Solomon ciphers), obtained by applying the Fujisaki–Okamoto transform to the Indistinguishability under Chosen Plaintext Attack (IND-CPA) public key encryption scheme. Among its advantages, HQC KEM inherits strong error-correcting properties from Hamming codes, enhancing data integrity and resilience; offers relatively smaller key sizes for a code-based system, aiding in practical key management; is flexible across various platforms, with efficient encryption, decryption, and key generation; and allows for adjustable security levels to meet diverse application requirements through parameter tuning. On the other hand, it presents potential efficiency concerns due to computational demands and larger key sizes compared to some non-code-based, quantum-resistant algorithms.

3.3. Lattice-Based Quantum-Resistant Algorithms

Lattice-based cryptography is the generic term for constructions of cryptographic primitives that involve lattices, either in the construction itself or in the proof of security. In a lattice, lines connect points to form a geometric structure. In lattice-based cryptography, this geometric structure encodes and decodes messages, using huge grids with billions of individual points, and an almost unlimited number of dimensions. Due to the nature of the lattice, it is difficult to break a lattice-based cryptosystem, as some patterns extend infinitely, allowing messages to be encoded in such a way that only someone who knows the correct key can decode them. This improves the achievable level of security making some lattice-based constructions resistant to attacks by classical and quantum computers. Other special features are speed and power consumption. Lattice-based algorithms allow for much faster computations and can be implemented in hardware, making them less power consuming than other algorithms. Some interesting references can be found in [21,22,23]. Lattice-based cryptography is relatively easy to implement and can be used for a number of different applications: homomorphic encryption, public key encryption, hash functions, key exchange, and digital signature, as we describe below (see

Table 1. Lattice-based quantum-resistant algorithms by function.

Primitive	Name	Description
Homomorphic encryption	Gentry	The first fully homomorphic encryption system capable of evaluating circuits of arbitrary depth (can evaluate addition and multiplication gates) using lattice-based cryptography. The process has two phases. First, a somewhat homomorphic encryption is performed; then, the noise level needs to be kept below a certain limit using squashing and bootstrapping.
	Zvika Brakerski, Craig Gentry, and Vinod Vaikuntanathan	A fully homomorphic scheme, based on Craig Gentry’s scheme, but not requiring ideal lattices. In this case, it is started from a simpler system based on integers but has similar properties in terms of homomorphism and efficiency.
Encryption	Goldreich–Goldwasser–Halevi	It is an asymmetric cryptosystem based on the Closest Vector Problem (CVP). Currently broken. The GGH encryption scheme has a flaw in the design. Each ciphertext reveals information about the plaintext. The decryption problem could become a much easier special nearest vector problem than general CVP.
	NTRU	Relatively new public key cryptosystem that operates with private and secret keys, used as an alternative to RSA and Elliptic Curve Cryptography. It is based on the shortest vector problem in a lattice. Its most relevant advantage is its high speed in key generation, encryption, and decryption processes. In addition, the cryptosystem can be implemented efficiently on very limited systems, such as single 8-bit processors, and it has a low memory usage. Fast key generation allows the use of disposable keys enabling the creation of a new key for each transaction.
Key exchange	CRYSTALS–Kyber	It is a secure key encapsulation mechanism indistinguishability under adaptive chosen ciphertext attack, designed to resist against quantum computer attacks. Its security is based on the difficulty of solving the Learning-With-Errors problem over module lattices. Among the advantages of this asymmetric cryptosystem are smaller encryption keys, easier exchange, and speed of execution.
	FrodoKEM	FrodoKEM is a secure IND-CCA2 KEM, whose security unlike other mechanisms such as Kyber or NTRU is based only on the “simple” or “unstructured” variant of LWE. Such a security model implies that FrodoKEM could remain secure even if the lattice structures break down one day. While this offers a potential security advantage, it also comes at a significant cost in performance (higher bandwidth and computational complexity), being discarded in the NIST standardization process for low performance reasons.
	NTRU Prime	NTRU requires similar hardware resources as SABER and has comparable encapsulation speed, but decapsulation is slightly slower and key generation is much slower.
	SABER	Kyber and SABER have fairly comparable performance, the difference being that Kyber requires slightly less hardware resources.
Digital signature	CRYSTALS–Dilithium	It is a lattice-based digital signature scheme whose security is based on the difficulty of finding short vectors in lattices. CRYSTALS–Dilithium keys can only be used for digital signature generation and verification, and their strength is represented by the size of their polynomial matrix. The larger the matrix size, the stronger the key.
	Falcon	It uses lattice-based cryptography, specifically the NTRU lattice structure along with fast Fourier transform techniques, for efficient computation. It stands out for its small signature sizes and high performance.
	SPHINCS+	It does not rely on number-theoretic assumptions but instead uses hash-based cryptography. It is less efficient than Falcon and has larger key sizes than Dilithium.

).

Regarding homomorphic encryption, it is a cryptographic method that allows mathematical operations to be performed on ciphertext, rather than on the data itself. The crucial property of homomorphic encryption is that the same result must be obtained by decrypting the ciphertext on which the operations have been performed, as by simply operating on the initial plain text. There are many interesting applications for a system that is capable of performing homomorphic operations, such as e-health data processing, privacy protection, outsourcing of financial operations, anonymous database queries, or enhanced privacy protection in advertising systems. There are three approaches for homomorphic encryption called somewhat, partially, and fully homomorphic schemes. In somewhat homomorphic encryption [24], addition and multiplication operations are allowed, but are limited to a certain number of operations because each operation adds noise and, after adding a certain amount of noise, it is no longer possible to recover the data. Partially homomorphic systems [25] admit any number of operations but are limited to only one type of operation (addition or multiplication). Then, fully homomorphic schemes [26] support both addition and multiplication, applied any number of times to the data. The latter is the most interesting for quantum computing. Two significant approaches in lattice-based PQC for homomorphic encryption are Gentry’s original scheme [27] and the proposals [28,29].

As public cryptography, we can highlight the Goldreich-Goldwasser-Halevy (GGH) [30] encryption scheme and the NTRUE [31,32]. The former represents an early effort to take advantage of lattice structures for cryptographic purposes, specifically encryption. The GGH encryption scheme’s security foundation rests on the hardness of the Closest Vector Problem (CVP) within lattice frameworks. Despite its pioneering status, the GGH scheme has been critiqued for vulnerabilities that potentially expose it to specific types of attacks, underscoring the challenges of balancing efficiency, security, and practicality in lattice-based cryptography. The latter, NTRU, offers an alternative to traditional systems like RSA and Elliptic Curve Cryptography (ECC) by focusing on the shortest vector problem in lattices. NTRU has evolved over time, resulting in a hybrid scheme used for the NIST selection process that combines NTRUEncrypt and NTRU-HRSS-KEM, known collectively as NTRU. This variant uses the SXY transform, a type of Fujisaka–Okamoto transformation [33], to enhance security, effectively preventing attackers from extracting useful information from manipulated ciphertexts. While NTRU is suitable for implementation on resource-constrained devices such as 8-bit processors and requires minimal memory, it lags behind other lattice-based schemes like Kyber and SABER, which will be explained later, in terms of key generation speed and efficiency. Furthermore, NTRU’s keys and ciphertexts are roughly 25% larger than those of its competitors, presenting challenges in storage and transmission efficiency. Despite these drawbacks, NTRU remains a critical player in the development of quantum-resistant cryptographic solutions.

For key exchange, CRYSTALS–Kyber [34,35] was the selected algorithm for standardization by NIST. Key exchange schemes are cryptographic methods used for two or more parties to securely agree on a shared encryption key without the need to transmit it directly. CRYSTALS–Kyber is a secure KEM designed to resist against quantum computer attacks and is classified as IND-CCA2. Its security is based on the difficulty of solving the Learning-With-Errors (LWE) problem over module lattices. Among the advantages of this asymmetric cryptosystem are compact key sizes, high performance, efficient bandwidth usage (but larger than that of SABER), and a versatile implementation. Several variants with different security levels have been defined: Kyber-512 with a NIST security level 1 (security approximately equivalent to AES-128), Kyber-768 with a NIST security level 3 (security approximately equivalent to AES-192), and Kyber-1024 with a NIST security level 5 (security approximately equivalent to AES-256). NIST has initiated the formal standardization process for CRYSTALS–Kyber, moving it from academic research towards formal standard documentation and eventually widespread deployment in secure web access and other applications. It is condensed under the FIPS 203 standard, named “Module-Lattice-Based Key-Encapsulation Mechanism Standard” ML-KEM [36], which presents three configurations each corresponding to the different Kyber variants. The key operational differences between CRYSTALS–Kyber and ML-KEM lie in their approach to secret key management, encapsulation algorithms, and randomness generation. CRYSTALS–Kyber’s secret key length varies to meet specific application needs, whereas ML-KEM uses a fixed 256-bit key that is immediately applicable as a symmetric key. ML-KEM also diverges in its use of the Fujisaki–Okamoto transform, employing a variant that differs from CRYSTALS–Kyber. Furthermore, ML-KEM eliminates an extra hashing step in the initial randomness process, relying instead on NIST-approved methods for randomness generation. This step is essential in CRYSTALS–Kyber to prevent errors during key generation.

FrodoKEM [37], NTRU Prime [32], and SABER [38] are three cryptographic mechanisms that were also evaluated together with Kyber for key exchange but did not reach the final standardization. FrodoKEM is based on a simple or unstructured variant of the LWE problem, distinguishing it from other lattice-based cryptographic algorithms like Kyber, NTRU, and SABER which use more structured lattice problems. This unstructured approach potentially offers more robust security since it may remain secure even if structured lattice solutions are compromised. However, this advantage comes at the cost of increased bandwidth usage and higher computational complexity. These performance drawbacks led to FrodoKEM being excluded from further consideration in the NIST standardization process after the third selection phase, despite its theoretical security benefits. FrodoKEM is particularly suitable for scenarios where maximum security assurance is required, even at the expense of performance. Then, NTRU Prime modifies the traditional NTRU cryptosystem to use the NTRU Prime Ring, incorporating large Galois groups to minimize the cryptographic attack surface. Unlike typical NTRU that uses random noise, NTRU Prime opts for deterministic operations such as rounding, which eliminates the chance of decryption errors due to random noise. This approach aims to enhance security but has not shown enough promise compared to other candidates, leading to its rejection by NIST. NTRU Prime includes two variants: Streamlined NTRU Prime (SNTRUP), which closely mirrors the original NTRU in performance but with slower key generation, and NTRU LPrime (NTRULPR), which merges characteristics of NTRU with those of Ring-LWE systems to achieve faster key generation rates comparable to Kyber and SABER. Finally, SABER utilizes the Module Learning With Rounding (MLWR) problem for its security framework, which requires less randomness than the LWE approach used in other schemes and hence reduces the overall bandwidth requirement. SABER is designed for simplicity, efficiency, and flexibility, allowing for straightforward implementations that avoid modular reductions and rejection sampling. It is structured to provide three levels of security: LightSABER for basic security (analogous to AES-128), SABER for substantial security (similar to AES-192), and FireSABER for maximum security (comparable to AES-256). Despite its efficient design and strong security, SABER was not selected for standardization by NIST, which preferred Kyber due to its foundation on the more extensively studied Module Learning With Errors (MLWE) problem.

Similarly, but for digital signature, NIST published [39] its decision to initiate the formal standardization process for three digital signature algorithms to verify identities during a digital transaction or to sign a document remotely. These are CRYSTALS–Dilithium [40], recommended as the primary algorithm by NIST; Falcon [41], for applications that need smaller signatures than CRYSTALS–Dilithium; and SPHINCS+ [42], a slower and heavier algorithm than the CRYSTALS–Dilithium and Falcon algorithms, but useful as a spare because it uses a different mathematical approach than the previous two algorithms. Specifically comparing CRYSTALS–Dilithium and Falcon, the signature generation with Dilithium is faster than with Falcon. However, the cost of data transmission in Falcon is lower than Dilithium, due to its public keys and smaller signature sizes. Unlike Falcon signatures, Dilithium signatures cannot fit in a single Internet packet, making it difficult to customize some applications. Finally, Falcon requires significantly more memory resources than Dilithium, limiting its use on restricted devices, e.g., Internet of Things (IoT).

3.4. Hash-Based Quantum-Resistant Algorithms

Introduced in the 1970s, hash functions have been widely employed in public key cryptography to provide integrity and authentication, e.g., as an essential part of digital signatures. In PQC, their use is maintained, especially for the construction of digital signatures. It is important to note that these algorithms are categorized into two types of schemes. The first one, called One-Time Signature (OTS), allow each key pair to securely sign only a single message. A private key can sign any message, but each private key must be used only once to sign a single message. Utilizing a private key to sign multiple messages compromises the security of the scheme. The second one is Many-Time Signature (MTS), where it is possible to sign multiple messages with a single public key by employing a structured arrangement of multiple one-time-use private keys. Each private key is utilized only once, ensuring security, but the collective framework allows for the repeated use of the public key. This hierarchical or layered configuration supports the secure generation of new private keys for each signing event, maintaining signature integrity in environments requiring frequent authentication tasks.

The advantages and disadvantages of the hash-based signature schemes that we will review, Extended Merkle Signature Scheme (XMSS) [43] and SPHINCS+, can be summarized as follows. Advantages include collision resistance, which ensures that two different messages do not produce the same hash value, therefore enhancing the uniqueness of digital signatures. These schemes also present a low processing time and reduced computational load, as signatures are generated from hash summaries rather than full messages. Furthermore, the fixed size of hashes typically results in smaller signatures that occupy less storage space and bandwidth. However, many hash-based signature methods are stateful, requiring the private key to be updated after each use to maintain security, and they require a system state management to track the usage of private keys. The security of these schemes strongly depends on the robustness of the underlying hash function; any compromise to this function weakens the entire signature scheme. There are stateless hash-based schemes, but they usually produce longer signatures and require longer processing times. In addition, the frequency of key usage for signature generation should be recorded.

XMSS is a stateful, hash-based cryptographic signature scheme that evolves from the traditional Merkle signature. XMSS combines multiple OTS schemes into a single, larger structure known as the XMSS tree. This allows for multiple signatures with a predefined usage limit. To overcome the limitation of one message per key, the XMSS tree aggregates the authenticity of several OTS verification keys into a single XMSS public key. PseudoRandom Fenerators (PRGs) are employed to generate OTS signing keys as needed, minimizing storage requirements. In the XMSS method, each public/private key pair is associated with a binary tree comprising a master seed, node keys derived from the master seed, tree nodes formed by aggregating the hash values of child nodes, and leaf nodes that store data to be signed. The signature path includes hash values required to validate a signature, covering sibling nodes of the signed leaves and other nodes along the path to the tree root, which contains the hash value of the entire tree structure and is used in signature verification. Each signature results in an update to the leaves of the tree. XMSS operations include key generation through multiple Merkle trees, each representing a message segment, and signing by applying OTS to chosen message blocks. Signatures are updated after each use to prevent exhaustion. When all leaves in an XMSS tree are used, a new tree is generated to restart the signing process and reduce vulnerability to repeat signature attacks.

As mentioned before, SPHINCS+ has been chosen as one of three digital signature algorithms by NIST. SPHINCS+ is a stateless, hash-based signature scheme that integrates features from XMSS, but it employs larger keys and signatures to eliminate the need for state management. This stateless structure allows each signature to be independently generated without the need to maintain a persistent state. The benefit is a simpler implementation that is less vulnerable to state manipulation attacks. In its operation, SPHINCS+ combines OTS, Few-Time Signatures (FTS), Merkle trees, and hypertrees to create a robust digital signature scheme suitable for general use. The OTS component ensures that each private key is used to generate only one signature, after which the key is considered expended. In contrast, FTS allows a private key to produce a limited number of signatures before it becomes compromised. Then, Merkle trees facilitate efficient integrity verification of large data sets and hypertrees, an extended form of Merkle trees, and provide a hierarchical hash structure for enhanced integrity verification in more complex or nested environments.

From SPHINCS+, NIST has proposed FIPS 205 “Stateless Hash-Based Digital Signature Algorithm (SLH-DSA)” [44]. This standard approves 12 out of the 36 parameter sets defined in SPHINCS+ version 3.1, specifically the simpler configurations that employ SHA2 or SHAKE [45] cryptographic functions. SLH-DSA is designed to secure and authenticate messages, relying on the computational difficulty of finding hash preimages and other hash function properties. The operation of SLH-DSA involves components like the FTS scheme, Forest of Random Subsets (FORS), Multiple-Time Signature (MTS), and the XMSS. It utilizes a combination of XMSS and OTS signatures within a Merkle hash tree structure, where each FORS key pair can sign a limited number of messages. The authentication information in an SLH-DSA signature includes a FORS signature and a hypertree signature, which authenticates the FORS public key using a sequence of XMSS signatures across multiple layers. The public key in SLH-DSA comprises the top XMSS layer’s public key and a public seed. This ensures domain separation among different SLH-DSA key pairs. The private key includes a secret seed for pseudo randomly generating all secret values for OTS and FORS keys and an additional secret key for message hash generation.

Finally, Picnic [46] is a digital signature scheme designed to secure against both classical and quantum computational attacks, utilizing Non-Interactive Zero-Knowledge (NIZK) proofs and relying on symmetric key primitives such as hash functions and block ciphers, particularly Low Multiplicative Complexity (LowMC). Unlike traditional public key cryptography, Picnic’s security is based on the integrity of its symmetric components. This approach uses NIZK to allow a prover to demonstrate possession of a secret key without revealing it or interacting in real-time, ensuring the confidentiality and authenticity of the information. LowMC supports the scheme by providing an efficient block cipher that optimizes for Multi-Party Computation (MPC), fully homomorphic encryption, and zero-knowledge proofs, making it suitable for resource-constrained environments like Internet of Things (IoT) devices. Despite its potential, Picnic faces challenges in implementation, particularly against side-channel attacks, and requires further analysis to match the extensively studied security of more traditional ciphers like AES. Advanced to the third phase of NIST selection, Picnic was not chosen primarily due to the low maturity of LowMC’s security evaluation compared to the established digital signature algorithms.

3.5. Isogeny-Based Quantum-Resistant Algorithms

Isogeny-Based Cryptography [47] represents a pioneering field in cryptographic research that utilizes the algebraic properties of super singular elliptic curves over finite fields to develop cryptographic systems. This emerging branch of cryptography is still under intensive research and development but has shown significant promise in being resistant to quantum attacks, positioning it as a potential cornerstone for future information security measures.

An isogeny is defined as a morphism between one elliptic curve to another, preserving the group structure of points, meaning the addition of points on the original curve corresponds to an equivalent operation on the target curve. The cryptographic strength of this approach lies in the conjectured difficulty of finding a specific isogeny between two given elliptic curves, a task that becomes computationally challenging as the complexity of the map increases. This foundational problem reinforces the encryption methods employed in isogeny-based cryptographic systems.

Among the key cryptographic systems derived from isogeny theory are the Super singular Isogeny Diffie–Hellman (SIDH), Super singular Isogeny Key Encapsulation (SIKE), and Commutative Super singular Isogeny Diffie–Hellman (CSIDH). SIDH is a key exchange protocol leveraging the mathematical properties of super singular elliptic curves and isogenies, offering a secure mechanism for key establishment that could be inherently resistant to quantum factorization algorithms. SIKE [48] extends this concept into a key encapsulation scheme, coupling the unique characteristics of super singular elliptic curves to generate and securely exchange cryptographic keys. CSIDH [49,50] builds on the principles of SIDH but introduces commutative properties of isogenies to enhance the efficiency and security of the key generation process. This protocol distinguishes itself by exploring these commutative properties, which not only facilitate more efficient key production but also bolster the system’s resistance to quantum attacks.

SIKE has demonstrated the ability to integrate seamlessly with conventional ECC, efficiently using optimized code for operations on these curves. This integration facilitates the creation of hybrid schemes that effectively merge classical and PQC principles, highlighting its potential in maintaining cryptographic security in the introduction of quantum computing. Compared to other encryption schemes and key encapsulation mechanisms, SIKE is distinguished by its very small public keys and significantly reduced ciphertext size, offering a compact solution in cryptographic applications. However, SIKE also presents several disadvantages, largely due to its relatively unexplored security landscape. For instance, SIKE’s reliance on finding isogenies between super singular elliptic curves has not been thoroughly investigated yet. In addition, SIKE exhibits slower encapsulation and decapsulation speeds compared to other proposed schemes. More importantly, the protocol requires the public disclosure of auxiliary torsion points, an operational necessity that potentially exposes additional information to attackers.

Despite being selected by NIST as an alternate candidate in the fourth round of its Post-Quantum Cryptography standardization process due to its promising potential and minimal key and ciphertext sizes, SIKE faced significant security challenges. On 5 August 2022, researchers Wouter Castryck and Thomas Decru detailed in [51] an effective attack exploiting the auxiliary torsion points disclosed by SIKE, which compromised the SIDH protocol within about an hour using basic computational resources. This attack utilized complex mathematical techniques and a 25-year-old theorem, fundamentally undermining confidence in SIKE’s security. Subsequent attempts to adjust the SIDH/SIKE framework to safeguard against such vulnerabilities would have led to unacceptable performance degradation and increased key sizes. As a result, on 21 September 2022, the SIKE team officially declared the scheme insecure to NIST, acknowledging that no variant of SIDH/SIKE could simultaneously maintain its performance parameters and ensure security, thus highlighting the critical challenges in developing isogeny-based cryptographic systems.

3.6. Braid Group-Based Quantum-Resistant Algorithms

Braid group cryptography presents a different approach in computer security, bringing the mathematical principles of braid theory—interlacing strands or threads—to develop advanced cryptographic systems once considered invulnerable to quantum computing attacks. The security foundation of this cryptography relies on the computational complexity of solving mathematical challenges such as the word problem in braid groups (Word Group Problem, WGP), the Conjugacy Subgroup Problem (CSP), the braid group isomorphism problem (Isomorphism Braid Problem, IBP), and the Complementary Subgroup Problem for Conjugacy (CSPC). These problems were previously considered exceedingly difficult to solve, even with the most advanced computers. However, recent research indicates that their complexity might be more manageable than initially expected.

In mathematical terms, a braid consists of a set of strands interlaced in a specific and orderly manner [52]. Each braid comprises a fixed number of strands, and the manner in which these strands intertwine defines the braid itself. Braid groups, also known as Artin groups, are non-commutative (non-abelian) groups composed of all possible braids that can be formed with a fixed number of strands. Elements of a braid group can be described as configurations of vertical or horizontal threads that do not intersect in a three-dimensional space, anchored at both ends to two parallel disks. Moreover, the threads move in one direction without backtracking, ensuring that any plane parallel to the disks cuts each thread exactly once. This complex structure underlies the potential for braid group cryptography to contribute significantly to the field.

Braid group cryptography was initially developed for secure public key encryption and digital signature applications. The process involves selecting a braid group to set up the cryptographic system, generating paired public and private keys, where the public key encrypts messages and the private key decrypts them. Messages are encoded into braids using a specific algorithm, and the encrypted braid is transmitted to the recipient who uses their private key to decrypt and recover the original message. Despite this innovative approach, some vulnerabilities have been exposed in almost all proposed cryptographic protocols based on braid groups. Notable among these are the Anshel–Anshel–Goldfeld (AAG) key exchange protocol [53], Diffie–Hellman adaptations for braid groups, and the Shpilrain–Zapata public key protocols [54], all of which utilize the mathematical challenges of braid conjugacy and the discrete logarithm problem within these groups. Further protocols also base their security on the conjugacy problem in braid groups, reflecting the diversity of attempts to apply braid theory to cryptographic security.

WalnutDSA [55] is a lightweight digital signature scheme designed for efficient operation in resource-constrained environments such as IoT devices and embedded systems. It distinguishes itself by the efficiency of its signature verification process, making it suitable for platforms with limited computational capabilities, including 8 and 16-bit systems. The cryptographic robustness of WalnutDSA derives from the difficulty of reversing the E-Multiplication function, a notable contrast to the conjugacy search problem from earlier braid group-based cryptographic systems. Notably, WalnutDSA is resistant to all types of attacks associated with the conjugacy search problem and does not require maintaining any state, thus allowing an unlimited number of signatures. The scheme operates by generating a public and private key pair, with the public key used openly for encrypting messages and the private key for decrypting received messages that were encrypted with the corresponding public key. Messages are encoded into a specific format such as SHA2-256 or SHA2-512 before being signed using the private key in conjunction with WalnutDSA’s signature function, E-Multiplication. This function utilizes a combination of operations in braid groups, matrices, and finite fields to produce a unique digital signature that verifies the authenticity and non-repudiation of the message.

Despite its initial promise and unique features, WalnutDSA faced significant challenges. It was the only braid group-based cryptosystem among the 82 proposals reviewed by NIST but did not advance to the second round due to a series of vulnerabilities identified during evaluation. These included factorization attacks that could forge a signature for any given message, and collision attacks that, despite being limited to specific messages, demonstrated potential for short forged signatures. A particularly effective attack described in [56] used a heuristic approach that bypassed the E-Multiplication altogether, allowing an adversary to compute an alternate secret key capable of producing valid signatures for any chosen message, leading to universal forgery. These security flaws highlight the inherent challenges in developing and securing braid group-based cryptographic systems and underscore the complexities of ensuring robust security in practical implementations.

3.7. Multivariate Quantum-Resistant Algorithms

Multivariate-based cryptography (MVC) refers to a class of public key cryptographic schemes that employ multivariate polynomials over a finite field. In these systems, a set of public multivariate polynomial functions are used to encrypt messages, transforming them into polynomial values, which the recipient can then decrypt by applying corresponding decryption functions. The core challenge and security of these schemes lie in the difficulty of solving systems of multivariate polynomial equations, recognized as an NP-complete problem, which makes the inversion of these functions without specific inputs complex and secure against both classical and quantum computational attacks.

However, multivariate encryption systems have faced challenges in terms of speed and public key sizes, similar to what occurred to RSA, making them more appropriate for digital signature systems where they can offer shorter signature sizes compared to other post-quantum candidates. Historical attempts to develop secure multivariate encryption systems have seen various failures. Notable examples include the Merkle–Hellman, which based its security on the knapsack problem and was eventually broken; the Hidden Field Equations (HFE) that experienced effective attacks against some of its variants; the Unbalanced Oil and Vinegar (UOV), which was compromised due to design weaknesses; and Rainbow, a more recent scheme that incorporates multiple layers of polynomial equations but has shown vulnerabilities to cryptanalytic attacks.

Despite these setbacks, there has been renewed interest in multivariate cryptography over the last decade due to its potential to withstand quantum attacks and its efficiency in generating smaller signatures. Among the nineteen signature schemes submitted to the NIST PQC standardization project, seven were multivariate schemes, with four advancing to the second round and one of them reaching the finalist stage. The four in the second round were Great Multivariate Short Signature (GeMSS), Lifted Unbalanced Oil and Vinegar (LUOV) [57], Multivariate Quadratic Digital Signature Scheme (MQDSS) [58], and Rainbow [59] as the last finalist. Nevertheless, Rainbow was eventually dismissed from the final selection due to significant security attacks that undermined its reliability.

Rainbow uses multiple layers of polynomial equations to encrypt and decrypt messages. Inspired by the Unbalanced Oil-Vinegar (UOV) scheme, Rainbow improves upon UOV’s efficiency and security by adding multiple layers, each increasing the complexity of the equations and, consequently, the security of the system. However, Rainbow is known for its notably slow key generation process and relatively large key sizes, which may not be suitable for all applications. Despite these drawbacks, Rainbow was chosen as a finalist in NIST’s PQC standardization process due to its interesting performance profile for applications requiring small signatures or quick verification. Nonetheless, significant vulnerabilities were exposed during the competition, leading to its exclusion from the final selection due to demonstrated security weaknesses.

GeMSS, on the other hand, is characterized by its large public key size, small signatures, quick verification, and slower signature process. Its security model incorporates the hash and sign approach, iterative Feistel–Patarin permutations adding randomness and nonlinearity, and the Hidden Field Equations variant (HFEv-) to enhance resistance against cryptographic attacks. Despite these advanced features, GEMSS has a notably larger public key, which poses challenges for implementation in low-resource devices. Similarly to Rainbow, GEMSS was also subjected to key recovery attacks during NIST’s standardization process. These attacks, introducing new MinRank instances, significantly compromised the scheme’s security by exposing its private key structure, leading to a loss of confidence in its robustness and its eventual exclusion from further consideration.

4. Discussion and Transition Process

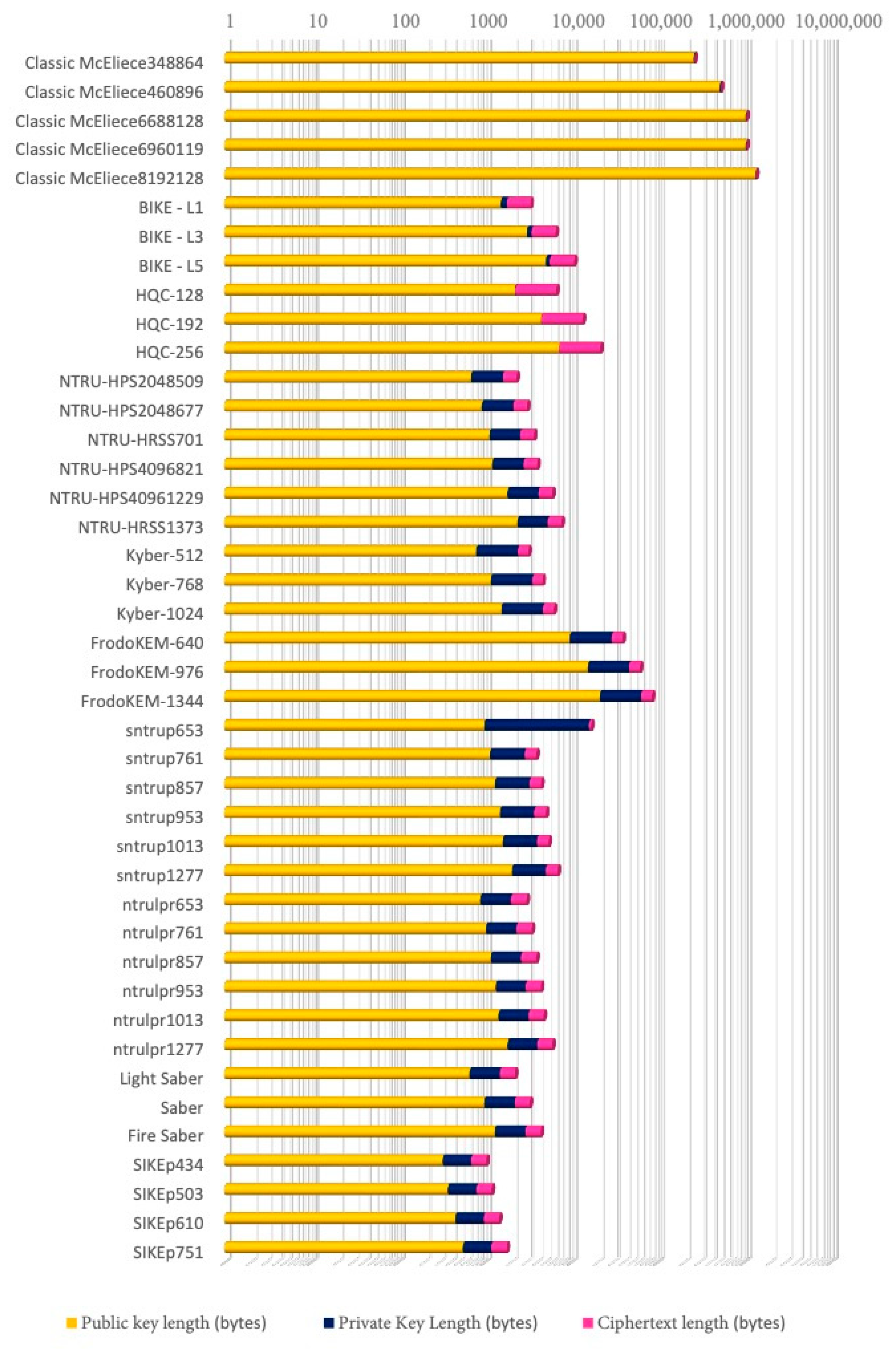
To start with, Figure 5 provides a comparative analysis of public key sizes in bytes for various KEM proposed in PQC. This is representative data, since stakeholders may need to balance security needs with resource constraints, particularly in environments where storage and bandwidth are limited. Thus, Figure 2 illustrates the diversity in storage requirements across different schemes. A detailed overview of the life-cycle of PQC algorithms during the NIST standardization process is summarized in

Table 2. Life-cycle of PQC algorithms * during NIST standardization process.

Algorithm	Phase 1	Phase 2	Phase 3	Phase 4	Standard
Classic McEliece	Yes	Yes	Yes	Yes	No
BIKE	Yes	Yes	Yes	Yes	No
HQC	Yes	Yes	Yes	Yes	No
NTRU	Yes	Yes	Yes	No	No
CRYSTALS–Kyber	Yes	Yes	Yes	-	Yes
FrodoKEM	Yes	Yes	Yes	No	No
SABER	Yes	Yes	Yes	No	No
CRYSTALS–Dilithium	Yes	Yes	Yes	-	Yes
Falcon	Yes	Yes	Yes	-	Yes
qTESLA	Yes	Yes	No	No	No
SPHINCS	Yes	Yes	Yes	-	Yes
Picnic	Yes	Yes	Yes	No	No
Rainbow	Yes	Yes	Yes	No	No
GeMSS	Yes	Yes	Yes	No	No
SIKE	Yes	Yes	Yes	Yes	No

* Only those that passed phase 2.

, showcasing the progression and current status of various algorithms through different phases. As mentioned before, BIKE (BIKE-1, BIKE-2, and BIKE-3) shows small public key size, demonstrating its high efficiency in terms of storage needs. In comparison, HQC (HQCs-128, HQCs-192, HQCs-256) also maintains relatively compact key sizes, with the size escalating with the security level denoted by the numerical suffix, indicative of bit strength. The NTRU family, including variants like NTRU-HRSS701 and several NTRU-HPS versions, shows larger key sizes, which reflect different security or efficiency trade-offs inherent to each variant. Similarly, Kyber variants (Kyber-512, Kyber-768, Kyber-1024) demonstrate an increase in key sizes with higher model numbers, remarking that enhanced security comes with larger keys. FrodoKEM variants are shown to have even larger key sizes, potentially impacting their usability in resource-constrained environments but offering stronger security assurances. At the top of the graph, classic McEliece variants have the largest key sizes among the schemes compared, which could challenge their practicality but may also signify robust security features.

Table 3. Key and signature lengths (bytes) for digital signatures. NIST security levels range from Level 1, Basic, suitable for low-risk environments, to Level 5, Maximum, designed for critical scenarios with potential severe consequences from data loss. Each level increases in security measures: Level 2 is Moderate, Level 3 Substantial, and Level 4 High.

Algorithm	Security Level (1–5)	Public Key Length (Bytes)	Private Key Length (Bytes)	Signature Length (Bytes)
Dilithium–2/ML–DSA–44	2	1312	2528	2420
Dilithium–3/ML–DSA–65	3	1952	4000	3293
Dilithium–5/ML–DSA–87	5	2592	4864	4595
FALCON-512	1	897	7553	666
FALCON-1024	5	1793	13,953	1280
qTESLA I	1	1280	2560	2416
qTESLA III	3	2048	4096	3840
SPHINCS+ −128s	1	32	64	7856
SPHINCS+ −128f	1	32	64	17,088
SPHINCS+ −192s	3	48	96	16,224
SPHINCS+ −192f	3	48	96	35,664
SPHINCS+ −256s	5	64	128	29,792
SPHINCS+ −256f	5	64	128	49,856
Picnic-L1-full	1	34	17	30,809
Picnic3-L1	1	34	17	12,359
Picnic-L3-full	3	48	24	68,493
Picnic3-L3	3	48	24	27,173
Picnic-L5-full	5	64	32	121,616
Picnic3-L5	5	64	32	46,282
Rainbow I	1/2	161,600	103,616	66
Rainbow III	3/4	882,080	626,016	164
Rainbow V	5	1,930,600	1,408,704	212
GeMSS128	1	352,168	16	33
GeMSS192	3	1,237,934	24	52
GeMSS256	5	3,040,659	32	72

includes a comparison of key and signature lengths for digital signature mechanisms. As expected, the increase in public key, private key, and signature sizes as the security level escalates reflects the strengthened cryptographic measures required for higher security demands. For instance, Dilithium 2, 3, and 5 display gradually larger public keys, private keys, and signatures as security levels rise from 2 to 5. Moreover, a comparison between different algorithms, even at the same security level, reveals significant variations in key and signature dimensions, emphasizing differences in cryptographic mechanisms and efficiency. As an example, at Level 1, FALCON-512 has a public key size of 897 bytes and a signature size of 666 bytes, which contrasts with qTESLA I, which has a public key size of 1280 bytes and a signature size of 2416 bytes. Additionally, SPHINCS+ presents notable variations in signature sizes, because of their cryptographic operations and intended applications. Particularly, SPHINCS+ versions, even at lower security levels, show significantly larger signature sizes, likely due to their stateless hash-based signature methodology. As a final note, specialized configurations are evident in algorithms like GeMSS, which features really large public key sizes compared to other algorithms, only being useful in scenarios where large key sizes are not a limiting factor.

Although algorithms such as SIKE and Rainbow have been broken and are no longer candidates for post-quantum cryptographic standardization, their initial promise and subsequent compromise provide valuable insights into the challenges of designing quantum-resistant cryptographic schemes. For example, Rainbow, a multivariate-based signature scheme, was considered a strong candidate due to its efficiency in specific use cases, but its vulnerabilities were exposed through cryptanalysis. Similarly, SIKE, an isogeny-based KEM, was eliminated following an efficient key-recovery attack in 2022.

Despite their exclusion from the final stages of the NIST competition, the lessons learned from their vulnerabilities offer crucial guidance for future cryptographic research. By understanding why these algorithms failed, we can identify potential weaknesses in other quantum-resistant schemes and design stronger alternatives. Therefore, while SIKE and Rainbow are no longer viable for practical deployment, their inclusion in this survey provides historical context and contributes to a broader understanding of the PQC landscape.

To address the challenge of PQC adoption, we consider that there are two key points to be discussed, starting with the phase-in strategy. Before any actual deployment, it is important to assess the existing cryptographic setting of the organization. This involves identifying the cryptographic systems currently in use, understanding their vulnerabilities, and recognizing the potential quantum threats. Then, organizations should evaluate the sensitivity of the data they protect and determine the urgency of migration to PQC, always in accordance with the corresponding regulations such as the General Data Protection Regulation (GDPR), California Consumer Privacy Act (CCPA), etc. The output of this stage should result in a comprehensive plan that outlines priorities for migration, considering factors like data sensitivity, system complexity, and available resources. According to [60], a detailed risk assessment is critical in identifying and prioritizing cryptographic assets for migration to PQC. In addition, the transition to PQC will require that all stakeholders understand the consequences and the need of PQC via education and training [61].

To allow for a gradual implementation and even pilot testing, a recommended option is the use of hybrid cryptography. Hybrid cryptographic systems combine traditional cryptographic techniques with quantum-resistant algorithms, ensuring security against both classical and quantum threats and backward compatibility. A hybrid approach involves using scheme combiners, where combined schemes operate in parallel, ensuring key generation speed is limited by the slower scheme [62]. NIST and the European Network and Information Security Agency (ENISA), as well as other national security agencies, emphasize the necessity of hybridization for future cryptographic security, deploying PQC as an additional layer to classical cryptography, with keys from both schemes combined to enhance encryption [63], for instance, combining Elliptic-Curve Diffie–Hellman (ECDH) with the Kyber post-quantum KEM scheme [64] or the incorporation of QKD PQC in the Transport Layer Security (TLS) protocol [65]. The Internet Engineering Task Force (IETF) has also started defining hybrid approaches in various protocols [66], emphasizing the importance of this strategy in transitioning to quantum-safe cryptography.

Second, the security implications during the transition process must be considered. In this period, hybrid systems might introduce new vulnerabilities. Attackers could potentially exploit weaknesses in the integration of these systems. For example, there is potential for downgrade attacks in hybrid cryptographic approaches where an adversary forces the system to use the less secure classical cryptographic methods [60]. System performance could also be affected during this process. PQC algorithms usually require more computational resources, which could be unaffordable in scenarios such as IoT [67,68]. As in any technology transition, backward compatibility and interoperability should be guaranteed. This involves maintaining seamless communication between systems using classical cryptography and those using PQC. Finally, regulation will evolve and organizations will have to adapt to comply with the forthcoming PQC-related security standards and recommendations.

Last, because of the novelty and to assure success in the PQC transition in the long-term, monitoring and maintenance activities should be part of the organization’s routines. Continuous monitoring is critical in detecting vulnerabilities introduced by evolving quantum threats. Specifically, this includes proactive surveillance of cryptographic implementations to identify emerging risks promptly, before they can be exploited, thereby ensuring systems remain resilient. It is important to note that the field of quantum computing is progressing quickly, and what we consider secure today may not be secure tomorrow. New vulnerabilities could be discovered as quantum capabilities expand. Additionally, ongoing maintenance involves updating cryptographic solutions to align with newly established standards, incorporating patches, and adopting more secure algorithms as they are developed. This process guarantees that cryptographic practices remain robust, especially in dynamic environments where quantum advancements may rapidly shift the threat landscape. The necessity of continuous monitoring and maintenance in cryptographic systems can be exemplified through the historical evolution of widely used standards like RSA and SHA. Over time, advances in computational power have necessitated periodic increases in RSA key lengths to maintain adequate security levels, with current recommendations advocating for key sizes of 2048 bits or higher, as opposed to the original 512-bit keys. Similarly, the transition from SHA-1 to SHA-256 was driven by vulnerabilities identified through ongoing cryptanalysis. These cases underscore the critical importance of monitoring cryptographic implementations and updating them as new vulnerabilities are discovered. By regularly assessing and adjusting cryptographic standards, organizations can proactively address emerging threats and ensure the long-term resilience of their security infrastructure.

5. Research Agenda

The rapid advancements in quantum computing present a pressing need to explore PQC solutions. In previous sections, we have provided a foundational analysis of promising PQC algorithms. At this point, there remain several areas where further research is crucial to ensure the effective implementation and long-term security of these cryptographic systems. The following research directions are proposed to guide future work in this evolving field.

5.1. Hybrid Cryptographic Systems

As organizations transition to quantum-resistant systems, hybrid cryptographic solutions, which combine traditional and post-quantum algorithms, have emerged as a practical strategy. Future research should focus on optimizing the integration of hybrid systems to maintain performance and achieving robust security against both classical and quantum threats. Specifically, studies are needed to evaluate how these systems perform in resource-constrained environments, such as IoT devices and embedded systems, where computational resources and energy efficiency are critical.

5.2. Performance and Scalability Analysis

The implementation of PQC algorithms introduces potential trade-offs in terms of computational efficiency, bandwidth, and latency. Future studies should focus on benchmarking the performance of PQC algorithms in diverse real-world scenarios, paying special attention to scalability for large-scale deployments. Establishing standardized metrics and performance benchmarks will be essential to guide organizations in selecting suitable algorithms based on their specific operational needs and constraints.

5.3. Security Assessment and Long-Term Viability

The security landscape for PQC remains uncertain as new quantum and classical attacks may emerge. Ongoing research is needed to assess the resilience of current PQC algorithms against both known and unknown threats. This includes heuristic-based evaluations and stress-testing of algorithms to identify potential vulnerabilities that may arise over time. Ensuring the long-term viability of these algorithms requires a dynamic approach, where continuous monitoring and updates are integral to maintaining cryptographic security.

5.4. Transition Strategies and Implementation Guidelines

The transition from classical cryptographic systems to quantum-resistant alternatives is a complex process that demands careful planning and phased implementation. In Section 4, we provide some preliminary guidelines, but further research is needed to develop comprehensive frameworks that guide organizations in migrating to PQC, keeping backward compatibility and minimal disruption to existing systems. Additionally, studies should investigate the impact of emerging regulatory requirements on the adoption of PQC, particularly in industries where data protection is critical.

6. Conclusions

Cryptographic technologies are advancing to face the challenges of quantum computing. Particularly, there is a strong interest in post quantum cryptography (PQC) and the transition process from classical cryptography to PQC. The National Institute of Standards and Technology (NIST) has played a fundamental role in this topic, evaluating and validating a variety of quantum-resistant cryptographic algorithms during the last years. In this work, we provide a unified, comprehensive understanding of the various algorithmic approaches, specifically, lattice, code, multivariate, braid, and isogeny-based cryptography. We see that each method offers unique strengths and, at the same time, presents specific challenges. The selection of algorithms such as CRYSTALS–Kyber, CRYSTALS–Dilithium, Falcon, and SPHINCS+ for standardization highlights their potential in establishing the backbone of future security systems. With this work, we address the existing literature gap by offering a comprehensive review of the most prominent PQC algorithms, focusing on their strengths, vulnerabilities, and implementation challenges, contextualizing their theoretical foundations and practical applications. In addition, we have explored the transition process, of interest for stakeholders navigating the path to post-quantum cryptographic solutions. The transition to PQC will be characterized by a strategic phase-in approach, emphasizing the hybridization of classical and quantum-resistant algorithms to ensure seamless integration and backward compatibility, as we have discussed. This dual-layered security strategy is essential for current systems to remain functional while gradually adopting quantum-resistant features. Nevertheless, the continuous discovery of vulnerabilities and the dynamic nature of quantum and classical threats will require an ongoing effort from all stakeholders in research, standardization, and implementation.