A Novel Two-Stage Hybrid Model Optimization with FS-FCRBM-GWDO for Accurate and Stable STLF
Abstract
1. Introduction
- Forecasting Stage: Utilizes FCRBM and deep learning techniques to accurately predict electrical energy consumption. The focus here is on capturing the random and complex patterns in load demand.
- Optimization Stage: Employs the GWDO algorithm to optimize the energy management process based on the predictions from the first stage. This stage aims to reduce costs, manage demand surges, and balance electricity expenses with customer convenience. During the training process, the model uses the Rectified Linear Unit (ReLU) as the loss function to ensure precise and stable forecasting outcomes.
- Prediction Accuracy and Stability: focusing on the model’s ability to provide consistent and accurate predictions of electrical energy consumption.
- Energy Management Efficiency: addressing the optimization of energy use, cost reduction, and demand surge management to enhance power system stability.
- Time-Shiftable Appliances: devices whose operation can be scheduled to non-peak times without affecting user comfort.
- Power-Shiftable Appliances: devices that can operate at different power levels based on availability and demand.
- Critical Appliances: essential devices that require a continuous power supply and cannot be easily rescheduled.
2. Preliminaries
2.1. Single and Combined Models for STLF
2.2. Existing ELM Strategies
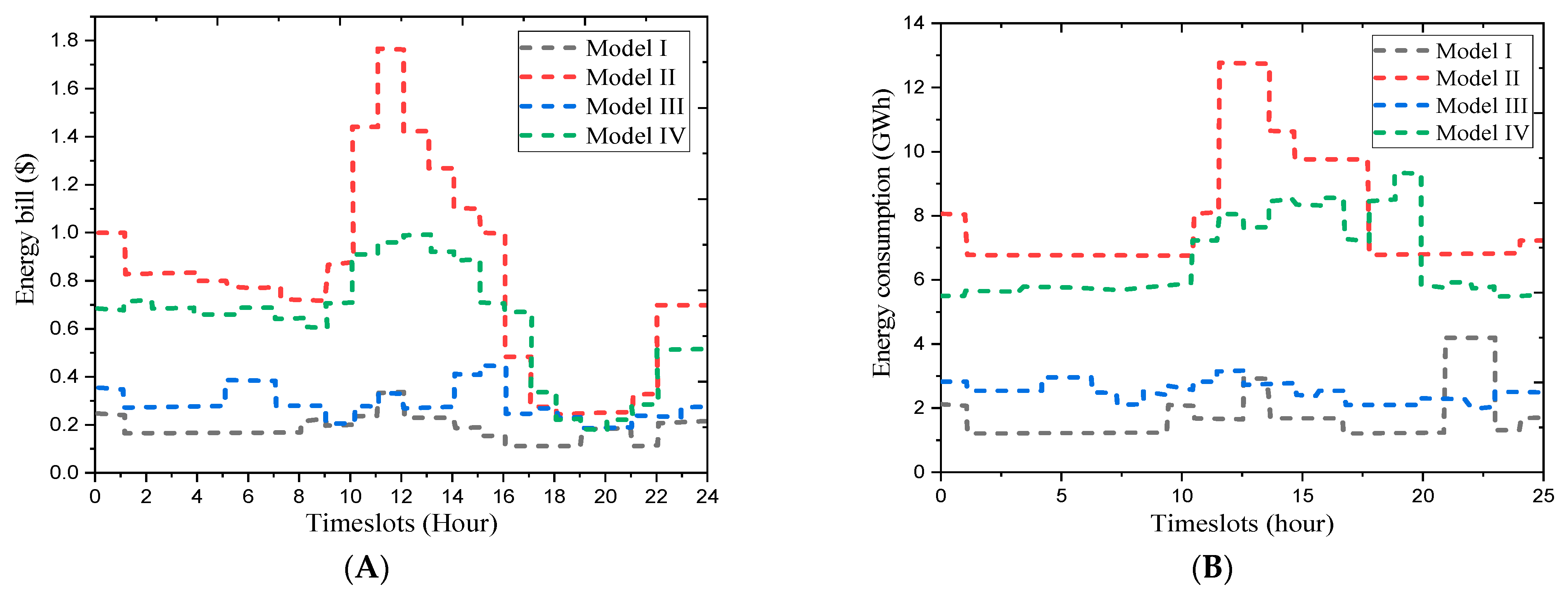
- Mode I: Consumers prioritize minimizing their electricity bill, even if it results in higher user discomfort. The weights are set to (γ1 = 1, γ2 = 0, γ3 = 0), aligning the optimization with the goal of cost reduction.
- Mode II: Consumers prioritize comfort over lower electricity costs. To accommodate this, the EMC adjusts the weights to (γ1 = 0, γ2 = 0, γ3 = 1), focusing on maximizing user comfort.
- Mode III: The priority is reducing the PAR, benefiting both consumers and electricity utility companies (EUCs). A lower PAR leads to a smoother demand curve, allowing EUCs to reduce the number of peak power plants in operation, ultimately lowering the energy cost per unit for consumers. The weights are set to (γ1 = 0, γ2 = 1, γ3 = 0) to achieve this goal.
- Mode IV: Consumers aim to balance all three objectives of minimizing the electricity bill, reducing the PAR, and achieving a satisfactory tradeoff between cost and comfort. The EMC assigns equal weights (γ1 = 1/3, γ2 = 1/3, γ3 = 1/3) to each objective, ensuring a balanced approach.
3. Proposed Methodologies
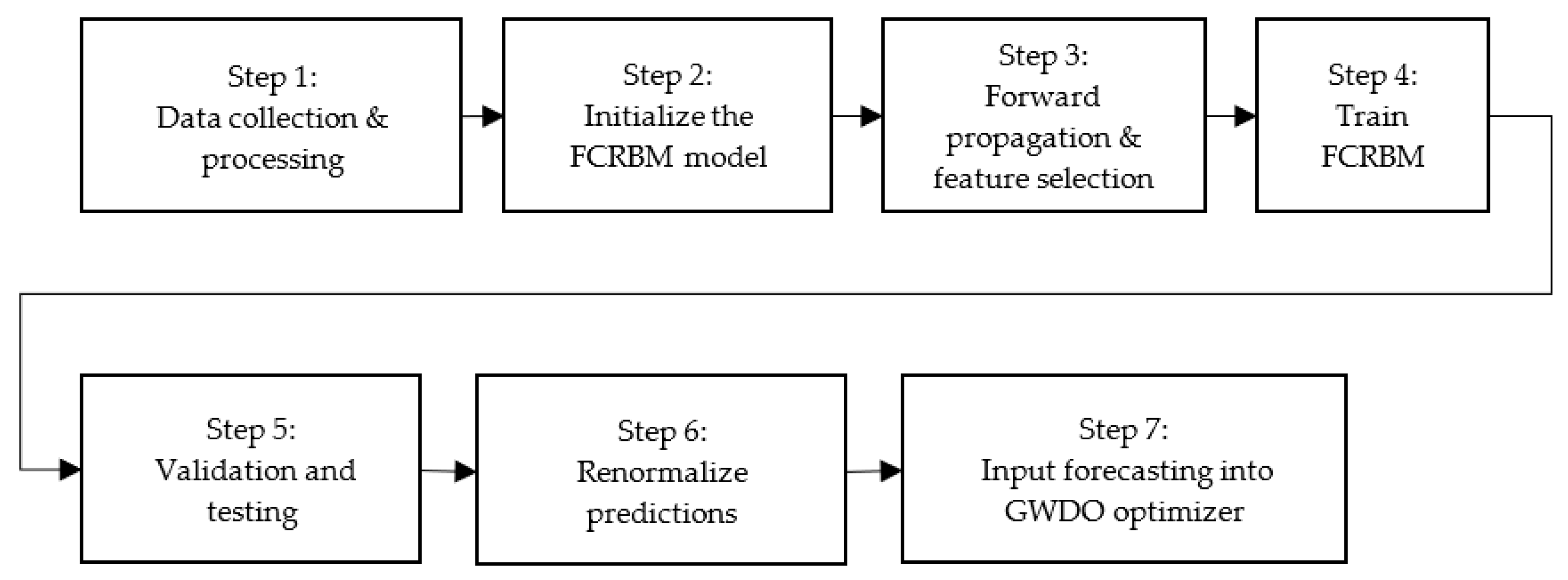
3.1. Electrical Load Forecasting with FCRBM Forecaster
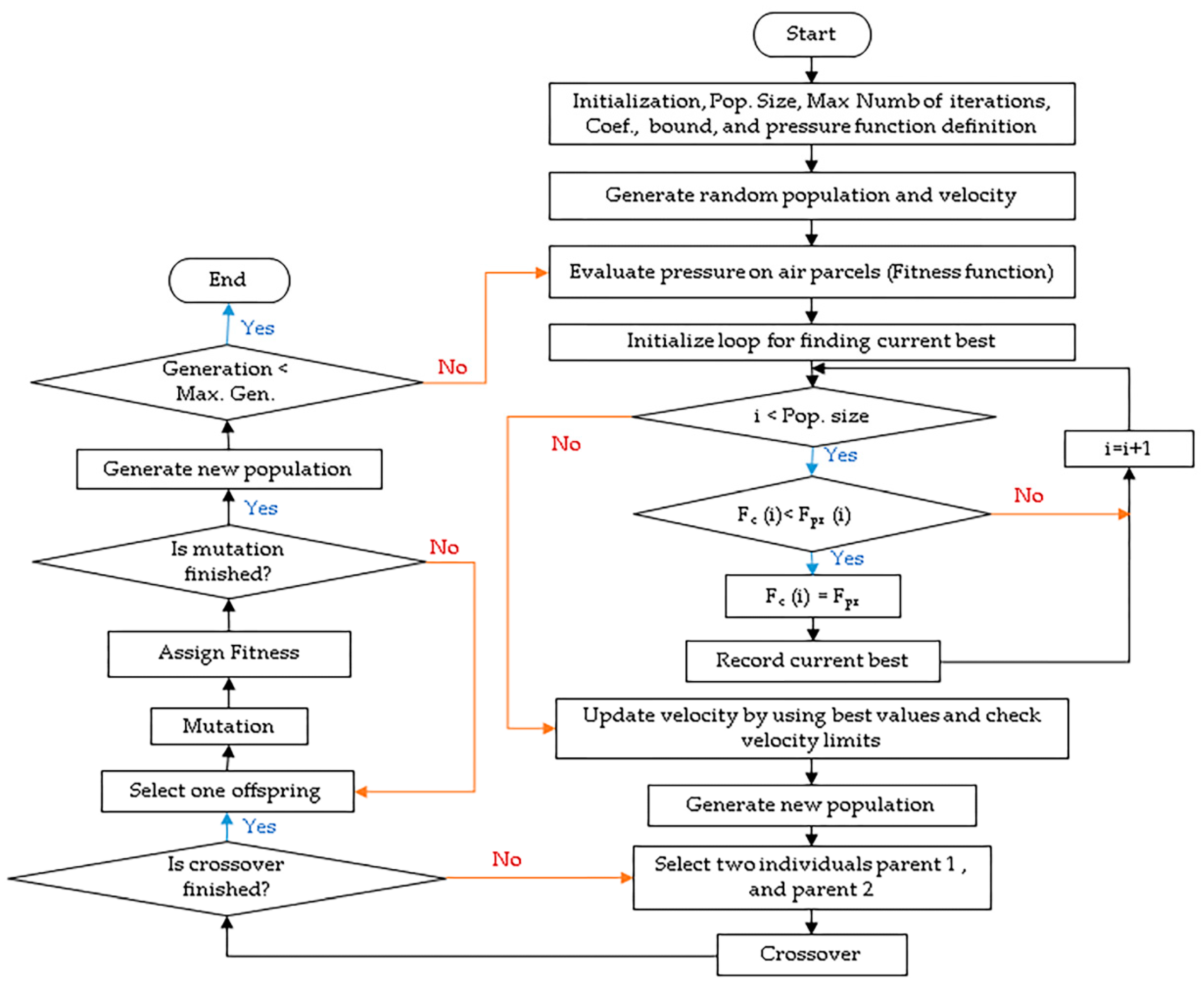
3.2. GWDO-Based Optimizer Model
4. Hybrid Framework Based on FS, FCRBM, and GWDO
Performance Metrics for Accuracy Evaluation
5. Experimental Results and Discussion
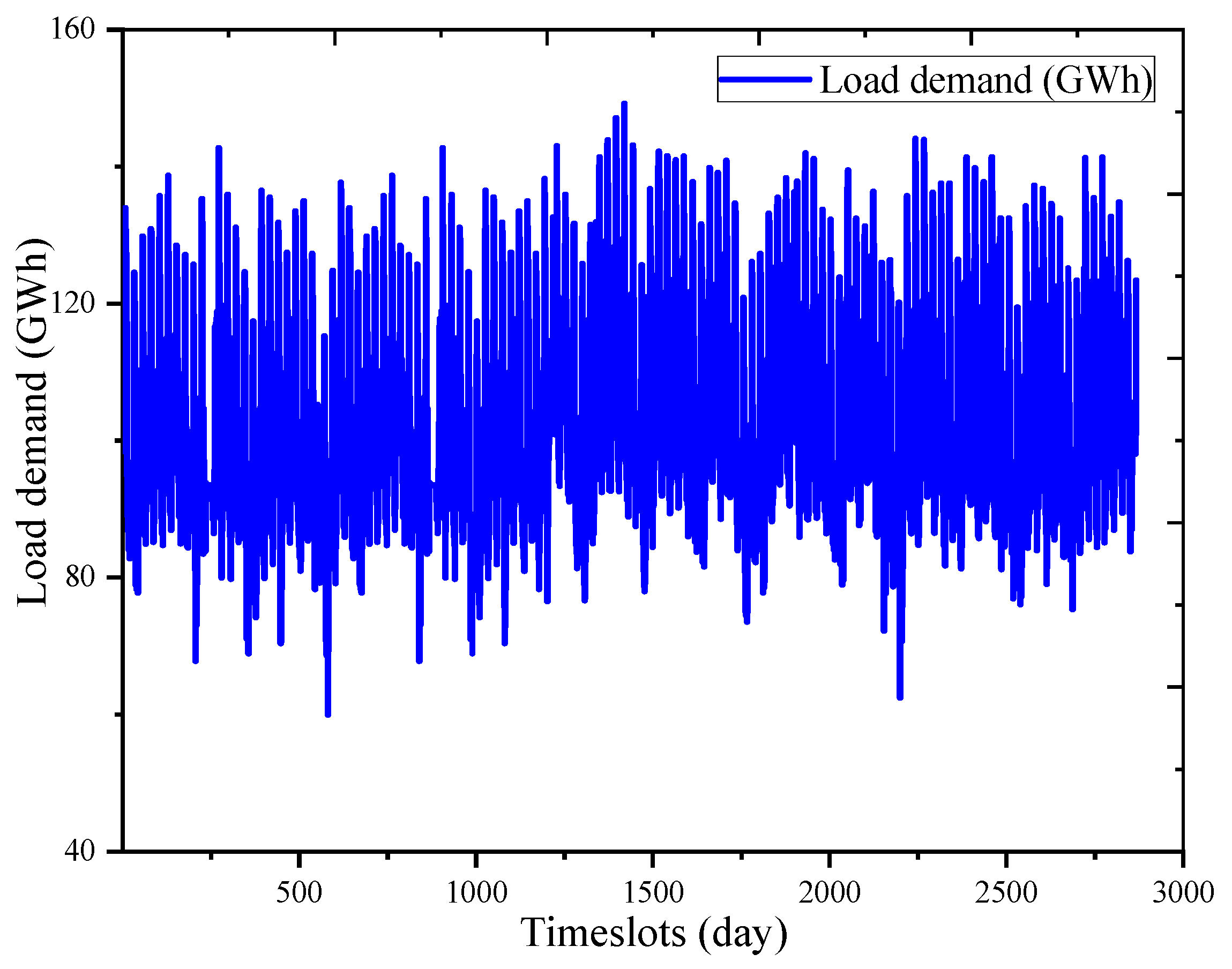
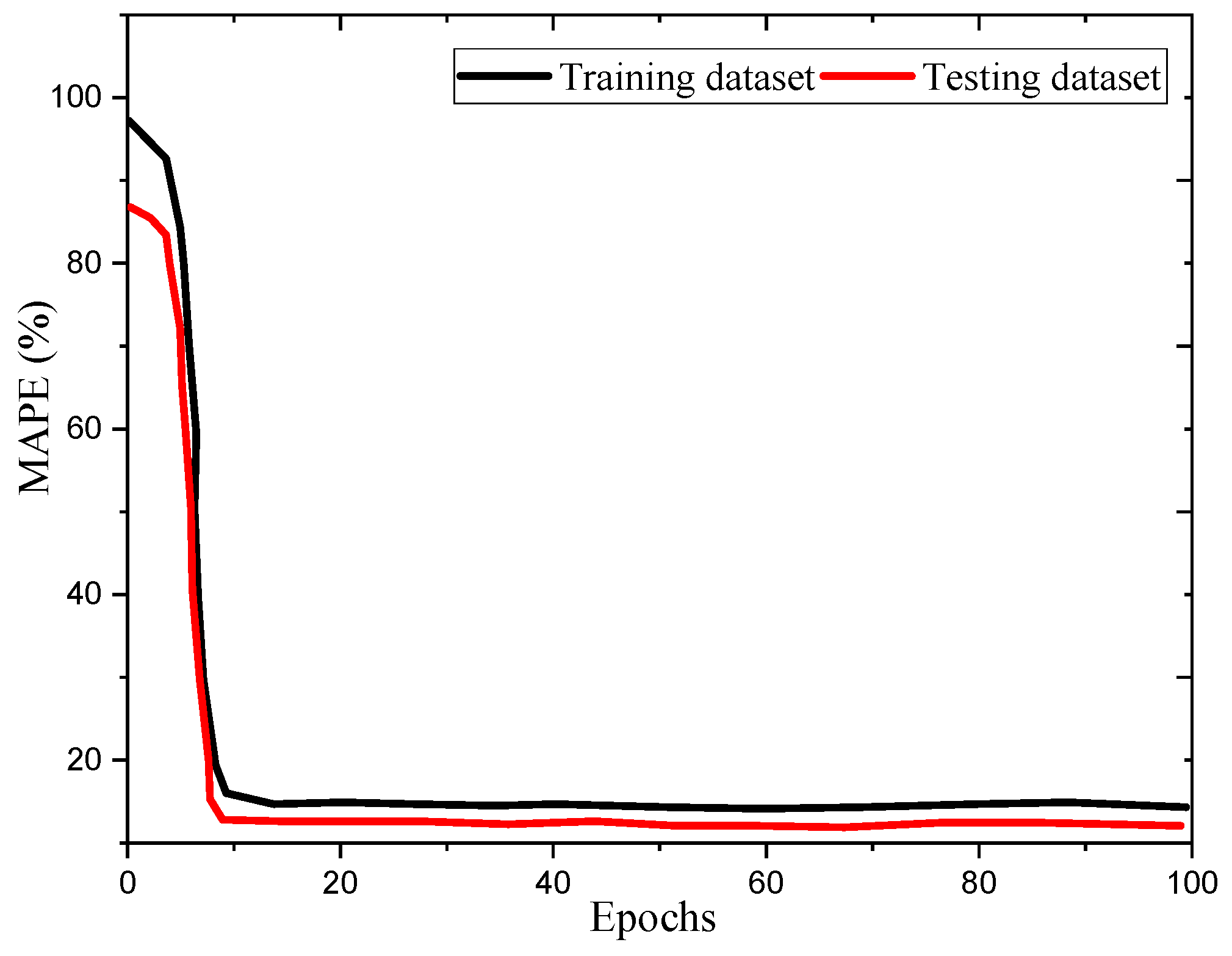
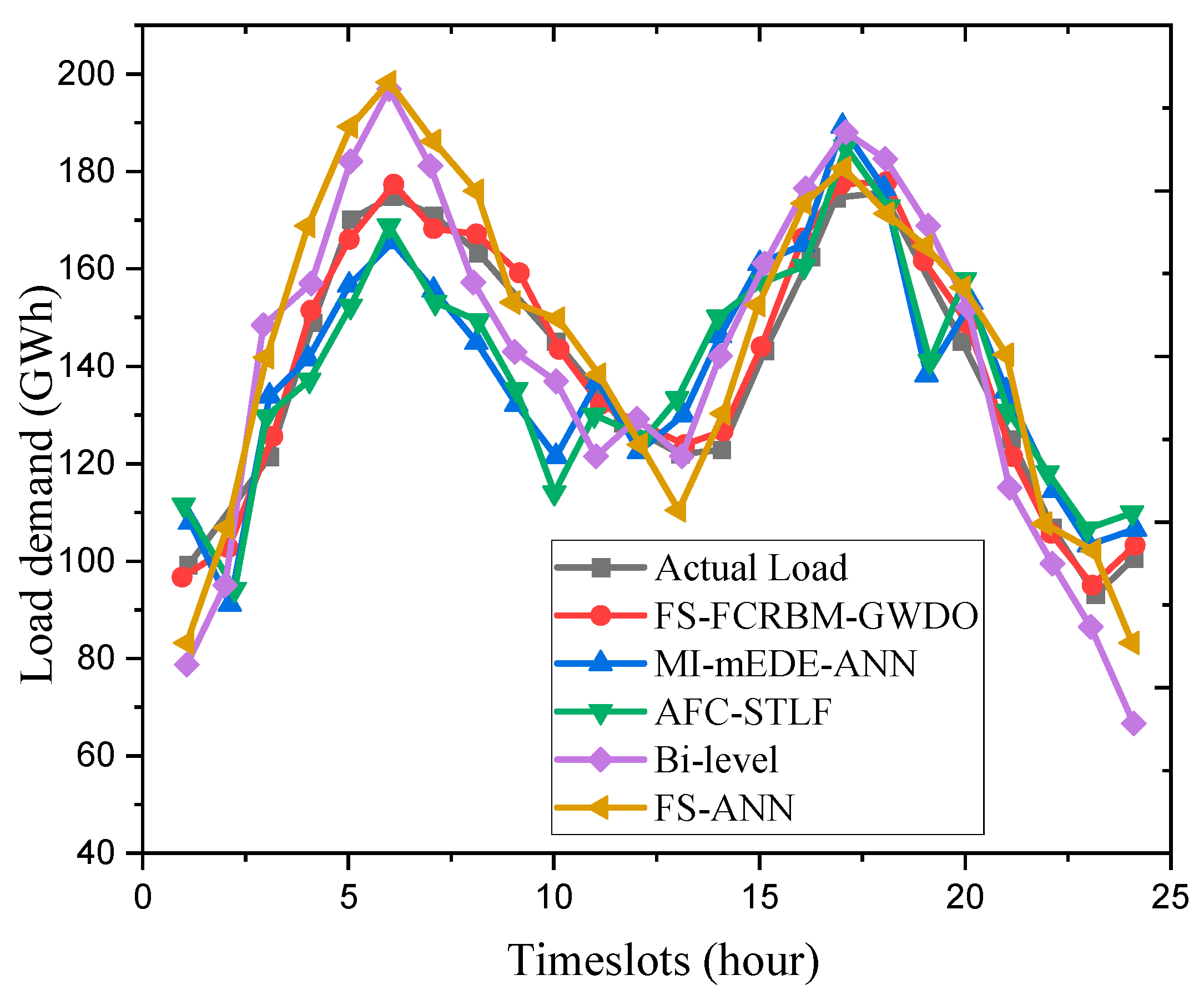
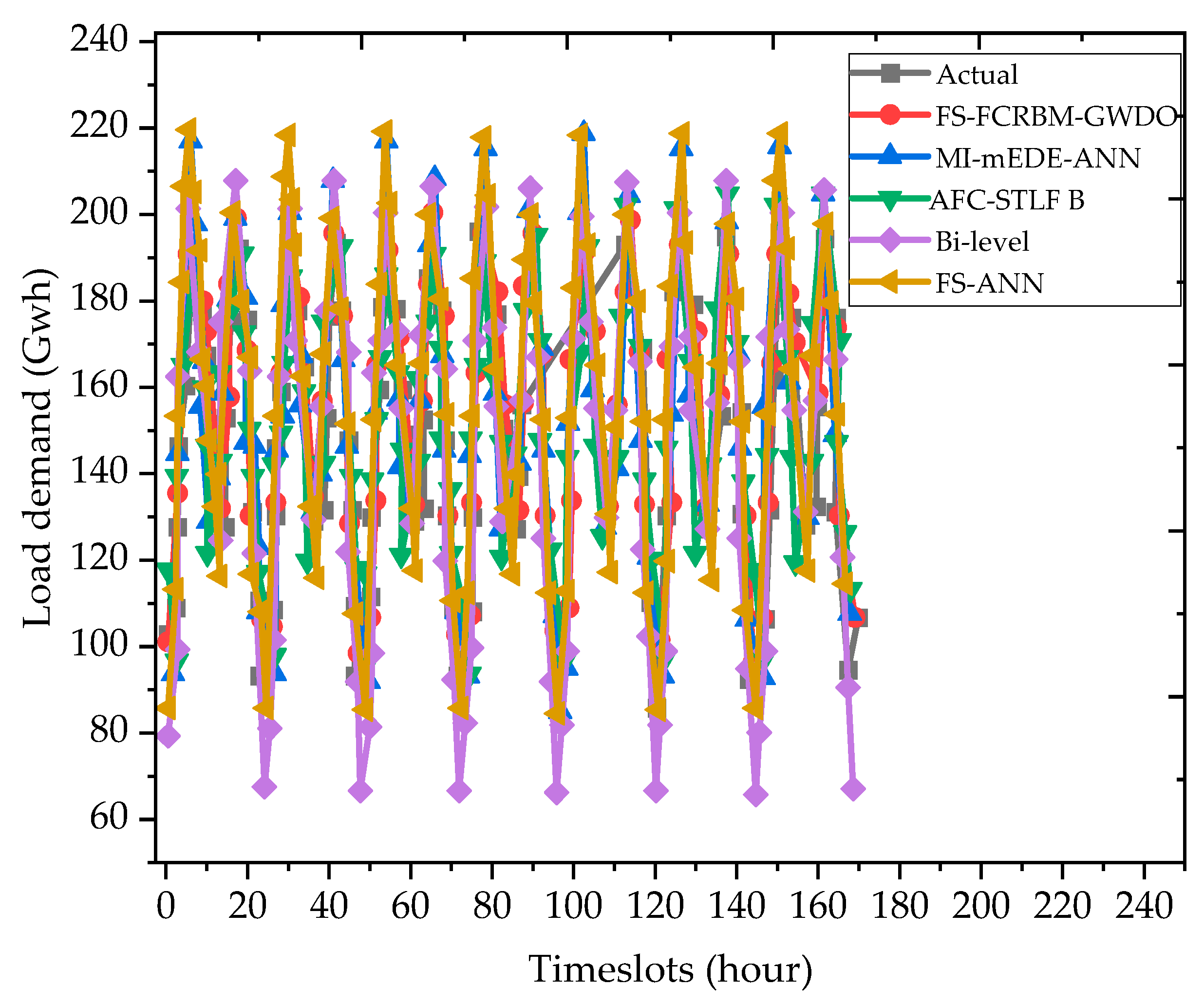
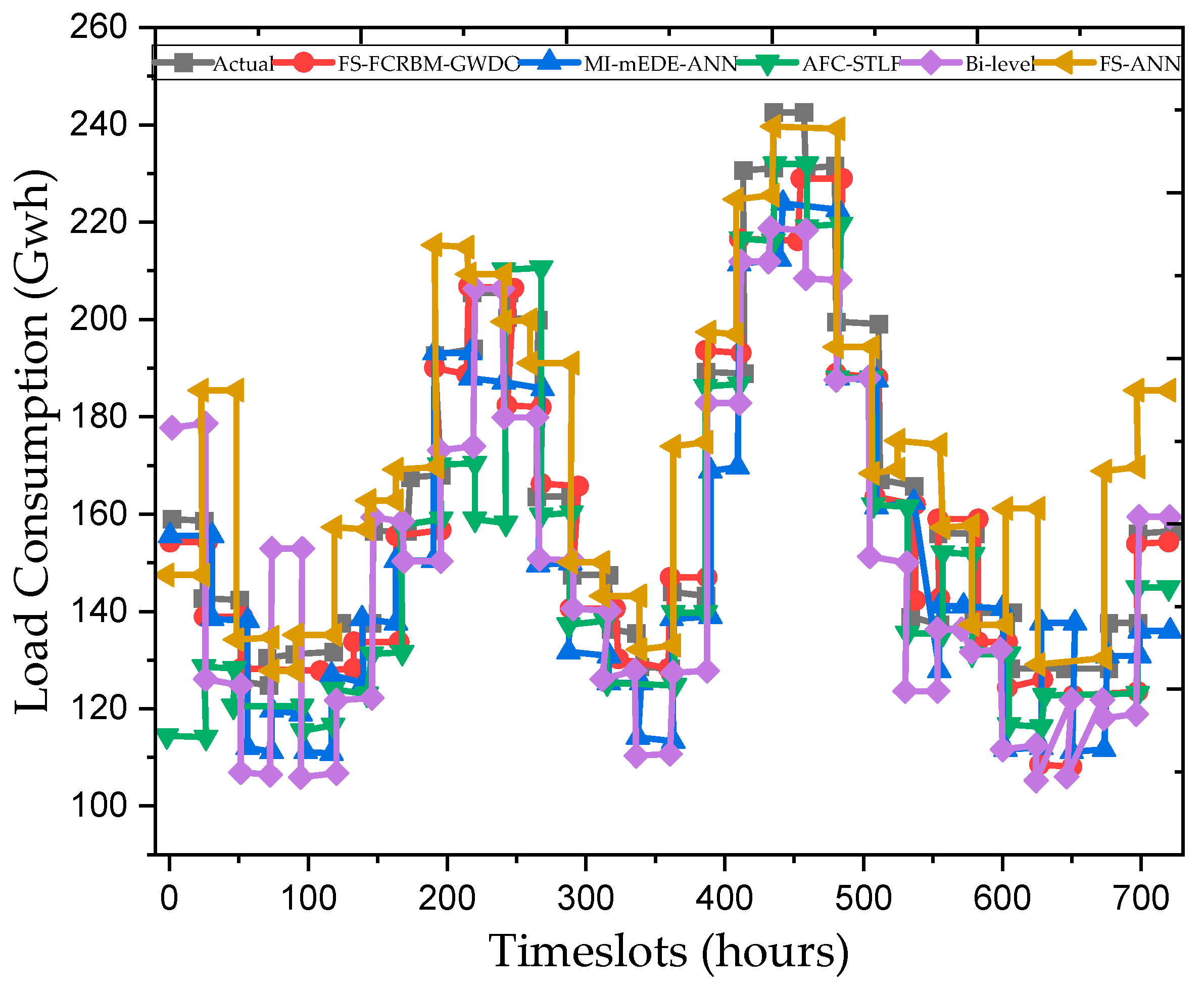
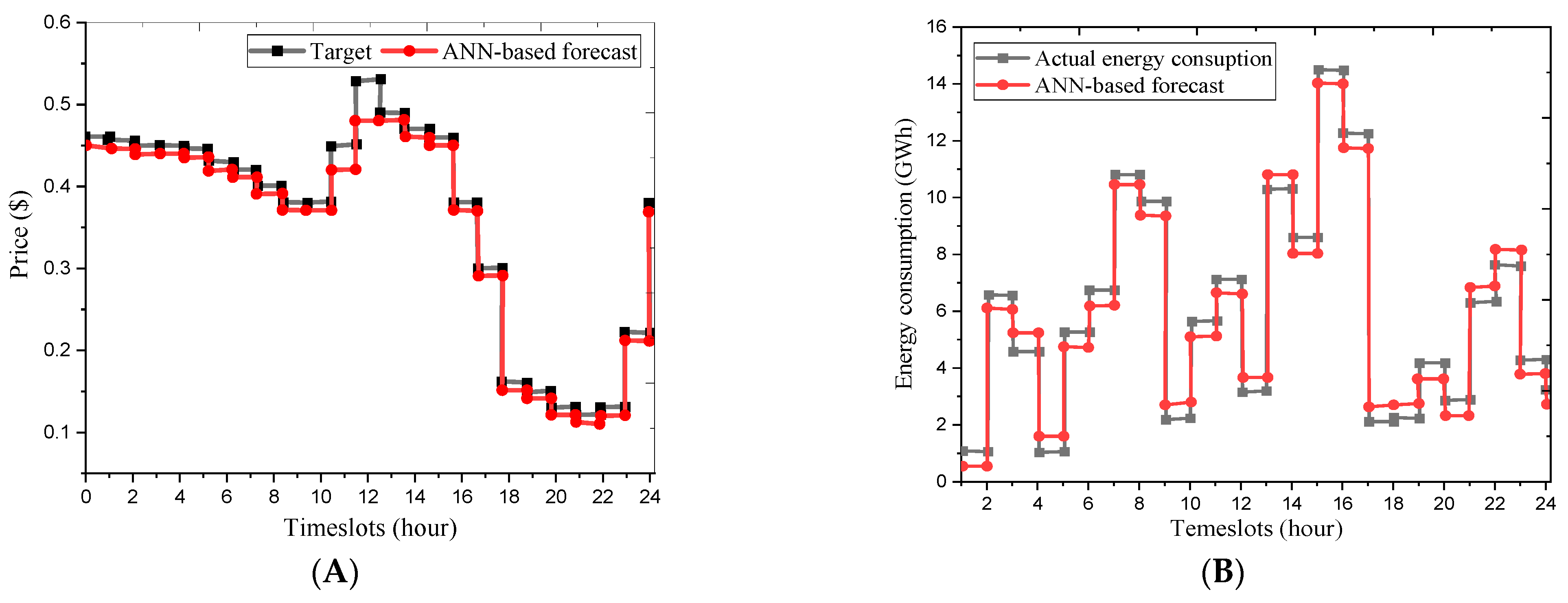
5.1. Stage One: Electrical Load Forecasting
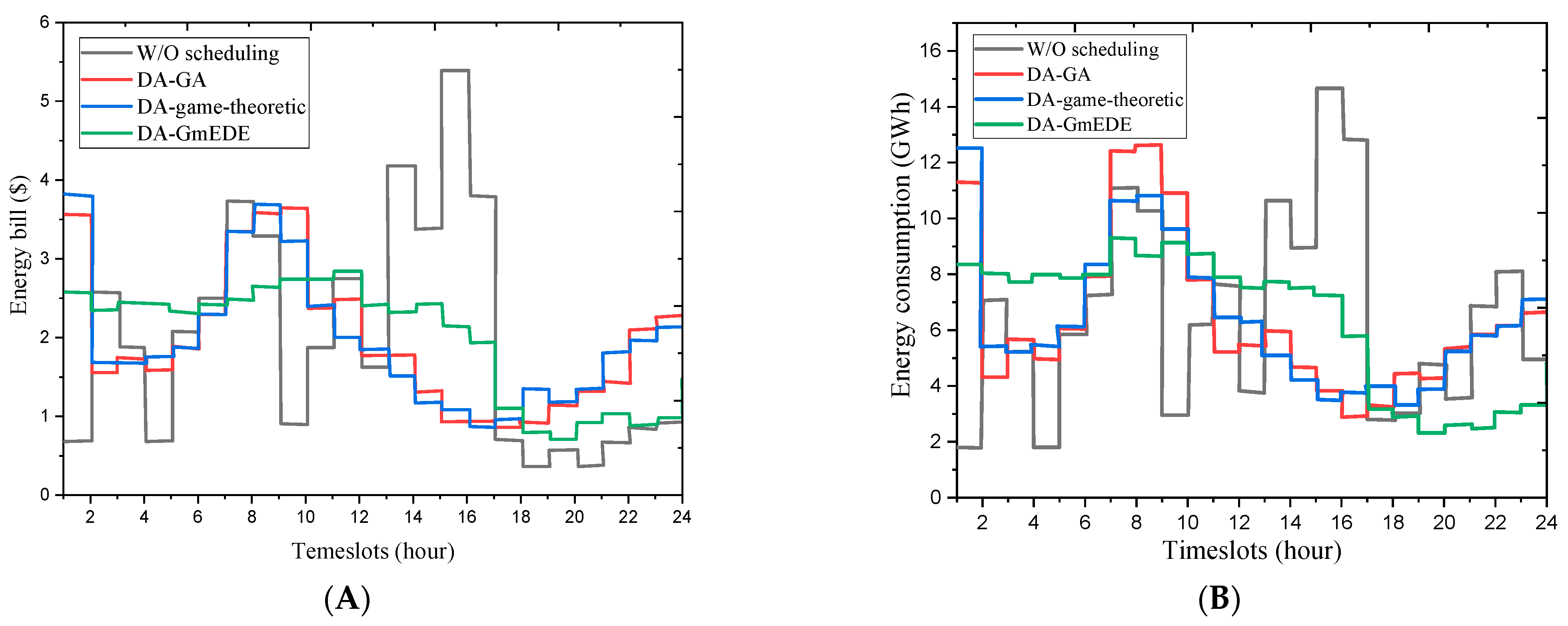
5.2. Energy Management Based on the DA-GmEDE Framework
5.3. Energy Consumption and Corresponding Electricity Bills across Four Different Modes of Operation
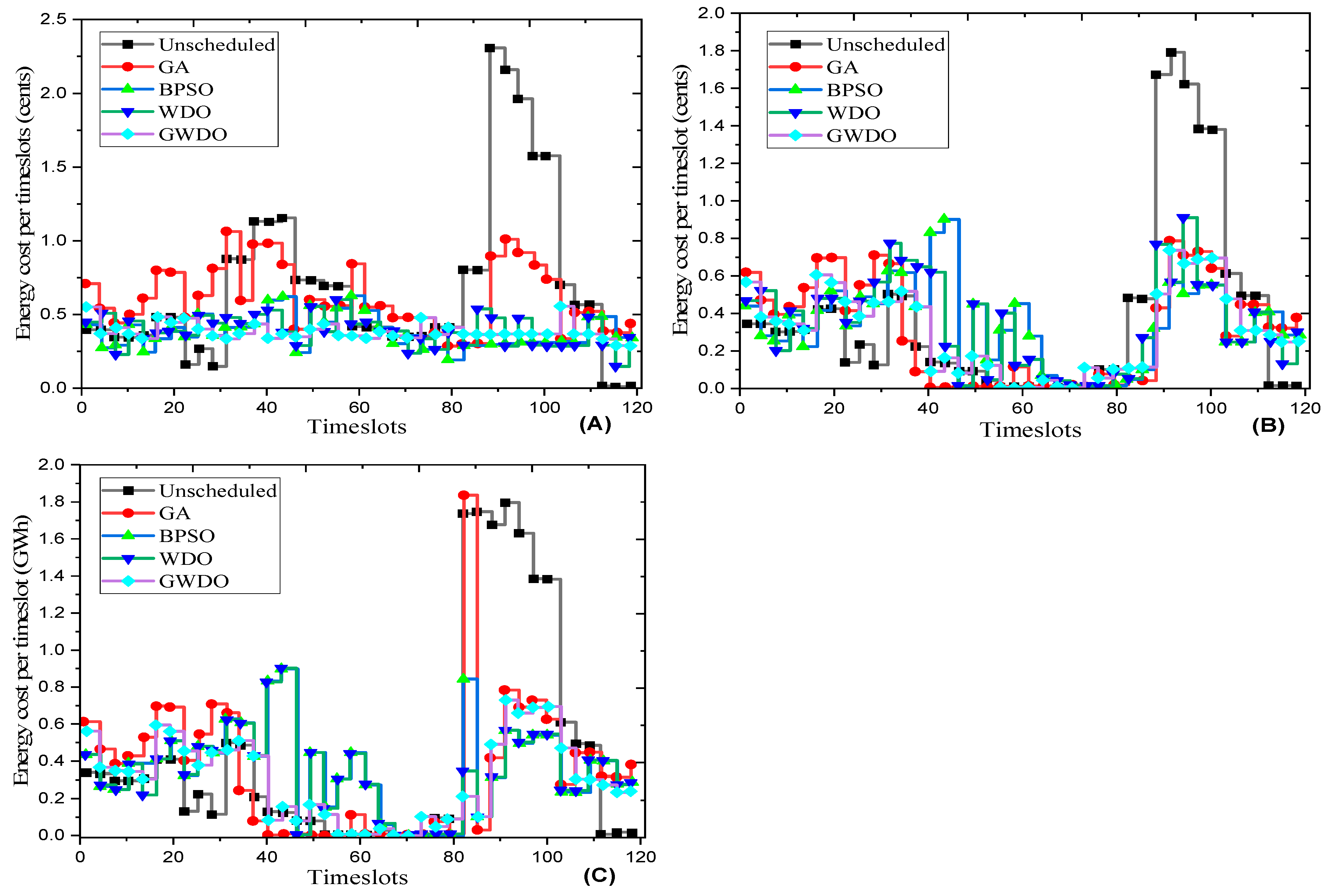
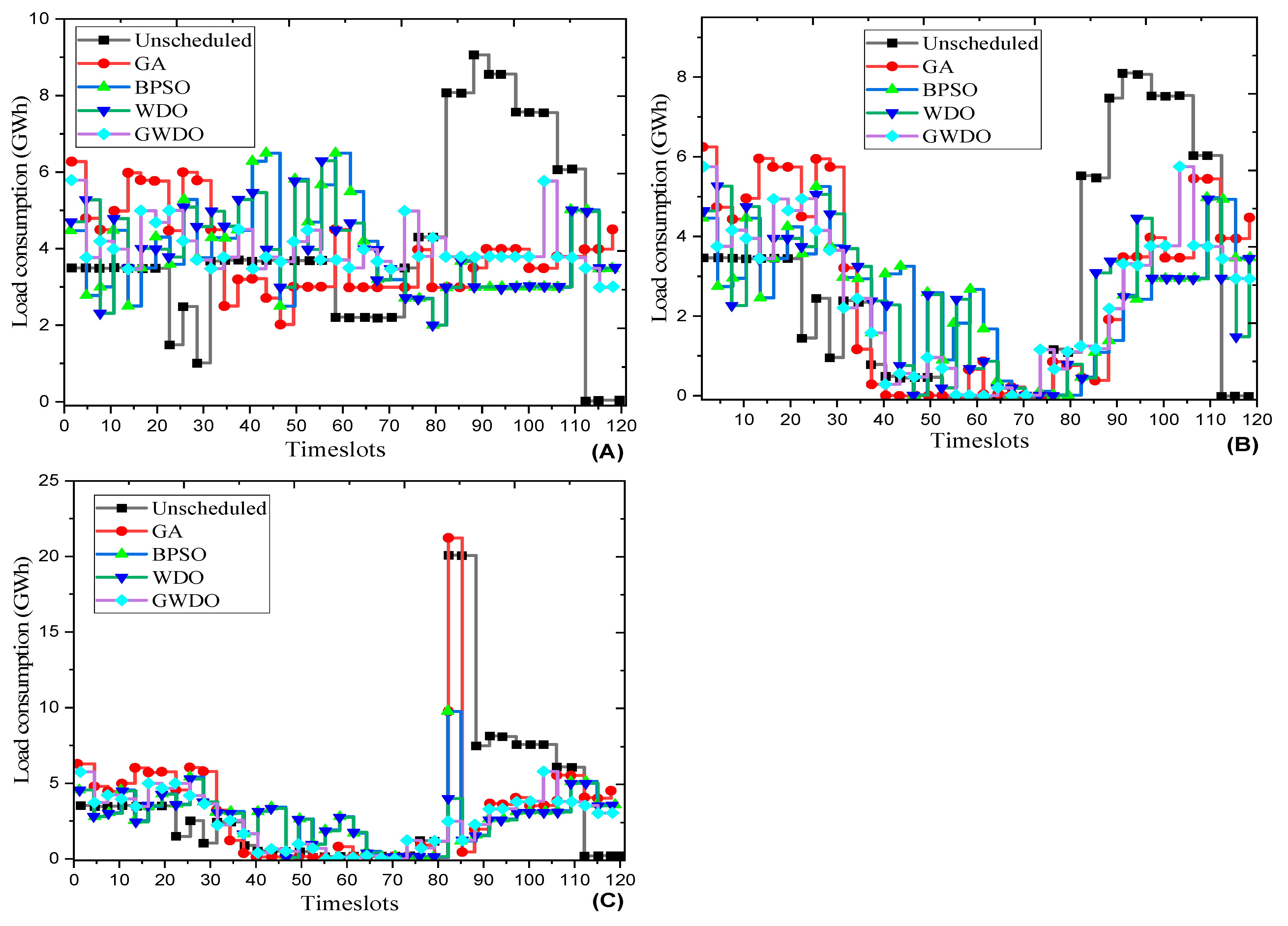
5.4. Energy Consumption of Residential Buildings within the Scheduling Time Horizon
5.5. Electricity Bill per Hour for a Home in a Residential Building within the Scheduling Time Horizon
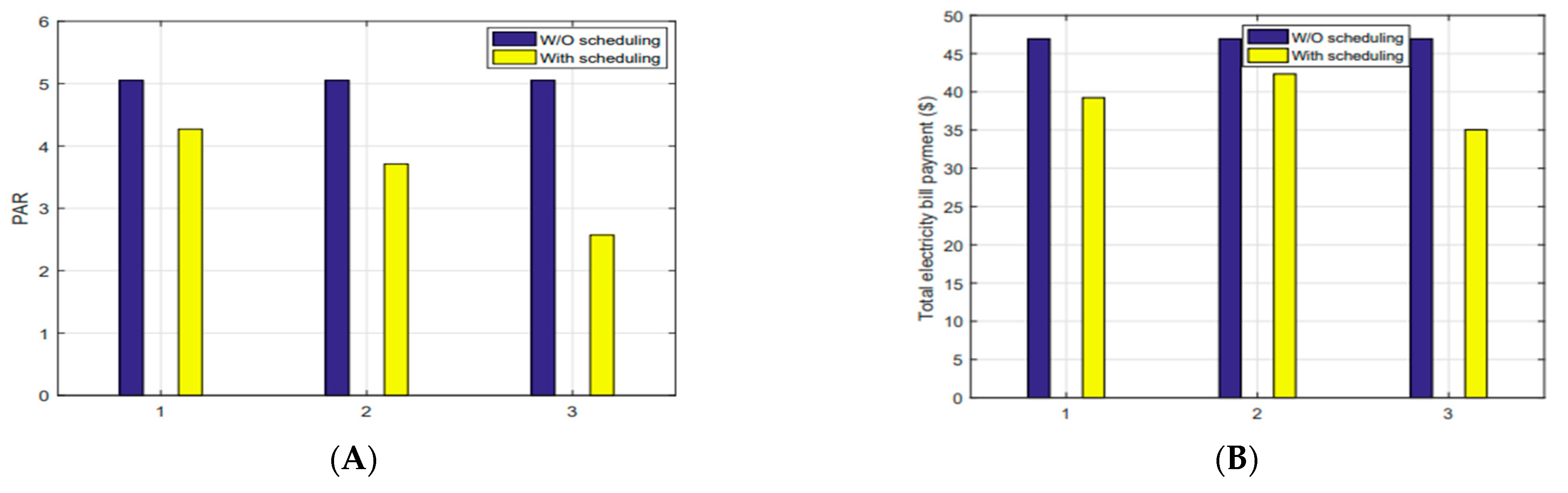
6. Performance Tradeoff Analysis
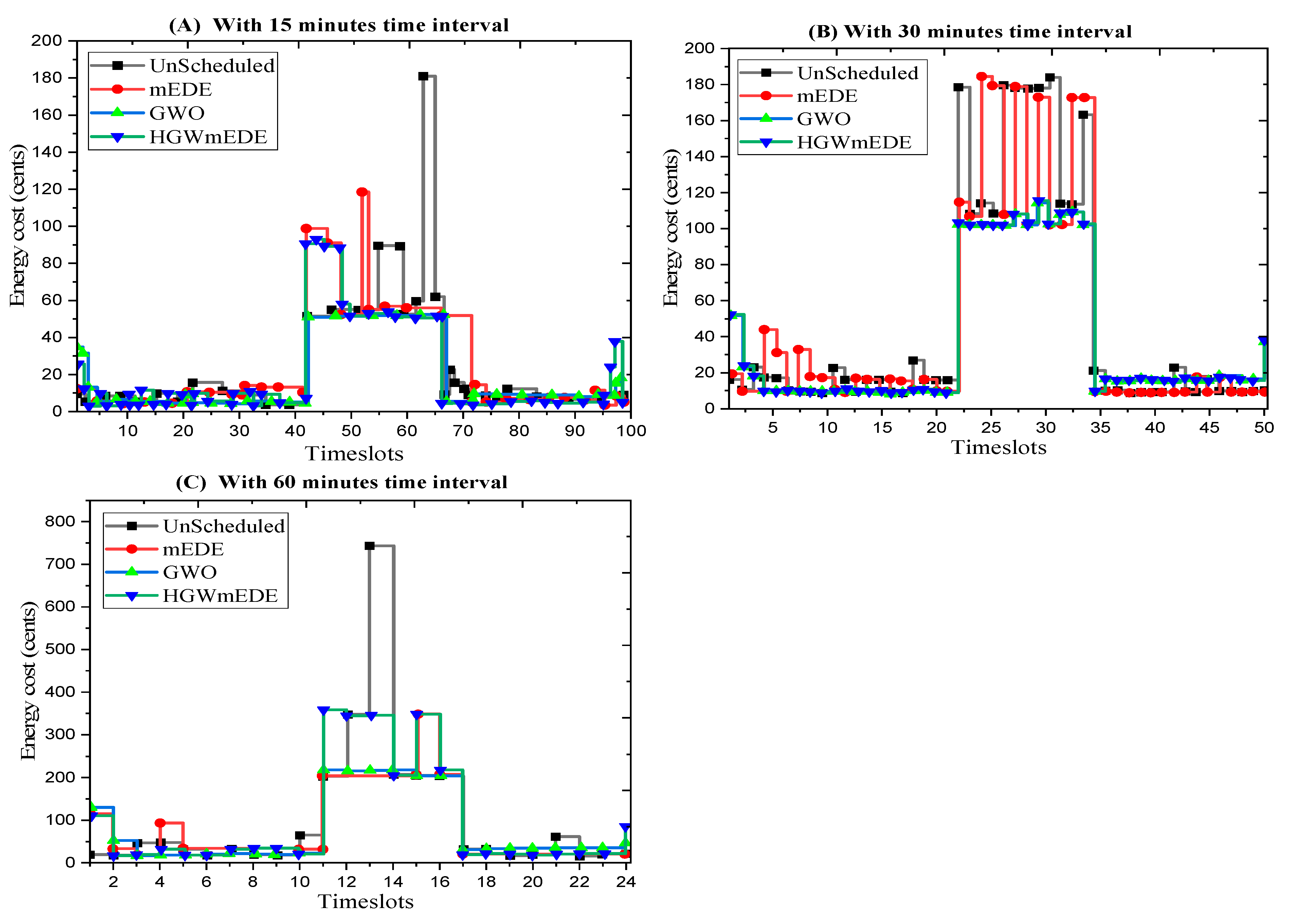
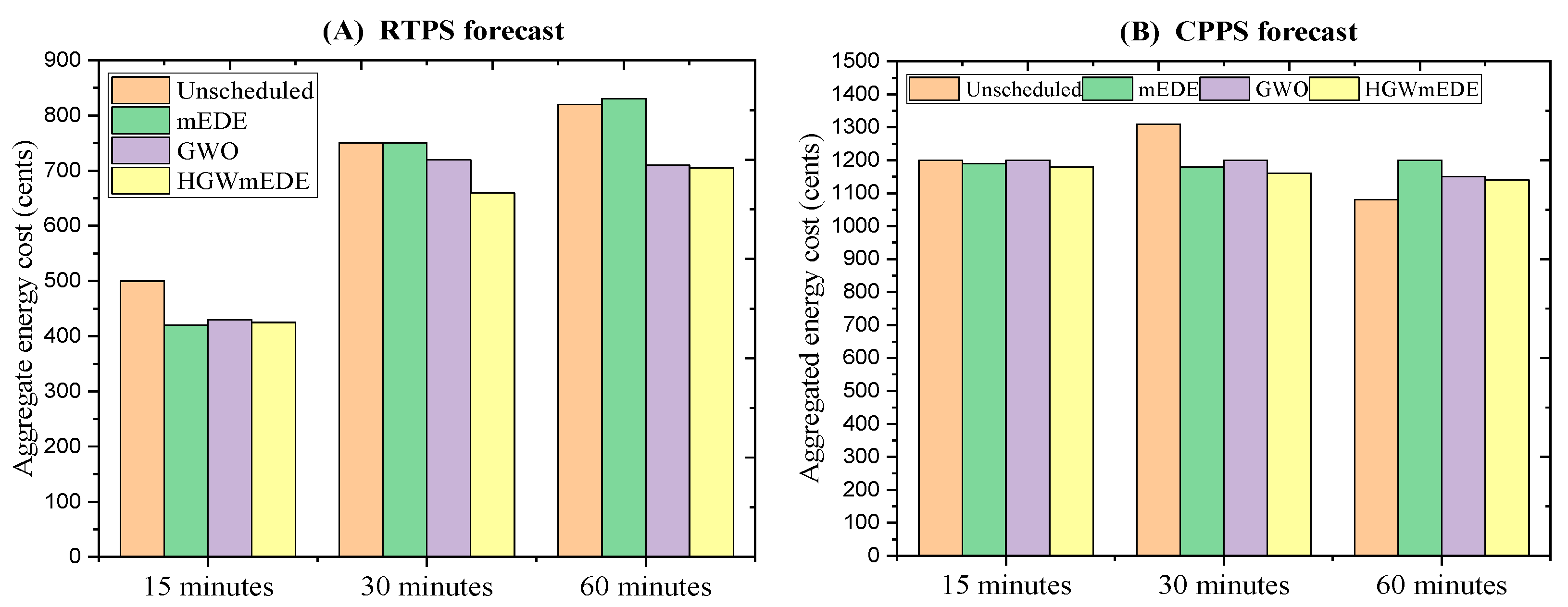
6.1. Electricity Cost Evaluation under a Price-Based DR Program
6.2. Electricity Cost Evaluation Using RTPS and CPPS under OTI
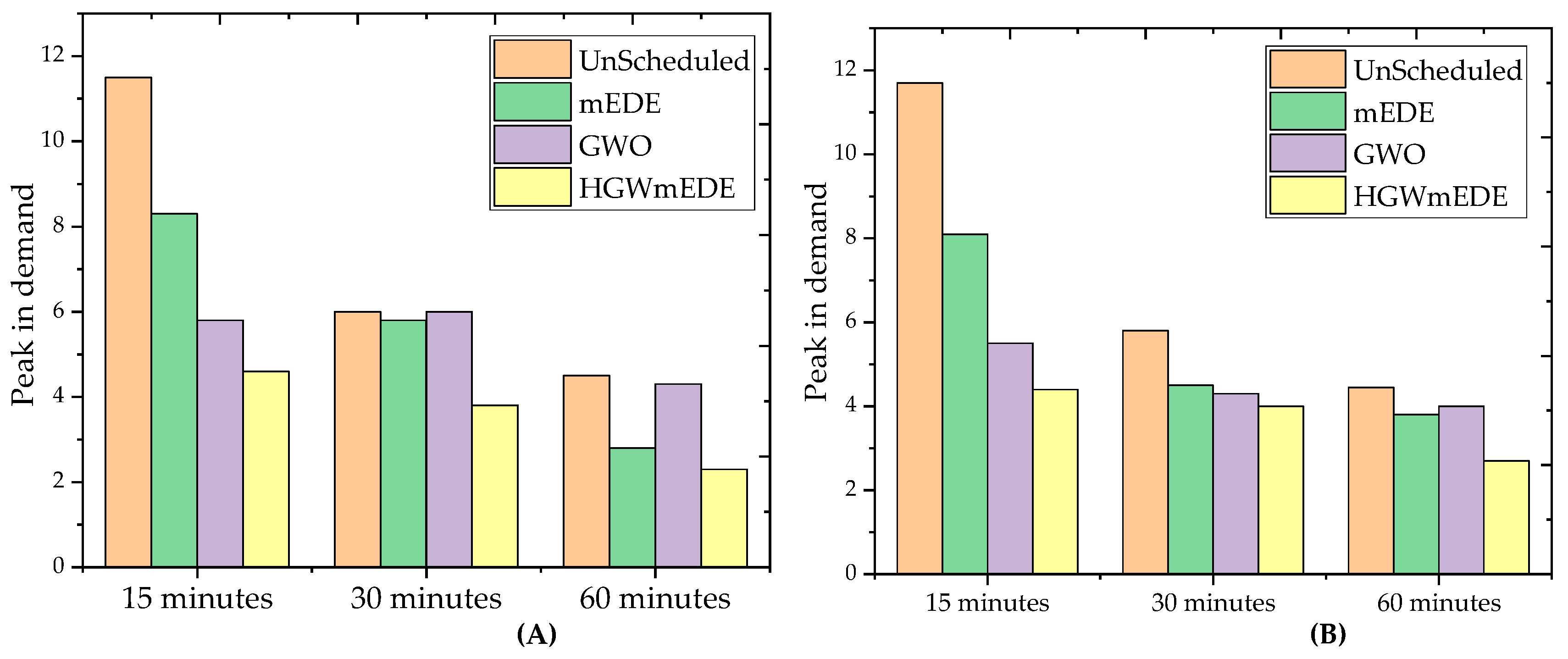
6.3. Peaks in Demand
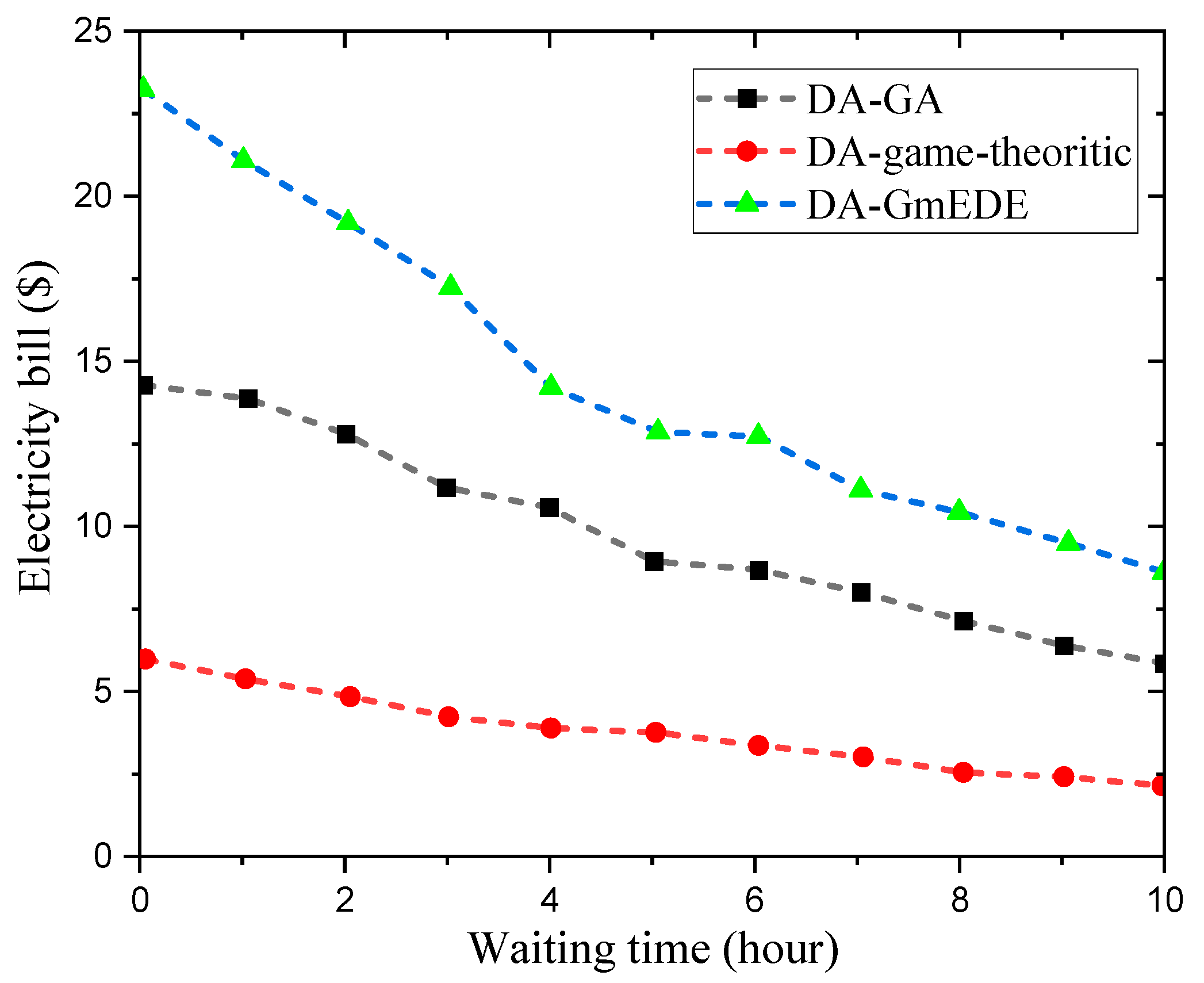
6.4. Waiting Time Evaluation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giamarelos, N.; Papadimitrakis, M.; Stogiannos, M.; Zois, E.N.; Livanos, N.-A.I.; Alexandridis, A. A Machine Learning Model Ensemble for Mixed Power Load Forecasting across Multiple Time Horizons. Sensors 2023, 23, 5436. [Google Scholar] [CrossRef]
- Zhao, W.; Fan, L. Short-Term Load Forecasting Method for Industrial Buildings Based on Signal Decomposition and Composite Prediction Model. Sustainability 2024, 16, 2522. [Google Scholar] [CrossRef]
- Xin, F.; Yang, X.; Beibei, W.; Ruilin, X.; Fei, M.; Jianyong, Z. Research on electric vehicle charging load prediction method based on spectral clustering and Deep Learning Network. Front. Energy Res. 2024, 12, 1294453. [Google Scholar] [CrossRef]
- Veeramsetty, V.; Chandra, D.R.; Grimaccia, F.; Mussetta, M. Short-term electric power load forecasting using principal component analysis and recurrent neural networks. Forecasting 2022, 4, 149–164. [Google Scholar] [CrossRef]
- Guo, X.; Gao, Y.; Li, Y.; Zheng, D.; Shan, D. Short-term household load forecasting based on long- and short-term time-series network. Energy Rep. 2021, 7, 58–64. [Google Scholar] [CrossRef]
- Li, D.; Liu, Q.; Feng, D.; Chen, Z. A Medium- and Long-Term Residential Load Forecasting Method Based on Discrete Cosine Transform-FED former. Energies 2024, 17, 3676. [Google Scholar] [CrossRef]
- Panigrahi, R.; Patne, N.R.; Pemmada, S.; Manchalwar, A.D. Regression model-based hourly aggregated electricity demand prediction. Energy Rep. 2022, 8, 16–24. [Google Scholar] [CrossRef]
- Hassnain, S.; Asar, A.; Mahmood, F. Performance of STLF model from the PSO, Time Series and regression perspectives. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009. [Google Scholar] [CrossRef]
- Harun, M.H.; Othman, M.M.; Musirin, I. Short-term load forecasting (STLF) using artificial neural network based multiple lags of Time Series. Adv. Neuro-Inf. Process. 2009, 5507, 445–452. [Google Scholar] [CrossRef]
- Zhu, K.; Geng, J.; Wang, K. A hybrid prediction model based on pattern sequence-based matching method and extreme gradient boosting for holiday load forecasting. Electr. Power Syst. Res. 2021, 190, 106841. [Google Scholar] [CrossRef]
- Al-Ani, B.R.K.; Erkan, E.T. A study of load demand forecasting models in electricity using artificial neural networks and Fuzzy Logic Model. Int. J. Eng. 2022, 35, 1111–1118. [Google Scholar] [CrossRef]
- Uwimana, E.; Zhou, Y.; Zhang, M. Long-term electrical load forecasting in Rwanda based on support vector machine enhanced with Q-SVM optimization kernel function. J. Power Energy Eng. 2023, 11, 32–54. [Google Scholar] [CrossRef]
- Kaskouras, C.D.; Krommydas, K.F.; Baltas, I.; Papaioannou, G.P.; Papayiannis, G.I.; Yannacopoulos, A.N. Assessing the Flexibility of Power Systems through Neural Networks: A Study of the Hellenic Transmission System. Sustainability 2024, 16, 5987. [Google Scholar] [CrossRef]
- Reppert, T. Local-level ownership of electricity grids: An analysis of Germany’s Distribution System Operators (DSOs). Util. Policy 2023, 85, 101678. [Google Scholar] [CrossRef]
- Anees, A.; Chen, Y.-P.P. True real-time pricing and combined power scheduling of electric appliances in Residential Energy Management System. Appl. Energy 2016, 165, 592–600. [Google Scholar] [CrossRef]
- Mujeeb, S.; Javaid, N.; Ilahi, M.; Wadud, Z.; Ishmanov, F.; Afzal, M.K. Deep Long Short-term memory: A new price and load forecasting scheme for big data in Smart Cities. Sustainability 2019, 11, 987. [Google Scholar] [CrossRef]
- Deng, B.; Peng, D.; Zhang, H.; Qian, Y. An intelligent hybrid short-term load forecasting model optimized by switching delayed PSO of micro-grids. J. Renew. Sustain. Energy 2018, 10, 024901. [Google Scholar] [CrossRef]
- Cecati, C.; Kolbusz, J.; Rozycki, P.; Siano, P.; Wilamowski, B.M. A novel RBF Training Algorithm for short-term Electric Load Forecasting and comparative studies. IEEE Trans. Ind. Electron. 2015, 62, 6519–6529. [Google Scholar] [CrossRef]
- Ahmad, A.; Javaid, N.; Guizani, M.; Alrajeh, N.; Khan, Z.A. An accurate and fast converging short-term load forecasting model for industrial applications in a smart grid. IEEE Trans. Ind. Inform. 2017, 13, 2587–2596. [Google Scholar] [CrossRef]
- Cai, M.; Pipattanasomporn, M.; Rahman, S. Day-ahead building-level load forecasts using deep learning vs. traditional time-series techniques. Appl. Energy 2019, 236, 1078–1088. [Google Scholar] [CrossRef]
- Mujeeb, S.; Alghamdi, T.A.; Ullah, S.; Fatima, A.; Javaid, N.; Saba, T. Exploiting deep learning for wind power forecasting based on Big Data Analytics. Appl. Sci. 2019, 9, 4417. [Google Scholar] [CrossRef]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep Learning for Estimating Building Energy Consumption. Sustain. Energy Grids Netw. 2016, 6, 91–99. [Google Scholar] [CrossRef]
- Gao, Y.; Matsunami, Y.; Miyata, S.; Akashi, Y. Operational optimization for off-grid renewable building energy system using Deep Reinforcement Learning. Appl. Energy 2022, 325, 119783. [Google Scholar] [CrossRef]
- Dedinec, A.; Filiposka, S.; Dedinec, A.; Kocarev, L. Deep belief network based electricity load forecasting: An analysis of Macedonian case. Energy 2016, 115, 1688–1700. [Google Scholar] [CrossRef]
- Fan, C.; Xiao, F.; Zhao, Y. A short-term building cooling load prediction method using deep learning algorithms. Appl. Energy 2017, 195, 222–233. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. Application of a new hybrid neuro-evolutionary system for day-ahead price forecasting of electricity markets. Appl. Soft Comput. 2010, 10, 784–792. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F.; Zareipour, H. Short-term load forecast of microgrids by a new bilevel prediction strategy. IEEE Trans. Smart Grid 2010, 1, 286–294. [Google Scholar] [CrossRef]
- Liu, D.; Zeng, L.; Li, C.; Ma, K.; Chen, Y.; Cao, Y. A distributed short-term load forecasting method based on local weather information. IEEE Syst. J. 2018, 12, 208–215. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Wadud, Z.; Shafiq, Z.; Ali Khan, M.U.; Khan, I.; Khan, F.A.; Derhab, A. A novel accurate and fast converging deep learning-based model for electrical energy consumption forecasting in a smart grid. Energies 2020, 13, 2244. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting—A novel pooling deep RNN. IEEE Trans. Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
- Huang, X.; Hong, S.H.; Li, Y. Hour-ahead price-based energy management scheme for Industrial Facilities. IEEE Trans. Ind. Inform. 2017, 13, 2886–2898. [Google Scholar] [CrossRef]
- Hora, C.; Dan, F.C.; Bendea, G.; Secui, C. Residential short-term load forecasting during atypical consumption behavior. Energies 2022, 15, 291. [Google Scholar] [CrossRef]
- Xu, X.; Niu, D.; Wang, Q.; Wang, P.; Wu, D.D. Intelligent forecasting model for regional power grid with distributed generation. IEEE Syst. J. 2017, 11, 1836–1845. [Google Scholar] [CrossRef]
- Li, L.; Ota, K.; Dong, M. When weather matters: IOT-based electrical load forecasting for smart grid. IEEE Commun. Mag. 2017, 55, 46–51. [Google Scholar] [CrossRef]
- Rai, A.; Shrivastava, A.; Jana, K.C. Differential attention net: Multi-directed differential attention based hybrid deep learning model for solar power forecasting. Energy 2023, 263, 125746. [Google Scholar] [CrossRef]
- Samuel, O.; Javaid, S.; Javaid, N.; Ahmed, S.H.; Afzal, M.K.; Ishmanov, F. An efficient power scheduling in smart homes using Jaya based optimization with time-of-use and critical peak pricing schemes. Energies 2018, 11, 3155. [Google Scholar] [CrossRef]
- Awais, M.; Javaid, N.; Aurangzeb, K.; Haider, S.I.; Khan, Z.A.; Mahmood, D. Towards effective and efficient energy management of single home and a smart community exploiting heuristic optimization algorithms with Critical Peak and real-time pricing tariffs in smart grids. Energies 2018, 11, 3125. [Google Scholar] [CrossRef]
- Pandey, A.K.; Jadoun, V.K.; Sabhahit, J.N. Real-time Peak Valley pricing based multi-objective optimal scheduling of a virtual power plant considering renewable resources. Energies 2022, 15, 5970. [Google Scholar] [CrossRef]
- Shewale, A.; Mokhade, A.; Lipare, A.; Bokde, N.D. Efficient techniques for residential appliances scheduling in Smart Homes for energy management using multiple Knapsack problem. Arab. J. Sci. Eng. 2023, 49, 3793–3813. [Google Scholar] [CrossRef]
- Du, Y.F.; Jiang, L.; Li, Y.; Wu, Q. A robust optimization approach for demand side scheduling considering uncertainty of manually operated appliances. IEEE Trans. Smart Grid 2018, 9, 743–755. [Google Scholar] [CrossRef]
- Kakran, S.; Chanana, S. Optimal Energy Scheduling method under Load Shaping Demand Response Program in a Home Energy Management System. Int. J. Emerg. Electr. Power Syst. 2019, 20, 20180147. [Google Scholar] [CrossRef]
- Derakhshan, G.; Shayanfar, H.A.; Kazemi, A. The optimization of demand response programs in smart grids. Energy Policy 2016, 94, 295–306. [Google Scholar] [CrossRef]
- Haider, H.T.; See, O.H.; Elmenreich, W. Residential demand response scheme based on adaptive consumption level pricing. Energy 2016, 113, 301–308. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, J.-W.; Cui, S.-C.; Wang, Y.-W. Distributed real-time demand response for energy management scheduling in Smart Grid. Int. J. Electr. Power Amp Energy Syst. 2018, 99, 233–245. [Google Scholar] [CrossRef]
- Eid, C.; Koliou, E.; Valles, M.; Reneses, J.; Hakvoort, R. Time-based pricing and electricity demand response: Existing barriers and next steps. Util. Policy 2016, 40, 15–25. [Google Scholar] [CrossRef]
- Khalid, R.; Javaid, N.; Rahim, M.H.; Aslam, S.; Sher, A. Fuzzy Energy Management Controller and scheduler for Smart Homes. Sustain. Comput. Inform. Syst. 2019, 21, 103–118. [Google Scholar] [CrossRef]
- Khalid, A.; Javaid, N.; Mateen, A.; Ilahi, M.; Saba, T.; Rehman, A. Enhanced time-of-use electricity price rate using game theory. Electronics 2019, 8, 48. [Google Scholar] [CrossRef]
- Mohseni, A.; Mortazavi, S.S.; Ghasemi, A.; Nahavandi, A.; Talaei Abdi, M. The application of household appliances’ flexibility by set of sequential Uninterruptible Energy Phases Model in the day-ahead planning of a residential microgrid. Energy 2017, 139, 315–328. [Google Scholar] [CrossRef]
- Tavakoli, S.; Nisol, G.; Hallin, M. Factor models for high-dimensional functional time series II: Estimation and forecasting. J. Time Ser. Anal. 2023, 44, 601–621. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Population size | 24 |
| Number of decision variables | 2 |
| Number of iterations | 100 |
| 3 | |
| 0.2 | |
| 0.4 | |
| −5 | |
| 5 | |
| 0.3 | |
| −0.3 | |
| 0.9 | |
| 0.1 | |
| Learning rate | 0.0001 |
| Weight decay | 0.0002 |
| Momentum | 0.5 |
| Control Parameters | Value |
|---|---|
| Number of hidden layers | 1 |
| Number of neurons in hidden layer | 10 |
| Output layer | 1 |
| Number of output neurons | 1 |
| Number of epochs | 100 |
| Number of iterations | 100 |
| Learning rate | 0.0019 |
| Momentum | 0.6 |
| Initial weight | 0.1 |
| Initial bias | 0 |
| Max | 0.9 |
| Min | 0.1 |
| Decision variables | 2 |
| Population size | 24 |
| Delay in weight | 0.0002 |
| Historical load data | 4 years |
| Exogenous parameters | 4 years |
| Electrical Load Consumption Forecasting Models | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Day | FS-FCRBM-GWDO | MI-mEDE-ANN | AFC-STLF | Bi-Level | FS-ANN | ||||||||||
| MAPE | r | MAPE | r | MAPE | r | MAPE | r | MAPE | r | ||||||
| 1 | 1.13 | 1.19 | 0.70 | 2.20 | 1.55 | 0.50 | 2.30 | 1.60 | 0.52 | 2.60 | 1.69 | 0.50 | 3.41 | 1.87 | 0.50 |
| 2 | 1.10 | 0.98 | 0.68 | 2.10 | 1.45 | 0.58 | 2.15 | 1.55 | 0.56 | 2.80 | 1.80 | 0.51 | 3.29 | 1.79 | 0.40 |
| 3 | 1.09 | 1.10 | 0.71 | 2.50 | 1.30 | 0.51 | 2.10 | 1.48 | 0.53 | 2.75 | 1.51 | 0.39 | 3.18 | 1.73 | 0.29 |
| 4 | 1.03 | 0.97 | 0.80 | 2.02 | 1.20 | 0.50 | 2.40 | 1.49 | 0.54 | 2.85 | 1.72 | 0.51 | 3.37 | 1.92 | 0.37 |
| 5 | 1.50 | 1.09 | 0.65 | 2.10 | 1.15 | 0.55 | 2.25 | 1.37 | 0.55 | 2.87 | 1.59 | 0.34 | 3.20 | 1.81 | 0.40 |
| 6 | 1.30 | 1.07 | 0.75 | 2.30 | 1.34 | 0.65 | 2.15 | 1.35 | 0.69 | 2.89 | 1.71 | 0.61 | 3.17 | 1.89 | 0.51 |
| 7 | 1.24 | 1.04 | 0.69 | 2.11 | 1.55 | 0.60 | 2.10 | 1.60 | 0.65 | 2.75 | 1.70 | 0.32 | 3.71 | 1.94 | 0.40 |
| 8 | 1.23 | 1.02 | 0.70 | 2.15 | 1.45 | 0.50 | 2.09 | 1.65 | 0.55 | 2.70 | 1.80 | 0.49 | 3.63 | 1.79 | 0.51 |
| 9 | 1.08 | 1.05 | 0.80 | 2.35 | 1.36 | 0.55 | 2.50 | 1.66 | 0.56 | 2.65 | 1.62 | 0.62 | 3.56 | 1.84 | 0.42 |
| 10 | 1.05 | 0.99 | 0.79 | 2.40 | 1.39 | 0.69 | 2. 44 | 1.67 | 0.60 | 2.63 | 1.81 | 0.57 | 3.08 | 1.93 | 0.49 |
| 11 | 1.15 | 1.10 | 0.87 | 2.01 | 1.45 | 0.77 | 2.35 | 1.55 | 0.75 | 2.70 | 1.58 | 0.42 | 3.04 | 1.9 | 0.50 |
| 12 | 1.25 | 1.11 | 0.65 | 2.06 | 1.50 | 0.55 | 2.12 | 1.58 | 0.55 | 2.60 | 1.70 | 0.39 | 3.68 | 1.81 | 0.40 |
| 13 | 1.10 | 0.96 | 0.81 | 2.10 | 1.55 | 0.71 | 2.20 | 1.43 | 0.75 | 2.63 | 1.73 | 0.34 | 3.29 | 1.72 | 0.29 |
| 14 | 1.12 | 0.99 | 0.79 | 2.12 | 1.37 | 0.75 | 2.23 | 1.47 | 0.70 | 2.36 | 1.68 | 0.39 | 3.43 | 1.62 | 0.28 |
| 15 | 1.10 | 1.03 | 0.78 | 2.13 | 1.46 | 0.78 | 2.27 | 1.30 | 0.73 | 2.50 | 1.62 | 0.52 | 3.67 | 1.91 | 0.53 |
| 16 | 1.18 | 1.05 | 0.79 | 2.00 | 1.39 | 0.70 | 2.13 | 1.35 | 0.78 | 2.58 | 1.71 | 0.61 | 3.31 | 1.9 | 0.48 |
| 17 | 1.19 | 1.08 | 0.80 | 2.13 | 1.48 | 0.60 | 2.35 | 1.55 | 0.65 | 2.56 | 1.65 | 0.63 | 3.36 | 1.81 | 0.51 |
| 18 | 1.21 | 1.09 | 0.85 | 2.19 | 1.29 | 0.85 | 2.10 | 1.36 | 0.64 | 2.65 | 1.69 | 0.67 | 3.82 | 1.78 | 0.50 |
| 19 | 1.25 | 1.12 | 0.90 | 2.16 | 1.36 | 0.50 | 2.14 | 1.55 | 0.59 | 2.54 | 1.64 | 0.62 | 3.44 | 1.69 | 0.39 |
| 20 | 1.44 | 0.95 | 0.67 | 2.17 | 1.47 | 0.60 | 2.15 | 1.45 | 0.48 | 2.50 | 1.59 | 0.61 | 3.16 | 1.72 | 0.54 |
| 21 | 1.39 | 0.90 | 0.71 | 2.34 | 1.51 | 0.58 | 2.19 | 1.54 | 0.58 | 2.59 | 1.80 | 0.53 | 3.31 | 1.91 | 0.43 |
| 22 | 1.17 | 0.99 | 0.75 | 2.10 | 1.50 | 0.75 | 2.10 | 1.40 | 0.59 | 2.80 | 1.58 | 0.50 | 3.51 | 1.73 | 0.41 |
| 23 | 1.15 | 1.01 | 0.86 | 2.30 | 1.45 | 0.64 | 2.13 | 1.34 | 0.39 | 2.75 | 1.71 | 0.61 | 3.35 | 1.72 | 0.52 |
| 24 | 1.08 | 1.07 | 0.87 | 2.01 | 1.34 | 0.73 | 2.24 | 1.60 | 0.58 | 2.65 | 1.63 | 0.39 | 3.92 | 1.81 | 0.41 |
| 25 | 1.03 | 1.11 | 0.92 | 1.99 | 1.35 | 0.82 | 2.13 | 1.49 | 0.67 | 2.67 | 1.53 | 0.61 | 3.89 | 1.8 | 0.39 |
| 26 | 1.05 | 1.05 | 0.90 | 2.00 | 1.56 | 0.09 | 2.26 | 1.61 | 0.49 | 2.85 | 1.70 | 0.68 | 3.75 | 1.59 | 0.52 |
| 27 | 1.03 | 1.10 | 0.88 | 2.10 | 1.40 | 0.58 | 2.10 | 1.48 | 0.77 | 2.55 | 1.75 | 0.62 | 3.79 | 1.79 | 0.49 |
| 28 | 1.25 | 1.11 | 0.76 | 2.09 | 1.35 | 0.56 | 2.15 | 1.50 | 0.58 | 2.60 | 1.75 | 0.55 | 3.35 | 1.81 | 0.38 |
| 29 | 1.27 | 1.13 | 0.77 | 2.08 | 1.32 | 0.55 | 2.13 | 1.53 | 0.59 | 2.62 | 1.76 | 0.49 | 3.36 | 1.78 | 0.39 |
| 30 | 1.25 | 1.21 | 0.81 | 2.01 | 1.21 | 0.43 | 2.21 | 1.48 | 0.51 | 2.58 | 1.69 | 0.51 | 3.34 | 1.74 | 0.36 |
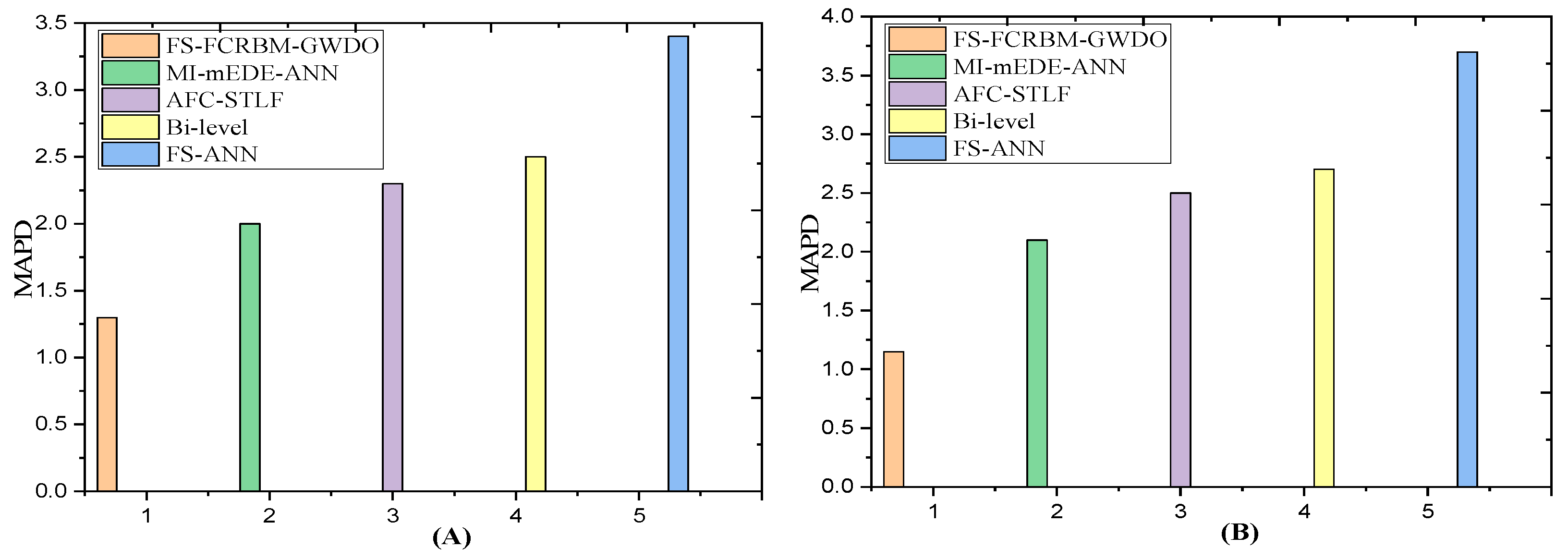
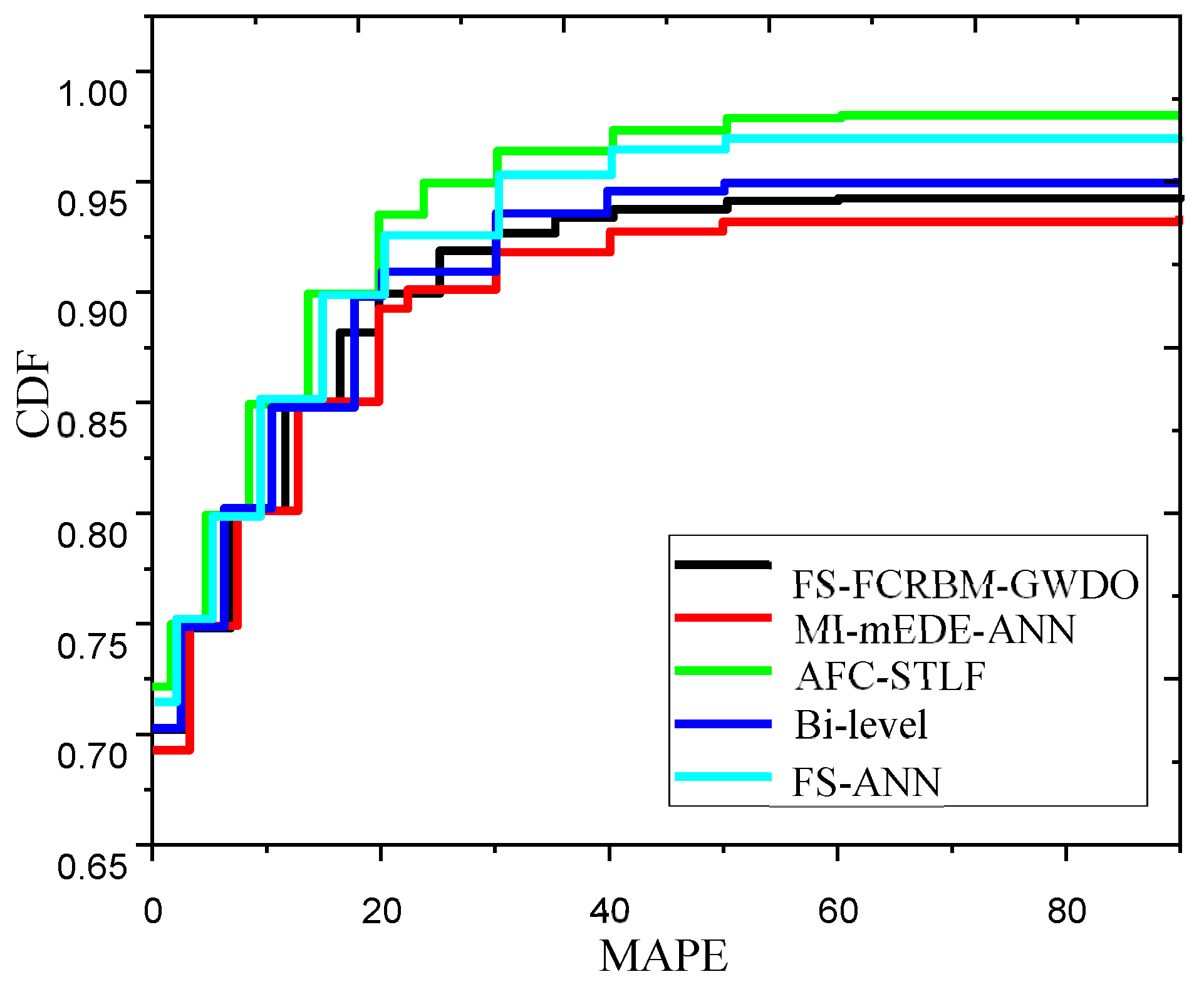
| Agg. | 1.10 | 1.03 | 0.79 | 2.20 | 1.25 | 0.65 | 2.10 | 1.35 | 0.60 | 2.6 | 1.70 | 0.52 | 3.4 | 1.80 | 0.43 |
| Electrical Load Consumption Forecasting Models | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month | FS-FCRBM-GWDO | MI-mEDE-ANN | AFC-STLF | Bi-Level | FS-ANN | ||||||||||
| MAPE | r | MAPE | r | MAPE | r | MAPE | r | MAPE | r | ||||||
| 1 | 1.09 | 1.12 | 0.81 | 2.22 | 1.38 | 0.81 | 2.3 | 1.28 | 0.69 | 2.49 | 1.61 | 0.39 | 3.61 | 1.9 | 0.49 |
| 2 | 1.37 | 1.01 | 0.7 | 2.09 | 1.5 | 0.58 | 2.09 | 1.51 | 0.51 | 2.48 | 1.59 | 0.61 | 3.19 | 1.59 | 0.51 |
| 3 | 1.32 | 1.20 | 0.59 | 2.1 | 1.47 | 0.62 | 2.2 | 1.6 | 0.49 | 2.59 | 1.7 | 0.5 | 3.64 | 1.82 | 0.29 |
| 4 | 1.12 | 0.89 | 0.77 | 1.99 | 1.19 | 0.43 | 2.35 | 1.52 | 0.6 | 2.9 | 1.81 | 0.38 | 3.32 | 1.78 | 0.4 |
| 5 | 1.28 | 1.12 | 0.68 | 2.21 | 1.5 | 0.54 | 2.29 | 1.6 | 0.58 | 2.62 | 1.69 | 0.6 | 3.37 | 1.83 | 0.48 |
| 6 | 1.09 | 1.11 | 0.92 | 2.29 | 1.38 | 0.59 | 2.08 | 1.28 | 0.42 | 2.68 | 1.72 | 0.62 | 3.17 | 1.69 | 0.52 |
| 7 | 1.1 | 1.20 | 0.58 | 2.07 | 1.6 | 0.57 | 2.03 | 1.57 | 0.7 | 2.69 | 1.57 | 0.38 | 3.73 | 1.78 | 0.41 |
| 8 | 1.18 | 1.07 | 0.69 | 2.04 | 1.39 | 0.43 | 2.11 | 1.59 | 0.6 | 2.95 | 1.8 | 0.62 | 3.61 | 1.91 | 0.39 |
| 9 | 1.3 | 1.09 | 0.62 | 2.1 | 1.46 | 0.62 | 2.21 | 1.61 | 0.49 | 2.54 | 1.6 | 0.34 | 3.6 | 1.64 | 0.41 |
| 10 | 1.09 | 1.10 | 0.81 | 2.05 | 1.42 | 0.68 | 2.08 | 1.42 | 0.8 | 2.59 | 1.79 | 0.61 | 3.18 | 1.93 | 0.53 |
| 11 | 1.08 | 1.06 | 0.92 | 2.07 | 1.56 | 0.82 | 2.29 | 1.64 | 0.72 | 2.63 | 1.8 | 0.29 | 3.09 | 1.79 | 0.5 |
| 12 | 1.15 | 1.15 | 0.79 | 2.3 | 1.32 | 0.91 | 2.09 | 1.45 | 0.7 | 2.72 | 1.69 | 0.63 | 3.85 | 1.93 | 0.51 |
| Agg. | 1.18 | 1.09 | 0.74 | 2.12 | 1.43 | 0.63 | 2.17 | 1.50 | 0.60 | 2.65 | 1.69 | 0.50 | 3.45 | 1.80 | 0.45 |
| Performance Parameters | Models | ||||
|---|---|---|---|---|---|
| FS-ANN | Bi-Level | AFC-STLF | MI-mEDE-ANN | FS-FCRBM-GWDO | |
| Computational complexity (level) | Low | High | Moderate | High | Moderate |
| Convergence rate (epochs) | 33rd | 28th | 26th | 21st | 11th |
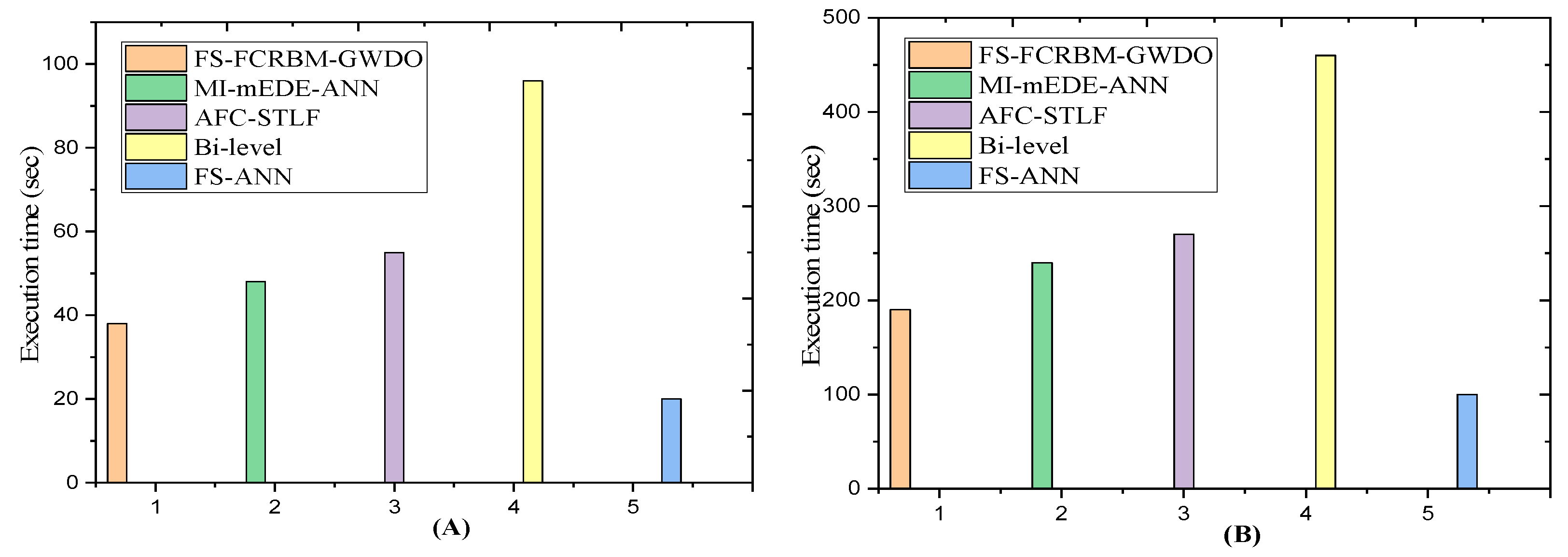
| Execution time (s) | 31 | 89 | 62 | 97.5 | 98.9 |
| Accuracy (%) | 96.4 | 97.4 | 97.9 | 97.8 | 98.7 |
| Parameters | Values |
|---|---|
| Population | 100 |
| Minimum lower population bound | 0.1 |
| Maximum lower population bound | 0.9 |
| Number of wolves in each pack | 17 |
| Maximum epochs | 100 |
| Decision variables | 2 |
| Learning rate | 0.002 |
| Weight decay | 0.0002 |
| Initial value of weight | 0.1 |
| Initial value of bias | 0 |
| Number of objectives | 2 |
| Momentum | 0.5 |
| Feature selection threshold | 0.5 |
| Distance from prey | Vary |
| Status of leader | 1 or 2 |
| Number of dimensions | 17 |
| Gradient of problem | Vary |
| Classification | Types of Application | Power Rating (GWh) | Operation Timeslots (h) | Priority |
|---|---|---|---|---|
| Power-shiftable appliances | Electric radiator | (0.5–1.5) | 10 | 2 |
| Water dispenser | (0.8–1.2) | 24 | ||
| Refrigerator | (0.5–1.2) | 24 | ||
| Air conditioner | (0.8–1.5) | 10 | ||
| Critical appliances | Hair dryer | 1.2 | 1 | 3 |
| Microwave | 1.8 | 3 | ||
| Electric iron | 1.8 | 4 | ||
| Electrical kettle | 1.5 | 1 | ||
| Time shiftable Appliances | Washing machine | 0.7 | 5 | 1 |
| Cloth dryer | 2 | 4 | ||
| Water pump | 0.4 | 2 |
| Scenarios and Algorithms | Electrical Energy Cost (USD) under RTPS | Electrical Energy Cost (USD) under CPPS | ||||
|---|---|---|---|---|---|---|
| 15 min | 30 min | 60 min | 15 min | 30 min | 60 min | |
| Without scheduling | 500.4821 | 743.4871 | 822.1561 | 1200.1561 | 1300.8910 | 1085.6481 |
| GWO | 426.0507 | 727.1431 | 717.9402 | 1190.5122 | 1200.9612 | 1080.4091 |
| mEDE | 420.5381 | 743.1951 | 831.2132 | 1178.4901 | 1164.4901 | 1190.6901 |
| GmEDE | 416.7468 | 658.6502 | 712.7292 | 1164.4901 | 1085.9022 | 1056.7891 |
| Scenarios | Peak Load in Demand under RTPS with Different OTIs | Peak Load in Demand under CPPS with Different OTIs | ||||
|---|---|---|---|---|---|---|
| 15 min | 30 min | 60 min | 15 min | 30 min | 60 min | |
| Without scheduling | 10.9698 | 6.0258 | 5.0258 | 10.9698 | 5.8035 | 5.0258 |
| mEDE | 8.1723 | 5.8425 | 3.6558 | 8.1723 | 5.2537 | 3.8425 |
| GWO | 5.676 | 5.9336 | 4.3509 | 5.6265 | 4.8166 | 3.9336 |
| GmEDE | 5.1531 | 3.6210 | 2.5369 | 5.5416 | 4.0264 | 3.6210 |
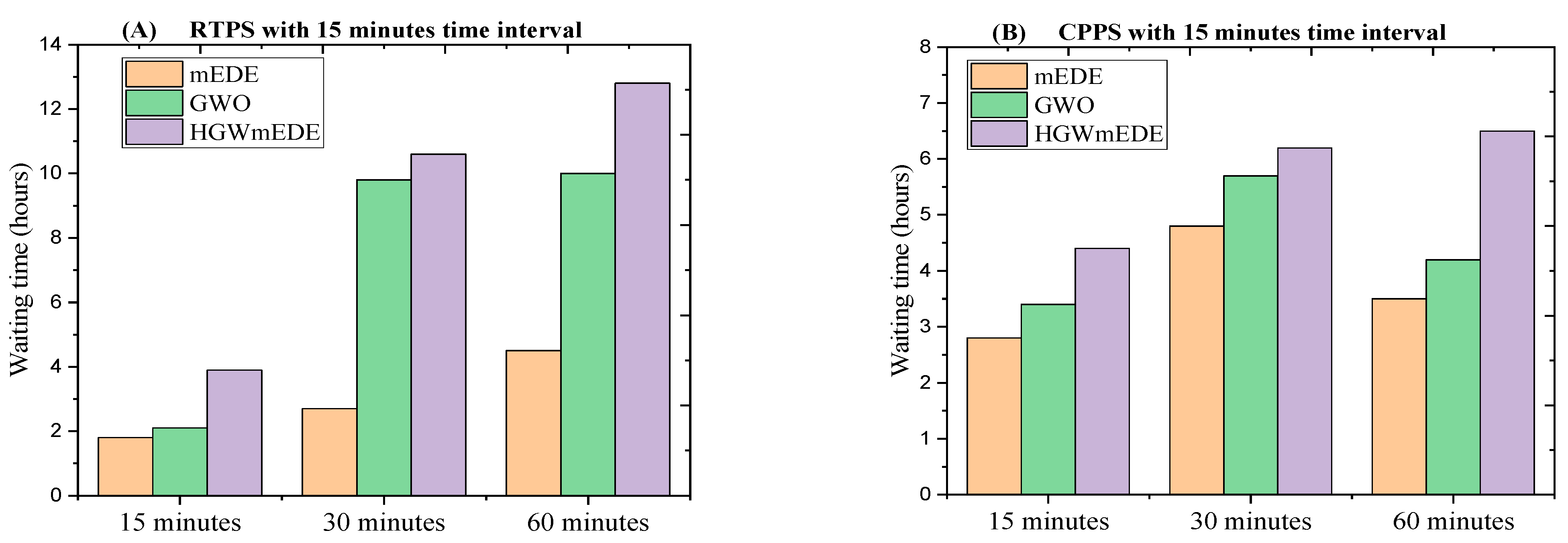
| Scenarios | Evaluation of Waiting under RTPS for Different OTI | Evaluation of Waiting under CPPS for Different OTI | ||||
|---|---|---|---|---|---|---|
| 15 min | 30 min | 60 min | 15 min | 30 min | 60 min | |
| mEDE | 4.3781 h | 4.5394 h | 2.6560 h | 3.3826 h | 4.8012 h | 2.8158 h |
| GWO | 9.7494 h | 10.0262 h | 2.2397 h | 4.2293 h | 5.7853 h | 3.3346 h |
| GmEDE | 10.4249 h | 12.7007 h | 3.8793 h | 6.4814 h | 6.1335 h | 4.3408 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uwimana, E.; Zhou, Y. A Novel Two-Stage Hybrid Model Optimization with FS-FCRBM-GWDO for Accurate and Stable STLF. Technologies 2024, 12, 194. https://doi.org/10.3390/technologies12100194
Uwimana E, Zhou Y. A Novel Two-Stage Hybrid Model Optimization with FS-FCRBM-GWDO for Accurate and Stable STLF. Technologies. 2024; 12(10):194. https://doi.org/10.3390/technologies12100194
Chicago/Turabian StyleUwimana, Eustache, and Yatong Zhou. 2024. "A Novel Two-Stage Hybrid Model Optimization with FS-FCRBM-GWDO for Accurate and Stable STLF" Technologies 12, no. 10: 194. https://doi.org/10.3390/technologies12100194
APA StyleUwimana, E., & Zhou, Y. (2024). A Novel Two-Stage Hybrid Model Optimization with FS-FCRBM-GWDO for Accurate and Stable STLF. Technologies, 12(10), 194. https://doi.org/10.3390/technologies12100194







