1. Introduction
Energy companies benefit from load demand forecasting once short-term is used for monitoring, operational safety, turbine control, network integration, stability, and resource reallocation; medium-term is used mostly for power system management, economic dispatch, load balancing, minor maintenance, and load shedding; and long-term is commonly used for maintenance planning, operations management, turbine generator coupling or decoupling planning, operation cost optimization, and generation capacity estimation.
Short-term load forecasting is useful and necessary for the economic generation of power due to the grid’s inability to store energy without specific equipment to do so, the economic allocation between plants (unit commitment scheduling), maintenance schedules, and for system security such as peak load shaving by power interchange with interconnected utilities [
1].
The behavior of the electrical energy demand is directly influenced by other variables such as climate, economic, and characteristic user behavior factors [
2,
3,
4,
5]. All involved load behavior factors bring difficulty and an extra challenge to the problem, but on the other hand, these factors bring a better and more efficient solution [
6]. The classical or stochastic models are commonly used in medium and long-term forecasting. The most used classical methods used to forecast are multiple linear regressions, Auto-Regressive Integrated Moving Average (ARIMA), including Seasonal ARIMA and variants, exponential smoothing, and spectral analysis. These forecasting methods stand out due to the prediction of linear factors efficiency and low cost [
4,
7].
Nowadays, many different approaches have been applied for short-term load forecasting (STLF) such as Artificial Intelligence (AI) and fuzzy systems. AI-based systems are mainly used due to their symbolic reasoning, flexibility, and explanation capabilities. Based on the problem of distributing and transmission companies to forecast the energy demand, there are many works using machine learning (ML) models, and the most cited studies used artificial neural networks to forecast the load demand and approved the notable accuracy of the models, but the computation time and processing necessity are elevated, much more than many other methods based on its sophisticated structure. A methodology using fuzzy rules to incorporate historical weather and load data was proposed by [
8] (1996) to increase the power and efficiency of the load forecasting solution [
9].
This paper presents two contributions. First, it addresses the problem of the accuracy of the probabilistic forecasting model for short-term time series where endogenous variables interfere by emphasizing a low computational cost white box approach such as Granular Weighted Multivariate Fuzzy Time Series (GranularWMFTS) based on the Fuzzy Information Granules (FIG) method and a univariate form such as Probabilistic Fuzzy Time Series. Secondly, it compares time series forecasting models based on algorithms such as Holt-Winters, ARIMA, High Order Fuzzy Time Series (HOFTS), Weighted High Order Fuzzy Time Series (WHOFTS) and Multivariate Fuzzy Time Series (MVFTS) where this paper is based on Root Mean Squared Error (RMSE), Symmetric Mean Absolute Percentage Error (sMAPE) and Theil’s U Statistic (U) relying on 5% error criteria.
The remainder of this article is organized as follows.
Section 2 presents the foundation of each approach evaluated in this paper and the changes over time that enhanced the forecasting models.
Section 3 describes the case of study, nuances founded on each forecasting model as well as the accuracy achieved in terms of RMSE, sMAPE, and U criteria with optimizations on short-term load demand forecasting.
2. Materials and Methods
This section aims to present some fundamentals of each chosen approach used in this article.
2.1. Data
This article used a public dataset from an electrical company in the United States fo America. PJM (Pennsylvania, New Jersey, and Maryland) is a regional transmission organization (RTO) that coordinates the movement of wholesale electricity in all or parts of Delaware, Illinois, Indiana, Kentucky, Maryland, Michigan, New Jersey, North Carolina, Ohio, Pennsylvania, Tennessee, Virginia, West Virginia, and the District of Columbia. The dataset provided is a time series of sample frequency of 1h for all those regions and there’s only the load demand on a specific timestamp so for increasing the model some variables such as seasonality, lags, and week days were created to enhance the model. More details of the statistical form of the data can be seen in
Table 1.
2.2. Holt-Winters
The Triple Exponential Smoothing method was the result of an extension of Double Exponential Smoothing by adding the seasonal component Equation (
3). Also, this one is used when the dataset has level, trend, and seasonality, and the equation addition is used to handle the seasonality. This method is named Holt-Winters (HW). There are two main models on HW depending on the type of seasonality: the additive and multiplicative seasonal models.
In HW represents the weight of the level component, represents the weight of the trend component, and represents the weight of the seasonal component. So, represents the current seasonal component based on current observation, previous level, trend, and seasonality component values , and as well. Hence, the next forecast value is the sum of all three components, where h is the number of forecast values, e.g., is the next forecast value once .
The
m was used to denote the frequency of the seasonality, so
represents monthly data. Additionally,
L was employed to guarantee that the seasonal index estimates utilized in the forecasting process originate from the time series last year,
where
The Multiplicative Seasonal Model is recommended when the amplitude of the seasonal pattern is proportional to the average level of the time series, the seasonal variation is changing proportionally to the level of the series.
2.3. ARIMA Model
Box-Jenkins approach applied to the ARIMA model, cited from now on as ARIMA, has three components: Auto-Regressive (AR), Integrated (I), and Moving Average (MA) components. The dependent relationship between an observation and a prior observation is used by the AR component. The I component employs the difference of raw data to make the time series stationary. Finally, the MA component leverages the dependence between an observation and a residual error from a moving average model applied to lag observations. We remove an observation from the preceding time step.
Each term of the ARIMA model has explicit components that function as parameters. ARIMA (p, d, q) where:
p: number of lag observations included in the model (parameter to AR component)
d: number of times that the raw observation is differenced (parameter to I component)
q: the size of the moving average window (parameter to MA component)
AR model is a regression where the current observation only depends on its lags. In the MA model,
depends linearly on the current and past errors evaluated. MA model is typically used with the AR model bringing the Auto Regressive Moving Average (ARMA) model. So, ARIMA is nothing more than the joining of the three components leading to Equation (
5) given by:
where
is the first lag of the series,
is the coefficient of the first AR term,
is the coefficient of the first MA term,
is the intercept term, also estimated by the model, and
is the error of a given point in time
t. If the mean of
y is zero,
is not be included.
2.4. Fuzzy Systems
Fuzzy logic was introduced by [
10] as fuzzy set theory. The term fuzzy logic refers to the observation which individuals frequently base their conclusions on non-numerical or imprecise information. Before fuzzy logic, the mathematical set representation of a value was Boolean logic: true if the value was in the set or false otherwise. The fuzzy logic has duality; an element may belong and simultaneously not belong to the same set at certain levels, like when the membership value is between [0, 1]. The fuzzy set has no boundaries and is usually overlapping.
Let X be a numerical variable where , this variable is called the universe of discourse, or its acronym, U and the highest and lowest value of the numerical variable is the universe of discourse’s interval, represented as . The step to represent numerical values into linguistic values is called fuzzification, where value is a linguistic term, so a fuzzy set is associated with this value. A fuzzy set is represented by where where is the fuzzy universe of discourse.
A Fuzzy Time Series (FTS) theory was laid out by [
11] using fuzzy set logic. In contrast to stochastic forecasting methods, FTS does not require large data sets, which makes it more suitable than conventional forecasting systems in some cases. However, if the data exhibit multiple seasonal patterns, a larger data set will be necessary. Otherwise, FTS can process both crisp and fuzzy values.
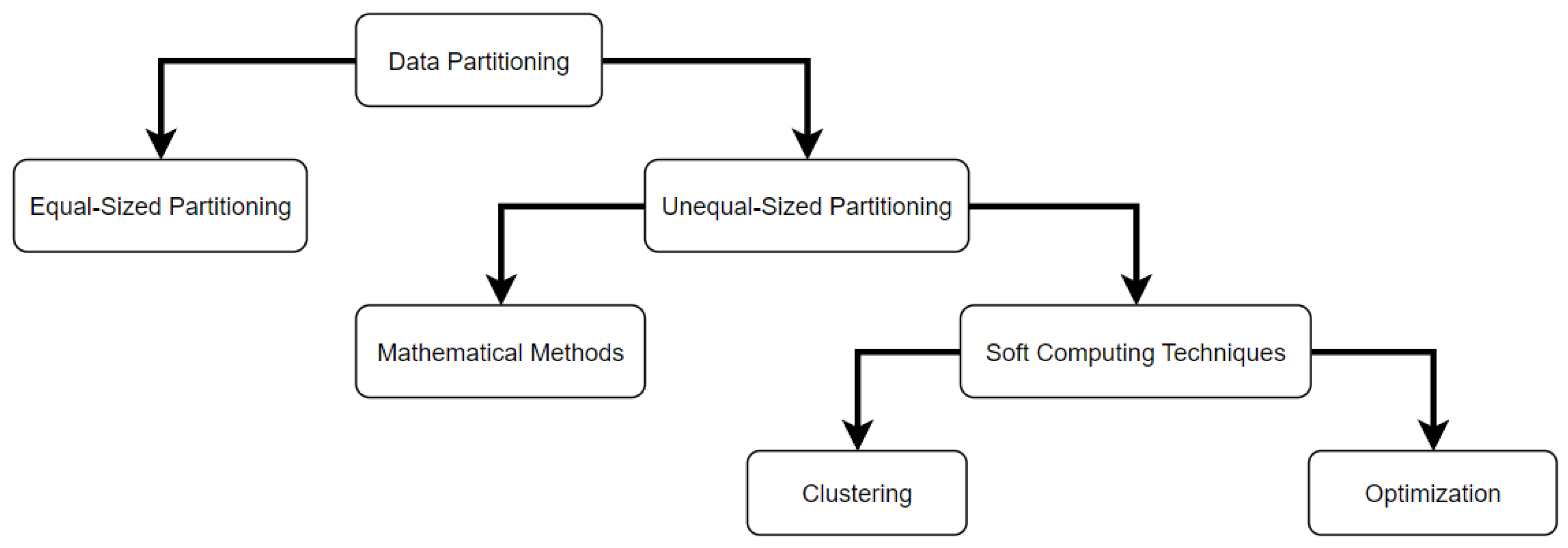
The FTS has basic components to represent the forecasting process using this approach [
12]. These components are: Define universe of discourse; Data partitioning; Fuzzification; Formulation of fuzzy logical relationship (FLR) and fuzzy logical relationship group (FLRG); Defuzzification.
With
J being the number of fuzzy sets, the universe of discourse partitioning technique seeks to divide the universe of discourse
U and produce linguistics variables
made up of the fuzzified datasets
. The lower and upper bounds
to the discourse universe are typically given a confidence margin when it comes to fuzzy set theory. Thus, Equation (
6) may be used to represent the universe of discourse, and as a rule,
l and
u have the same value. The purpose of these margins is to aid in the forecasting process’ fuzzification to account for variations in the discourse universe’s limits.
Three key model hyperparameters, namely the membership function
, the partitioning strategy, and the number of needed partitions
k, determine the
throughout the partitioning process. Depending on the discourse universe, the number of partitions can be any integer that establishes the number of fuzzy sets. In the interval [0, 1], the membership function determines the extent to which a crisp value belongs to a fuzzy set.
Figure 1 illustrates the partitioning scheme approaches from the point of view of the ML engineer and his options, depending on each type of problem. Model accuracy is directly correlated with the
k value; however, this correlation becomes non-linear for small values of
k, which results in a few fuzzy sets representing the discourse universe, underfitting the model by generating a crude generalization with oversimplified patterns. On the other hand, a high value of
k results in minor noisy fluctuations and excessive specificity, which overfits the model and creates a large number of fuzzy sets.
The degree to which a value belongs to a fuzzy set in the interval [0, 1] is defined by the membership function . There are several methods to map a value’s membership on fuzzy sets; the most often employed ones are the generalized bell, triangular, trapezoidal, and Gaussian mappings. Although this phase has little bearing on the accuracy, it is crucial for improving the model’s readability and explainability.
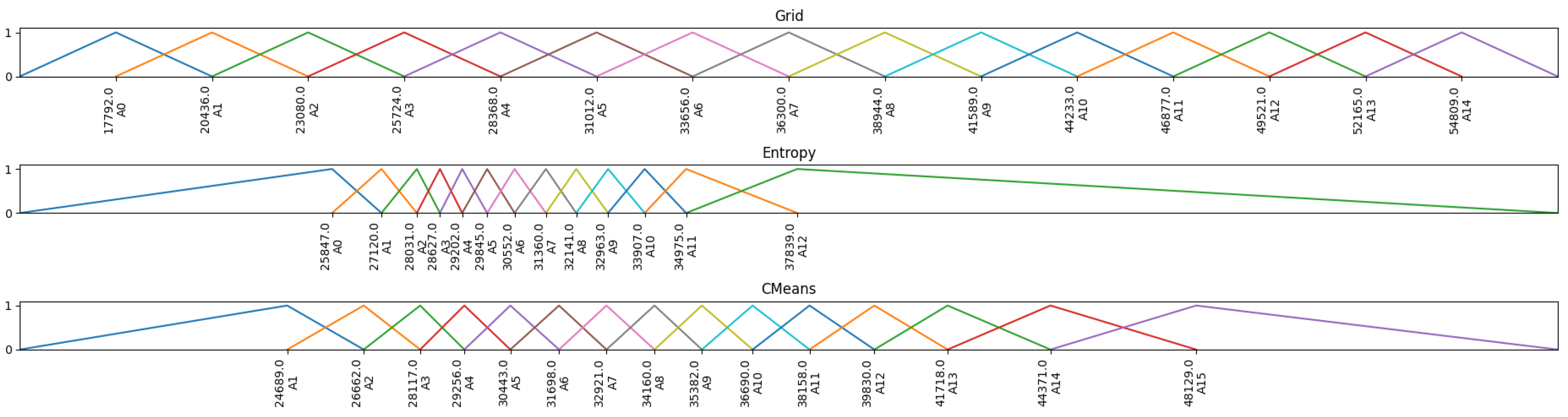
The procedure utilized in the partition phase to divide the discourse universe itself and determine the boundaries, middle point, and length of the fuzzy set is referred to as the partitioning scheme. An equal-size Partitioning is a logical way to solve the partitioning problem but is not always the best approach. The partitioning scheme directly affects the accuracy of the model and this partitioning approach gives the same importance for all fuzzy sets, that might not be the case for all datasets. The unequal-sized partitioning scheme has multiple subtopics that will not be discussed here but include entropy and clustering approaches. Entropy is an alternative to equal-sized partitioning, where there is a weight on fuzzy sets to give more importance to some and a high level of coverage to others.
Entropy based methods begins by assuming an equal-size fuzzy set split and applying the weight to transform the fuzzy set length and numbers according to necessity. The clustering partitioning scheme, on the other hand, is based on discovering the number of clusters according to the distance of the centroids. In response to the previously mentioned optimization issue, this approach is far more costly and difficult to fit, but the outcome may be much more accurate. To exemplify the partitioning schemes discussed above,
Figure 2 shows a visual reference.
The fuzzification aims to determine the degree of allegiance between the input and the fuzzy set. The fuzzification process maps every into a fuzzy set based on the membership function chosen. The fuzzification process began during the partitioning explanation phase. However, in order to extract its meaning, the next step is to build a relationship and divide the fuzzy sets into a group.
The FLR is a fuzzy rule regarding
or even
. This rule describes the temporal relationship pattern
, thus the dataset
D generates
fuzzy logical relationships [
13]. Therefore, FLR generates a matrix
fulfilled with the
of each combination; this matrix is also called a fuzzy rule matrix.
Aiming to decrease the complexity of processing a high-dimensional matrix, FLRG, proposed by Chen in [
14], extracts the relationship of precedence combinations. FLRG is based on grouping
. For example,
Figure 3 shows a fuzzified set extracted based on a grid partitioning scheme of
Figure 2 where FLRG brings the relationship between two sets to a group of relationship with that set and helps a one-step-ahead forecasting finding
.
Given a , FLRG finds this set on the antecedent part of the rules and finds out all possibilities on consequence to perform the one-step-ahead forecasting bringing a better reliability and readability to the model separating the fuzzy sets into groups and consequences, improving performance while making more easier.
2.5. High Order Fuzzy Time Series (HOFTS)
HOFTS model, proposed by [
15], uses high order
parameters to enhance the prediction with lagged values. This order (
) parameter is the memory size of the model, but even with multiple lagged values, it’s still a univariate approach. Also, an order
has a negative impact in this model accuracy [
14].
FLR is the basis of HOFTS once many antecedents
imply a consequence
, e.g., if precedence is a load demand on lag
the consequence corresponds to the outputs that were experienced in the estimation period
. Accordingly, the high-order FLR was introduced in [
14] as illustrated in Equation (
7) where each precedence item’s weight must add up to 1.
2.6. Weighted High Order Fuzzy Time Series (WHOFTS)
WHOFTS unlike HOFTS assumes that all precedence do not have the same importance in the defuzzyfication and FLRG steps; however, FLR is the same as HOFTS. There are some ways to calculate the weights, one of them, demonstrated in [
16], is shown on Equation (
8). Another way, like in [
14,
17], is to set a higher constant to older lags.
The entire number of temporal patterns with the same predecessor, such as , is represented by , or Right Hand Side, in this instance . The number of occurrences of on temporal patterns with the same antecedent is represented by under this scenario.
2.7. Multivariate Fuzzy Time Series
Indeed, managing multivariate time series is not a simple operation, but a common approach used is a clustering model to reduce multivariate data to multiple univariate data, like Fuzzy C-Means in [
18,
19,
20].
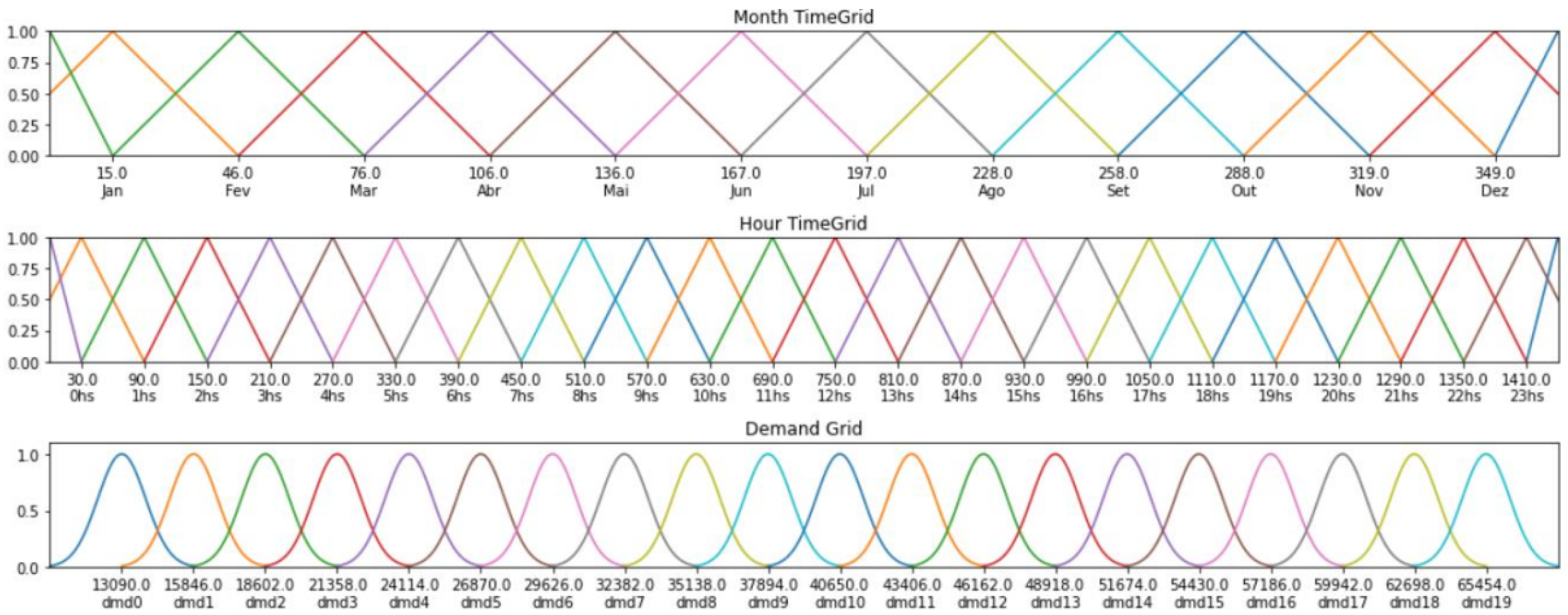
Multivariate Fuzzy Time Series (MVFTS) is a point forecasting model of type Multiple Input/Single Output (MISO) with order
. MVFTS starts to differ on the partition step once each endogenous variable can have different membership functions and partitions, like grid and seasonal time grid in the case of cyclic variables such as month and hour. The logic of FLR and FLRG stays the same despite the multivariate nature of the data, and only the fuzzyfication process handles this uncoupled. Weighted Multivariate Fuzzy Time Series (WMVFTS) differ from MVFTS once it assumes that not all precedence have equal the same importance in the defuzzyfication and FLRG steps; however, FLR is the same as MVFTS and the equation of weights can be one of many possible ways to reach a proper weight for the data, like Equation (
8).
2.8. GranularWMFTS Model
The foundation of GranularWMFTS is Fuzzy Information Granules (
), a method of defining entities that represent subsets of a broader domain that was introduced by [
21]. Every
functions as a multivariate fuzzy set, or a composite of distinct fuzzy sets from various variables, enabling the replacement of a vector with a scalar containing the data point’s greatest membership value. When the variables are treated as target and endogenous,
-FTS serves as a Multiple Input/Multiple Output (MIMO) model, enabling multivariate forecasting.
Given a multivariate time series . Each have a corresponding variable . Data points that represent a series of fuzzy information granules are then assembled to generate the resultant FTS F. The global linguistic variable is the union of all . In GranularWMVFTS, each variable is independent and has its linguistic variables . These granules are the combination of a fuzzy set for each variable, such as . Each variable’s membership function adheres to the minimal triangular norm (T-norm), and the midpoints () of its internal fuzzy sets serve as the set’s index. That is, once , each multivariate data point may be transformed by the linguistic variable in the fuzzyfication stage into .
After the fuzzification process, the fuzzified data can feed a Probabilistic Weighted Fuzzy Time Series (PWFTS) model to continue the process (FLR, FLRG, and so on) with point, interval, or probabilistic forecasting. This PWFTS model creates a Fuzzy Temporal Pattern (FTP) that is quite similar to FLR, in terms of representation:
, despite the temporal dependency that involves the consideration of time intervals and the relationships between events over time. Moreover, despite the time dependence of FTP, a FLRG-like Fuzzy time Pattern Group (FTPG). When a certain set
is recognized at time t (the antecedent), each FTPG may be interpreted as the set of possible outcomes that could occur at a particular time
(the consequent) [
16].
Finally, the empirical probability is computed using Probabilistic Weighted FTPG (PWFTPG), in which the precedence and consequence sides are weighted to measure their fuzzy empirical probabilities. Given that the fuzzy set is identified at time t, the weights can be interpreted as the empirical conditional probability of the fuzzy set on time .
3. Results and Discussion
Regarding the methodologies provided in the preceding part, each method behaves differently with the same data set; hence, a comparison is made to demonstrate forecasting accuracy. For this study, the PyFTS library was used and 48 steps ahead in the forecasting. Since the data set is univariate, the best multivariate model was used. Hour and month variables were introduced using the grid partitioning schema, and for demand variables, a Gaussian partitioning scheme was used, as shown in
Figure 4.
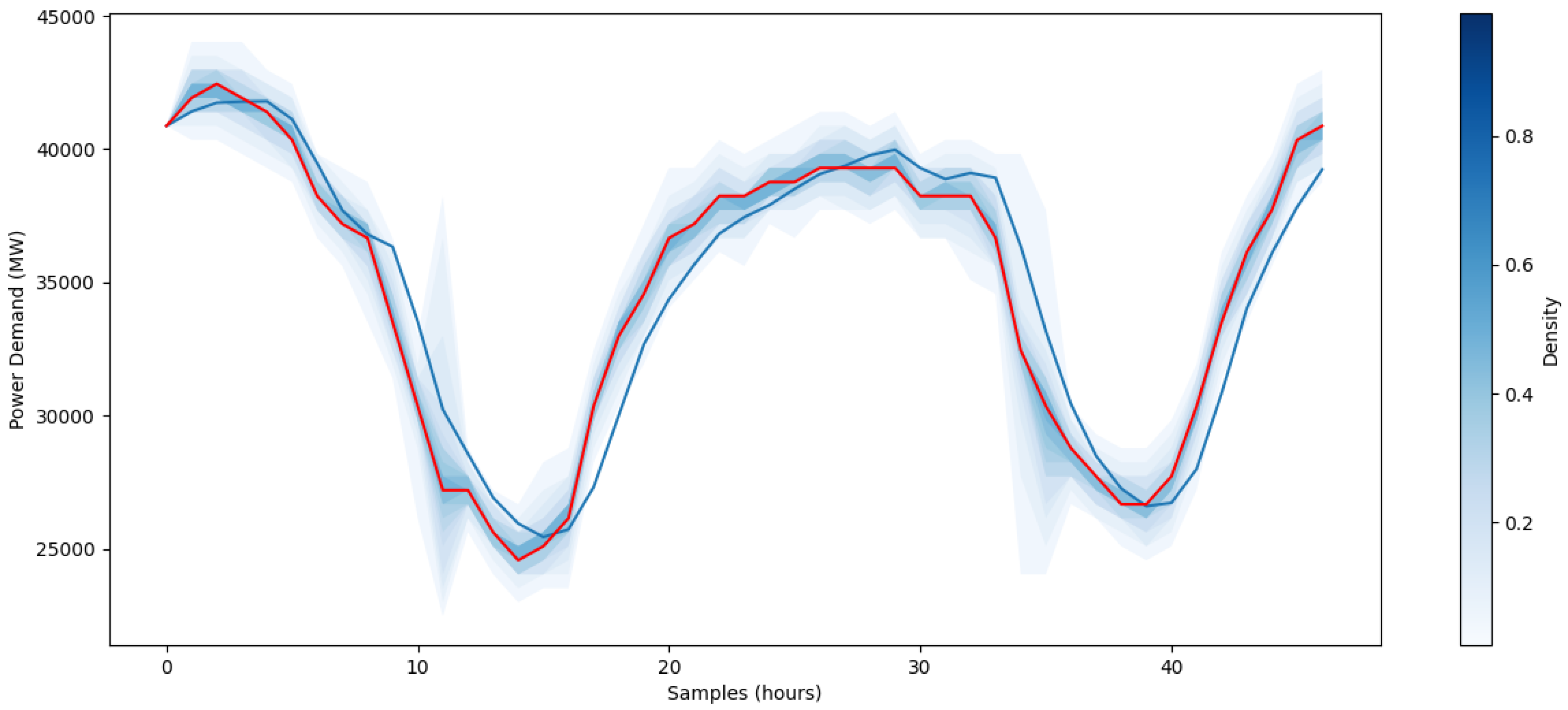
Regarding STLD, it’s common to expect a value as a result, or a point prediction, on the data set at
, but a probability prediction tells a lot more and follows the path to be usable to any application, carrying the interval expected the true value to be and the error based on the distribution of the data. The last model, GranularWMVFTS, supports a forecasting distribution probability and returns a graphical resource with probabilistic information carrying the uncertainty of each
as shown on
Figure 5. Despite that, all results from all models tested are presented in
Table 2.
Root mean square error is one of the most used error evaluation metrics of a model in forecasting quantitative data. Formally RMSE is defined by Equation (
9) where
are predicted values,
are observed values, and
n is the number of observations. The meaning of RMSE is a Euclidian distance of these points, ignoring the number of observations (
n). Now considering the whole rooted variables, RMSE can be thought of as the normalized distance of the forecasted values from the observed ones. Once RMSE is a statistical evaluation based on variance and mean of the error, it expects that the observed data can be decomposed as Equation (
9) where error represents distributed random noise with mean zero.
RMSE has a double purpose in data science, such as serving as a heuristic for training models or evaluating trained models for usefulness. In case of use to evaluate the model’s accuracy, RMSE metrics output is strongly dependent on unity. RMSE reliability should be rated, an RMSE too small can represent an overfitting issue due to the number of parameters exceeding the number of data points. So, the result should be evaluated, and think if the small result is an overfitting or a good forecasting.
sMAPE is also a well-known error evaluation metric because the output is a percentage error, which does not depend on the unity itself. The sMAPE is computed as the average of the absolute % errors between the actual values, y, and the anticipated values,
. Each error is weighted by the total of the absolute values of the actual and predicted values. A score of 0 denotes an exact match between the actual and anticipated values, while a score of 1 denotes no match at all. The final score falls between 0 and 1. A lower sMAPE number is preferable, and the percentage error is often calculated by multiplying it by 100%. The optimal score is 0; lower values are preferable.
The Auto-Regressive method performed better as the p parameter grew but when the q parameter was added, turning into an ARMA model, the accuracy did not grow as expected, the ARIMA model brings up a better accuracy, in comparison of the best AR model. Probably an AutoARIMA can result in a better accuracy next time, but analytically the best result found was for ARIMA (p, q, d = 14, 1, 4). HW did not perform well, regarding ARIMA, but could help analyze the trend component. Entering fuzzy-based paradigms, the univariate performs better than any stochastic method tested and was enhanced using a weighted form, and when a multivariate strategy was added, the accuracy grew much more, showing the usability of the multiple seasonality as an input variable to the forecasting problem. Other important variables, such as weather, temperature, and so forth, could enhance the results more. We optimized fuzzy hyperparameters such as partitions k, partitioning schemes, membership functions, and order as follows:
RMSE and sMAPE grew from
to
as
k increased as the time of fit and prediction increased, according to an analysis of partition
k. The other hyperparameters were fixed on order as
, grid partitioning, and the triangular membership function. Regarding the partitioning scheme, shown in
Figure 2, three partitioning schemes were analyzed: grid (equal-sized partitioning), entropy (mathematical method), and CMeans (clustering algorithms), where other hyperparameters were fixed on order as
, triangular membership function, and partition as
.
Grid partitioning had the best result, followed by CMeans and entropy, which had a significant jump compared to grid partitioning. In terms of RMSE CMeans was 63% worse and Entropy was 149% worse than grid partitioning on this dataset with these hyperparameters fixed. Regarding the membership function, three functions were analyzed, such as triangular, trapezoidal, and Gaussian where all other hyperparameters were fixed on order as
, grid partitioning, and partition as
. There was no difference between triangular and trapezoidal membership functions regarding RMSE and sMAPE but Gaussian had a 7% worse performance. Analyzing order
has few options once [
14] demonstrate that
affects performance, but on
Table 3 what happens to RMSE and sMAPE on orders above 3 and the time taken to fit and predict the data. Thus, the hyperparameters chosen for this paper to FTS models are
,
,
and
, used to achieve the results on
Table 2. To achieve these times, it was used a 32 GB RAM (random access memory) computer with Intel i7-12700 (Intel, Santa Clara, CA, USA). No GPU (Graphics Processing Unit) was used during the tests.
Using the criteria of 5% to choose forecasting methods for short-term Term Load Demand Forecasting, the approved approaches can be seen in
Table 2. The 5% criteria were based on how much a company can miss without changing the resultant action regarding the forecasting; the information was provided directly by the technical team. Hence, these approaches could be used to enhance a load-shedding process and even a grid reconfiguration starter, ensuring the availability and reliability of the network. The case of load shedding is quite critical, so the lowest RMSE is required. These approaches could be an exogenous variable in the energy stock to evaluate the price of the energy due to the power demand.
The Granular WMVFTS was chosen as the favorite rather than Weighted MVFTS, despite the best performance of this version, due to ability of GWMVFTS to forecast a set of values inside a universe of possible values, instead of the point prediction of WVMFTS. This decision was made because in short time forecasting, in cases of operational safety, turbine control, network integration, stability, or resource reallocation, a set of statistical proven values gives a confidence to act properly when needed.