Abstract
This paper focuses on the economic power dispatch (EPD) operation of a microgrid in an OPAL-RT environment. First, a long short-term memory (LSTM) network is proposed to forecast the load information of a microgrid to determine the output of a power generator and the charging/discharging control strategy of a battery energy storage system (BESS). Then, a deep reinforcement learning method, the deep deterministic policy gradient (DDPG), is utilized to develop the power dispatch of a microgrid to minimize the total energy expense while considering power constraints, load uncertainties and electricity price. Moreover, a microgrid built in Cimei Island of Penghu Archipelago, Taiwan, is investigated to examine the compliance with the requirements of equality and inequality constraints and the performance of the deep reinforcement learning method. Furthermore, a comparison of the proposed method with the experience-based energy management system (EMS), Newton particle swarm optimization (Newton-PSO) and the deep Q-learning network (DQN) is provided to evaluate the obtained solutions. In this study, the average deviation of the LSTM forecast accuracy is less than 5%. In addition, the daily operating cost of the proposed method obtains a 3.8% to 7.4% lower electricity cost compared to that of the other methods. Finally, a detailed emulation in the OPAL-RT environment is carried out to validate the effectiveness of the proposed method.
1. Introduction
The use of microgrids has drawn significant attention in recent years due to their potential to improve the stability and reliability of power distribution systems. A microgrid is a small-scale power grid that can operate independently or in connection with the main power grid [1,2]. Each microgrid can not only operate independently using its own control mechanism, but also can integrate the renewable energy resources, isolate the failed grid and save operation costs through peak shaving. A microgrid typically includes a combination of renewable energy resources (RERs), such as a photovoltaic (PV) plant, wind turbine generator (WTG) and battery energy storage system (BESS), as well as distributed energy sources (DESs), such as a gas turbine and diesel generators. Although the microgrid with RER integration provides flexibility and sustainability benefits, it also faces challenges in stable and power dispatch due to the uncertainties of intermittency that are unexpected and dynamic power variations resulting in real-time balancing operation. To solve these problems and ensure the cost effectiveness of microgrid systems, it is essential to minimize the operation costs via economic power dispatch (EPD). The EPD problem arises in microgrid systems and involves minimizing the total fuel cost of power generation, while ensuring that the power demand is met, and the generation limits are respected [3,4,5]. The objective is to optimize the generation schedule of multiple generators in the microgrid, such that the overall fuel cost is minimized without violating any operational constraints. The EPD problem can be formulated with different fuel cost functions, depending on the type of generators used in the microgrid. However, the complexity of the EPD problem increases with the integration of more RERs in the microgrid system. Therefore, it is necessary to develop an efficient and effective method to solve the EPD problem.
The EPD problem has been extensively studied in the literature, and various techniques have been proposed to solve the problem. Traditional methods such as linear programming (LP), quadratic programming (QP), and mixed-integer programming (MIP) have been widely used for solving the EPD problem in power systems [6,7,8]. However, these methods have some limitations, such as high computational complexity and the inability to handle the nonlinearities of the system [9,10,11]. Moreover, metaheuristic algorithms, such as the genetic algorithm (GA), particle swarm optimization (PSO), and differential evolution (DE), have shown good performance in solving the EPD problem in microgrid systems [12,13,14]. Nevertheless, it is worth noting that these methods may converge to suboptimal solutions and suffer from slow convergence rates [15,16,17].
Load forecasting is an important component of microgrid operation, as it can help predict the power demand of a microgrid in advance. Accurate load forecasting allows microgrid operators to plan and allocate resources effectively, which can improve the efficiency and reliability of microgrid operation [18,19]. In recent years, deep learning algorithms have shown promising results in solving various optimization problems in power systems. Long short-term memory (LSTM) networks are a type of recurrent neural network (RNN) that are well-suited for time series data, such as load forecasting. LSTM networks can capture long-term dependencies in time series data and are able to remember information from previous time steps. In this study, an LSTM network is utilized to predict the load demand of a microgrid. The LSTM network is trained on historical load data and can predict the load demand for the next time step based on the current and previous load values [20,21].
Deep reinforcement learning (DRL) has shown great potential for solving complex control problems in various domains. It combines the power of deep neural networks with the principles of reinforcement learning to enable agents to learn complex decision-making policies directly from high-dimensional inputs, without the need for hand-crafted features. Some popular DRL algorithms, such as the deep Q-network (DQN) and deep deterministic policy gradient (DDPG), have been applied to optimize the EPD strategy of microgrids [22,23]. The DQN is a model-free, off-policy algorithm that uses a deep neural network to approximate the Q-value function. The Q-value function estimates the expected total reward an agent will receive by taking a certain action in a certain state. Moreover, the DQN employs experience replay, and this helps to break the correlation between consecutive samples and stabilize the learning process [24,25]. On the other hand, the DQN aims to obtain the Q-value estimates in discrete action space. Therefore, in the continuous action domains, such as the EPD problem, the performance of the DQN is less than outstanding. In addition, the DDPG is an actor–critic algorithm that learns a deterministic policy function and a Q-value function simultaneously. The policy function maps states to actions, while the Q-value function estimates the expected total reward an agent will receive by taking a certain action in a certain state, following the policy function. DDPG uses a target network, a delayed copy of the Q-network and the policy network, to update the networks, which reduces the variance of the gradients and stabilizes the learning process [26,27,28]. Since DDPG can learn the policies in high-dimensional space and possess great potential to process continuous action problems, it will achieve better performance on the EPD problem than the DQN will.
DRL algorithms have several advantages in solving the EPD problem of power systems. Firstly, they can learn from experience and adapt to changes in a microgrid system, making them more flexible and adaptable than traditional methods. Secondly, DRL algorithms can handle stochastic and uncertain conditions, which are common in renewable energy sources such as solar and wind power. Thirdly, DRL algorithms can handle non-linear and non-convex optimization problems, which are often encountered in microgrid systems. Lastly, DRL algorithms can provide near-optimal solutions in a relatively short time, which is important for real-time applications. These advantages make DRL algorithms a promising solution for efficient and sustainable microgrid operation [29,30,31]. Therefore, this study proposes a novel approach that combines LSTM-based load forecasting with the DDPG algorithm to optimize the EPD strategy of microgrid systems. The proposed method uses historical load data to train the LSTM network to forecast the load demand for the next time step. The forecasted load demand is then used as input to the DDPG algorithm to determine the optimal dispatch strategy for the microgrid system. The objective of this research is to minimize the overall fuel cost of a microgrid while meeting the demand and supply constraints.
This study focuses on the EPD of a microgrid system on Cimei Island [32], which is connected to the main grid via submarine power cables. The microgrid system includes PV and WTG sources with a predetermined output power provided by a Taiwan power company (Taipower). To optimize the EPD strategy of the microgrid system, control strategies are developed for the efficient operation of the diesel generator, gas turbine generator, and the BESS to minimize electricity bills. Moreover, the proposed method is implemented using a hardware-in-the-loop (HIL) mechanism developed with OPAL-RT real-time simulator OP4510 and a floating-point digital signal processor (DSP) from Texas Instruments TMS320F28335 for BESS control. The rest of this study is organized as follows. The modeling, formulations and configurations of the microgrid are presented in Section 2, and the DDPG with LSTM method for EPD is proposed in Section 3. Some test cases with different EPD methods are investigated to verify the performance of the proposed methodology in Section 4. The emulation in an OPAL-RT real-time environment is presented in Section 5. Finally, some conclusions are presented in Section 6.
2. Microgrid Model
The microgrid model of Cimei Island [32] is utilized in this study. A single-line diagram of the island is shown in Figure 1, which includes a diesel generator, a gas turbine generator, a 355 kWp PV system, a 1000 kWh BESS, a wind farm with a 305 kW WTG system, loads, and some demand response resources. The BESS is capable of charging or discharging power from/to the microgrid, where the negative and positive signs indicate the charging and discharging power of the BESS, respectively. Moreover, power variations of PV and WTG systems for a day are provided by Taipower. Furthermore, the microgrid is connected to the main grid and actively participates in real-time electricity markets to take advantage of the real-time electricity prices. Thus, the power can flow between the main grid and the microgrid, where the positive sign indicates power consumption in the microgrid, and the negative sign indicates power flowing into the main grid. Table 1 lists the three-stage electricity rates of Taipower in USD. This study aims to minimize the costs of fuel generators and electricity bills to ensure profitability for microgrid operators while providing additional support to the main grid. The mathematical formulations used to solve this problem are presented below.
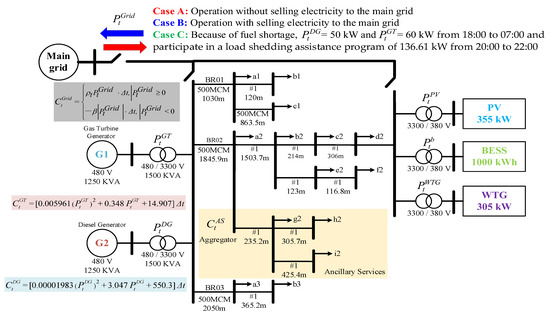
Figure 1.
Single-line diagram of Cimei Island power system.

Table 1.
Three-stage electricity cost of Taipower.
2.1. Conventional Power Generator
The microgrid system model, shown in Figure 1, involves the control of the total cumulative power consumption and the peak power to minimize the expenses incurred from fuel generators and electricity bills. The model encompasses a comprehensive representation of the DESs, the BESS, main grid, and power balance, along with their respective physical properties and technical constraints. Detailed descriptions of the model are presented below.
2.1.1. Diesel Generator
To take into account technical constraints, the power output of the diesel generator at each time slot, , is represented as and formulated as follows:
The minimum and maximum power limits of the diesel generator are denoted as and , respectively. To calculate the generation cost of the diesel generator, a conventional quadratic cost function is used as follows:
where is the duration of a time slot; , and are positive coefficients.
2.1.2. Gas Turbine Generator
The power output of the gas turbine generator at each time slot, t, is represented as and formulated as follows:
where the minimum and maximum power limits of the gas turbine generator are denoted as and , respectively. To calculate the generation cost of the gas turbine generator, a conventional quadratic cost function is used as follows:
where is the duration of a time slot; , and are positive coefficients.
2.2. Renewable Power Generator and Loads
The power generation curves of PV and WTG systems are shown in Figure 2, and they are downsized proportionally to meet the capacity of the systems in this study. These curves are based on the daily average solar and wind power production curves provided by Taipower for the Taiwan area. Moreover, the hourly power output of PV and WTG systems varies according to the corresponding values shown in Figure 2. Let and denote the power production of PV and WTG systems, respectively. The load connected to the microgrid varies according to the predicted value of the LSTM load forecasting model and is denoted by . The net load of the microgrid at time slot is defined by Equation (5):
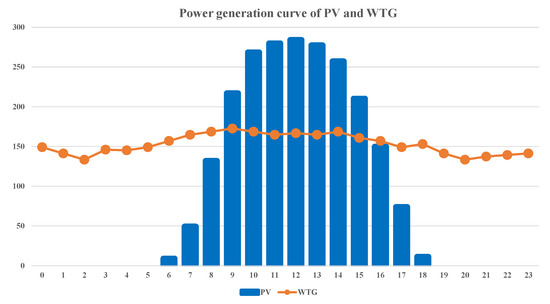
Figure 2.
Piecewise solar power generation curve of PV system and power generation curve of WTG system.
2.3. BESS
To control the charging or discharging of the BESS in each time slot, , the power output is denoted by , with negative values indicate charging and positive values indicate discharging. The power output is constrained by Equation (6) to prevent over charging or discharging.
where is the maximum discharging power and represents the maximum charging power. Moreover, the BESS has a state of charge (SOC) denoted as , which follows a certain dynamic behavior described by the following:
where is the capacity of BESS. Additionally, to ensure safe operation, it is important to maintain the SOC of the BESS within a secure range via the following:
where, to prevent over-discharging or over-charging, the lower and upper limits of SOC of the BESS are denoted as and, respectively, and they represent the acceptable minimum and maximum SOC values.
2.4. Electricity Trade and Power Balance
2.4.1. Purchase/Sell Electricity from/to Main Grid
The microgrid in this research has the option to purchase electricity from or sell electricity to the main grid through a contract with the utility. The real-time purchasing price at time slot is denoted as in the formulation, while the selling price is represented as . As a result, the microgrid’s transaction cost can be expressed as Equation (9):
The power flow between the main grid and microgrid is denoted by . The cost of purchasing electricity from the main grid is represented by , and the cost of selling electricity to the main grid is denoted by . At each time slot,, the microgrid can either purchase or sell electricity. Therefore, is subject to the following constraints:
The maximum power that the microgrid can handle at the point of common coupling (PCC) is denoted as .
2.4.2. Ancillary Services
To maintain the operation of the main grid during power shortages, the microgrid can offer ancillary services such as a demand response, which can be purchased by the main grid at a price denoted by . Moreover, the aggregator can be found in Figure 1. The payment for the transaction can be expressed as follows:
The aggregate power consumed by the dispatchable loads within the microgrid is denoted as .
2.4.3. Power Balance
To ensure the reliable and secure operation of the microgrid system, it is crucial to schedule sufficient power generation to meet the demand. An energy management strategy is employed for the coordinated control of the generating units to maintain the power balance. In this study, as the main objective is to optimize the energy management of a grid-connected microgrid, the power generation dispatch at each time slot must satisfy the following power balance constraint:
Equation (12) represents the power balance constraint, where the left-hand side represents the total power supplied by the generating units and the right-hand side represents the total power consumed by the loads. It is necessary to ensure that the power balance constraint is always satisfied.
In order to verify the performance of the proposed method for optimal EPD and power generation using the HIL mechanism, the active/reactive power control structure of the BESS proposed in [32] is adopted, and the controllers of the BESS are modeled in the DSP board control system. Additionally, since synchronous generators are typically used in diesel generator and gas turbine generator systems, the active/reactive power control structures of these systems are designed using virtual synchronous generators with inertia [33,34]. The controllers of the diesel generator and gas turbine generator systems are modeled in OP4510.
3. Proposed Methodology
3.1. Deep Reinforcement Learning
Deep reinforcement learning (DRL) is the combination of deep learning (DL) and reinforcement learning (RL) approaches. DL, which consists of a deep neural network divided into three parts, input, hidden and output layers, is able to perform learning in a complex and comprehensive data environment. RL includes the agent, environment, action and reward. The agent explores the environmental state, takes action under the dynamic environment, and looks forward to maximizing the reward.
The DQN, one of the DRL algorithms, can provide a stable solution to deep value-based RL. It has three main components, replay buffer, Q-network and target network as shown in Figure 3. The DQN employs experience replay, a technique that stores past experiences of the agent in a replay buffer and randomly samples batches of these experiences to update the Q-network. Moreover, the Q-network and target network comprise three main components: input, hidden and output layers. The input layer receives the state of the environment, which is usually represented as a set of features or raw sensory data. The hidden layer uses nonlinear functions as the activation function to transform the input into a high-level representation that captures the relevant information for decision-making. Finally, the output layer computes the Q-values for each action in the action space, which represents the expected future rewards if that action is taken.
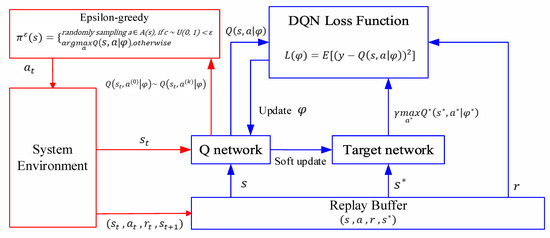
Figure 3.
Workflow of DQN algorithm.
3.2. MDP Model
In this section, the EPD operation of a microgrid is formulated as a Markov decision process (MDP). Firstly, the agent observes the state, , of the environment, and then it selects and takes an action, , which is based on the observed state. After that, the agent receives a reward, , from environment and observes a new state, , of the environment. The MDP model of EPD operation is defined by the tuple {S, A, T, R}, and the elements for the MDP model are defined in the following.
- System sate
The system state, , of the microgrid at time step t is denoted as = (, ) including the total load demand of the microgrid, , the SOC of BESS, , the power output of PV, , the power output of wind turbine, , and the present electricity price, .
- Action
denotes the action at time step t and is taken by the agent under the current system state. It is described as = (, ) including the output power of the gas turbine generator, , the output power of the diesel generator, and the BESS charging or discharging power, .
- Transition probability
The transition function, , denotes the transition probability from the system state, , to state under the action as Equation (13):
As the above distribution is determined, the state transition is determined by system state and action .
- Reward function
The reward function, , is the negative equivalent of the microgrid operational cost at time step t. It consists of three parts: (1) defined in (2), which is the operational cost of the diesel generator at time step t, (2) defined in (4), which is the operational cost of gas turbine generator at time step t, and (3) the electricity cost from power grid defined in (9). Thus, the reward function can be defined as Equation (14):
In order to ensure the safety of the microgrid system, the power utility operator should guarantee enough power to supply the demand, so the power supplied from power grid, which is calculated as shall satisfy the power balance defined in (5).
3.3. Proposed DDPG with LSTM Method
A LSTM network is utilized to forecast the load demand information of the proposed microgrid model. It will be treated as one of the system state variables in the MDP model. Then, the DRL algorithm DDPG, which follows the MDP model to come out from the optimal power dispatch of power grid, is applied.
3.3.1. LSTM Network
The LSTM network architecture consists of one or several memory cells, with each cell comprising three main gates: the forget gate, the input gate, and the output gate. Each gate performs a specific function within the LSTM network [35]. In the LSTM network, the first step, forget gate , is to decide whether the information coming from the previous timestamp should be kept or forgotten as the definition in Equation (15):
where is the activation function; is the input information at time step t; is the information coming from the previous time step, t − 1; and represent the weight and bias of the forget gate. A sigmoid function is adopted as the activation function that will make a number between 0 and 1, and the previous information, , will be forgotten if = 0. In the next step, the input gate is used to decide the new information to be stored in the cell state. The equation of the input gate, , at time step t is defined in Equation (16):
where and represent the weight and bias of the input gate. A sigmoid function is also adopted as the activation function of the input gate, which will let the value of be between 0 and 1. At the same time, an activation function, tanh, will be applied to new information as denotes in Equation (17), so that the new information will be a value between −1 and 1. However, the new information will not be memorized directly in the cell state, and it will be calculated and updated to the cell state as the equation defined in Equation (18).
As the last step, the output gate is used to decide what would be the output. Also, the equation of the output gate, , at time state t is defined in Equation (19):
where and represent the weight and bias of the output gate. Again, a sigmoid function as an activation function is adopted in the output gate. The cell state, , using the tanh function and being multiplied by the output gate, , is the output information, , as defined in Equation (20):
Following the configuration in the LSTM network and using a single-layer memory cell with a mean squared error (MSE) loss function, the whole year hourly training data as the input information is denoted as = (, ), where is the load demand of the microgrid in Cimei Island at timestamp . The result of one particular day of forecast performance is shown in Figure 4, and the average deviation is less than 5%.
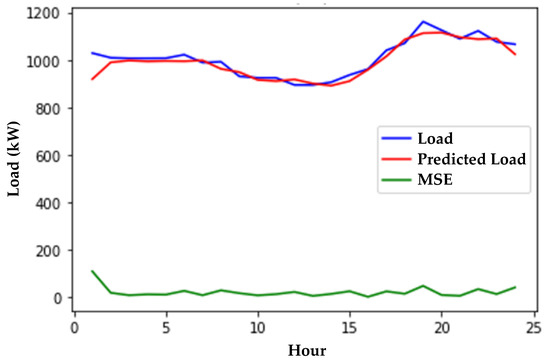
Figure 4.
Load demand forecast performance of LSTM.
3.3.2. Procedure of DDPG with LSTM Method
The proposed DDPG with LSTM method for the power dispatch optimization of the microgrid will be described in detail as follows with the workflow shown in Figure 5. The DDPG is an actor–critic, model-free algorithm which operates over continuous action spaces to learn a Q-function and uses the Q-function to learn the policy. It includes four neural networks, the evaluated actor with weights, the evaluated critic with weights, the target actor with weights and the target critic with weights. The weights of the evaluated actor, , and evaluated critic network, are randomly initialized and the weights of the target network are set as = and = . Moreover, an additional experience replay buffer, , which stores the past transition tuple , is used and cleared at the beginning. At the first of each episode, , and the normal distributed noise, , is initialized and obtains the initial observation state Following each time step, , of the episode, the evaluated actor selects and executes an action, , with exploration noise, Then, it observes a reward, , and new state, , from the system environment of the microgrid with the load demand forecast from the LSTM network. This transition will be stored in the experience replay buffer, . In the next step, a minibatch of size N is sampled from the experience replay buffer, and the evaluated critic network calculates the estimation Q-value, , with the input information, ), and the target actor network chooses a target action, . After that, target action and state are treated as the inputs of the target critic network. By adding the discounted target Q-value, which comes from the target critic network to the immediate reward, , the target critic network will come out the moving target, , that the evaluated critic tries to achieve. In addition, is denoted as Equation (21):
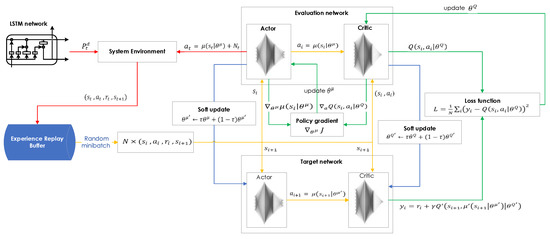
Figure 5.
Workflow of proposed DDPG with LSTM method.
Then, the loss function, L, based on temporal difference error computation is defined in Equation (22):
It is used to minimize the loss and update the weights of the evaluated critic network. Also, the policy gradient for updating the evaluated actor network can be calculated using Equation (23):
The weights of the evaluated critic and actor networks are updated sequentially as defined in Equation (24):
where and represent the learning rates for the gradient descent algorithm. In the last step, the target critic network and target actor network are also updated sequentially and softly at each episode defined in Equation (25):
where τ is a tiny gain value for the weight replacement between 0 and 1 that is based on the running average method, and the state machine will keep on going until the time step equal to and then return to the first step when starting the next episode. The following Algorithm 1 are the pseudo codes of the training process for the proposed DDPG with LSTM method.
| Algorithm 1: Proposed DDPG with LSTM method |
| 1. Initialize and train the LSTM network with = (, ). 2. Randomly initialize evaluated actor network, , and critic network, , with weights and . 3. Initialize target actor and critic network and with weights and . 4. Initialize experience replay buffer, 5. For episode = 1 to , carry out the following. 6. Initialize the Gaussian exploration noise, . 7. Receive the initial observation state . 8. For time step t = 1 to , carry out the following: 9. Select action with for the exploration noise. 10. Execute action in the system environment with the load demand forecast from the LSTM network and observe reward and new state . 11. Store transition into experience replay buffer . 12. Sample a random minibatch of the size N transition, , from experience replay buffer 13. Set 14. Update the evaluated critic network by minimizing the loss, L, as follows: 15. Update the evaluated actor policy using the sampled policy gradient: 16. Softly update the target actor and critic network with the update rate, , as follows: 17. End for. 18. End for. |
To improve the understanding of the proposed DDPG with LSTM method, the flowchart of the kernel of the DDPG algorithm is shown in Figure 6. Moreover, Figure 7 shows the training process of the DDPG with LSTM method for the EPD of the Cimei Island power system. The maximum value of episode is set to be 20,000 and one can see the trend of the average reward reaching convergence.
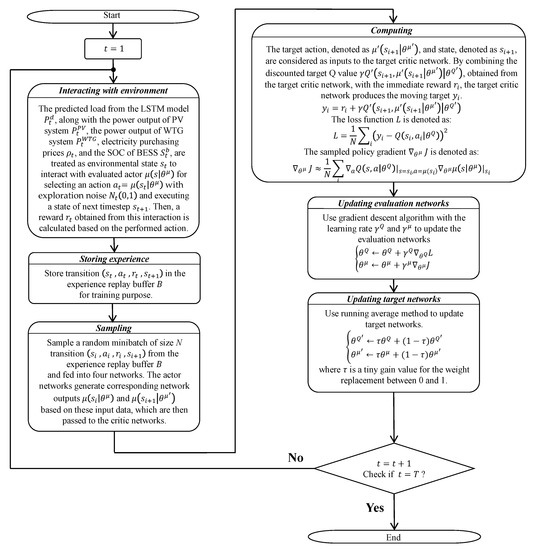
Figure 6.
Flowchart of kernel of DDPG algorithm.
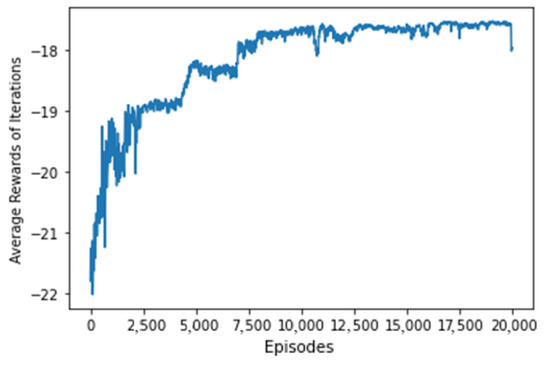
Figure 7.
Training process of DDPG with LSTM method.
4. Benchmarking
In this study, the proposed method is compared with the experience-based EMS, Newton-PSO, and DQN methods in terms of optimization performance. Additionally, to use the experience-based EMS and Newton-PSO method, reasonable assumptions must be made about the stochastic and uncertain conditions in the microgrid. Therefore, the power output of the BESS needs to be scheduled and processed as shown in the flowchart in Figure 8 and is described as below.
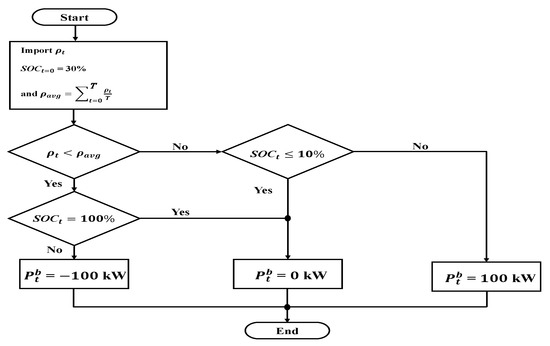
Figure 8.
Flowchart of BESS process.
- Set the initial values
Import the purchasing price of the main grid, and the SOC of the last hour with = 30% at hour 0; the average purchasing price is denoted as Equation (26)
where is the total duration of the economic dispatch operation. The objective of this study is to minimize the overall fuel cost within one day, so is set to 24.
- Check the purchasing price of the main grid.Check if the purchasing price of the main grid is cheaper than the average purchasing price.
- Make the decision.If the purchasing price of the main grid is cheaper than the average purchasing price, the BESS will charge at 100 kW; otherwise, the BESS will discharge at 100 kW.Check the SOC and decide the power output of the BESS.
- The SOC of the BESS is set to be 10% ≦ ≦ 100%. If the SOC is not within the range of the constraint conditions, the BESS does not charge or discharge; otherwise, the BESS follows the decision to charge or discharge. Moreover, the SOC of the BESS will carry on over to the next hour and proceed to the next optimization calculation.
4.1. Experience-Based EMS
The experience-based EMS is designed based on the power company expert who in charge of the power dispatch process. Its flowchart is shown in Figure 9 and described as follows.
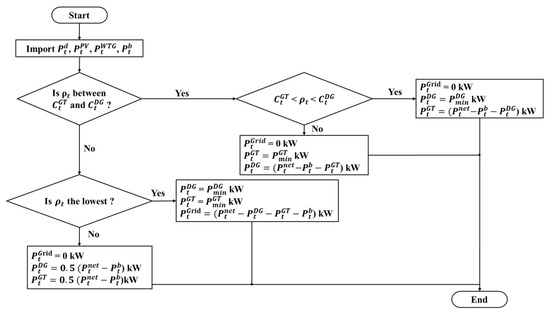
Figure 9.
Flowchart of experience-based EMS method.
- Set the initial values.Import the predictive load of the microgrid, the value of PV, the value of WTG, and the power output of the BESS.
- Check the purchasing price of main grid.Examine the purchasing price of main grid, and then calculate the fuel cost of the diesel generator and that of the gas turbine generator separately. Check if the buying price of the main grid is between the fuel cost of the diesel generator and that of the gas turbine generator.
- Make the decision.If the buying price of the main grid is between the fuel cost of the diesel generator and that of the gas turbine generator or the buying price of the main grid is the most expensive, then the output powers will be shared by the gas turbine and diesel generators; otherwise, the main grid will predominantly supply the load of the microgrid.
- Output the power of generator.The results of the EMS consist of the power commands of the diesel generator, gas turbine generator and the BESS and then are sent to the individual control blocks.
4.2. Newton-PSO
The Newton–Raphson method has been a standard solution algorithm to use for the power flow problem for decades. Newton’s method is a useful solution algorithm but has the disadvantage of slow convergence if it is not near the solution. Moreover, PSO is a population stochastic global optimizer, in which several particles form a swarm that evolve or fly throughout the problem hyperspace to search for an optimal or near-optimal solution. Many studies on Newton–Raphson-based power flow programs combined with PSO, i.e., Newton-PSO, have been proven to be effective in economic power dispatch [36,37]. Figure 10 explains the implementation of the Newton-PSO method. Initially, a swarm of random particles is created, and random positions of generator voltages are assigned to them; then, the best position is stored when they move through the search space. The best-fit particle of the minimum operation cost, , shown in Equation (27) is tracked by the algorithm, and the position of each particle is affected by that of the best-fit particle in the entire swam. Information regarding the best solution is shared throughout the swarm by updating the position and velocity. Furthermore, the loop is ended when the predefined voltage error is met, or the maximum iterations are obtained. A series of experiments are conducted to properly tune the Newton-PSO parameters to suit the targeted optimal economic dispatch problem, which considers the fuel cost and electricity billing as an objective.
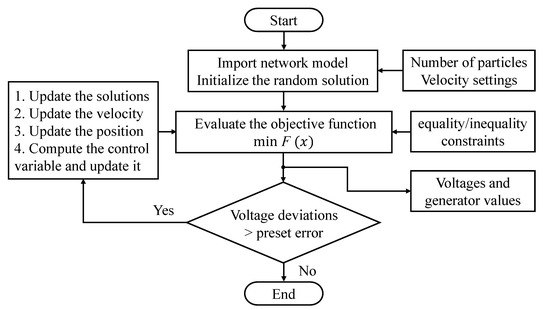
Figure 10.
Flowchart of Newton-PSO method.
4.3. DQN
The classic DQN method is a value based DRL algorithm that has shown remarkable performance in various domains. The DQN algorithm architecture is shown in Figure 3. It employs experience replay, target network, and epsilon-greedy exploration to enhance learning stability and efficiency. It is an extension of the Q-learning algorithm that uses a Q-network, which is a deep neural network with weight parameters, , as an approximator for the action value function, , as shown by Equation (28):
Based on the Bellman equation, the expression of the Q-network model can be represented as Equation (29):
where and are the training state and the action to be performed at the next time step; is the reward received by the agent during the training process at each step; is the learning rate of the Q network; is the discount factor. The target network is a separate neural network that is periodically updated to provide stable targets for the Q-value function as in Equation (30):
The Q-value targets are computed using the target network and subsequently define the objective function using the mean square error as the loss function of the neural network as in Equation (31):
which has its weights fixed for a certain number of iterations, and then is updated using the soft update technique as in Equation (32):
where is the soft update rate between 0 and 1; is the weights of target network.
4.4. Performance Comparison
In this study, three different scenarios, Case A, Case B, and Case C, are designed to compare the impact of the experience-based EMS, Newton-PSO, DQN, and the proposed DDPG with LSTM methods on the optimization performance of a microgrid. The coefficients of the cost functions shown in Equations (2) and (4) and the minimum and maximum values of the generators are shown in Table 2. The values of different limits and coefficients in Table 2 are selected based on the nominal specifications of gas turbines and diesel generators with a similar capacity to that of Taipower generators.

Table 2.
Coefficients of fuel cost and power limits of generators in microgrid.
The load variation throughout the day, as depicted in Figure 4, is obtained from a well-trained LSTM load prediction model. The hourly solar and wind power generation curves shown in Figure 2 are utilized as the values for the PV and WTG system’s output powers. To quantify the outcomes, both the experience-based EMS and Newton-PSO methods employ the same SOC policy for charging and discharging the BESS as illustrated in Figure 8. For the quantification process, a particle count of 40 is set, and 5 independent runs are executed with a maximum of 100 iterations for each parameter variation. Moreover, the velocity settings shown in Figure 10, including the inertia weight and two acceleration constants, are set to −0.1618, 1.8903, and 2.1225, respectively. These parameters are determined through trial and error, considering the requirements of optimal performance and reasonable convergence speed within a maximum of 100 iterations. Furthermore, in the DQN method, the network consists of 2 fully connected hidden layers with 256 and 256 rectified linear unit (ReLU) neurons, respectively. The output layer is also a fully connected layer with 75 linear neurons. In addition, Case A and Case B represent the operation of the Cimei Island microgrid without selling electricity to the main grid and with the sale of electricity to the main grid, respectively. Case C is designed for a scenario in which the microgrid experiences sudden fuel shortage, requiring the gas turbine and diesel generator in the microgrid to operate at a minimum load of 60 kW and 50 kW, respectively, from 18:00 to 07:00. Additionally, the microgrid is obligated to participate in a load-shedding assistance program of 136.61 kW from 20:00 to 22:00 and transfer the load to the gas turbine and diesel generator units upon receiving the assistance instruction from the power company.
Figure 11, Figure 12 and Figure 13 represent the comparison of optimization results using the experience-based EMS, Newton-PSO, DQN, and DDPG with LSTM methods under three different scenarios: Case A, Case B, and Case C. Owing to the multiple particle optimization of the Newton-PSO method and the end-to-end learning capabilities of the DQN method, the total cost is well-reduced compare to that of the experience-based EMS method. Moreover, the degree of convergence of the DDPG with the LSTM method is more stable than that of the DQN method in continuous action space. Thus, the DDPG with LSTM method has the lowest average cost compared to that of the other methods. Furthermore, the results of optimization based on the DDPG with LSTM method are shown in Table 3, Table 4 and Table 5. Table 3 presents the results for Case A, where the utility company implements a peak-shaving strategy with three different electricity prices. The main grid purchases electricity at a lower price than the average price from 22:00 to 07:00, while during the high or semi-high peak periods from 07:00 to 22:00, the main grid purchases electricity at a higher price than the average. In addition, Table 4 displays the outcomes for Case B, where the microgrid, based on the generation plan from Case A, fulfills its contractual obligation with the utility company by selling 500 kW of electricity to the main grid from 13:00 to 17:00 at an agreed price of 0.149 USD/kWh. In Case C, as illustrated in Table 5, a simulation is conducted to represent a sudden fuel shortage in the microgrid. During this period, the gas turbine and diesel generators operate at the minimum power output from 18:00 to 07:00 on the next day to conserve the fuel inventory. The microgrid purchases electricity from the main grid to supply the load. Additionally, the microgrid operator receives a notification to implement an auxiliary service plan, reducing the load by 136.61 kW from 20:00 to 22:00 at an agreed price of 0.237 USD/kWh. The load is then transferred to the gas turbine and diesel generators without any power outage.
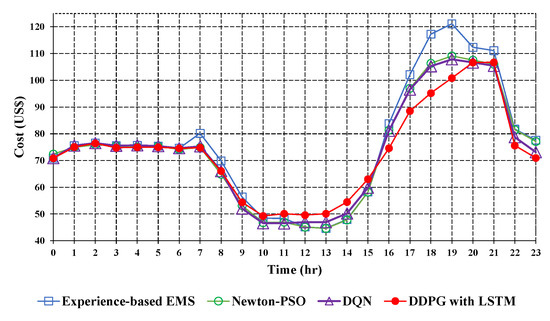
Figure 11.
Optimization results of various methods in Case A.
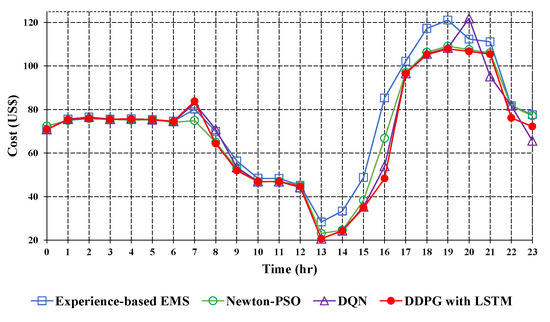
Figure 12.
Optimization results of various methods in Case B.
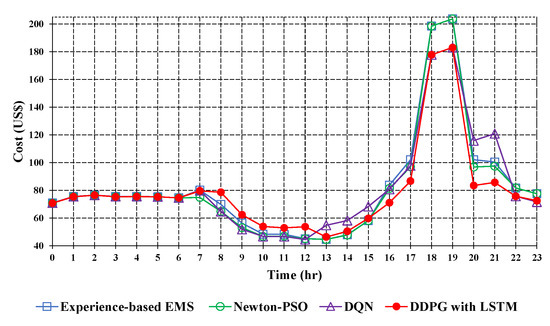
Figure 13.
Optimization results of various methods in Case C.

Table 3.
Optimization results of DDPG with LSTM method in Case A.

Table 4.
Optimization results of DDPG with LSTM method in Case B.

Table 5.
Optimization results of DDPG with LSTM method in Case C.
Table 6 is the comparison of the daily total operating costs for the four methods using the experience-based EMS, Newton-PSO, DQN and DDPG with LSTM. As one can see, in Table 6, the performance judged according to the daily total cost of the proposed DDPG with LSTM method is better than that of the experience-based EMS, Newton-PSO and DQN methods. Though the Newton-PSO and DQN methods can possibly achieve overall optimization results, the proposed DDPG with LSTM method is still able to find the best results.

Table 6.
Comparison of fuel cost and electricity billings of various methods in Case A, B and C.
5. Experimentation
5.1. OPAL-RT Environment and Implementation
Figure 14 depicts the experimental setup of HIL utilized to optimize the energy management of a microgrid. Testing the performance of a real microgrid system is challenging due to the complexity of power components and consumer loads. To overcome this, a real-time simulator is employed as a crucial tool for exploring the power system’s characteristics. In this study, the OPAL-RT real-time high-speed simulator, manufactured by OPAL-RT Co., Ltd., in Montreal, QC, Canada, is chosen for its excellent integration capabilities with simulation software such as MATLAB and LabVIEW. The proposed method’s optimal solutions are verified through the HIL mechanism, making it practical for the Cimei Island microgrid. Moreover, the testing platform consists of various components, including an oscilloscope, a host computer equipped with an EMS containing different EPD methods, peripheral circuits, a CANalyst SN65HVD230 CAN bus transceiver communication module, and a DSP TMS320F28335 control board integrated with the HIL mechanism built with the OPAL-RT real-time simulator OP4510 and the RT-LAB environment. The OP4510 simulator features two 16-channel digital-to-analog converter modules (OP5330), one 16-channel analog-to-digital converter module (OP5340), and one 32-channel digital signal conditioning module (OP5353). The BESS controller is implemented using the C language on Texas Instruments TMS320F28335 DSP, and the observed signals are transferred to the oscilloscope via the serial peripheral interface (SPI). Furthermore, a dedicated CAN bus transceiver communication module is employed to receive active/reactive power commands of the BESS from the EMS.

Figure 14.
Experimental setup of HIL.
Figure 15 provides an illustration of the OPAL-RT structure and its peripherals. The entire Cimei Island microgrid, with the exception of the BESS controller, is modeled in the host system and then transferred to OP4510 through Ethernet communication. In HIL, the inverter models are designed by the authors based on specifications [32,33,34]. The microgrid components, including the inverters of the BESS and the virtual synchronous generators of the diesel generator and gas turbine generator, are modeled in the field programmable gate array (FPGA) of OP4510. On the other hand, the PV, the BESS, WTG modules, and the diesel generator and gas turbine generator are modeled in the CPU of OP4510. Additionally, the active/reactive power commands for the diesel generator and gas turbine generator are transmitted from the EMS in the host system to the OP4510 CPU using Ethernet communication as well. The control blocks of the BESS operate with a sampling time of 1 ms, and the PWM switching frequency for the BESS inverter is set at 16 kHz.
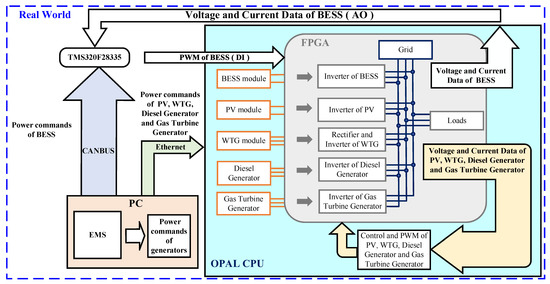
Figure 15.
Structure of OPAL-RT and peripherals.
5.2. Emulation Result
To minimize fuel costs based on changes in predictive load, PV, and WTG power, this study designed three cases and used the proposed DDPG with LSTM method to emulate the optimization results in real time using the HIL system depicted in Figure 14. In Case A, where no electricity is sold to the main grid, Figure 16a presents the emulated responses of the predictive load, , PV , and WTG around 07:00. Moreover, the power outputs of the gas turbine generator, , and diesel generator, , are illustrated in Figure 16b, while the power flow in the main grid, , and the power output of the BESS, , are depicted in Figure 16c. In Case B, where 500 kW of power is supplied to the main grid from 13:00 to 17:00, Figure 17a presents the emulated responses of the predictive load, , PV , and WTG around 13:00. Furthermore, the power outputs of the gas turbine generator, , and diesel generator, , are illustrated in Figure 17b, while the power flow in the main grid, , and the power output of the BESS, , are depicted in Figure 17c. In addition, Case C involves a load reduction agreement between the microgrid and power company, transferring 136.61 kW of the load to the gas turbine and diesel generator units from 20:00 to 22:00. Figure 18a presents the emulated responses of the predictive load, , PV , and WTG around 22:00. The power outputs of the gas turbine generator, , and diesel generator, , are illustrated in Figure 18b, while the power flow in the main grid, , and the power output of the BESS, , are depicted in Figure 18c.
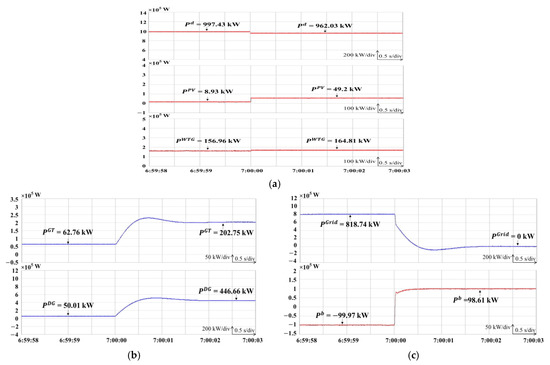
Figure 16.
Emulated responses of DDPG with LSTM at 7 a.m. in Case A. (a) Power command of PV, WTG, and predictive load; (b) power outputs of gas turbine and diesel generator; (c) power flow in main grid and power output of BESS.
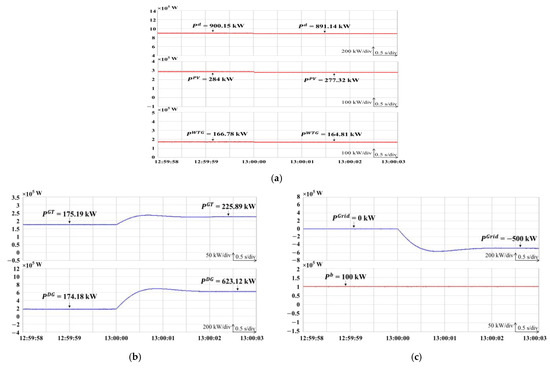
Figure 17.
Emulated responses of DDPG with LSTM at 1 p.m. in Case B. (a) Power command of PV, WTG, and predictive load; (b) power outputs of gas turbine and diesel generator; (c) power flow in main grid and power output of BESS.
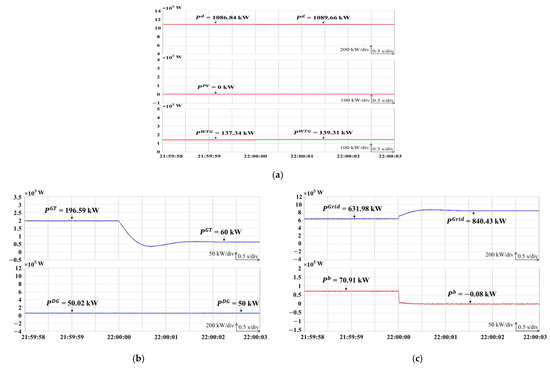
Figure 18.
Emulated responses of DDPG with LSTM at 10 p.m. in Case C. (a) Power command of PV, WTG, and predictive load; (b) power outputs of gas turbine and diesel generator; (c) power flow in main grid and power output of BESS.
6. Conclusions
In this study, a novel DRL algorithm, which is the DDPG algorithm combined with LSTM, was proposed to obtain the optimal EPD solution for a microgrid. Compared to the experience-based EMS, Newton-PSO and DQN methods, the proposed DDPG with LSTM method has a much lower electricity cost and features superior optimization performance. Moreover, the microgrid built in Cimei Island was investigated to examine the compliance with the requirements of equality and inequality constraints and the performance of the proposed method. Furthermore, the HIL mechanism was conducted to verify the effectiveness of the proposed DDPG with LSTM method to prove it to be pragmatic. From the emulation results, it has been verified that the proposed DDPG with LSTM method could obtain the best optimal EPD solution owing to its capability to learn the policies in high-dimensional space, which is very helpful to reduce costs for the operation of the microgrid. The significant contributions of the proposed DDPG with LSTM method include (1) the easy adjustment of the mathematical models of a microgrid subjected to the power balance constraints according to parameter and load variations; (2) the successfully improved accuracy of load forecasting using LSTM, resulting in more efficient EPD; (3) the successful development of solving the optimal economic dispatch solution with the ability to handle the uncertainties and dynamic characteristics of microgrid systems effectively, making it a promising solution for EPD in real-world microgrid systems; (4) the successful implementation of the results of optimal economic dispatch and power generation using the proposed method in a microgrid system built with a HIL real-time simulator to prove to be pragmatic.
Author Contributions
F.-J.L. and C.-F.C. designed and developed the main parts of research work including theory derivation and analyses of the obtained results. F.-J.L. and C.-F.C. were also mainly responsible for the preparation of the paper. Y.-C.H. and T.-M.S. contributed to the DSP-based control platform and writing parts. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministry of Science and Technology of Taiwan, R.O.C., through grant number MOST 111-3116-F-008-003.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bani-Ahmed, A.; Rashidi, M.; Nasiri, A.; Hosseini, H. Reliability Analysis of a Decentralized Microgrid Control Architecture. IEEE Trans. Smart Grid 2018, 10, 3910–3918. [Google Scholar] [CrossRef]
- Yang, P.; Yu, M.; Wu, Q.; Hatziargyriou, N.; Xia, Y.; Wei, W. Decentralized Bidirectional Voltage Supporting Control for Mul-ti-Mode Hybrid AC/DC Microgrid. IEEE Trans. Smart Grid 2020, 11, 2615–2626. [Google Scholar] [CrossRef]
- Li, C.; de Bosio, F.; Chen, F.; Chaudhary, S.K.; Vasquez, J.C.; Guerrero, J.M. Economic Dispatch for Operating Cost Minimization Under Real-Time Pricing in Droop-Controlled DC Microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 587–595. [Google Scholar] [CrossRef]
- Anglani, N.; Oriti, G.; Colombini, M. Optimized Energy Management System to Reduce Fuel Consumption in Remote Military Microgrids. IEEE Trans. Ind. Appl. 2017, 53, 5777–5785. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M.; Guerrero, J.M. Energy Management System for an Islanded Microgrid with Convex Relaxation. IEEE Trans. Ind. Appl. 2019, 55, 7175–7185. [Google Scholar] [CrossRef]
- Paul, T.G.; Hossain, S.J.; Ghosh, S.; Mandal, P.; Kamalasadan, S. A Quadratic Programming Based Optimal Power and Battery Dispatch for Grid-Connected Microgrid. IEEE Trans. Ind. Appl. 2018, 54, 1793–1805. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, L.; Li, J. A Fast LP-Based Approach for Robust Dynamic Economic Dispatch Problem: A Feasible Region Projection Method. IEEE Trans. Power Syst. 2020, 35, 4116–4119. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, F.; Li, A.; Su, Y.; Yang, X.; Zheng, J. An Optimal Generation Scheduling Approach Based on Linear Relaxation and Mixed Integer Programming. IEEE Access 2020, 8, 168625–168630. [Google Scholar] [CrossRef]
- Lin, C.; Wu, W.; Chen, X.; Zheng, W. Decentralized Dynamic Economic Dispatch for Integrated Transmission and Active Dis-tribution Networks Using Multi-Parametric Programming. IEEE Trans. Smart Grid 2018, 9, 4983–4993. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Vilaplana, D.G.; Bordons, C.; Roncero-Sanchez, P.; Ridao, M.A. Optimal Management of Microgrids with External Agents Including Battery/Fuel Cell Electric Vehicles. IEEE Trans. Smart Grid 2019, 10, 4299–4308. [Google Scholar] [CrossRef]
- Liu, C.; Ma, H.; Zhang, H.; Shi, X.; Shi, F. A MILP-Based Battery Degradation Model for Economic Scheduling of Power System. IEEE Trans. Sustain. Energy 2023, 14, 1000–1009. [Google Scholar] [CrossRef]
- Kalakova, A.; Nunna, H.S.V.S.K.; Jamwal, P.K.; Doolla, S. A Novel Genetic Algorithm Based Dynamic Economic Dispatch with Short-Term Load Forecasting. IEEE Trans. Ind. Appl. 2021, 57, 2972–2982. [Google Scholar] [CrossRef]
- Jordehi, A.R. A mixed binary-continuous particle swarm optimisation algorithm for unit commitment in microgrids considering uncertainties and emissions. Int. Trans. Electr. Energy Syst. 2020, 30, e12581. [Google Scholar]
- Jordehi, A.R. An improved particle swarm optimisation for unit commitment in microgrids with battery energy storage systems considering battery degradation and uncertainties. Int. J. Energy Res. 2021, 45, 727–744. [Google Scholar] [CrossRef]
- Ponciroli, R.; Stauff, N.E.; Ramsey, J.; Ganda, F.; Vilim, R.B. An Improved Genetic Algorithm Approach to the Unit Commit-ment/Economic Dispatch Problem. IEEE Trans. Power Syst. 2020, 35, 4005–4013. [Google Scholar] [CrossRef]
- Abbas, G.; Gu, J.; Farooq, U.; Raza, A.; Asad, M.U.; El-Hawary, M.E. Solution of an Economic Dispatch Problem through Particle Swarm Optimization: A Detailed Survey—Part II. IEEE Access 2017, 5, 24426–24445. [Google Scholar] [CrossRef]
- Raghav, L.P.; Kumar, R.S.; Raju, D.K.; Singh, A.R. Optimal Energy Management of Microgrids Using Quantum Teaching Learning Based Algorithm. IEEE Trans. Smart Grid 2021, 12, 4834–4842. [Google Scholar] [CrossRef]
- Muzumdar, A.A.; Modi, C.N.; Vyjayanthi, C. Designing a Robust and Accurate Model for Consumer-Centric Short-Term Load Forecasting in Microgrid Environment. IEEE Syst. J. 2022, 16, 2448–2459. [Google Scholar] [CrossRef]
- Trivedi, R.; Patra, S.; Khadem, S. A Data-Driven Short-Term PV Generation and Load Forecasting Approach for Microgrid Applications. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 911–919. [Google Scholar] [CrossRef]
- Alavi, S.A.; Mehran, K.; Vahidinasab, V.; Catalao, J.P.S. Forecast-Based Consensus Control for DC Microgrids Using Distributed Long Short-Term Memory Deep Learning Models. IEEE Trans. Smart Grid 2021, 12, 3718–3730. [Google Scholar] [CrossRef]
- Han, H.; Liu, H.; Zuo, X.; Shi, G.; Sun, Y.; Liu, Z.; Su, M. Optimal Sizing Considering Power Uncertainty and Power Supply Reliability Based on LSTM and MOPSO for SWPBMs. IEEE Syst. J. 2022, 16, 4013–4023. [Google Scholar] [CrossRef]
- Zhao, J.; Li, F.; Mukherjee, S.; Sticht, C. Deep Reinforcement Learning-Based Model-Free On-Line Dynamic Multi-Microgrid Formation to Enhance Resilience. IEEE Trans. Smart Grid 2022, 13, 2557–2567. [Google Scholar] [CrossRef]
- Zhang, H.; Yue, D.; Dou, C.; Hancke, G.P. PBI Based Multi-Objective Optimization via Deep Reinforcement Elite Learning Strategy for Micro-Grid Dispatch With Frequency Dynamics. IEEE Trans. Power Syst. 2023, 38, 488–498. [Google Scholar] [CrossRef]
- Sharma, J.; Andersen, P.-A.; Granmo, O.-C.; Goodwin, M. Deep Q-Learning with Q-Matrix Transfer Learning for Novel Fire Evacuation Environment. IEEE Trans. Syst. 2021, 51, 7363–7381. [Google Scholar] [CrossRef]
- Liu, Z.; Hou, L.; Zheng, K.; Zhou, Q.; Mao, S. A DQN-Based Consensus Mechanism for Blockchain in IoT Networks. IEEE Internet Things J. 2022, 9, 11962–11973. [Google Scholar] [CrossRef]
- Xu, Y.-H.; Yang, C.-C.; Hua, M.; Zhou, W. Deep Deterministic Policy Gradient (DDPG)-Based Resource Allocation Scheme for NOMA Vehicular Communications. IEEE Access 2020, 8, 18797–18807. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Gao, Z.; He, X. An Improved DDPG and Its Application Based on the Double-Layer BP Neural Network. IEEE Access 2020, 8, 177734–177744. [Google Scholar] [CrossRef]
- Ye, Y.; Qiu, D.; Sun, M.; Papadaskalopoulos, D.; Strbac, G. Deep Reinforcement Learning for Strategic Bidding in Electricity Markets. IEEE Trans. Smart Grid 2020, 11, 1343–1355. [Google Scholar] [CrossRef]
- Lin, L.; Guan, X.; Peng, Y.; Wang, N.; Maharjan, S.; Ohtsuki, T. Deep Reinforcement Learning for Economic Dispatch of Virtual Power Plant in Internet of Energy. IEEE Internet Things J. 2020, 7, 6288–6301. [Google Scholar] [CrossRef]
- Fang, D.; Guan, X.; Hu, B.; Peng, Y.; Chen, M.; Hwang, K. Deep Reinforcement Learning for Scenario-Based Robust Economic Dispatch Strategy in Internet of Energy. IEEE Internet Things J. 2021, 8, 9654–9663. [Google Scholar] [CrossRef]
- Shan, X.; Xue, F. A Day-Ahead Economic Dispatch Scheme for Transmission System with High Penetration of Renewable Energy. IEEE Access 2022, 10, 11159–11172. [Google Scholar] [CrossRef]
- Lin, F.-J.; Liao, J.-C.; Chen, C.-I.; Chen, P.-R.; Zhang, Y.-M. Voltage Restoration Control for Microgrid with Recurrent Wavelet Petri Fuzzy Neural Network. IEEE Access 2022, 10, 12510–12529. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed Power System Virtual Inertia Implemented by Grid-Connected Power Con-verters. IEEE Trans. Power Electron. 2018, 33, 8488–8499. [Google Scholar] [CrossRef]
- Tan, K.-H.; Lin, F.-J.; Shih, C.-M.; Kuo, C.-N. Intelligent Control of Microgrid with Virtual Inertia Using Recurrent Probabilistic Wavelet Fuzzy Neural Network. IEEE Trans. Power Electron. 2020, 35, 7451–7464. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual: Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Khan, N.A.; Sidhu, G.A.S.; Gao, F. Optimizing Combined Emission Economic Dispatch for Solar Integrated Power Systems. IEEE Access 2016, 4, 3340–3348. [Google Scholar] [CrossRef]
- Loyarte, A.S.; Clementi, L.A.; Vega, J.R. A Hybrid Methodology for a Contingency Constrained Economic Dispatch under High Variability in the Renewable Generation. IEEE Lat. Am. Trans. 2019, 17, 1715–1723. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).