Abstract
In the energy-planning sector, the precise prediction of electrical load is a critical matter for the functional operation of power systems and the efficient management of markets. Numerous forecasting platforms have been proposed in the literature to tackle this issue. This paper introduces an effective framework, coded in Python, that can forecast future electrical load based on hourly or daily load inputs. The framework utilizes a recurrent neural network model, consisting of two simpleRNN layers and a dense layer, and adopts the Adam optimizer and tanh loss function during the training process. Depending on the size of the input dataset, the proposed system can handle both short-term and medium-term load-forecasting categories. The network was extensively tested using multiple datasets, and the results were found to be highly promising. All variations of the network were able to capture the underlying patterns and achieved a small test error in terms of root mean square error and mean absolute error. Notably, the proposed framework outperformed more complex neural networks, with a root mean square error of 0.033, indicating a high degree of accuracy in predicting future load, due to its ability to capture data patterns and trends.
1. Introduction
Electric load forecasting (ELF) in a power system is crucial for the operation planning of the system, and it also generates an increasing academic interest [1]. For the management and planning of the power system, forecasting demand factors such as load per hour, maximum (peak) load, and the total amount of energy is crucial. As a result, forecasting according to the time horizon is beneficial for meeting the various needs according to their application, as indicated in Table 1. The ELF is divided into three groups [2]:

Table 1.
Applications of the forecasting processes based on time horizons.
- Long-term forecasting (LTF): 1–20 years. The LTF is crucial for the inclusion of new-generation units in the system and the development of the transmission system.
- Medium-term forecasting (MTF): 1 week–12 months. The MTF is most helpful for the setting of tariffs, the planning of the system maintenance, financial planning, and the scheduling of fuel supply.
- Short-term forecasting (STF): 1 h–1 week. The STF is necessary for the data supply to the generation units to schedule their start-up and shutdown time, to prepare the spinning reserves, and to conduct an in-depth analysis of the restrictions in the transmission system. STF is also crucial for the evaluation of power system security.
Various approaches can be used based on the model found. Although MTF and LTF forecasting will rely on techniques such as trend analysis [3,4], end-use analysis [5], neural network technique [6,7,8,9,10], and multiple linear regressions [11], STF requires an approach based on regression [12], analysis of time series [13], implementation of artificial neural networks [14,15,16], expert systems [17], fuzzy logic [18,19], and support vector machines [20,21]. STF is important for both the Transmission System Operators (TSOs) in the case of extreme weather conditions to maintain the reliable operation of the system [22,23] and for the Distribution System Operators (DSOs) due to the constant increase of microgrids affecting the total load [24,25] as well as the difficulty of matching varying renewable energy to the demand with diminishing margins.
The MTF and LTF require both expertise in data analysis and experience of how power systems and the liberated markets function, but the STF relies more on data modeling (trying to fit data into models) than on in-depth knowledge of how a power system operates [26]. The load forecast of the day ahead (STF) is a work that the operational planning department of every TSO must establish every day of the year. The forecast must be as accurate as possible because its accuracy will depend on which units will participate in the power system energy production the next day, to produce the required amount of energy to cover the requested system load. The historical data on load patterns, the weather, air temperature, wind speed, calendar seasonal data, economic events, and geographical data are only a few of the many variables that influence load forecasting.
The strategic actions of several entities, including companies involved in power generation, retailers, and aggregators, depend on the precise load projections, nevertheless, as a result of the liberalization and increased competitiveness of contemporary power markets. Additionally, a robust forecasting model for prosumers would result in the best resource management, such as energy generation, management, and storage.
The augmentation of “active consumers” [27] and the penetration of renewable energy sources (RES) by 2029–2049 [28] will result in very different planning and operation challenges in this new scenario [29]. Toolboxes from the past will not function the same way they do now. For instance, it becomes increasingly difficult for the future energy mix to match load demands whenever creating intriguing prospects for new players on both the supply and demand sides of a power system. The literature raises questions about how to handle the availability of energy outputs from RES and the adaptability of customers in light of the uncertainty and unpredictability concerns associated with power consumption. An imperfect solution to this problem can be found in the new and sophisticated forecasting techniques [30,31,32]. To assess and predict future electricity consumption, a deep learning (DL) forecasting model was developed, investigating electricity-load strategies in an attempt to prevent future electricity crises.
In this work, we suggest a framework based on a recurrent neural network (RNN) for the prediction of energy consumption in Greece. The RNN consists of two simpleRNN layers and a dense layer, using the Adam optimizer and as loss function during the training process. The dataset consists of the hourly energy consumption in Greece for 746 days. We provide the results for several values of the time step parameter, i.e., 12, 24, and 48, which is responsible for the inclusion of that number of previous points, in the prediction of the following value. Our experiments show that a time step equal to 24 provides the best results in the test set. In other words, this time step results in the least root mean square error (RMSE), illustrating that there is a strong periodicity every 24 h.
The rest of the paper is organized as follows: Section 2 presents the Theoretical Background. Section 3 presents the dataset and the proposed methodology, and Section 4 describes the experimental results, discusses the work and presents a comparison between the proposed methodology and other state-of-the-art neural networks, while Section 5 presents a conclusion and future work.
2. Theoretical Background
In this paper, the underlying model of predicting energy consumption is that of Artificial Neural Network (ANN) and, specifically, that of RNN [33,34]. The theory of RNN was brought up in 1986, while the well-known Long Short-Term Memory (LSTM) [35] networks were initially presented in 1997. The proposed literature architectures of RNN are fewer than the Convolutional Neural Network (CNN) [36] architectures. The evolution of RNN may be divided into three phases, the Overloaded Single Memory for Vanilla RNN [37], the Multiple Gate Memories for LSTM, and the Pay Attention for Encoder-Decoder architecture with RNN, respectively. Through these three phases, researchers were making an effort to recall the biggest amount of past information to predict the future more accurately. Gated Recurrent Unit (GRU) [38] is a type of recurrent neural network (RNN) architecture used for processing sequential data. Unlike traditional RNNs, GRUs have two memory gates (Update gate and Reset gate) that control the flow of information in and out of the memory cell, allowing them to efficiently capture long-term dependencies in sequential data. GRUs are widely used in natural language processing, speech recognition, and time-series forecasting tasks.
2.1. RNN for Variable Inputs/Outputs
The task of handling input and output of varied sizes is considered to be challenging in the field of normal neural networks. Part of the use cases that normal neural networks are incapable of handling are shown in Figure 1, where “many” does not stand for a fixed number for each input or output to the models.
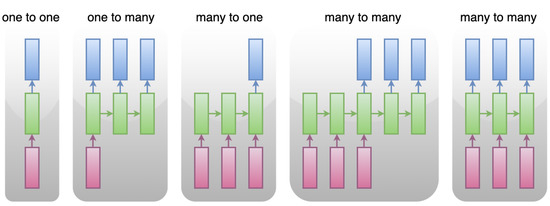
Figure 1.
RNN for Variable Inputs/Outputs.
The cases presented in Figure 1 may be summarized in the following three categories.
- One to Many, applied in fields of image captioning, text generation
- Many to One, applied in fields of sentiment analysis, text classification
- Many to Many, applied in fields of machine translation, voice recognition
However, RNN may deal with the above-mentioned cases as it includes a recursive processing unit with single or multiple layers of cells) plus a hidden state extracted from past data.
The use of a recursive processing unit has advantages and disadvantages. The main advantage is that the network may handle inputs and outputs of varied sizes. Unfortunately, the main disadvantages are the difficulty of storing past data and the complication of vanishing/exploding gradients.
2.2. Vanilla RNN
A Vanilla RNN is a type of neural network that can process sequential data, such as time-series data or natural language text, by maintaining an internal state. In a vanilla RNN, the output of the previous time step is fed back into the network as input for the current time step, along with the current input. This allows the network to capture information from previous inputs and use it to inform the processing of future inputs. The term “vanilla” is used to distinguish this type of RNN from more complex variants, such as LSTMs (Long Short-Term Memory) and GRUs (Gated Recurrent Units), which incorporate additional mechanisms to better handle long-term dependencies in sequential data. Despite their simplicity, vanilla RNNs can be effective for a range of tasks, such as language modeling, speech recognition, and sentiment analysis. However, they can struggle with long-term dependencies and suffer from vanishing or exploding gradients, which can make training difficult. In Figure 2 the main RNN architecture incorporating self-looping or recursive pointer is presented. Let us consider input, output, and hidden state as x, o, and h, respectively, while U, W, and V are the corresponding parameters. In this architecture, an RNN cell (in green) may include one or more layers of normal neurons or other types of RNN cells.
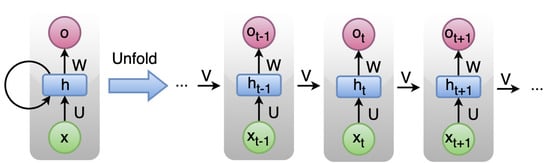
Figure 2.
Basic RNN architecture.
The main concept of RNN is the recursive pointing structure which is based on the following rules:
- Inputs and outputs are of variable size
- In each stage the hidden state from the previous stage as well as the current input is utilized to compute the current hidden state that feeds the next stage. Consequently, knowledge from past data is transmitted through the hidden states to the next stages. Hence, the hidden state is a means of connecting the past with the present as well as input with output.
- The set of parameters U, V, and W as well as the activation function are common to all RNN cells.
Unfortunately, the shared among all cells set of parameters (U, V, W) constitutes a serious bottleneck when the RNN raises enough. In this case, a brain consisting of only one set of memory may be overloaded. Therefore, Vanilla RNN cells that have multi-layers may easily enhance the performance.
2.3. Long Short-Term Memory
LSTM networks are a type of RNN designed to handle long-term dependencies in data. LSTMs were first introduced by Hochreiter and Schmidhuber in 1997 and have since become widely used due to their success in solving a variety of problems. Unlike standard RNNs, LSTMs are specifically created to address the issue of long-term dependency, making it their default behavior.
LSTMs consist of a chain of repeating modules, similar to all RNNs, but the repeating module in LSTMs is structured differently. Instead of a single layer, LSTMs have four interacting layers. The key component of LSTMs is the cell state, a horizontal line that runs through the modules and enables an easy flow of information. The LSTMs regulate the flow of information in the cell state through gates, which consist of a sigmoid neural network layer and a pointwise multiplication operation. The sigmoid layer outputs numbers between 0 and 1 to determine the amount of information to let through.
LSTMs have three gates to control the cell state: the forget gate, the input gate, and the output gate. The forget gate uses a sigmoid layer to decide which information to discard from the cell state. The input gate consists of two parts: a sigmoid layer that decides which values to update, and a tanh layer that creates new candidate values. The new information is combined with the cell state to create an updated state. Finally, the output gate uses a sigmoid layer to decide which parts of the cell state to output, then passes the cell state through tanh and multiplies it by the output of the sigmoid gate to produce the final output.
2.4. Convolutional Neural Network
CNN [36] is a type of deep learning neural network commonly used in image recognition and computer vision tasks. It is based on the concept of convolution operation, where the network learns to extract features from the input data through filters or kernels. The filters move over the input data and detect specific features such as edges, lines, patterns, and shapes, which are then processed and passed through multiple layers of the network. These multiple layers allow the CNN to learn increasingly complex representations of the input data. The final layer of the CNN outputs predictions for the input data based on the learned features. In addition to image recognition, CNNs can be applied to various other tasks including natural language processing, audio processing, and video analysis.
2.5. Gated Recurrent Unit
The GRU [38] operates similarly to an RNN, but with different operations and gates for each GRU unit. To address issues faced by standard RNNs, GRUs incorporate two gate mechanisms: the Update gate and the Reset gate. The Update gate determines the amount of previous information to pass on to the next stage, enabling the model to copy all previous information and reduce the risk of vanishing gradients. The Reset gate decides how much past information to ignore, deciding whether previous cell states are important. The Reset gate first stores relevant past information into a new memory then multiplies the input and hidden states with their weights, calculates the element-wise multiplication between the Reset gate and the previous hidden state, and applies a non-linear activation function to generate the next sequence.
3. Materials and Methods
3.1. Dataset
The dataset consists of the hourly energy consumption in Greece for 746 days starting from 31 November 2020 to 16 December 2022, according to IPTO S.A. (Independent Power Transmission Operator S.A.) [39]. IPTO S.A. is the Owner and Operator of the Hellenic Electricity Transmission System (HETS). The IPTO mission is the operation, control, maintenance, and development of the Hellenic Electricity Transmission System. Each data point indicates the hourly energy consumption in terms of MWh, i.e., for each day, there are 24 energy indices in MWh showing the energy consumption per hour.
3.2. Proposed Methodology
Toward the prediction of energy consumption, we propose an artificial neural network, specifically, an RNN. An RNN is specialized in extracting patterns and making predictions for time series and sequential data. Contrary to a dataset with independent data points, where a feed-forward neural network is the best choice, the existence of data points that depend upon the previous ones, demands the incorporation of a memory concept. This memory provides the prediction model with the capability of storing the previous states and considering them for the prediction of the following output. At the first stage of our pipeline, there is an input layer where the raw data are imported and scaled appropriately to be fed into the hidden layers described previously. The data are scaled in the range (0, 1) and, in turn, divided into train and test sets. After experimentation, we conclude with an 80–20 split, meaning that the train set is the 80% and the test set is the 20% of the whole dataset, respectively. Our network consists of two simpleRNN layers and a dense layer as shown in Figure 3. A simpleRNN layer has a feedback loop that can be unrolled in x time steps as shown in Figure 2 where x is the number of previous observations taken into account for the prediction of the next point.
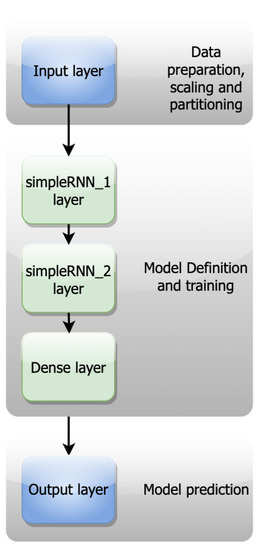
Figure 3.
The proposed prediction pipeline.
In our case, the time step parameter is equal to 24, assuming there is a periodicity every 24 h. The network has 50 hidden units created via the SimpleRNN layers and one dense unit created via the dense layer. The model has 7.701 trainable parameters, i.e., 2600, 5050, and 51 for the first simpleRNN layer, the second simpleRNN layer, and the dense layer, respectively. For training purposes, a root mean square error (RMSE) function was applied as a loss function and the network was trained for 40 epochs.
4. Results and Discussion
In this Section, a comparison between the variations of the proposed methodology, the RNN network, is presented along with a comparison with the other neural networks. As mentioned above, the procedure of performance evaluation was divided into four variations, i.e., time steps equal to 12, 24, 48, and 72. In all those variations 80% of the data set was initially used as a training set and the rest 20% as a test set. Given that the dataset consists of 17,904 measurements of the hourly energy consumption in Greece for 746 days (31 November 2020 till 16 December 2022) according to IPTO S.A. [39], the proposed framework may handle mainly the two load-forecasting categories, i.e., short-term and medium-term on the time horizon.
In Figure 4 and Figure 5 the actual ground truth values against the predicted ones for a parameter time step equal to 24 are presented during the training and testing process, respectively. All variations of the proposed network capture the underlined patterns and present a small test error in terms of RMSE and MAE.
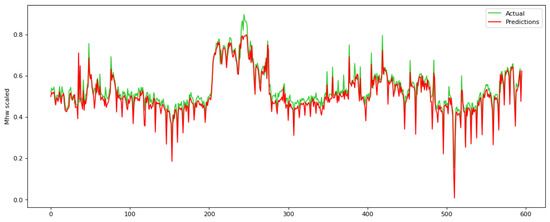
Figure 4.
Actual ground truth values against the predicted ones during the training process for a parameter time step equal to 24 for the proposed RNN.
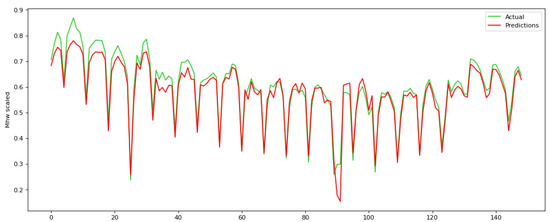
Figure 5.
Actual ground truth values against the predicted ones during the testing process for a parameter time step equal to 24 for the proposed RNN.
Our experiments show that a time step equal to 24 provides the best results in the test set. Time step equal to 24 results in the least RMSE, illustrating that there is a strong periodicity every 24 h. When the time step is equal to 24, then RMSE = 0.033 in the test set, while for the time step equal to 12 and 48, RMSE is 0.048 and 0.041, respectively. In addition, when the time step is equal to 12, then MAE = 0.163 in the test set, while for the time step equal to 12 and 48 MAE is 0.165 and 0.187, respectively. Subsequently, at a time step of 72, the RNN network demonstrates proficiency within the training set; however, the outcomes within the testing set lack encouragement, indicating an overfitting occurrence within the system. RMSE and MAE in training and test set for all four time steps are shown in Table 2, as well as in Figure 6.

Table 2.
RMSE and MSE in training and test set for all three neural networks and four time steps.
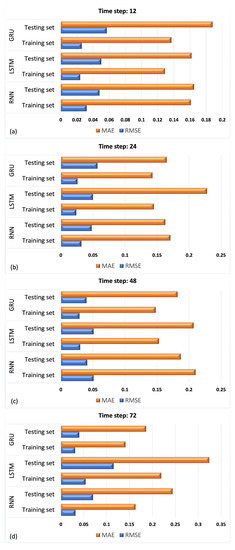
Figure 6.
RMSE and MSE in training and test set for GRU, LSTM and RNN for time steps 12 (a), 24 (b), 48 (c) and 72 (d).
In Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 the actual ground truth values against the predicted ones are presented, for a parameter time step equal to 12, 48, and 72 during the training and testing process, respectively.
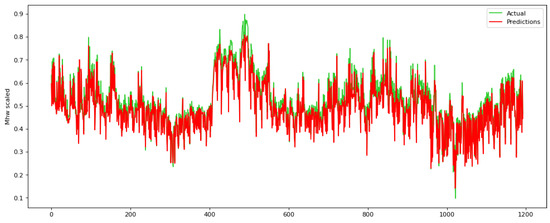
Figure 7.
Actual ground truth values against the predicted ones during the training process for a parameter time step equal to 12 for the proposed RNN.
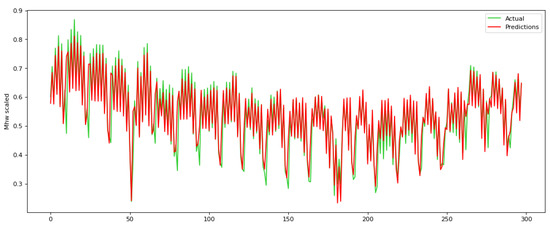
Figure 8.
Actual ground truth values against the predicted ones during the testing process for a parameter time step equal to 12 for the proposed RNN.
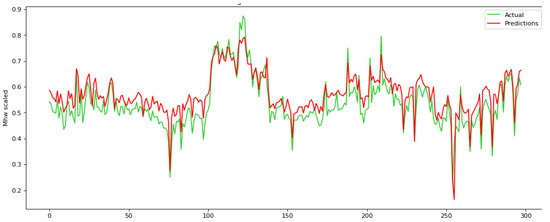
Figure 9.
Actual ground truth values against the predicted ones during the training process for a parameter time step equal to 48 for the proposed RNN.
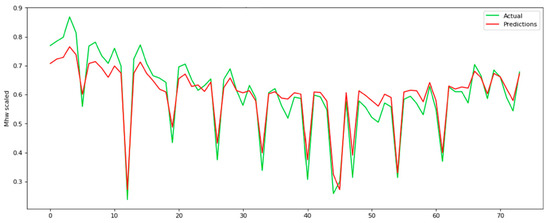
Figure 10.
Actual ground truth values against the predicted ones during the testing process for a parameter time step equal to 48 for the proposed RNN.
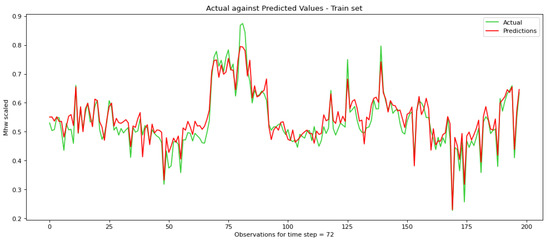
Figure 11.
Actual ground truth values against the predicted ones during the training process for a parameter time step equal to 72 for the proposed RNN.
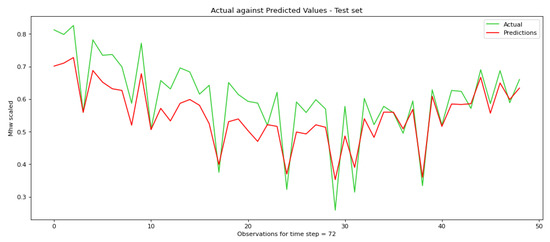
Figure 12.
Actual ground truth values against the predicted ones during the training process for a parameter time step equal to 72 for the proposed RNN.
The experimental results of the previous Section attest that all variations of the proposed network capture the underlined patterns and present a small test error in terms of RMSE and Mean Absolute Error (MAE). To highlight its performance, a comparison with two more complex neural networks, a Long Short-Term Memory (LSTM) and a Gated Recurrent Unit (GRU), is demonstrated in Table 2. The GRU network consists of a Gated Recurrent Unit (GRU) layer followed by a dropout layer, a second Gated Recurrent Unit (GRU) followed by a dropout layer, and a dense layer. The dropout rate was set to 0.2 in both dropout layers and the network counts 23,301 trainable parameters. The Long Short-Term Memory (LSTM) network has a similar structure with an LSTM layer followed by a dropout layer and a second LSTM layer followed by a dropout layer and a dense one. The dropout rate was also equal to 0.2 and the network counts 30,651 parameters. All variants, i.e., time step equal to 12, 24, 48 and 72, trained for 40 epochs.
All networks show lower RMSE and MAE for time step equal to 24, declaring it as the best choice for the examined task. In general, the RNN network outperforms both the LSTM and GRU networks except for time steps 48 and 72, where the GRU has a slightly lower RMSE and MAE. For a time step equal to 12 RNN outperforms both networks in RMSE and MAE, with the LSTM performing better than GRU in both metrics.
Considering the best variation for time step equal to 24, RNN outperforms the LSTM and GRU networks regarding MAE, while it shows lower RMSE than the LSTM network and equal to the GRU network, i.e., RMSE = 0.033. The LSTM is a more complex network than the GRU, with three gates and far more trainable parameters, and it is a very efficient solution for long-lasting dependencies. Though, GRU performs better for smaller datasets and dependencies, as is shown in our study. RNN measurements are the most promising, indicating that for specific tasks such as electricity-load consumption with few features, RNNs with the appropriate architecture and parameters can perform better than more complex and sophisticated networks.
Finally, Figure 13 includes three subfigures, one for each model: RNN, LSTM, and GRU, illustrating the evolution of the loss function throughout the training epochs. The observed trend in most cases demonstrates a continuous decrease in the loss function, followed by a plateau, indicating the convergence of the proposed networks towards a stable solution. This suggests that the models have successfully captured the underlying patterns and are performing well on the training data. The convergence of the loss function curve indicates an appropriate selection of the learning rate, as it exhibits a smooth convergence pattern. However, in a few instances, slight fluctuations are observed, suggesting the possibility of an excessively large learning rate. These fluctuations, however, are transient as the loss function converges to a low value within one to five epochs. Thus, it can be concluded that these fluctuations represent momentary instabilities during the training process.
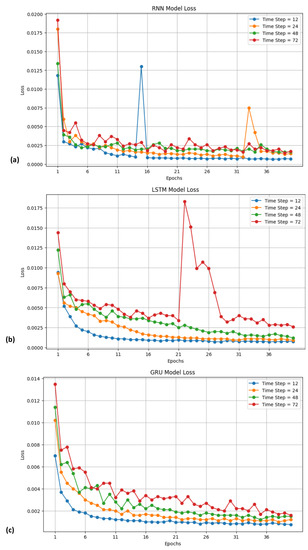
Figure 13.
Loss function evolution throughout the training epochs for RNN (a), LSTM (b), GRU (c) for time steps 12, 24, 48, and 72.
5. Conclusions
In this study, an RNN was trained on a dataset of electricity-load data and was able to accurately predict future energy load values. Performance was evaluated using RMSE and MAE metrics, and compared with other well-known neural networks such as LSTM and GRU that handle time dependencies and sequential data. The models were examined at four different time steps and all performed best with a time step of 24. The RNN had the best performance (RMSE of 0.033 and MAE of 0.163), demonstrating its ability to learn the underlying patterns and trends in the data series and make accurate predictions, even better than more complex neural networks. It should be noted that with only 17,904 hourly energy consumption measurements in the dataset, long-term forecasting of electricity load is not possible due to insufficient training data. Additionally, to improve the accuracy of short- and medium-term forecasting, social, economic, or environmental factors such as temperature, precipitation, humidity, and wind should be taken into consideration in the model training and prediction processes.
Author Contributions
Conceptualization, C.P.; V.M. and E.M.; methodology, G.F.; software, E.M.; validation, C.P. and V.V.; formal analysis, G.F.; V.V. and V.M.; investigation, G.F. and C.P.; resources, G.F.; writing—original draft preparation, C.P., E.M. and G.F.; writing—review and editing, E.M.; visualization, V.V.; supervision, C.P. and V.M.; project administration, G.F. and V.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AGC | Automatic Generation Control |
| ANN | Artificial Neural Network |
| CNN | Convolutional Neural Network |
| DSO | Distribution System Operators |
| ELD | Economic Load Dispatch |
| GRU | Gated Recurrent Unit |
| HETS | Hellenic Electricity Transmission System |
| IPTO | Independent Power Transmission Operator |
| LD | Linear dichroism |
| LSTM | Long Short-Term Memory |
| LTF | Long-term forecasting |
| MAE | Mean Absolute Error |
| MTF | Medium-term forecasting |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
| STF | Short-term forecasting |
| TSO | Transmission System Operator |
References
- Kang, C.; Xia, Q.; Zhang, B. Review of power system load forecasting and its development. Autom. Electr. Power Syst. 2004, 28, 1–11. [Google Scholar]
- Shi, T.; Lu, F.; Lu, J.; Pan, J.; Zhou, Y.; Wu, C.; Zheng, J. Phase Space Reconstruction Algorithm and Deep Learning-Based Very Short-Term Bus Load Forecasting. Energies 2019, 12, 4349. [Google Scholar] [CrossRef]
- Zhang, K.; Tian, X.; Hu, X.; Guo, Z.N. Partial Least Squares regression load forecasting model based on the combination of grey Verhulst and equal-dimension and new-information model. In Proceedings of the 7th International Forum on Electrical Engineering And Automation (IFEEA), Hefei, China, 25–27 September 2020; pp. 915–919. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Pan, S.; Zhang, M.; Ji, Y.Z. Midterm Power Load Forecasting Model Based on Kernel Principal Compo-nent Analysis. Big Data 2019, 7, 130–138. [Google Scholar] [CrossRef] [PubMed]
- Al-Hamadi, H.; Soliman, S.A. Long-term/mid-term electric load forecasting based on short-term correlation and annual growth. Electr. Power Syst. Res. 2005, 74, 353–361. [Google Scholar] [CrossRef]
- Baek, S. Mid-term Load Pattern Forecasting with Recurrent Artificial Neural Network. IEEE Access 2019, 7, 172830–172838. [Google Scholar] [CrossRef]
- Nalcaci, G.; Ozmen, A.; Weber, G.W. Long-term load forecasting: Models based on MARS, ANN and LR methods. Cent. Eur. J. Oper. Res. 2019, 27, 1033–1049. [Google Scholar] [CrossRef]
- Adhiswara, R.; Abdullah, A.G.; Mulyadi, Y. Long-term electrical consumption forecasting using Artificial Neural Network (ANN). J. Phys. Conf. Ser. 2019, 1402, 033081. [Google Scholar] [CrossRef]
- Tsakoumis, A.C.; Vladov, S.S.; Mladenov, V.M. Electric load forecasting with multilayer perceptron and Elman neural network. In Proceedings of the 6th Seminar on Neural Network Applications in Electrical Engineering, Belgrade, Yugoslavia, 26–28 September 2002; pp. 87–90, ISBN 0-7803-7593-9. [Google Scholar] [CrossRef]
- Dondon, P.; Carvalho, J.; Gardere, R.; Lahalle, P.; Tsenov, G.; Mladenov, V. Implementation of a feed-forward Artificial Neural Network in VHDL on FPGA. In Proceedings of the 12th Symposium on Neural Network Applications in Electrical Engineering, Belgrade, Serbia, 25–27 November 2014; pp. 37–40, ISBN 978-147995888-7. [Google Scholar] [CrossRef]
- Abu-Shikhah, N.; Aloquili, F.; Linear, O.; Regression, N. Smart Grid and Renewable Energy. Smart Grid Renew. Energy 2011, 2, 126–135. [Google Scholar] [CrossRef]
- Pappas, S.; Ekonomou, L.; Moussas, V.C.; Karampelas, P.; Katsikas, S.K. Adaptive Load Forecasting Of The Hellenic Electric Grid. J. Zhejiang Univ. Sci. 2008, 2, 1724–1730. [Google Scholar] [CrossRef]
- Pappas, S.; Ekonomou, L.; Karampelas, P.; Karamousantas, D.C.; Katsikas, S.K.; Chatzarakis, G.E.; Skafidas, P.D. Electricity Demand Load Forecasting of the Hellenic Power System Using an ARMA Model. Electr. Power Syst. Res. 2010, 80, 256–264. [Google Scholar] [CrossRef]
- Ekonomou, L.; Oikonomou, S.D. Application and comparison of several artificial neural networks for forecasting the Hellenic daily electricity demand load. In Proceedings of the 7th WSEAS International Conference on Artificial Intelligence, Knowledge Engineering and Data Bases (AIKED’ 08), Cambridge, UK, 20–22 February 2008; pp. 67–71. [Google Scholar]
- Ekonomou, L.; Christodoulou, C.A.; Mladenov, V. A short-term load forecasting method using artificial neural networks and wavelet analysis. Int. J. Power Syst. 2016, 1, 64–68. [Google Scholar]
- Karampelas, P.; Pavlatos, C.; Mladenov, V.; Ekonomou, L. Design of artificial neural network models for the prediction of the Hellenic energy consumption. In Proceedings of the 10th Symposium on Neural Network Applications in Electrical Engineering, Belgrade, Serbia, 23–25 September 2010. [Google Scholar]
- Hwan, K.J.; Kim, G.W. A short-term load forecasting expert system. In Proceedings of the 5th Korea-Russia International Symposium on Science and Technology, Tomsk, Russia, 26 June–3 July 2001; Volume 1, pp. 112–116. [Google Scholar]
- Ali, M.; Adnan, M.; Tariq, M.; Poor, H.V. Load Forecasting through Estimated Parametrized Based Fuzzy Inference System in Smart Grids. IEEE Trans. Fuzzy Syst. 2021, 29, 156–165. [Google Scholar] [CrossRef]
- Bhotto, M.Z.A.; Jones, R.; Makonin, S.; Bajić, I.V. Short-Term Demand Prediction Using an Ensemble of Linearly-Constrained Estimators. IEEE Trans. Power Syst. 2021, 36, 3163–3175. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Y.; Muljadi, E.; Zhang, J.J.; Gao, D.W. A Short-Term and High-Resolution Distribution System Load Forecasting Using Support Vector Regression with Hybrid Parameters Optimization. IEEE Trans. Smart Grid 2018, 9, 3341–3350. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Roozitalab, F. Midterm Load Forecasting: A Multistep Approach Based on Phase Space Reconstruction and Sup-port Vector Machine. IEEE Syst. J. 2020, 14, 4967–4977. [Google Scholar] [CrossRef]
- Zafeiropoulou, M.; Sijakovic, I.; Terzic, N.; Fotis, G.; Maris, T.I.; Vita, V.; Zoulias, E.; Ristic, V.; Ekonomou, L. Forecasting Transmission and Distribution System Flexibility Needs for Severe Weather Condition Resilience and Outage Management. Appl. Sci. 2022, 12, 7334. [Google Scholar] [CrossRef]
- Fotis, G.; Vita, V.; Maris, I.T. Risks in the European Transmission System and a Novel Restoration Strategy for a Power System after a Major Blackout. Appl. Sci. 2023, 23, 83. [Google Scholar] [CrossRef]
- Sambhi, S.; Kumar, H.; Fotis, G.; Vita, V.; Ekonomou, L. Techno-Economic Optimization of an Off-Grid Hybrid Power Generation for SRM IST Delhi-NCR Campus. Energies 2022, 15, 7880. [Google Scholar] [CrossRef]
- Sambhi, S.; Bhadoria, H.; Kumar, V.; Chaurasia, P.; Chaurasia, G.S.; Fotis, G.; Vita, G.; Ekonomou, V.; Pavlatos, C. Economic Feasibility of a Renewable Integrated Hybrid Power Generation System for a Rural Village of Ladakh. Energies 2022, 15, 9126. [Google Scholar] [CrossRef]
- Khuntia, S.; Rueda, J.; Meijden, M. Forecasting the load of electrical power systems in mid- and long-term horizons: A review. IET Gener. Transm. Distrib. 2016, 10, 3971–3977. [Google Scholar] [CrossRef]
- Directive (EU) 2019/944 of the European Parliament and of the Council of 5 June 2019 on Common Rules for the Internal Market for Electricity and Amending Directive 2012/27/EU. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?qid=1570790363600&uri=CELEX:32019L0944 (accessed on 29 December 2022).
- IRENA. Innovation Landscape Brief: Market Integration of Distributed Energy Resources; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Commission, M.; Company, D. Integrating Renewables into Lower Michigan Electric Grid. Available online: https://www.brattle.com/wp-content/uploads/2021/05/15955_integrating_renewables_into_lower_michigans_electricity_grid.pdf (accessed on 29 December 2022).
- Wang, F.C.; Hsiao, Y.S.; Yang, Y.Z. The Optimization of Hybrid Power Systems with Renewable Energy and Hydrogen Gen-eration. Energies 1948, 11, 1948. [Google Scholar] [CrossRef]
- Wang, F.; Lin, K.-M. Impacts of Load Profiles on the Optimization of Power Management of a Green Building Employing Fuel Cells. Energies 2019, 12, 57. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, C. A Hybrid BA-ELM Model Based on Factor Analysis and Similar-Day Approach for Short-Term Load Forecasting. Energies 2018, 11, 1282. [Google Scholar] [CrossRef]
- Goller, C.; Kuchler, A. Learning task-dependent distributed representations by backpropagation through structure. In Proceedings of the International Conference on Neural Networks (ICNN’96), Washington, DC, USA, 3–6 June 1996; Volume 1, pp. 347–352. [Google Scholar]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Moustafa, N.; Hawash, H. Dive Into Recurrent Neural Networks. In Deep Learning Approaches for Security Threats in IoT Environments; IEEE: Piscataway, NJ, USA, 2023; pp. 209–229. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Available online: https://www.data.gov.gr/datasets/admie_realtimescadasystemload/ (accessed on 29 December 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).