Design and Analysis of Guidance Function of Permanent Magnet Electrodynamic Suspension
Abstract
1. Introduction
2. Operation and Principles
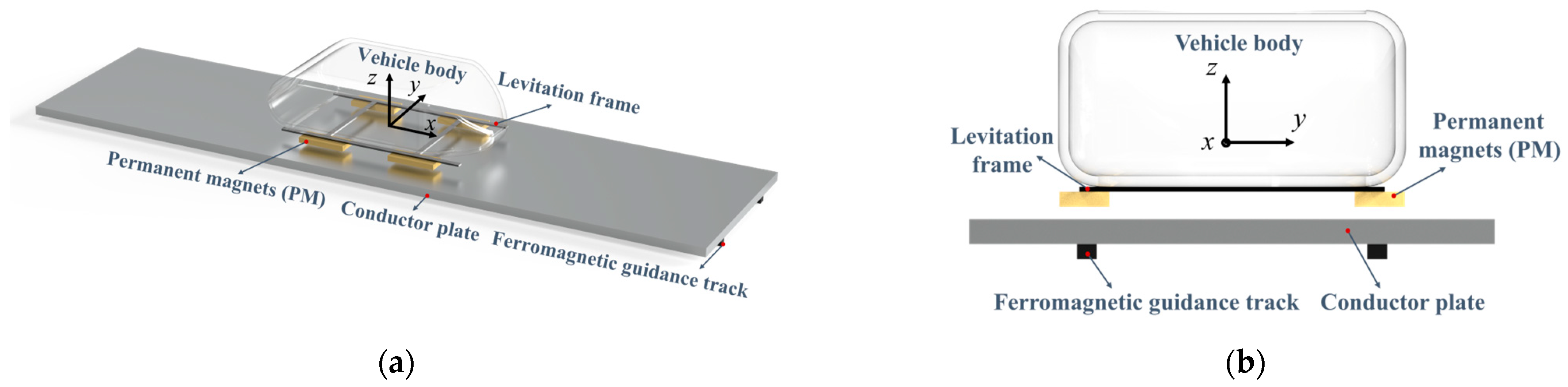
2.1. Presentation of a New Structure
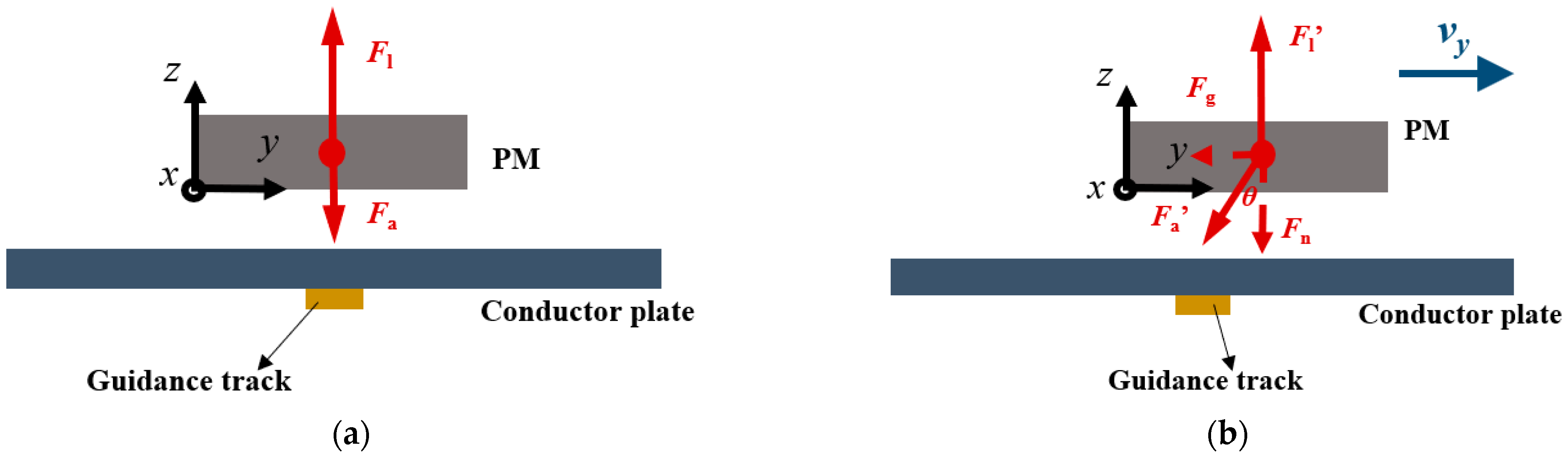
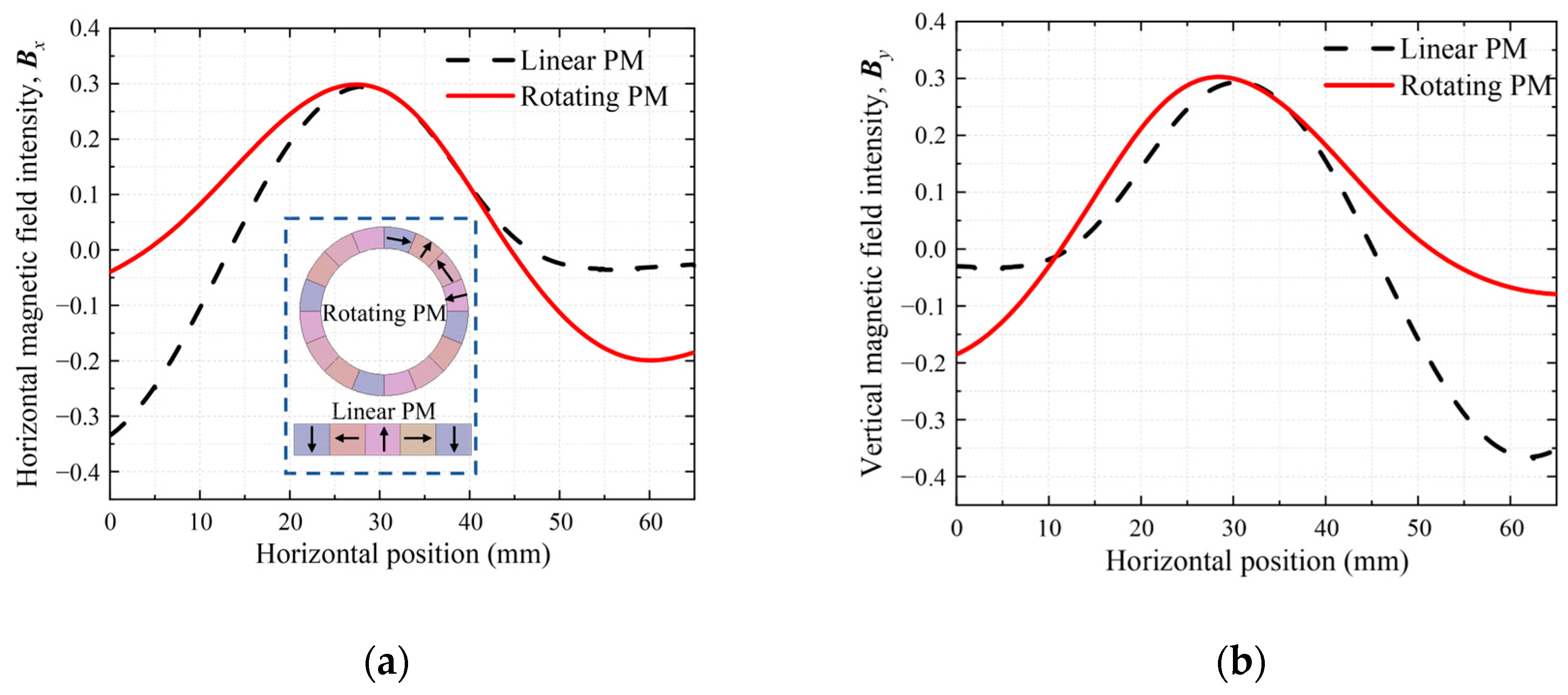
2.2. Basic Principles of the New Structure
3. FEM Experimental Verification
3.1. Establishment of Finite Element Model
3.2. Experimental Verification
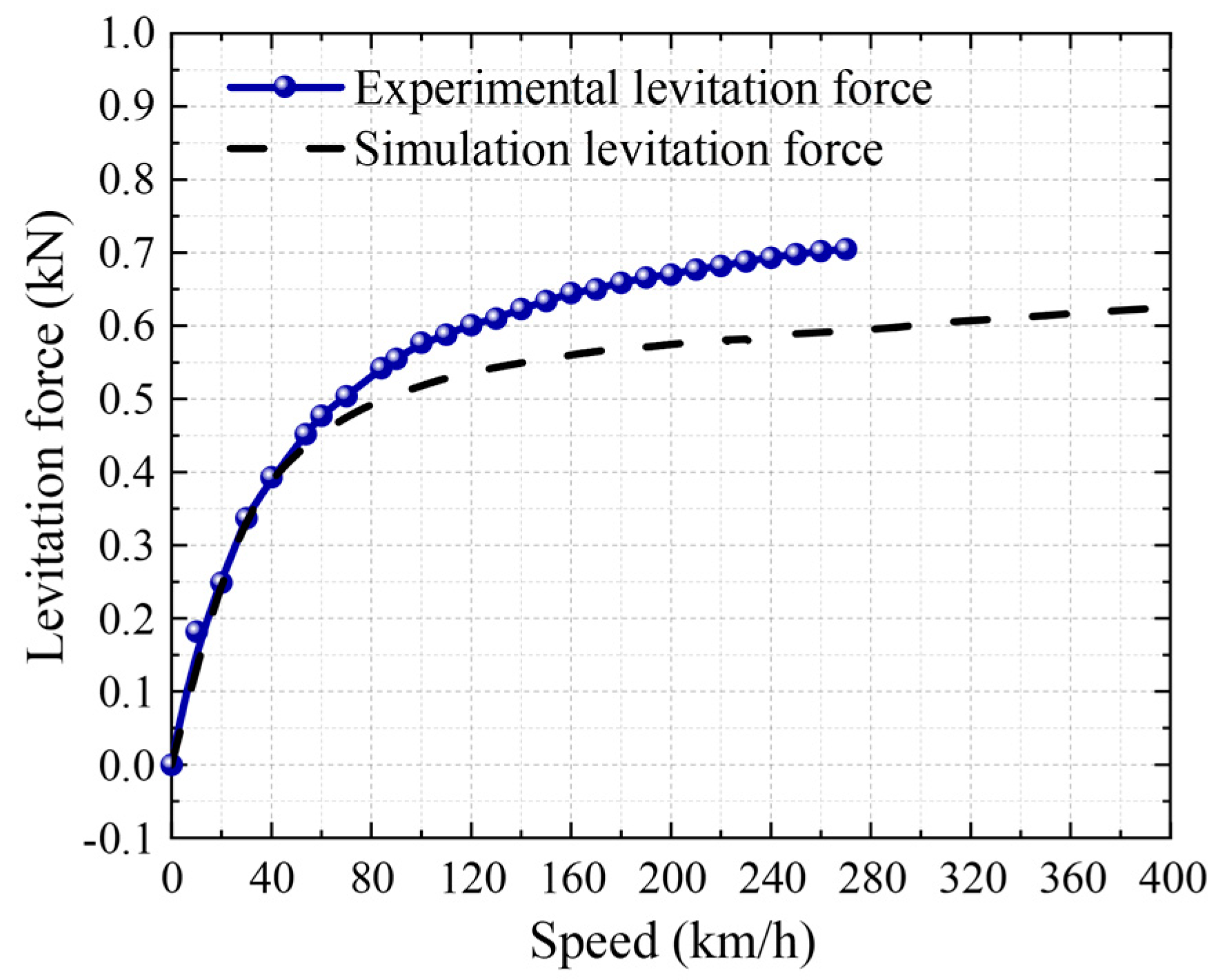
3.3. Results Comparison
4. Analysis on Guidance Performance and Parameter Optimization
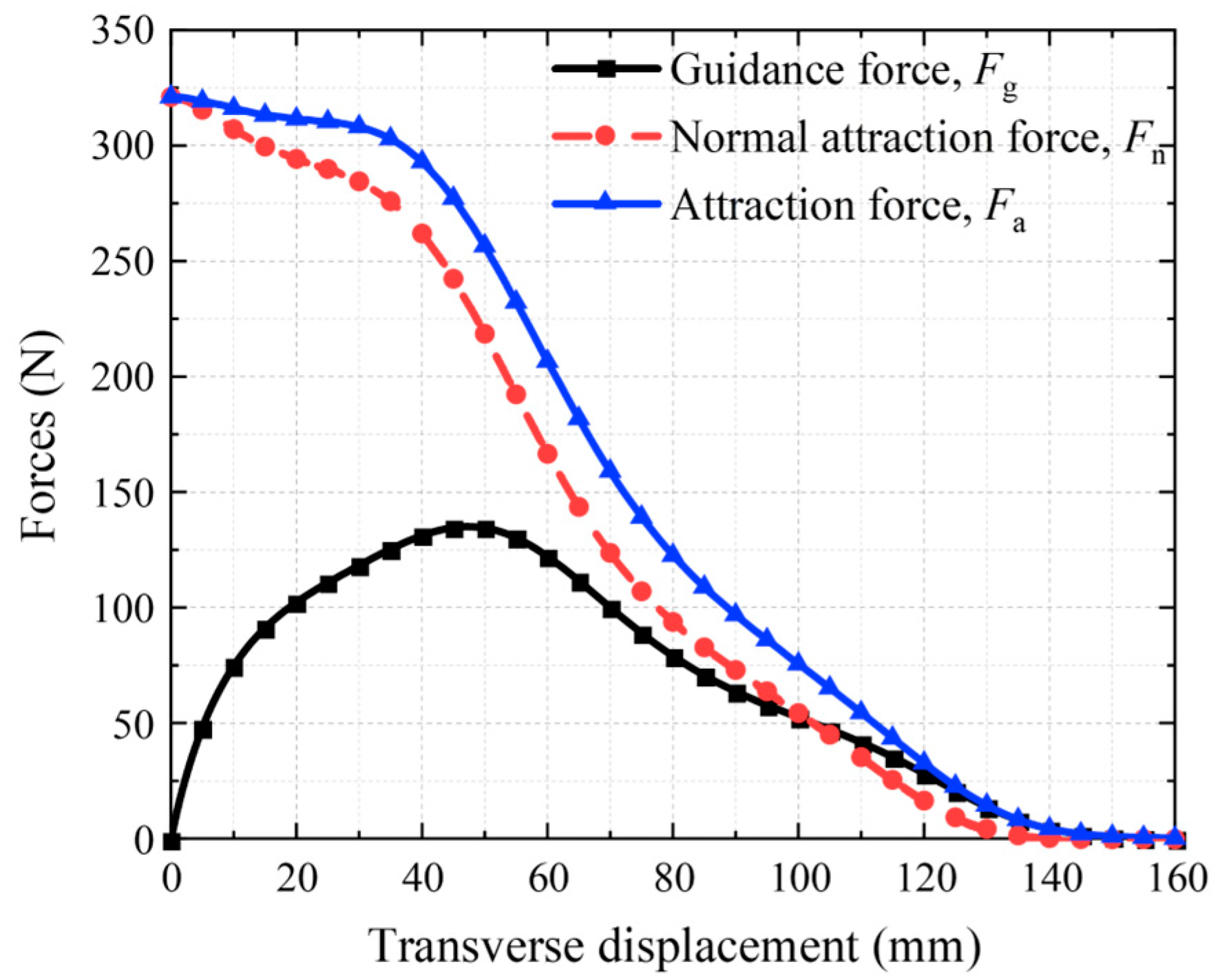
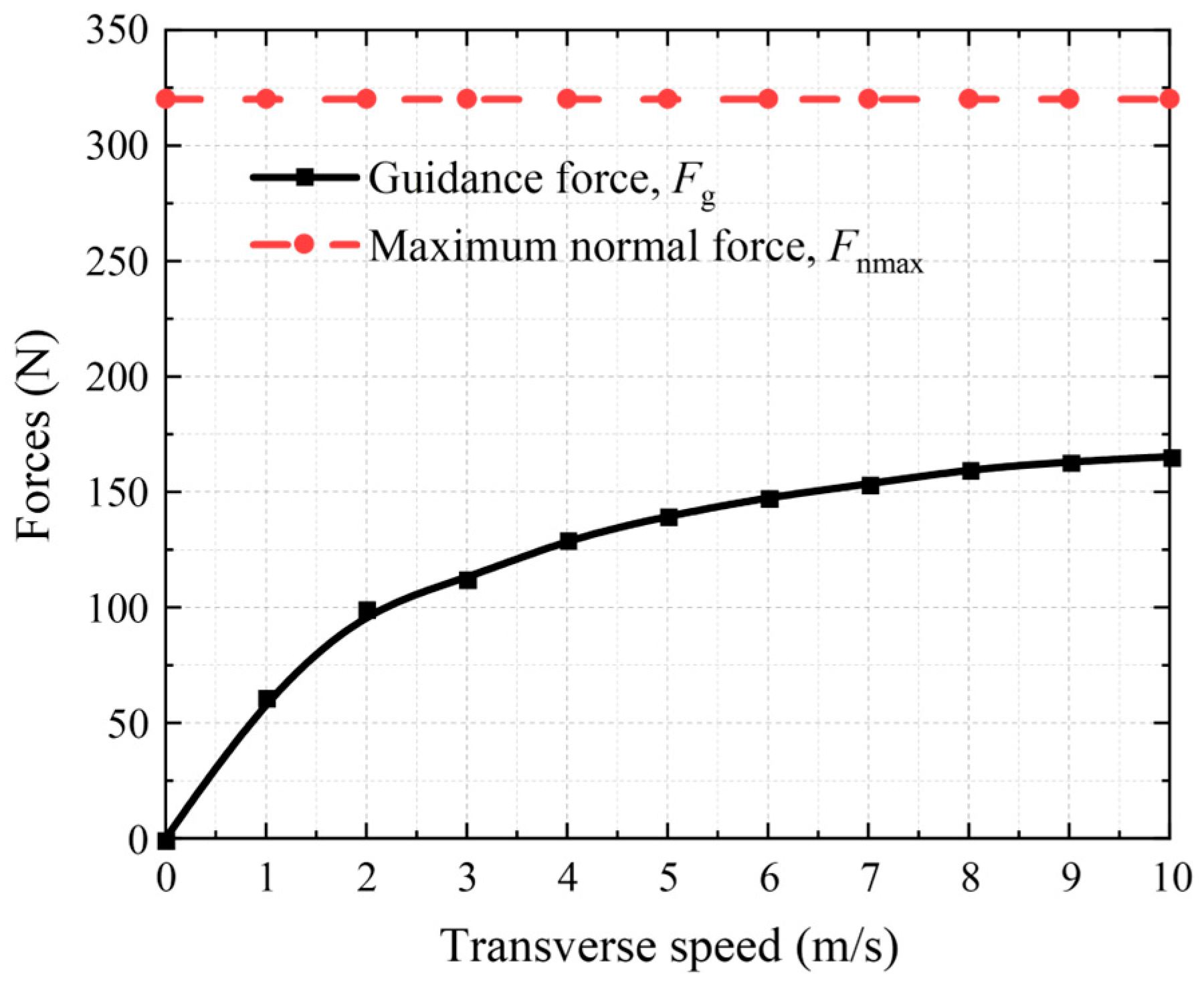
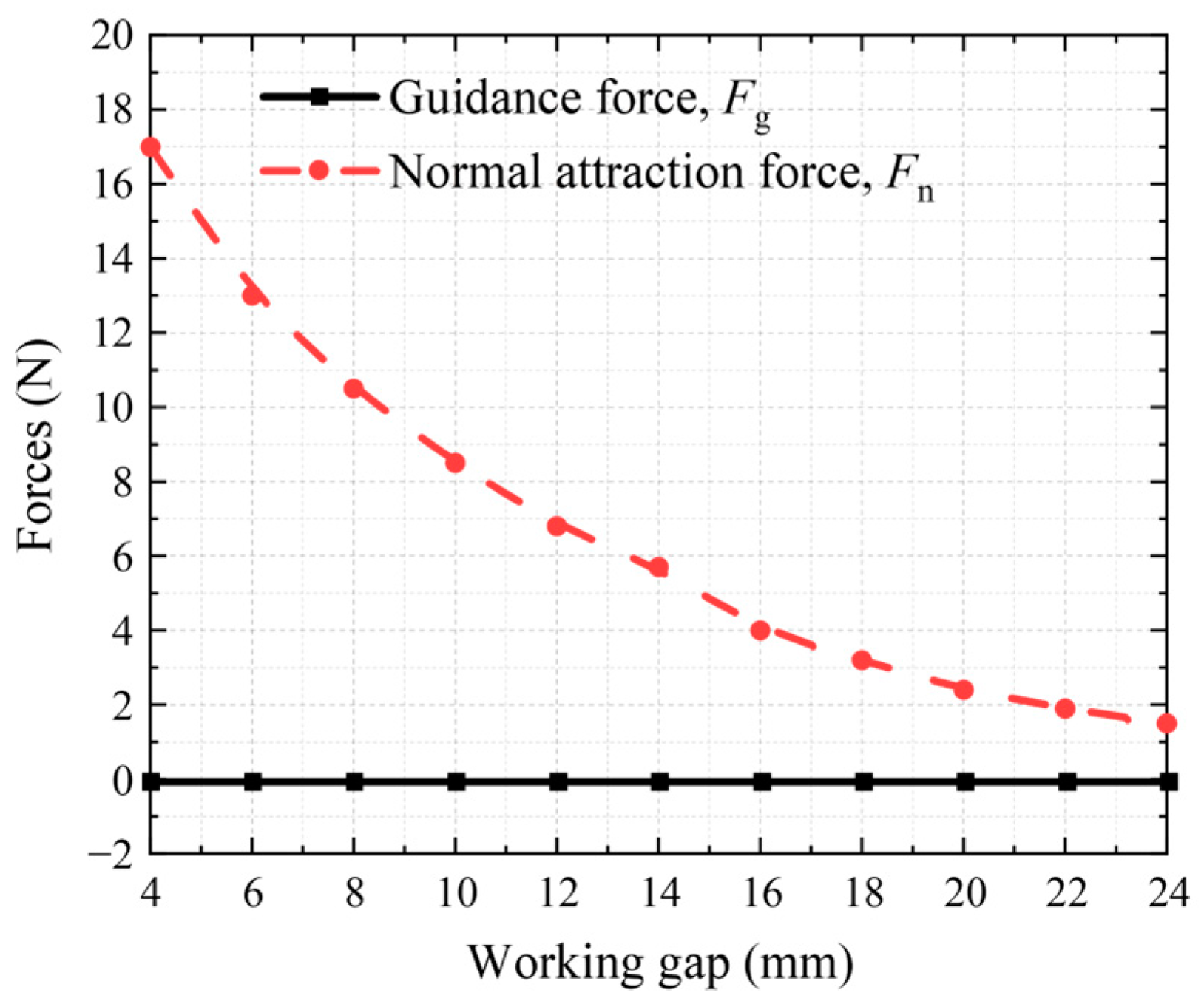
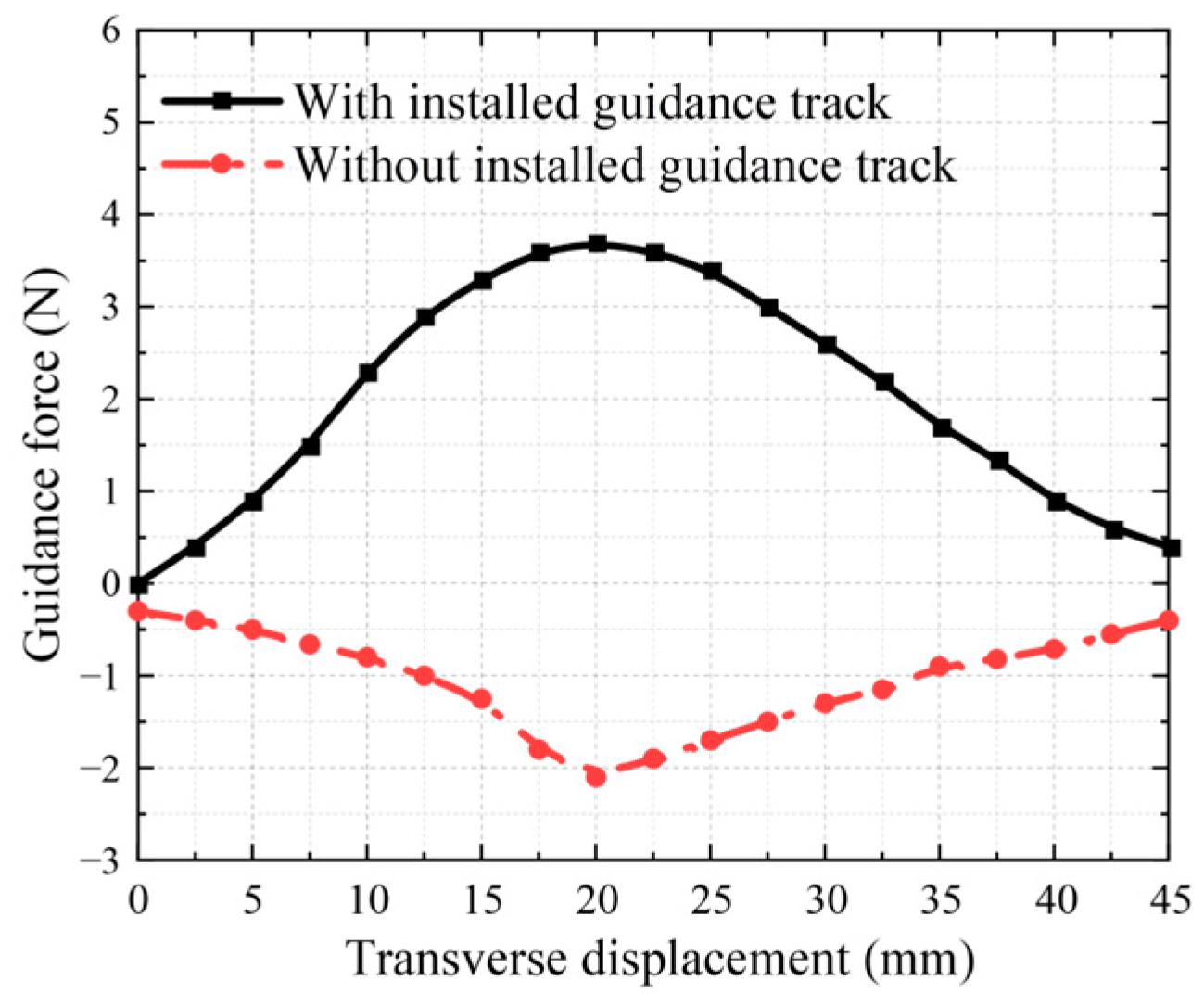
4.1. Guidance Performance Analysis
4.2. Parameters Optimization Analysis
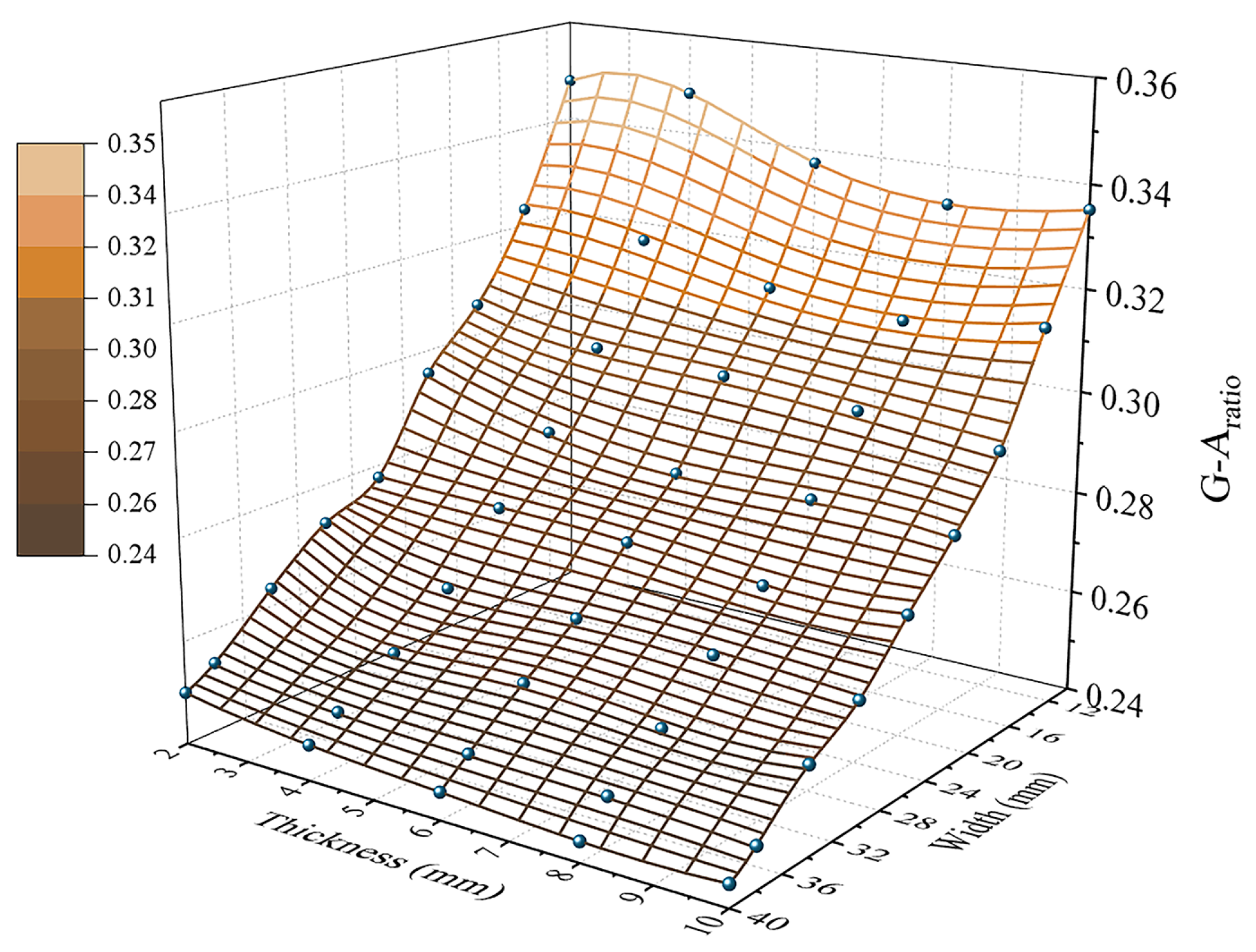
4.3. Geometric Parameters Analysis
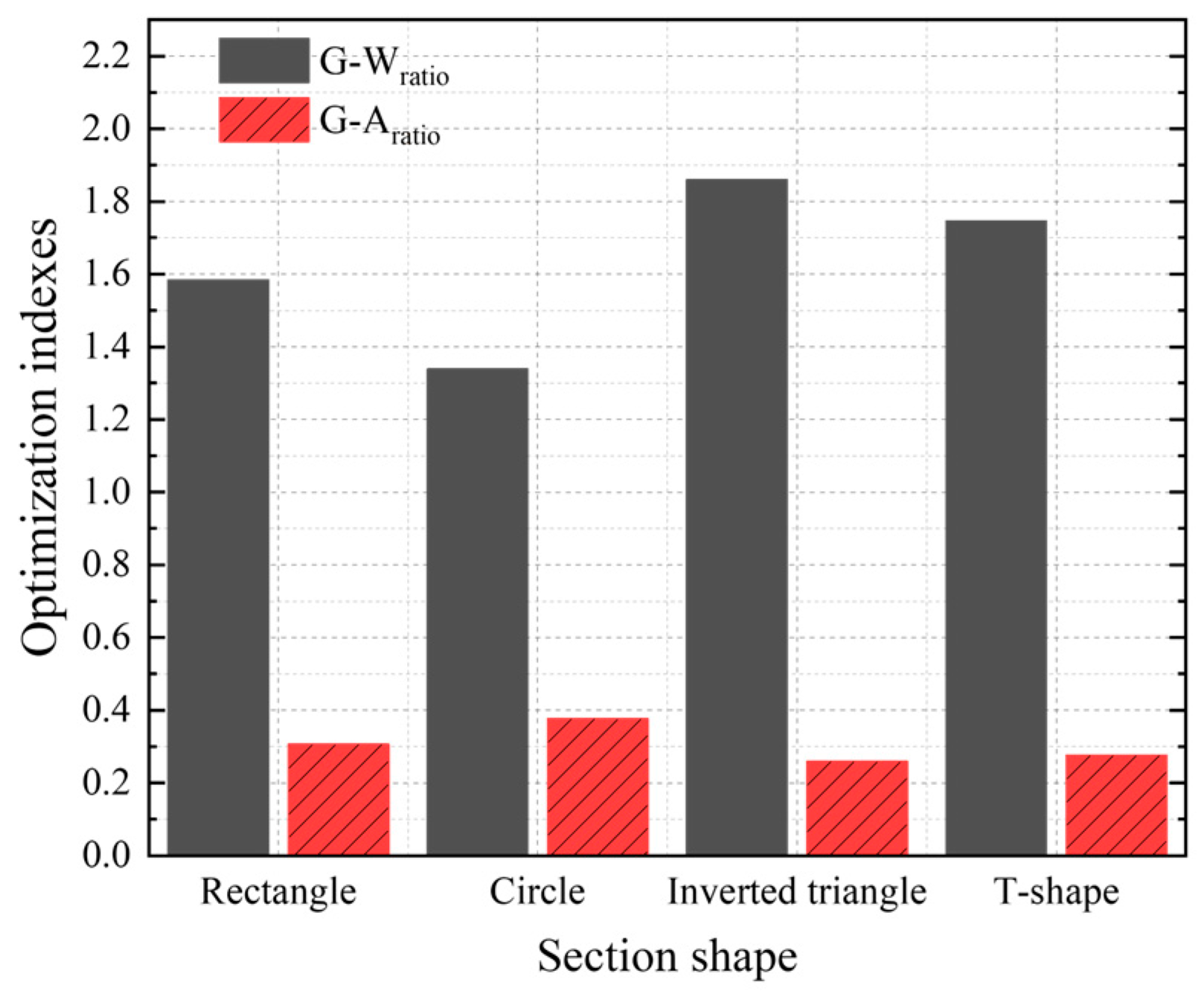
4.4. Shape Section Analysis
4.5. Installation Position Analysis
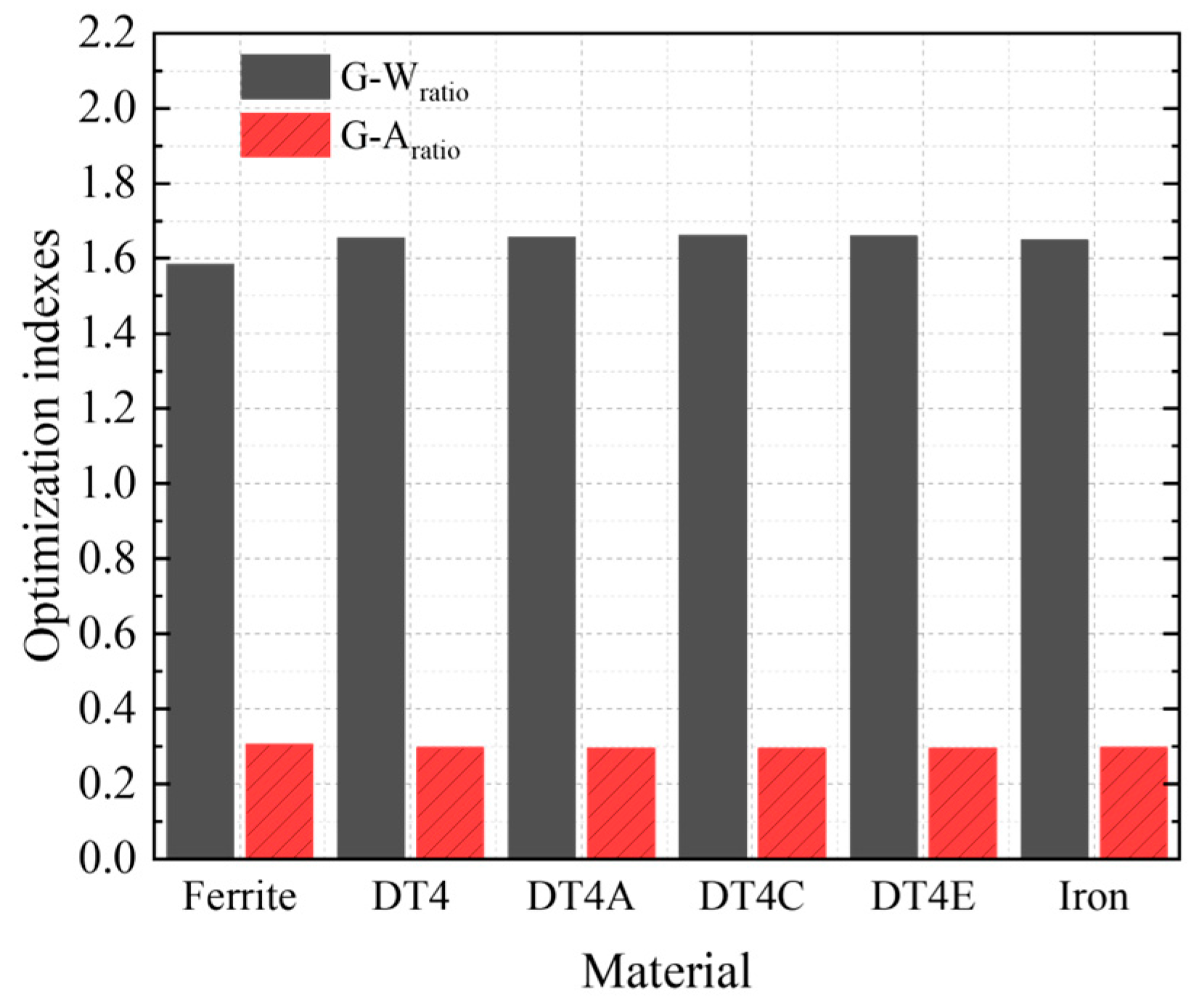
4.6. Material Selection Analysis
5. Equivalent Experimental Verification
5.1. Experimental Prototype
5.2. Analysis of Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, F.; Luo, S.; Deng, Z. Study on key technologies and whole speed range application of maglev rail transport. J. China Railw. 2019, 41, 40–49. [Google Scholar] [CrossRef]
- Franca, T.N.; Shi, H.; Deng, Z.; Stephan, R.M. Overview of electrodynamic levitation technique applied to maglev vehicles. IEEE Trans. Appl. Supercon. 2021, 31, 3602605. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, K.; Duan, J.; Jing, Y. Study of permanent magnet electrodynamic suspension system with a novel Halbach array. J. Elecrt. Eng. Technol. 2020, 15, 969–977. [Google Scholar] [CrossRef]
- Paden, B.A.; Snyder, S.T.; Paden, B.E.; Ricci, M.R. Modeling and control of an electromagnetic variable valve actuation system. IEEEASME Trans. Mechatron. 2015, 20, 2654–2665. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, F.; Jin, J.; Pei, W.; Xu, F.; Oka, K.; Zhang, M. Research of permanent magnetic levitation system: Analysis, control strategy design, and experiment. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2022, 14, 7617–7628. [Google Scholar] [CrossRef]
- Hu, J.; Ma, W.; Chen, X.; Luo, S. Levitation stability and Hopf bifurcation of EMS maglev trains. Math. Probl. Eng. 2020, 2020, 2936838. [Google Scholar] [CrossRef]
- Ding, J.; Yang, X.; Long, Z. Structure and control design of levitation electromagnet for electromagnetic suspension medium-speed maglev train. J. Vib. Control 2019, 25, 1179–1193. [Google Scholar] [CrossRef]
- Lv, G.; Liu, Y.; Zhou, T.; Zhang, Z. Analysis of suspension and guidance system of EDS maglev based on a novel magnetomotive force model. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2923–2933. [Google Scholar] [CrossRef]
- Hu, Y.; Long, Z.; Zeng, J.; Wang, Z. Analytical optimization of electrodynamic suspension for ultrahigh-speed ground transportation. IEEE Trans. Magn. 2021, 57, 1–11. [Google Scholar] [CrossRef]
- Deng, Z.; Li, J.; Zhang, W.; Gou, Y. High-temperature superconducting magnetic levitation vehicles: Dynamic characteristics while running on a ring test line. IEEE Veh. Technol. Mag. 2017, 12, 95–102. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, W.; Zheng, J. A high-temperature superconducting maglev ring test line developed in Chengdu, China. IEEE Trans. Appl. Supercond. 2016, 26, 3602408. [Google Scholar] [CrossRef]
- Rote, D.M.; Cai, Y.G. Review of dynamic stability of repulsive-force maglev suspension systems. IEEE Trans. Mag. 2002, 38, 1383–1390. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, K.; Liang, D.; Jing, Y. Stability control of permanent magnet and electromagnetic hybrid Halbach array electrodynamic suspension system. Compel-Int. J. Comp. Math. Electr. Electron. Eng. 2021, 40, 905–920. [Google Scholar] [CrossRef]
- Li, Y.; Hu, W.; Gong, Z.; Wang, D.; Liu, Y. A Guiding Device and a Maglev train. CHN. Patent CN208069680U, 9 November 2018. [Google Scholar]
- Rogg, D. The development of high-speed magnetic levitation system in the Federal Republic of Germany, objective and present state. In Proceedings of the 10th Int. Conf. on Maglev System, Hamburg, West Germany, 9 June 1988; pp. 3–5. [Google Scholar]
- Zhao, C.X. Research on Guidance Dynamics of EMS High-Speed Maglev Train. 2014. Available online: https://lib.gdqy.edu.cn/asset/detail/0/20447122922 (accessed on 8 November 2022).
- Wang, Y.; Yang, J.; Cui, Y. Characteristic analysis of permanent magnet electromagnetic hybrid suspension guidance system for maglev train. Electr. Driv. Locomo. 2021, 6, 1–8. [Google Scholar] [CrossRef]
- Hu, Q.; Sun, B.; Yu, H.; Meng, Q. Maglev air-gap altitude control of single electromagnetic guiding actuator for linear elevator. J. Shenyang Univ. Technol. 2013, 35, 251–256. [Google Scholar] [CrossRef]
- Kim, M.; Jeong, J.H.; Lim, J.; Kim, C.H.; Won, M. Design and control of levitation and guidance systems for a semi-high-speed maglev train. J. Electr. Eng. Technol. 2017, 12, 117–125. [Google Scholar] [CrossRef]
- Wang, Z.; Cai, Y.; Gong, T.Y.; Liu, K.; Li, J.; Ma, G.T. Characteristic studies of the superconducting electrodynamic suspension train with a field-circuit-motion coupled model. Pro. CSEE 2019, 39, 1162–1171. [Google Scholar] [CrossRef]
- Wang, X.; Huang, J. Levitation and guidance characteristics of superconducting electrodynamic maglev train. J. Tongji Univ. (Nat. Sci.) 2022, 50, 1482–1489. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, C.; Feng, X.; Ren, X. Study on mechanical characteristics of the electrodynamic levitation and guidance system for the superconducting maglev train. Machinery 2020, 47, 25–32. [Google Scholar] [CrossRef]
- Montgomery, D.B.; Technology, M.; Drive, H. Overview of the 2004 magplane design. In Proceedings of the Maglev’2004, Shanghai, China, 26–28 October 2004; pp. 106–113. [Google Scholar]
- Wu, H.; Li, P.; Hu, Y.; Zhang, L.; Ran, S.; Cheng, X. A Guidance Device for Vacuum Pipeline Maglev Train. CHN. Patent 201810060683.8, 14 August 2018. [Google Scholar]
- Liu, S.J. Permanent Magnet Induction Suspension and Guidance Device. CHN. Patent 01128905.8, 3 November 2004. [Google Scholar]
- Chen, Y.; Zhang, K. Calculation of electromagnetic force of plate type null double side permanent magnet electrodynamic suspension. Trans. China Electrotec. 2016, 31, 150–156. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, W.; Kou, L.; Cheng, Y.; Huang, H.; Wang, L. An ultra-high-speed maglev test rig designed for HTS pinning levitation and electrodynamic levitation. IEEE Trans. Applied. Supercond. 2021, 31, 3603605. [Google Scholar] [CrossRef]











| Parameter | Value |
|---|---|
| Length of a single magnet (x axis) | 30 mm |
| Width of a single magnet (y axis) | 100 mm |
| Thickness of a single magnet (z axis) | 30 mm |
| Number of PM | 9 |
| Magnetization angle | 90° |
| Remanence of PM | 1.45 T |
| Width of aluminum track (y axis) | 165 mm |
| Thickness of aluminum track (z axis) | 30 mm |
| Parameter | Value |
|---|---|
| Length of a single magnet (x axis) | 30 mm |
| Width of a single magnet (y axis) | 100 mm |
| Thickness of a single magnet (z axis) | 30 mm |
| Number of PM | 9 |
| Magnetization angle | 90° |
| Remanence of PM | 1.45 T |
| Width of aluminum track (y axis) | 165 mm |
| Thickness of aluminum track (z axis) | 12 mm |
| Width of guidance track (y axis) | 10 mm |
| Thickness of guidance track (z axis) | 4 mm |
| Suspension gap | 15 mm |
| Parameter | Value |
|---|---|
| Length of a single linear magnet | 16 mm |
| Width of a single linear magnet | 35 mm |
| Thickness of a single linear magnet | 17.5 mm |
| Number of linear PM | 5 |
| Outer diameter of PM wheel | 50 mm |
| Inner diameter of PM wheel | 32.5 mm |
| Width of PM wheel | 35 mm |
| Pole pairs of PM wheel | 4 |
| Remanence of PM | 1.19 T |
| Material of PM | NdFeB-N35 |
| Parameter | Value |
|---|---|
| Material of PM | NdFeB-N35 |
| External diameter of PM | 50 mm |
| Inner diameter of PM | 32.5 mm |
| Width of PM | 35 mm |
| Remanence of PM | 1.19 T |
| Pole pairs of PM | 4 |
| Density of PM | 7500 kg/m3 |
| Material of aluminum track | 1060 |
| Conductivity of aluminum track | 3.4 × 107 s/m |
| Width of aluminum track | 60 mm |
| Thickness of aluminum track | 6.8 mm |
| Maximum idling speed of motor | 8000 rpm |
| Torque of motor | 2 N·m |
| Width of guidance track | 8 mm |
| Thickness of guidance track | 4 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Y.; Deng, Z.; Shi, H.; Li, K.; Cao, T.; Deng, B.; Liang, L.; Zheng, J. Design and Analysis of Guidance Function of Permanent Magnet Electrodynamic Suspension. Technologies 2023, 11, 3. https://doi.org/10.3390/technologies11010003
Xiang Y, Deng Z, Shi H, Li K, Cao T, Deng B, Liang L, Zheng J. Design and Analysis of Guidance Function of Permanent Magnet Electrodynamic Suspension. Technologies. 2023; 11(1):3. https://doi.org/10.3390/technologies11010003
Chicago/Turabian StyleXiang, Yuqing, Zigang Deng, Hongfu Shi, Kaiwen Li, Ting Cao, Bin Deng, Le Liang, and Jun Zheng. 2023. "Design and Analysis of Guidance Function of Permanent Magnet Electrodynamic Suspension" Technologies 11, no. 1: 3. https://doi.org/10.3390/technologies11010003
APA StyleXiang, Y., Deng, Z., Shi, H., Li, K., Cao, T., Deng, B., Liang, L., & Zheng, J. (2023). Design and Analysis of Guidance Function of Permanent Magnet Electrodynamic Suspension. Technologies, 11(1), 3. https://doi.org/10.3390/technologies11010003








