An Automatic, Contactless, High-Precision, High-Speed Measurement System to Provide In-Line, As-Molded Three-Dimensional Measurements of a Curved-Shape Injection-Molded Part
Abstract
:1. Introduction
2. Part and Measurement Properties
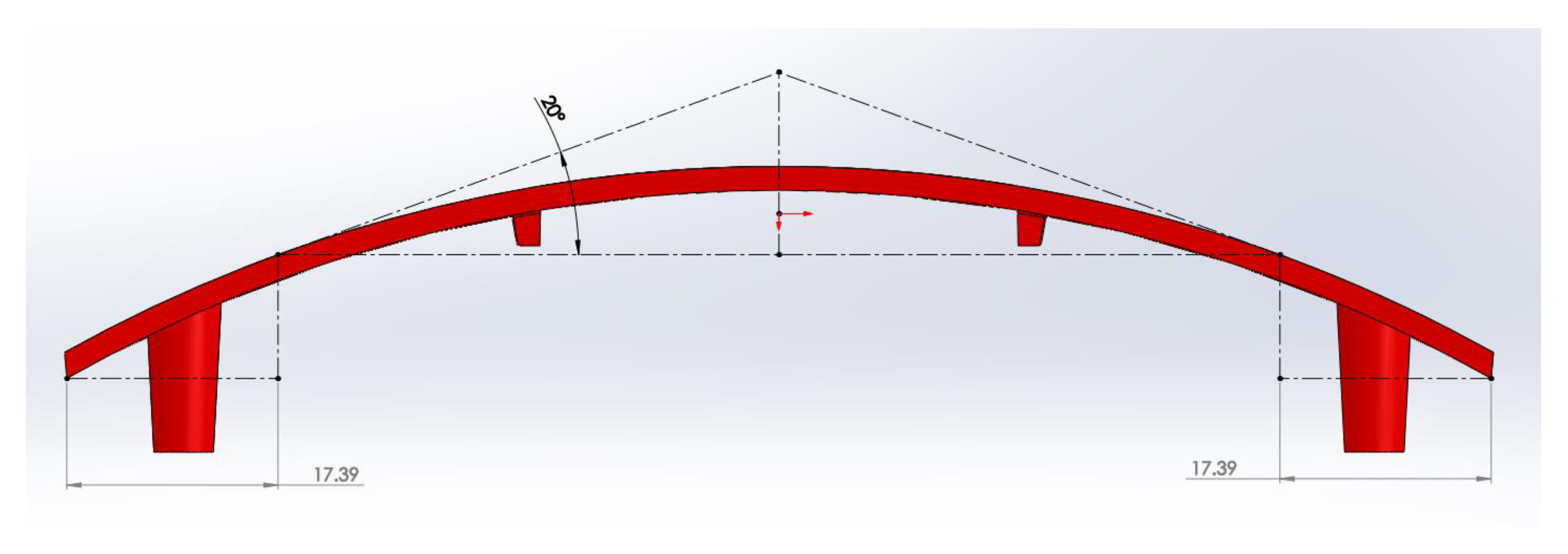
2.1. Part Properties
2.2. Measurement Requirements
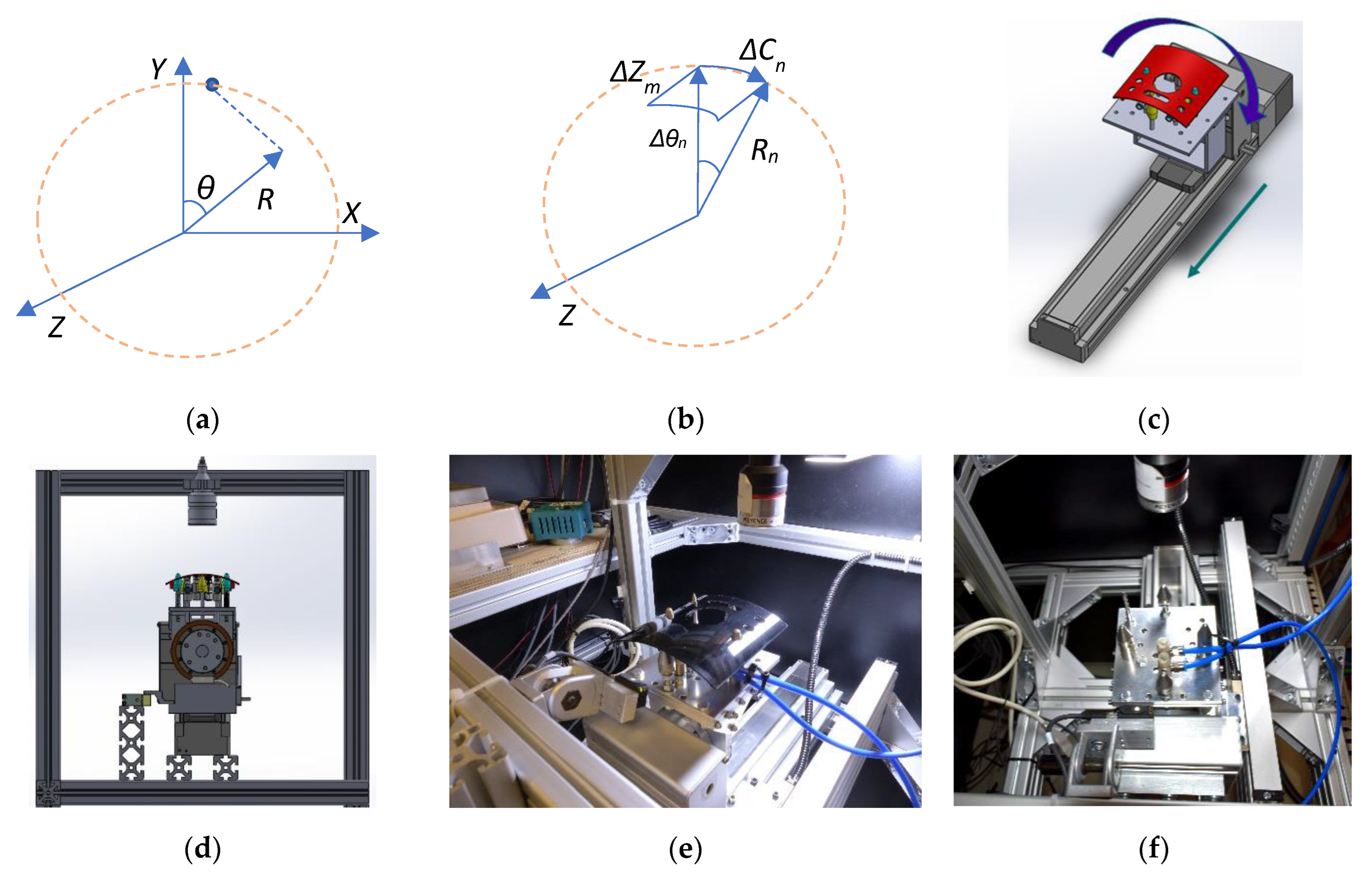
2.3. Part Manipulation: Gripper
2.4. Fixture on the Measurement Stations
3. Measurement System and Experiments
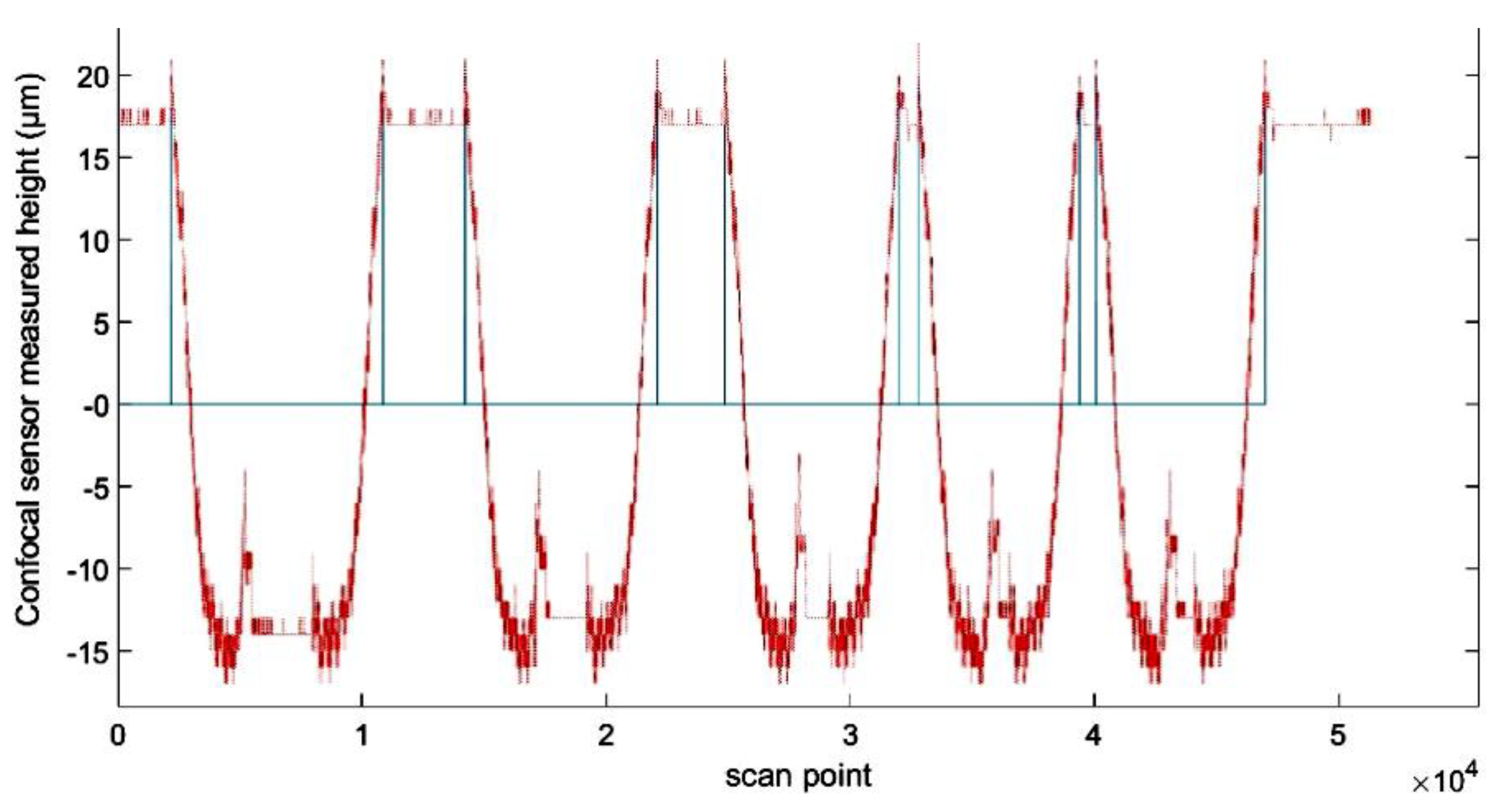
3.1. Feasibility Test
3.2. Measurement Methodology
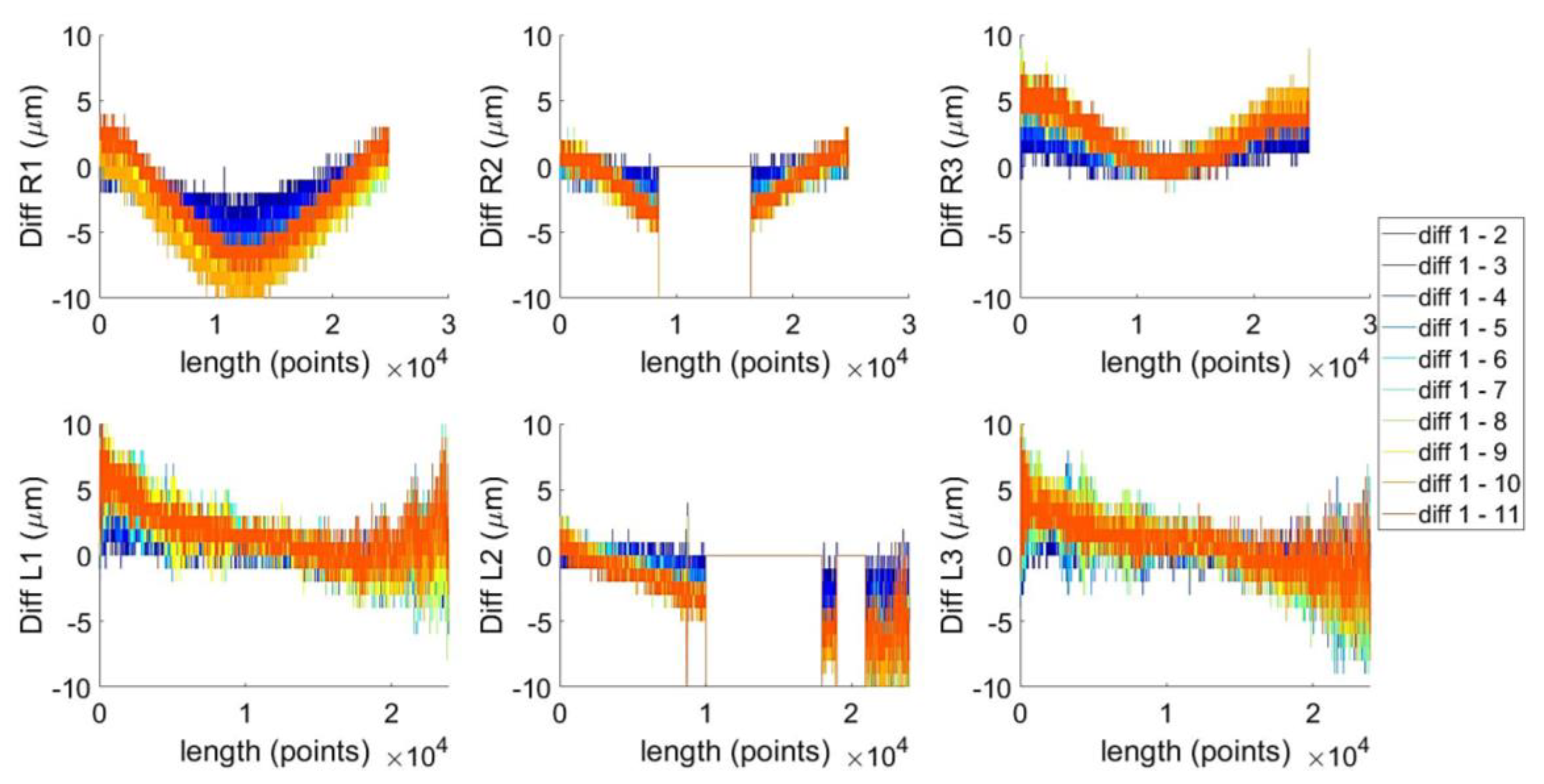
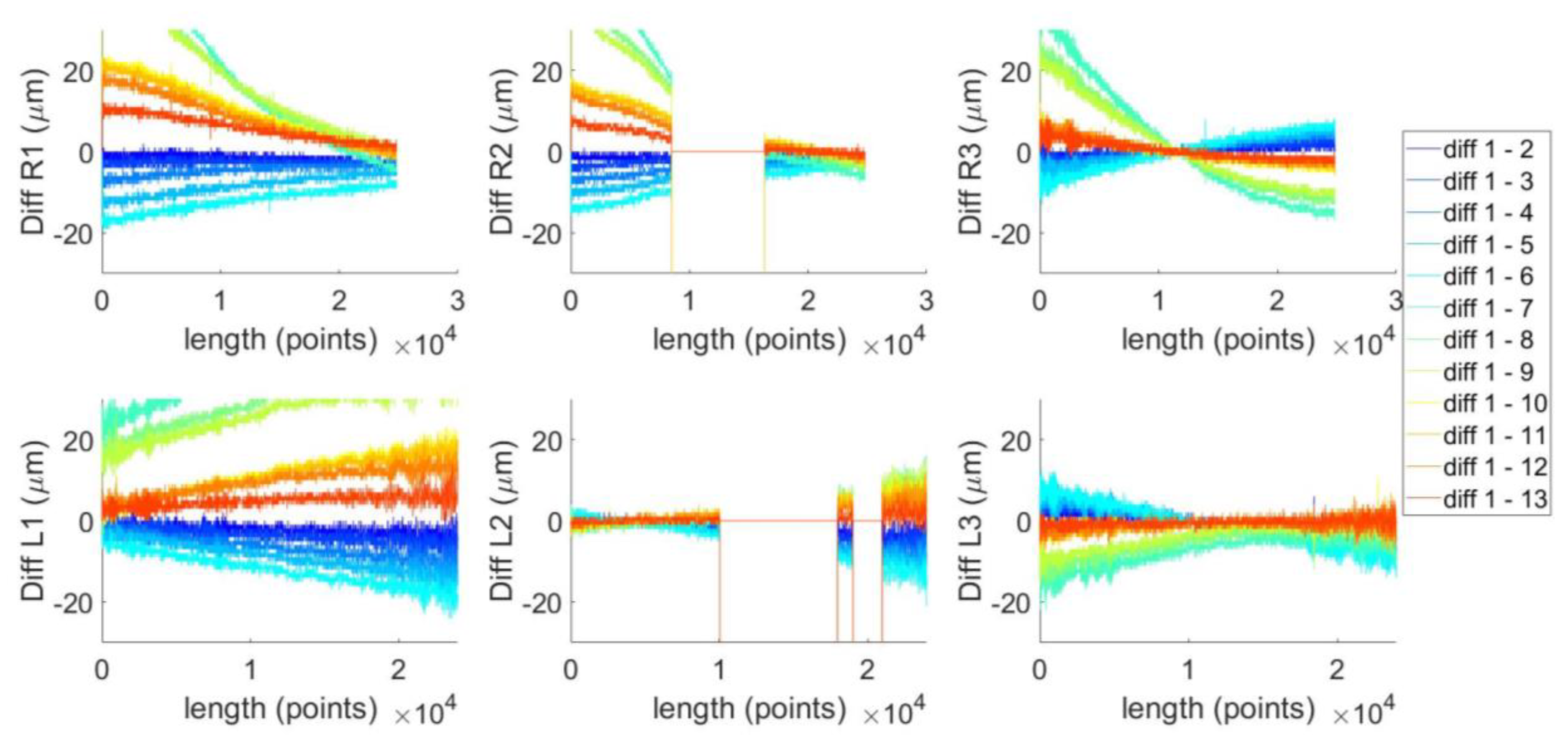
3.3. Experiment 1: Precision Validation Using a Self-Built Gauge
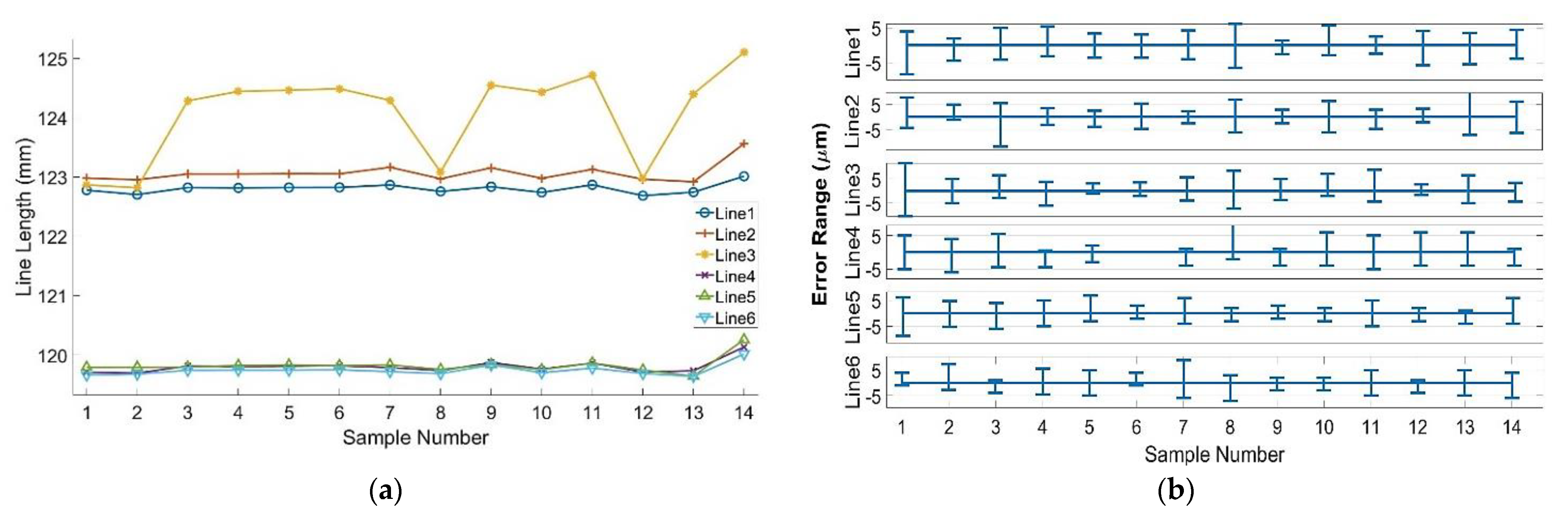
3.4. Experiment 2: Precision Validation on the Molded Part
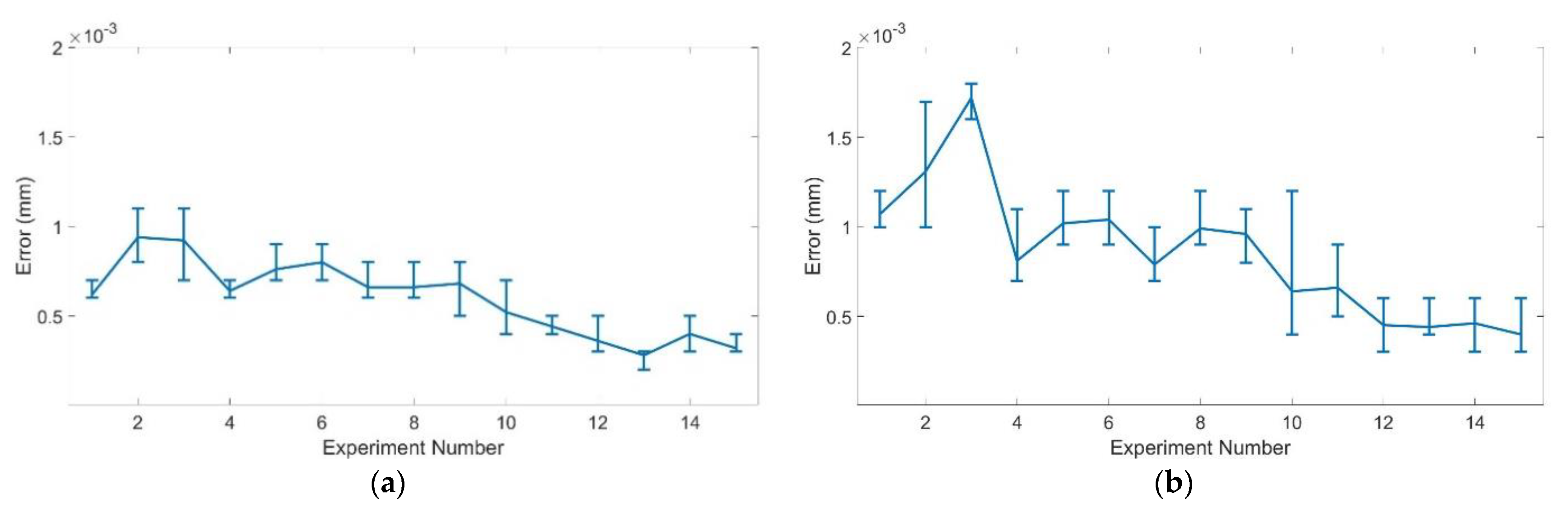
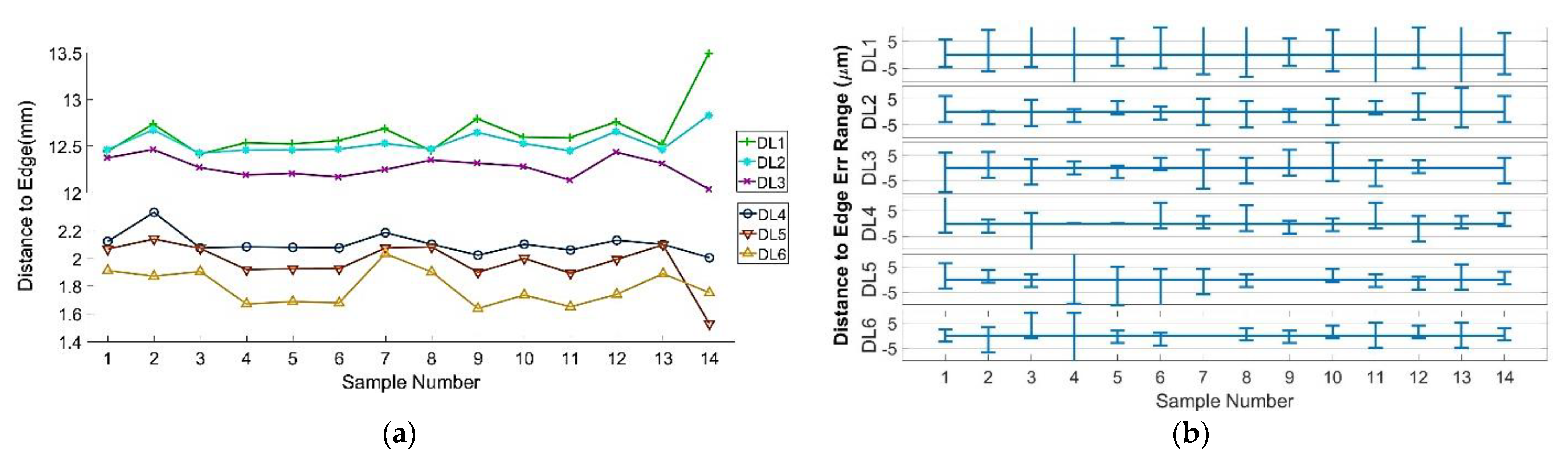
3.5. Experiment 3: Positioning Error on the Fixture
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmed, T.; Sharma, P.; Karmaker, C.L.; Nasir, S. Warpage Prediction of Injection-Molded PVC Part Using Ensemble Machine Learning Algorithm. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Singh, G.; Pradhan, M.K.; Verma, A. Multi Response Optimization of Injection Moulding Process Parameters to Reduce Cycle Time and Warpage. Mater. Today Proc. 2018, 5, 8398–8405. [Google Scholar] [CrossRef]
- Gruber, D.P.; Buder-Stroisznigg, M.; Wallner, G.; Strauss, B.; Jandel, L.; Lang, R.W. A Novel Methodology for the Evaluation of Distinctness of Image of Glossy Surfaces. Prog. Org. Coat. 2008, 63, 377–381. [Google Scholar] [CrossRef]
- Gruber, D.P. Method for Automatically Detecting a Defect on a Surface of a Molded Part. WO2010102319, 16 September 2010. [Google Scholar]
- Gruber, D.P.; Buder-Stroisznigg, M.; Wallner, G.; Strauß, B.; Jandel, L.; Lang, R.W. Characterization of Gloss Properties of Differently Treated Polymer Coating Surfaces by Surface Clarity Measurement Methodology. Appl. Opt. 2012, 51, 4833–4840. [Google Scholar] [CrossRef]
- Gruber, D.P. Method and Device for the Optical Analysis of the Surface of an Object. EP14186013, 1 April 2015. [Google Scholar]
- Masato, D.; Rathore, J.; Sorgato, M.; Carmignato, S.; Lucchetta, G. Analysis of the Shrinkage of Injection-Molded Fiber-Reinforced Thin-Wall Parts. Mater. Des. 2017, 132, 496–504. [Google Scholar] [CrossRef]
- Sreedharan, J.; Jeevanantham, A.K. Analysis of Shrinkages in ABS Injection Molding Parts for Automobile Applications. Mater. Today Proc. 2018, 5, 12744–12749. [Google Scholar] [CrossRef]
- Azad, R.; Shahrajabian, H. Experimental Study of Warpage and Shrinkage in Injection Molding of HDPE/RPET/Wood Composites with Multiobjective Optimization. Mater. Manuf. Processes 2019, 34, 274–282. [Google Scholar] [CrossRef]
- Barghash, M.A.; Alkaabneh, F.A. Shrinkage and Warpage Detailed Analysis and Optimization for the Injection Molding Process Using Multistage Experimental Design. Qual. Eng. 2014, 26, 319–334. [Google Scholar] [CrossRef]
- Chen, W.-C.; Fu, G.-L.; Tai, P.-H.; Deng, W.-J.; Fan, Y.-C. ANN and GA-Based Process Parameter Optimization for MIMO Plastic Injection Molding. In Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; Volume 4, pp. 1909–1917. [Google Scholar] [CrossRef]
- Ozcelik, B.; Erzurumlu, T. Comparison of the Warpage Optimization in the Plastic Injection Molding Using ANOVA, Neural Network Model and Genetic Algorithm. J. Mater. Process. Technol. 2006, 171, 437–445. [Google Scholar] [CrossRef]
- Petrova, T.; Kazmer, D. Hybrid Neural Models for Pressure Control in Injection Molding. Adv. Polym. Technol. 1999, 18, 19–31. [Google Scholar] [CrossRef]
- Kazmer, D.O. Injection Mold Design Engineering. In Injection Mold Design Engineering, 2nd ed.; Kazmer, D.O., Ed.; Hanser Publishers: Munich, Germany, 2016; pp. I–XXIV. ISBN 978-1-56990-570-8. [Google Scholar]
- Liao, S.J.; Chang, D.Y.; Chen, H.J.; Tsou, L.S.; Ho, J.R.; Yau, H.T.; Hsieh, W.H.; Wang, J.T.; Su, Y.C. Optimal Process Conditions of Shrinkage and Warpage of Thin-Wall Parts. Polym. Eng. Sci. 2004, 44, 917–928. [Google Scholar] [CrossRef]
- Jansen, K.M.B.; Van Dijk, D.J.; Husselman, M.H. Effect of Processing Conditions on Shrinkage in Injection Molding. Polym. Eng. Sci. 1998, 38, 838–846. [Google Scholar] [CrossRef]
- Pomerleau, J.; Sanschagrin, B. Injection Molding Shrinkage of PP: Experimental Progress. Polym. Eng. Sci. 2006, 46, 1275–1283. [Google Scholar] [CrossRef]
- Régnier, G.; Trotignon, J.P. Local Orthotropic Shrinkage Determination in Injected Moulded Polymer Plates. Polym. Test. 1993, 12, 383–392. [Google Scholar] [CrossRef]
- Gao, J.; Gindy, N.; Chen, X. An Automated GD&T Inspection System Based on Non-Contact 3D Digitization. Int. J. Prod. Res. 2006, 44, 117–134. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Liu, Y.; Yu, X.; Hou, Y.; Chen, W. High-Speed 3D Shape Measurement Using a Rotary Mechanical Projector. Opt. Express 2021, 29, 7885–7903. [Google Scholar] [CrossRef]
- Li, W.; Zhou, L.; Yan, S.-J. A Case Study of Blade Inspection Based on Optical Scanning Method. Int. J. Prod. Res. 2015, 53, 2165–2178. [Google Scholar] [CrossRef]
- Alkmal, J.S. Investigation of Optical Distance Sensors for Applications in Tool Industry: Optical Distance Sensors. Master’s Thesis, Saimaa University of Applied Science, South Kariland, Finland, 2013. [Google Scholar]
- Boltryk, P.J.; Hill, M.; McBride, J.W.; Nascè, A. A Comparison of Precision Optical Displacement Sensors for the 3D Measurement of Complex Surface Profiles. Sens. Actuators A Phys. 2008, 142, 2–11. [Google Scholar] [CrossRef]
- Jordan, H.-J.; Wegner, M.; Tiziani, H. Highly Accurate Non-Contact Characterization of Engineering Surfaces Using Confocal Microscopy. Meas. Sci. Technol. 1998, 9, 1142–1151. [Google Scholar] [CrossRef]
- Yang, L.; Wang, G.; Wang, J.; Xu, Z. Surface Profilometry with a Fibre Optical Confocal Scanning Microscope. Meas. Sci. Technol. 2000, 11, 1786–1791. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, Z.; Meng, Y.; Shao, C. Data-Driven Intelligent 3D Surface Measurement in Smart Manufacturing: Review and Outlook. Machines 2021, 9, 13. [Google Scholar] [CrossRef]
- Nouira, H.; El-Hayek, N.; Yuan, X.; Anwer, N.; Salgado, J. Metrological Characterization of Optical Confocal Sensors Measurements (20 and 350 Travel Ranges). J. Phys. Conf. Ser. 2014, 483, 012015. [Google Scholar] [CrossRef]
- Keyence Confocal Displacement Sensors CL-3000. 2019. Available online: www.keyence.com (accessed on 24 March 2019).
- Berkovic, G.; Zilberman, S.; Shafir, E. Temperature Effects in Chromatic Confocal Distance Sensors. In Proceedings of the SENSORS, 2013 IEEE, Baltimore, MD, USA, 3–6 November 2013; pp. 1–3. [Google Scholar] [CrossRef]
- Geometrical Product Specifications (GPS)—Roundness 2011, no. ISO12181-2. Available online: https://www.iso.org/standard/53621.html (accessed on 20 March 2021).
- Geometrical Product Specifications (GPS)—Geometrical Tolerancing—Tolerances of Form, Orientation, Location and Run-Out, 2017, no. ISO1101. Available online: https://www.iso.org/obp/ui/#iso:std:iso:1101:ed-4:v1:en (accessed on 20 March 2021).
- Sun, C.; Wang, H.; Liu, Y.; Wang, X.; Wang, B.; Li, C.; Tan, J. A Cylindrical Profile Measurement Method for Cylindricity and Coaxiality of Stepped Shaft. Int. J. Adv. Manuf. Technol. 2020, 111, 2845–2856. [Google Scholar] [CrossRef]
- Zeng, W.; Jiang, X.; Scott, P.J. Roundness Filtration by Using a Robust Regression Filter. Meas. Sci. Technol. 2011, 22, 035108. [Google Scholar] [CrossRef]
- Gosar, Z.; Gruber, D.P. IN-LINE Quality Inspection of Freeform Plastic High Gloss Surfaces Aided by Multi-Axial Robotic Systems. In Proceedings of the International Electrotechnical and Computer Science Conference (ERK’2017), Portotoz, Slovenia, 26 September 2017; pp. 445–448. [Google Scholar]
- Chiariotti, P.; Fitti, M.; Castellini, P.; Zitti, S.; Zannini, M.; Paone, N. High-Accuracy Dimensional Measurement of Cylindrical Components by an Automated Test Station Based on Confocal Chromatic Sensor. In Proceedings of the 2018 Workshop on Metrology for Industry 4.0 and IoT, Brescia, Italy, 16–18 April 2018; pp. 58–62. [Google Scholar] [CrossRef]
- Brinkmann, O.B.; Schmachtenberg, O. International Plastics Handbook; HANSER: Munich, Germany, 2012; pp. 547–553. [Google Scholar]










| Exp. | Position | Type | Speed | Unit |
|---|---|---|---|---|
| 1-1 | PL1 | Linear | 30 | mm/s |
| 1-2 | PL1 | Linear | 60 | mm/s |
| 1-3 | PL1 | Linear | 120 | mm/s |
| 1-4 | PL2 | Linear | 30 | mm/s |
| 1-5 | PL2 | Linear | 60 | mm/s |
| 1-6 | PL2 | Linear | 120 | mm/s |
| 1-7 | PL3 | Linear | 30 | mm/s |
| 1-8 | PL3 | Linear | 60 | mm/s |
| 1-9 | PL3 | Linear | 120 | mm/s |
| 1-10 | RP1 | Rotary | 30 | °/s |
| 1-11 | RP1 | Rotary | 60 | °/s |
| 1-12 | RP2 | Rotary | 30 | °/s |
| 1-13 | RP2 | Rotary | 60 | °/s |
| 1-14 | RP3 | Rotary | 30 | °/s |
| 1-15 | RP3 | Rotary | 60 | °/s |
| Line | Mean Val. | Min | Max | Error |
|---|---|---|---|---|
| R1 | 122.742 | 122.736 | 122.747 | 0.011 |
| R2 | 122.943 | 122.940 | 122.948 | 0.008 |
| R3 | 122.831 | 122.822 | 122.834 | 0.012 |
| L1 | 119.704 | 119.700 | 119.710 | 0.010 |
| L2 | 119.785 | 119.780 | 119.790 | 0.010 |
| L3 | 119.657 | 119.660 | 119.655 | 0.005 |
| Distance to Line | Min | Max | Difference |
|---|---|---|---|
| R1 | 2488 | 2490 | 2 |
| R2 | 2492 | 2494 | 2 |
| R3 | 2474 | 2477 | 3 |
| L1 | 425 | 426 | 1 |
| L2 | 414 | 416 | 2 |
| L3 | 383 | 384 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeidi Aminabadi, S.; Jafari-Tabrizi, A.; Gruber, D.P.; Berger-Weber, G.; Friesenbichler, W. An Automatic, Contactless, High-Precision, High-Speed Measurement System to Provide In-Line, As-Molded Three-Dimensional Measurements of a Curved-Shape Injection-Molded Part. Technologies 2022, 10, 95. https://doi.org/10.3390/technologies10040095
Saeidi Aminabadi S, Jafari-Tabrizi A, Gruber DP, Berger-Weber G, Friesenbichler W. An Automatic, Contactless, High-Precision, High-Speed Measurement System to Provide In-Line, As-Molded Three-Dimensional Measurements of a Curved-Shape Injection-Molded Part. Technologies. 2022; 10(4):95. https://doi.org/10.3390/technologies10040095
Chicago/Turabian StyleSaeidi Aminabadi, Saeid, Atae Jafari-Tabrizi, Dieter Paul Gruber, Gerald Berger-Weber, and Walter Friesenbichler. 2022. "An Automatic, Contactless, High-Precision, High-Speed Measurement System to Provide In-Line, As-Molded Three-Dimensional Measurements of a Curved-Shape Injection-Molded Part" Technologies 10, no. 4: 95. https://doi.org/10.3390/technologies10040095
APA StyleSaeidi Aminabadi, S., Jafari-Tabrizi, A., Gruber, D. P., Berger-Weber, G., & Friesenbichler, W. (2022). An Automatic, Contactless, High-Precision, High-Speed Measurement System to Provide In-Line, As-Molded Three-Dimensional Measurements of a Curved-Shape Injection-Molded Part. Technologies, 10(4), 95. https://doi.org/10.3390/technologies10040095






