Performance Analysis of 2D and 3D Bufferless NoCs Using Markov Chain Models
Abstract
:1. Introduction
2. Related Work
- It estimates expected latency (number of hops) between individual nodes, as well as the average for a given topology and traffic pattern, more accurately than current state-of-the-art static models.
- It raises the level of abstraction from cycle-accurate simulation, reducing the estimation time by at least four orders of magnitude, from minutes and hours to milliseconds.
3. Proposed Methodology
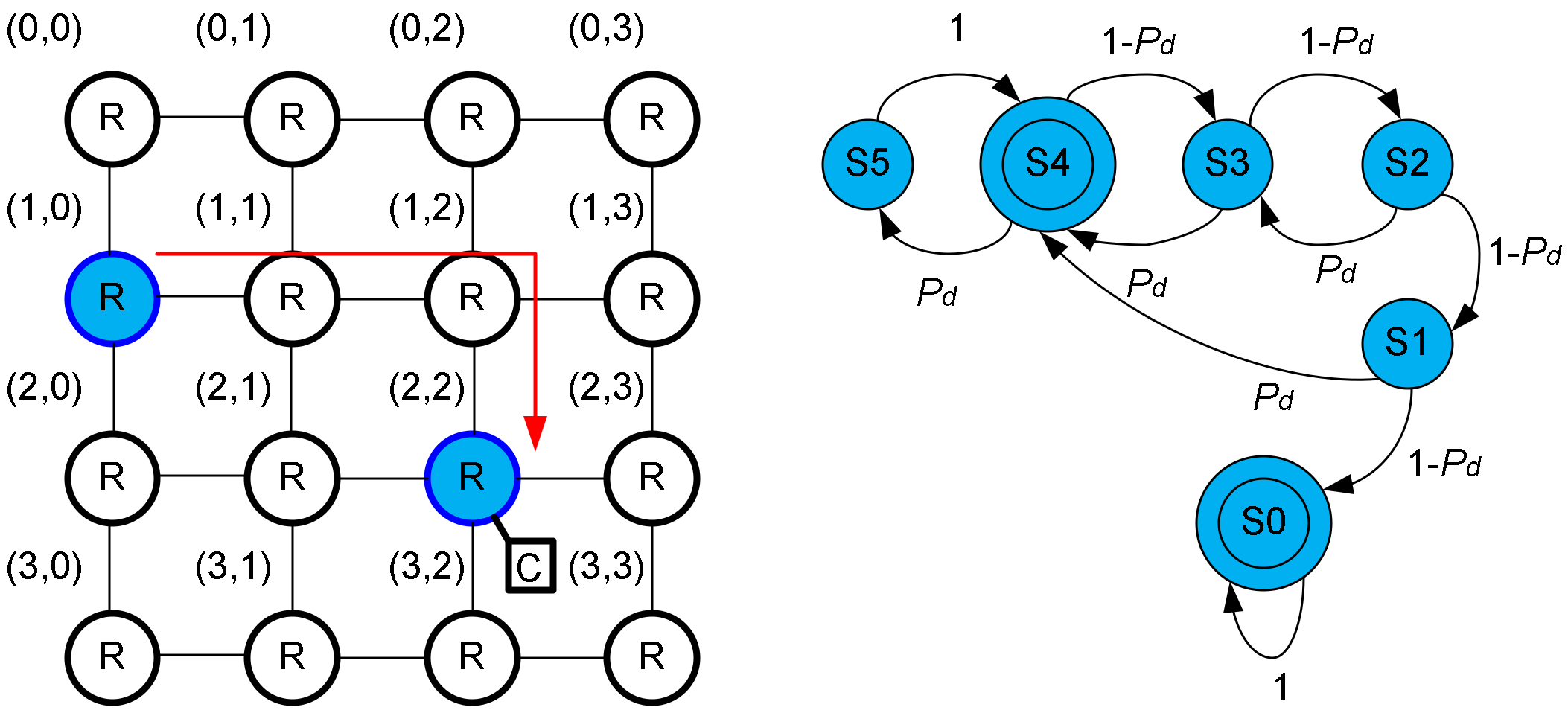
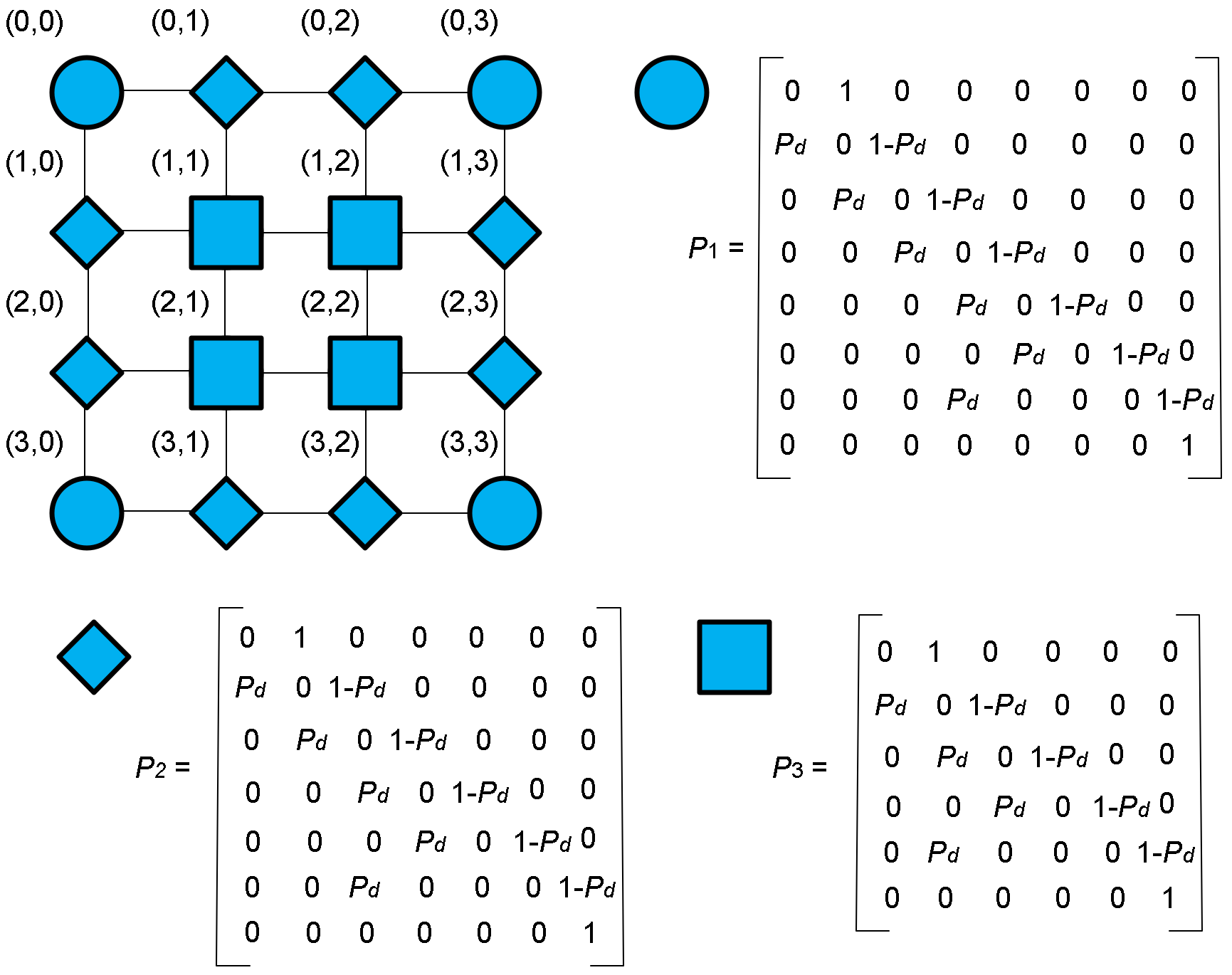
3.1. Topology Modeling
3.2. Traffic Modeling
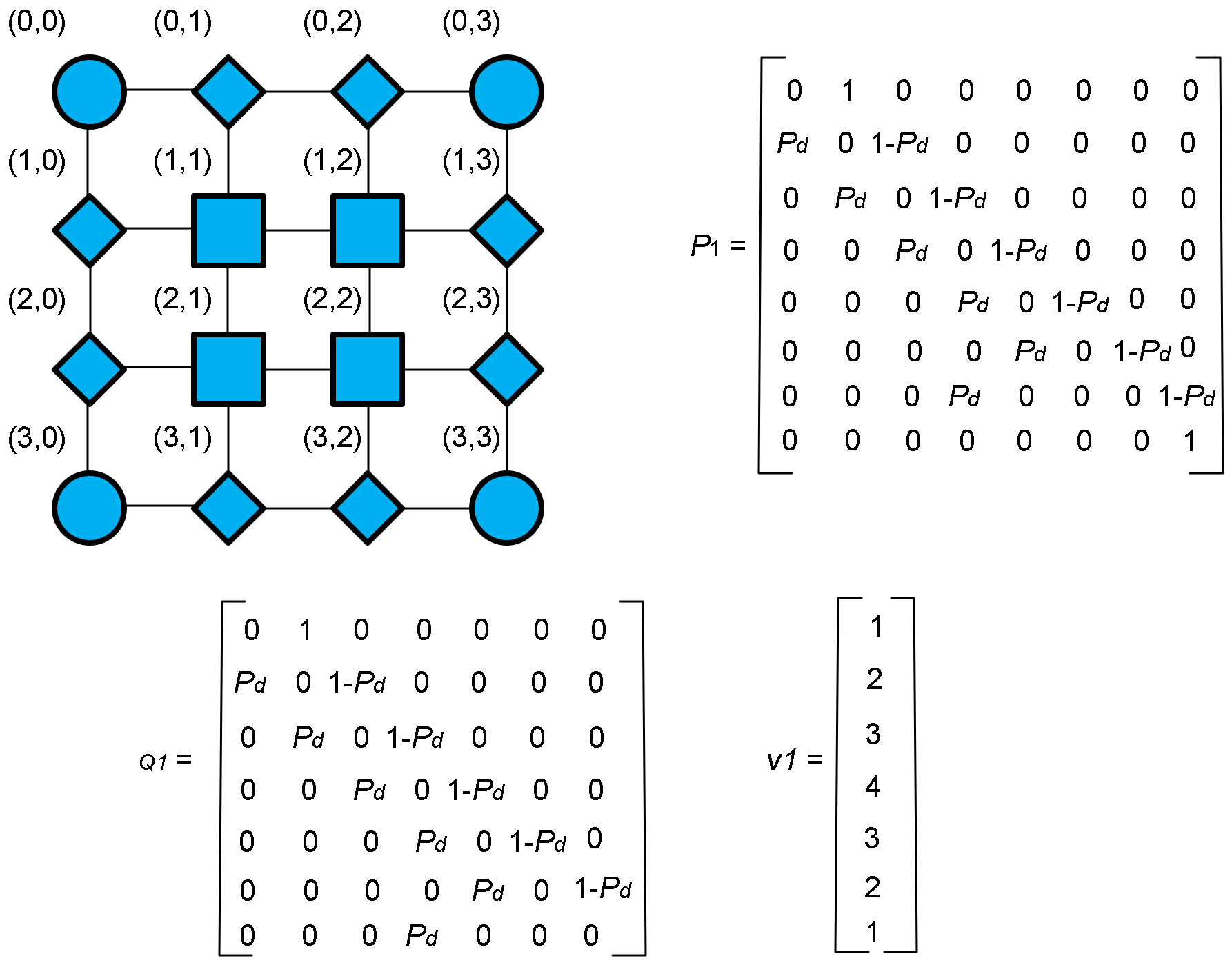
- Given a NoC topology, determine node distance classes and therefore the minimum number of Markov Chains.
- Fill each Markov chain transition matrix with the transition probabilities.
- Use Equations (1)–(3) to obtain the expectations for each source–destination node pair.
- Use Equation (4) to obtain the mean expected latency for the entire network based on the traffic pattern.
4. Experimental Results
4.1. Deflection Probability Simulation
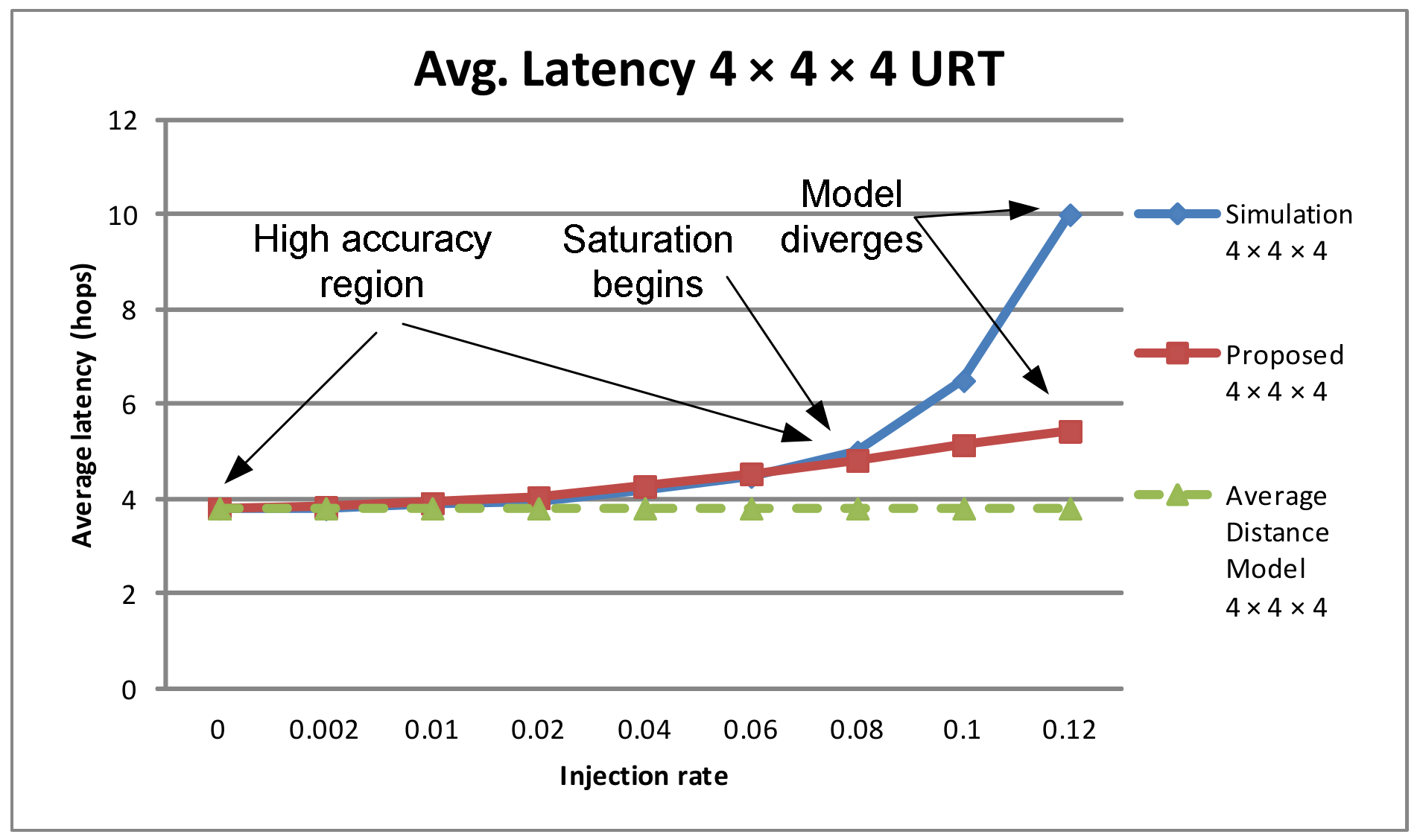
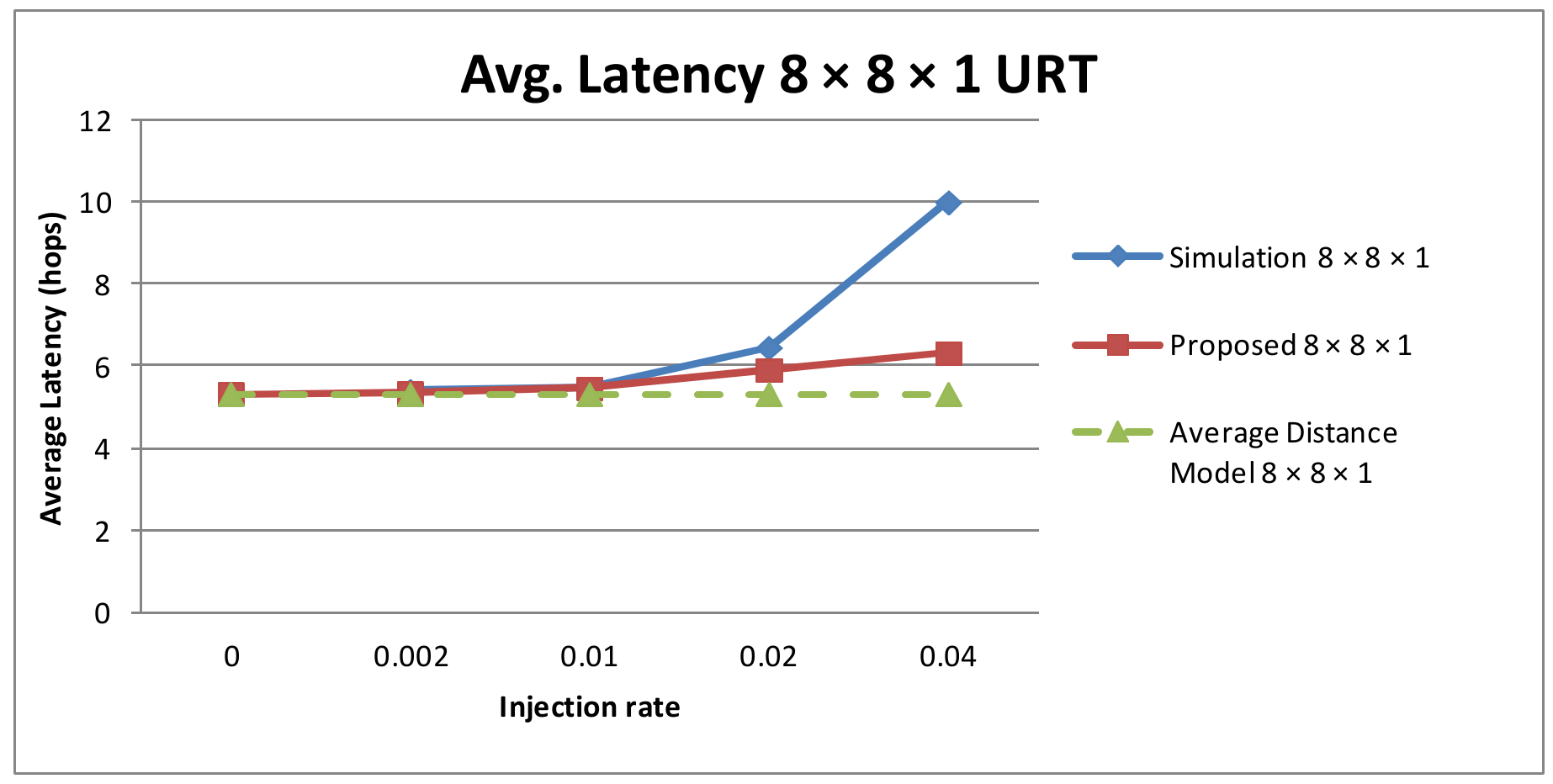
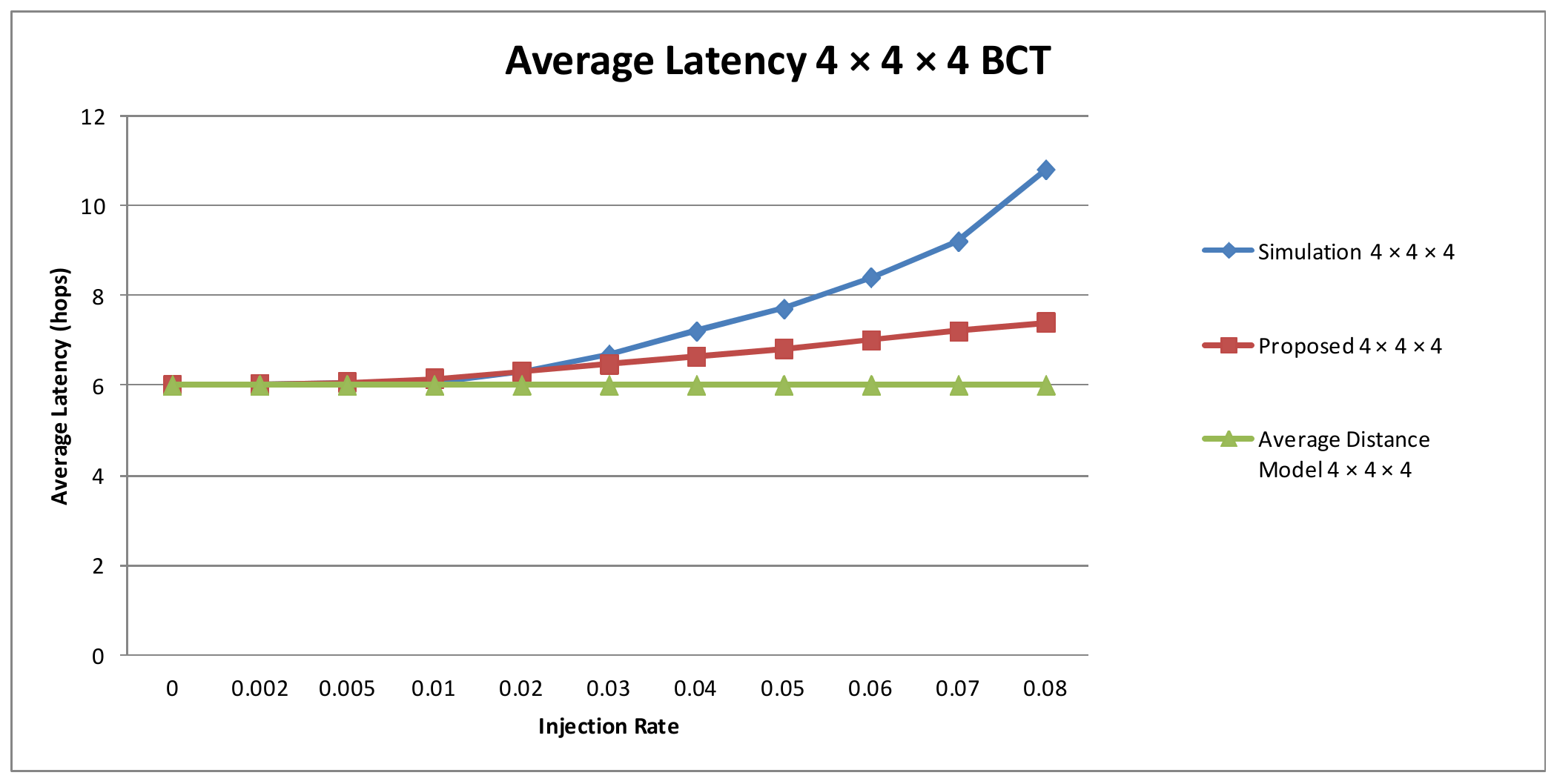
4.2. Average Latency Analysis
4.3. Model Accuracy Evaluation
5. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NoC | Network-on-Chip |
| URT | Uniform Random Traffic |
| BCT | Bit-Complement Traffic |
| ADM | Average Distance Model |
References
- Tatas, K.; Siozios, K.; Soudris, D.; Jantch, A. Designing 2D and 3D Network-on-Chip Architectures; Springer: New York, NY, USA, 2014. [Google Scholar]
- Bohr, M.T. Interconnect scaling—The real limiter to high performance ULSI. In Proceedings of the International Electron Devices Meeting, Washington, DC, USA, 10–13 December 1995; pp. 241–244. [Google Scholar]
- Swarbrick, I.; Gaitonde, D.; Ahmad, S.; Jayadev, B.; Cuppett, J.; Morshed, A.; Gaide, B.; Arbel, Y. Versal Network-on-Chip (NoC). In Proceedings of the 2019 IEEE Symposium on High-Performance Interconnects (HOTI), Santa Clara, CA, USA, 14–16 August 2019. [Google Scholar]
- Ivanov, M.; Sergyienko, O.; Tyrsa, V.; Lindner, L.; Flores-Fuentes, W.; Rodríguez-Quiñonez, J.C.; Hernandez, W.; Mercorelli, P. Influence of data clouds fusion from 3D real-time vision system on robotic group dead reckoning in unknown terrain. IEEE/CAA J. Automatica Sinica 2020, 7, 368–385. [Google Scholar] [CrossRef]
- Choi, W.; Duraisamy, K.; Kim, R.G.; Doppa, J.R.; Pande, P.P.; Marculescu, D.; Marculescu, R. On-Chip Communication Network for Efficient Training of Deep Convolutional Networks on Heterogeneous Manycore Systems. IEEE TC 2018, 67, 672–686. [Google Scholar] [CrossRef] [Green Version]
- Guerrier, P.; Greiner, A. A Generic Architecture for On-Chip Packet-Switched Interconnections. In Proceedings of the Design, Automation and Test in Europe Conference and Exhibition (DATE), Paris, France, 27–30 March 2000. [Google Scholar]
- Jafari, F.; Lu, Z.; Jantsch, A.; Yaghmaee, M.H. Buffer Optimization in Network-on-Chip Through Flow Regulation. IEEE TCAD 2010, 29, 1973–1986. [Google Scholar] [CrossRef] [Green Version]
- Ramanujam, R.; Soteriou, V.; Lin, B.; Li-Shiuan, P. Design of a High-Throughput Distributed Shared-Buffer NoC Router. In Proceedings of the International Symposium on Networks-on-Chip (NOCS), Grenoble, France, 3–6 May 2010; pp. 69–78. [Google Scholar]
- Wang, L.; Zhang, J.; Yang, X.; Wen, D. Router with Centralized Buffer for Network-on-Chip. In Proceedings of the Great Lakes Symposium on VLSI (GLSVLSI), Orange County, CA, USA, 6–8 June 2009; pp. 469–474. [Google Scholar]
- Kodi, A.; Louri, A.; Wang, J. Design of energy-efficient channel buffers with router bypassing for network-on-chips (NoCs). In Proceedings of the 2009 10th International Symposium on Quality Electronic Design, San Jose, CA, USA, 16–18 March 2009; pp. 826–832. [Google Scholar]
- Moscibroda, T.; Mutlu, O. A Case for Bufferless Routing in On-Chip Networks. In Proceedings of the 36th Annual International Symposium on Computer Architecture, New York, NY, USA, 11–15 June 2009; pp. 196–207. [Google Scholar]
- Fallin, C.; Craik, C.; Mutlu, O. Chipper: A low-complexity bufferless deflection router. In Proceedings of the 17th IEEE International Symposium on High Performance Computer Architecture, San Antonio, TX, USA, 12–16 February 2011; pp. 144–155. [Google Scholar]
- Feng, C.; Lu, Z.; Jantch, A.; Zhang, M. A 1-Cycle 1.25 GHz Bufferless Router for 3D Network-on-Chip. IEICE Trans. Inf. Syst. 2012, E95D, 1519–1522. [Google Scholar] [CrossRef] [Green Version]
- Feng, C.; Lu, Z.; Jantsch, A.; Zhang, M.; Xing, Z. Addressing transient and permanent faults in NoC with efficient fault-tolerant deflection router. IEEE Trans. Large Scale Int. Syst. TVLSI 2013, 21, 1053–1066. [Google Scholar] [CrossRef] [Green Version]
- Tatas, K. High-performance 3D NoC bufferless router with approximate priority comparison. In Proceedings of the 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018. [Google Scholar]
- Tatas, K.; Savva, S.; Kyriacou, C. 3DBUFFBLESS: A Novel Buffered-Bufferless Hybrid Router for 3D Networks-on-Chip. In Proceedings of the 27th International Symposium on Power and Timing Modeling, Optimization and Simulation (PATMOS 2017), Thessaloniki, Greece, 25–27 September 2017. [Google Scholar]
- Audsley, N. Applying new scheduling theory to static priority pre-emptive scheduling. Softw. Eng. J. 1993, 8, 284–292. [Google Scholar] [CrossRef] [Green Version]
- Qian, Z.L.Y.; Dou, W. Analysis of worst-case delay bounds for on-chip packet switching networks. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2010, 29, 802–815. [Google Scholar] [CrossRef] [Green Version]
- Bekooij, M.; Hoes, R.; Moreira, O.; Poplavko, P.; Pastrnak, M.; Mesman, B.; Mol, J.D.; Stuijk, S.; Gheorghita, V.; van Meerbergen, J. Dataflow analysis for real-time embedded multiprocessor system design. In Dynamic and Robust Streaming in and between Connected Consumer-Electronic Devices; Springer: Berlin/Heidelberg, Germany, 2005; pp. 81–108. [Google Scholar]
- Bogdan, P.; Marculescu, R. Non-stationary traffic analysis and its implications on multicore platform design. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2011, 30, 508–519. [Google Scholar] [CrossRef]
- Weldezion, A.Y.; Grange, M.; Jantsch, A.; Tenhunen, H.; Pamunuwa, D. Zero-load predictive model for performance analysis in deflection routing NoCs. Microprocess. Microsyst. 2015, 39, 634–647. [Google Scholar] [CrossRef] [Green Version]
- Tatas, K. Towards an Analytical Model of Latency in Deflection Routing: A Stochastic Process Approach for Bufferless NoCs. In Proceedings of the 10th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 5–7 July 2021. [Google Scholar]
- Brémaud, P. Markov Chains: Gibbs Fields, Monte Carlo Simulation and Queues, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Selvi, T.; Vaidhyanathan. Maximum Distance in Graphs. IJMTT 2018, 58, 16–19. [Google Scholar] [CrossRef]
- Haggstrom, O. Finite Markov Chains and Algorithmic Applications; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ben-Itzhak, Y.; Zahavi, E.; Cidon, I.; Kolodny, A. HNOCS: Modular open-source simulator for Heterogeneous NoCs. In Proceedings of the International Conference on Embedded Computer Systems (SAMOS), Samos, Greece, 16–19 July 2012; pp. 51–57. [Google Scholar]






| Topology | γ | Absolute Error URT/BCT | Percentage Error (%) URT/BCT | Normalized Error (%) URT/BCT |
|---|---|---|---|---|
| 4 × 4 × 4 | 0.002 | 0.0945/0.0296 | 2.48/0.49 | 2.48/0.49 |
| 0.01 | 0.0824/0.1005 | 2.11/1.66 | 2.16/1.67 | |
| 0.04 | 0.0434/0.5588 | 1.04/7.76 | 1.13/9.31 | |
| 0.06 | 0.1403/1.3748 | 3.34/16.60 | 3.68/23.24 | |
| 0.08 | 0.127 | 2.83 | 3.33 | |
| 8 × 4 × 2 | 0.002 | 0.2385/0.0299 | 5.32/0.42 | 5.36/0.43 |
| 0.01 | 0.2006/0.0695 | 4.36/0.92 | 4.51/0.99 | |
| 0.04 | 0.208 | 4.42 | 4.68 | |
| 0.06 | 0.14 | 2.8 | 3.15 | |
| 0.08 | 0.306 | 5.36 | 6.88 | |
| 8 × 8 × 1 | 0.002 | 0.29/0.0379 | 5.47/0.47 | 5.54/0.47 |
| 0.01 | 0.35/0.4073 | 6.46/4.74 | 6.61/5.09 | |
| 0.04 | 0.49 | 7.65 | 9.26 |
| Topology/Traffic Pattern | Average Distance | Topology Regularity (R) | ADM | Proposed | Range ADM | Range Proposed | |
|---|---|---|---|---|---|---|---|
| 4 × 4 × 4/URT | 3.8 | 1 | 0.04 | 0.09 | 0.12 | 33% | 75% |
| 8 × 4 × 2/URT | 4.44 | 1.1667 | 0.04 | 0.06 | 0.08 | 50% | 75% |
| 8 × 8 × 1/URT | 5.33 | 1.41667 | 0.015 | 0.02 | 0.06 | 25% | 33% |
| 4 × 4 × 4/BCT | 6 | 1 | 0.03 | 0.05 | 0.08 | 37.5% | 62.5% |
| 8 × 4 × 2/BCT | 7 | 1.1667 | 0.015 | 0.018 | 0.04 | 37.5% | 45% |
| 8 × 8 × 1/BCT | 8 | 1.41667 | 0.009 | 0.011 | 0.025 | 36% | 44% |
| Topology/Traffic Pattern | R | |||
|---|---|---|---|---|
| 4 × 4 × 4/URT | 3.8 | 1 | 3.8 | 0.12 |
| 8 × 4 × 2/URT | 4.44 | 1.1667 | 3.8 | 0.08 |
| 8 × 8 × 1/URT | 5.33 | 1.41667 | 3.76 | 0.06 |
| 4 × 4 × 4/BCT | 6 | 1 | 6 | 0.08 |
| 8 × 4 × 2/BCT | 7 | 1.1667 | 6 | 0.04 |
| 8 × 8 × 1/BCT | 8 | 1.41667 | 5.65 | 0.025 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tatas, K. Performance Analysis of 2D and 3D Bufferless NoCs Using Markov Chain Models. Technologies 2022, 10, 27. https://doi.org/10.3390/technologies10010027
Tatas K. Performance Analysis of 2D and 3D Bufferless NoCs Using Markov Chain Models. Technologies. 2022; 10(1):27. https://doi.org/10.3390/technologies10010027
Chicago/Turabian StyleTatas, Konstantinos. 2022. "Performance Analysis of 2D and 3D Bufferless NoCs Using Markov Chain Models" Technologies 10, no. 1: 27. https://doi.org/10.3390/technologies10010027
APA StyleTatas, K. (2022). Performance Analysis of 2D and 3D Bufferless NoCs Using Markov Chain Models. Technologies, 10(1), 27. https://doi.org/10.3390/technologies10010027






