Abstract
Global environmental goals and the Paris agreement declared the need to avoid dangerous climate change by reducing emissions of greenhouse gases with an ultimate goal to transform today’s policies and reach climate neutrality before the end of the century. In the medium to long-term, climate policies imply rising CO price and consequent financial risk for carbon-intensive producers. In this context, there is a need for tools to buffer CO prices within the period of transition to greener technologies when the emission offsetting markets expose high volatility. Contracts for optional future purchase of carbon credits could provide emitters with a cost-efficient solution to address existing regulatory risks. At the same time, this would help to create much needed financing for the projects generating carbon credits in the future. This work presents the concept of a flobsion—a flexible option with benefit sharing—and demonstrates its advantages in terms of risk reduction for both seller and buyer as compared to both a “do nothing” strategy (offsetting at future market price) and a traditional option with a fixed strike price. The results are supported analytically and numerically, employing as a benchmark the dataset on historical CO prices from the European Emission Trading Scheme. Flobsion has the potential to extend the traditional option in financial applications beyond compliance markets.
1. Introduction
The sustainable development agenda United Nations Development Programme (2016) and the need to restrain climate change UNFCCC (2015) limit greenhouse gas (GHG) emissions into the Earth’s atmosphere and thus constrain the future use of fossil fuel. While concrete mechanisms of achieving these goals are not yet in place, there is a clear move in this direction. On the technological side, there is a substantial progress on electric vehicles that were considered as a potential future development a decade ago and already in 2016 the global electric car stock surpassed two million vehicles after crossing the 1 million threshold in 2015; the registrations of electric cars hit a record in 2016, with over 750 thousand sales worldwide International Energy Agency (2017). The energy used by the industry and households (also to recharge car’s batteries) is coming partially from renewable sources, and that share is increasing, so between 2010 and 2014, renewable energy consumption of the top countries has effectively doubled from 168 million tons to 316 million tons of oil equivalent WordAtlas (2018). However, in the energy sector that is responsible for about 40% of global GHG emissions The Shift Project Data Portal (2019), there is still a big (over 80%) share of fossil fuels in total energy production BP p.l.c. (2018). The main reason for that is apparently lower costs, but also other considerations e.g., electric grid stabilization needs as wind mills can generate fluctuations of capacity Hannele Holttinen et al. (2006), societal attitude to avoid operation and construction of new nuclear power plants U.S. Congress, Office of Technology Assessment (1984). Although one may foresee drastic changes in the energy generation technologies in the coming decades, it seems that fossil fuel-based (i.e., CO intensive technologies) will maintain a reasonable share in the total power generation mix throughout that transitional period.
The mechanisms for CO pricing are not established yet beyond regional scale and the legal background is missing with the exception for the European Emission Trading Scheme (EU–ETS) and the Cap-and-Trade Program in California, USA. However, in the mid– to long–term, the CO price is likely to upscale to a larger geographical extent, be it in a form of a carbon tax, cap-and-trade, or a mix thereof. This would inevitably create a distortion in the energy sector, with the highest impact on those companies that have large share of fossil fuel in their power generation technologies mix. Because of the system role of those companies, they would need to be supported with enough supply of emission allowances/offsets. Creating such a supply by legal/policy means would raise a question on diminishing the purpose of the CO price geographical upscaling, while subsidizing these companies would mean spending taxpayers money against the principles they were spent to support renewable technologies in the previous period. From this perspective, there seem to be a need for tools supporting a smooth transition from a few regional CO pricing models to a larger scale implementation.
In this context, contracting at current relatively low price levels the future delivery of CO credits is one of the possibilities to reduce regulatory risk for carbon-intensive emitters that have limited possibilities of technological change. These carbon credits could be supplied in the future by projects on reducing emissions in the industry and energy sectors UNFCCC (2012).
As the future development of the CO price is highly uncertain, a hedging strategy protecting a regulated entity from excessive price peaks seems to be a reasonable approach for managing the associated risk. One of the potential candidates from available financial instruments to provide hedging capabilities is a traditional call option Collins and Fabozzi (2008), which (in our setting) is the right purchased in advance to buy in the future a specified amount of carbon credits at a specified price. The call option provides financing to the seller before the actual delivery, which is advantageous in the context of financing a project implementation that is needed to generate carbon credits.
The contribution of this paper is in the introduction and proofs of analytical properties of a new financial instrument—a flexible option with a benefit sharing mechanism, a flobsion in short, which is an extension of a call option concept combined with the idea of benefit (and loss) sharing between the contracting parties explored in earlier publications Krasovskii et al. (2016, 2017). A flobsion has advantages in terms of risk reduction for both buyer and seller as compared to a “do nothing” strategy (offsetting at future market price) and a traditional option with a fixed strike price. We illustrate analytical results with benchmarking examples employing historical data on CO prices in the European Emission Trading Scheme (EU-ETS).
2. Literature Review and Motivation
There is a rich set of literature sources devoted to the multiple concepts that we employed in this manuscript: risk management in general and that connected to an uncertain future CO price for emissions offsetting in particular; principles of indifference prices, benefit sharing, and optionality to address future uncertainty. In this section we provide a condensed review of selected publications in order to position our manuscript and provide the reader with an entry point to the relevant literature.
In the general risk management context a key role plays a notion of a risk measure and in particular a “coherent” measure of risk that possesses desirable properties Artzner et al. (1999). While there exist many risk measures used in practice e.g., variance, value-at-risk, conditional value-at-risk—not all of them are coherent. In practice, there are deficiencies associated also with coherent risk measures e.g., inability to differentiate between market risk and model uncertainty Cont (2006). As a proxy for risk associated with the future asset market price we use variance and to address risk associated with a potential price model uncertainty, in the spirit of Cont (2006), demonstrate that flobsion (as compared to an option) has a lower sensitivity to a wrong assumption on a price scenario.
The employed idea of benefit (revenue) and risk sharing is rather general and was earlier explored within various contexts e.g., revenue-risk-sharing for public-private partnerships in construction Rouhani et al. (2018), game theoretic setting for contracts in electricity market Ma et al. (2019), coordination of supply chains Liu et al. (2017), emission offsetting context for a forward contract Krasovskii et al. (2017). In this paper, we merge the concept of benefit sharing with a financial option to create a new instrument.
There is an vast body of literature starting from early works Black and Scholes (1973); Cox and Ross (1976) further developed and summarized in comprehensive books on extensive treatment of theoretical and computational aspects of options-style derivatives pricing Detemple (2005); Pierre Henry-Labordere (2009). In these works a stochastic price process has to belong to a specific family (e.g., Brownian motion) and the problem of derivatives’ pricing requires specific treatment depending on the time moment when an option can be executed (American or European option). We employ a different and a more general approach that deals with a rather generic form of a discrete price distribution and does not specify the instrument’s execution date.
Financial instruments including those of option-type are becoming increasingly important for risk management in particular in electricity markets due to uncertainty of consumption and limited fungibility of energy Kudryavtsev and Zanette (2013). The link to volatile emission permit markets leads to more complexity in risk management as the permits may expose features that are distinctive from other financial assets Medina and Pardo (2013). An earlier research on pricing European emission allowances Chesney and Taschini (2012) suggested a closed-form formula for option-pricing, while admitting its rather limited utility because of the specific model assumptions. Our results are less price-centric due to the established link to existing options pricing and more oriented towards risk reduction properties of a flobsion.
With regard to risk reduction, a paper Andrew and Chen (2017) examines the effect of imposing various permit price-containment policies on spot market such as a price ceiling, floor, or collar within an electricity market context. While addressing the same problem of market volatility, unlike the paper Andrew and Chen (2017), we suggest an instrument that is bilateral and does not require market-level intervention by a regulator. From this perspective, the two approaches are complementary to each other.
The motivation of this research is in the high uncertainty and risks associated with the future CO prices in the context of emissions offsetting of regulated entities. The research question was whether it is possible to reduce these risks even further as compared to a traditional option respecting the concerns of both regulated entity (buyer) and the offset supplier (seller). In parallel to suggesting a new financial instrument, our work is addressing the need of evaluating “the new contractual forms that are constantly emerging in response to evolving economic conditions and regulations” Detemple (2005).
3. Flobsion Description
There exist two flavors of an option—“put” and “call”, and for the purposes of the manuscript we will only use the call-option, further referring to it for simplicity as just “option”. An option for an asset (e.g., for an emission offset) implies that a buyer pays an amount to the seller of the option for the future possibility to purchase the asset at an agreed “strike” price . The owner of the option decides in the future whether to make such a purchase or not, so for them it is a possibility, but not an obligation. The time component of an option is specified in the contract and can be e.g., a specific day on which the purchase of the asset can be executed a “European option”, or a time period within which that purchase can be made an “American option”. Our discussion below is applicable to both cases as we do not explicitly model dynamic prices and instead refer to two time moments: (1) the time of purchase of an option and (2) the time of executing the option.
A flobsion is similar, yet has a more general construction than the option. A buyer pays the amount to the seller of a flobsion for the future possibility to purchase the asset at the agreed “strike” price plus the discounted difference between the asset’s market price x and , if that difference is positive (or just otherwise). So, in case if the flobsion holder decides to make a purchase of an asset within the period of validity of a flobsion, they would pay the amount
meaning that an asset is being purchased at a market price x and the flobsion is not being executed if . Here is a discount to the market price using as a base. In case of a flobsion, a future asset purchase is still optional for the buyer as in case of a standard option. The price for future purchase of an asset in case of a flobsion is not fixed, yet tied to the market price, so based on this general trait, the flobsion is a new, so far unknown, member of a loosely defined set of financial instruments commonly called “exotic options” Buchen (2012); Collins and Fabozzi (2008).
Remark 1.
For , a flobsion turns into an option, so that the amount paid for an underlying asset in the future conditional on the market price x would be
Remark 2.
For the amount paid in the future for an underlying asset equals the market price x, which corresponds to the “do nothing” alternative (naturally assuming i.e., nothing was paid for a zero future discount to the market price).
4. Analytical Results
Below, we present the proofs for a probabilistic market price x described for simplicity by a discrete distribution in the form
which is practical for numerical modeling and is sufficient for our application. Analytical results on discrete approximations of continuous distributions are available in the literature Kennan (2006).
Definition 1.
The price is a “fair price” of a flobsion with the strike price if the expected total amount paid for an asset by a flobsion holder equals the expected market price of the asset:
Theorem 1.
Let , where is the strike price of an option and that one of a flobsion. Then the fair prices of an option and a flobsion are connected through the flobsion’s discount to the future market price d:
Proof.
Theorem 2.
Let be the strike prices of a flobsion and an option, and and the corresponding fair prices for the same price distribution Equation (3). Then for any alternative price distribution , , , the following equality holds:
where the expectation is calculated over the price distribution .
Proof.
□
Remark 3.
In Theorem 2, the prices , (also respective ones for an option, if ) while being fair for the price distribution Equation (3) are not necessarily fair for the alternative price distribution , so that generally speaking
and the meaning of the term
is the average expected profit or loss as compared to “do nothing” approach where no flobsions/options are contracted and only the market price for an asset is being paid. The practical implication of Theorem 2 is that the flobsion is less sensitive to a wrong assumption on price distribution than the option in terms of reducing both expected profit and loss (both contradict the principle of a fair price) under an alternative price scenario.
Definition 2.
We would call a function a compressing transform of a distribution Equation (3) if there exist a number such that
where .
Definition 3.
We would call a function a pair-wise compressing transform of a distribution Equation (3) with additionally ordered values if
Lemma 1.
A flobsion is a pair-wise compressing transform of the price distribution Equation (3).
Proof.
Let us denote , where is defined in Equation (1). Without changing connotation we may assume that the values are ordered, so that , for all . Let us consider all three possible options for any fixed :
□
Lemma 2.
Any pair-wise compressing transform in the sense of Definition 3 is a compressing transform in the sense of Definition 2.
Proof.
Let us denote the distribution under consideration as and the transform as . Then from Definition 3 it follows that
Let us consider the value of the index such that
From Equation (11) it follows that
and hence there exist such a shifting parameter , such that the following inclusion of the intervals is valid:
furthermore, because of Equation (12) and the value of shifting parameter in Equation (14) can be refined in such a way that also belongs to the interval implying the following chain of inequalities:
that for easier reference we split into a set of inequalities:
Let us fix an arbitrary index i and consider two cases:
Let us start with the case “A”:
So, the lemma is proven for the case “A”. Equation (9) holds for . Let us consider also the case “B”:
The lemma is proven also for the case “B”: Equation (9) holds for . □
Lemma 3.
Proof.
Let us denote and , then
□
Theorem 3.
A flobsion reduces risk (decreases cost variance) for any future discount d, strike price , and flobsion price :
where the amount paid in the second period is conditional on the market price and is defined in Equation (1).
Proof.
According to Lemma 1, a flobsion is a pair-wise compressing transform of the price distribution Equation (3), hence, by Lemma 2, a flobsion is a compressing transform of the price distribution, hence for the function transforming the market price into a price paid for an underlying asset by a flobsion owner the Lemma 3 is valid and hence Equation (21) holds where , that implies the validity of Equation (22) as for any (a constant defined in the first time period). □
Remark 4.
In Theorem 3 the flobsion price does not have to be the fair price as for any (a constant defined in the first time period).
Remark 5.
Theorem 4.
Let the prices of a flobsion and an option satisfy the same equation Equation (4) as the fair prices. Then in terms of total cost of offsets, a flobsion with the strike price s and a discount d is equivalent to a portfolio of offsets to be purchased in the future at a market price and options with the same strike price s, and .
Proof.
We denote the total cost of v offsets when acquiring them on the market, via option, and via flobsion as , , and respectively. For any offset price x materialized in the future, we consider two possible cases: case A: that implies
Case B: that implies
□
Remark 6.
The prices in Theorem 4 for a flobsion and an option do not necessarily have to be fair prices, yet naturally the theorem holds for fair prices.
5. Benchmarking Results
For numerical illustration we employ the dataset on historical CO prices (emission allowances, EUA) from the European Emission Trading Scheme (ETS) Fusion Media (2018) spanning the time period August 2005–February 2018 (further referred to as the “historical period”). These prices are presented in Figure 1.
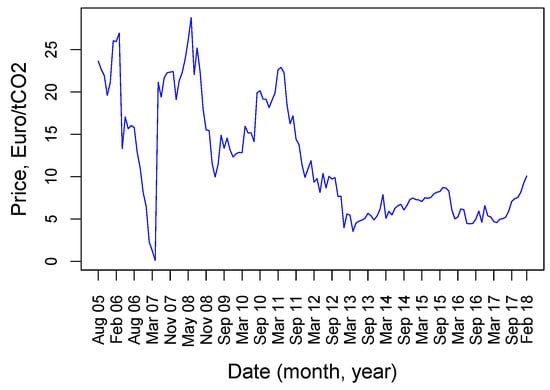
Figure 1.
Historical CO prices from the European Emission Trading Scheme (ETS) Fusion Media (2018).
For the purposes of benchmarking a flobsion against an option, we consider a hypothetic scenario where both an option and a flobsion for EUA were purchased before August 2005 and were executed (or expired without execution) at a random date uniformly distributed within the historical period. The market price distribution at the time of execution/expiration of a flobsion/option is shown in the form of a histogram in Figure 2.
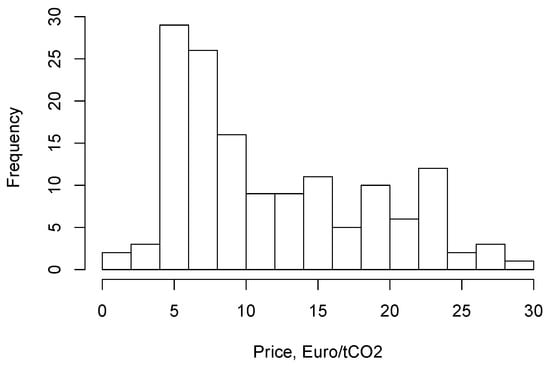
Figure 2.
CO-price distribution from the EU ETS for the period August 2005–February 2018.
We assume that the contracted volume of allowances was actually used to offset emissions either through an option (flobsion) or via direct purchase on the market, so that the total price paid per one ton of emitted CO is the sum of the option (flobsion) price plus either market price (in case the option/flobsion was not executed) or the option’s strike price (flobsion’s strike price plus discounted market price).
For the purposes of numerical calculations we arbitrarily set the flobsion’s discount d to and the strike price to 8 Euro/tCO (both for the option and the flobsion). The total amount that was paid in three possible cases: just paying actual market price for emissions, using a flobsion or an option is presented in Figure 3 for three price scenarios: original historical prices, those doubled, and halved, where the initial purchase prices for both option and flobsion are “fair” for the original (historical) price distribution. The total amount paid per unit of emissions when flobsion is involved for all possible market prices stays between those of an option and the market price as illustrated in Figure 3.
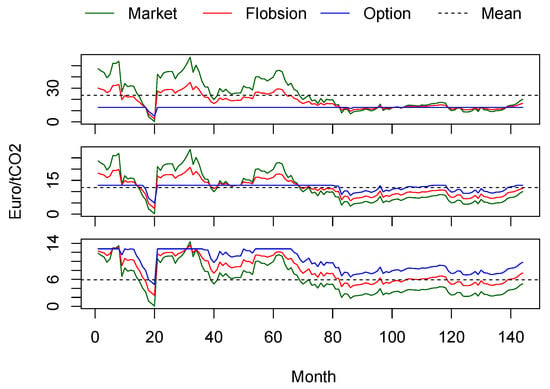
Figure 3.
The total amount paid for emissions offsetting depending on the date (month since August 2005) in three cases: just paying a market price, using an option or a flobsion for three price scenarios: original historical prices (middle panel), those doubled (top panel), and halved (bottom panel).
The expected deviations from zero-expected profit (loss) in case of an option and a flobsion are presented in Table 1. The smaller scale of profits and losses provided by a flobsion numerically illustrates the analytical results obtained in Theorem 2.

Table 1.
Expected deviations from zero-expected profit (loss) in Euro/tCO in case of an option and a flobsion. Positive numbers are profits, negative numbers are losses.
The flobsion’s and option’s reduction in offset cost variance for the original market price scenario is presented in Table 2. According to Theorem 4, purchasing a flobsion was similar to buying an option for a share of needed offsets and then actual emissions offsetting in the future using that option and purchasing the rest of needed offsets at a market price. The variance of the total cost of emissions offsetting supported by a flobsion is between that of an option and the “do nothing in advance” approach. Table 2 illustrates numerically the results of Theorem 3 i.e., the variance of the offsetting cost supported by a flobsion is smaller than the “original” variance of the market price (15.58 < 46.21).

Table 2.
Variance of the emission offsetting costs for the historical price distribution and three alternatives: paying just the marked price (“do nothing”), contracting a flobsion, and an option.
The numbers in Table 1 and Table 2 indicate a trade-off between lower sensitivity to a wrong assumption on the price scenario (lower absolute values for flobsion in Table 1) and higher variance of offsetting costs within a fixed price scenario (higher value for flobsion than for option in Table 2). This links to the concepts of “model uncertainty” and “market risk” discussed earlier in Section 2 and illustrates the fact that a better performance in the sense of “model uncertainty” (price scenario) comes at the expense of lower performance in the sense of “market risk”. At the same time, contracting a flobsion is better than buying an option if the price scenario is uncertain (Table 1) and better than “do nothing” if a price scenario is fixed (Table 2).
6. Discussion
The construction of a flobsion possesses universal properties that make it advantageous (or at least more flexible) as compared to contracting an option or “doing nothing” (implying a future purchase at a market price). This flexibility allows for shaping financial risk of an economic entity (flobsion buyer) in the face of future uncertain marked developments and in a sense “soft” hedging against unfavorable situation where the flobsion’s underlying asset price increases. While this risk is not fully absorbed by a flobsion (as opposed to an option), it allows for a flexibility on flobsion’s seller side who would like to avoid finding themselves in a situation where they have to sell an underlying asset to the option holder at the pre-defined strike price regardless of how high the market price turns out to be in the future. The flobsions’ discount construction allows for balancing the benefit (between buyer and seller) created by a possible future price increase. So, in case if such an increase materializes in the future, the buyer and seller are factually sharing profits stemming from the discount to the actual market price. In case if the market price stays below the flobsions’ strike price, the instrument is not being executed and there is no difference with the option.
A similar idea of controlling the volatility of the final price paid for an underlying asset, however under more specific conditions imposed on the stochastic price process, was explored earlier for the barrier options and capped options Detemple (2005). The fobsion’s concept of a discount seems to be a “smoother” way of controlling that volatility as compared to barrier/capped options which are inherently controlled by respective thresholds. A quantitative comparison of these approaches within a problem-specific stochastic price processes may be useful in potential applications.
Selection of a particular risk measure is application-specific, depends on a particular problem context, and involves consideration of the complexity in interpretation of the risk measure and tractability of the resulting risk minimization problem. We have chosen variance for our analysis despite its known limitations Rockafellar et al. (2002) in addressing fat-tails and equal penalty to ups and downs of a distribution. While latter seems of a smaller problem in our setting that is intended to address the concerns of both buyer and seller (ups for a seller are downs for a buyer and vice versa), the fat-tail limitation is accepted assuming the interpretation of variance as a risk proxy employed for benchmarking rather than a risk measure used in an application-specific formulation of an optimization problem.
The options-style derivatives pricing Detemple (2005); Pierre Henry-Labordere (2009) assume a specific family of the stochastic price process to estimate the derivative’s price. Our approach, based on a rather generic form of a discrete price distribution, allows us to capitalize on existing results for options pricing (both American and European style) and reduce the flobsion’s pricing problem to those extensively explored earlier for options. To make the link between a traditional option and a flobsion we employ the “fair price” principle, which is similar to the utility-indifference pricing concept Hobson (2005) and the no-arbitrage principle widely used in the options pricing literature Buchen (2012); Chesney and Taschini (2012); Cox and Ross (1976); Detemple (2005).
As stated by Theorem 4, flobsion is similar to a portfolio with fixed shares of offsets to be purchased in the future at a market price and those covered by an option. Although mathematically, flobsion delivers the same distribution of the total cost of offsetting as such a portfolio, it allows for a legal contract for the whole amount of offsets, not only those covered by an option. In the sense of a portfolio-style point of view, this seems to be similar to the result obtained for the problem of pricing and hedging using oil and copper futures and forward contracts Kenichiro Shiraya et al. (2016), where the authors found that using three different futures contracts to hedge long-term contracts outperformed the traditional hedge based on a single futures position.
Here for simplicity, we have considered the properties of emission costs associated with the CO price employing financial instruments independently from other emission costs reduction options that may be available to a concerned emitter, e.g., energy producers who have a portfolio of technologies varying in emission rates (per produced energy unit) may have a flexibility in adapting to an increased CO price by adjusting the shares of individual technologies used in production Krasovskii et al. (2016, 2017). So, the cost structure of an energy producer may change for higher CO prices as these would lead to a different ranking of technologies in the total production portfolio. Therefore, the construction of a flobsion has to be applied to such cases and studied in more detail. As energy producers who have only CO-intensive technologies in their portfolios lack this flexibility, they are largely limited in managing their costs to financial instruments including a flobsion.
A more complex problem setting than that considered in this paper, could include the case of asymmetric information where the flobsion buyer and seller have different views on the future CO prices, so their fair price estimates would be different. Depending on the mathematical sign of that difference, it can make it easier or more difficult to come to a purchase agreement Krasovskii et al. (2017). A similar consideration is valid in the context of risk preferences of a buyer and a seller (risk taking or risk averse attitudes). We expect that the risk context would influence the flobsion price in a similar way as it influences the price of a forward contract, however, this has to be proven by a numerical modeling similar to earlier works Krasovskii et al. (2016).
In this paper, we carried out an indicative benchmarking of a flobsion’s performance employing a historical dataset with real market prices to avoid the complexity of price process modeling. As demonstrated in the earlier literature (see e.g., Fuss et al. (2012); Fortin et al. (2008)), the price process can be represented by a multi-parametric family of distributions, where the parameters of a distribution determine the results of numerical modeling. In this study we illustrated possible outcomes of contracting flobsions employing original historical data (and simple transformations thereof) to avoid the necessity of finding a suitable distribution family and prove its fit to historical prices.
The flobsion concept carries potential for supporting initiatives on reducing emissions from deforestation and forest degradation (REDD), while the problem associated with the acceptance of REDD-based offsets for emission reduction compliance at both national and international levels is still open and the future fungibility of REDD-based offsets with emission allowances and clean development mechanism (CDM) offsets is unknown Beltran et al. (2013); Dooley and Gupta (2017). This uncertainty creates additional risk associated with contracting REDD-offsets that a flobsion might help to mitigate.
7. Conclusions
Analytical results on the flobsion’s properties presented in this paper cover a rich enough family of discrete price distributions and make this work complete for practical applications. These applications can be more general and not necessarily connected to the current and future CO markets and the emission offsetting context.
The simple relation between the option and flobsion price based on Theorem 1 allows for easy determination of the flobsion price for any given discount based on the price of an option which is familiar to many market players. Flobsion’s reduction of cost variance is less than that provided by the option, however, in case that the initially assumed price scenario turns out to be wrong, flobsion leads to smaller implied losses and gains, which reduces the risk for both buyer and seller.
While the flobsion construct is apparently applicable more universally, we see its good fit within the emission offsetting context. Despite technical details of potential future regulation remain uncertain, there is a progress towards more climate-aware policies. As policy changes can create not only opportunities, but also risks for certain market players, there is a need to accommodate and alleviate those risks. The flobsion’s properties presented in this paper prove it to be a potential candidate helping in addressing these challenges and ultimately enabling or accelerating the implementation of new policies.
Further research might be directed towards exploration of a flobsion in more general financial risk management contexts as well as in the context of more detailed economic models that inherently include a regulated entity’s possibility to adapt to rising CO prices e.g., by adjusting technological portfolios.
Author Contributions
N.K. designed the study. N.K. and R.L. developed the concept of a flobsion. N.K., R.L., A.K., and M.O. discussed preliminary results. N.K. obtained analytical results, carried out numerical experiments, and wrote the manuscript with contributions from all the authors.
Funding
This work was supported by the project “Delivering Incentives to End Deforestation: Global Ambition, Private/Public Finance and Zero-Deforestation Supply Chains” funded by the Norwegian Agency for Development Cooperation under agreement number QZA-0464, QZA-16/0218.
Acknowledgments
Nikolay Khabarov would like to acknowledge Elena Moltchanova from the University of Canterbury, New Zealand, for help, useful discussions, and motivating the work in analytical direction. The authors express their gratitude to Michaela Rossini from the IIASA Library for supporting this work. The authors are thankful to two anonymous reviewers whose critical feedback and constructive suggestions helped to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| EUA | emission allowances from the European Emission Trading Scheme |
| EU ETS | European Emission Trading Scheme |
| CDM | Clean Development Mechanism |
References
- Andrew, L. Liu, and Yihsu Chen. 2017. Price containment in emissions permit markets: Balancing market risk and environmental outcomes. IISE Transactions 49: 1129–49. [Google Scholar] [CrossRef]
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Beltran, Angelica Mendoza, Arild Angelsen, Michel den Elzen, Caroline Wang Gierløff, and Hannes Böttcher. 2013. Analysing the Options and Impacts of Including REDD Credits in Carbon Markets. Technical Report, PBL Working Paper 17. Available online: https://www.pbl.nl/sites/default/files/cms/publicaties/pbl-2013-working-paper-analysing-the-options-and-impacts-of-including-redd-credits-in-carbon-markets.pdf (accessed on 17 September 2018).
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- BP p.l.c. 2018. BP Statistical Review of World Energy 2018. Available online: https://www.bp.com/content/dam/bp/en/corporate/pdf/energy-economics/statistical-review/bp-stats- review-2018-full-report.pdf (accessed on 17 September 2018).
- Buchen, Peter. 2012. An Introduction to Exotic Option Pricing. Boca Raton: CRC Press. [Google Scholar]
- Chesney, Marc, and Luca Taschini. 2012. The endogenous price dynamics of emission allowances and an application to co2 option pricing. Applied Mathematical Finance 19: 447–75. [Google Scholar] [CrossRef]
- Collins, B., and F. J. Fabozzi. 2008. Financial Markets and Instruments (Chapter 15). In OTC Equity Derivatives. Hoboken: John Wiley & Sons, vol. 1, pp. 181–89. [Google Scholar]
- Cont, Rama. 2006. Model uncertainty and its impact on the pricing of derivative instruments. Mathematical Finance 16: 519–47. [Google Scholar] [CrossRef]
- Cox, John C., and Stephen A. Ross. 1976. The valuation of options for alternative stochastic processes. Journal of Financial Economics 3: 145–66. [Google Scholar] [CrossRef]
- Detemple, Jerome. 2005. American-Style Derivatives. Boca Raton: CRC Press. [Google Scholar]
- Dooley, Kate, and Aarti Gupta. 2017. Governing by expertise: The contested politics of (accounting for) land-based mitigation in a new climate agreement. International Environmental Agreements: Politics, Law and Economics 17: 483–500. [Google Scholar] [CrossRef]
- Fortin, Ines, Sabine Fuss, Jaroslava Hlouskova, Nikolay Khabarov, and Michael Obersteiner. 2008. An integrated CVaR and real options approach to investments in the energy sector. The Journal of Energy Markets 1: 61–85. [Google Scholar] [CrossRef][Green Version]
- Fusion Media. 2018. Carbon Emissions Futures Historical Data. Available online: https://www.investing.com/commodities/carbon-emissions-historical-data (accessed on 18 September 2018).
- Fuss, Sabine, Jana Szolgayová, Nikolay Khabarov, and Michael Obersteiner. 2012. Renewables and climate change mitigation: Irreversible energy investment under uncertainty and portfolio effects. Energy Policy 40: 59–68. [Google Scholar] [CrossRef]
- Hannele Holttinen, Peter Meibom, Antje Orths, Frans Van Hulle, Cornel Ensslin, Lutz Hofmann, John McCann, Jan Pierik, John Olav Tande, Ana Estanqueiro, and et al. 2006. Design and Operation of Power Systems with Large Amounts of Wind Power. Available online: https://www.webcitation.org/61DCFd3dj?url=http://www.ieawind.org/AnnexXXV/Meetings/Oklahoma/IEA%20SysOp%20GWPC2006%20paper_final.pdf (accessed on 17 September 2018).
- Hobson, D. G. 2005. Bounds for the utility-indifference prices of non-traded assets in incomplete markets. Decisions in Economics and Finance 28: 33–52. [Google Scholar] [CrossRef]
- International Energy Agency. 2017. Global EV Outlook 2017. Available online: https://www.iea.org/publications/freepublications/publication/GlobalEVOutlook2017.pdf (accessed on 17 September 2018).
- Kenichiro Shiraya, Akihiko Takahashi, M. A. H. Dempster, and Ke Tang, eds. 2016. Pricing and Hedging of Long-Term Futures and Forward Contracts with a Three-Factor Model. Boca Raton: CRC Press, Taylor & Francis Group, pp. 31–52. ISBN 978-1-4987-1233-0. [Google Scholar]
- Kennan, John. 2006. A note on Discrete Approximations of Continuous Distributions. Available online: http://www.ssc.wisc.edu/~jkennan/research/DiscreteApprox.pdf (accessed on 18 September 2018).
- Kudryavtsev, Oleg, and Antonino Zanette. 2013. Efficient pricing of swing options in Lévy-driven models. Quantitative Finance 13: 627–35. [Google Scholar] [CrossRef][Green Version]
- Krasovskii, Andrey, Nikolay Khabarov, and Michael Obersteiner. 2016. Fair pricing of REDD-based emission offsets under risk preferences and benefit-sharing. Energy Policy 96: 193–205. [Google Scholar] [CrossRef]
- Krasovskii, Andrey, Nikolay Khabarov, and Michael Obersteiner. 2017. CO2-intensive power generation and REDD-based emission offsets with a benefit-sharing mechanism. Energy Systems 8: 857–83. [Google Scholar] [CrossRef]
- Liu, Xiaofang, Jian Li, Jun Wu, and Guoqing Zhang. 2017. Coordination of supply chain with a dominant retailer under government price regulation by revenue sharing contracts. Annals of Operations Research 257: 587–612. [Google Scholar] [CrossRef]
- Ma, Kai, Congshan Wang, Jie Yang, Changchun Hua, and Xinping Guan. 2019. Pricing mechanism with noncooperative game and revenue sharing contract in electricity market. IEEE Transactions on Cybernetics 49: 97–106. [Google Scholar] [CrossRef] [PubMed]
- Medina, Vicente, and Angel Pardo. 2013. Is the eua a new asset class? Quantitative Finance 13: 637–53. [Google Scholar] [CrossRef]
- Pierre Henry-Labordere. 2009. Analysis, Geometry, and Modeling in Finance: Advanced Methods in Option Pricing. Boca Raton: CRC Press. [Google Scholar]
- Rockafellar, R. Tyrrell, Stanislav P. Uryasev, and Michael Zabarankin. 2002. Deviation Measures in Risk Analysis and Optimization. In SSRN. vol. 2002-7. [Google Scholar] [CrossRef]
- Rouhani, Omid M., Richard R. Geddes, Wooseok Do, H. Oliver Gao, and Arash Beheshtian. 2018. Revenue-risk-sharing approaches for public-private partnership provision of highway facilities. Case Studies on Transport Policy 6: 439–48. [Google Scholar] [CrossRef]
- The Shift Project Data Portal. 2019. Breakdown of World GHG Emissions by Sector in 2010. Available online: http://www.tsp-data-portal.org/Breakdown-of-GHG-Emissions-by-Sector#tspQvChart (accessed on 22 February 2019).
- UNFCCC. 2012. Kyoto Protocol CDM Passes One Billionth Certified Emission Reduction Milestone. Available online: https://cdm.unfccc.int/CDMNews/issues/issues/I_P0QZOY6FWYYKFKOSAZ5GYH2250DRQK/ viewnewsitem.html (accessed on 22 February 2019).
- UNFCCC. 2015. Cop 21 Paris Climate Conference. Available online: http://www.cop21paris.org/about/cop21 (accessed on 7 June 2018).
- United Nations Development Programme. 2016. Sustainable Development Goals. Available online: http://www.undp.org/content/undp/en/home/sustainable-development-goals.html (accessed on 4 May 2018).
- U.S. Congress, Office of Technology Assessment. 1984. Nuclear Power in an Age of Uncertainty. Chapter 8: Public Attitudes Toward Nuclear Power; Washington: U.S. Government Printing Office, pp. 211–251. Available online: http://govinfo.library.unt.edu/ota/Ota_4/DATA/1984/8421.PDF (accessed on 17 September 2018).
- WordAtlas. 2018. Renewable Energy by Country: China, the United States, Brazil, and Canada Lead the World in Renewable Energy Production. Available online: https://www.worldatlas.com/articles/top-15-countries-using-renewable-energy.html (accessed on 17 September 2018).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).