Abstract
In this paper, we develop a contingent claim model to examine the optimal bank interest margin, i.e., the spread between the domestic loan rate and the deposit market rate of an international bank in distress. The framework is used to evaluate the cross-border lending efficiency for a bank that participates in a government capital injection program, a government intervention used in response to the 2008 financial crisis. This paper suggests that government capital injection is an appropriate way to recapitalize the distressed bank, enhancing the bank interest margin and survival probability. Nevertheless, the government capital injection lacks efficiency when the bank’s cross-border lending is high. Stringent capital regulation, suggested to prevent future crises by literature, leads to superior lending efficiency when the government capital injection is low.
JEL Classification:
G21; G28
1. Introduction
The 2007/2008 global financial crisis raises fundamental issues about the banking strategies of international loan portfolio diversification, especially from the standard of return/risk efficiency.1 Figure 1 reports the overall cross-border claims on banks of BIS (Bank of International Settlements) reporting banks from 1998 to 2018. Clearly, these claims have cycled over time, with the home bias evident in the decline in the cross-border claims since the peak in 2007. The contrasting trends in cross-border lending reflect bank needs to deleverage because of changes in risk perceptions.2 In addition, policy interventions having aimed at stabilizing domestic banking systems also provide incentives for banks to concentrate more on their economies.3 Cross-border diversification in bank lending, however, is barely understood, as shown by the concern that it is not considered in recapitalization for distressed banks during the recent financial crisis. Particularly, distressed banks receive government bailout package of capital infusion during the financial crisis (Bayazitova and Shivdasani 2012), public outcries for more capital from banks tend to be greater after the financial crisis, and stringent capital regulation as a post-crisis reform proposal should adapt to prevent future crises (Kashyap et al. 2008). Our analysis of cross-border bank lending and recapitalization was motivated by the above observations. The aim of this paper is to investigate whether cross-border bank lending under capital regulation is an interest for bank equity holders when the bank in distress participates in a financial rescue program of government capital injections.
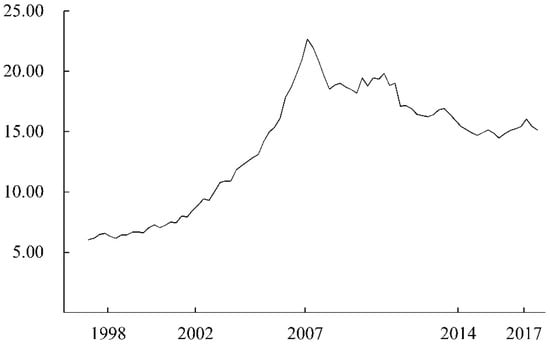
Figure 1.
Cross-border bank lending, 1998Q1–2018Q3: Claims (in trillions of US dollars) on bank sector of banks in all reporting countries. Source: Locational statistics, International banking, BIS Statistics.
The effects of cross-border lending diversification on bank interest margin (commonly used to proxy lending-to-deposit rate spread), bank equity risk, and diversification efficiency are important issues that concern bank managers (e.g., Iskandar-Datta and McLaughlin 2007; de Blas and Russ 2013; Bremus 2015; Barrell and Nahhas 2019). The bank interest margin is crucial in strategic decisions made by banks because the interest margin is one of the principal elements of bank profitability and is often used as a proxy for the efficiency of financial intermediation (Saunders and Schumacher 2000). Bank equity risk in relation to bank survival is central not only in strategic decisions made by banks, but also in decisions made by the regulatory authority about banking stability (Berger and Bouwman 2013). Diversification efficiency/deficiency is an important evaluation for cross-border lending (Rossi et al. 2009; García-Herrero and Vázquez 2013), and banks often assess their performance to each other on this basis. Comprehending whether higher cross-border loan portfolio diversification has significant effects on the bank interest margin, the bank equity risk, and the diversification efficiency gain, and how these effects differ depending on the distressed bank’s participation in a government capital injection program are important for the regulatory authority to achieve a desired level of banking stability. In the light of the recent financial crisis, this topic has become of uttermost important to the discussion of bank efficiency and stability.
To investigate diversification effects on bank interest margin and efficiency, we construct a contingent claim model along the line of Episcopos (2008) for the valuation of a bank’s equity. According to Episcopos (2008), default can occur at any time before the maturity date that the risk of a premature default to the liability valuation is explicitly captured by a simple knock-out barrier option feature of different components of liabilities. However, the assumption of Episcopos’ (2008) approach is not applicable to domestic loan markets since such markets are virtually always highly concentrated where cross-border banks set loan rates and face random loan levels (Claessens 2006). We complement this by extending Episcopos’ (2008) model to be able to capture the effects of the international loan portfolio diversification on the bank’s interest margin, and then on the bank’s equity risk and diversification efficiency. We do this by using a so-called firm-theoretic barrier option framework.
Our paper is also motivated by the observations of financial default events related to the 2007/2008 global financial crisis (Breitenfellner and Wagner 2010). The observations illustrate that, during a financial crisis, bank capital is depleted. A government capital injection program is expected to stabilize banks by providing a source of capital when public market alternatives are unavailable.4 Further, as previously pointed out by Berger and Bouwman (2013), several post-crisis reform proposals tend to focus on how capital regulation should adapt to prevent future crises. Hence, from a policy standpoint, it is interesting to examine how government capital injections affect bank interest margin and cross-border lending efficiency at various levels of loan portfolio diversification, and how stringent capital regulation affects bank interest margin and cross-border lending efficiency at various levels of government capital injection.
Our results have distinct bank strategy and regulatory policy implications. Increasing international loan portfolio diversification by the bank increases not only the risk of foreign loan repayments due to additional exchange rate volatility and country risk (Rajan and Friedman 1997) but also the risk of domestic loan repayments due to the bank’s more prone to loan risk-taking at a reduced margin, thereby increasing the bank’s equity risk. Further, diversification efficiency increases after increasing the cross-border lending. As a result, a financially disadvantaged bank can use the cross-border lending strategy to benefit from the diversification efficiency gain. We also show that: (i) these augmented risk and efficiency are reduced when the government capital injection increases; and (ii) the augmented risk is decreased, and the augmented efficiency is increased when the capital regulation is increasingly stringent. Result (i) suggests that, from a safety viewpoint, a bank strategy of the cross-border loan portfolio diversification is encouraged when the bank participates in the bailout program of government capital injection although strategy itself is not efficient. Our result provides an explanation that the success of a financial rescue program of the government capital injection depends critically on the willingness of distressed banks to participate in it. Result (ii) suggests that a bank strategy of the cross-border loan portfolio diversification is also encouraged when the bank’s capital requirement in the domestic market is increased. Our suggestion is consistent with the stability argument of Berger and Bouwman (2013). Overall, from a normative standpoint, our results sound a note to the adaption of government capital injection mechanism that reduces efficiency but contributes to stability, while the adaption of capital regulation mechanism after a financial crisis that increases efficiency and stability in the context of cross-border loan portfolio diversification.
2. Related Literature
The following sketch is intended to provide broad motivation for our international lending theory. The first is the literature on bank interest margin including the recent studies of Saunders and Schumacher (2000), Kasman et al. (2010), de Blas and Russ (2010, 2013), and Bremus (2015). Saunders and Schumacher (2000) investigated the impact of the structure of bank competition and macro interest-rate volatility on interest margins in six selected European countries and the US over the 1988–1995 period. Their results suggest an important trade-off between assuring bank solvency (captured by high capital-to-asset ratios) and lowering the cost of consumer financial services (measured by low net interest margins). Kasman et al. (2010) investigated the effects of the financial reforms on the determinants of bank net interest margin over the period 1995–2006 in the banking systems of the European countries. Their paper shows that increases in bank size and managerial efficiency significantly decrease the bank interest margins. Regulators also should promote merger and acquisition and market entry to increase the scale and efficiency of banks in the countries.
de Blas and Russ (2010) theoretically studied the implications of financial liberalization on bank net interest margins, and lending interest rates. They concluded that foreign-owned banks not only lead to superior efficiency to their host markets but also charge higher markups on borrowed funds than their domestically owned rivals when countries liberalize their financial sectors. de Blas and Russ (2013) studied both cross-border takeovers and cross-border lending on the structure of lending costs, bank profit, and interest rates charged to borrowers. They found that aggregate effects are more significant for cross-border lending than cross-border takeovers. Liberalization toward cross-border lending decreases net interest margins, and increases efficiency and competitive pressure (contestability), while liberalization toward cross-border takeovers increases net interest margins and do not lead to competitive pressure. Both the policies can increase aggregate out.
Bremus (2015) studied the role that international banking plays for market structures in the banking industry. The author suggested that bank foreign direct investment (FDI) is more stability-enhancing than cross-border lending. Further, an increase in bank interest margins in case of FDI increases the resistibility of banks against adverse shocks due to higher margins boosting bank profits. We add to the literature on bank interest margin by providing a theoretical illustration of how the cross-border lending can affect bank interest margin related to bank loan pricing behavior, bank equity risk, and efficiency gain from cross-border loan portfolio diversification for a bank in distress.
The second is the literature on international loan portfolio diversification versus focus. Conventional wisdom in the banking literature argues that banks should be as diversified as possible (Diamond 1984). Proponents of diversification suggest that diversified banks can benefit from leveraging managerial skills and abilities across products and geographic regions (Iskandar-Datta and McLaughlin 2007) and gaining economies of scope through spreading fixed costs over products and region (Drucker and Puri 2009). Diversified banks may also reduce the expected costs of financial distress or bankruptcy by lowering risks through spreading operations across different products or economic environment (Boot and Schmeits 2000). Rossi et al. (2009) found that diversification deteriorates cost efficiency, ameliorates profit efficiency, reduces bank’ realized risk, and has a positive impact on banks’ capitalization. Focusing on the anatomy of bank diversification, Elsas et al. (2010) investigated how revenue diversification affects bank value. They concluded that diversification does not reduce shareholder value but rather improves bank profitability and thereby bank value. Elsas et al. (2010) showed that diversification increases profitability and thus, indirectly, it also increases bank value.
On the other hand, some studies, for example, by Berger and Ofek (1996) and Denis et al. (1997) argue that the costs of diversification might outweigh the benefits. Proponents of focus argue that diversified banks can suffer from diluting the comparative advantage of management by going beyond their existing expertise (Klein and Saidenberg 1998), competition induced by diversification (Winton 1999), and increased agency costs resulting from value-decreasing activities of the managers who have lowered their personal risk (Laeven and Levine 2007). Diversification of banking activities across international boards can lead to increased political risk, and foreign exchange risk, which can destroy shareholder value (Deng and Elyasiani 2008). Tabak et al. (2011) found that loan portfolio concentration increases returns as well as reduces default risk; in particular, the impact of concentration on bank’s return is decreasing on bank’s risk; there are significant size effects; and foreign and state-owned banks seem to be less affected by the degree of diversification.
Cole and Obstfeld (1991) evaluated the social gains from international risk sharing in some simple general-equilibrium models with output uncertainty. They found that the direct welfare gains from cross-border portfolio diversification may be quite small as far as large industrialized economies are concerned. Cetorelli and Goldberg (2012a) provide some results to support the conjecture that banking globalization has a deep and pervasive impact on the consequences of domestic and international liquidity shocks. Cetorelli and Goldberg (2012b) contributed to further the understanding of global banking funding dynamics by taking a closer view from the perspective of a host country. Chakraborty et al. (2017) highlighted the benefits of financial integration that Europe enjoyed before the crisis and the costs of financial disintegration since then. They argued that, while financial separation is useful to limit contagion during a crisis, such ringfencing comes at certain costs borne by firms and consumers at other times. Barrell and Nahhas (2019) considered the cross-border lending stock from 19 advanced countries to European countries using quarterly data for 1999–2016. Their results suggest EU integration has had a large effect on cross-border lending, although this has been partly reversed after Euro debt crisis; this reversal probably arises more from the actions of home country bank regulators rather than from the rise in risk premia in host countries. While we also examine diversification, our focus on the bank spread management aspects of efficiency gain from international loan portfolio diversification takes our analysis in a different direction.
The third strand is the literature on bank equity capital during a financial crisis. Most theories (e.g., Acharya et al. 2011; Allen et al. 2011) predict that capital reduces bank equity risk and enhances bank survival probability. However, some theories (e.g., Koehn and Santomero 1980; Besanko and Kanatas 1996) suggest that increasing bank capital could be counterproductive because it perversely increases bank risk taking. Harris et al. (2013) examined the impact of the TARP capital injections on the operational efficiency of commercial banks. They showed a deteriorating pattern in the operating efficiency for banks that received the capital injection from TARP funds that is not evident in non-TARP banks. Lin and Li (2017) took a contingent claim approach to the market valuation of equity and default risk in a financial services holding company. They showed that an increase in bank capital requirement results in an increased default risk in the consolidated bank’s equity return. This paper also examines the effect of capital, in particular capital regulation after government capital injection to a bank in distress. After establishing the effects of capital on bank performance, we turn our attention to understanding the efficiency gain from international loan portfolio diversification through which these effects work.
3. The Model Basics
This section mainly consists of two parts. In the first part, a few simplifying assumptions are made to get tractable solutions. The remaining part of this section focuses on the valuation of the international bank’s equity and risk, and of the efficiency gain from international loan portfolio diversification.
3.1. The Framework and Assumptions
We consider an international bank whose planning horizon extends over a given time interval with two dates, 0 and 1, . can be considered as the time at which the bank subject to a comprehensive on-site audit by regulatory authorities, who assess the net worth of the bank and check that it is solvent. If assets are found to be less than liabilities at , the bank’s assets are costlessly transferred to liability holders. Equity holders are residual claimants on the bank’s assets after all other liabilities have been met. The book value of the bank’s liabilities can be treated as the strike price in the contingent valuation. When the value of the bank’s assets is less than the strike price, the equity value is zero. Several important assumptions of the framework are described as follows.
First, at time , the bank’s balance sheet looks like what is shown in Table 1. For the sake of simplicity, the initial portfolio of assets is assumed to include domestic loans , foreign loans , and liquid asset where denotes the degree of international loan portfolio diversification. This is a decision variable of the bank. The cost structure of the bank at includes deposits , capital stock , and government capital injection where is a regulatory parameter. These variables are used in a later part when the model is developed.

Table 1.
The bank’s balance sheet at . 1
Second, an international bank is assumed to diversify its loan portfolio across international regions including domestic and foreign markets. Our focus is on international loan portfolio diversification in the spirit of García-Herrero and Vázquez (2013): financial globalization since the mid-1990s has produced a massive expansion of bank activities overseas. We also follow Damanpour (1986) that the bank finds itself facing stiffer competition from banks in the foreign lending operation. This reflects an assumption in our model, relatively speaking, that the domestic loan market faced by the bank is imperfectly competitive and its foreign loan market is perfectly competitive. Except the domestic loan market faced by the bank, competitive markets are assumed for all financial assets. The bank is a rate-taker and, therefore, the interest rate it will have to pay on deposits is market determined.
Third, domestic loans, foreign loans, and liquid assets in the bank’s earning-asset portfolio are assumed to be complete in the sense that any financial claim can be replicated in the market place by a combination of other financial assets. Therefore, the price of any asset is identical to the value of the replicating portfolio to avoid arbitrage opportunities (Crouhy and Galai 1991). This complete feature assumption allows the model to be silent on the separation of management from ownership, and to focus on market determined value for the financial claims on the bank’s assets.
Fourth, government intervention in response to the subprime-related 2007/2008 financial crisis generally included three possible means: government guaranteed debt issuance programs, purchases of distressed assets by the government, and direct equity injections (Breitenfellner and Wagner 2010). The introduction of government capital injection in the model is understood because the bank in distress suddenly needs a source of new capital due to a liquidity shock event, as pointed out by Bayazitova and Shivdasani (2012). A government capital injection program assisting liquidity demand, in particular focusing on international loan portfolio diversification, can stabilize the bank by providing a source of capital when public market alternatives are unavailable.
3.2. Model Specifications
As shown in Table 1, the bank’s liquidity constraint at is given by the following balance sheet:
In Equation (1), the demand for domestic loans faced by the bank is governed by a downward-sloping demand function where is the domestic loan rate chosen by the bank. The bank can also have foreign loans normalizing exchange rate between domestic and foreign currencies to one on its balance sheet. The foreign loans earn the foreign market loan rate of . In the earning-asset portfolio, the bank can also hold an amount of liquid assets, for example, central bank reserves or Treasury bills, during the period horizon. These assets earn the security-market interest rate of . The larger is, the higher degree is the international diversification relative to the focus case. The total assets are financed partly by deposits. The supply of deposits faced by the bank is perfectly elastic at the deposit market rate of . The bank’s equity capital is tied by regulation to be a fixed proportion of its deposits, where is specified as a regulatory capital-to-deposits ratio (VanHoose 2007). The condition of can be motivated based on a binding argument that is sufficiently larger than (Wong 1997).
The bank’s objective is to set to maximize the value of a European down-and-out call () option function, subject to Equation (1). We now apply the model and adapt it to evaluate bank claims. The market value of the bank’s underlying assets follows a geometric Brownian motion of the form:
where
and where is the value of the bank’s total loan repayments including the domestic loan repayment and the foreign loan repayments , with an instantaneous drift , and an instantaneous weighted-average disaggregated volatility where is the domestic-loan volatility and is the foreign-loan volatility.5 is a standard Wiener process. In the model, the weighted-average parameter is denoted by country risk because the bank may expose itself to foreign country risk perhaps due to business cycles across countries not perfectly synchronized (García-Herrero and Vázquez 2013).
In this context, the value of the bank’s equity is given by a formula:
where
The objective function in Equation (3) is interpreted as follows. The first term is recognized as a standard call option on the underlying value of the bank’s total loan repayments where is the strike price of the call. is specified as the net-obligation payments, i.e., the difference between the payments to depositors and the repayments from the investment in the liquid-asset market. is the risk-free discounted rate. is the cumulative density function of the standard normal distribution. The second term is interpreted as the net value between the expected domestic-loan repayment value and the present value of the weighted-average () net-obligation payments using the down-and-in call option view of the bank. The is explained as the value of domestic loans which creditors cannot force dissolution. We assume that is proportional to by a barrier-to-debt ratio , where . Similarly, the third term is the down-and-in call on the bank’s foreign-loan repayments with the strike price of the weighted-average () net-obligation payments . The barrier is proportional to by a barrier-to-debt ratio where . It is seen easily that the barrier option is a wider class than the standard call option because as and approach zero in Equation (3), and vanish, and we arrive at the usual Merton (1974) call option price that captures the bank’s equity.
With the equity function well described, one can now move on to considering the equity risk of the bank. The equity risk is used below when the efficiency gain from international loan portfolio diversification is measured. For this purpose, we define the variance of the return on in Equation (3) in the spirit of Ronn and Verma (1986) as follows:
where
The first term on the right-hand side of Equation (4), , can be interpreted as the call-based equity deviation with a corresponding underlying value of the bank’s total loan repayments. The second term, , can be interpreted as the knock-out value deviation with a corresponding underlying value of the domestic loan repayments. The third term, , can be interpreted as that of the foreign loan repayments.
Given the preceding settings, it is interesting to compare the equity risk/return efficiency of the international loan portfolio with that of the domestic loan portfolio and determine the efficiency gains if existent from international diversification, from the viewpoint of shareholder investment. Toward that end, let denote the ratio excess equity return to equity volatility when for the international loan portfolio and the same ratio when for the domestic loan portfolio. In other words,
and
where is the risk-free equity return, implying the opportunity cost of the shareholder investment including government capital injection. Then, the efficiency gains from international loan portfolio diversification can be measured by the differential:
measures the equity return differential, per unit of equity risk, that accrues from holding the international loan portfolio in lieu of the domestic loan portfolio. Note that in our model is treated as the benchmark of the equity risk/return efficiency that is assumed to be positive in sign. yields the efficiency gain from the international loan portfolio diversification, whereas yields the efficiency loss.
4. Solution and Results
In this section, we first discuss the theoretic modeling of solution and comparative static results. Then, several numerical examples are employed to explain the comparative static results derived from the theoretical model.
4.1. Optimum and Comparative Static Analysis
With all assumptions in place, we are ready to solve for the bank’s optimal choice of domestic loan rate. Partially differentiating Equation (3) with respect to , the first-order condition is given by:
We require that the second-order condition be satisfied, . The optimal domestic loan rate can be chosen based on Equation (8) where the marginal value of equals to the marginal total knock-out values of . We can further substitute the optimal domestic loan rate to obtain in Equation (7) remaining on the optimization.
Consider next the impact on the differential from changes in international loan portfolio diversification degree, government capital injection, and capital regulation. Differentiation of Equation (7) evaluated at the optimal domestic loan rate with respect to parameter (where , , and ) yields:
where
The first term on the right-hand side of Equation (9) can be identified as the direct effect, while the second term can be identified as the indirect effect. The direct effect captures the change in due to an increase in parameter , holding the optimal domestic loan rate constant. The indirect effect arises because an increase in changes the bank’s profits by in every possible state. In general, the added complexity of path dependent options in Equation (9) does not always lead to clear-cut results, but we can certainly speak of tendencies for reasonable parameter levels corresponding roughly to a hypothetical bank. A numerical exercise is designed to investigate the comparative static results of Equation (9) in the following subsection.
4.2. Parameter Basics
The formulas for the values of the equity claim, the equity risk, the efficiency measure, and the comparative static results of Equation (9) presented above are truly closed formulas that can be readily implemented once the relevant parameters are given. In the following, we assume that the case parameter levels, unless otherwise indicated, are as follows: , , , , , , , , , , and . Let change from (4.5, 350) to (5.1, 329) due to . These parameter levels used for simulation exercises are interpreted as follows.
- (i)
- The conditions of and indicate the scope of earning-asset portfolio substitution (Kashyap et al. 2002). captures the binding condition of the capital constraint (Wong 1997). demonstrates the bank interest margin as an element of after-tax earnings (Saunders and Schumacher 2000).
- (ii)
- The specification of capital adequacy requirement is set by the capital-to-deposits ratio (VanHoose 2007). In the case, without government capital injection where , the capital-to-asset ratio at is = 7.18%, where , , and , which does not meet the capital adequacy requirement of 8.00%. This indicates a situation of the bank’s depleted capital. This possible case is supportive to an argument of Bayazitova and Shivdasani (2012): the government capital injection is anticipated by the distressed bank when raising new capital in public markets by the bank is difficult.
- (iii)
- The condition of indicates that the standard deviation of domestic loan repayments is less than the standard deviation of foreign loan repayments. This can be understood that international portfolio investment involves, at the very least, two additional sources of risk, exchange rate volatility and country risk (Rajan and Friedman 1997). Accordingly, we further assume the condition of , implying that the bank with high asset volatility are more likely to exhibit a higher probability of hitting the barrier before the expiration date than the bank without such the characteristic.
4.3. International Loan Portfolio Diversification Effect
In this subsection, three sets of comparative statics are computed and used to assess the effects of the increased international loan portfolio diversification degree of the bank on its domestic loan rate, equity risk, and diversification efficiency at various levels of capital (increased government capital injection or stringent capital regulation).
Equation (9) with captures the response of the diversification efficiency to a change in international loan portfolio diversification degree. The findings are shown in Table 2. First, we have the result of with an approximate optimal domestic loan rate of 4.6% in the shaded area according to the equilibrium condition of Equation (8). The result of demonstrates that an increase in the international loan portfolio diversification degree decreases the bank’s domestic loan rate (and thus on the bank’s interest margin since the foreign market loan rate and the deposit market rate are not choice variables of the bank). As the bank increases its international loan portfolio diversification, it must now provide a return to a larger foreign loan base. One way the bank may attempt to augment its total returns is by shifting its investments to its domestic loan portfolio and away from the liquid-asset market. If domestic loan demand is relatively rate-elastic, a larger loan portfolio is possible at a reduced margin. de Blas and Russ (2013) found that cross-border lending decreases bank interest margins. Thus, their finding lends support to our result.

Table 2.
Effects of international loan portfolio diversification degree on domestic loan rate, equity risk, and diversification efficiency. 1
Second, the effect of international diversification on bank equity risk is reported in the third panel of Table 2. The direct effect captures the change in due to an increase in , holding the optimal bank interest margin constant. It is unambiguously positive because an increase in the extent of diversification makes the loan portfolio riskier to grant due to an increase in high-risk foreign loans with a decrease in low-risk domestic loans in the down-and-in call options. The indirect effect arises because an increase in changes the equity volatility by in every possible state. An increase in increases domestic loan risk-taking at a reduced optimal margin; consequently, increasing the bank’s equity volatility. Since the indirect effect reinforces the direct effect to give an overall positive response of to an increase in , we conclude that loan portfolio diversification increases bank equity volatility. Our result is consistent with a theory (e.g., Denis et al. 1997; Deng and Elyasiani 2008) that predicts a deterioration in the effectiveness of international loan portfolio diversification on the bank’s equity risk.
Third, as indicated in the fourth panel of Table 2, the efficiency gain from international loan portfolio diversification at various levels of diversification degree is positive in sign. This effect simply reflects an efficiency gain required by the bank for the international diversification. Further, the last panel demonstrates both the direct effect and the indirect effect evaluated at the optimal domestic loan rate are positive. The positive direct effect reflects an increasing gain required by the bank for the increasing diversification decision it makes. The indirect effect is therefore positive and reinforces the direct effect. The result is understood because the bank with broad global exposure should be better positioned to diversify away country-specific risks since business cycles across countries are not perfectly synchronized. Our result is consistent with Rossi et al. (2009): the benefits of international diversification in loan portfolio could be potentially existent.
The computed comparative static results are listed in Table 3. The negative effect of the international loan portfolio diversification on the bank’s interest margin is increased as the government capital injection increases. This result suggests a positive relation between capital and domestic loan market share in the domestic loan market. This is understood that a high-capital international bank is able to compete more effectively for its domestic loans (Calomiris and Wilson 2004), providing some support. We also show that the positive effect on international loan portfolio diversification on the bank’s equity risk is decreased as the government capital injection increases. This result suggests that a negative relation between capital and equity risk. Thus, we argue that higher capital helps bank safety because the higher-capital bank engages in more monitoring investment, thereby reducing the bank’s equity risk, and implicitly reducing the probability of default of the bank. Our argument is largely supported by Holmstrom and Tirole (1997). Overall, the international bank views a relatively large amount of government capital injection to be beneficial when the bank’s international loan portfolio diversification is efficient and increased.

Table 3.
Effects of international loan portfolio diversification degree on diversification efficiency at various levels of government capital injection. 1
There are interesting results obtained, as shown in Table 4. First, the negative effect of international loan portfolio diversification on the bank’s interest margin is decreased as the capital-to-deposits ratio increases. This result suggests that a lower-capital international bank due to stringent capital requirements is less likely to compete more effectively for domestic loans when its cross-border lending is increased. Our theory demonstrates a positive relation between capital and market share in the domestic loan market. Second, when the international loan portfolio diversification is high, the positive effect of international loan portfolio diversification on the bank’s equity risk is decreased as the capital requirement is increased. We argue that capital regulation helps from the standpoint of bank survival, consistent with Holmstrom and Tirole (1997). Third, the positive effect of the international diversification on the diversification efficiency is increased as the capital requirement is increased. This suggests that the bank views a relatively high capital regulation to be beneficial when the bank’s international loan portfolio diversification is increased. Our result is largely supported by the argument of Berger and Bouwman (2013): post-crisis reform proposals tend to focus on how capital regulation should adapt to prevent future crises.

Table 4.
Effects of international loan portfolio diversification degree on diversification efficiency at various levels of capital-to-deposits ratio. 1
4.4. Government Capital Injection Effect
In this subsection, we compute the effects of government capital injection on bank interest margin, equity risk, and diversification efficiency at various levels of cross-border lending diversification.
To study the overall effect of government capital injections, we report the findings in Table 5. We show that government capital injection produces an increase in bank interest margin and a decrease in bank equity risk. As can be seen from the last panel, however, an increase in the government capital injection decreases the efficiency gain from the international loan portfolio diversification. The result is understood because the positive impact on the bank’s interest margin from increases in the government’s capital injection, making the bank less prone to risk-taking, is less likely to vanish and the negative impact on the bank’s equity risk is less likely to come into effect. From a normative standpoint, our results sound a cautionary note to the adoption of increasing government capital injections that discourage international loan portfolio diversification although government capital injection is an efficient way to stabilize the bank. Our results complement the analysis of the efficiency gain from international diversification as proposed in Rossi et al. (2009).

Table 5.
Effects of government capital injection on domestic loan rate, equity risk, and diversification efficiency. 1
Table 6 depicts the effect of government capital injection on bank interest margin, equity risk, and international diversification efficiency at various levels of international loan portfolio diversification. We show that the positive effect on the bank’s interest margin and the negative effect on the bank’s equity risk are decreased as the degree of international loan portfolio diversification increases. These results indicate that capital significantly enhances the bank’s interest margin (and thus the bank’s profit) and survival probability in particular when the international loan portfolio diversification status is not high. Moreover, the negative effect on diversification efficiency is increased as the degree of international loan portfolio diversification increases. This result demonstrates that capital significantly deteriorates efficiency in particular when the international loan portfolio diversification is high. Complementing Bayazitova and Shivdasani (2012), we suggest that a government capital injection program can stabilize a distressed bank when the bank does not take an active part in cross-border lending.

Table 6.
Effects of government capital injection on diversification efficiency at various levels of international loan portfolio diversification. 1
4.5. Capital Regulation Effect
It is necessary to elaborate on the capital regulation issue based on Equation (9) where . The findings are summarized in Table 7. It is interesting that, as the capital-to-deposits ratio increases, a larger domestic loan portfolio is possible at a reduced interest margin, resulting in increasing risk-taking. In the problem at hand, increases in the capital-to-deposits ratio have a positive effect on bank equity risk. However, the efficiency gain from the international loan portfolio diversification is robust to a wide range of capital regulation. We conclude that increased capital regulation is likely to deteriorate the international bank’s equity risk, but ameliorate the international bank’s efficiency gain. The former can be motivated based on an argument about the presence of market power in the domestic loan market, and the latter can be motivated based on an argument about the importance of international loan portfolio diversification when the justification of capital regulation is focused.

Table 7.
Effects of capital-to-deposits ratio on domestic loan rate, equity risk, and diversification efficiency. 1
As shown in Table 8, the negative impact on the bank’s interest margin is increased and the positive impact on the bank’s equity risk is increased as well when the total amount of the government’s capital injections is increased. The government’s capital injection effect reinforces the capital regulation effect to give an overall positive response of the bank’s equity risk. Relying on a comprehensive framework for bank equity risk measurement, we find evidence against strategic substitutes between capital regulation and government capital injection, unlike studies concerned with government intervention packages. However, the positive effect of capital regulation on the bank’s international loan portfolio diversification efficiency is weakened when the government’s capital injection is increased. We suggest that bank diversification efficiency is from capital regulation, not from government capital injection.

Table 8.
Effects of capital-to-deposits ratio on diversification efficiency at various levels of government capital injection. 1
5. Conclusions
Recently, international lending dropped significantly and has remained at a comparatively low level since the 2007/2008 global financial crisis. This trend occurs at a time where an unprecedented tide of financial internationalization has raised growing concerns among investors, claimholders, and regulators. By relying on a barrier option valuation framework, the model presented in this paper tries to study international loan portfolio diversification efficiency, particularly concerning an international bank in distress. International loan portfolio diversification status, government capital injection, and capital regulation are considered. Their respective effects on the distressed bank has been assessed.
First, we suggest that, from an efficiency viewpoint, international loan portfolio diversification conducted by the distressed bank be encouraged although diversification produces higher domestic lending and equity risk for the bank. The effect of the diversification encouragement is relatively low when the government capital injection is at a high level. Second, we show that an increase in the government capital injection significantly decreases the bank’s international loan portfolio diversification efficiency when the bank’s diversification degree is high. Third, we find that an increase in the capital regulation significantly increases diversification efficiency when the bank helped by the government capital injection is low. Three insights on regulation have been given in banking diversification.
The valuation framework presented here is fairly general and should open at least one further avenues of research. One issue that has not been addressed is the efficiency gain from international loan portfolio diversification with credit swaps of domestic loan portfolio. Credit swaps as such may make the distressed bank shift the focus on local geographic diversification instead of international geographic diversification. Such concerns are beyond the scope of this paper and thus are not addressed here. What this paper does demonstrate, however, is the important role played by efficiency gains from international loan portfolio diversification related to bank performance and safety and thereby the stability of the banking system during a financial crisis.
Author Contributions
Conceptualization, J.-H.L.; Formal analysis, S.C.; Funding acquisition, F.-W.H.; Investigation, F.-W.H.; Methodology, J.-H.L.; Project administration, J.-H.L.; Resources, P.-C.L.; Software, S.C.; Validation, P.-C.L.; Visualization, P.-C.L.; Writing—original draft, F.-W.H.; and Writing—review and editing, F.-W.H.
Funding
This research was funded by National Natural Science Foundation of China, grant number 71603217.
Acknowledgments
We would like to thank Mila Marinkovic (assistant editor), two anonymous referees, and the English editor for their helpful comments and suggestions. The usual disclaimer applies.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Acharya, Viral V., Hamid Mehran, Til Schuermann, and Anjan V. Thakor. 2011. Robust capital regulation. Staff Report no. 490, Federal Reserve Bank of New York, New York, NY. Available online: https://www.newyorkfed.org/medialibrary/media/research/staff_reports/sr490.pdf (accessed on 31 January 2019).
- Allen, Franklin, Elena Carletti, and Robert Marquez. 2011. Credit market competition and capital regulation. Review of Financial Studies 24: 983–1018. [Google Scholar] [CrossRef]
- Barrell, Ray, and Abdulkader Nahhas. 2019. The role of lender country factors in cross border bank lending. International Review of Financial Analysis. in press. [Google Scholar] [CrossRef]
- Bayazitova, Dinara, and Anil Shivdasani. 2011. Assessing TARP. Review of Financial Studies 25: 377–407. [Google Scholar] [CrossRef]
- Berger, Allen N., and Christa H. S. Bouwman. 2013. How does capital affect bank performance during financial crises? Journal of Financial Economics 109: 146–76. [Google Scholar] [CrossRef]
- Berger, Philip G., and Eli Ofek. 1996. Bustup takeovers of value-destroying diversified firms. Journal of Finance 51: 1175–200. [Google Scholar] [CrossRef]
- Besanko, David, and George Kanatas. 1996. The regulation of bank capital: Do capital standards promote bank safety? Journal of Financial Intermediation 5: 160–83. [Google Scholar] [CrossRef]
- Boot, Arnoud W. A., and Anjolein Schmeits. 2000. Market discipline and incentive problems in conglomerate firms with applications to banking. Journal of Financial Intermediation 9: 240–73. [Google Scholar] [CrossRef]
- Breitenfellner, Bastian, and Niklas Wagner. 2010. Government intervention in response to the subprime financial crisis: The good into the pot, the bad into the crop. International Review of Financial Analysis 19: 289–97. [Google Scholar] [CrossRef]
- Bremus, Franziska M. 2015. Cross-border banking, bank market structures and market power: Theory and cross-country evidence. Journal of Banking & Finance 50: 242–59. [Google Scholar] [CrossRef][Green Version]
- Bremus, Franziska, and Marcel Fratzscher. 2014. Drivers of Structural Change in Cross-Border Banking Since the Global Financial Crisis. DIW Berlin Discussion Paper No. 1411. Berlin: German Institute for Economic Research. [Google Scholar] [CrossRef]
- Calomiris, Charles W., and Berry Wilson. 2004. Bank capital and portfolio management: The 1930s “capital crunch” and the scramble to shed risk. Journal of Business 77: 421–55. [Google Scholar] [CrossRef]
- Cetorelli, Nicola, and Linda S. Goldberg. 2012a. Banking globalization and monetary transmission. Journal of Finance 67: 1811–43. [Google Scholar] [CrossRef]
- Cetorelli, Nicola, and Linda S. Goldberg. 2012b. Follow the money: Quantifying domestic effects of foreign bank shocks in the great recession. American Economic Review 102: 213–18. [Google Scholar] [CrossRef]
- Chakraborty, Indraneel, Rong Hai, Hans A. Holter, and Serhiy Stepanchuk. 2017. The real effects of financial (dis)integration: A multi-country equilibrium analysis of Europe. Journal of Monetary Economics 85: 28–45. [Google Scholar] [CrossRef]
- Claessens, Stijn. 2006. Competitive Implications of Cross-Border Banking. Policy Research Working Paper 3854. Washington: World Bank. [Google Scholar] [CrossRef]
- Cole, Harold L., and Maurice Obstfeld. 1991. Commodity trade and international risk sharing: How much do financial markets matter? Journal of Monetary Economics 28: 3–24. [Google Scholar] [CrossRef]
- Committee on the Global Financial System. 2018. Structural Changes in Banking after the Crisis. CGFS Papers No 60, Bank for International Settlements. Available online: https://www.bis.org/publ/cgfs60.pdf (accessed on 3 April 2019).
- Crouhy, Michel, and Dan Galai. 1991. A contingent claim analysis of a regulated depository institution. Journal of Banking & Finance 15: 73–90. [Google Scholar] [CrossRef]
- Damanpour, Faramarz. 1986. A survey of market structure and activities of foreign banking in the US. Columbia Journal of World Business 21: 35–46. [Google Scholar]
- de Blas, Beatriz, and Katheryn Niles Russ. 2010. FDI in the Banking Sector. Working Paper No. 10–8, University of California, Davis, Department of Economics, Davis, CA. Available online: https://ssrn.com/abstract=1647347 (accessed on 31 January 2019).
- de Blas, Beatriz, and Katheryn Niles Russ. 2013. All Banks Great, Small, and Global: Loan Pricing and Foreign Competition. International Review of Economics & Finance 26: 4–24. [Google Scholar] [CrossRef]
- Deng, Saiying, and Elyas Elyasiani. 2008. Geographic diversification, bank holding company value, and risk. Journal of Money, Credit and Banking 40: 1217–38. [Google Scholar] [CrossRef]
- Denis, David J., Diane K. Denis, and Atulya Sarin. 1997. Agency problems, equity ownership, and corporate diversification. Journal of Finance 52: 135–60. [Google Scholar] [CrossRef]
- Diamond, Douglas W. 1984. Financial intermediation and delegated monitoring. Review of Economic Studies 51: 393–414. [Google Scholar] [CrossRef]
- Drucker, Steven, and Manju Puri. 2009. On loan sales, loan contracting, and lending relationships. Review of Financial Studies 22: 2835–72. [Google Scholar] [CrossRef]
- Elsas, Ralf, Andreas Hackethal, and Markus Holzhäuser. 2010. The anatomy of bank diversification. Journal of Banking & Finance 34: 1274–87. [Google Scholar] [CrossRef]
- Episcopos, Athanasios. 2008. Bank capital regulation in a barrier option framework. Journal of Banking & Finance 32: 1677–86. [Google Scholar] [CrossRef]
- García-Herrero, Alicia, and Francisco Vázquez. 2013. International diversification gains and home bias in banking. Journal of Banking & Finance 37: 2560–71. [Google Scholar] [CrossRef]
- Harris, Oneil, Daniel Huerta, and Thanh Ngo. 2013. The impact of TARP on bank efficiency. Journal of International Financial Markets, Institutions & Money 24: 85–104. [Google Scholar] [CrossRef]
- Holmstrom, Bengt, and Jean Tirole. 1997. Financial intermediation, loanable funds, and the real sector. Quarterly Journal of Economics 112: 663–91. [Google Scholar] [CrossRef]
- Iskandar-Datta, Mai, and Robyn McLaughlin. 2007. Global diversification: New evidence from corporate operating performance. Corporate Ownership and Control 4: 228–50. Available online: http://www.virtusinterpress.org/IMG/pdf/COC__Volume_4_Issue_4_Summer_2007_Continued_.pdf#page=68 (accessed on 31 January 2019). [CrossRef]
- Kashyap, Anil K., Raghuram G. Rajan, and Jeremy C. Stein. 2002. Banks as liquidity providers: An explanation for the coexistence of lending and deposit-taking. Journal of Finance 57: 33–73. [Google Scholar] [CrossRef]
- Kashyap, Anil K., Raghuram G. Rajan, and Jeremy C. Stein. 2008. Rethinking capital regulation. In Maintaining Stability in a Changing Financial System. Kansas City: Federal Reserve Bank of Kansas City, pp. 431–71. [Google Scholar]
- Kasman, Adnan, Gokce Tunc, Gulin Vardar, and Berna Okan. 2010. Consolidation and commercial bank net interest margins: Evidence from the old and new European Union members and candidate countries. Economic Modelling 27: 648–55. [Google Scholar] [CrossRef]
- Klein, Peter G., and Marc R. Saidenberg. 1998. Diversification, Organization, and Efficiency: Evidence from Bank Holding Companies. Working Paper, Federal Reserve Bank of New York, New York, NY. Available online: https://ssrn.com/abstract=98653 (accessed on 31 January 2019).
- Koehn, Michael, and Anthony M. Santomero. 1980. Regulation of bank capital and portfolio risk. Journal of Finance 35: 1235–44. [Google Scholar] [CrossRef]
- Laeven, Luc, and Ross Levine. 2007. Is there a diversification discount in financial conglomerates? Journal of Financial Economics 85: 331–67. [Google Scholar] [CrossRef]
- Lin, Jyh-Horng, and Xuelian Li. 2017. Regulatory policies on Gramm-Leach-Bliley consolidation of commercial banking, shadow banking, and life insurance. Journal of International Financial Markets, Institutions & Money 50: 69–84. [Google Scholar] [CrossRef]
- Merton, Robert C. 1974. On the pricing of corporate debt: The risk structure of interest rates. Journal of Finance 29: 449–70. [Google Scholar] [CrossRef]
- Rajan, Murli, and Joseph Friedman. 1997. An examination of the impact of country risk on the international portfolio selection decision. Global Finance Journal 8: 55–70. [Google Scholar] [CrossRef]
- Ronn, Ehud I., and Avinash K. Verma. 1986. Pricing risk-adjusted deposit insurance: An option-based model. Journal of Finance 41: 871–95. [Google Scholar] [CrossRef]
- Rose, Andrew K., and Tomasz Wieladek. 2011. Financial Protectionism: The First Tests. NBER Working Paper No. 17073, National Bureau of Economic Research, Cambridge, MA. Available online: https://www.nber.org/papers/w17073.pdf (accessed on 31 January 2019).
- Rossi, Stefania P.S., Markus S. Schwaiger, and Gerhard Winkler. 2009. How loan portfolio diversification affects risk, efficiency and capitalization: A managerial behavior model for Austrian banks. Journal of Banking & Finance 33: 2218–26. [Google Scholar] [CrossRef]
- Saunders, Anthony, and Liliana Schumacher. 2000. The determinants of bank interest rate margins: An international study. Journal of International Money and Finance 19: 813–32. [Google Scholar] [CrossRef]
- Tabak, Benjamin M., Dimas M. Fazio, and Daniel O. Cajueiro. 2011. The effects of loan portfolio concentration on Brazilian banks’ return and risk. Journal of Banking & Finance 35: 3065–76. [Google Scholar] [CrossRef]
- VanHoose, David. 2007. Theories of bank behavior under capital regulation. Journal of Banking & Finance 31: 3680–97. [Google Scholar] [CrossRef]
- Winton, Andrew. 1999. Don’t Put All Your Eggs in One Basket? Diversification and Specialization in Lending. Working Paper, University of Minnesota, Minneapolis, MN. Available online: https://ssrn.com/abstract=173615 (accessed on 31 January 2019).
- Wong, Kit Pong. 1997. On the determinants of bank interest margins under credit and interest rate risks. Journal of Banking & Finance 21: 251–71. [Google Scholar] [CrossRef]
| 1 | We are a bit informal here and use “international” and “cross-border” synonymously. The terms “efficiency” or “diversification efficiency” refer to “efficiency from international loan portfolio diversification”. |
| 2 | The decade since the onset of the global financial crisis has brought about significant structural changes in the banking sector. The Committee on the Global Financial System (2018) pointed out that, while many large advanced economy banks have moved away from trading and cross-border activities, there does not appear to be clear evidence of a systemic retrenchment from core credit provision. Bremus and Fratzscher (2014) found that total cross-border bank claims have significantly decreased in response to the global financial crisis and did not resume the pre-crisis upward trend since then. The authors analyzed the effects of changes to regulatory policy and to monetary policy on cross-border bank lending since the global financial crisis. We would like to thank an anonymous reviewer for pointing these effects out to us. |
| 3 | Incentives, for example, include nationalizations, guarantees, or regulatory rules (see Rose and Wieladek 2011). |
| 4 | A cornerstone of the Troubled Asset Relief Program (TARP) is the government’s purchase of equity capital in financial institutions. |
| 5 | Note that, in the standard context of the aggregated approach (e.g., Episcopos 2008), shareholders are indifferent among various asset compositions so long as the portfolio attains a specific level of overall portfolio risk instead of the used disaggregated approach and in our model. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).