Explanatory Power of Pre-Issue Financial Strength for Long-Term Market Performance: Evidence from Initial Equity Offerings on an Emerging Market
Abstract
:1. Introduction
2. Related Literature
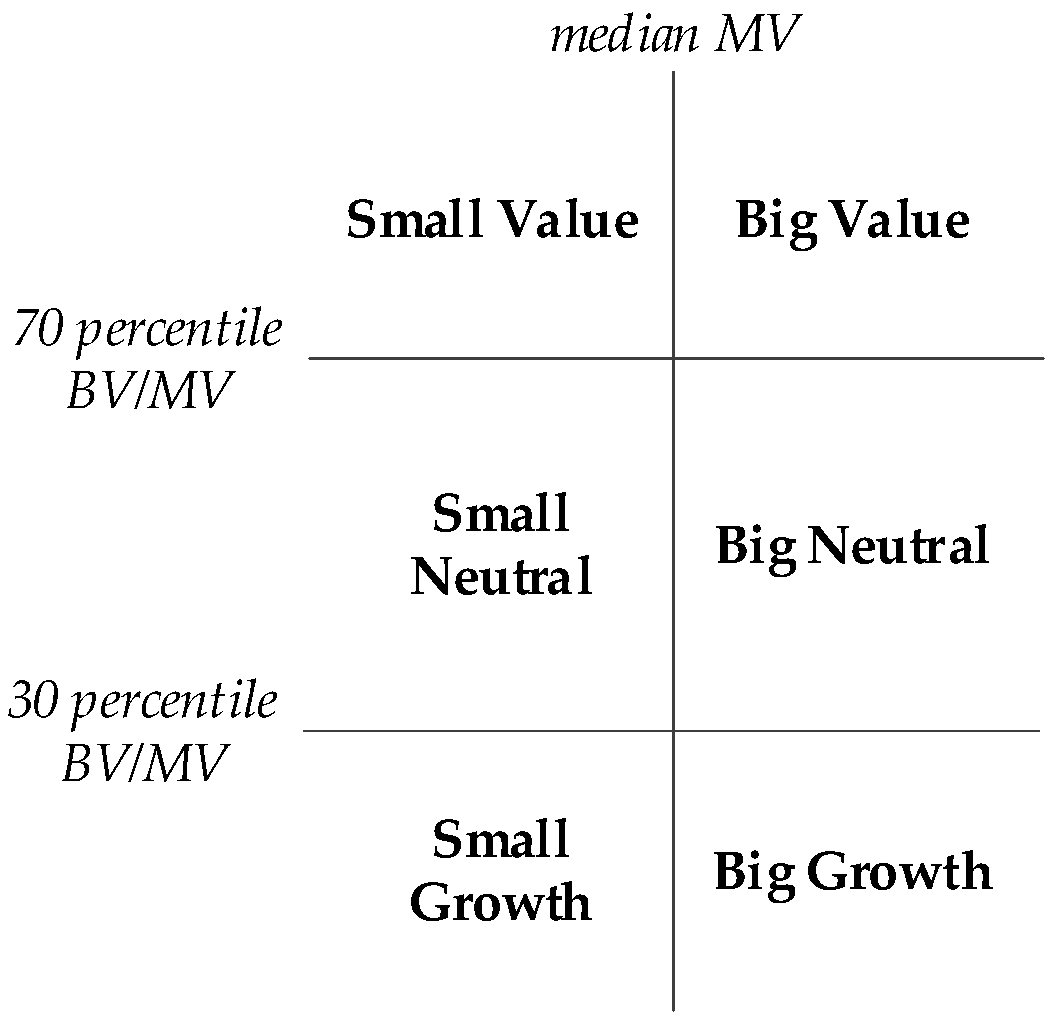
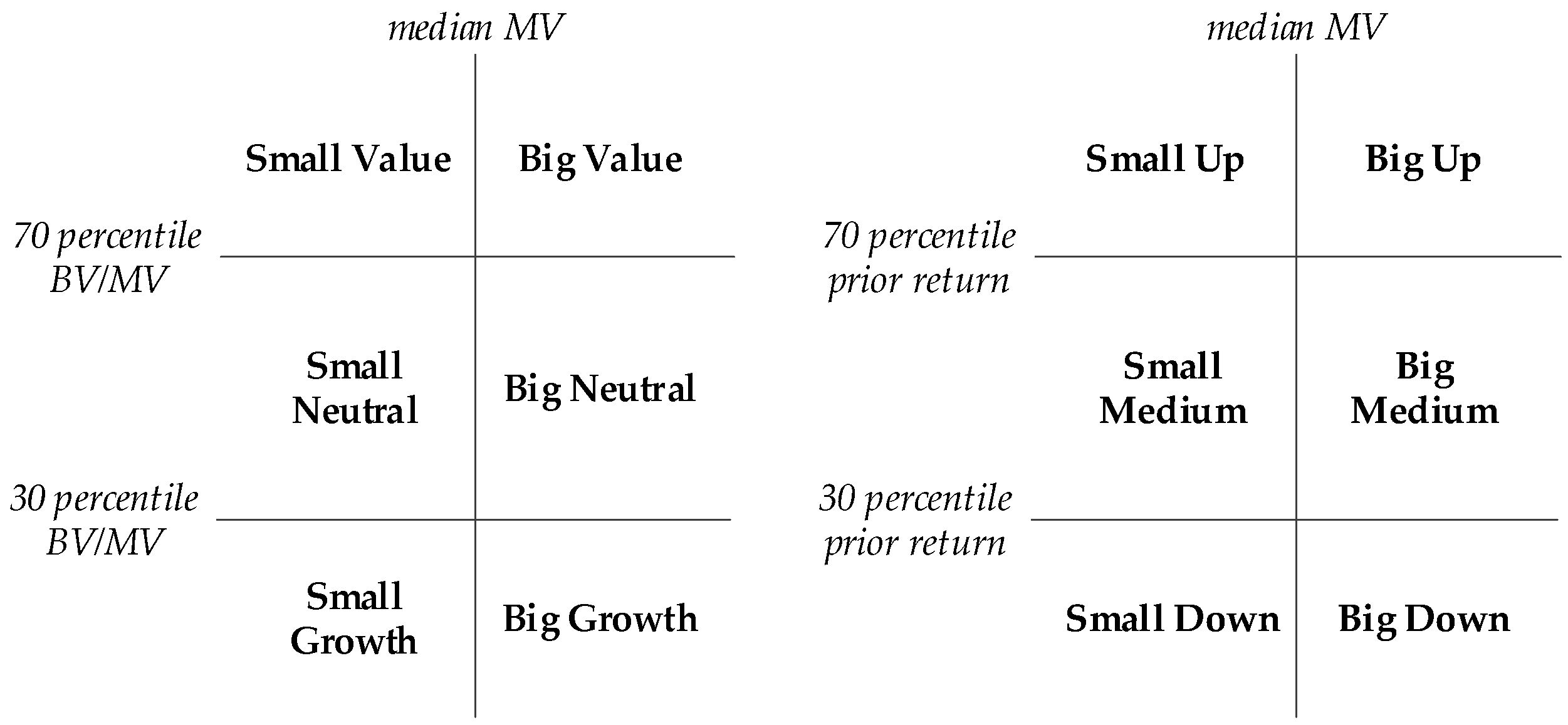
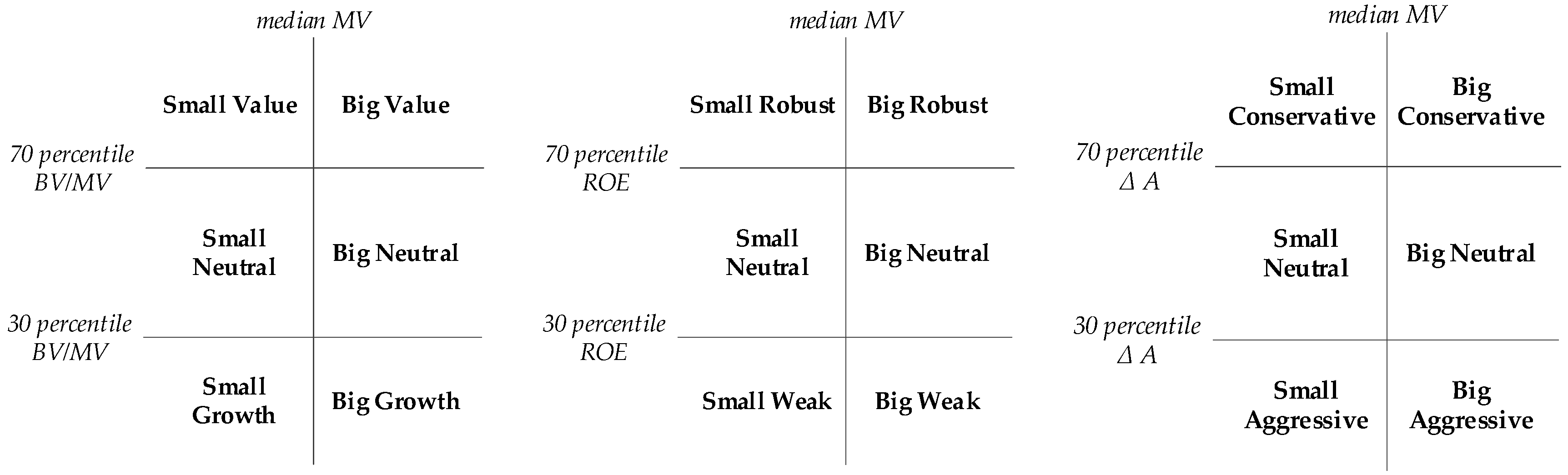
3. Empirical Modelling
4. Empirical Results
4.1. Long-Term IPO Performance According to the Calendar-Time Portfolio Approach for All Issuers
4.2. Net Profitability and Long-Term IPO Performance
4.3. Operating Profitability and Long-Term IPO Performance
4.4. Cash-Flow Efficiency and Long-Term IPO Performance
5. Robustness Checks
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ali, Fahad, RongRong He, and Yue Xiang Jiang. 2018. Size, Value and Business Cycle Variables. The Three-Factor Model and Future Economic Growth: Evidence from an Emerging Market. Economies 6: 14. [Google Scholar] [CrossRef]
- Alvarez, Susana, and Victor M. González. 2001. Long-Run Performance of Initial Public Offerings (IPOs) in the Spanish Capital Market. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Aussenegg, Wolfgang. 2000. Privatization versus Private Sector Initial Public Offerings in Poland. Multinational Finance Journal 4: 69–99. Available online: https://ssrn.com/abstract=2627710 (accessed on 4 January 2019). [CrossRef]
- Ball, Ray, and Lakshmanan Shivakumar. 2006. The Role of Accruals in Asymmetrically Timely Gain and Loss Recognition. Journal of Accounting Research 44: 207–42. [Google Scholar] [CrossRef]
- Barber, Brad M., and John D. Lyon. 1997. Detecting long-run abnormal stock returns: The empirical power and specification of test statistics. Journal of Financial Economics 43: 341–72. [Google Scholar] [CrossRef]
- Brav, Alon, Christopher Geczy, and Paul A. Gompers. 2000. Is the abnormal return following equity issuances anomalous? Journal of Financial Economics 56: 209–49. [Google Scholar] [CrossRef]
- Brav, Alon, and Paul A. Gompers. 1997. Myth or Reality? The Long-Run Underperformance of Initial Public Offerings: Evidence from Venture and Nonventure Capital-Backed Companies. Journal of Finance 52: 1791–1821. [Google Scholar] [CrossRef]
- Brycz, Bogumiła, Tadeusz Dudycz, and Michał J. Kowalski. 2017. Is the success of an issuer an investor success? Evidence from Polish IPOs. Baltic Journal of Economics 17: 57–77. [Google Scholar] [CrossRef]
- Carhart, Mark M. 1997. On Persistence in Mutual Fund Performance. Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Dechow, Patricia M., and Ilia D. Dichev. 2002. The Quality of Accruals and Earnings: The Role of Accrual Estimation Errors. Accounting Review 77: 35–59. [Google Scholar] [CrossRef]
- Dechow, Patricia M., Richard G. Sloan, and Amy P. Sweeney. 1995. Detecting Earnings Management. Accounting Review 70: 193–225. Available online: http://www.jstor.org/stable/248303 (accessed on 4 January 2019).
- Diether, Karl B., Christopher J. Malloy, and Anna Scherbina. 2002. Differences of Opinion and the Cross Section of Stock Returns. Journal of Finance 57: 2113–41. [Google Scholar] [CrossRef]
- Eckbo, B. Espen, Ronald W. Masulis, and Øyvind Norli. 2000. Seasoned public offerings: resolution of the ‘new issues puzzle’. Journal of Financial Economics 56: 251–91. [Google Scholar] [CrossRef]
- Ewen, Martin. 2018. Where is the Risk Reward? The Impact of Volatility-Based Fund Classification on Performance. Risks 6: 80. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1998. Market efficiency, long-term returns, and behavioral finance. Journal of Financial Economics 49: 283–306. [Google Scholar] [CrossRef]
- Fama, Eugene F., Lawrence Fisher, Michael C. Jensen, and Richard Roll. 1969. The Adjustment of Stock Prices to New Information. International Economic Review 10: 1–21. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2015. A five-factor asset pricing model. Journal of Financial Economics 116: 1–22. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2016. Dissecting Anomalies with a Five-Factor Model. Review of Financial Studies 29: 69–103. [Google Scholar] [CrossRef]
- Fu, Chengbo. 2018. Alpha Beta Risk and Stock Returns—A Decomposition Analysis of Idiosyncratic Volatility with Conditional Models. Risks 6: 124. [Google Scholar] [CrossRef]
- Gao, Yan, Connie X. Mao, and Rui Zhong. 2006. Divergence of opinion and long-term performance of initial public offerings. Journal of Financial Research 29: 113–29. [Google Scholar] [CrossRef]
- Ibbotson, Roger G. 1975. Price performance of common stock new issues. Journal of Financial Economics 2: 235–72. [Google Scholar] [CrossRef]
- Jegadeesh, Narasimhan, and Jason Karceski. 2009. Long-run performance evaluation: Correlation and heteroskedasticity-consistent tests. Journal of Empirical Finance 16: 101–11. [Google Scholar] [CrossRef]
- Jegadeesh, Narasimhan, and Sheridan Titman. 1993. Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency. Journal of Finance 48: 65–91. [Google Scholar] [CrossRef]
- Jelic, Ranko, and Richard Briston. 2003. Privatisation Initial Public Offerings: the Polish Experience. European Financial Management 9: 457–84. [Google Scholar] [CrossRef]
- Jewartowski, Tomasz, and Joanna Lizińska. 2012. Short- and Long-Term Performance of Polish IPOs. Emerging Markets Finance and Trade 48: 59–75. [Google Scholar] [CrossRef]
- Jones, Jennifer J. 1991. Earnings Management During Import Relief Investigations. Journal of Accounting Research 29: 193–228. [Google Scholar] [CrossRef]
- Kahneman, Daniel, and Amos Tversky. 1982. The psychology of preferences. Scientific American 246: 160–73. [Google Scholar] [CrossRef]
- Kooli, Maher, Jean-François L’Her, and Jean-Marc Suret. 2006. Do IPOs really underperform in the long-run? New evidence from the Canadian market. Journal of Private Equity 9: 48–58. [Google Scholar] [CrossRef]
- Kothari, Sagar P., Andrew J. Leone, and Charles E. Wasley. 2005. Performance matched discretionary accrual measures. Journal of Accounting and Economics 39: 163–97. [Google Scholar] [CrossRef]
- Kothari, Sagar P., and Jerold B. Warner. 2007. Econometrics of event studies. Handbook of Empirical Corporate Finance 1: 3–36. [Google Scholar] [CrossRef]
- Levis, Mario. 1993. The Long-Run Performance of Initial Public Offerings: The UK Experience 1980–1988. Financial Management 22: 28–41. [Google Scholar] [CrossRef]
- Lintner, John. 1969. The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets: A Reply. The Review of Economics and Statistics 51: 222–24. [Google Scholar] [CrossRef]
- Lizińska, Joanna, and Leszek Czapiewski. 2014. Performance of Polish IPO firms: size and profitability effect. Gospodarka Narodowa 1: 53–71. [Google Scholar] [CrossRef]
- Lizińska, Joanna, and Leszek Czapiewski. 2016. Is the IPO Anomaly in Poland Only Apparent or Real? In The Essence and Measurement of Organizational Efficiency. Edited by Tadeusz Dudycz, Grażyna Osbert-Pociecha and Bogumiła Brycz. Springer Proceedings in Business and Economics. Cham: Springer, pp. 175–94. [Google Scholar]
- Loughran, Tim, and Jay R. Ritter. 1995. The New Issues Puzzle. Journal of Finance 50: 23–51. [Google Scholar] [CrossRef]
- Lyn, Esmeralda O., and Edward J. Zychowicz. 2003. The performance of new equity offerings in Hungary and Poland. Global Finance Journal 14: 181–95. [Google Scholar] [CrossRef]
- Lyon, John D., Brad M. Barber, and Chih-Ling Tsai. 1999. Improved Methods for Tests of Long-Run Abnormal Stock Returns. Journal of Finance 54: 165–201. [Google Scholar] [CrossRef]
- McNichols, Maureen F. 2000. Research design issues in earnings management studies. Journal of Accounting and Public Policy 19: 313–45. [Google Scholar] [CrossRef]
- McNichols, Maureen F. 2002. Discussion of the quality of accruals and earnings: Multiples. Journal of Accounting Research 40: 135–72. [Google Scholar]
- Miller, Edward M. 1977. Risk, uncertainty, and divergence of opinion. Journal of Finance 32: 1151–68. [Google Scholar] [CrossRef]
- Mitchell, Mark L., and Erik Stafford. 2000. Managerial Decisions and Long-Term Stock Price Performance. The Journal of Business 73: 287–329. [Google Scholar] [CrossRef]
- Rajan, Rabhuram, and Henri Servaes. 1997. Analyst Following of Initial Public Offerings. Journal of Finance 52: 507–29. [Google Scholar] [CrossRef]
- Ritter, Jay R. 1991. The Long-Run Performance of initial Public Offerings. Journal of Finance 46: 3–27. [Google Scholar] [CrossRef]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19: 425–42. [Google Scholar] [CrossRef]
- Shen, Zhe, Limin Chen, and Qian Sun. 2015. Do Chinese IPOs really underperform in the long run? Journal of Portfolio Management 41: 84–91. [Google Scholar] [CrossRef]
- Teoh, Siew Hong, Ivo Welch, and Tak J. Wong. 1998. Earnings Management and the Long-Run Market Performance of Initial Public Offerings. Journal of Finance 53: 1935–74. [Google Scholar] [CrossRef]
| CAPM | 3FF | 4C | 5FF | |
|---|---|---|---|---|
| Panel A: 36-month portoflio | ||||
| α | −0.008 ** | −0.010 *** | −0.008 ** | −0.011 *** |
| (−2.503) | (−3.308) | (−2.570) | (−3.977) | |
| RMP | 0.864 *** | 0.823 *** | 0.811 *** | 0.763 *** |
| (16.648) | (17.112) | (16.457) | (16.795) | |
| SBM | 0.491 *** | 0.511 *** | 0.649 *** | |
| (5.312) | (5.367) | (7.005) | ||
| HML | 0.326 *** | 0.264 ** | 0.496 *** | |
| (2.724) | (2.176) | (4.136) | ||
| WML | −0.100 * | |||
| (−1.689) | ||||
| RMW | 0.067 | |||
| (0.711) | ||||
| CMA | −0.575 *** | |||
| (−4.785) | ||||
| p-value for F | 0.000 | 0.000 | 0.000 | 0.000 |
| adj. R2 | 0.699 | 0.759 | 0.761 | 0.800 |
| Panel B: 24-month portfolio | ||||
| α | −0.008 ** | −0.010 *** | −0.008 ** | −0.010 *** |
| (−2.372) | (−2.958) | (−2.339) | (−3.050) | |
| RMP | 0.867 *** | 0.834 *** | 0.826 *** | 0.786 *** |
| (15.680) | (15.347) | (14.723) | (15.063) | |
| SBM | 0.365 *** | 0.376 *** | 0.528 *** | |
| (3.856) | (3.855) | (5.381) | ||
| HML | 0.175 | 0.125 | 0.239 ** | |
| (1.498) | (1.080) | (2.131) | ||
| WML | −0.070 | |||
| (−1.038) | ||||
| RMW | 0.007 | |||
| (0.072) | ||||
| CMA | −0.543 *** | |||
| (−4.233) | ||||
| p-value for F | 0.000 | 0.000 | 0.000 | 0.000 |
| adj. R2 | 0.651 | 0.683 | 0.682 | 0.721 |
| CAPM (L) | CAPM (H) | 3FF (L) | 3FF (H) | 4C (L) | 4C (H) | 5FF (L) | 5FF (H) | |
|---|---|---|---|---|---|---|---|---|
| α | −0.012 *** | −0.005 | −0.014 *** | −0.006 * | −0.011 *** | −0.006 * | −0.015 *** | −0.008 *** |
| (−2.793) | (−1.593) | (−3.675) | (−1.961) | (−2.643) | (−1.856) | (−3.906) | (−2.748) | |
| RMP | 0.922 *** | 0.809 *** | 0.867 *** | 0.782 *** | 0.841 *** | 0.786 *** | 0.804 *** | 0.729 *** |
| (13.458) | (16.163) | (13.831) | (15.643) | (13.192) | (15.224) | (13.067) | (15.178) | |
| SBM | 0.682 *** | 0.291 *** | 0.703 *** | 0.311 *** | 0.821 *** | 0.468 *** | ||
| (5.662) | (3.031) | (5.704) | (3.122) | (6.548) | (4.780) | |||
| HML | 0.429 *** | 0.209 * | 0.320 ** | 0.196 | 0.553 *** | 0.421 *** | ||
| (2.747) | (1.677) | (2.037) | (1.541) | (3.400) | (3.318) | |||
| WML | −0.187 ** | −0.009 | ||||||
| (−2.439) | (−0.148) | |||||||
| RMW | −0.043 | 0.186 * | ||||||
| (−0.332) | (1.856) | |||||||
| CMA | −0.616 *** | −0.503 *** | ||||||
| (−3.787) | (−3.961) | |||||||
| p-value for F | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| adj. R2 | 0.602 | 0.686 | 0.689 | 0.707 | 0.697 | 0.706 | 0.722 | 0.749 |
| α(H)–α(L) | 0.086 ** | 0.099 ** | 0.058 | 0.081 ** |
| CAPM (L) | CAPM (H) | 3FF (L) | 3FF (H) | 4C (L) | 4C (H) | 5FF (L) | 5FF (H) | |
|---|---|---|---|---|---|---|---|---|
| α | −0.012 *** | −0.006 * | −0.014 *** | −0.007 ** | −0.011 *** | −0.006 * | −0.014 *** | −0.009 *** |
| (−2.790) | (−1.668) | (−3.676) | (−2.091) | (−2.811) | (−1.700) | (−3.923) | (−2.791) | |
| RMP | 0.924 *** | 0.804 *** | 0.871 *** | 0.774 *** | 0.854 *** | 0.769 *** | 0.810 *** | 0.720 *** |
| (14.154) | (15.377) | (14.581) | (14.992) | (13.938) | (14.453) | (13.846) | (14.424) | |
| SBM | 0.648 *** | 0.346 *** | 0.668 *** | 0.366 *** | 0.783 *** | 0.516 *** | ||
| (5.644) | (3.481) | (5.640) | (3.561) | (6.571) | (5.079) | |||
| HML | 0.413 *** | 0.235 * | 0.324 ** | 0.199 | 0.536 *** | 0.436 *** | ||
| (2.776) | (1.826) | (2.152) | (1.517) | (3.471) | (3.309) | |||
| WML | −0.144 * | −0.056 | ||||||
| (−1.951) | (−0.878) | |||||||
| RMW | −0.040 | 0.162 | ||||||
| (−0.330) | (1.551) | |||||||
| CMA | −0.603 *** | −0.515 *** | ||||||
| (−3.901) | (−3.901) | |||||||
| p-value for F | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| adj. R2 | 0.626 | 0.664 | 0.708 | 0.694 | 0.711 | 0.694 | 0.740 | 0.735 |
| α(H)–α(L) | 0.073 ** | 0.084 ** | 0.065 * | 0.068 * |
| CAPM (L) | CAPM (H) | 3FF (L) | 3FF (H) | 4C (L) | 4C (H) | 5FF (L) | 5FF (H) | |
|---|---|---|---|---|---|---|---|---|
| α | −0.011 *** | −0.006 * | −0.013 *** | −0.007 ** | −0.012 *** | −0.005 | −0.014 *** | −0.009 *** |
| (−2.641) | (−1.741) | (−3.222) | (−2.436) | (−2.700) | (−1.597) | (−3.795) | (−2.898) | |
| RMP | 0.915 *** | 0.817 *** | 0.874 *** | 0.775 *** | 0.869 *** | 0.756 *** | 0.795 *** | 0.738 *** |
| (13.746) | (15.983) | (13.751) | (15.972) | (13.170) | (15.420) | (13.178) | (15.233) | |
| SBM | 0.565 *** | 0.417 *** | 0.567 *** | 0.454 *** | 0.754 *** | 0.550 *** | ||
| (4.623) | (4.478) | (4.447) | (4.792) | (6.132) | (5.567) | |||
| HML | 0.305 * | 0.347 *** | 0.246 | 0.279 ** | 0.526 *** | 0.469 *** | ||
| (1.925) | (2.869) | (1.515) | (2.309) | (3.300) | (3.664) | |||
| WML | −0.077 | −0.128 ** | ||||||
| (−0.969) | (−2.165) | |||||||
| RMW | 0.056 | 0.106 | ||||||
| (0.448) | (1.044) | |||||||
| CMA | −0.777 *** | −0.344 *** | ||||||
| (−4.872) | (−2.682) | |||||||
| p-value for F | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| adj. R2 | 0.612 | 0.681 | 0.670 | 0.732 | 0.665 | 0.742 | 0.724 | 0.752 |
| α(H)–α(L) | 0.067 * | 0.065 * | 0.080 * | 0.066 * |
| CAPM (L) | CAPM (H) | 3FF (L) | 3FF (H) | 4C (L) | 4C (H) | 5FF (L) | 5FF (H) | |
|---|---|---|---|---|---|---|---|---|
| Panel A: 36-month portoflio | ||||||||
| α (ROS) | −0.012 *** | −0.005 | −0.014 *** | −0.006 * | −0.011 *** | −0.006 * | −0.015 *** | −0.008 *** |
| (−2.793) | (−1.593) | (−3.675) | (−1.961) | (−2.643) | (−1.856) | (−3.906) | (−2.748) | |
| α(H)–α(L) | 0.086 ** | 0.099 ** | 0.058 | 0.081 ** | ||||
| α (OROS) | −0.012 *** | −0.006 * | −0.014 *** | −0.007 ** | −0.011 *** | −0.006 * | −0.014 *** | −0.009 *** |
| (−2.790) | (−1.668) | (−3.676) | (−2.091) | (−2.811) | (−1.700) | (−3.923) | (−2.791) | |
| α(H)–α(L) | 0.073 ** | 0.084 ** | 0.065 * | 0.068 * | ||||
| α (OCFS) | −0.011 *** | −0.006 * | −0.013 *** | −0.007 ** | −0.012 *** | −0.005 | −0.014 *** | −0.009 *** |
| (−2.641) | (−1.741) | (−3.222) | (−2.436) | (−2.700) | (−1.597) | (−3.795) | (−2.898) | |
| α(H)–α(L) | 0.067 * | 0.065 * | 0.080 * | 0.066 * | ||||
| α (ROA) | −0.014 *** | −0.003 | −0.016 *** | −0.004 | −0.012 *** | −0.005 | −0.017 *** | −0.006 ** |
| (−3.099) | (−0.970) | (−4.094) | (−1.298) | (−2.880) | (−1.465) | (−4.384) | (−2.001) | |
| α(H)–α(L) | 0.126 *** | 0.146 *** | 0.084 ** | 0.129 *** | ||||
| α (OROA) | −0.013 *** | −0.004 | −0.015 *** | −0.005 | −0.013 *** | −0.005 | −0.016 *** | −0.008 ** |
| (−3.032) | (−1.275) | (−4.092) | (−1.624) | (−3.152) | (−1.343) | (−4.361) | (−2.389) | |
| 0.104 ** | 0.118 *** | 0.094 ** | 0.098 ** | |||||
| α (OCFA) | −0.011 *** | −0.006 * | −0.013 *** | −0.007 ** | −0.012 *** | −0.005 | −0.014 *** | −0.009 *** |
| (−2.654) | (−1.782) | (−3.279) | (−2.448) | (−2.799) | (−1.569) | (−3.777) | (−2.927) | |
| α(H)–α(L) | 0.067 * | 0.066 * | 0.084 ** | 0.067* | ||||
| Panel B: 24-month portfolio | ||||||||
| α (ROS) | −0.010 ** | −0.006 * | −0.013 *** | −0.007 ** | −0.011 ** | −0.007 * | −0.012 *** | −0.008 ** |
| (−2.221) | (−1.818) | (−2.846) | (−2.102) | (−2.204) | (−1.887) | (−2.864) | (−2.237) | |
| α(H)–α(L) | 0.045 | 0.062 | 0.039 | 0.057 | ||||
| α (OROS) | −0.010 ** | −0.007 * | −0.012 *** | −0.008 ** | −0.011 ** | −0.007 * | −0.012 *** | −0.009 ** |
| (−2.247) | (−1.972) | (−2.787) | (−2.244) | (−2.262) | (−1.669) | (−2.697) | (−2.348) | |
| α(H)–α(L) | 0.034 | 0.050 | 0.051 | 0.038 | ||||
| α (OCFS) | −0.009 ** | −0.007 ** | −0.011 ** | −0.009 *** | −0.011 ** | −0.006 * | −0.011 *** | −0.008 ** |
| (−2.182) | (−2.043) | (−2.490) | (−2.656) | (−2.345) | (−1.689) | (−2.753) | (−2.415) | |
| α(H)–α(L) | 0.024 | 0.016 | 0.055 | 0.033 | ||||
| α (ROA) | −0.014 *** | −0.003 | −0.017 *** | −0.003 | −0.013 *** | −0.004 | −0.016 *** | −0.004 |
| (−3.015) | (−0.744) | (−3.853) | (−0.844) | (−2.787) | (−0.924) | (−3.743) | (−0.984) | |
| α(H)–α(L) | 0.132 *** | 0.163 *** | 0.111 *** | 0.146 *** | ||||
| α (OROA) | −0.015 *** | −0.001 | −0.018 *** | −0.002 | −0.015 *** | −0.001 | −0.017 *** | −0.002 |
| (−3.285) | (−0.258) | (−4.040) | (−0.428) | (−3.102) | (−0.369) | (−3.916) | (−0.676) | |
| α(H)–α(L) | 0.173 *** | 0.198 *** | 0.162 *** | 0.171 *** | ||||
| α (OCFA) | −0.009 ** | −0.008 ** | −0.011 ** | −0.010 *** | −0.010 ** | −0.008 ** | −0.011 *** | −0.010 *** |
| (−2.046) | (−2.260) | (−2.457) | (−2.813) | (−2.175) | (−2.006) | (−2.777) | (−2.663) | |
| α(H)–α(L) | 0.007 | 0.005 | 0.029 | 0.016 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czapiewski, L.; Lizińska, J. Explanatory Power of Pre-Issue Financial Strength for Long-Term Market Performance: Evidence from Initial Equity Offerings on an Emerging Market. Int. J. Financial Stud. 2019, 7, 16. https://doi.org/10.3390/ijfs7010016
Czapiewski L, Lizińska J. Explanatory Power of Pre-Issue Financial Strength for Long-Term Market Performance: Evidence from Initial Equity Offerings on an Emerging Market. International Journal of Financial Studies. 2019; 7(1):16. https://doi.org/10.3390/ijfs7010016
Chicago/Turabian StyleCzapiewski, Leszek, and Joanna Lizińska. 2019. "Explanatory Power of Pre-Issue Financial Strength for Long-Term Market Performance: Evidence from Initial Equity Offerings on an Emerging Market" International Journal of Financial Studies 7, no. 1: 16. https://doi.org/10.3390/ijfs7010016
APA StyleCzapiewski, L., & Lizińska, J. (2019). Explanatory Power of Pre-Issue Financial Strength for Long-Term Market Performance: Evidence from Initial Equity Offerings on an Emerging Market. International Journal of Financial Studies, 7(1), 16. https://doi.org/10.3390/ijfs7010016





