On the Impact of Policy Uncertainty on Oil Prices: An Asymmetry Analysis
Abstract
:1. Introduction
2. The Models and Methods
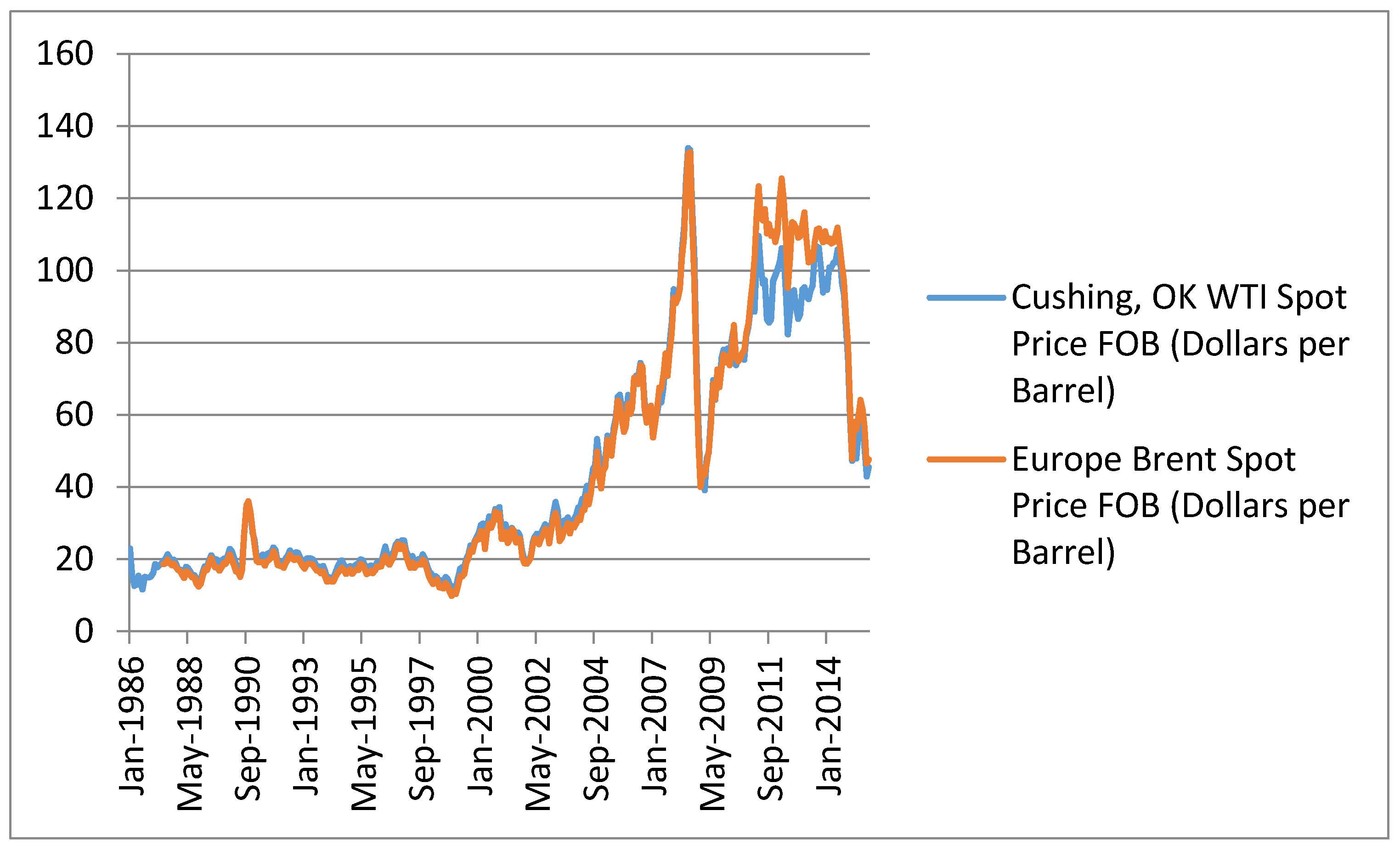
3. Empirical Results
4. Summary
Author Contributions
Conflicts of Interest
Appendix A. Data Definition and Sources
References
- Aftab, Muhammad, Karim Bux Shah Syed, and Naveed Akhter Katper. 2017. Exchange Rate Volatility and Malaysian-Thai Bilateral Industry Trade Flows. Journal of Economic Studies 44: 99–114. [Google Scholar] [CrossRef]
- Al-Shayeb, Abdulrahman, and Abdulnasser Hatemi-J. 2016. Trade openness and economic development in the UAE: an asymmetric approach. Journal of Economic Studies 43: 587–97. [Google Scholar] [CrossRef]
- Baghestani, Hamid, and Samer Kherfi. 2015. An error-correction modeling of US consumer spending: are there asymmetries? Journal of Economic Studies 42: 1078–94. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, Mohsen, and Hadise Fariditavana. 2015. Nonlinear ARDL Approach, Asymmetric Effects and the J-Curve. Journal of Economic Studies 42: 519–30. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, Mohsen, and Seyed H. Ghodsi. 2017. Policy Uncertainty and House Prices in the United States of America. Journal of Real Estate Portfolio Management 23: 73–85. [Google Scholar]
- Bahmani-Oskooee, Mohsen, and Saha Sujata. 2015. On the Relation between Stock Prices and Exchange Rates: A Review Article. Journal of Economic Studies 42: 707–32. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, Mohsen, Sahar Bahmani, Alice Kones, and Ali Kutan. 2015. Policy Uncertainty and the Demand for Money in the United Kingdom. Applied Economics 47: 1151–57. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, Mohsen, Ali Kutan, and Alice Kones. 2016. Policy Uncertainty and the Demand for Money in the United States. Applied Economics Quarterly 62: 37–49. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, and Steven J. Davis. 2016. Measuring Economic Policy Uncertainty. Quarterly Journal of Economics 131: 1593–636. [Google Scholar] [CrossRef]
- Bekiros, Stelios, Rangan Gupta, and Alessia Paccagnini. 2015. Oil Price Forecast ability and Economic Uncertainty. Economics Letters 132: 125–28. [Google Scholar] [CrossRef]
- Bernanke, Ben S. 1983. Irreversibility, Uncertainty, and Cyclical Investment. Quarterly Journal of Economics 98: 85–106. [Google Scholar] [CrossRef]
- Brennan, Michael. 1990. Latent Assets. Journal of Finance 45: 709–30. [Google Scholar] [CrossRef]
- Brennan, Michael, and Eduardo Schwartz. 1985. Evaluating Natural Resource Investment. Journal of Business 58: 1135–57. [Google Scholar] [CrossRef]
- Brogaard, Jonathan, and Andrew Detzel. 2015. The Asset-Pricing Implications of Government Economic Policy Uncertainty. Management Science 61: 3–18. [Google Scholar] [CrossRef]
- Delatte, Anne-Laure, and Antonio Lopez-Villavicencio. 2012. Asymmetry Exchange Rate Pass-Through: Evidence from Major Countries. Journal of Macroeconomics 34: 833–44. [Google Scholar] [CrossRef]
- Demir, Ender, and Giray Gozgor. 2016. The impact of economic policy uncertainty on the vehivle miles traveled (VMT) in the U.S. Eurasian Journal of Business and Management 4: 39–48. [Google Scholar] [CrossRef]
- Durmaz, Nazif. 2015. Industry Level J-Curve in Turkey. Journal of Economic Studies 42: 689–706. [Google Scholar] [CrossRef]
- 2009. Edelstein, Paul, and Lutz Kilian 2009. How Sensitive Are Consumer Expenditures to Retail Energy Prices? Journal of Monetary Economics 56: 766–79.
- 2010. Elder, John, and Apostolos Serletis 2010. Oil Price Uncertainty. Journal of Money, Credit, and Banking 42: 1137–59.
- Finn, Mary G. 2000. Perfect Competion and the Effects of Energy Price Increases on Economic Activity. Journal of Money, Credit, and Banking 32: 400–16. [Google Scholar] [CrossRef]
- Gregoriou, Andros. 2017. Modelling non-linear behaviour of block price deviations when trades are executed outside the bid-ask quotes. Journal of Economic Studies 44: 206–13. [Google Scholar] [CrossRef]
- Hooker, Mark A. 1996. What happened to the Oil-Price Macroeconomy Relationship? Journal of Monetary Economics 38: 195–213. [Google Scholar] [CrossRef]
- Kang, W., Ronald A. Ratti, and Joaquin L.Vespignani. 2017a. Oil price shocks and policy uncertainty: new evidence on the effect of US and non-US oil production. Energy Economics 66: 536–46. [Google Scholar] [CrossRef]
- Kang, Wensheng, de Garcia Fernando Perez, and Ronald A. Ratti. 2017b. Oil price shocks, policy uncertainty, and stock returns of oil and gas corporations. Journal of International Money and Finance 70: 344–59. [Google Scholar] [CrossRef]
- Kim, In-Moo, and Prakash Loungani. 1992. The Role of Energy in Real Business Cycle Models. Journal of Monetary Economics 29: 173–89. [Google Scholar] [CrossRef]
- Ko, Jun-Hyung, and Chnag-Min Lee. 2015. International Economic Policy Uncertainty and Stock Prices: Wavelet Approach. Economics Letters 134: 118–22. [Google Scholar] [CrossRef]
- Lima, Luiz, Claudio Foffano Vasconcelos, Jose Simão, and Helder de Mendonça. 2016. The quantitative easing effect on the stock market of the USA, the UK and Japan: An ARDL approach for the crisis period. Journal of Economic Studies 43: 1006–21. [Google Scholar] [CrossRef]
- Majd, Saman, and Robert S. Pindyck. 1987. Time to Build, Option Value, and Investment Decisions. Journal of Financial Economics 18: 7–27. [Google Scholar] [CrossRef]
- Nusair, Salah A. 2017. The J-curve Phenomenon in European Transition Economies: A Nonliear ARDL Approach. International Review of Applied Economic 31: 1–27. [Google Scholar] [CrossRef]
- Pal, Debdatta, and Subrata K. Mitra. 2016. Asymmetric Oil Product Pricing in India: Evidence from a Multiple Threshold Nonlinear ARDL Model. Economic Modelling 59: 314–28. [Google Scholar] [CrossRef]
- Pastor, Lubos, and Pietro Veronesi. 2012. Uncertainty about Government Policy and Stock Prices. The Journal of Finance 67: 1219–64. [Google Scholar] [CrossRef]
- Pastor, Lubos, and Pietro Veronesi. 2013. Political Uncertainty and Risk Premia. Journal of Financial Economics 110: 520–45. [Google Scholar] [CrossRef]
- Pesaran, Hashem M., Yongcheol Shin, and Richard J. Smith. 2001. Bounds Testing Approach to the Analysis of Level Relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling Asymmetric Cointegration and Dynamic Multipliers in a Nonlinear ARDL Framework. In Festschrift in Honor of Peter Schmidt: Econometric Methods and Applications. Edited by Robin Sickels and William Horrace. New York: Springer, pp. 281–314. [Google Scholar]
- Triantis, Alexander J., and James E. Hodder. 1990. Valuing Flexibility as a Complex Option. Journal of Finance 45: 549–66. [Google Scholar] [CrossRef]
| 1 | The site is: http://www.policyuncertainty.com/index.html. |
| 2 | For some other application of this measure of policy uncertainty see (Pastor and Veronesi 2012, 2013; Ko and Lee 2015; Brogaard and Detzel 2015; Bahmani-Oskooee et al. 2015, 2016; Bahmani-Oskooee and Ghodsi 2017). |
| 3 | For more on the application of these methods see (Delatte and Lopez-Villavicencio 2012; Bahmani-Oskooee and Fariditavana 2015; Bahmani-Oskooee and Saha 2015; Durmaz 2015; Baghestani and Kherfi 2015; Pal and Mitra 2016; Al-Shayeb and Hatemi-J 2016; Lima et al. 2016; Nusair 2017; Aftab et al. 2017; Gregoriou 2017). |
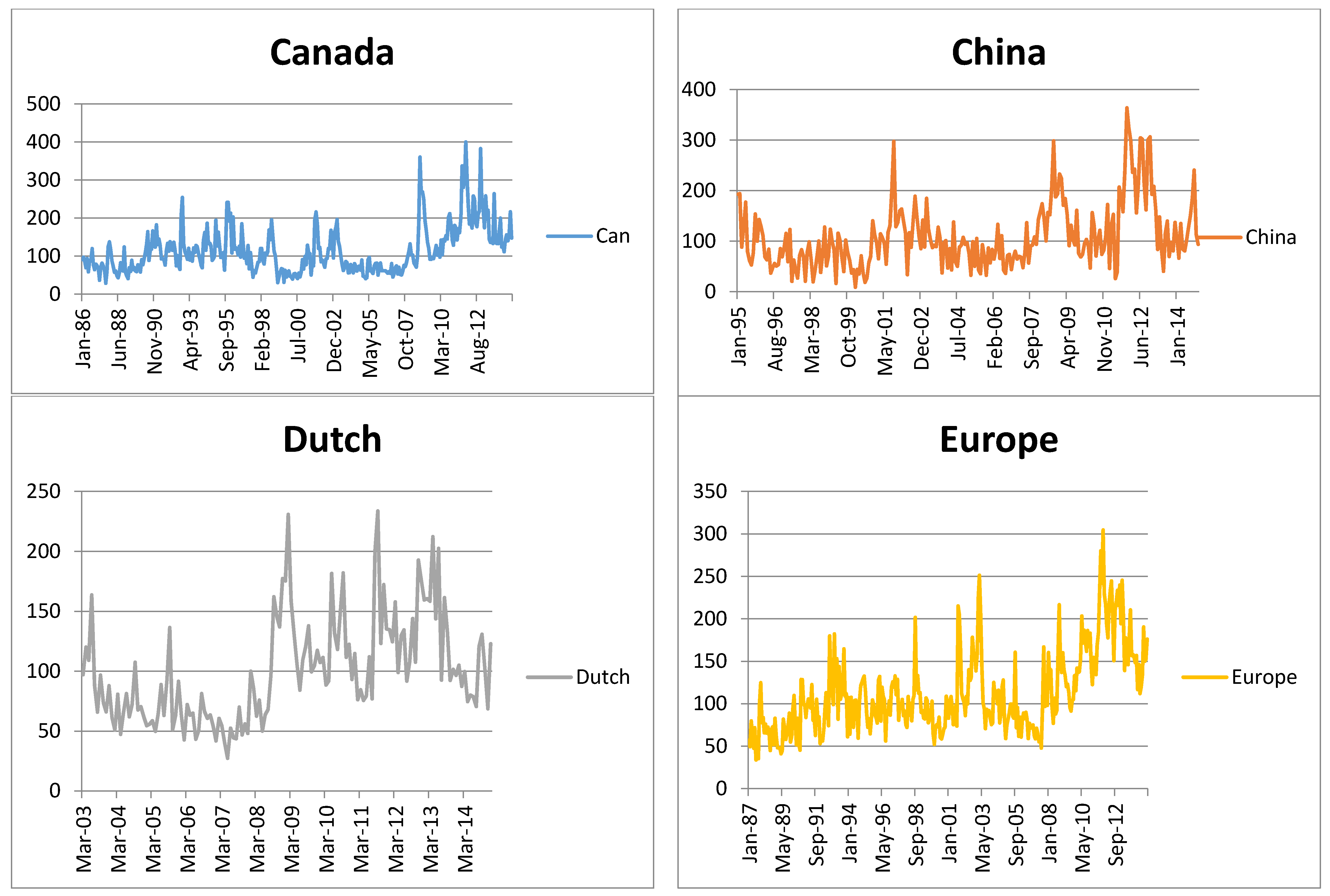
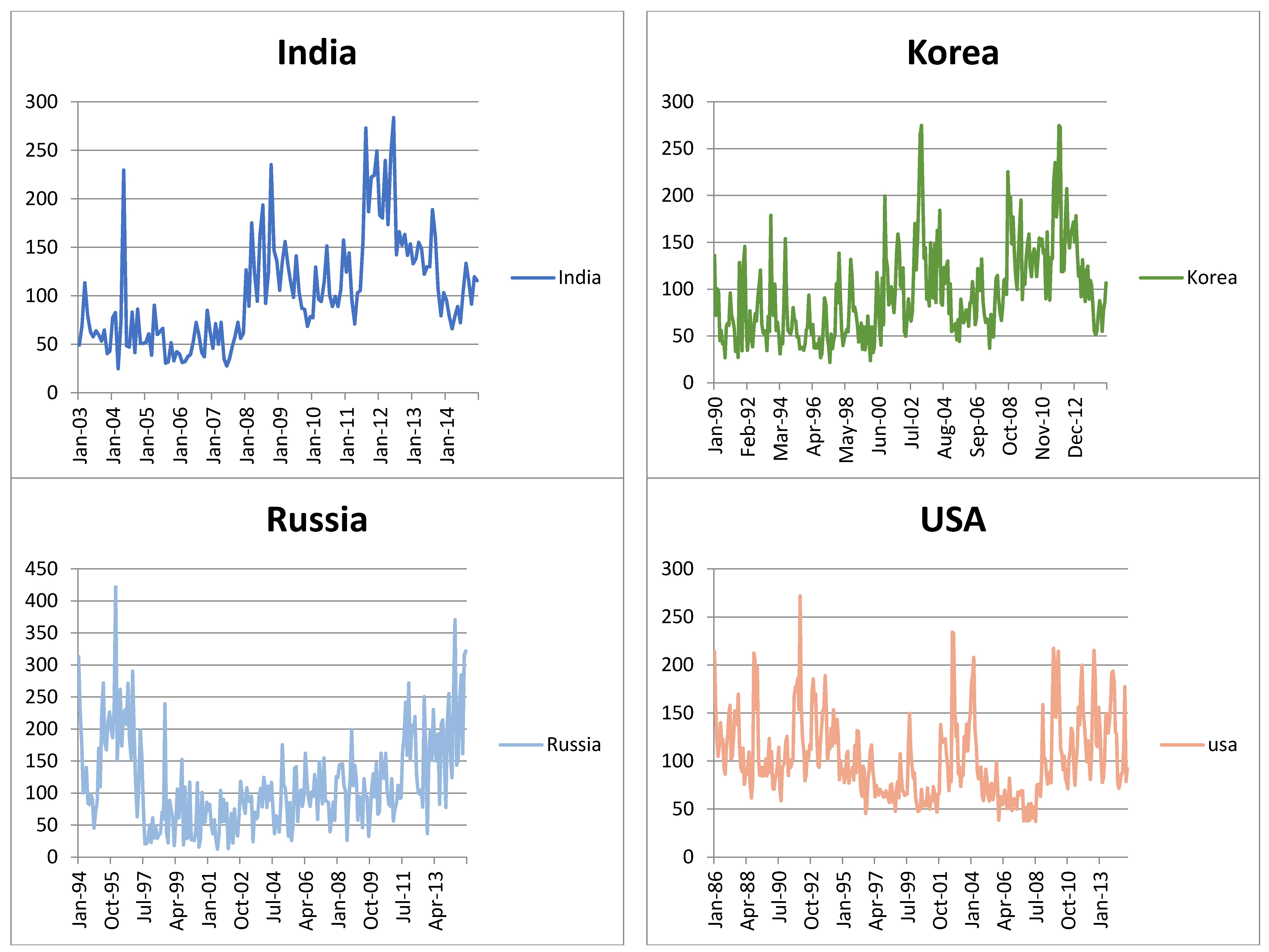
| Canada | China | Dutch | ||||
| L-ARDL | NL-ARDL | L-ARDL | NL-ARDL | L-ARDL | NL-ARDL | |
| Panel A: Short–Run Estimates | ||||||
| ΔlnOPt-1 | 0.24 (4.45) ** | 0.28 (5.24) ** | 0.25 (3.82) ** | 0.24 (3.68) ** | 0.28 (3.22) ** | 0.29 (3.34) ** |
| ΔlnOPt-2 | 0.13 (1.98) ** | 0.23 (2.57) ** | 0.24 (2.66) ** | |||
| ΔlnOPt-3 | ||||||
| ΔlnOPt-4 | ||||||
| ΔlnOPt-5 | ||||||
| ΔlnOPt-6 | ||||||
| ΔlnPUt | −0.04 (2.61) ** | −0.01 (0.93) | −0.04 (1.57) | |||
| ΔlnPUt-1 | −0.06 (3.73) ** | |||||
| ΔlnPUt-2 | −0.03 (2.38) ** | |||||
| ΔlnPUt-3 | −0.02 (1.79) * | |||||
| ΔlnPUt-4 | ||||||
| ΔlnPUt-5 | ||||||
| ΔlnPUt-6 | ||||||
| ΔlnPUt-7 | ||||||
| ΔPOSt | −0.05 (2.52) ** | −0.07 (1.36) | −0.05 (1.23) | |||
| ΔPOSt-1 | −0.09 (2.57) ** | |||||
| ΔPOSt-2 | ||||||
| ΔPOSt-3 | ||||||
| ΔPOSt-4 | ||||||
| ΔPOSt-5 | ||||||
| ΔPOSt-6 | ||||||
| ΔPOSt-7 | ||||||
| ΔNEGt | −0.07 (1.26) | 0.02 (0.57) | −0.07 (1.43) | |||
| ΔNEGt-1 | −0.14 (2.43) ** | 0.09 (1.79) * | ||||
| ΔNEGt-2 | ||||||
| ΔNEGt-3 | ||||||
| ΔNEGt-4 | ||||||
| ΔNEGt-5 | ||||||
| ΔNEGt-6 | ||||||
| ΔNEGt-7 | ||||||
| Panel B: Long-Run Estimates | ||||||
| ln PU | −2.03 (0.56) | −0.89 (0.62) | 0.15 (0.57) | |||
| POS | −1.87 (1.62) | −0.95 (2.05) ** | −0.44 (1.21) | |||
| NEG | −2.01 (1.72) * | −1.05 (2.23) ** | −0.54 (1.44) | |||
| Constant | 13.47 (0.78) | 2.06 (5.11) ** | 8.19 (1.20) | 2.62 (10.57) ** | 3.67 (3.17) | 3.83 (24.41) ** |
| Panel C: Diagnostic Statistics | ||||||
| F | 1.33 | 3.66 | 1.80 | 5.81 * | 4.89 * | 4.66 |
| ECMt-1 | −0.01 (0.82) | −0.03 (2.33) | −0.01 (1.15) | −0.08 (3.57) ** | −0.07 (3.07) * | −0.12 (3.64) ** |
| LM | 15.39 | 15.12 | 11.94 | 10.83 | 15.35 | 14.63 |
| RESET | 5.91 ** | 1.45 | 5.31 ** | 3.69 * | 8.13 ** | 8.44 ** |
| Adjusted R2 | 0.11 | 0.08 | 0.06 | 0.07 | 0.14 | 0.14 |
| CS (CS2) | S (S) | S (S) | S (S) | S (S) | S (US) | S (US) |
| WALD–S | 0.81 | 4.43 ** | 0.07 | |||
| WALD–L | 17.47 ** | 72.42 ** | 5.37 ** | |||
| Europe | India | Japan | ||||
| L-ARDL | NL-ARDL | L-ARDL | NL-ARDL | L-ARDL | NL-ARDL | |
| Panel A: Short–Run Estimates | ||||||
| ΔlnOPt-1 | 0.28 (5.20) ** | 0.29 (5.43) ** | 0.28 (3.22) ** | 0.30 (3.59) ** | 0.29 (5.18) ** | 0.29 (5.37) ** |
| ΔlnOPt-2 | 0.22 (2.39) ** | 0.26 (2.98) ** | ||||
| ΔlnOPt-3 | −0.07 (0.78) | |||||
| ΔlnOPt-4 | −0.01 (0.15) | |||||
| ΔlnOPt-5 | 0.08 (0.91) | |||||
| ΔlnOPt-6 | −0.23 (2.66) ** | |||||
| ΔlnPUt | −0.03 (1.51) | 0.002 (0.14) | −0.05 (3.06) ** | |||
| Δln PUt-1 | −0.05 (2.83) ** | −003 (1.84) * | ||||
| ΔlnPUt-2 | −0.06 (3.11) ** | |||||
| ΔlnPUt-3 | −0.04 (2.38) ** | |||||
| ΔlnPUt-4 | ||||||
| ΔlnPUt-5 | ||||||
| ΔlnPUt-6 | ||||||
| ΔlnPUt-7 | ||||||
| ΔPOSt | −0.03 (0.54) | −0.002 (0.07) | −0.05 (0.78) | |||
| ΔPOSt-1 | −0.14 (2.43) ** | −0.19 (2.75) | ||||
| ΔPOSt-2 | −0.04 (0.74) | −0.02 (0.27) | ||||
| ΔPOSt-3 | 0.06 (1.10) | −0.06 (0.94) | ||||
| ΔPOSt-4 | 0.02 (0.49) | −0.09 (1.36) | ||||
| ΔPOSt-5 | 0.12 (2.20) ** | −0.18 (2.86) ** | ||||
| ΔPOSt-6 | ||||||
| ΔPOSt-7 | ||||||
| ΔNEGt | 0.09 (2.49) ** | −0.01 (0.34) | −0.19 (2.89) ** | |||
| ΔNEGt-1 | ||||||
| ΔNEGt-2 | ||||||
| ΔNEGt-3 | ||||||
| ΔNEGt-4 | ||||||
| Panel B: Long-Run Estimates | ||||||
| ln PU | −1.00 (0.34) | 0.04 (0.15) | −1.92 (0.82) | |||
| POS | −2.27 (1.86) * | −0.02 (0.07) | −0.86 (0.86) | |||
| NEG | −2.46 (1.96) ** | −0.10 (0.34) | −0.97 (0.97) | |||
| Constant | 8.63 (0.62) | 2.68 (5.39) ** | 4.15 (3.08) ** | 3.84 (24.77) ** | 12.63 (1.16) | 3.65 (5.40) ** |
| Panel C: Diagnostic Statistics | ||||||
| F | 1.03 | 3.68 | 3.08 | 5.49 * | 1.69 | 2.74 |
| ECMt-1 | −0.01 (0.90) | −0.03 (2.74) | −0.05 (2.02) | −0.12 (3.60) ** | −0.01 (1.37) | −0.04 (2.74) |
| LM | 11.46 | 13.66 | 8.04 | 15.52 | 9.49 | 8.92 |
| RESET | 3.89 * | 4.06 ** | 3.59 * | 7.02 ** | 1.07 | 0.48 |
| Adjusted R2 | 0.12 | 0.12 | 0.15 | 0.09 | 0.11 | 0.13 |
| CS (CS2) | S (S) | S (S) | S (S) | S (S) | S (S) | S (S) |
| WALD–S | 0.10 | 0.49 | 4.36 ** | |||
| WALD–L | 21.88 ** | 6.81 ** | 24.91 ** | |||
| Russia | South Korea | United States | ||||
| L-ARDL | NL-ARDL | L-ARDL | NL-ARDL | L-ARDL | NL-ARDL | |
| Panel A: Short–Run Estimates | ||||||
| ΔlnOPt-1 | 0.26 (4.11) ** | 0.24 (3.77) ** | 0.26 (4.55) ** | 0.26 (4.64) ** | 0.28 (5.60) ** | 0.31 (5.86) ** |
| ΔlnOPt-2 | 0.15 (2.32) ** | |||||
| ΔlnOPt-3 | ||||||
| ΔlnOPt-4 | ||||||
| ΔlnOPt-5 | ||||||
| ΔlnOPt-6 | ||||||
| ΔlnPUt | −0.01 (0.71) | −0.02 (1.45) | −0.34 (0.01) | |||
| ΔlnPUt-1 | −0.02 (1.52) | −0.08 (4.79) ** | −0.07 (2.43) ** | |||
| ΔlnPUt-2 | −0.02 (2.29) ** | −0.05 (2.89) ** | −0.04 (1.53) | |||
| ΔlnPUt-3 | −0.06 (4.07) ** | |||||
| ΔlnPUt-4 | −0.04 (2.36) ** | |||||
| ΔlnPUt-5 | −0.03 (2.25) ** | |||||
| ΔlnPUt-6 | −0.04 (2.65) ** | |||||
| ΔlnPUt-7 | −0.02 (1.66) * | |||||
| ΔPOSt | −0.005 (0.15) | 0.03 (0.55) | −0.01 (0.06) | |||
| ΔPOSt-1 | −0.07 (2.16) ** | −0.05 (1.11) | −0.28 (2.83) ** | |||
| ΔPOSt-2 | −0.12 (3.48) ** | −0.05 (1.05) | −0.14 (1.47) | |||
| ΔPOSt-3 | −0.06 (1.72) * | −0.15 (3.36) ** | ||||
| ΔPOSt-4 | ||||||
| ΔPOSt-5 | ||||||
| ΔPOSt-6 | ||||||
| ΔPOSt-7 | ||||||
| ΔNEGt | −0.003 (0.17) | −0.09 (1.65) | 0.01 (0.26) | |||
| ΔNEGt-1 | −0.14 (2.39) ** | |||||
| ΔNEGt-2 | ||||||
| ΔNEGt-3 | ||||||
| ΔNEGt-4 | ||||||
| ΔNEGt-5 | ||||||
| ΔNEGt-6 | ||||||
| ΔNEGt-7 | ||||||
| Panel B: Long-Run Estimates | ||||||
| Ln PU | −0.10 (0.10) | 1.21 (1.52) | −0.36 (0.19) | |||
| POS | 0.03 (0.15) | −0.85 (1.22) | 0.51 (0.46) | |||
| NEG | −0.04 (0.17) | −0.99 (1.38) | 0.29 (0.26) | |||
| Constant | 4.54 (0.99) | 3.07 (14.00) ** | −1.60 (0.45) | 1.91 (3.94) ** | 5.41 (0.61) | 3.06 (6.79) ** |
| Panel C: Diagnostic Statistics | ||||||
| F | 1.08 | 5.58 * | 1.50 | 4.31 | 1.28 | 2.15 |
| ECMt-1 | −0.01 (1.31) | −0.08 (3.74) * | −0.01 (1.72) | −0.05 (3.38) ** | −0.01 (1.44) | −0.03 (2.53) |
| LM | 14.73 | 11.42 | 14.07 | 6.15 | 13.18 | 15.85 ** |
| RESET | 10.08 ** | 9.68 ** | 14.24 ** | 4.29 ** | 4.05 ** | 6.08 |
| Adjusted R2 | 0.08 | 0.08 | 0.14 | 0.16 | 0.07 | 0.08 |
| CS (CS2) | S (S) | S (S) | S (S) | S (S) | S (S) | S (S) |
| WALD–S | 4.21 ** | 0.41 | 3.39 * | |||
| WALD–L | 97.47 ** | 10.79 ** | 20.68 ** | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahmani-Oskooee, M.; Harvey, H.; Niroomand, F. On the Impact of Policy Uncertainty on Oil Prices: An Asymmetry Analysis. Int. J. Financial Stud. 2018, 6, 12. https://doi.org/10.3390/ijfs6010012
Bahmani-Oskooee M, Harvey H, Niroomand F. On the Impact of Policy Uncertainty on Oil Prices: An Asymmetry Analysis. International Journal of Financial Studies. 2018; 6(1):12. https://doi.org/10.3390/ijfs6010012
Chicago/Turabian StyleBahmani-Oskooee, Mohsen, Hanafiah Harvey, and Farhang Niroomand. 2018. "On the Impact of Policy Uncertainty on Oil Prices: An Asymmetry Analysis" International Journal of Financial Studies 6, no. 1: 12. https://doi.org/10.3390/ijfs6010012
APA StyleBahmani-Oskooee, M., Harvey, H., & Niroomand, F. (2018). On the Impact of Policy Uncertainty on Oil Prices: An Asymmetry Analysis. International Journal of Financial Studies, 6(1), 12. https://doi.org/10.3390/ijfs6010012




