Has IPO Market Structure Fundamentally Changed? Evidence from Negative Binomial Regression with Structural Breaks

Highlights

What are the main findings?

• Bai-Perron testing identifies six distinct IPO regimes with notably different variances
• Thirty-two-fold variance increase across regimes post-dot-com (from 37.1 to 1208.5)
• Statistically significant overdispersion emerges during the 2008 financial crisis, subsides post-recession, and returns with unprecedented intensity after May 2020

What are the implications of the main findings?

• IPO markets operate under distinct regimes; timing strategies that ignore structural breaks may produce misleading signals
• OLS without structural breaks produce wrong-signed coefficients; count modeling with regime controls corrects inference
• Negative binomial regression nests Poisson and accommodates varying dispersion across regimes

Abstract

This paper introduces Bai-Perron structural break detection combined with negative binomial regression to model overdispersed U.S. IPO count data. Using monthly data from 1995 to 2024, we identify five breaks that partition IPO activity into six distinct regimes, each with fundamentally different variance characteristics. We then employ negative binomial regression that incorporates these breaks. IPO data show substantial overdispersion (variance-to-mean ratios: 2.77 to 33.74). The negative binomial model reveals that market uncertainty (as measured by the VIX) and financing costs (as indicated by 10-year Treasury rates) reduce IPO activity, while lagged IPO volume drives activity in the current period. Regime-specific likelihood ratio tests reveal that statistically significant overdispersion first emerges during the 2008 financial crisis, subsides during the post-recession period, and returns with unprecedented intensity after May 2020. An OLS model without the identified structural breaks incorrectly suggests positive interest rate effects.

1. Introduction

IPO markets exhibit pronounced non-linearities, structural instability, and time-varying dynamics that render standard linear models inadequate. The dramatic swings from dot-com euphoria to post-financial crisis paralysis to pandemic-era surges suggest that IPO activity operates under distinct market regimes rather than following a stable data-generating process. Modeling these dynamics requires an approach that can both identify regime boundaries endogenously and account for the count data properties of IPO volume.

Our study extends Greene’s (2008) negative binomial regression framework by incorporating endogenous structural breaks identified through Bai-Perron multiple breakpoint regression testing to model the dynamics of U.S. IPO volume. We hypothesize that the decision to pursue an IPO is time- and state-dependent, captured simultaneously by structural breaks, market uncertainty, financing costs, and momentum effects. We focus on net IPOs (IPOs), defined as traditional IPOs excluding SPACs, direct listings, and other non-standard offerings.

To test this hypothesis, we first employ a Bai-Perron multiple breakpoint regression to identify structural breaks in IPO volume. We then examine the variance and median for IPOs for each of the Bai-Perron structural break regimes to assess if there are differences across time periods. Next, we model IPO activity with a negative binomial regression model. Our independent variables are the one-month lag of IPOs, the Chicago Board Options Exchange Volatility Index (VIX), and the market yield on U.S. Treasury securities at 10-year constant maturity (DGS10). We include five structural break indicator variables to capture the non-linearities and regime switches in the IPO market.

The results confirm our hypothesis, revealing distinct IPO regimes with notably different variances and medians. A traditional OLS model1 without breaks incorrectly suggests that higher interest rates increase IPO activity, which contradicts sound financial theory. In contrast, our negative binomial regression with structural breaks reveals that market uncertainty (VIX) and financing costs (10-year rates) reduce IPO activity, while the one-month lag of IPO volume drives current period activity, properly accounting for count data characteristics and severe overdispersion.

2. Literature Review

2.1. What We Know About the Market Drivers of IPO Volume

Core IPO timing research establishes strong links between market conditions and IPO activity. Lowry (2003) demonstrates that firms’ capital demands, information asymmetry, and investor sentiment significantly affect IPO volume, with periods of high investor optimism associated with increased IPO activity. Beaulieu and Bouden (2015) and Dicle and Levendis (2018) demonstrate that elevated VIX values are associated with lower IPO volumes. Ibbotson and Jaffe (1975) identify hot and cold issue markets and examine the relationship between IPO volume and returns. Loughran et al. (1994) show that stock market performance affects IPO volume. Ritter and Welch (2002) emphasize that market conditions are primary drivers of IPO decisions, with bear markets dramatically reducing IPO volumes. Pástor and Veronesi (2005) provide a theoretical foundation for rational IPO waves driven by market valuations.

2.2. Regime-Switching and Structural Break Approaches to IPO Modeling

Brailsford et al. (2000) apply Markov regime-switching to identify hot and cold IPO periods, building on the work of Ritter (1984) and Ibbotson and Jaffe (1975). They find that hot regimes exhibit higher means and substantially higher volatility. While structural break detection has been applied to count data in other fields (Beauregard et al., 2023, using sequential Chow tests), such methods have not been combined with financial count data modeling. Recent work confirms the need to account for regime changes in IPO count data. Wang and Ning (2022) use Markov regime-switching models with negative binomial distributions to identify hot and cold IPO markets. Batnini and Hammami (2015) apply a count regression model to predict IPO volume, utilizing quasi-Poisson methods with principal components analysis for dimensionality reduction of lagged variables, rather than structural break identification.

2.3. Why Existing Methods Fall Short

These studies provide important insights, but they do not simultaneously address the structural shifts of the IPO market (see Figure 1), the discrete nature of IPO volume, and its severe overdispersion. Brailsford et al. (2000) employ a two-state switching model, which provides formal regime identification; however, it requires assumptions about latent state variables and, like their subsequent VAR model, treats IPO volume as continuous rather than count data. Wang and Ning’s (2022) approach captures market cycles through probabilistic state transitions but requires estimating hidden states and transition probabilities. Thus, although count methods have been applied to IPO data to a degree, these implementations have not incorporated multiple structural break detection. Moreover, the quasi-Poisson specification in Batnini and Hammami (2015) can only partially address overdispersion, as it cannot adequately model IPO data where the variance substantially exceeds the mean. While our analysis identifies six distinct regimes, attempting to estimate a six-state Markov switching model would face severe identification and convergence challenges, further highlighting the advantages of the Bai-Perron approach for detecting multiple structural changes.

2.4. Why Bai-Perron + Negative Binomial Works

The Bai-Perron method identifies the points at which the IPO market transitions between distinct operating regimes, each with fundamentally different characteristics. Unlike two-state regime-switching models, which assume the market cycles between hot and cold periods, our approach reveals that major economic shifts create new regimes of market behavior that persist until the next structural break. The power and elegance of combining Bai-Perron breakpoint analysis with negative binomial regression allow us to model IPO dynamics properly. These distinct regimes are clearly visible in Figure 1.

The negative binomial regression framework addresses the limitations of Poisson models when the variance exceeds the mean (Cameron & Trivedi, 1986; Greene, 2008). Cohn et al. (2022) further demonstrate that log-linear regressions on count data can produce coefficients with the wrong sign due to heteroskedasticity, recommending Poisson or negative binomial specifications, which remain unbiased even when the mean-variance equality restriction is violated. Our approach improves upon the regime-switching approaches of Brailsford et al. (2000) and Wang and Ning (2022) for IPO activity. Recent work demonstrates a growing precedent for sophisticated regime-switching and count modeling in financial contexts: Orlowski (2023) successfully implements Bai-Perron multiple breakpoint detection with European financial time series, Domfeh et al. (2024) employ non-homogeneous Poisson processes with seasonal dependencies for catastrophe frequency modeling, and Marchese et al. (2023) use regime-switching structural break models for energy commodity correlations. Our Bai-Perron method identifies multiple statistically significant structural break dates, without limiting us to a hot and cold framework or relying on an unobservable switching mechanism.

Count models have been used sparingly to model IPO activity (Ivanov & Lewis, 2008; Wang & Ning, 2022). To our knowledge, Bai-Perron breakpoint detection has not been applied to overdispersed IPO count data. Our approach extends Greene’s (2008) negative binomial framework by incorporating structural breaks via Bai-Perron breakpoint regression, addressing both the overdispersion and structural instability that characterize IPO markets. Hence, we provide a more parsimonious alternative to Markov-switching models that rely on latent state variables.

3. Data

Our research is based on the monthly IPO volume for NYSE-, Nasdaq-, and AMEX-listed stocks, as reported on Jay Ritter’s website (Ritter, 2025). This series includes only completed offerings; withdrawn filings are excluded, and re-registered offerings that are ultimately completed are counted once at their completion date. The average monthly values of VIX and DGS10, quoted on an investment basis, were extracted from the St. Louis FRED Database for the January 1995 to December 2024 sample period, which includes 360 observations. We begin our sample in 1995 to focus on the modern IPO market structure, avoiding potential confounding effects from the Savings and Loan crisis resolution and early Nasdaq structural changes.

We select explanatory variables based on established theories of IPO timing. VIX captures market uncertainty, which Dicle and Levendis (2018) and Beaulieu and Bouden (2015) show significantly affects IPO activity. The 10-year Treasury rate (DGS10) represents financing costs, as higher rates increase the cost of capital and make equity issuance relatively less attractive (Pástor & Veronesi, 2005). Consistent with prior research, we include lagged IPO volume to capture persistence in IPO activity (Brailsford et al., 2004).

Table 1. Descriptive statistics.

	IPOS	VIX	DGS10
Mean	25.369	19.935	3.745
Median	19.000	18.180	3.750
Maximum	151.00	62.670	7.780
Minimum	0.000	10.130	0.620
Std. Dev.	22.143	7.779	1.600
Skewness	2.089	1.953	0.190
Kurtosis	8.658	9.300	2.175
Jarque-Bera	742.068	824.288	12.371
Probability	0.000	0.000	0.002
Observations	360	360	360
ADF	−3.216 *	−5.517 ***	−2.194
ADF Breakpoint	−7.113 ***	−6.517 ***	−5.159 **

***, **, * denote significance at 1%, 5%, and 10% levels.

shows the descriptive statistics for the examined variables. The data distributions of IPOs, VIX, and DGS10 are leptokurtic, with excess kurtosis values of 8.658, 9.300, and 2.175, respectively, indicating a strong prevalence of tail risks. The wide range of 0 to 151 for IPOs, along with its high excess kurtosis, reflects the volatile, cyclical, and time-varying nature of the IPO market.

The ADF and ADF Breakpoint are the Dickey–Fuller and Dickey–Fuller breakpoint unit root tests for the trend and intercept. IPO volume shows marginal evidence of stationarity (p-value = 0.083) under standard tests but clear stationarity (p < 0.01) when structural breaks are accounted for. Similarly, interest rates are non-stationary under conventional tests but achieve stationarity at the 5% level when breaks are modeled (p = 0.0199), demonstrating that ignoring structural breaks can lead to unnecessary variable transformations, which can result in incorrect statistical inference and inappropriate model specifications. VIX is stationary at 1% under both specifications, with the break test providing stronger evidence. The dramatic improvement in stationarity evidence when accounting for breaks (p < 0.01 versus p = 0.083 for IPOs) validates that our identified regimes represent genuine structural shifts in market dynamics.

4. Results

To identify structural breaks in IPO volume, we employ the Bai and Perron (2003) multiple breakpoint test:

$${IPO}_t={\displaystyle {\sum }_{j=1}^6{c}_j{I}_{jt}}+{\epsilon }_t$$

(1)

where c_j represents the mean IPO level in regime j, I_jt is an indicator variable equal to 1 when observation t belongs to regime j (and 0 otherwise), and the break dates are endogenously determined by minimizing the sum of squared residuals of the time periods and statistically testing them with F-statistics. We test sequentially for L + 1 versus L breaks with 10% trimming and a maximum of five breaks.

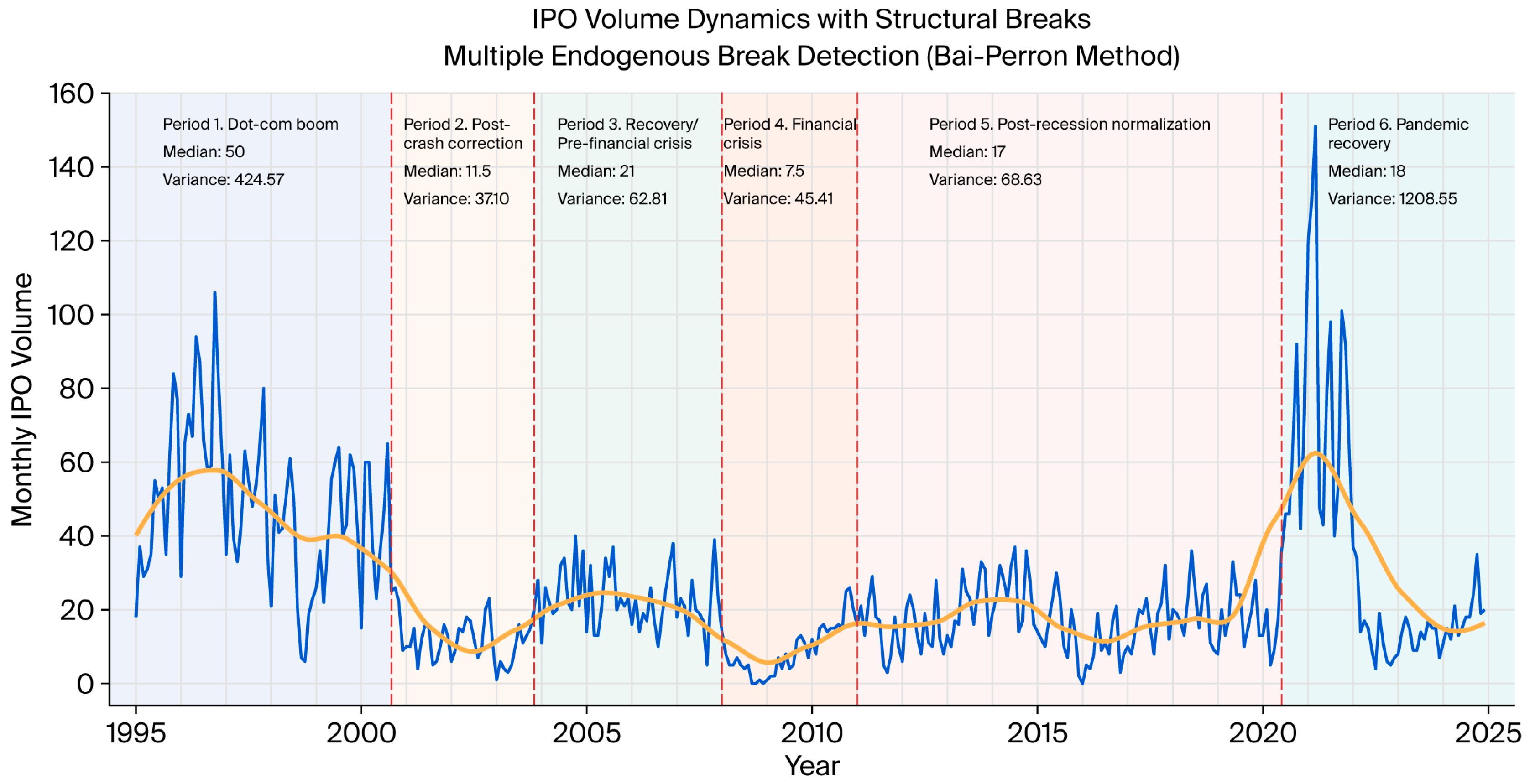
Our Bai-Perron analysis identifies structural shifts in the mean IPO rate through endogenous structural breaks, revealing the time-varying nature of IPO volume. The model identifies five structural breaks, corresponding to six distinct regimes of IPO activity. The economic significance of our endogenously identified breaks—coinciding with the dot-com crash, financial crisis, and pandemic—provides validation for the use of Bai-Perron for break detection, even in contexts involving count data of macroeconomic variables. Notably, the model identifies the pandemic-era break as May 2020, just two months after the World Health Organization declared the pandemic, demonstrating the method’s precision in detecting structural shifts. These periods include the dot-com boom (January 1995–August 2000), post-crash correction (September 2000–October 2003), recovery period/pre-financial crisis (November 2003–December 2007), financial crisis (January 2008–December 2010), post-recession normalization/pandemic onset (January 2011–May 2020), and pandemic recovery with inflation management (June 2020–December 2024).

Table 2. Bai-Perron breakpoints.

Variable	Coefficient	t-Statistic
1995M01 to 2000M08: 68 observations
C	48.544 ***	19.265
2000M09 to 2003M10: 38 observations
C	12.053 ***	12.095
2003M11 to 2007M12: 50 observations
C	22.700 ***	20.084
2008M01 to 2010M12: 36 observations
C	9.083 ***	8.020
2011M01 to 2020M05: 113 observations
C	17.186 ***	21.868
2020M06 to 2024M12: 55 observations
C	35.818 ***	7.577

*** denotes significance at 1% level.

presents the Bai-Perron breakpoint test results, confirming all identified breaks are statistically significant at the 1% level.

As in Herley et al. (2023), we examine how variance and median IPO volumes differ across structural breaks (

Table 3. IPO volume statistics by market regime.

Period	Date Range	Observations	Median	Mean	Variance	Variance-to-Mean
Overall *	January 1995–December 2024	360	19.00	25.37	488.94	19.27
1	January 1995–August 2000	68	50.00	48.54	424.57	8.75
2	September 2000–October 2003	38	11.50	12.05	37.10	3.08
3	November 2003–December 2007	50	21.00	22.7	62.81	2.77
4	January 2008–December 2010	36	7.50	9.08	45.41	5.00
5	January 2011–May 2020	113	17.00	17.19	68.63	3.99
6	June 2020–December 2024	55	18.00	35.82	1208.55	33.74

* Represents statistics for the entire sample period without structural break adjustments.

). The variance in IPO volume is dramatic across regimes, ranging from 37.1 in the post-dot-com crash period from September 2000 to October 2003 to 1208.5 during the more recent period from June 2020 to December 2024, representing a 32-fold difference. Most strikingly, Period 6’s variance-to-mean ratio of 33.74 dwarfs all previous periods (which ranged from 2.77 to 8.75), suggesting a fundamental shift in IPO market dynamics rather than a temporary shock. Median IPO volumes vary from 7.5 to 50 IPOs per month across regimes. The wide variance and median ranges indicate fundamental instability in IPO activity, supporting the endogenous structural framework of our research. Refer to Table 3 and Figure 1 for additional details.

Using Greene’s (2008) framework, the negative binomial framework is specified as:

$$Conditional Mean: \mathsf{{\rm E}}\left[y_i|x_i\right]={\lambda }_i$$

(2)

$$Conditional Variance: Var[y_i |x_i]={\lambda }_i (1+\alpha {\lambda }_i)$$

(3)

$$Link Function: {\lambda }_i=\mathrm{e}\mathrm{x}\mathrm{p}\left(x_i^{\prime }\beta \right)$$

(4)

We extend Greene’s (2008) framework in Equation (5) by incorporating endogenous structural breaks identified through Bai-Perron multiple breakpoint regression testing. The time-varying nature of IPOs is captured in our negative binomial regression model by indicator variables $D_{2 }$–$D_6$, with Period 1 (January 1995–August 2000) serving as the baseline captured in the intercept:

$${\lambda }_i=exp\left({\beta }_0+ {\beta }_1{IPOS}_{t-1}+{\beta }_2{VIX}_t+{\beta }_3{DGS10}_t+{\beta }_4{D}_2+{\beta }_5{D}_3+{\beta }_6{D}_4+{\beta }_7{D}_5+{\beta }_8{D}_6\right)+{ϵ}_t$$

(5)

Upon inspection, our IPO data exhibit severe overdispersion with an overall variance-to-mean ratio of 19.27 (see Table 3), which violates the equidispersion assumption of a Poisson regression. Formal testing using the likelihood-ratio (LR) statistic, where our null hypothesis is $\alpha =0 \left(Poisson\right)$ and our alternative hypothesis is $\alpha >0 \left(Negative Binomial\right),$ confirms this with an LR statistic of 153.92 and a p < 0.001 (see

Table 4. Negative binomial regression results.

Variable	Coefficient	z-Statistic
Constant	4.971 ***	7.07
IPOSt−1	0.017 ***	4.73
VIX	−0.038 ***	−3.75
DGS10	−0.187 **	−2.26
D2	−0.871 ***	−3.24
D3	−0.817 ***	−2.87
D4	−1.388 ***	−3.97
D5	−1.375 ***	−3.39
D6	−0.975 ***	−2.75
Model Diagnostics
LR statistic	153.92
Prob(LR statistic)	0.00
Log likelihood	−1450.15
AIC	8.129
BIC	8.226
Observations	359

***, ** denote significance at 1% and 5% levels.

). The overdispersion is also evident across all time periods, with the variance-to-mean ratio ranging from 2.77 to 33.74, further underscoring the need to use a negative binomial regression approach for modeling IPO volume.

While Markov-switching models have been applied to IPO research assuming recurring hot and cold dynamics, our identification of six distinct regimes makes such approaches infeasible. A two-state Markov-switching specification, although estimable, cannot accommodate the six distinct regimes identified by our structural break analysis. Our Bai-Perron approach, which utilizes fixed regime indicators, offers a practical alternative that accommodates non-recurring structural changes. The proportion of months with zero IPOs is low (4 months, 1.1%), indicating that a standard negative binomial regression model can adequately accommodate them. Zero-inflated specifications address excess zeros beyond what a count distribution predicts; with only 1.1% zeros, such complexity is unwarranted. As Cohn et al. (2022) note, zero-inflated models are suitable when data exhibit excessive zeros, but identifying factors that affect exposure can be challenging.

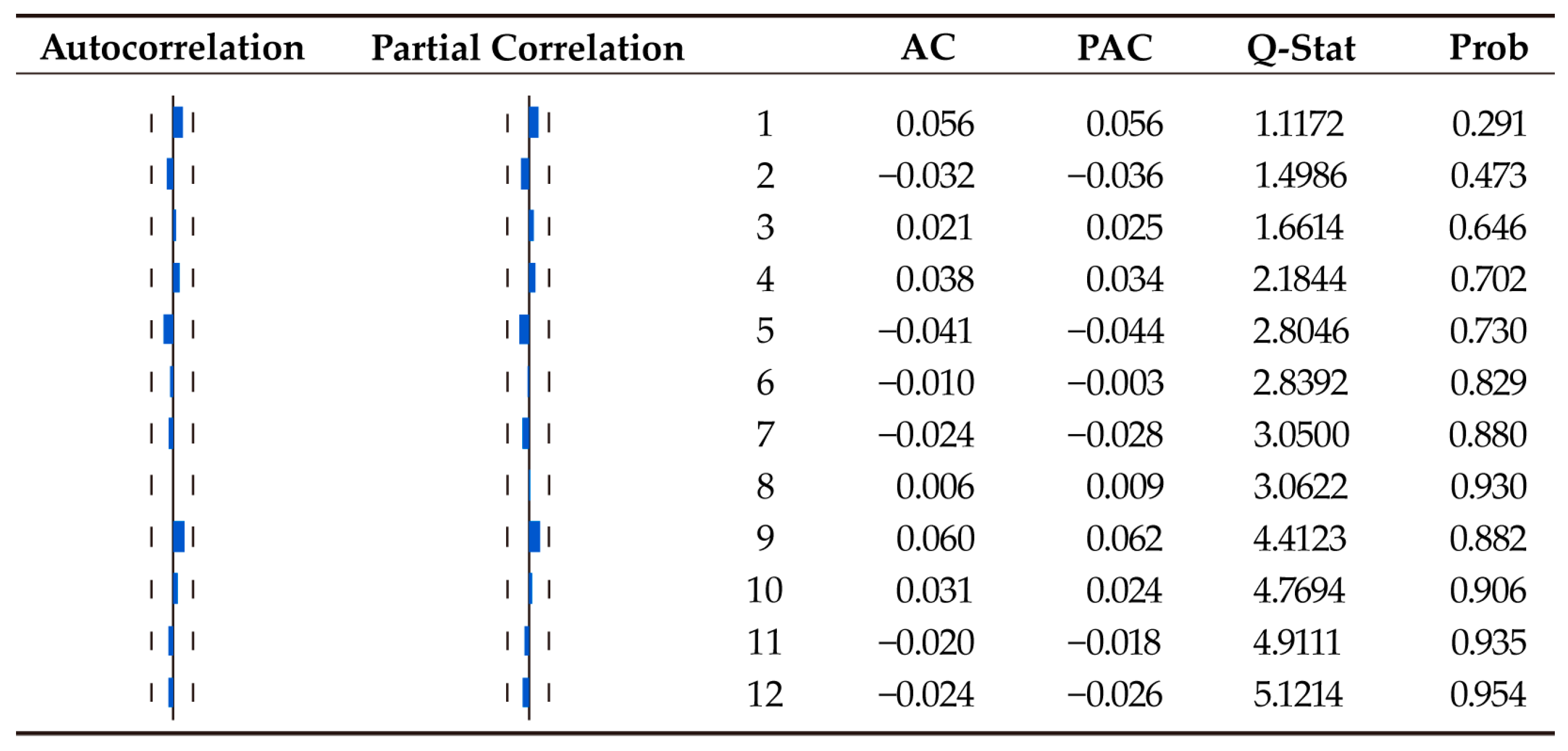
All variables, including the constant (which represents the baseline IPO activity), are statistically significant at the 1% level, except for DGS10, which is significant at the 5% level. Tests on squared residuals confirm the absence of heteroskedasticity or ARCH effects (maximum autocorrelation = 0.060, all p-values > 0.29). Standard serial correlation diagnostics are less reliable for count model residuals, though the absence of patterns in squared residuals suggests adequate model specification. See Figure A1 in Appendix A.

Our regression coefficients are logarithmic; accordingly, we exponentiate them into count effects for economic interpretation. For example, with β₁ = 0.017, we have exp(0.017) = 1.017. A practical interpretation of the coefficient is that each additional IPO in the previous month increases expected current IPOs by 1.7% (holding all other variables constant). Each one-point increase in VIX reduces expected IPOs by 3.7%, corroborating that market uncertainty deters or tempers IPO activity. Each one percentage point increase in 10-year Treasury rates reduces expected IPOs by 17.1%, reflecting the significant impact of financing costs on IPO decisions.

The post-crash correction period (D2) has 58.2% fewer IPOs than our baseline. The recovery period/pre-financial crisis period (D3) has 55.8% fewer IPOs. The financial crisis period (D4) has 75.1% fewer IPOs than the baseline, consistent with the frozen capital markets that followed Lehman’s collapse. The post-recession normalization/pandemic onset period (D5) has 74.7% fewer IPOs than the baseline. The pandemic recovery with the inflation management period (D6) has 62.3% fewer IPOs than the baseline. The constant represents the Period 1 baseline, which had the highest median IPO volume (50) and sustained high activity. All subsequent periods show significant reductions from this baseline (55.8–75.1%), indicating that the consistent high volume of the dot-com era was a historical anomaly.

To examine whether overdispersion varies across regimes, we estimate separate negative binomial models for each regime.

Table 5. Regime-specific overdispersion tests.

Regime	Date Range	LR Statistic	p-Value
1	January 1995–August 2000	5.48	0.70
2	September 2000–October 2003	2.68	0.95
3	November 2003–December 2007	0.58	0.99
4	January 2008–December 2010	19.19 **	0.014
5	January 2011–May 2020	8.52	0.38
6	June 2020–December 2024	33.40 ***	<0.001

***, ** denote significance at 1% and 5% levels.

presents the likelihood ratio tests for overdispersion across all six regimes.

Pre-crisis periods (Zones 1–3) exhibit no statistically significant overdispersion, as indicated by LR statistics that fail to reject the Poisson null. The 2008 financial crisis marks a structural shift: Zone 4 is the first period where overdispersion becomes statistically significant (LR = 19.19, p = 0.014). Notably, Zone 5 (post-recession normalization) exhibits no significant overdispersion (p = 0.38), suggesting that markets stabilized during this period. Post-May 2020, overdispersion returns with unprecedented intensity (LR = 33.40, p < 0.001). The negative binomial specification remains appropriate throughout, as it nests the Poisson distribution, yielding efficient estimates when overdispersion is minimal while accommodating the extreme variance observed in later periods.

The importance of our structural break specification is further illustrated by examining S&P 500 returns. In a baseline OLS model, log returns appear significant (β = 54.03, p = 0.035). However, this relationship becomes insignificant (β = 1.02, p = 0.430) in our structural break-adjusted negative binomial model, suggesting the apparent relationship reflects both variables responding to the same economic shifts rather than market returns directly driving IPO activity.

Robustness

We test whether our results hold with alternative specifications. Including a second lag IPO (−2) and Economic Policy Uncertainty (EPU) alongside our original variables, all structural breaks remain significant at the 1% level. The second lag is significant (p < 0.001), and EPU is marginally significant (p = 0.074). Our core finding remains: structural breaks identify distinct IPO regimes regardless of the specification used.

We also examine potential endogeneity concerns.

Table A1. Negative binomial regression results|endogeneity check.

Variable	Coefficient	z-Statistic
Constant	4.898 ***	6.73
IPOSt−1	0.016 ***	4.48
VIXt−1	−0.031 ***	−3.09
DGS10t−1	−0.193 **	−2.30
D2	−0.939 ***	−3.47
D3	−0.815 ***	−2.78
D4	−1.447 ***	−4.10
D5	−1.384 ***	−3.32
D6	−1.023 ***	−2.79
Model Diagnostics
LR statistic	150.15
Prob(LR statistic)	0.00
Log likelihood	−1452.04
AIC	8.139
BIC	8.237
Observations	359

***, ** denote significance at 1% and 5% levels.

in Appendix A presents results using lagged values of VIX and DGS10. The results remain virtually unchanged, with both market uncertainty and financing costs continuing to have negative and statistically significant effects on IPO activity. The stability of coefficients across specifications (VIX: −0.031 vs. −0.038; DGS10: −0.193 vs. −0.187) confirms that our findings are robust to concerns about endogeneity.

To test whether our structural breaks capture autoregressive dynamics rather than genuine structural changes, we re-estimated the Bai-Perron model including three lags of IPO volume.

Table A2. Structural break stability.

Regime	Date Range (Original)	Date Range (W-Lags)	Shift
1	January 1995–August 2000	April 1995–August 2000	Stable
2	September 2000–October 2003	September 2000–October 2003	Identical
3	November 2003–December 2007	November 2003–October 2007	2 months
4	January 2008–December 2010	November 2007–April 2018	Variable
5	January 2011–May 2020	May 2018–March 2021	Variable
6	June 2020–December 2024	April 2021–December 2024	~11 months

presents the results. Early regimes show remarkable stability: Regime 1 remains stable, Regime 2 is identical across specifications, and Regime 3 shifts by only two months. The middle regimes (4–5) exhibit greater sensitivity to lag inclusion, reflecting the complex post-crisis dynamics of this period. Specifically, the lag-augmented model merges the 2008–2010 financial crisis with the subsequent post-Dodd–Frank normalization period into a single regime (2007M11–2018M04), obscuring a key structural distinction in IPO market conditions. Importantly, a distinct post-2020 regime persists across specifications, confirming that our core finding—the unprecedented overdispersion in recent years—is robust to model specification. We retain the original specification because its regime boundaries align with identifiable economic events (the dot-com crash, the financial crisis onset in January 2008, the post-crisis normalization beginning January 2011, and the pandemic), enhancing practical applicability.

Finally, to address concerns about the two-step procedure, we test for structural breaks in the residuals of the negative binomial model. The Bai-Perron test finds no significant breaks, confirming that our zone independent variables adequately capture the structural shifts.

5. Conclusions

To our knowledge, this study is the first to apply Bai-Perron breakpoint regression tests to financial count data, demonstrating that U.S. IPO volume dynamics necessitate the identification of multiple structural breaks and the use of proper count methods that account for overdispersion. The 32-fold variance increase across regimes post-dot-com (from 37.1 to 1208.5), coupled with persistent overdispersion, reveals instability in market structure that neither traditional OLS models nor two-state regime-switching approaches can adequately capture. Regime-specific likelihood ratio tests reveal that statistically significant overdispersion first emerges with the 2008 financial crisis (LR = 19.19, p = 0.014), subsides during the post-recession normalization period (p = 0.38), and returns with unprecedented intensity after May 2020 (LR = 33.40, p < 0.001). This suggests the financial crisis disrupted IPO market dynamics; markets partially healed during the subsequent decade, but the pandemic shattered this stability, creating the most volatile IPO environment in our sample.

The failure of IPO volumes to recover to their dot-com era baseline across multiple market cycles suggests that structural breaks represent permanent regime changes, not temporary shocks. The shift to higher variance regimes suggests that standard IPO timing models may require reconsideration. A baseline OLS specification without structural breaks yields a positive coefficient on DGS10 (+3.05, p < 0.001), implying that higher interest rates increase IPO activity—directly contradicting financial theory. This sign reversal is consistent with Cohn et al.’s (2022) finding that log-linear approaches can produce wrong-signed coefficients when applied to count data. After accounting for structural breaks, the coefficient reverses to −0.187 (p < 0.05), aligning with corporate finance theory.

Our methodology provides policymakers and practitioners with more accurate tools for monitoring IPO market health and timing market entry, as traditional methods often mask critical regime changes or employ a limited hot and cold approach. The identification of six distinct regimes—with statistically significant overdispersion emerging in 2008 and returning with unprecedented intensity after May 2020—suggests that IPO timing strategies based on pre-crisis patterns may no longer be applicable. Future research might examine whether similar patterns exist in other capital markets.