Anomalies and Investor Sentiment: International Evidence and the Impact of Size Factor
Abstract
1. Introduction
2. Literature Review
3. Data and Methodology
3.1. Data
3.2. Models
4. Results
4.1. Pure Anomaly Strategies
4.2. Fixing the Size Factor
4.3. Robustness Checks
4.3.1. Combination Portfolios Instead of Portfolios Formed Based on a Single Anomaly
4.3.2. Using Equally Weighted Portfolios Instead of Value-Weighted Portfolios
4.3.3. Examining Size Anomaly While Controlling Other Factors
4.3.4. Calculating Size Anomaly Returns from Various Combination Portfolios
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | “Direct” indicators are sentiment measures obtained by surveys. “Indirect” indicators, on the other hand, are calculated by using market data such as put/call parity and discounts on closed-end funds. |
| 2 | Available on http://www.cao.go.jp/index-e.html (accessed on 15 January 2020). |
| 3 | https://ec.europa.eu/info/business-economy-euro/indicators-statistics/economic-databases/business-and-consumer-surveys_en (accessed on 16 January 2020). |
| 4 | Based on surveys, the economic sentiment indicator (ESI) of Europe consists of five different sub-indicators, namely industrial confidence (40%), service confidence (30%), consumer confidence (20%), retail trade confidence (5%) and construction confidence (5%). |
| 5 | Stambaugh and Yuan (2017) suggest a new model with two mispricing factors, which having predictive relationship with investor sentiment, in order to explain anomaly returns. |
| 6 | https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html (accessed on 10 January 2020). |
| 7 | Other anomaly returns are not available for Europe, Japan, North America and global markets. |
| 8 | Due to the lack of data for other regions, we do this check only for the US market. |
References
- Ali, Ashiq, and Umit G. Gurun. 2009. Investor Sentiment, Accruals Anomaly, and Accruals Management. Journal of Accounting, Auditing & Finance 24: 415–31. [Google Scholar]
- Altanlar, Ali, Jiaqi Guo, and Phil Holmes. 2019. Do culture, sentiment, and cognitive dissonance explain the “above suspicion” anomalies? European Financial Management 25: 1168–95. [Google Scholar] [CrossRef]
- Ang, Andrew, Robert J. Hodrick, Yuhang Xing, and Xiaoyan Zhang. 2006. The cross-section of volatility and expected returns. Journal of Finance 61: 259–99. [Google Scholar] [CrossRef]
- Baker, Malcolm, and Jeffrey Wurgler. 2006. Investor Sentiment and the Cross-Section of Stock Returns. Journal of Finance 61: 1645–80. [Google Scholar] [CrossRef]
- Baker, Malcolm, Jeffrey Wurgler, and Yu Yuan. 2012. Global, local, and contagious investor sentiment. Journal of Financial Economics 104: 272–87. [Google Scholar] [CrossRef]
- Banz, Rolf W. 1981. The relationship between return and market value of common stocks. Journal of Financial Economics 9: 3–18. [Google Scholar] [CrossRef]
- Basu, Sanjoy. 1977. Investment Performance of Common Stocks in Relation to Their Price-Earning Ratios: A Test ofthe Efficient Market Hypothesis. Journal of Finance 32: 663–82. [Google Scholar] [CrossRef]
- Basu, Sanjoy. 1983. The Relationship between Earnings’ Yield, Market Value and Return for NYSE Common Stocks: Further Evidence. Journal of Financial Economics 12: 129–56. [Google Scholar] [CrossRef]
- Bathia, Deven, and Don Bredin. 2013. An examination of investor sentiment effect on G7 stock market returns. The European Journal of Finance 19: 909–37. [Google Scholar] [CrossRef]
- Brown, Gregor. W., and Michael T. Cliff. 2005. Investor Sentiment and Asset Valuation. The Journal of Business 78: 405–40. [Google Scholar] [CrossRef]
- Calluzzo, Paul, Fabio Moneta, and Selim Topaloglu. 2019. When Anomalies Are Publicized Broadly, Do Institutions Trade Accordingly? Management Science 65: 4555–74. [Google Scholar] [CrossRef]
- Chan, Louis K. C., Yasushi Hamao, and Josef Lakonishok. 1991. Fundamentals and stock returns in Japan. Journal of Finance 46: 1739–64. [Google Scholar] [CrossRef]
- Chen, Long, Robert Novy-Marx, and Lu Zhang. 2011. An Alternative Three-Factor Model. Available online: https://ssrn.com/abstract=1418117 (accessed on 15 January 2020).
- Cooper, Michael J., Huseyin Gulen, and Michael J. Schill. 2008. Asset Growth and the Cross Section of Stock Returns. Journal of Finance 63: 1069–652. [Google Scholar] [CrossRef]
- Daniel, Kent, and Sheridan Titman. 2006. Market reactions to tangible and intangible information. Journal of Finance 61: 1605–43. [Google Scholar] [CrossRef]
- De Bondt, Werner F. M., and Richard Thaler. 1985. Does the stock market overreact? Journal of Finance 40: 793–805. [Google Scholar] [CrossRef]
- De Bondt, Werner F. M., and Richard H. Thaler. 1987. Further evidence on investor overreaction and stock market seasonality. Journal of Finance 42: 557–81. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1992. The Cross-Section of Expected Stock Returns. Journal of Finance 47: 427–65. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2015. A five-factor asset pricing model. Journal of Financial Economics 116: 1–22. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2016. Disecting Anomalies with a Five-Factor Model. The Review of Financial Studies 29: 69–103. [Google Scholar] [CrossRef]
- Ferreira, Paulo, and Andreia Dionísio. 2014. Revisiting serial dependence in the stock markets of the G7 countries, Portugal, Spain and Greece. Applied Financial Economics 24: 319–31. [Google Scholar] [CrossRef]
- Frazzini, Andrea, and Lasse Heje Pedersen. 2014. Betting against beta. Journal of Financial Economics 111: 1–25. [Google Scholar] [CrossRef]
- Griffin, John M., Xiuqing Ji, and J. Spencer Martin. 2003. Momentum investing and business cycle risk: Evidence from pole to pole. Journal of Finance 58: 2515–47. [Google Scholar] [CrossRef]
- Hackel, Kenneth S., Joshua Livnat, and Atul Rai. 2000. A Free Cash Flow Investment Anomaly. Journal of Accounting, Auditing & Finance 15: 1–24. [Google Scholar]
- Han, Chunmao, and Yongdong Shi. 2022. Chinese stock anomalies and investor sentiment. Pacific-Basin Finance Journal 73: 101739. [Google Scholar] [CrossRef]
- Jacobs, Heiko. 2015. What explains the dynamics of 100 anomalies? Journal of Banking and Finance 57: 65–85. [Google Scholar] [CrossRef]
- Jacobs, Heiko, and Sebastian Müller. 2019. Anomalies across the globe: Once public, no longer existent? Journal of Financial Economics 135: 213–30. [Google Scholar] [CrossRef]
- Jegadeesh, Narasimhan. 1990. Evidence of predictable behavior of security returns. Journal of Finance 45: 881–98. [Google Scholar] [CrossRef]
- Jegadeesh, Narasimhan, and Sheridan Titman. 1993. Returns to buying winners and selling losers: Implications for stock market efficiency. Journal of Finance 48: 65–91. [Google Scholar] [CrossRef]
- Jiang, Lei, Jinyu Liu, Lin Peng, and Baolian Wang. 2021. Investor Attention and Asset Pricing Anomalies. Review of Finance 26: 563–93. [Google Scholar] [CrossRef]
- Keim, Donald B. 1983. Size-related anomalies and stock return seasonality: Further empirical evidence. Journal of Financial Economics 12: 13–32. [Google Scholar] [CrossRef]
- Kim, Dongcheol, and Haejung Na. 2018. Investor Sentiment, Anomalies, and Macroeconomic Conditions. Asia-Pacific Journal of Financial Studies 47: 751–804. [Google Scholar] [CrossRef]
- Lee, Wayne Y., Christine X. Jiang, and Daniel C. Indro. 2002. Stock market volatility, excess returns, and the role of investor sentiment. Journal of Banking and Finance 26: 2277–99. [Google Scholar] [CrossRef]
- Loughran, Tim, and Jay R. Ritter. 1995. The new issues puzzle. Journal of Finance 50: 23–51. [Google Scholar] [CrossRef]
- Lu, Xiaomeng, Robert F. Stambaugh, and Yu Yuan. 2017. Anomalies Abroad: Beyond Data Mining (No. w23809). National Bureau of Economic Research. Available online: https://www.nber.org/papers/w23809 (accessed on 15 January 2020).
- Naranjo, Andy, M. Nimalendran, and Mike Ryngaert. 1998. Stock Returns, Dividend Yields, and Taxes. Journal of Finance 53: 2029–57. [Google Scholar] [CrossRef]
- Narayan, Paresh Kumar, and Susan Sunila Sharma. 2015. Does data frequency matter for the impact of forward premium on spot exchange rate? International Review of Financial Analysis 39: 45–53. [Google Scholar] [CrossRef]
- Narayan, Paresh Kumar, Huson Ali Ahmed, and Seema Narayan. 2015. Do momentum-based trading strategies work in the commodity futures markets? Journal of Futures Market 35: 868–91. [Google Scholar] [CrossRef]
- Reinganum, Marc R. 1983. The anomalous stock market behavior of small firms in January: Empirical tests for tax-loss selling effects. Journal of Financial Economics 12: 89–104. [Google Scholar] [CrossRef]
- Salur, Bayram Veli, and Cumhur Ekinci. 2023. Can Investor Sentiment Indicators Based on Fund Flows and Stock Intensity Predict Stock Returns? Unpublished Working Paper. Istanbul: Istanbul Technical University. [Google Scholar]
- Schwert, G. William. 2003. Anomalies and Market Efficiency. In Handbook of Economics of Finance. Edited by George Constantinides, Milton Harris and René M. Stulz. Amsterdam: Elsevier, pp. 939–74. [Google Scholar]
- Sloan, Richard G. 1996. Do stock prices fully reflect information in accruals and cash flows about future earnings? The Accounting Review 71: 289–315. [Google Scholar]
- Stambaugh, Robert F., and Yu Yuan. 2017. Mispricing Factors. The Review of Financial Studies 30: 1270–315. [Google Scholar] [CrossRef]
- Stambaugh, Robert F., Jianfeng Yu, and Yu Yuan. 2012. The short of it: Investor sentiment and anomalies. Journal of Financial Economics 104: 288–302. [Google Scholar] [CrossRef]
- Yang, Heejin, Doojin Ryu, and Doowon Ryu. 2017. Investor sentiment, asset returns and firm characteristics: Evidence from the Korean Stock Market. Investment Analysts Journal 46: 132–47. [Google Scholar] [CrossRef]
- Zaremba, Adam. 2016. Investor sentiment, limits on arbitrage, and the performance of cross-country stock market anomalies. Journal of Behavioral and Experimental Finance 9: 136–63. [Google Scholar] [CrossRef]
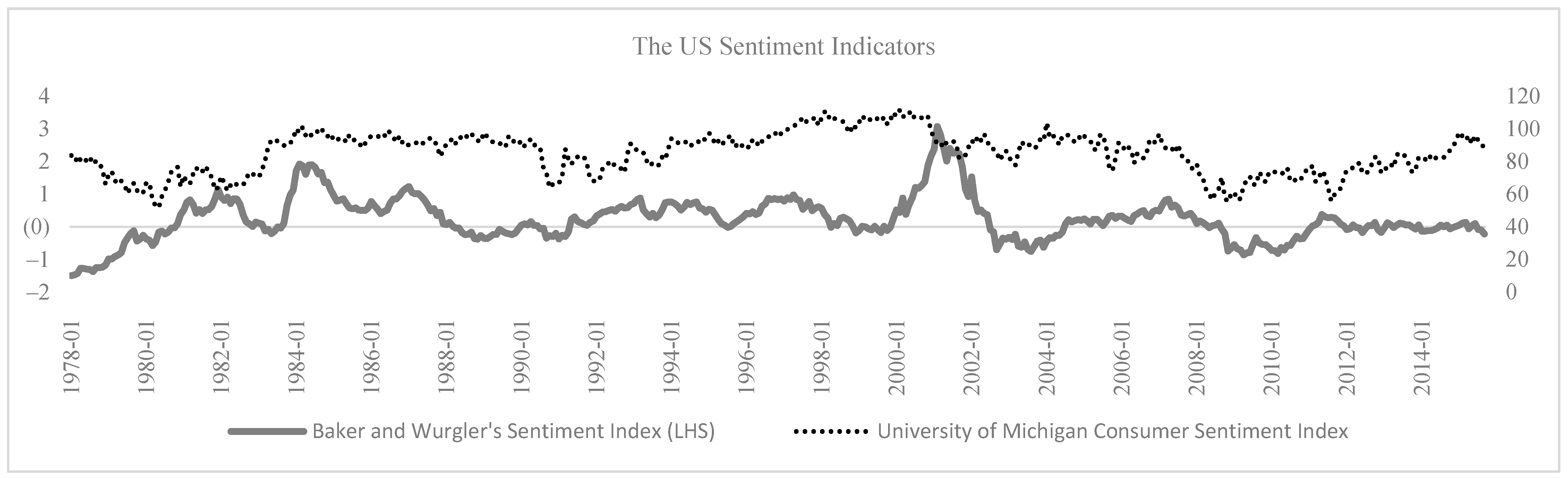
| Country/Region | Data Period | Nb of Months | Sentiment Indicators |
|---|---|---|---|
| US | January 1978–September 2015 | 453 | Baker and Wurgler, U Michigan |
| Japan | March 2004–October 2018 | 176 | Japanese CCI |
| Europe | July 1990–October 2018 | 340 | ESI |
| North America | November 1990–September 2015 | 299 | Baker and Wurgler, U Michigan |
| Global | November 1990–September 2015 | 299 | Baker and Wurgler, U Michigan |
| Anomaly | Reference | Strategy |
|---|---|---|
| Size | Banz (1981) | Decile 1–Decile 10 |
| Book-to-market | Fama and French (1992) | Decile 10–Decile 1 |
| Momentum | Jegadeesh and Titman (1993) | Decile 10–Decile 1 |
| Operating profitability | Fama and French (2016); Chen et al. (2011) | Decile 10–Decile 1 |
| Investments (asset growth) | Cooper et al. (2008) | Decile 1–Decile 10 |
| Short-term reversal | Jegadeesh (1990) | Decile 1–Decile 10 |
| Long-term reversal | De Bondt and Thaler (1987) | Decile 1–Decile 10 |
| Accruals | Sloan (1996) | Decile 1–Decile 10 |
| Cashflow/price | Hackel et al. (2000) | Decile 10–Decile 1 |
| Dividend yield | Naranjo et al. (1998) | Decile 10–Decile 1 |
| Earnings/price | Basu (1977, 1983) | Decile 10–Decile 1 |
| Market beta | Frazzini and Pedersen (2014) | Decile 1–Decile 10 |
| Net share issues | Loughran and Ritter (1995); Daniel and Titman (2006); Fama and French (2016) | Decile 1–Decile 10 |
| Residual variance | Ang et al. (2006) | Decile 1–Decile 10 |
| Variance | Ang et al. (2006) | Decile 1–Decile 10 |
| Pf 1 | Pf 2 | Pf 3 | Pf 4 | Pf 5 | Pf 6 | |
|---|---|---|---|---|---|---|
| Size | Small | Small | Small | Big | Big | Big |
| Book-to-market | Low | Mid | High | Low | Mid | High |
| Variable | Mean | Std Dev | Min | Max | N |
|---|---|---|---|---|---|
| Size | 0.2 | 4.6 | −21.0 | 32.1 | 453 |
| Book-to-market | 0.4 | 4.7 | −20.2 | 24.3 | 453 |
| Momentum | 1.2 | 7.5 | −45.6 | 26.2 | 453 |
| Short-term-reversal | 0.2 | 5.6 | −25.0 | 21.4 | 453 |
| Long-term-reversal | 0.2 | 4.8 | −13.9 | 23.7 | 453 |
| Accruals | −0.3 | 2.8 | −12.4 | 8.8 | 453 |
| Cashflow/price | 0.3 | 4.1 | −13.4 | 15.1 | 453 |
| Dividend yield | 0.0 | 5.5 | −22.1 | 26.4 | 453 |
| Earnings/price | 0.3 | 4.2 | −14.1 | 15.3 | 453 |
| Investments | −0.5 | 3.2 | −15.8 | 10.7 | 453 |
| Market beta | 0.1 | 6.6 | −24.0 | 25.0 | 453 |
| Net share issues | −0.5 | 3.1 | −10.9 | 11.9 | 453 |
| Operating profitability | 0.4 | 4.3 | −23.4 | 19.1 | 453 |
| Residual variance | −0.8 | 7.4 | −33.6 | 30.8 | 453 |
| Variance | −0.6 | 8.2 | −35.2 | 36.0 | 453 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Baker and Wurgler index | |||||||||||||||||
| 2 | Uni. Michigan | 0.36 *** | ||||||||||||||||
| 3 | Size | −0.06 | −0.03 | |||||||||||||||
| 4 | Book-to-market | 0.14 *** | 0.07 | 0.32 *** | ||||||||||||||
| 5 | Momentum | 0.06 | 0.05 | −0.01 | −0.27 *** | |||||||||||||
| 6 | Short-term reversal | 0.00 | 0.01 | 0.13 *** | 0.08 | −0.38 *** | ||||||||||||
| 7 | Long-term reversal | 0.05 | −0.04 | 0.41 *** | 0.56 *** | −0.20 *** | 0.09 * | |||||||||||
| 8 | Accruals | 0.07 | 0.09 ** | −0.15 *** | −0.05 | 0.13 *** | −0.02 | −0.06 | ||||||||||
| 9 | Cashflow/price | 0.14 *** | 0.03 | −0.02 | 0.58 *** | 0.00 | −0.10 ** | 0.19 *** | 0.06 | |||||||||
| 10 | Dividend yield | 0.17 *** | 0.04 | −0.13 *** | 0.31 *** | −0.16 *** | −0.06 | 0.28 *** | 0.05 | 0.42 *** | ||||||||
| 11 | Earnings/price | 0.17 *** | 0.01 | −0.05 | 0.58 *** | 0.00 | −0.05 | 0.22 *** | 0.02 | 0.84 *** | 0.45 *** | |||||||
| 12 | Investments | 0.13 *** | 0.07 | 0.16 *** | 0.44 *** | 0.10 ** | −0.09 ** | 0.46 *** | 0.14 *** | 0.35 *** | 0.34 *** | 0.35 *** | ||||||
| 13 | Market beta | 0.20 *** | 0.07 | −0.43 *** | 0.00 | 0.20 *** | −0.25 *** | −0.06 | 0.10 ** | 0.36 *** | 0.65 *** | 0.39 *** | 0.26 *** | |||||
| 14 | Net share issues | 0.21 *** | 0.08 * | −0.37 *** | −0.01 | 0.10 ** | −0.13 *** | −0.07 | 0.09 * | 0.28 *** | 0.35 *** | 0.24 *** | 0.36 *** | 0.56 *** | ||||
| 15 | Operating profitability | 0.20 *** | 0.02 | −0.51 *** | −0.21 *** | 0.18 *** | −0.17 *** | −0.28 *** | −0.04 | 0.22 *** | 0.27 *** | 0.26 *** | 0.05 | 0.60 *** | 0.53 *** | |||
| 16 | Residual variance | 0.22 *** | 0.02 | −0.60 *** | −0.08 | 0.25 *** | −0.24 *** | −0.13 *** | 0.08 | 0.30 *** | 0.48 *** | 0.38 *** | 0.25 *** | 0.81 *** | 0.59 *** | 0.73 *** | ||
| 17 | Variance | 0.22 *** | 0.00 | −0.50 *** | −0.07 | 0.23 *** | −0.23 *** | −0.11 ** | 0.06 | 0.32 *** | 0.53 *** | 0.40 *** | 0.23 *** | 0.84 *** | 0.60 *** | 0.71 *** | 0.95 *** |
| US | Japan | Europe | North America | Global | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anomaly No | Anomaly | FF3F | FF5F | FF3F | FF5F | FF3F | FF5F | FF3F | FF5F | FF3F | FF5F |
| 1 | Size | −0.11 | 0.05 | 0.16 * | 0.14 | −0.02 | 0.03 | 0.19 * | 0.36 *** | 0.22 *** | 0.25 *** |
| 0.24 | 0.61 | 0.07 | 0.11 | 0.82 | 0.67 | 0.08 | 0.00 | 0.01 | 0.00 | ||
| 2 | Book-to-market | −0.26 ** | −0.06 | 0.12 * | 0.11 | 0.26 *** | 0.12 ** | 0.29 *** | 0.15 ** | 0.30 *** | 0.18 *** |
| 0.02 | 0.57 | 0.10 | 0.13 | 0.00 | 0.01 | 0.00 | 0.03 | 0.00 | 0.00 | ||
| 3 | Momentum | 1.61 *** | 1.06 *** | 0.02 | −0.37 | 1.17 *** | 0.68 *** | 0.95 *** | 0.72 *** | 0.96 *** | 0.69 *** |
| 0.00 | 0.00 | 0.69 | 0.31 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | ||
| 4 | Investments | 0.33 ** | 0.08 | 0.11 | 0.05 | 0.26 *** | 0.11 ** | 0.59 *** | 0.36 *** | 0.36 *** | 0.22 *** |
| 0.01 | 0.47 | 0.37 | 0.35 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 5 | Operating profitability | 0.64 *** | −0.03 | 0.11 | 0.05 | 0.41 *** | −0.33 *** | 0.19 * | −0.22 *** | 0.14 | −0.17 *** |
| 0.00 | 0.73 | 0.27 | 0.42 | 0.00 | 0.00 | 0.09 | 0.00 | 0.04 ** | 0.00 | ||
| 6 | Short-term reversal | −0.11 | 0.04 | ||||||||
| 0.67 | 0.90 | ||||||||||
| 7 | Long-term reversal | −0.15 | −0.05 | ||||||||
| 0.43 | 0.76 | ||||||||||
| 8 | Accruals | 0.38 *** | 0.38 *** | ||||||||
| 0.00 | 0.00 | ||||||||||
| 9 | Cashflow/price | 0.10 | 0.00 | ||||||||
| 0.46 | 0.99 | ||||||||||
| 10 | Dividend yield | −0.02 | 0.02 | ||||||||
| 0.93 | 0.92 | ||||||||||
| 11 | Earnings/price | 0.06 | −0.05 | ||||||||
| 0.68 | 0.73 | ||||||||||
| 12 | Market beta | 0.47 ** | 0.10 | ||||||||
| 0.01 | 0.56 | ||||||||||
| 13 | Net share issues | 0.65 *** | 0.30 *** | ||||||||
| 0.00 | 0.01 | ||||||||||
| 14 | Residual variance | 1.27 *** | 0.52 *** | ||||||||
| 0.00 | 0.00 | ||||||||||
| 15 | Variance | 1.17 *** | 0.37 * | ||||||||
| 0.00 | 0.08 | ||||||||||
| US (Baker and Wurgler) | US (U Michigan) | Japan | Europe | North America | Global | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An No | Anomaly | FF3F | FF5F | FF3F | FF5F | FF3F | FF5F | FF3F | FF5F | FF3F | FF5F | FF3F | FF5F |
| 1 | Size | 1.53 *** | 1.69 *** | 0.06 *** | 0.06 *** | 0.05 | 0.05 | 0.09 ** | 0.10 ** | 0.07 ** | 0.06 ** | 0.00 | −0.00 |
| 0.01 | 0.01 | 0.01 | 0.01 | 0.35 | 0.33 | 0.04 | 0.03 | 0.01 | 0.02 | 0.99 | 0.95 | ||
| 2 | Book-to-market | 0.72 | 0.88 | 0.01 | 0.01 | −0.06 | −0.04 | 0.04 | 0.04 | 0.00 | 0.00 | −0.00 | 0.00 |
| 0.31 | 0.19 | 0.65 | 0.67 | 0.20 | 0.37 | 0.25 | 0.23 | 0.83 | 0.76 | 0.96 | 0.88 | ||
| 3 | Momentum | −0.43 | −0.73 | −0.18 ** | −0.18 ** | −0.36 ** | −0.23 | −0.04 | −0.06 | −0.18 *** | −0.18 *** | −0.12 ** | −0.11 ** |
| 0.84 | 0.72 | 0.04 | 0.03 | 0.03 | 0.11 | 0.75 | 0.62 | 0.00 | 0.00 | 0.01 | 0.02 | ||
| 4 | Investments | 1.32 * | 1.27 ** | −0.03 | −0.02 | −0.16 ** | 0.04 | −0.02 | 0.00 | 0.02 | 0.01 | −0.00 | 0.00 |
| 0.10 | 0.05 | 0.46 | 0.49 | 0.03 | 0.25 | 0.65 | 0.86 | 0.33 | 0.37 | 0.94 | 0.69 | ||
| 5 | Operating profitability | 1.55 | 1.01 * | 0.01 | 0.01 | 0.11 * | 0.05 | 0.00 | −0.02 | −0.00 | 0.01 | 0.01 | 0.01 |
| 0.12 | 0.09 | 0.76 | 0.78 | 0.08 | 0.19 | 0.95 | 0.50 | 0.96 | 0.39 | 0.69 | 0.33 | ||
| 6 | Short-term reversal | 1.03 | 1.10 | 0.00 | 0.01 | ||||||||
| 0.52 | 0.49 | 0.93 | 0.94 | ||||||||||
| 7 | Long-term reversal | 0.40 | 0.58 | −0.03 | −0.03 | ||||||||
| 0.73 | 0.58 | 0.47 | 0.47 | ||||||||||
| 8 | Accruals | 0.81 | 0.85 | −0.01 | −0.00 | ||||||||
| 0.32 | 0.29 | 0.88 | 0.99 | ||||||||||
| 9 | Cashflow/price | −0.12 | −0.22 | −0.00 | −0.01 | ||||||||
| 0.89 | 0.80 | 0.95 | 0.87 | ||||||||||
| 10 | Dividend yield | −0.23 | −0.17 | −0.03 | −0.02 | ||||||||
| 0.84 | 0.88 | 0.59 | 0.62 | ||||||||||
| 11 | Earnings/price | 0.38 | 0.27 | −0.01 | −0.01 | ||||||||
| 0.66 | 0.74 | 0.86 | 0.78 | ||||||||||
| 12 | Market beta | −0.46 | −0.69 | 0.02 | 0.03 | ||||||||
| 0.68 | 0.51 | 0.61 | 0.51 | ||||||||||
| 13 | Net share issues | 0.93 | 0.72 | −0.01 | −0.01 | ||||||||
| 0.23 | 0.30 | 0.79 | 0.85 | ||||||||||
| 14 | Residual variance | −0.22 | −0.76 | −0.06 | −0.05 | ||||||||
| 0.87 | 0.48 | 0.30 | 0.23 | ||||||||||
| 15 | Variance | 0.90 | 0.35 | −0.07 | −0.06 | ||||||||
| 0.54 | 0.78 | 0.27 | 0.23 | ||||||||||
| Pf 1 | Pf 2 | Pf 3 | Pf 4 | Pf 5 | Pf 6 | |
| Size | Small | Small | Small | Big | Big | Big |
| Book-to-market | Low | Mid | High | Low | Mid | High |
| Pf 1 | Pf 2 | Pf 3 | Pf 4 | Pf 5 | Pf 6 | |
| Size | Small | Small | Small | Big | Big | Big |
| Investments | Low | Mid | High | Low | Mid | High |
| Pf 1 | Pf 2 | Pf 3 | Pf 4 | Pf 5 | Pf 6 | |
| Size | Small | Small | Small | Big | Big | Big |
| Operating profitability | Low | Mid | High | Low | Mid | High |
| Pf 1 | Pf 2 | Pf 3 | Pf 4 | Pf 5 | Pf 6 | |
| Size | Small | Small | Small | Big | Big | Big |
| Momentum | Low | Mid | High | Low | Mid | High |
| Panel A: US | Equally Weighted | Controlling Size Factor | |||||||
| Sentiment | t-Stat | p-Value | Adj R-Square | Sentiment | t-Stat | p-Value | Adj R-Square | ||
| Book-to-market | 0.70 | 0.99 | 0.32 | 0.66 | When size is small | −0.31 | −0.53 | 0.60 | 0.67 |
| When size is big | 1.24 *** | 3.29 | 0.00 | 0.83 | |||||
| Investments | 1.99 ** | 2.41 | 0.02 | 0.21 | When size is small | 1.25 ** | 2.24 | 0.03 | 0.19 |
| When size is big | 0.83 | 1.64 | 0.10 | 0.52 | |||||
| Operating profitability | −1.94 * | −1.77 | 0.08 | 0.23 | When size is small | −1.54 ** | −1.98 | 0.05 | 0.17 |
| When size is big | 0.97 | 1.25 | 0.21 | 0.14 | |||||
| Momentum | −0.95 | −0.50 | 0.62 | 0.02 | When size is small | −0.26 | −0.20 | 0.84 | 0.02 |
| When size is big | −0.10 | −0.07 | 0.94 | 0.09 | |||||
| Panel B: Europe | Equally Weighted | Controlling Size Factor | |||||||
| Sentiment | t-Stat | p-Value | Adj R-Square | Sentiment | t-Stat | p-Value | Adj R-Square | ||
| Book-to-market | 0.04 | 1.14 | 0.25 | 0.84 | When size is small | 0.08 * | 1.65 | 0.10 | 0.59 |
| When size is big | −0.01 | −0.18 | 0.86 | 0.78 | |||||
| Investments | −0.02 | −0.46 | 0.65 | 0.49 | When size is small | 0.00 | 0.04 | 0.97 | 0.39 |
| When size is big | −0.04 | −0.78 | 0.44 | 0.43 | |||||
| Operating profitability | 0.00 | 0.06 | 0.95 | 0.11 | When size is small | −0.02 | −0.36 | 0.72 | 0.03 |
| When size is big | 0.02 | 0.43 | 0.67 | 0.21 | |||||
| Momentum | −0.04 | −0.32 | 0.74 | 0.12 | When size is small | −0.10 | −0.88 | 0.38 | 0.08 |
| When size is big | 0.02 | 0.16 | 0.88 | 0.14 | |||||
| Panel C: Japan | Equally Weighted | Controlling Size Factor | |||||||
| Sentiment | t-Stat | p-Value | Adj R-Square | Sentiment | t-Stat | p-Value | Adj R-Square | ||
| Book-to-market | −0.06 | −1.30 | 0.20 | 0.85 | When size is small | −0.05 | −0.50 | 0.62 | 0.60 |
| When size is big | −0.08 | −1.26 | 0.21 | 0.78 | |||||
| Investments | −0.16 ** | −2.17 | 0.03 | 0.34 | When size is small | −0.14 * | −1.73 | 0.09 | 0.34 |
| When size is big | −0.18 ** | −2.06 | 0.04 | 0.24 | |||||
| Operating profitability | 0.11 * | 1.77 | 0.08 | 0.35 | When size is small | 0.09 | 1.30 | 0.20 | 0.41 |
| When size is big | 0.14 * | 1.65 | 0.10 | 0.19 | |||||
| Momentum | −0.36 ** | −2.26 | 0.03 | 0.13 | When size is small | −0.32 * | −1.97 | 0.05 | 0.07 |
| When size is big | 0.40 ** | −2.20 | 0.03 | 0.14 | |||||
| Panel D: North America | Equally Weighted | Controlling Size Factor | |||||||
| Sentiment | t-Stat | p-Value | Adj R-Square | Sentiment | t-Stat | p-Value | Adj R-Square | ||
| Book-to-market | 0.27 | 0.63 | 0.53 | 0.89 | When size is small | −0.11 | −0.17 | 0.86 | 0.80 |
| When size is big | 0.64 | 1.41 | 0.16 | 0.87 | |||||
| Investments | 0.99 * | 1.68 | 0.09 | 0.62 | When size is small | 1.29 * | 1.84 | 0.07 | 0.35 |
| When size is big | 0.71 | 1.04 | 0.30 | 0.69 | |||||
| Operating profitability | −0.69 | −1.03 | 0.31 | 0.42 | When size is small | −2.22 *** | −2.94 | 0.00 | 0.31 |
| When size is big | 0.85 | 1.13 | 0.26 | 0.44 | |||||
| Momentum | 0.11 | 0.07 | 0.95 | 0.10 | When size is small | −0.08 | −0.05 | 0.96 | 0.04 |
| When size is big | 0.29 | 0.17 | 0.87 | 0.14 | |||||
| Panel E: Global Portfolios | Equally Weighted | Controlling Size Factor | |||||||
| Sentiment | t-Stat | p-Value | Adj R-Square | Sentiment | t-Stat | p-Value | Adj R-Square | ||
| Book-to-market | 0.02 | 0.06 | 0.95 | 0.90 | When size is small | −0.46 | −1.20 | 0.23 | 0.79 |
| When size is big | 0.49 | 1.42 | 0.16 | 0.85 | |||||
| Investments | 0.47 | 1.22 | 0.22 | 0.64 | When size is small | 0.50 | 1.22 | 0.22 | 0.43 |
| When size is big | 0.44 | 0.92 | 0.36 | 0.67 | |||||
| Operating profitability | −0.12 | −0.30 | 0.76 | 0.37 | When size is small | −0.99 ** | −2.22 | 0.03 | 0.25 |
| When size is big | 0.75 | 1.60 | 0.11 | 0.37 | |||||
| Momentum | 0.64 | 0.54 | 0.59 | 0.13 | When size is small | 0.74 | 0.66 | 0.51 | 0.08 |
| When size is big | 0.54 | 0.40 | 0.69 | 0.16 | |||||
| Equally Weighted | Combination Portfolio | |||||||
|---|---|---|---|---|---|---|---|---|
| Anomalies | Sentiment | t-Stat | p-Value | Adj R-Square | Sentiment | t-Stat | p-Value | Adj R-Square |
| Size | 2.84 *** | 3.16 | 0.00 | 0.59 | 1.37 ** | 2.22 | 0.03 | 0.59 |
| Book-to-market | 0.70 | 0.99 | 0.32 | 0.66 | 0.46 | 1.29 | 0.20 | 0.84 |
| Momentum | −0.95 | −0.50 | 0.62 | 0.02 | −0.18 | −0.14 | 0.89 | 0.05 |
| Investments | 1.99 ** | 2.41 | 0.02 | 0.21 | 1.04 ** | 2.47 | 0.01 | 0.45 |
| Operating profitability | −1.94 * | −1.77 | 0.08 | 0.23 | −0.29 | −0.41 | 0.68 | 0.16 |
| Equally Weighted | Value-Weighted | |||||||
|---|---|---|---|---|---|---|---|---|
| Anomalies | Sentiment | T-Stat | p-Value | Adj R-Square | Sentiment | t-Stat | p-Value | Adj R-Square |
| Size | 2.84 *** | 3.16 | 0.00 | 0.59 | 1.53 *** | 2.78 | 0.01 | 0.83 |
| Book-to-market | 0.70 | 0.99 | 0.32 | 0.66 | 0.72 | 1.02 | 0.31 | 0.74 |
| Momentum | −0.95 | −0.50 | 0.62 | 0.02 | −0.42 | −0.20 | 0.84 | 0.07 |
| Short-term reversal | 2.62 * | 1.76 | 0.08 | 0.07 | 1.02 | 0.65 | 0.52 | 0.09 |
| Long-term reversal | 2.64 ** | 2.24 | 0.03 | 0.23 | 0.40 | 0.35 | 0.73 | 0.34 |
| Accruals | 1.08 ** | 2.20 | 0.03 | 0.02 | 0.81 | 1.00 | 0.32 | 0.02 |
| Cashflow/price | 0.18 | 0.30 | 0.77 | 0.54 | −0.11 | −0.13 | 0.89 | 0.47 |
| Dividend yield | 0.57 | 0.67 | 0.50 | 0.46 | −0.23 | −0.20 | 0.84 | 0.53 |
| Earnings/price | 0.14 | 0.23 | 0.82 | 0.55 | 0.38 | 0.44 | 0.66 | 0.51 |
| Investments | 1.99 ** | 2.41 | 0.02 | 0.21 | 1.32 * | 1.66 | 0.10 | 0.29 |
| Market beta | −1.56 | −1.59 | 0.11 | 0.65 | −0.46 | −0.41 | 0.68 | 0.67 |
| Net share issues | −0.47 | −0.54 | 0.59 | 0.40 | 0.93 | 1.21 | 0.23 | 0.31 |
| Operating profitability | −1.94 * | −1.77 | 0.08 | 0.23 | 1.55 | 1.57 | 0.12 | 0.39 |
| Residual variance | −1.81 | −1.34 | 0.18 | 0.57 | −0.22 | −0.17 | 0.87 | 0.65 |
| Variance | −1.40 | −1.02 | 0.31 | 0.58 | 0.89 | 0.61 | 0.54 | 0.63 |
| Size Anomaly with Different Stock Characteristics | ||||
|---|---|---|---|---|
| Sentiment | t-Stat | p-Value | Adj R-Square | |
| When book-to-market is low | 2.39 *** | 2.96 | 0.00 | 0.52 |
| When book-to-market is medium | 0.87 | 1.55 | 0.12 | 0.62 |
| When book-to-market is high | 0.84 | 1.18 | 0.24 | 0.50 |
| When investment is low | 2.25 ** | 2.50 | 0.01 | 0.48 |
| When investment is medium | 0.54 | 1.11 | 0.27 | 0.62 |
| When investment is high | 1.84 *** | 2.80 | 0.00 | 0.47 |
| When operating profit is low | 2.73 *** | 3.08 | 0.00 | 0.38 |
| When operating is medium | 0.23 | 0.51 | 0.61 | 0.58 |
| When operating profit is high | 0.22 | 0.46 | 0.64 | 0.65 |
| When momentum is low | 1.32 | 1.27 | 0.21 | 0.36 |
| When momentum is medium | 0.65 | 1.38 | 0.17 | 0.60 |
| When momentum is high | 1.16 ** | 2.00 | 0.05 | 0.46 |
| Size anomaly | 2.84 *** | 3.16 | 0.00 | 0.59 |
| Parameter Estimate | t-Stat | p-Value | Adj R-Square | |
|---|---|---|---|---|
| Panel A: European Portfolios | ||||
| Size strategy return from book-to-market combination | 0.09 ** | 2.03 | 0.04 | 0.66 |
| Size strategy return from investment combination | 0.09 ** | 2.01 | 0.05 | 0.66 |
| Size strategy return from operating profit combination | 0.11 *** | 2.61 | 0.01 | 0.69 |
| Size strategy return from momentum combination | 0.08 * | 1.65 | 0.10 | 0.62 |
| Panel B: Japanese Portfolios | ||||
| Size strategy return from book-to-market combination | 0.05 | 0.93 | 0.35 | 0.75 |
| Size strategy return from investment combination | 0.04 | 0.77 | 0.44 | 0.75 |
| Size strategy return from operating profit combination | 0.04 | 0.67 | 0.51 | 0.74 |
| Size strategy return from momentum combination | 0.11 * | 1.96 | 0.05 | 0.67 |
| Panel C: North America Portfolios | ||||
| Size strategy return from book-to-market combination | 2.01 *** | 3.13 | 0.00 | 0.64 |
| Size strategy return from investment combination | 1.89 *** | 3.12 | 0.00 | 0.59 |
| Size strategy return from operating profit combination | 1.29 ** | 2.49 | 0.01 | 0.62 |
| Size strategy return from momentum combination | 1.73 *** | 2.69 | 0.01 | 0.51 |
| Panel D: Global Portfolios | ||||
| Size strategy return from book-to-market combination | 1.67 *** | 3.53 | 0.00 | 0.60 |
| Size strategy return from investment combination | 1.57 *** | 3.48 | 0.00 | 0.58 |
| Size strategy return from operating profit combination | 1.27 *** | 3.05 | 0.00 | 0.61 |
| Size strategy return from momentum combination | 1.43 *** | 2.99 | 0.00 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salur, B.V.; Ekinci, C. Anomalies and Investor Sentiment: International Evidence and the Impact of Size Factor. Int. J. Financial Stud. 2023, 11, 49. https://doi.org/10.3390/ijfs11010049
Salur BV, Ekinci C. Anomalies and Investor Sentiment: International Evidence and the Impact of Size Factor. International Journal of Financial Studies. 2023; 11(1):49. https://doi.org/10.3390/ijfs11010049
Chicago/Turabian StyleSalur, Bayram Veli, and Cumhur Ekinci. 2023. "Anomalies and Investor Sentiment: International Evidence and the Impact of Size Factor" International Journal of Financial Studies 11, no. 1: 49. https://doi.org/10.3390/ijfs11010049
APA StyleSalur, B. V., & Ekinci, C. (2023). Anomalies and Investor Sentiment: International Evidence and the Impact of Size Factor. International Journal of Financial Studies, 11(1), 49. https://doi.org/10.3390/ijfs11010049






