Abstract
We studied the Japanese dialect by calculating aggregated PMI Levenshtein distances among local Japanese dialects using data from 2400 locations and 141 items from the Linguistic Atlas of Japan Database (LAJDB). Through factor analysis, we found the latent linguistic variables underlying the aggregated distances. We found two factors, the first of which reflects a division into five groups, and the second of which reflects the long-standing East/West cultural contrast in mainland Japan, also known as the AB division. In the latter division, the eastern group includes the Okinawa islands. We paid special attention to the Tokyo dialect, which is associated with Standard Japanese. In a second factor analysis, only distances to the Tokyo dialect were considered. Although the patterns represented by the four factors vary, they consistently show that dialects geographically closer to Tokyo are more similar to the Tokyo dialect. Additionally, the first three factors reflected the similarity of the Hokkaido varieties to Tokyo’s local dialect. The results of the factor analyses were linked back to the individual variation patterns of the 141 items. A more precise analysis of Tokyo’s position within the Japanese dialect continuum revealed that it is situated within a region of local dialects characterized by relatively small average linguistic distances to other dialects. This area includes the more central area of mainland Japan and Hokkaido. When the influence of geographical distance is filtered out, only the local dialects of Hokkaido remain as dialects with the smallest average distance to other local dialects. Additionally, we observed that dialects geographically close to Tokyo are most closely related to it. However, when we again use distances that are controlled for geographical distance, the local dialects on Hokkaido stand out as being very related to the Tokyo dialect. This probably indicates that the Tokyo dialect has had a relatively large influence on Hokkaido.
1. Introduction
The great advantage of dialectometry is that it makes it possible to view dialect variation at an aggregated level. On the basis of large amounts of data, and without having to make subjective choices, an overall picture can be given of the dialect variation in a particular region.
Multiple Japanese dialectometric studies have been carried out. Here, we provide a brief overview of the studies that are most closely related to ours.
Inoue and Kasai (1989) counted the frequency of 82 standard Japanese word forms in 47 prefectures using data of 2400 localities from the Linguistic Atlas of Japan (LAJ). Per prefecture the frequencies were converted to percentages. Thus, a vector of 82 percentages was obtained per prefecture. Similarities among the prefectures were calculated by correlating their corresponding frequency vectors. On the basis of the correlation coefficients, the prefectures were classified into 3 main groups by cluster analysis, or at a more detailed level in 10 groups. Additionally, vectors of 47 frequencies per word form were derived and correlated to each other. On the basis of these correlations, the 82 word forms were classified by means of cluster analysis as well.
Kumagai (2016) measured similarities among 2400 Japanese local dialects using 55 items from the Linguistic Atlas of Japan Database (LAJDB). Linguistic similarity between any pair two localities was measured by calculating the number of linguistic features shared by the localities.
Huisman et al. (2019) and Huisman (2021) measured dialectometric distances among Japanese dialects using Levenshtein distance. They used a newly compiled “comparative dataset based on the 100-item Swadesh List”. Ward’s clustering was applied to the linguistic distances that were obtained.
Jeszenszky et al. (2019) calculated aggregated distances between 2400 Japanese local dialects based on 37 items. They used data from the Linguistic Atlas of Japan Database (LAJDB). Linguistic distances among the 2400 locations were calculated. The distance between two locations was calculated as the sum of the differences for each of the 37 variables divided by the number of variables with answers from both respondents. As for the responses, a distinction was made between categories and variants within categories adopting the categorization of the responses in the legends of the 37 variables in the LAJ maps. Categories represent different lexemes, and forms within categories are forms that are somehow related to each other. When the responses are variants within the same category, the difference counts only for 20%. The measurements were subjected to a three-dimensional multidimensional scaling procedure based on which a color continuum map was created. In order to explain the results, many explanatory factors were considered: geographic factors such as great-circle distance, travel distance and travel times, historical factors such as least cost paths, modeling contact before the industrial revolution, and a linguistic influence index based on settlement hierarchy. Additionally, the impact of administrative boundaries was tested.
Heeringa and Inoue (2023) measured distances among the same 2400 localities using the same dataset, but used PMI Levenshtein distance following Wieling et al. (2009) and Wieling (2012). Instead of (classical) multidimensional scaling, they used t-Distributed Stochastic Neighbor Embedding (t-SNE) (Van der Maaten & Hinton, 2008; Van der Maaten, 2014). Using Ward’s clustering, they obtained a map that divides the Japanese dialect area into five groups. This result agreed well with results from earlier studies.
Inoue and Yarimizu (2024) used data from the Grammar Atlas of Japanese Dialects (GAJ). By applying the Levenshtein distance to dialectal data, the authors assessed how phonetic variations correlate with factors such as geographical proximity and accessibility, particularly in relation to railway and walking distances. This approach enables them to explore the impact of transportation networks on language standardization and the distribution of dialectal features.
The studies of Inoue and Kasai (1989), Kumagai (2016), Huisman et al. (2019), Huisman (2021), Jeszenszky et al. (2019), Heeringa and Inoue (2023) and Inoue and Yarimizu (2024) provide a well-founded and clear overall picture of the Japanese dialect variation. But once this overall picture has been obtained, one may ask what the most important linguistic variables are that underlie this overall picture.
To gain insights into this, Nerbonne (2006) and Grieve (2014) used a statistical technique known as factor analysis. Factor analysis is one of the techniques that comprises the category of multivariate analyses. Multivariate analyses are statistical techniques that are used to analyze data in which multiple variables are examined simultaneously, and they make it possible to understand more complex relationships and patterns in the data. The goal of factor analysis is to discover the underlying structure of the data by grouping variables into factors. These factors often represent underlying concepts that are not directly measurable. The factors are also referred to as latent variables, which are variables that are not directly measurable or observable, but that do influence other observable variables.
Nerbonne (2006) used data from the Atlas of the Middle and South Atlantic States (LAMSAS), particularly data from the southern states in the USA. He applied factor analysis to the vowels that were involved in the aggregate analysis. His goal was “to show how to proceed from the aggregate characterizations of dialectometry to the identification of the linguistic factors responsible for the aggregate differences, e.g., the different pronunciations of a single vowel phoneme”.
Grieve (2014) analyzed the acoustic vowel data from the Atlas of North American English. He identifies common patterns of regional variation “by using a factor analysis to analyze correlations between linguistic variables that are first smoothed using a local spatial autocorrelation analysis”. He concluded that this approach “identifies clearer patterns of aggregated regional linguistic variation than the standard approach to dialectometry”.
Pickl and Pröll (2019) applied factor analysis to data from the Bavarian Dialect Database (1408 locations, 100 variables) and the Atlas zur deutschen Alltagssprache ‘Atlas of German Everyday Language’ (934 locations, 245 varieties). For each possible pair of locations, the strength of their linguistic correspondence, when viewed across all variants and aggregated, was quantified. The results of cluster analysis, multidimensional scaling and factor analysis were compared to each other. The results of multidimensional scaling and factor analysis were shown in color continuum maps. The authors found that factor analysis explained a higher percentage of variance in the original distances than multidimensional scaling.
In this paper, we continue the work of Heeringa and Inoue (2023). First, we apply their methodology to a significantly larger dataset. Second, we perform factor analysis on the newly obtained measurements to identify the latent linguistic variables underlying the overall pattern. In other words, instead of focusing on the geographical aspect of the data as Heeringa and Inoue (2023) did, we will concentrate on the linguistic background (or basis). Unlike Nerbonne (2006) and Pickl and Pröll (2019), our factor analyses are based on the correlations among individual distance matrices, each of which contains Levenshtein distances among the variants of a word item.
We apply two different approaches. In the first approach, aggregated distances among all 2400 local dialects are considered, i.e., (2400 × (2400−1))/2 = 2,878,800 distances. On the basis of these distances, Heeringa and Inoue (2023) obtained their area map. In the second approach, only distances to the dialect of Tokyo are considered, i.e., 2399 distances. On the basis of these distances, Heeringa and Inoue (2023) made a reference point map in which the distances between Tokyo and the other 2399 local dialects are shown. This second approach is interesting given the historical dominance of the dialect of Tokyo and its close relationship to the standard Japanese language.
Once we have found the latent linguistic variables, we want to go one step further by investigating which measured variables underlie each of the latent linguistic variables. Here, by measured variables, we mean the respective variables that represent the variation in each of the items. The basic idea of this paper is that the overall picture based on aggregated dialectometric distances is the starting point. In order to understand this picture well, we will then unravel it step by step, first by means of factor analysis in a number of latent linguistic variables, and then by unraveling the latent linguistic variables into the original measured variables.
Tokyo has had a significant impact on the Japanese dialects throughout the country. As the nation’s political, cultural, and economic center, Tokyo is associated with standard Japanese, which is based on the Tokyo dialect. Over time, this standard form of Japanese has influenced other dialects across the country, leading to a decrease in dialectal diversity in some regions (Inoue & Hanzawa, 2024). We aim to determine whether Tokyo has exerted a greater influence on other dialects than the remaining varieties. For each of the 2400 local dialects, we calculated the average linguistic distance to the remaining 2399 dialects. These linguistic distances were then compared with the corresponding geographic distances. A dialect was considered influential if its average linguistic distance to other dialects was smaller than expected based on geographic distance alone.
We answer the following research questions:
- Which latent linguistic variables underlie the dialectometrically determined overall picture of Japanese dialect variation?
- Which measured variables underlie the latent linguistic variables?
- Which latent linguistic variables underlie the part of the overall picture that represents the relationships of the local Japanese dialects to the Tokyo variety?
- Which measured variables underlie the latent linguistic variables when Tokyo is the reference point?
- Is Tokyo the most influential dialect?
- Which local dialects are particularly influenced by the Tokyo dialect?
This paper is structured as follows. In Section 2, we briefly describe the LAJDB, the Levenshtein distance and several statistical techniques for visualizing the dialectal variation; more extensively, we describe factor analysis. In Section 3, we apply factor analysis in order to determine the latent linguistic variables that determine the big picture of Japanese dialect variation, and we will have a closer look at the latent linguistic variables using representative words. In Section 4, we analyze the same data making use of Tokyo’s usage as a reference point. In Section 5, we study the influence of Tokyo on the Japanese dialects. We end with a discussion and conclusions in Section 6.
We would like to emphasize that although the methodology presented in this article has been applied to Japanese dialects, it can, in principle, be applied to any set of dialect data. We hope that this article will encourage many readers to carry this out.
2. Methods
In this section, we describe several techniques that are more extensively described in Heeringa and Inoue (2023). For the convenience of the reader, the techniques are only briefly described here. Factor analysis, however, is described in much more detail.
2.1. Data Source of Linguistic Atlas of Japan (LAJ)
We use data from the Linguistic Atlas of Japan Database (LAJDB). The LAJDB includes both the original survey card images and the geographical distribution data of word forms of the Linguistic Atlas of Japan (LAJ) in digital format. The Linguistic Atlas of Japan (LAJ) is based on a survey that was conducted from 1957 to 1965 by the National Language Research Institute (NLRI). In 2016, 119 items were completed, corresponding to 43% of the 285 surveyed items (Kumagai, 2016). We use data from the LAJDB, which is available at https://www.lajdb.org/lajdb_data/LAJDB_data_download001_v20180328_rev.html (accessed on 10 February 2025). On this site, data are found for 143 items. For each of the items, an Excel table is provided. For our analysis, we used the column 語形 ‘word form’. The transcriptions in that column represent word forms that may either lexically or phonemically vary. We excluded item Q258(-1), which shows only pronunciation differences in the HI sound of HIGE (mustache), and item Q280, which shows only variation in the realization of /-g-/ in kagami, ‘mirror’. Therefore, 141 items remained. The items are listed in Table 1. All items vary both lexically and phonetically. There are several romanization systems in Japanese, and the so-called Hepburn (Hebon) system based on English is widely used nowadays. However, a special system based on phonological description is used in LAJ. For example, “shi chi fu” in the Hepburn system is spelled as “si ci hu”. In this paper, the Hepburn system is used in explanatory sentences, and the special LAJ system is used in figures and tables.

Table 1.
The 141 items from the LAJDB.
In order to convert the transcriptions for IPA transcriptions, we performed a series of simple steps. First, we replaced CY with [tʃ], SY with [ʃ], ZY with [ʒ], CI with [tʃi], SI with [ʃi] and ZI with [ʒi]. Subsequently, the single C, S, Z and J were replaced with [ts], [s], [z] and [j], respectively. The remaining uppercase symbols were converted into lowercase. Thus, we obtained transcriptions that could be used for measuring linguistic distances between the Japanese varieties. Text between 〔 and 〕 or between << and >> was removed. When ( and ) were used in the transcriptions itself, we split them into multiple transcriptions. For example, IS(Y)ATUU is split into ISATUU and ISYATUU, which are in turn converted into IPA [isatuu] and [iʃatuu]. A double vowel indicates a long vowel, and a double consonant indicates a geminate consonant, which we have kept.
When using this material, we need to realize that the word forms in the LAJDB correspond with the word forms presented in the legends in the LAJ. These word forms are the representative forms of the classifications of the variations in the survey materials. Each word form in a legend has its phonetic variations recorded in the materials. Therefore, the relationship between a word form or linguistic form in a legend and the variations it represents is not straightforward.
2.2. Levenshtein Distance
Using the LAJDB, we measured aggregated normalized PMI (Pointwise Mutual Information) Levenshtein distances among 2400 localities on the basis of 141 items from the LAJDB. The Levenshtein distance was introduced into dialectology by Kessler (1995), who used this measure for the comparison of Irish Gaelic dialects.
The algorithm calculates the cost of changing one string of characters into another. In our case, the characters are phonetic segments. The basic idea of the Levenshtein distance is shown in the example in Figure 1. The realization of shimoyake, ‘frostbite’, in the dialect of Motoyoshi1 can be changed into the realization of the dialect of Setouchi2 by deleting [j] and [u], substituting [g] with [s], inserting [m] and [o], and substituting [g] with [k].

Figure 1.
Alignment of the realizations of shimoyake, ‘frostbite’, in the local dialects of Motoyoshi and Setouchi.
Since [jugijage] can be changed into [simojake] by six operations, the Levenshtein distance is equal to 6. Many different operation sequences map [jugijage] → [simojake], but the Levenshtein algorithm always gives the cost of the cheapest mapping.
Given that the cumulative maximal cost is 10, the normalized Levenshtein distance is 6/10, i.e., 0.6. This means that the two realizations of shimoyake in the local dialects of Motoyoshi and Setouchi differ from each other by 60%.
When we compare two dialects by comparing n word pairs with the Levenshtein distance, we need to calculate the aggregated distance. The principle of aggregation is illustrated by the example in Table 2. In this example, the sum of the word pair distances is equal to 4.13. Then, we calculate the aggregated distance by dividing the sum of the word pair distances by the number of word pair distances: 4.13/6 = 0.69 or 69%.

Table 2.
Normalized Levenshtein distances calculated between Motoyoshi and Setouchi on the basis of six word pairs. The aggregated distance is 4.13/6 = 0.69 or 69%.
We use an approach that was coined as VC-sensitive by Wieling et al. (2009), meaning that a vowel may only match a vowel, and a consonant may only match a consonant. However, we allow for some exceptions: the [w] and the [j] may also match vowels, and the [u] and the [i] may also match consonants. The schwa may match a sonorant (see Bolognesi & Heeringa, 2002; Heeringa, 2004).
For more details on the procedure and choices regarding the measurement methods, the reader is referred to Heeringa and Inoue (2023), pp. 7–10.
We use Pointwise Mutual Information (PMI) Levenshtein as a method for comparing dialects (Wieling et al., 2009; Wieling, 2012).3 This version of Levenshtein distance learns the segment distances by analyzing the alignments (such as in Figure 1) that underly the distance measurements. Segment distances are based on how often segments correspond to each other in the alignments. The more frequently segments correspond to each other in an alignment, the smaller the distance between those segments. These segment distances are used as operation weights, rather than the binary weights that we used in the example above. Thus, it is taken into account that, for example, [i] and [ɒ] are more distant to each other than [i] and [ɪ].
As we mentioned in Section 2.1, we used the transcriptions from the LAJDB Excel tables that were found in the column 語形 ‘word form’. Sometimes, multiple transcriptions were given per location and per item. When multiple transcriptions are given in one location and one transcription is given in another location for an item, then all transcriptions in the first location are compared to the transcription in the other location, and the average distance is calculated. When multiple transcriptions are found in both locations, pairs are formed so that the average distance of the pairs is minimized.4
In order to check whether the number of items in the dataset is large enough to extract a reliable signal, we calculate Cronbach’s α coefficient, which is derived from the inter-item correlation of the items (Cronbach (1951); see Heeringa (2004, pp. 170–173) too for more details). The coefficient ranges between zero and one. A higher value indicates greater consistency between the items.
2.3. Factor Analysis
We illustrate the use of factor analysis by means of a small example in which we measure Levenshtein distances among five local dialects in Japan and six items.5 The locations of the local dialects are shown in Figure 2. First, we calculate distances among the five localities for each item individually. The result is shown in Table 3, where we find 10 distance values for each item, 1 distance for each dialect pair. Then, we correlate the item variables to each other. The correlations are given in Table 4. These correlations are the basis for the factor analysis.
Before applying factor analysis, we need to check whether there are highly correlated variables, and if so, to remove them. According to Field et al. (2012), variables correlate highly when r > 0.8. High correlations we found for the pairs oyayubi/shimoyake (0.97), shimoyake/shiasatte (0.96) and shiasatte/oyayubi (0.87). Using an automatic procedure, the items shimoyake and shiasatte were removed and the item oyayubi was retained. Thus, four items were left over.
In order to determine whether the data can produce reliable and meaningful factors, we performed the Kaiser–Meyer–Olkin (KMO) test. The test gives a value between 0 and 1. If the value is higher than 0.5, the data is suitable for factor analysis. Unfortunately, we obtained a value of 0.389, which means that the data are not suitable for factor analysis.6
We applied Bartlett’s test in order to assess whether the observed correlations among variables are strong enough to justify the application of factor analysis. The outcome of the test is p < 0.01, which indicates that there are significant correlations among the variables, and factor analysis is likely appropriate.
We calculated the determinant of the correlation matrix, a single value calculated from the matrix elements that summarizes certain properties of the matrix. A very small determinant (close to zero) suggests multicollinearity, and a large determinant (≥0.00001) suggests that the variables are not overly correlated and are more likely to provide unique information. We found a determinant of 0.187.
In the final step before we conducted the factor analysis, we determined the number of factors to which the data should be reduced. In order to develop an initial idea for this, we created a scree plot (Cattell, 1966). The plot is shown in Figure 3. The eigenvalues correspond to the amount of variance in the data that is explained by each factor. In the plot, the last, large drop is found between the second and third factor. Therefore, the plot suggests that the number of factors is equal to two. A more solid way of determining the number of factors is running a parallel analysis (Horn, 1965). A parallel analysis helps to determine which factors explain more variance than would be expected by chance. The eigenvalues of the real data are compared to eigenvalues that were obtained on the basis of random datasets (e.g., 1000 or more) with the same number of variables and observations as the actual dataset. Factors where the actual eigenvalues are greater than the mean eigenvalues from the random data should be retained. We performed a parallel analysis using 1000 simulated random datasets. The outcome of this test confirms that two factors should be retained.
When running the factor analysis, we need to choose a method of factor rotation. We choose ‘oblimin’, since factors may correlate to each other to a certain extent (see Field et al., 2012, pp. 767, 788). In Table 5, the main results of the factor analysis are given, namely the factor loadings. The factor loadings represent the correlations between the observed variables and the extracted factors.
We classify the items so that each factor determines a group. Each item is assigned to the factor on which the loading is strongest. When determining this, we consider the absolute loadings. This is visualized in Figure 4, where the x-axis represents the loadings of the first factor, and the y-axis the loadings of the second factor. The items monomorai and oyayubi have the largest loadings on factor 1, while the items kooru and toomorokoshi have the largest absolute loadings on factor 2. The colors red and turquoise mark the respective groups.
Figure 2.
Locations of the five dialects that are used in the example in Section 2.3 and Section 2.4.7

Table 3.
Levenshtein distances among five local dialects in Japan for each of six items.
Table 3.
Levenshtein distances among five local dialects in Japan for each of six items.
| monomorai | oyayubi | shimoyake | shiasatte | kooru | toomorokoshi | ||
|---|---|---|---|---|---|---|---|
| Kesennuma | Akitakata | 0.86 | 0.29 | 0.25 | 0.40 | 0.67 | 0.63 |
| Kitahiroshima | Akitakata | 0.00 | 0.00 | 0.00 | 0.13 | 0.67 | 0.80 |
| Kitahiroshima | Kesennuma | 0.86 | 0.29 | 0.25 | 0.36 | 0.00 | 0.00 |
| Motoyoshi | Akitakata | 0.86 | 0.29 | 0.25 | 0.40 | 0.63 | 0.63 |
| Motoyoshi | Kesennuma | 0.00 | 0.00 | 0.00 | 0.00 | 0.63 | 0.43 |
| Motoyoshi | Kitahiroshima | 0.86 | 0.29 | 0.25 | 0.36 | 0.63 | 0.89 |
| Setouchi | Akitakata | 0.71 | 0.43 | 0.50 | 0.80 | 0.50 | 0.63 |
| Setouchi | Kesennuma | 0.80 | 0.71 | 0.60 | 0.70 | 0.88 | 0.29 |
| Setouchi | Kitahiroshima | 0.71 | 0.43 | 0.50 | 0.78 | 0.88 | 0.90 |
| Setouchi | Motoyoshi | 0.80 | 0.71 | 0.60 | 0.70 | 0.89 | 0.43 |

Table 4.
Correlations among the six items.
Table 4.
Correlations among the six items.
| oyayubi | shimoyake | shiasatte | kooru | toomorokoshi | |
|---|---|---|---|---|---|
| monomorai | 0.69 | 0.67 | 0.66 | −0.08 | 0.09 |
| oyayubi | 0.97 | 0.87 | 0.39 | −0.41 | |
| shimoyake | 0.96 | 0.37 | −0.30 | ||
| shiasatte | 0.32 | −0.11 | |||
| kooru | −0.46 |
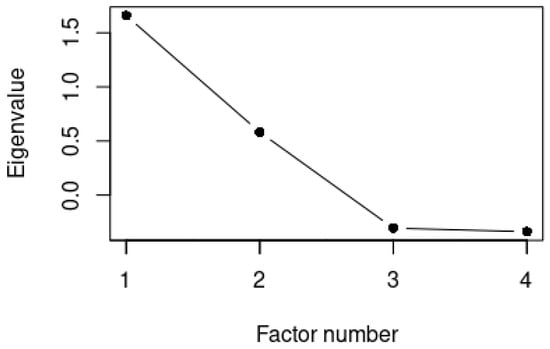
Figure 3.
Scree plot on the basis of four variables.

Table 5.
Factor loadings obtained by factor analysis.
Table 5.
Factor loadings obtained by factor analysis.
| Factor 1 | Factor 2 | |
|---|---|---|
| monomorai | 0.974 | −0.165 |
| oyayubi | 0.704 | 0.571 |
| kooru | −0.114 | 0.666 |
| toomorokoshi | 0.133 | −0.720 |
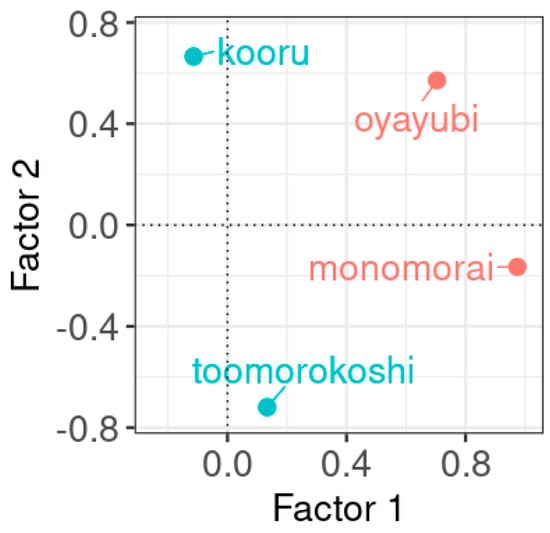
Figure 4.
The items in red (monomorai and oyayubi) load mainly on factor 1, and the items in turquoise (kooru and toomorokoshi) load mainly on factor 2.
When correlating items, we should pay special attention to the large number of missing values in the LAJDB data. If there is a large number of missing values, imputations might lead to unreliable results because there is not enough observed data to accurately estimate the missing values. Therefore, we decided not to impute missing values, but rather correlate any pair of items only on the basis of the locations that they share.
Another technique that proceeds from a matrix of correlations among variables, and based on these, aims to simplify the structure of the variables, is principal component analysis. Although both factor analysis and principal component analysis have the same goal, they are different. We prefer to use factor analysis. Nerbonne (2006) writes that
a factor analysis only models patterns of variation that are shared by the variables in the dataset, whereas a principal component analysis model totals variation, including variation that is unique to a single variable. A factor analysis is thus the more appropriate technique for identifying common patterns of regional variation and is also less likely to be affected by noise.
2.4. Finding Dialect Areas
We apply hierarchical cluster analysis to the linguistic distances among the 2400 localities. The result is a hierarchically structured tree or dendrogram, where the leaves are the dialects (Jain & Dubes, 1988). The branches in a dendrogram represent the distances between dialects and clusters. Given the aggregated distances in Table 6, we obtain the dendrogram shown in Figure 5.

Table 6.
Aggregated Levenshtein distances among five local Japanese dialects.
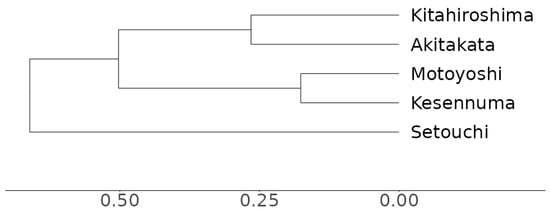
Figure 5.
Dendrogram obtained on the basis of the distance matrix in Table 6 using hierarchical agglomerative cluster analysis.
Areas can be derived from the dendrogram by drawing a vertical line somewhere in the dendrogram and counting the horizontal lines matching it. Local dialects connecting to the matching horizontal lines will then belong to the same cluster (or group or area).
The vertical line should be drawn between the two successive nodes that are most distant to each other. In Figure 6, the numbers reflect the order in which the clusters were generated. Therefore, the pairs of successive nodes are nodes 1 and 2, nodes 2 and 3, and nodes 3 and 4. We find the largest distance between successive nodes 2 and 3. The vertical line between those two nodes intersects with two horizontal lines that connect with two groups, which are the optimal groups.8 See Heeringa and Inoue (2023) for a more detailed description of this procedure.
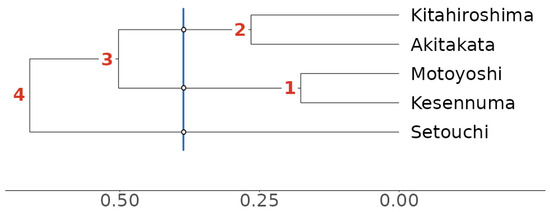
Figure 6.
The largest distance between two successive nodes is between nodes 2 and 3. A vertical line is drawn in the middle of these two nodes and intersects with two horizontal lines that connect with two groups.
When the dialect areas that are represented by the cluster groups are drawn in a map, each area takes a unique color. The way colors are assigned to the areas is described in Section 2.6 of the paper of Heeringa and Inoue (2023).
There are different clustering methods. We use a method known as Ward’s method (Ward, 1963). This method minimizes the variance in the clusters (Ward, 1963). Gere (2023) extensively validated several clustering methods, and concluded that using Ward’s method seems to be a safe and reasonable choice, producing clusters that were most significantly different from each other.
2.5. Visualizing the Dialect Landscape from the Perspective of a Reference Point
Reference point maps were introduced by Goebl (1981) and show the similarity of or difference in local dialects compared to a reference point. We adopted the approach of Goebl (2002), who used a rainbow scheme—red, orange, yellow, green, blue—where dialects most similar to the reference point are red, and the most distant dialects are blue.
Reference point maps with Tokyo will be analyzed in Section 4.
3. Unraveling the Big Picture of LAJ by Factor Analysis of Levenshtein Distance
The factor analyses were based on aggregated PMI Levenshtein distances calculated across 2400 local dialects. We found a Cronbach’s α value of 0.9647. A widely accepted threshold is 0.70 (Nunnally, 1978; Nunnally & Bernstein, 1994). That fact that our Cronbach’s α value is higher than 0.70 indicates that 141 items are enough to provide reliable results (see Section 2.2). When applying Ward’s cluster to the distance measures, we obtained a division of five natural groups. The result is shown in Figure 7. This result is consistent with that from the previous analysis of Inoue (2001) and Heeringa and Inoue (2023). It also agrees with the findings of Jeszenszky et al. (2019, p. 6).
Figure 7.
Natural groups obtained on the basis of aggregated PMI Levenshtein distances calculated on the basis of 141 items using Ward’s clustering. The five groups represent five areas that are distinguished by five different colors. Note that Hokkaido, located in the far north, is clustered with the Eastern dialect group.
However, the boundaries are different. First, the east–west boundary is not the boundary of the Japanese Alps, but the Shiga–Gifu prefectural border (Sekigahara). Second, the Noto Peninsula is now in the same cluster as the Kinki–Chugoku–Shikoku region as an enclave. This phenomenon was pointed out by Fujiwara (1990) based on grammar, phonology, etc., as a Japan Sea branch, and was also advocated by other researchers. Whether the special distribution of a small number of items had an effect or not requires further scrutiny.
3.1. Finding the Latent Linguistic Variables of Word Forms and Geography
We applied the factor analysis as described in Section 2.3. Given 141 items and 2400 local Japanese dialects, the number of distance values per item is maximally (2400 × (2400-1))/2 = 2,878,800 distances. With each item represented as a vector of maximally 2,878,800 distances, the items are correlated to each other by correlating their respective distance vectors. As we mentioned in Section 2.3, there are missing values. Therefore, two items were correlated on the basis of the shared locations.
There were two highly correlated items, i.e., items with r > 0.8, which we removed.
The value of Kaiser–Meyer–Olkin (KMO) statistics was initially lower than 0.5, namely 0.058, which is unacceptable. Although a KMO statistic of at least 0.5 is considered acceptable, we aimed for a KMO statistics of at least 0.7, which is labeled as ‘middling’ in this test. In 10 steps, we removed the item with the lowest individual KMO statistics and obtained a KMO value of 0.777. Thus, 129 items were left over.
Bartlett’s test of sphericity was highly significant with p < 0.001, indicating that there are some relationships between the variables.
The determinant score was initially 4.58339 × 10−26, which is smaller than 0.00001, and displays that there is multicollinearity. In each of the 55 steps, we determined which item lowered the determinant score most, and removed it. Thus, we obtained an acceptable determinant score that was larger than 0.00001, namely 0.0000107. Thus, 74 items were left over.
For this set, we again calculated the KMO statistic, which was 0.92 (labeled as ‘marvelous’ in the test), and again conducted Bartlett’s test of sphericity, with the result still being highly significant (p < 0.001).
In order to find the number of factors, we ran a parallel analysis which suggested 24 factors. In Figure 8, a scree plot is included which shows the eigenvalues of the factors. The decrease in eigenvalues between two successive factors is relatively larger up to the third factor than from the third factor onwards. Therefore, we will focus on the first two factors. The loadings of the first three factors are shown in Figure 9. To provide a clear picture, only items with a loading of 0.4 or higher are shown.
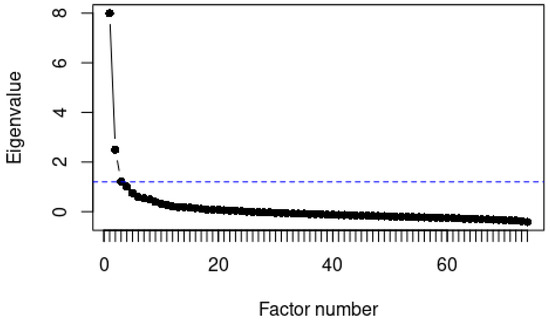
Figure 8.
Scree plot on the basis of 67 variables. The drop in eigenvalues between successive factors is relatively greater up to the third factor—whose corresponding dot is intersected by the dash line—than it is from the third factor onward.
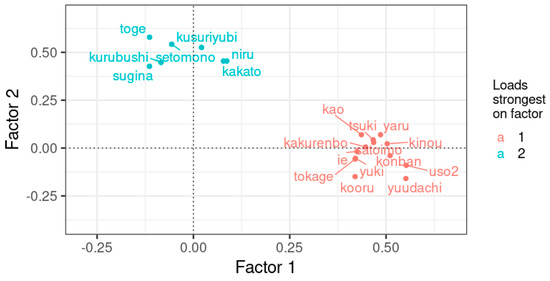
Figure 9.
Factor loadings of factor 1 versus factor loadings for factor 2. Only items with a loading of 0.4 or higher are shown.
We classified the items according to the factor on which they loaded the most strongly. There were 47 items that loaded most strongly on the first factor, and 27 items that loaded most strongly on the second factor. For each of the two item groups, the aggregated PMI Levenshtein distances were calculated on the basis of the items in the group.9 Subsequently, with Ward’s clustering, the natural dialect groups were found (see Section 2.4). The results are shown in Figure 10.
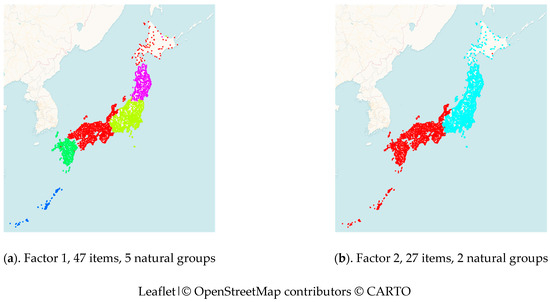
Figure 10.
Natural groups obtained on the basis of aggregated PMI Levenshtein distances calculated for each of the two item groups (a,b). The areas that were found for each of the two factors are distinguished by different colors. See Section 3.1 for more details.
In Figure 10a (factor 1), we find five groups which are almost the same as those in Figure 7. However, the boundaries are different. First, the east–west boundary is not the western boundary of the Japanese Alps. Second, in addition to the Noto Peninsula, Sado Island is in the same cluster as Kinki, Chugoku, and Shikoku. Note also that Hokkaido is clustered with the dialect area that is colored in red southwest of the Japanese mainland.
Figure 10b (factor 2) apparently looks like a simplification of the map in Figure 10a. However, note that Hokkaido is clustered with the northeastern group, and the Okinawa islands are clustered together with the southwestern dialects on the Japanese mainland. Notably, the latter finding is a trend that did not emerge in earlier analyses and requires further scrutiny as an issue in the future.
In summary, the two and five divisions of Japanese dialects are the same as before. Since we increased the data, we were able to pick up distributional trends that were previously noted only by some researchers.
3.2. Examining the Original Variables of Word Forms
In Section 3.1, for each factor, we showed the geographical pattern that we obtained when calculating distances on the basis of the items that loaded most strongly on that factor. In Figure 10, we found that Factor 1 suggests a division into five groups and Factor 2 a division into a northeastern group (including Hokkaido) and a southwestern group (including the Okinawa Islands).
In this section, we examine the original variables—each variable representing the dialectal variation in an item (word)—that underlie the factors. We will not discuss all 74 variables, but we will focus on the two variables that load the most strongly on any of the two factors. Items with their factor loadings are shown in Figure 7. In Table 7, the items with their loadings are given per factor. For each factor, we focus on the two items with the highest loadings. For Factor 1, we focus on uso (2) and yuudachi. For Factor 2, we focus on toge and setomono.

Table 7.
Factor loadings of items with loadings larger than 0.4. For each item, the highest loading is shown in bold.
Area maps of these four items (words) are shown in Figure 11. For practical reasons, these maps were obtained on the basis of a random subset of 400 locations. Each map was created as follows. First, PMI Levenshtein distances were calculated among the maximally 2400 realizations of the item. Then, Ward’s clustering was applied and the number of natural groups was determined. Then, within each group, we found the realization that had the smallest average distance to all other realizations in the group. This realization was considered the most representative realization and was used as label in the legend.10 The four maps are described in turn.
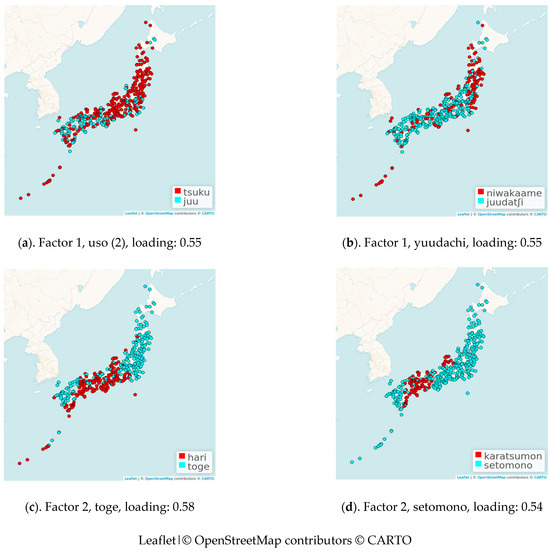
Figure 11.
Area maps for the two items that load the most strongly on the first factor (a,b), and the two items that load the most strongly on the second factor (c,d). The areas represent the natural groups found with Ward’s clustering. For each group, the most representative form is given.
Maps 11a and b show the distribution of the realizations of the items uso (2) and yuudachi, which load the most strongly on Factor 1. In Map 11a, we find that the red form [tsuku] runs from north to south. The blue form [juu] is predominantly found in the southwestern part of the Japanese mainland. In Map 11b, the red form [niwakaame] is mainly found in the northeast and on the Okinawa islands; in the other areas, the blue form [juudatʃi] is dominant, in Chugoku–Shikoku and Kanto.
The distinction of a southwestern part, a northeastern part and the Okinawa islands partly explains the division into five groups in Figure 7. But we have to realize that this division into five groups emerged from more than two items, and that the pattern that was obtained on the basis of the aggregate over multiple items does not necessarily correspond exactly with the patterns of the individual items.
Maps 11c and d show the distribution of the realizations of the items toge and setomono. In Map 11c, we see the red form [hari] mainly the south and the blue form [toge] mainly in the north. In Map 11d, we see that the red form [karatsumon] is distributed in Chugoku–Shikoku and Noto Peninsula, while the blue form [setomono] (or a variant of this) is distributed almost nationwide. Seto is the ceramics production area of Aichi Prefecture in central Japan, and Karatsu is the ceramics production area of Kyushu in western Japan. This is a special distribution pattern and is related to the actual production, sales and transportation routes of ceramics.
4. Unraveling the Latent Linguistic Variables with Tokyo as a Reference Point
4.1. Finding the Latent Linguistic Variables with Tokyo as a Reference Point
While we analyzed aggregated distances among all pairs of local dialects in Section 3.1, we focus on analyzing the distances between the local dialects and Tokyo in this section. In other words, in Section 3.1, we analyzed the big picture, and in this section, we analyze only the part of the big picture that represents the relationships between the local dialects and Tokyo.
In Figure 12, the Japanese local dialects are compared to the dialect spoken in or close to Tokyo. Distances are visualized by colors according to a rainbow scheme. Red means that a local dialect is identical to the dialect of Tokyo, and darker blue means that a local dialect is maximally different from the dialect of Tokyo.11
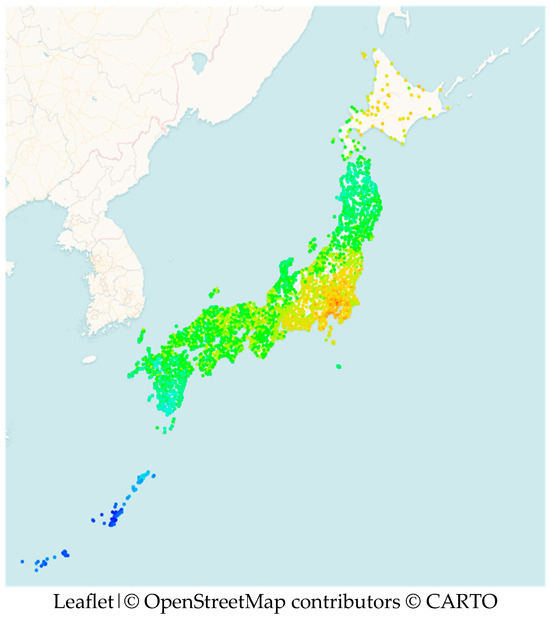
Figure 12.
Reference point map showing the distances of 2399 local Japanese dialects relative to point no. 5698.69 (Tokyo). Distances are visualized by colors according to a rainbow scheme. Red means that the local dialect is identical to the dialect of Tokyo, and darker blue means that the local dialect is maximally different from the dialect of Tokyo. Note the reddish dots near Tokyo and the (darker) blue dots on the Ryukyu Islands to the southwest.
The result aligns with previous analyses, including those conducted by Inoue (2001) and Heeringa and Inoue (2023). Figure 12 effectively captures continuity. The findings are reliable and provide a representative reflection of Japan as a whole. Tokyo exhibits similarities with the Kanto region, while analogous linguistic patterns are distributed along the Pacific side. Furthermore, linguistic distance closely corresponds to geographical distance, with noticeable distinctions at the country’s borders. Also note the similarity of the Hokkaido varieties to the local dialect of Tokyo.
For each of the 141 items and 2399 locations, distances are calculated with respect to Tokyo (no. 5698.69, Nishihara-cho, Bunkyo-ku in the LAJDB, a typical Yamanote Uptown locality). The number of distance values per item is maximally 2399. With each item represented as a vector of maximally 2399 distances, the items are correlated to each other by correlating their respective distance vectors. As we mentioned in Section 2.3, there are missing values. Therefore, two items are correlated on the basis of their shared locations.
There were 46 items that were not recorded in Tokyo (see Table 1). They were left out of the analysis, and 95 items were left over. There were two highly correlated items, i.e., items with r > 0.8, which we removed.
The value of the Kaiser–Meyer–Olkin (KMO) statistic was initially low, namely 0.532, which is labeled as ‘miserable’ by the test. Although a KMO statistic of at least 0.5 is considered acceptable, we aimed for a KMO statistic of at least 0.7, which is labeled as ‘middling’ in this test. In one step, we removed the item with the lowest individual KMO statistics and obtained a KMO value of 0.816. Thus, 92 items were left over.
Bartlett’s test of sphericity was highly significant, at p < 0.001, indicating that there are some relationships between the variables.
The determinant score was initially 4.089197 × 10−25, which is smaller than 0.00001, and displays that there is multicollinearity. In each of 43 steps, we determined which item lowered the determinant score most, and removed it. Thus, we obtained an acceptable determinant score that was larger than 0.00001, namely 0.00001039809. Thus, 49 items were left over.
For this set, we again calculated the KMO statistic, which was 0.85 (labeled as ‘meritorious’ in the test), and again conducted Bartlett’s test of sphericity, with the result of the latter still being highly significant (p < 0.001).
In order to find the number of factors, we ran a parallel analysis which suggested 16 factors. In Figure 13, a scree plot is included which shows the eigenvalues of the factors. The decrease in eigenvalues between two successive factors is relatively larger up to the fifth factor than from the fifth factor onwards. Therefore, we will focus on the first four factors. The loadings of the first four factors are shown in Figure 14, Figure 15 and Figure 16. To provide a clear picture, only items (words) with a loading of 0.4 or higher are shown.
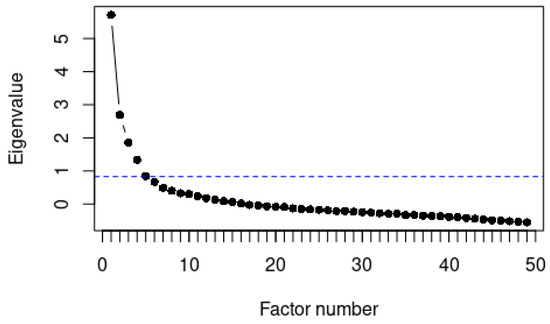
Figure 13.
Scree plot on the basis of 49 variables, where each variable includes distances to Tokyo. The drop in eigenvalues between successive factors is relatively greater up to the fifth factor—whose corresponding dot is intersected by the dash line—than it is from the fifth factor onward.
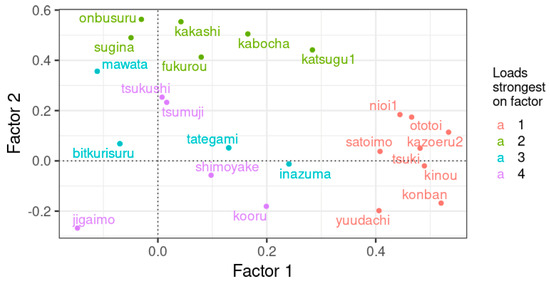
Figure 14.
Factor loadings of factor 1 versus factor loadings for factor 2. Only items with a loading of 0.4 or higher are shown.
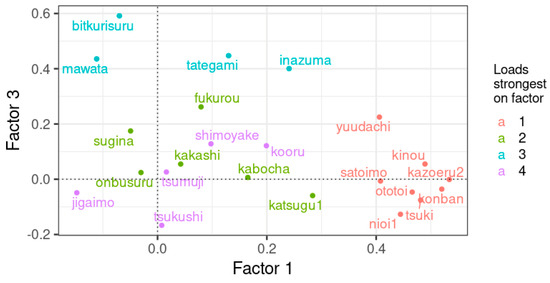
Figure 15.
Factor loadings of factor 1 versus factor loadings for factor 3. Only items with a loading of 0.4 or higher are shown.
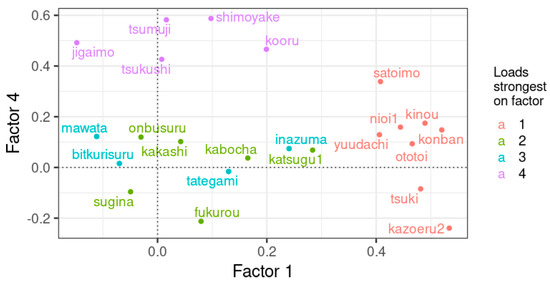
Figure 16.
Factor loadings of factor 1 versus factor loadings for factor 4. Only items with a loading of 0.4 or higher are shown.
We classified the items according to the factor on which they load the most strongly. There were 18 items that loaded the most strongly on the first factor, 8 items that loaded the most strongly on the second factor, 14 items that loaded the strongly on the third factor, and 9 items that loaded the most strongly on the fourth factor. For each of the four item groups, the aggregated PMI Levenshtein distances with respect to Tokyo were calculated on the basis of the items in the group.12 Subsequently, a reference point map using a rainbow scheme (see Section 2.5) was created for each item group. The results are shown in Figure 17.
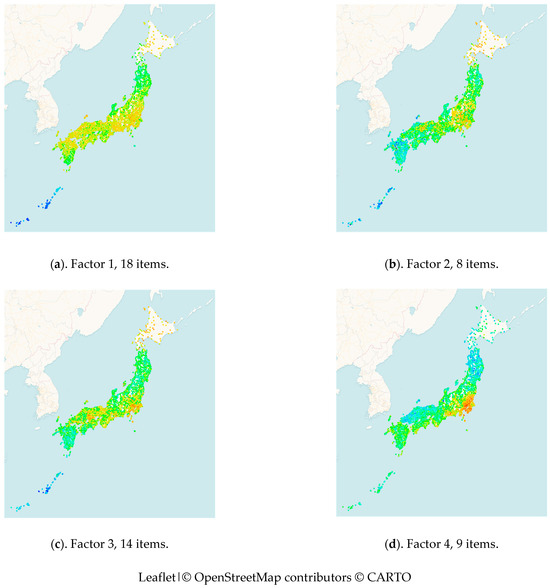
Figure 17.
Reference point maps obtained on the basis of aggregated PMI Levenshtein distances. Distances were calculated with respect to Tokyo for each of the four item groups (a–d).
The maps in Figure 17 show four different patterns. In Figure 17a, we find the broad area of Kanto, central Chugoku, to be similar to Tokyo. Kyushu, Tohoku and central Kinki are less similar to Tokyo. Okinawa is completely different. This map provides a good overall representation of Japan, closely matching geographical distances and aligning with common sense expectations.
Figure 17b shows that the dialect in the area of Kanto and the area north of it is similar to the Tokyo dialect. The dialects in the area close to the frontier and central Kinki area less similar. Enclaves exist in the Chugoku region, which have not been focused on so far. These should be further investigated in the future. The dialect in the southernmost part of the mainland is more distant to that in Tokyo than to that in any of the other maps in Figure 17.
Figure 17c resembles Figure 17a but more explicitly highlights two centers of locations that are linguistically close to the Tokyo dialect. Local dialects related to Tokyo are found in Kanto, Chubu, and Chugoku, and some related dialect areas are found close to the frontier and in the Central Kinki region. Enclaves in the Chugoku region that are linguistically similar to the Tokyo dialect have not yet been a focus and should be thoroughly investigated in future research.
In Figure 17d, we find a dialect in a remarkable large area in Kanto (east side and along Tokaido Highway) which is similar to the local dialect of Tokyo. This has been observed in the past and fits with common sense. Figure 17d is the only figure in which Hokkaido’s local dialects appear far from that of Tokyo, while the Okinawa island varieties are depicted as less distant.
4.2. Examining the Original Variables with Tokyo as a Reference Point
In Section 4.1, for each factor, we showed the geographical pattern that we obtained when calculating distances on the basis of the items that loaded the most strongly on that factor. The distances were measured between the Tokyo dialect and each of the 2399 local dialects. The patterns for each factor are shown in reference point maps in Figure 17. All four maps show that the most closely related varieties are found close to Tokyo. In Figure 17a, the mainland area that looks relatively close to Tokyo is largest. In Figure 17b, the southernmost part of the mainland is more distant to Tokyo than in any of the other maps in Figure 17. Figure 17c resembles Figure 17a but more explicitly highlights two centers of locations that are linguistically close to the Tokyo dialect. Figure 17d is the only figure in which the local dialects of Hokkaido are shown at a large distance from Tokyo and the varieties on the Okinawa islands are shown as less distant.
In this section, we examine the original variables—each variable representing the dialectal variation in an item (word)—that underlie the factors. For each factor, we examine the two items that load the most strongly on that factor. Items with their factor loadings are shown in the graphs in Figure 14, Figure 15 and Figure 16. In Table 8, the items, with their loadings, are given per factor. For Factor 1, we focus on kazoeru (2) and konban. For Factor 2, we focus on onbusuru and kakashi. For Factor 3, we focus on bikkurisuru (2) and tategami. For Factor 4, we focus on shimoyake and tsumuji.

Table 8.
Factor loadings of items with loadings larger than 0.4. For each item, the highest loading is shown in bold.
Area maps of these eight items are shown in Figure 18 and Figure 19. For practical reasons, these maps are obtained on the basis of a random subset of 400 locations plus Tokyo. Each of the maps was created as follows. First, PMI Levenshtein distances were calculated among the maximally 400 realizations of the item. Then, Ward’s clustering was applied and the number of natural groups was determined. Then, within each group, we found the realization that had the smallest average distance to all other realizations in the group. This realization was considered the most representative realization and was used as the label in the legend. Then, the average distance of the realizations in the group to the realization of Tokyo was calculated and projected on the rainbow color scheme. Then, the rainbow color that was found was assigned to all the locations within the group.13
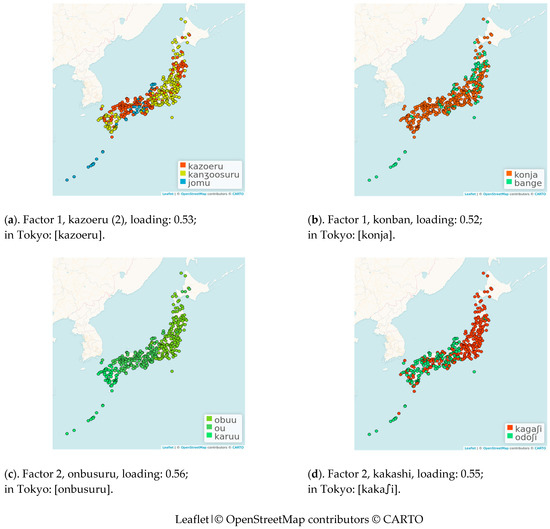
Figure 18.
Area maps for the two items that load the most strongly on the first factor (a,b), and the two items that load the most strongly on the second factor (c,d). The areas represent the natural groups found with Ward’s clustering. For each group, the most representative form is given. The colors of the groups represent the average distances to Tokyo according to a rainbow scheme. Red means that the dialect in that area is identical to the dialect of Tokyo, and darker blue means that the dialect in that area is maximally different from the dialect of Tokyo.
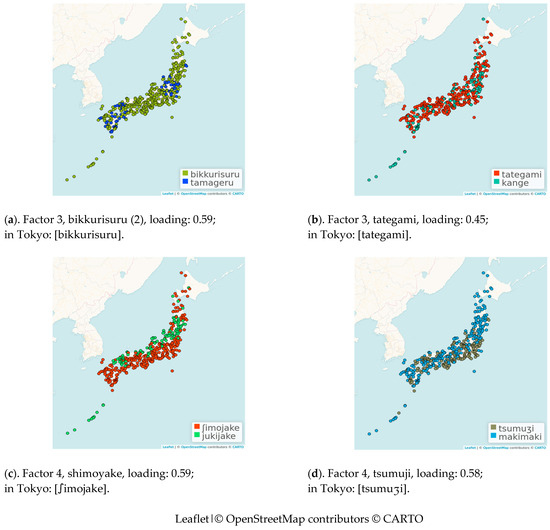
Figure 19.
Area maps for the two items that load the most strongly on the third factor (a,b), and the two items that load the most strongly on the fourth factor (c,d). The areas represent the natural groups found with Ward’s clustering. For each group, the most representative form is given. The colors of the groups represent the average distances to Tokyo according to a rainbow scheme. Red means that the dialect in that area is identical to the dialect of Tokyo, and darker blue means that the dialect in that area is maximally different from the dialect of Tokyo.
Figure 18 shows the reference point maps for the two items that load strongest on the first factor (kazoeru and konban) and the second factor (onbusuru and kakashi).
In Figure 18a, we find the red form [kazoeru] distributed in Tohoku and Kinki–Chugoku–Shikoku. It is distributed as an archaic word. The blue form [jomu] is also an archaic form with a distant distribution in the Kinki and Okinawa regions. The yellow form [kanʒoosuru] is of Chinese origin and has been distributed since the Ancient Ages. This does not coincide with the theory of dialectal concentric propagation theory. It is an item (word) with a special distribution pattern.
The red form [konja] in Figure 18b is of Chinese origin and became widespread in the Early Middle Ages. It is used throughout Japan except in Okinawa and the northeast. The green form [bange] is partly of Chinese origin, and is distributed in remote areas. The areas where the forms [kazoeru] and [konja] are spoken more or less correspond with the areas in Figure 17a (Factor 1) that were found to be more related to Tokyo.
Onbu suru is a colloquial Tokyo word consisting of two morphemes. Its transcription does not appear in the map in Figure 18c since it is found in the area where green [obuu] has the smallest average distance to the other realizations of it. On the map, we see three groups represented by three different shades of green that are difficult to distinguish. This means that the average distances of the three groups to the Tokyo form are approximately equal.
In Tokyo, the standard pronunciation of kakashi is [kakaʃi]. In Figure 18d, this pronunciation is found in the area that is labeled with the red form [kagaʃi]. West of Kinki, [kagaʃi] is based on kagasu, the transitive verb form of the verb “to sniff,” but this has been changed to refer to a doll. In Tohoku, [kagaʃi] is based on the voicing of the mid-word consonant of the standard form, kakashi. The blue form, [odoʃi], is of a different origin from the standard form, [kakaʃi], and is based on “bird scare” by cloth or sound. The original LAJ map also neatly shows the east–west difference.
The areas labeled as [obuu] in Figure 18c and [kagaʃi] in Figure 18d largely coincide and may reveal the southern border of the area that is linguistically closest to Tokyo in Figure 17b (Factor 2).
In Figure 19, reference point maps are shown for the items that load the most strongly on the third factor (bikkurisuru and tategami) and the fourth factor (shimoyake and tsumuji).
In Figure 19a, we find two areas that are labeled with the forms [bikkurisuru] and [tamageru], respectively. The green form [bikkurisuru] spread throughout Japan. It is of onomatopoeic origin. The form blue [tamageru] is derived from tama(shii) kieru, and remains in both east and west as an archaic word. The standard word form is [odoroku], and it is found in the area that is labeled with the form [bikkurisuru].
Figure 19b shows two forms, [tategami] and [kange], meaning horse’s hair. The red form [tategami] is the standard form and is found almost everywhere in Japan. The blue form [kange] is mainly found in Okinawa, but is also scattered in the mainland. Neither of these two forms is widely distributed throughout the country.
When comparing Figure 19a and Figure 19b, we see some similarity in the distribution of the forms [tamageru] and [kange], which more or less correspond with the two ‘centers’ in Figure 17c (Factor 3).
The forms [ʃimojake] and [jukijake] indicate a bisection in Figure 19c. The red form [ʃimojake] is the standard form and is distributed on the Pacific side, where there is little snow. The green form [jukijake] is distributed on the Sea of Japan side, where there is a lot of snow.14 In the original LAJ map, local word forms appear in various regions, but the “snow”-based form is more common on the Sea of Japan side and the “frost”-based form is more common on the Sea of Japan side.
In Figure 19d, two groups are shown that are labeled with forms [tsumuʒi] and [makimaki]. The gray form [tsumuʒi] is a revived form of an archaic word, and is distributed on the Pacific Ocean side. The blue form [makimaki] is of a different etymology, derived from the verb “to roll,” and is distributed nationwide.
In Figure 19c, we find a division into a group along the coast of the Sea of Japan (with form [jukijake]) and a group along the coast of the Pacific Ocean (with forms [ʃimojake]). This pattern is less sharply visible in Figure 19d. A similar pattern is found in Figure 17d (Factor 4), where local dialects that are linguistically more distant to Tokyo are found along the coast of the Sea of Japan, while the local dialects on the side of the Pacific Ocean are more similar to the local dialect of Tokyo.
5. The Influence of Tokyo on the Japanese Dialects
In Section 1, we wrote that Tokyo has had a significant impact on the Japanese dialects throughout the country. Standard Japanese is said to be derived from the language spoken historically in the Yamanote Uptown area of Tokyo (Shibatani, 1990; Inoue, 2010). The core vocabulary, grammar, and pronunciation of standard Japanese are rooted in the Tokyo dialect.
In this section, we investigate (1) whether the Tokyo dialect is the most influential variety, and (2) which local dialects are particularly influenced by the Tokyo dialect.
5.1. Is Tokyo the Most Influential Dialect?
As a first step, we computed the average linguistic distance between each local dialect and the other 2399, replicating the approach of Jeszenszky et al. (2019). The result is shown in Figure 20. The local dialects are indicated by dots. The redder a dot, the smaller the average distance to the other dialects, red being the color of similarity. The bluer a dot, the larger the average distance, blue being the color of distance.
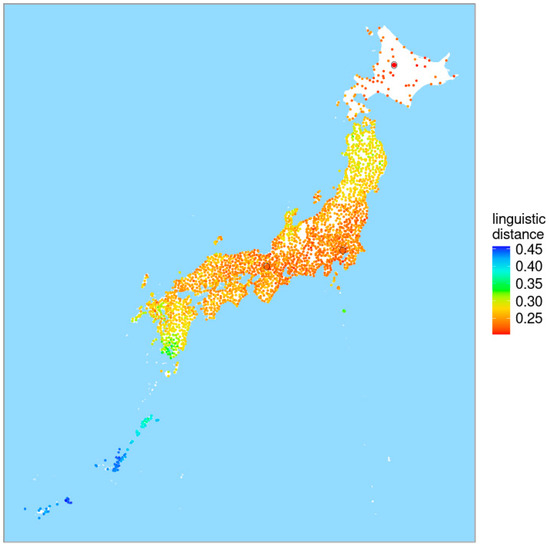
Figure 20.
Average linguistic distance map. The locations are indicated by dots, and the color of a dot represents the average distance to all other locations. The redder a dot, the smaller the average distance, and the bluer a dot, the larger the average distance. The encircled dot on the island of Hokkaido represents Nagayama, which has the smallest average distance. Tokyo (in the eastern part of the mainland) and Kyoto (to the west of Tokyo) are also indicated by circled dots.
In the map, three locations are encircled. The one more to the north is Nagayama15, which has the smallest average distance to the other locations. The one more to the south is Tokyo. We also encircled Kyoto, which is found more to the southwest. In Section 1, we mentioned the historical dominance of the dialect of Tokyo and its close relationship to the standard Japanese language. However, Tokyo’s linguistic dominance is relatively recent, emerging shortly before the Meiji era. Prior to this period, the Nara–Kyoto region—which later came to encompass Kyoto and Osaka—held greater linguistic influence.
The overall distribution appears continuous, with Tokyo at its center. However, Tohoku and Kyushu share little in common. A shift in color is noticeable from southern Kyushu, and even Amami–Okinawa exhibits continuity. Notably, the highest linguistic commonality with other regions was found not in Tokyo but in Nagayama, which is found on the island Hokkaido. This pattern was also observed by Jeszenszky et al. (2019, p. 5). This phenomenon can be attributed to factors such as the role of a lingua franca, the emergence of new dialect formation, and linguistic homogenization in modern colonial settings. While it has been suggested that the spread of a common language in Hokkaido was driven top–down by textbook-based written norms, non-standard language forms are also widely used. It is believed that various regional dialects, as part of everyday spoken language, have gradually converged at the colloquial level, reflecting a bottom–up linguistic change.
When ranking the dialects according to their average distance, Tokyo is found at position 206, which means that 91.4% of the local dialects have a higher average distance. Kyoto is found at position 134, which means that 94.4% of the local dialects have a higher average distance. A strong influence of both Tokyo and Kyoto on the other Japanese dialects may explain why the average linguistic distance of these two local dialects is relatively small.
What does the picture look like if we filter out the role of geographical distance? To determine this, we calculated the direct distances among the local dialects. We measured great-circle distances among the locations.16 The great-circle distance is the shortest distance between two points on the surface of a sphere, measured along the surface rather than through the interior (Onishi, 2019). Then, we ran a generalized additive model (gam) with smoothed great-circle distance as the predictor and linguistic distance as the dependent variable.17 The adjusted R-square of this model was 0.52.18 In Figure 21, the linguistic distance is plotted against the great-circle distance. The red line shows the linguistic distances as predicted by the gam model. This graph is notable for its curved rather than straight line. The gradual shift observed between 500 and 1500 km can be attributed to the inclusion of Hokkaido. Distances beyond 1500 km correspond to Okinawa, where the linguistic differences from other dialects are so pronounced that internal variations within Okinawa itself are not distinctly visible.
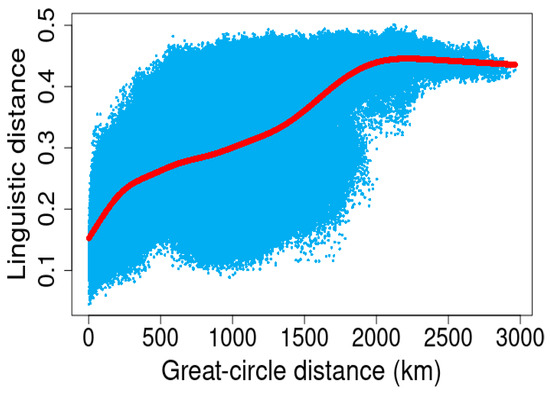
Figure 21.
Linguistic distance plotted against the great-circle distance. The red line shows the linguistic distances that were predicted by the gam model.
We also considered travel distances and travel times,19 but found that for some pairs of locations, travel distances and times could not be obtained, which was also observed by Jeszenszky et al. (2019). Jeszenszky et al. (2019) found that both the travel distance and the travel time strongly correlate with the great-circle distance. The respective correlations were r = 0.99 and r = 0.98. Given these high correlations, we focused only on the great-circle distance.
The residues obtained by the gam model represent the distances among the 2400 localities, with geographic distance being filtered out. They were calculated as the originally measured linguistic distances minus the linguistic distances as predicted by the gam model on the basis of the geographic distances. The result is shown in Figure 22. The map looks different from the map in Figure 20. The encircled location in the north of Hokkaido is Tokoro20, and it has the smallest average distance. This will be explained later.
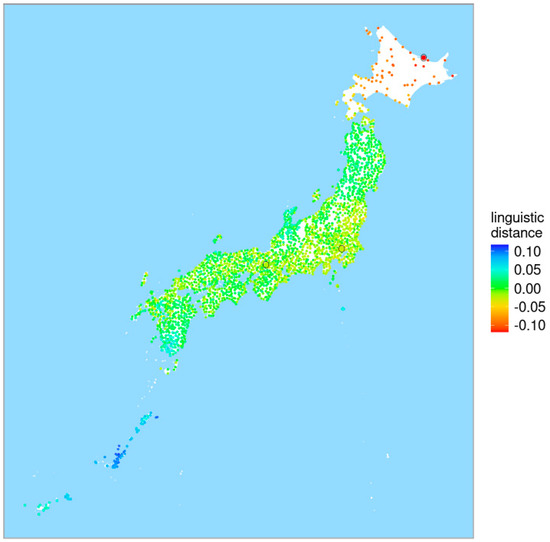
Figure 22.
The average linguistic distance of each local dialect to the other local dialects controlled for geographic distance. The encircled dot in the north of Hokkaido represents Tokoro, which has the smallest average distance. On the mainland, Tokyo (further east) and Kyoto (further west) are also indicated by circled dots.
In the ranking, according to the smallest average distance, Tokyo is found at position 197, so 91.8% of the local dialects have a higher average distance. Kyoto is found at position 309, so 87.1% of the local dialects have a higher average distance. Both varieties are highly ranked, but Tokyo now surpasses Kyoto in ranking. This may suggest that Tokyo’s influence on other Japanese dialects is less determined by geographic distance compared to Kyoto’s.
5.2. Which Local Dialects Are Particularly Influenced by the Tokyo Dialect?
In Figure 12, the distances between the local dialects and Tokyo are visualized. The dialects in the vicinity of Tokyo are most related. Towards the southwest, the distances become greater, with the greatest distances on the islands in the southwest. As we go north, the distances initially become greater, but in Hokkaido, they then become smaller again.
In Figure 23, the distances to Tokyo are visualized on the basis of the residues that were obtained by the gam model. On this map, dialects geographically closer to Tokyo appear less related to it, whereas the more distant Hokkaido dialects show a stronger connection. This unusual pattern in the Hokkaido dialect was previously observed by Inoue (2001) and Onishi (2019). One possible explanation is the development of a new dialect formation among settlers in newly established communities.
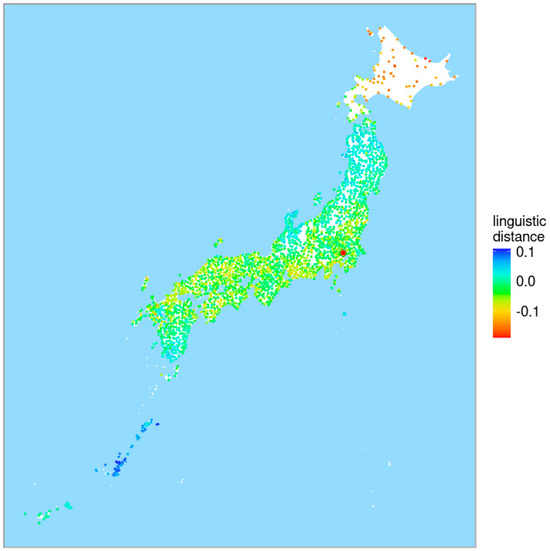
Figure 23.
Linguistic distances of local dialects to Tokyo controlled for geographic distance. Tokyo is indicated by the encircled dot.
6. Discussions and Conclusions
6.1. Direct Results of LAJ
In this paper, we unraveled the big picture of Japanese dialects as it was presented by Heeringa and Inoue (2023) and largely confirmed using a much larger dataset in this paper. This picture was obtained on the basis of aggregated distances using data on 141 items from the LAJDB. Factor analysis proved to be a very effective method for unraveling this picture. The division into five groups (see Figure 7) appeared to be based on mainly two different patterns (see Figure 10).
The first pattern in Figure 10a reveals a five-way division similar to that in Figure 7. A comparison of the two maps shows only slight differences in dialect boundaries. In the second pattern in Figure 10b, Japan is divided into northeastern Japan versus southwestern Japan and the islands southwest of the Japanese mainland. For each pattern, we showed the items that (partially) underlie the respective patterns (see Figure 11).
Heeringa and Inoue (2023) also presented a reference point map illustrating the distances between Tokyo’s local dialect and the other 2399 local dialects. The pattern shown in their map was confirmed by the map that we obtained using a larger dataset (see Figure 12). We performed a factor analysis in order to find the underlying patterns of this map as well. The distribution shown in the reference point map is mainly based on four patterns (see Figure 17). Although the patterns of the four maps vary, they consistently show that dialects closer to Tokyo are more similar to the Tokyo dialect. For each pattern, the items that support the respective patterns in particular are shown (see Figure 18 and Figure 19).
We have further investigated the position of Tokyo in the Japanese dialect continuum by determining the influence of Tokyo on the other local dialects. Indeed, Tokyo is located in an area with local dialects, whose average distance from other dialects is relatively small. This area includes the more central area of mainland Japan and Hokkaido. However, if we filter out the influence of geographical distance, only the local dialects of Hokkaido remain as dialects with the smallest average distance to the other local dialects. Originally, Hokkaido was primarily inhabited by the Ainu people, but it was annexed and colonized by Japan in 1869, following the Meiji Restoration. Japanese settlers forced the Ainu to assimilate (Mason, 2012; Jolliffe, 2020).
In Figure 17, we can see that the local dialects in the vicinity of Tokyo in particular are most related to Tokyo. But when using distances that were controlled for geographic distance again, the local dialects on Hokkaido stood out as very related to the Tokyo dialect. This probably indicates that the Tokyo dialect has had a relatively large influence on that in Hokkaido.
6.2. Evaluation of the Factor Analyses
As for the factor analyses that we performed, we observed a couple of things. First, making the data suitable for application of factor analysis was somewhat laborious. In the first factor analysis involving all mutual dialect distances, 74 out of 141 items eventually remained. In the second factor analysis involving only the distances relative to Tokyo, 46 items were initially removed since they were not recorded in Tokyo, so 95 items were left over. Then, for the purpose of factor analysis, another group of 46 items were removed, so 49 items remained. The removal of numerous items indicates that they either lacked a strong common structure or exhibited too much variability for meaningful factor extraction.
Second, the identification of 24 factors in the first analysis and 16 factors in the second suggests that dialectal differences are highly complex and multidimensional. Factor analysis is typically most useful when a small number of strong factors explain most of the variation, but here, the high number of factors implies that the variation is fragmented across many influences.
Third, the highest factor loadings did not exceed 0.55 in the first analysis and 0.53 in the second, even for the most important factor. This indicates that no single factor strongly explains the variation in dialect distances, meaning that dialectal relationships are not easily reducible to a few dominant trends.
These findings do not indicate that the factor analyses have failed; rather, they reveal both the nature of the data and the power of data aggregation. By combining multiple items, an underlying structure becomes apparent—one that is much less visible when examining factors or items individually.
6.3. Comparison to Earlier Works of LAJ
The results in this paper combine and summarize the main theories about the distribution patterns of Japanese dialects. The main characteristics and main streams of dialect distribution are now concretely documented on the basis of objective data.
Inoue’s (2010) previous analysis, in the 20th century, of LAJ 82 words was based on the Kasai data (numerical data counted by a student named Hisako Kasai) or on standard word forms and mean values (or sums) by prefectures. By applying multivariate analyses to these data, the East Japan factor and the West Japan factor were obtained. Since middleclass Tokyo speech had been interpreted as being the basis of the Japanese Standard Language, the hidden power of the former cultural center, Kyoto, was both impressive and surprising. At the end of various analyses, Japanese dialects were classified into five divisions, namely Tohoku, Kanto–Chubu, Western Japan (Kinki-Chugoku Shikoku), Kyusyu and Okinawa, five areas which beautifully agree with the five divisions acquired by our current analysis, as shown in Figure 7 or Map 3 in Heeringa and Inoue (2023).
Lexical analysis of the whole dataset was also applied to Kasai data. Usage frequency, year of first appearance in literature, etc., were added and analyzed. This attempt was a little different compared to the western dialectometry in that it paid attention to non-geographical, linguistic dimension of the data. The distribution pattern for each word of Kasai data was also analyzed. The east–west factor turned out to be important. Yarimuzu’s analysis of a different set of data, the Grammar Atlas of Japanese Dialect (GAJ), showed basically similar results (Yarimizu, 2007; Inoue & Yarimizu, 2024).
Inoue (2001) examined the first recorded occurrence of standard forms in dictionaries and other sources. By correlating these dates with their geographical distribution, the speed of linguistic propagation could be determined. Similarly, in this study, the first recorded occurrence of key word forms (dialectal variations) can be identified and compared with their distribution range. This approach represents a practical application in the emerging field of spatio-temporal linguistics.
Heeringa and Inoue (2023)’s analysis includes both standard forms and many colloquial dialectal forms, although the number of items (words) was smaller, namely 37. The Levenshtein distance was calculated for all the dialectal words, which resulted in objective distances and clear results, especially after applying cluster analysis. A similar dialect division into five areas was obtained in this paper.
Although the emphasis in dialectometry is on obtaining the big picture, studying the distribution pattern of individual items (words) is useful in order to explain the global patterns, including those obtained by factor analysis. We found the east–west division being reflected in multiple items. The number of dialectal forms may differ per item, but by applying factor analysis to aggregated Levenshtein distances, the main patterns or latent linguistic variables that underly the big picture can be found.
Author Contributions
Formal analysis, W.H.; Writing—original draft, W.H. and F.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available at: https://www.lajdb.org/lajdb_data/LAJDB_data_withCord_download002_v20180328_rev.html (accessed on 10 February 2025).
Acknowledgments
We are indebted to the National Institute of Japanese Language and Linguistics (NINJAL), especially Yasuo Kumagai, for digitizing and making available some of the data on the Linguistic Atlas of Japan. Our sincere thanks also go to John Nerbonne for his valuable comments and suggestions on an earlier version of this paper. Section 5, in particular, emerged from this. We also thank the two anonymous reviewers for their constructive remarks. They referred us to a much larger dataset than the one we initially used, which had a great impact on this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | Since 2009, Motoyoshi no longer exists as an independent city, but has been merged into the expanded city of Kesennuma. |
| 2 | Respectively codes 4716.20 and 0257.12 in the LAJDB. |
| 3 | We used LED-A for calculating the PMI Levenshtein distances. The implementation of PMI-Levenshtein in LED-A differs in details from Wieling (2012). It is beyond the scope of this paper to go into this. |
| 4 | For more details about the exact procedure see Heeringa (2004), pp. 134–135. |
| 5 | In this example we used transcriptions from LAJDB. Since this example data set is small, it is not possible to learn the weights well using PMI Levenshtein distance. We therefore applied plain Levenshtein distance where insertions, deletions and substitutions have a weight of 1, as we did in Figure 1 and Table 2. |
| 6 | Since we are only giving an example here, we will continue with the analysis. |
| 7 | The LAJDB codes of the locations are 4706.53 (Kesennuma), 4716.20 (Motoyoshi), 6450.45 (Atikata), 6359.62 (Kitahiroshima), and 0257.12 (Setouchi). |
| 8 | For more information about this procedure see https://statsandr.com/blog/files/Hierarchical-clustering-cheatsheet.pdf (accessed on 23 May 2025). This procedure is implemented in LED-A. |
| 9 | For the two groups we found Cronbach’s α values of 0.8765 and 0.8776. A widely accepted threshold is 0.70 (Nunnally, 1978), therefore the number of items was sufficient in order to produce reliable results. |
| 10 | The maps give a general idea of the variation of the items across the regions so that the reader can develop an idea of the basis for the division into areas, but should by no means be seen as a substitute for the much more precise and accurate maps in the LAJ. |
| 11 | In the LAJDB all localities are represented by codes. We determined location 5698.69 closest to Tokyo just by eyeballing. |
| 12 | Actually distances among all 2400 sites were calculated, and subsequently the distances to Tokyo were selected from the respective distance matrices. Considering the full datasets the Cronbach’s α values of the four groups are, respectively, 0.7738, 0.6518, 0.6738 and 0.3864. Since three coefficients are (slightly) lower than the threshold of 0.70 (see Section 2.2) the results should be interpreted with care. |
| 13 | We emphasize again that these maps are a highly simplified representation, the number of different forms in the original LAJ maps is always much larger. |
| 14 | [juki] means “snow” and [ʃimo] means “frost”. |
| 15 | In the LAJDB this location has code 1719.17. Historically, Nagayama was an independent town but merged with Asahikawa in 1961, becoming one of its districts. |
| 16 | The function distHaversine() from the R package geosphere (Hijmans, 2024) was used, see also Sinnott (1984). |
| 17 | We used the function gam from the R package mgcv (Wood, 2011). |
| 18 | We obtained a lower adjusted R-square value of 0.4912 when using a linear regression model. When using logarithmic geographic distances, the adjusted R-square dropped to 0.4648, and when using the square root of the geographic distance, we obtained a higher value of 0.5005. |
| 19 | We used the function find_route() from the R package osrm which retrieves these data from Open Street Map. |
| 20 | In the LAJDB this location has code 0896.22. Originally an independent town, Tokoro merged with Kitami in 2006. |
References
- Bolognesi, R., & Heeringa, W. (2002). De invloed van dominante talen op het lexicon en de fonologie van Sardische dialecten [The influence of dominant languages on the lexicon and phonology of Sardinian dialects]. Gramma/TTT: Tijdschrift voor taalwetenschap, 9(1), 45–84. Available online: http://www.wjheeringa.nl/papers/rom01.pdf (accessed on 23 May 2025).
- Cattell, R. B. (1966). The scree test for the number of factors. Multivariate Behavioral Research, 1(2), 245–276. [Google Scholar] [CrossRef] [PubMed]
- Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16, 297–334. Available online: http://cda.psych.uiuc.edu/psychometrika_highly_cited_articles/cronbach_1951.pdf (accessed on 23 May 2025). [CrossRef]
- Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R. Sage. [Google Scholar]
- Fujiwara, Y. (1990). Nihongo hogen bunpa ron [Dialect propagation theory of Japanese]. Musashino Shoin. [Google Scholar]
- Gere, A. (2023). Recommendations for validating hierarchical clustering in consumer sensory projects. Current Research in Food Science, 6, 100522. [Google Scholar] [CrossRef]
- Goebl, H. (1981). Eléments d’analyse dialectométrique (avec application à l’ais). Revue de Linguistique Romane, 45, 349–420. [Google Scholar]
- Goebl, H. (2002). Analyse dialectométrique des structures de profondeur de l’ALF. Revue de Linguistique Romane, 66(261–262), 5–63. [Google Scholar]
- Grieve, J. (2014). A comparison of statistical methods for the aggregation of regional linguistic variation. In B. Szmrecsanyi, & B. Wälchli (Eds.), Aggregating dialectology, typology, and register analysis: Linguistic variation in text and speech (pp. 53–88). De Gruyter. [Google Scholar] [CrossRef]
- Heeringa, W. (2004). Measuring dialect pronunciation differences using levenshtein distance [Unpublished doctoral dissertation, University of Groningen]. Available online: http://www.wjheeringa.nl/thesis/ (accessed on 23 May 2025).
- Heeringa, W., & Inoue, F. (2023). Exploring the Japanese dialect geography dialectometrically: Division and continuity. Studies in Geolinguistics, 3, 1–44. [Google Scholar] [CrossRef]
- Hijmans, R. (2024). _geosphere: Spherical trigonometry_. R package version 1.5-20. Available online: https://CRAN.R-project.org/package=geosphere (accessed on 3 April 2025).
- Horn, J. L. (1965). A rationale and test for the number of factors in factor analysis. Psychometrika, 30(2), 179–185. [Google Scholar] [CrossRef]
- Huisman, J. L. A. (2021). Variation in form and meaning across the Japonic language family: With a focus on the Ryukyuan languages [Doctoral dissertation, Radboud University Nijmegen]. Available online: https://pure.mpg.de/rest/items/item_3311139/component/file_3311141/content (accessed on 23 May 2025).
- Huisman, J. L. A., Majid, A., & van Hout, R. (2019). The geographical configuration of a language area influences linguistic diversity. PLoS ONE, 14(6), e0217363. [Google Scholar] [CrossRef]
- Inoue, F. (2001). Keiryoteki hogen kukaku [Quantificational dialect classification]. Meiji Shoin. [Google Scholar]
- Inoue, F. (2010). Real and apparent time clues to the speed of dialect diffusion. Dialectologia: Revista Electrònica, 2010(5), 45–64. [Google Scholar]
- Inoue, F., & Hanzawa, Y. (2024). New dialect and obsolescence in hamaogi glottogram survey―Dialect vocabulary change in 250 years. Dialectologia: Revista Electrònica, 32, 47–116. [Google Scholar]
- Inoue, F., & Kasai, H. (1989). Dialect classification by standard Japanese forms. Japanese Quantitative Linguistics, 39, 220–235. [Google Scholar]
- Inoue, F., & Yarimizu, K. (2024). Language standardization and railway-walking distance–Levenshtein distance and distribution in GAJ. Dialectologia et Geolinguistica, 32, 79–97. [Google Scholar] [CrossRef]
- Jain, A. K., & Dubes, R. C. (1988). Algorithms for clustering data. Prentice Hall. [Google Scholar]
- Jeszenszky, P., Hikosaka, Y., Imamura, S., & Yano, K. (2019). Japanese lexical variation explained by spatial contact patterns. ISPRS International Journal of Geo-Information, 8(9), 400. [Google Scholar] [CrossRef]
- Jolliffe, P. M. (2020). Forced Labour in Imperial Japan’s First Colony: Hokkaidō. The Asia–Pacific Journal, 18(20), e7. [Google Scholar] [CrossRef]
- Kessler, B. (1995, March 27–31). Computational dialectology in Irish Gaelic. 7th Conference of the European Chapter of the Association for Computational Linguistics (pp. 60–67), Dublin, Ireland. Available online: https://arxiv.org/pdf/cmp-lg/9503002.pdf (accessed on 23 May 2025).
- Kumagai, Y. (2016). Developing the linguistic atlas of Japan database and advancing analysis of geographical distributions of dialects. In M.-H. Côté, R. Knooihuizen, & J. Nerbonne (Eds.), The future of dialects. Selected papers from methods in dialectology XV (= Language Variation 1) (pp. 333–362). Language Science Press. [Google Scholar]
- Mason, M. (2012). Dominant narratives of colonial Hokkaido and imperial Japan: Envisioning the periphery and the modern nation-state (pp. 7–9). Palgrave Macmillan. [Google Scholar]
- Nerbonne, J. (2006). Identifying linguistic structure in aggregate comparison. Literary and Linguistic Computing, 21(4), 463–475. [Google Scholar] [CrossRef]
- Nunnally, J. C. (1978). Psychometric theory. McGraw-Hill. [Google Scholar]
- Nunnally, J. C., & Bernstein, I. H. (1994). Psychometric theory (3rd ed.). McGraw-Hill. [Google Scholar]
- Onishi, T. (2019). On the relationship of the degrees of correspondence of dialects and distances. Languages, 4(2), 37. [Google Scholar] [CrossRef]
- Pickl, S., & Pröll, S. (2019). Geolinguistische querschnitte und tiefenbohrungen in bayern und darüber hinaus. In Methodik moderner Dialektforschung. Erhebung, Aufbereitung und Auswertung von Daten am Beispiel des Oberdeutschen (pp. 141–143). Georg Olms Verlag. [Google Scholar]
- Shibatani, M. (1990). The languages of Japan. Cambridge University Press. [Google Scholar]
- Sinnott, R. W. (1984). Virtues of the haversine. Sky and Telescope, 68(2), 159. [Google Scholar]
- Van der Maaten, L. (2014). Accelerating t-SNE using tree-based algorithms. Journal of Machine Learning Research, 15, 3221–3245. Available online: https://www.jmlr.org/papers/volume15/vandermaaten14a/vandermaaten14a.pdf (accessed on 23 May 2025).
- Van der Maaten, L., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9, 2579–2605. Available online: https://www.jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf (accessed on 23 May 2025).
- Ward, J. H., Jr. (1963). Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association, 58, 236–244. [Google Scholar] [CrossRef]
- Wieling, M. (2012). A quantitative approach to social and geographical dialect variation [Doctoral dissertation, University of Groningen]. Available online: https://hdl.handle.net/11370/cd637817-572f-4826-98c1-08272775fb64 (accessed on 23 May 2025).
- Wieling, M., Prokić, J., & Nerbonne, J. (2009). Evaluating the pairwise alignment of pronunciations. In L. Borin, & P. Lendvai (Eds.), Proceedings of the EACL 2009 workshop on language technology and resources for cultural heritage, social sciences, humanities, and Education, (LaTeCH–SHELT&R 2009). Workshop at the 12th meeting of the European chapter of the association for computational linguistics. Athens, 30 March 2009 (pp. 26–34). Association for Computational Linguistics (ACL). Available online: https://aclanthology.org/W09-0304.pdf (accessed on 23 May 2025).
- Wood, S. N. (2011). Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society Series B, 73(1), 3–36. [Google Scholar] [CrossRef]
- Yarimizu, K. (2007). Hogen bunpo zenkoku chizu ni okeru kyotsugoka no jokyo (The situation of common language in GAJ). Nihongogaku, 26(11), 112–119. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).