Numerical Simulation of the Flow in Two-Phase Supersonic Underexpanded Gas–Particle Jets Exhausting into a Slotted Submerged Space
Abstract
:1. Introduction
2. Problem Statement
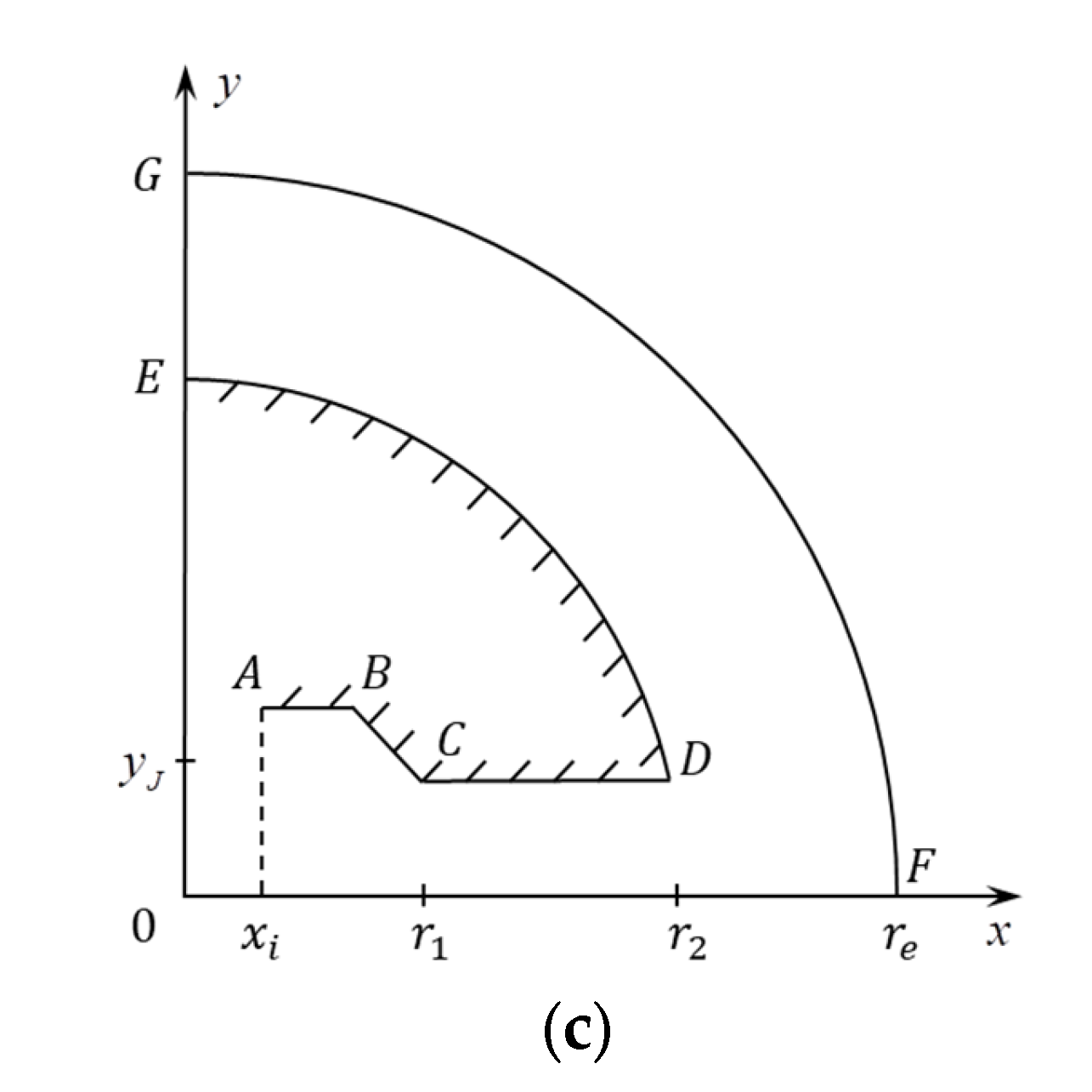
2.1. Calculation Procedure
2.2. Equations for Gas Flow in the Channel Approximation
2.3. Equations for Gas and Particles in the Channel Approximation
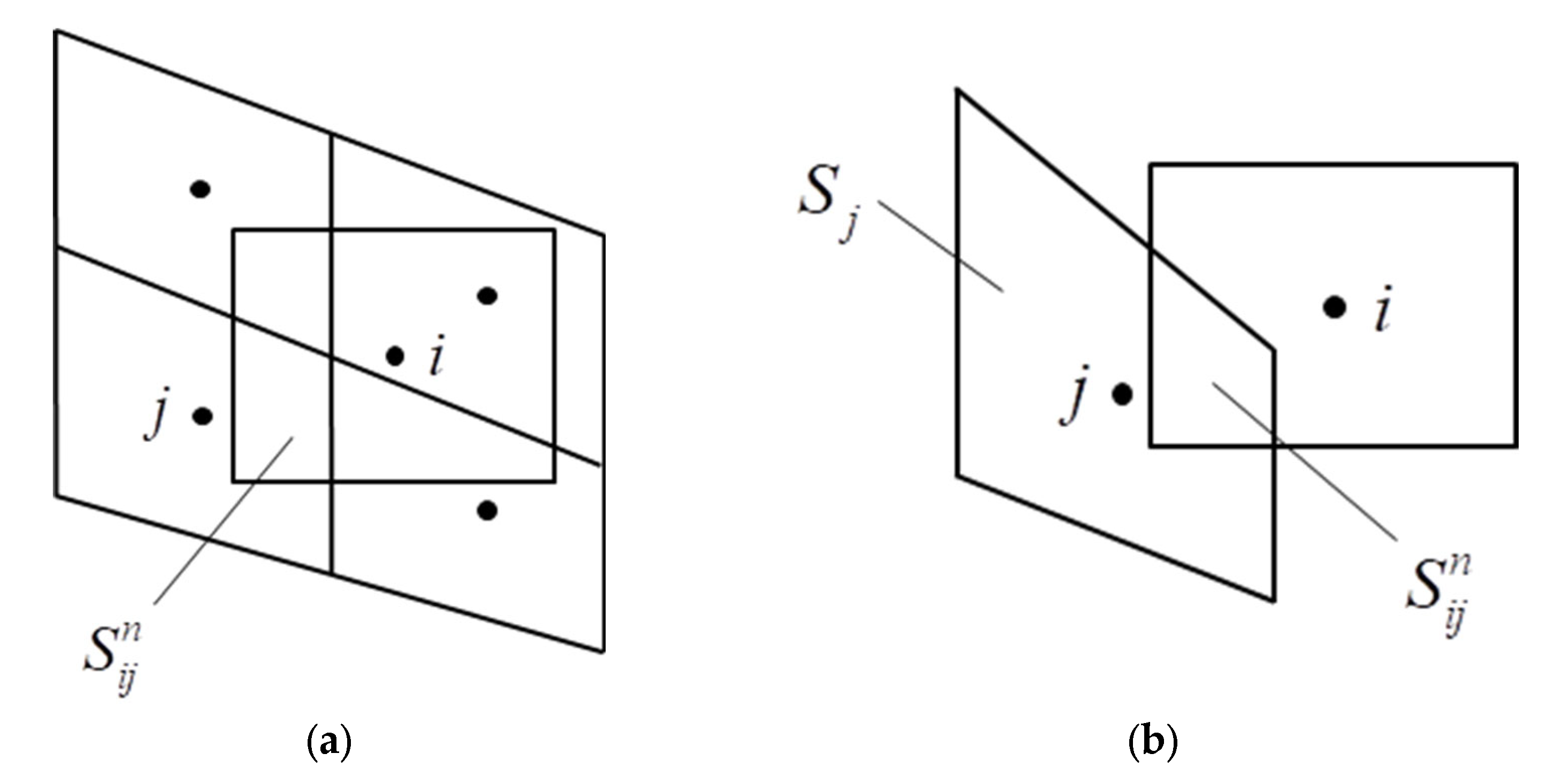
2.4. Method for Calculating Gas–Particle Flows
2.5. Calculated Parameters of the Problem
3. Results and Discussion
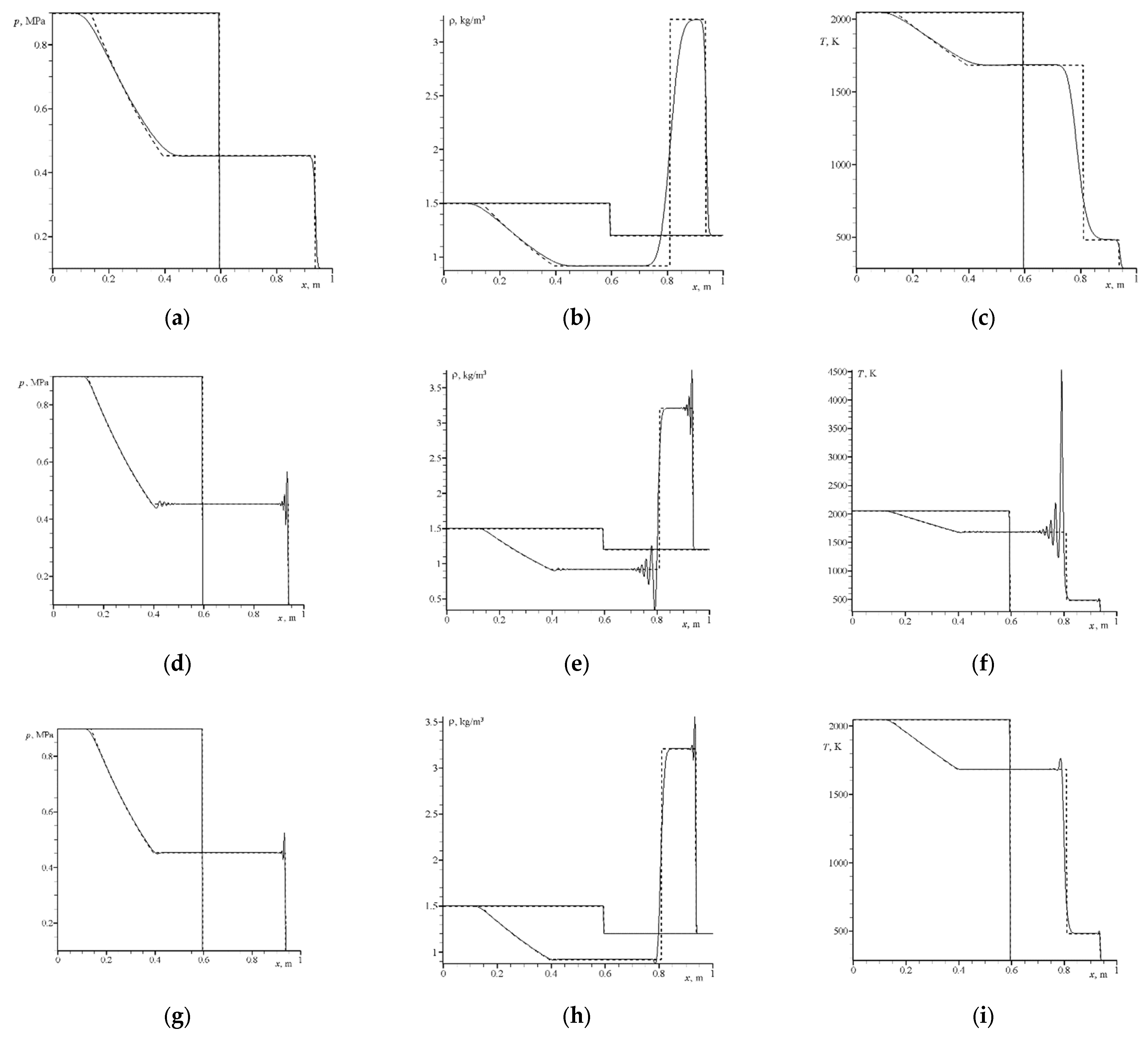
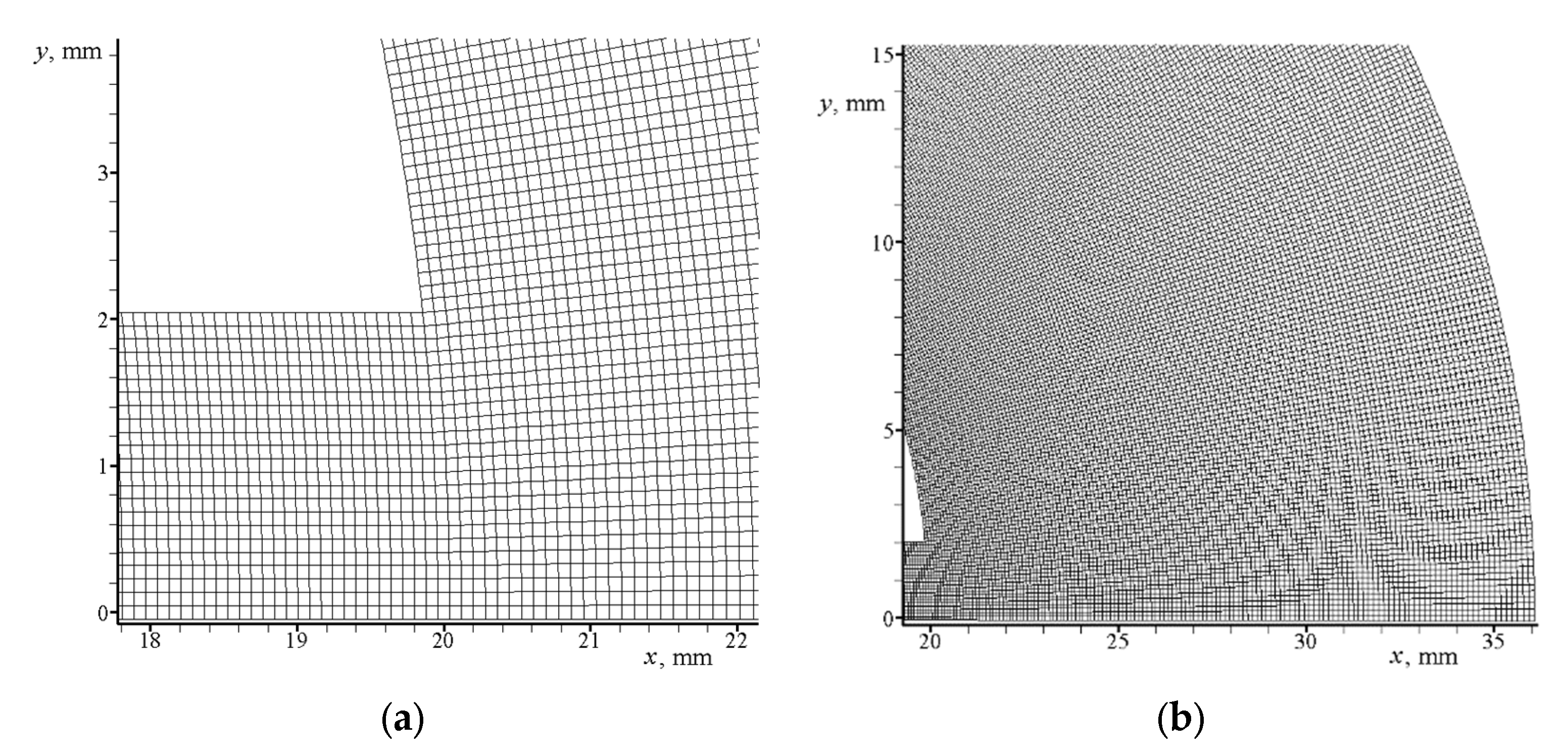
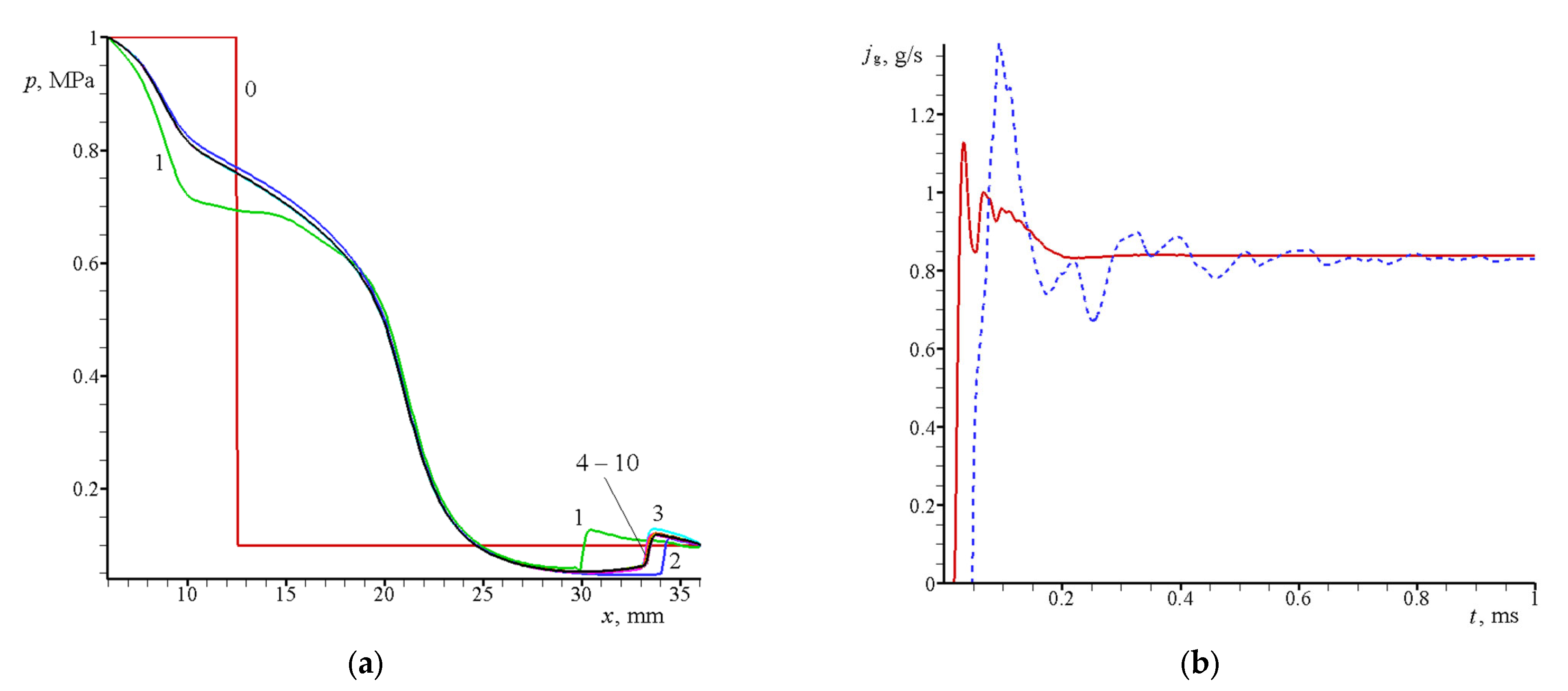
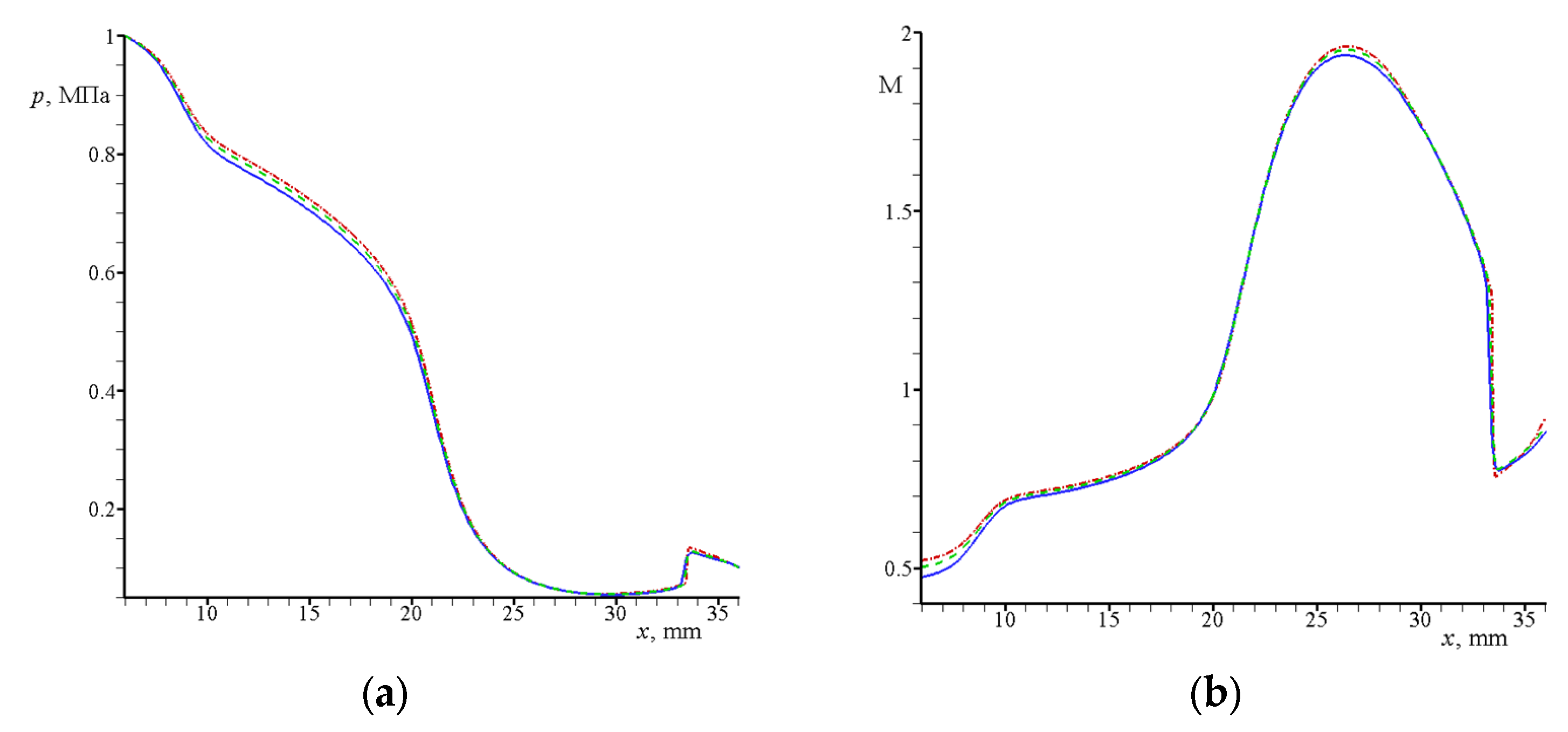
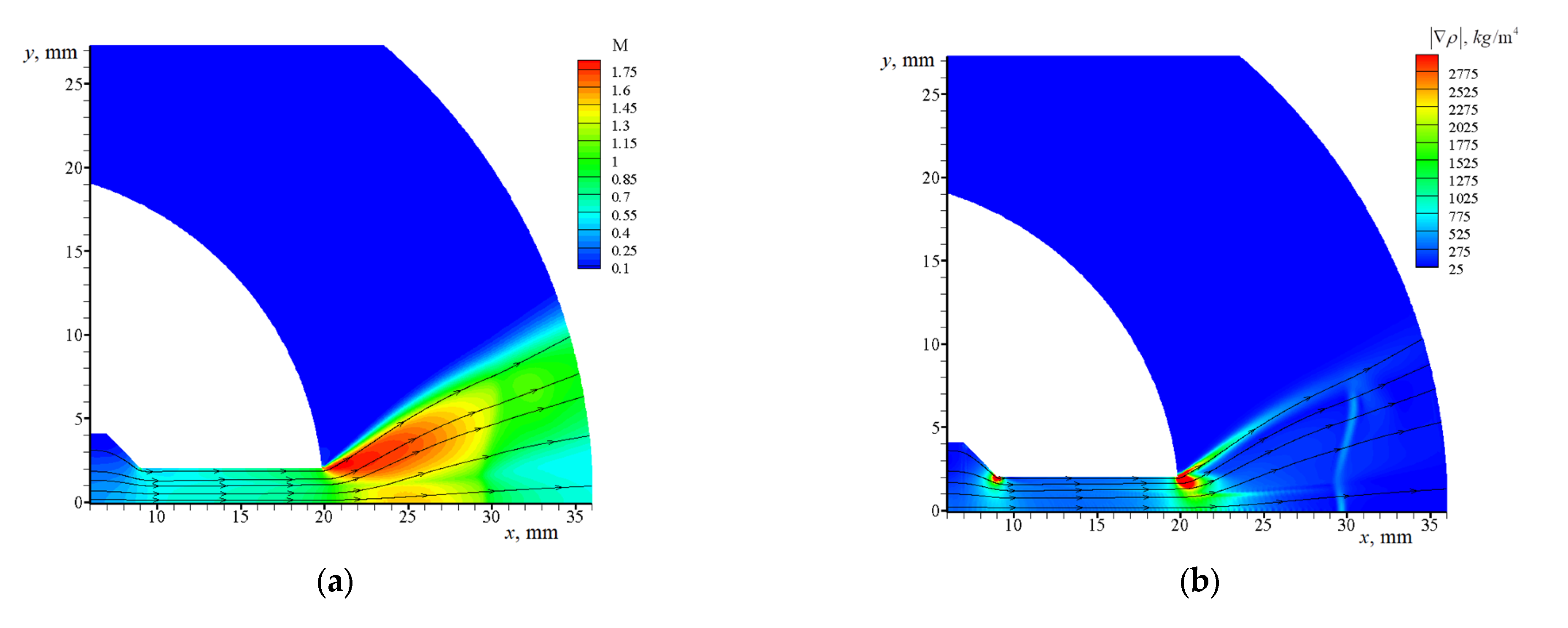
3.1. Calculation of the Gas Flow without Particles
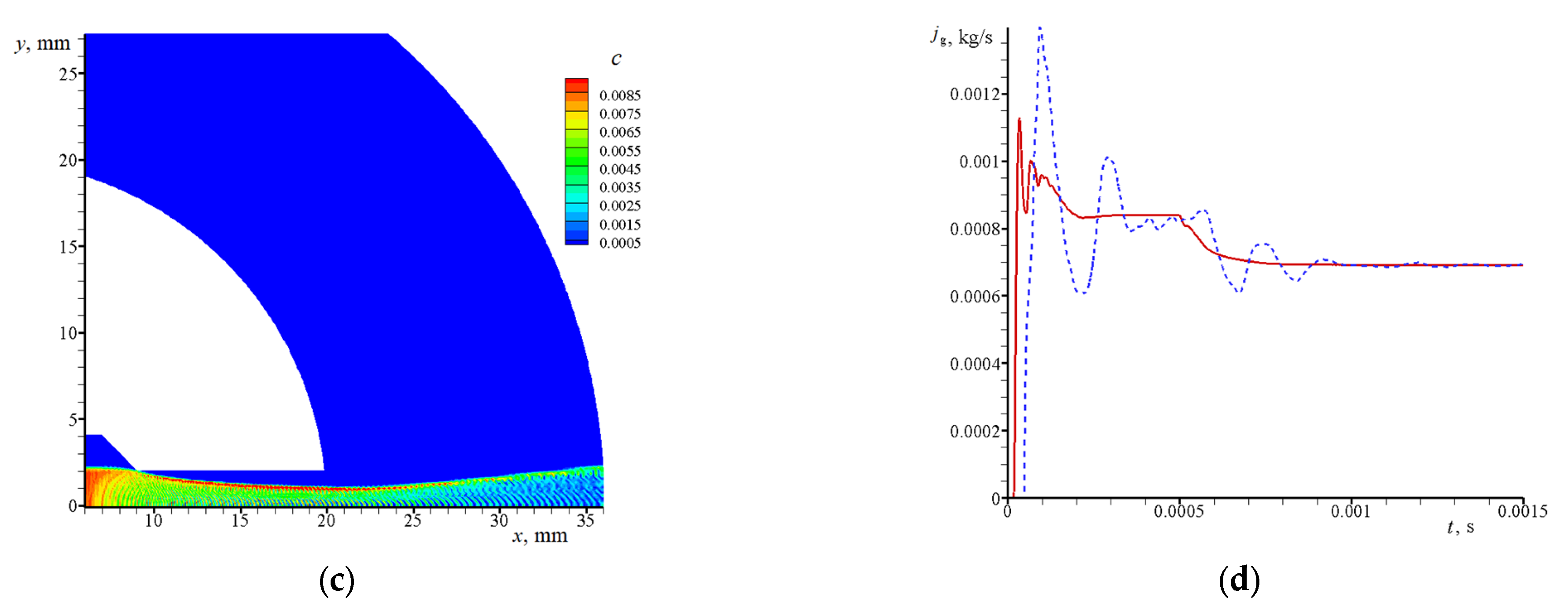
3.2. Calculated Data for a Gas–Particle Jet
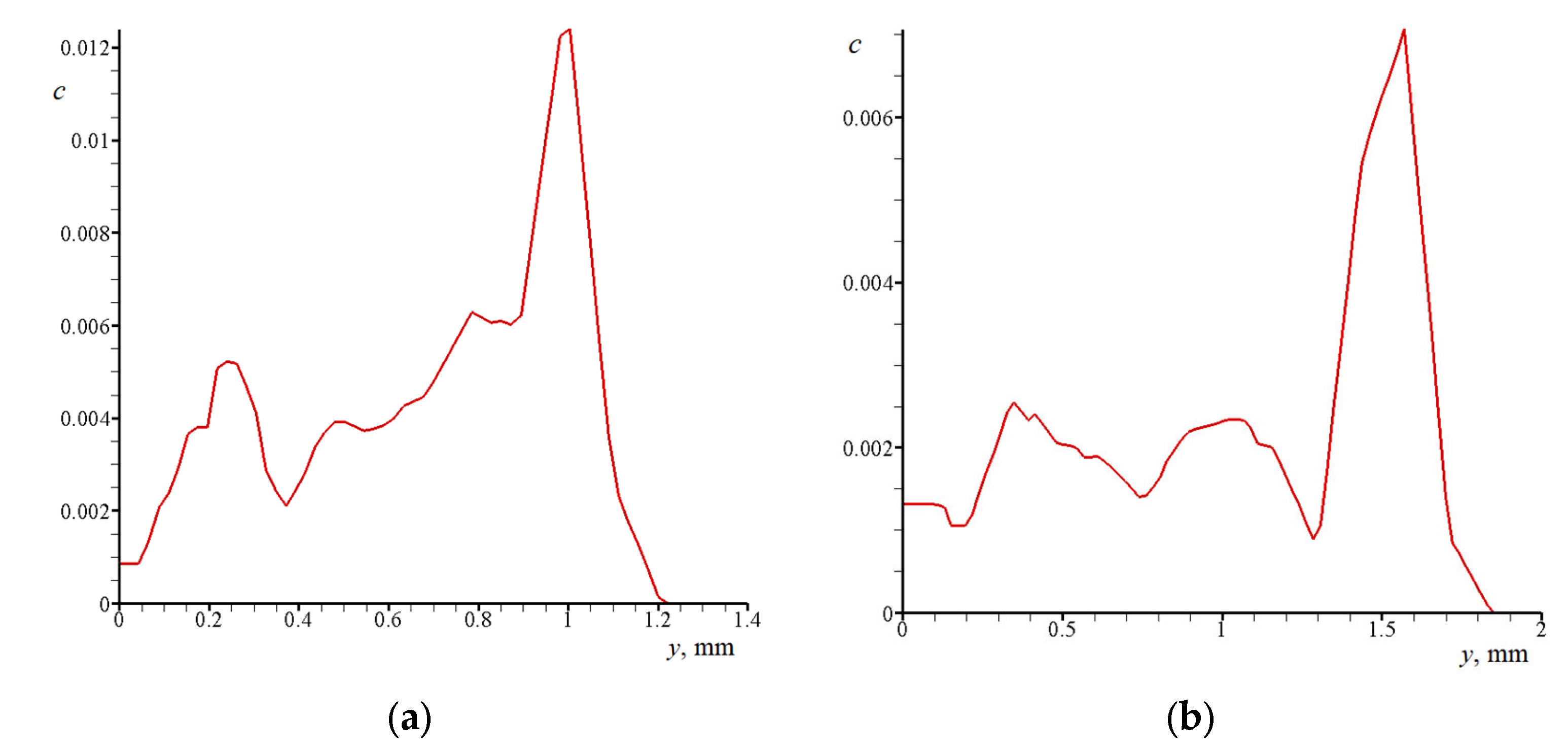
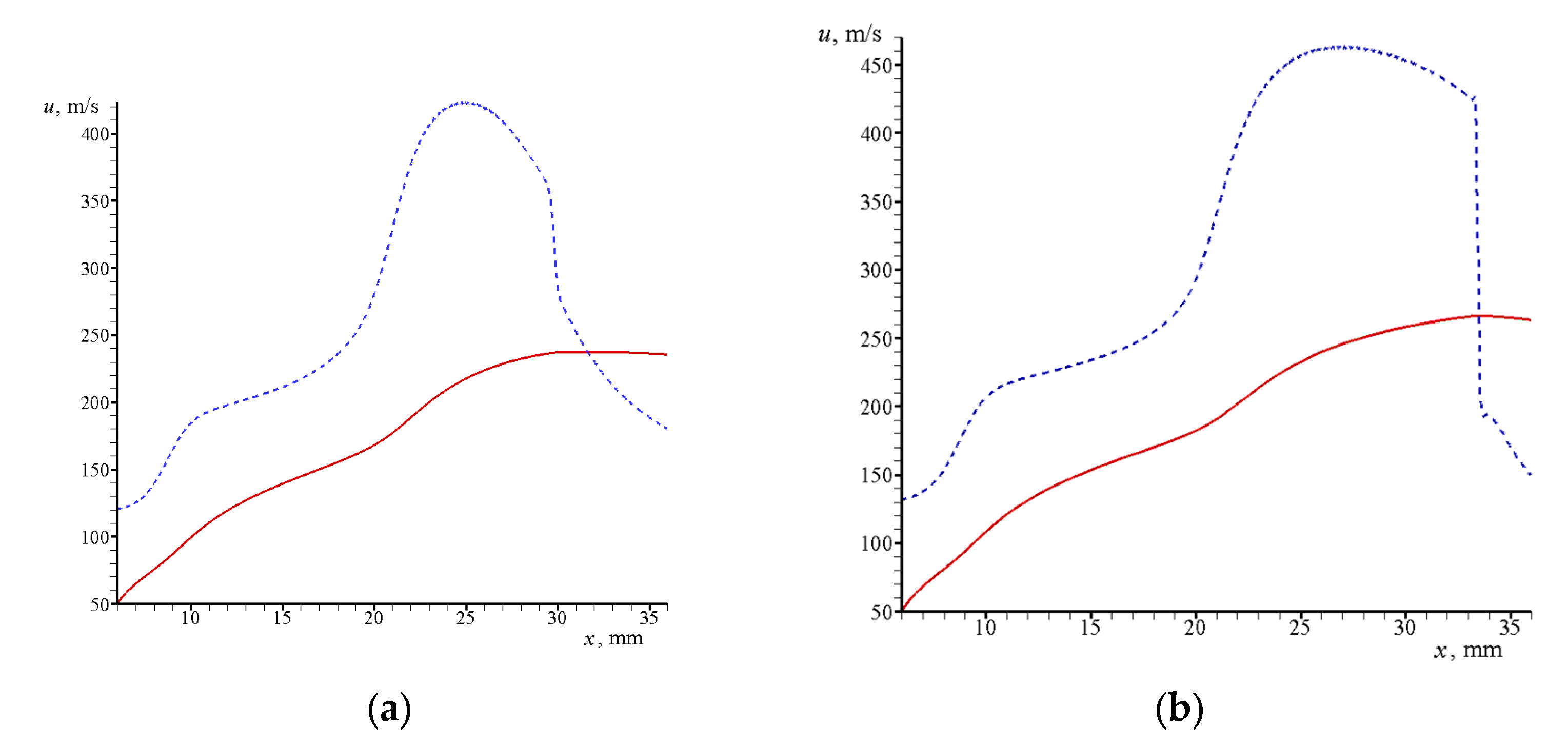
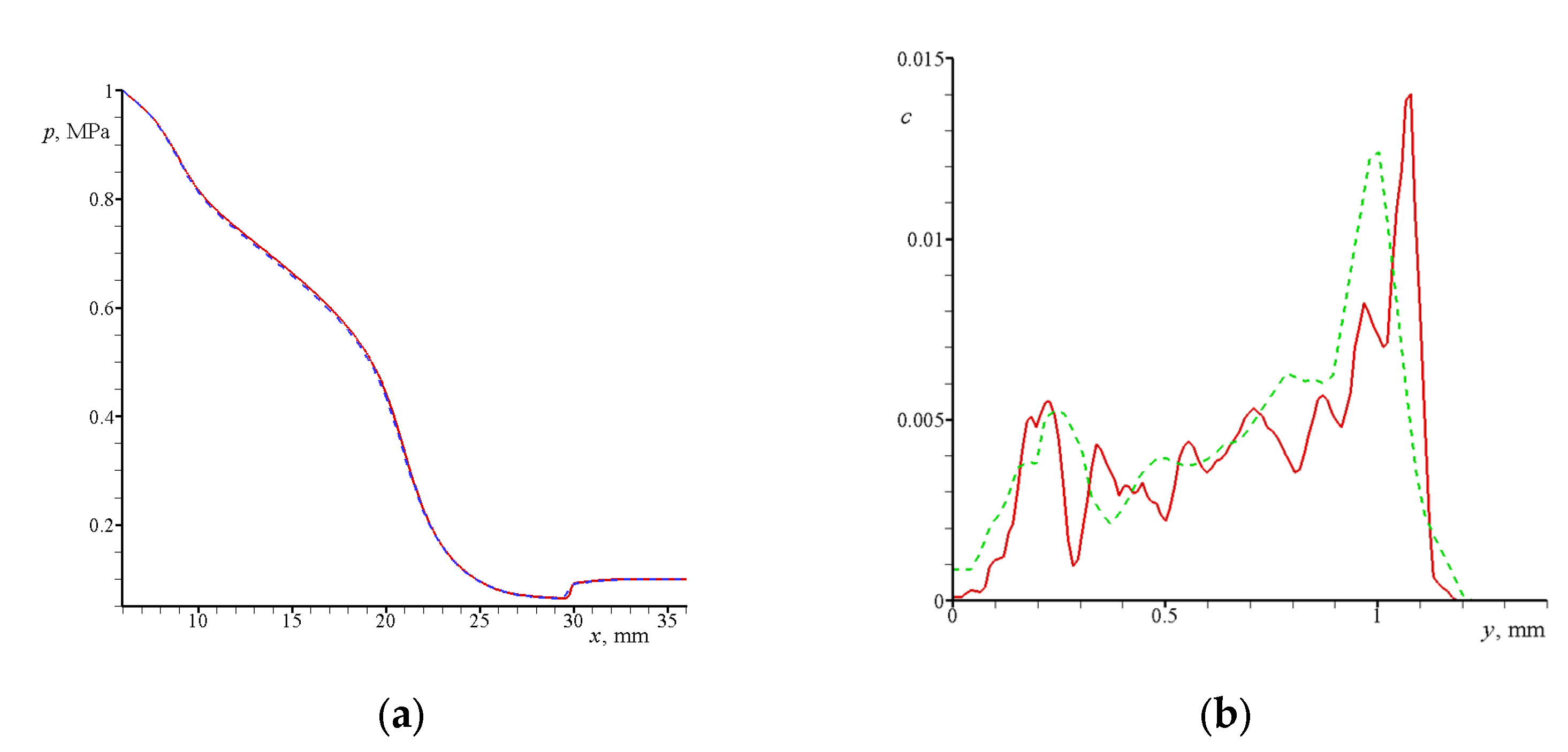
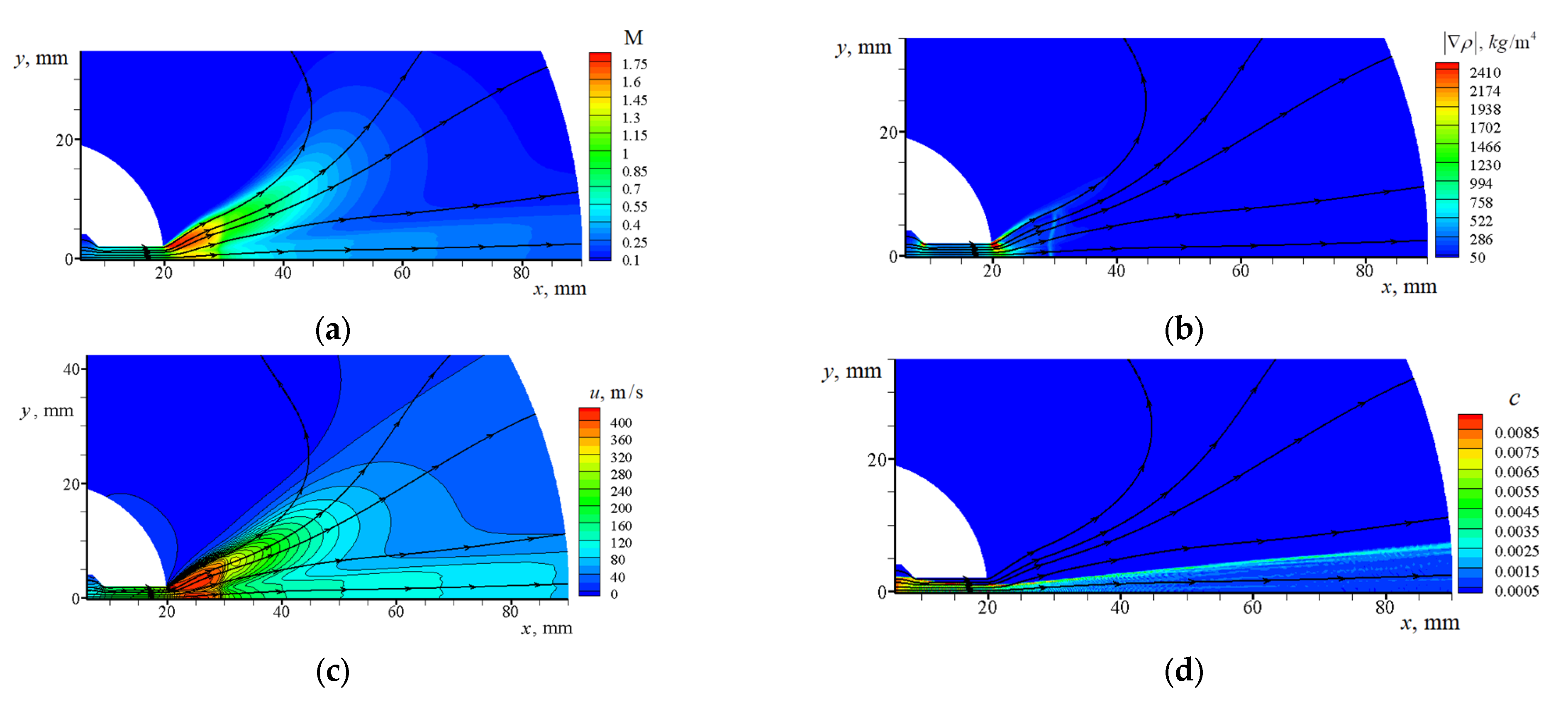
3.2.1. Jet in between Narrow Disks
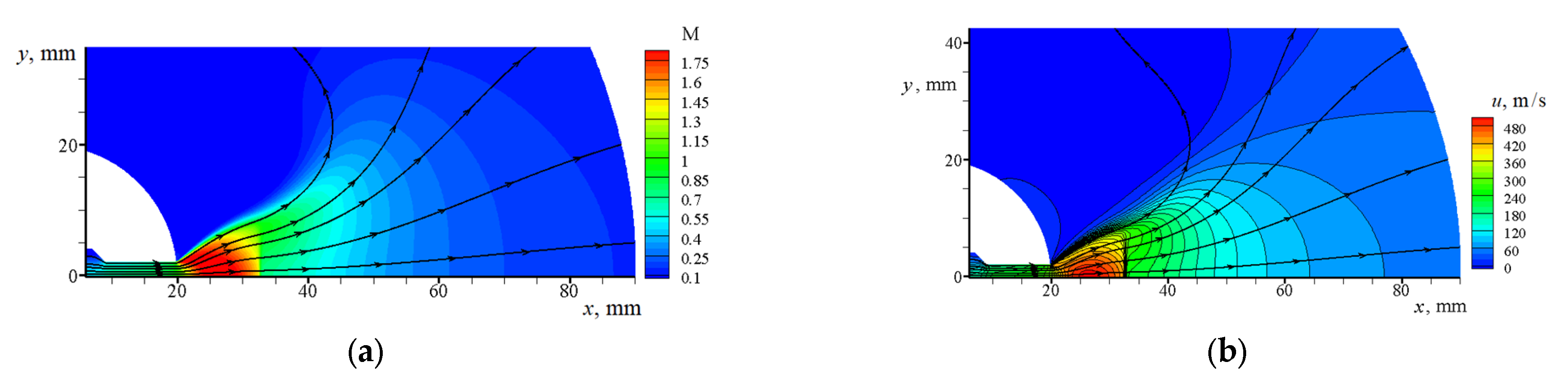
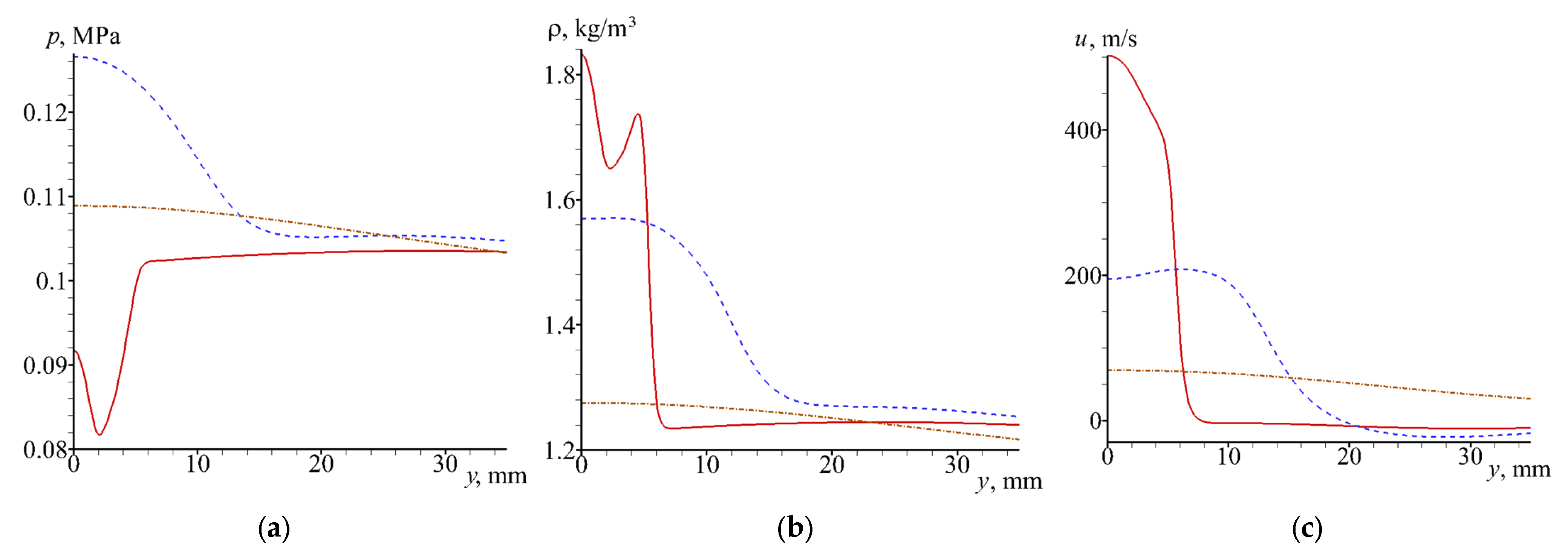
3.2.2. Jet in between Widely Spaced Disks
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| t | Time |
| x | Longitudinal coordinate axis |
| y | Transversal coordinate axis |
| u | Longitudinal gas velocity |
| v | Transversal gas velocity |
| q | Velocity vector modulus |
| p | Gas pressure |
| ρ | Gas density |
| E | Gas specific internal energy |
| T | Gas temperature |
| a | Speed of sound |
| μ | Dynamic viscosity |
| M | Mach number |
| λ | Thermal conductivity |
| Cv | Heat capacity in the pas at constant volume |
| Cp | Heat capacity in the pas at constant pressure |
| γ | Poisson’s adiabatic exponent |
| Re | Reynolds number |
| Pr | Prandtl number |
| Nu | Nusselt number |
| Re12 | Relative Reynolds number |
| M12 | Relative Mach number |
| f | Distribution function of particles |
| n | Concentration of particles |
| ρP | Density of the particle |
| dp | Diameter of the particle |
| xP | Longitudinal particle coordinate |
| yP | Transversal particle coordinate |
| uP | Longitudinal particle velocity |
| vp | Transversal particle velocity |
| TP | Particle temperature |
| apx | Longitudinal particle acceleration |
| apy | Transversal particle acceleration |
| qP | Flux of heat to the particle |
| Cd | Drag coefficient of the particle |
| Cs | Heat capacity of the particle material |
| Cw | Drag coefficient of the friction force acting from the disk |
| τx | Longitudinal component of the friction force acting from the disk |
| τy | Transversal component of the friction force acting from the disk |
| Fx | Longitudinal component of the friction force acting from the particles |
| Fy | Transversal component of the friction force acting from the particles |
| Q | Flux of energy from particles |
| Number of gas cells | |
| Number of particle cells | |
| Jet width | |
| Momentum flux | |
| Average pressure | |
| Average gas density | |
| Average longitudinal gas velocity |
Appendix A
- 1.
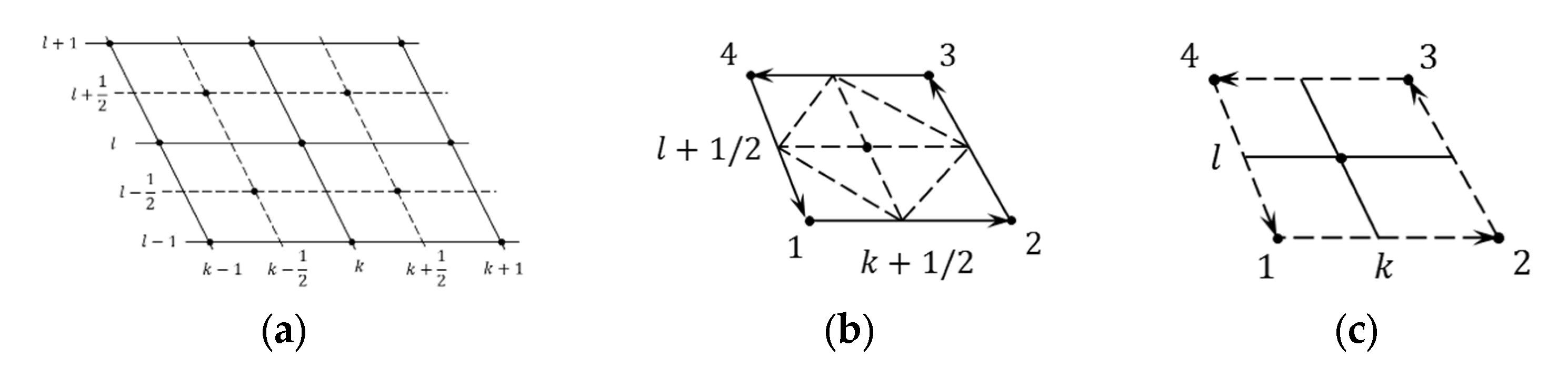
- Numerical calculation scheme.
- 2.
- Numerical scheme for 2D calculation on an irregular difference grid.
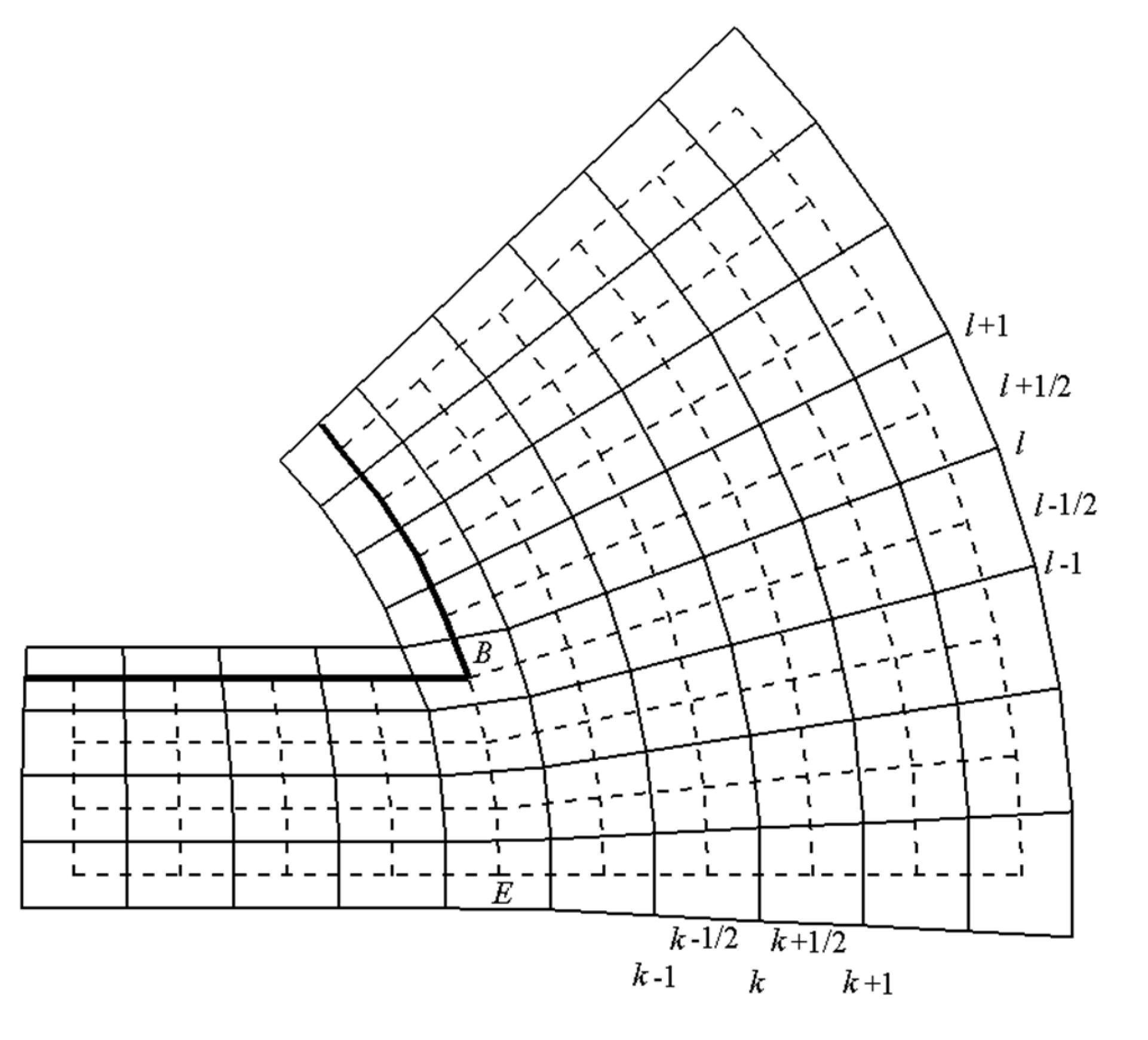
References
- Kiselev, S.P.; Kiselev, V.P.; Klinkov, S.V.; Kosarev, V.F.; Zaikovskii, V.N. Study of the gas-particle radial supersonic jet in the cold spraying. Surf. Coatings Technol. 2017, 313, 24–30. [Google Scholar] [CrossRef]
- Kiselev, S.P.; Kiselev, V.P.; Zaikovskii, V.N. Gas flows in radial micro-nozzles with pseudo-shocks. Shock Waves 2017, 28, 829–849. [Google Scholar] [CrossRef]
- Marayikkottu, A.V.; Levin, D.A. Influence of particle non-dilute effects on its dispersion in particle-laden blast wave systems. J. Appl. Phys. 2021, 130, 034701. [Google Scholar] [CrossRef]
- Volkov, A.N.; Tsirkunov, Y.M.; Olsterle, B. Numerical simulation of a supersonic gas-solid flow over a blunt body: The role of inter-particle collisions and two-way coupling effects. Int. J. Multiph. Flow 2005, 31, 1244–1275. [Google Scholar] [CrossRef]
- Li, M.; Li, L.; Shao, L.; Li, Q.; Zou, Z.; Li, B. Numerical analysis of the particle dynamics in a supersonic gas stream with a modified point-particle Euler-Lagrange approach. Metallurg. Mater. Trans. B 2021, 52, 1034–1051. [Google Scholar] [CrossRef]
- Capacelatro, J. Modeling high-speed gas-particle flows relevant to spacecraft landings. Int. J. Multiph. Flow 2022, 150, 104008. [Google Scholar] [CrossRef]
- Mehta, Y.; Salari, K.; Jackson, T.L.; Balachandar, S. Effect of Mach number and volume fraction in air-shock interacting with a bed of randomly distributed spherical particles. Phys. Rev. Fluids 2019, 4, 014303. [Google Scholar] [CrossRef]
- Mehta, Y.; Jackson, T.L.; Balachandar, S. Pseudo-turbulence in inviscid simulations of shock interacting with a bed of randomly distributed particles. Shock Waves 2020, 30, 49–62. [Google Scholar] [CrossRef]
- Kiselev, S.P.; Vorozhtsov, E.V.; Fomin, V.M. Foundations of Fluid Mechanics with Applications: Problem Solving Using Mathematica; Birkhauser: Boston, MA, USA, 1999; ISBN 978-1-4612-7198-7. [Google Scholar]
- Boiko, V.; Kiselev, V.; Kiselev, S.; Papyrin, A.; Poplavsky, S.; Fomin, V. Shock wave interaction with a cloud of particles. Shock Waves 1997, 7, 275–285. [Google Scholar] [CrossRef]
- Kiselev, S.P.; Kiselev, V.P.; Vorozhtsov, E.V. Interaction of a shock wave with a particle cloud of finite size. Shock Waves 2006, 16, 53–64. [Google Scholar] [CrossRef]
- Crowe, C.T. Review—Numerical models for dilute gas-particle flows. J. Fluids Eng. 1982, 104, 297–303. [Google Scholar] [CrossRef]
- Crowe, C.T.; Sharma, M.P.; Stock, D.E. The Particle-Source-In Cell (PSI-CELL) Model for Gas-Droplet Flows. J. Fluids Eng. 1977, 99, 325–332. [Google Scholar] [CrossRef]
- Jacobs, G.B.; Don, W.S. A high-order WENO-Z finite difference based particle-source-in cell method for computation of particle-laden flows with shocks. J. Comput. Phys. 2009, 228, 1365–1379. [Google Scholar] [CrossRef]
- Davis, S.L.; Dittmann, T.B.; Jacobs, G.B.; Don, W.S. Dispersion of a cloud of particles by a moving shock: Effects of the shape, angle of rotation, and aspect ratio. J. Appl. Mech. Tech. Phys. 2013, 54, 900–912. [Google Scholar] [CrossRef]
- Kiselev, S.P.; Kiselev, V.P. Numerical Simulation of nanoparticle acceleration in a Laval micronozzle with subsequent deceleration in a wall compression layer. Int. J. Aerosp. Innov. 2009, 1, 117. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, J.; Yin, Z.; Bao, F. Numerical simulation of non-spherical submicron particle acceleration and focusing in a converging-diverging micronozzle. Appl. Sci. 2022, 12, 343. [Google Scholar] [CrossRef]
- Shershnev, A.; Kudryavtsev, A.N. Numerical simulation of particle beam focusing in a supersonic nozzle with rectangular cross-section. J. Phys. Conf. Ser. 2019, 1404, 012042. [Google Scholar] [CrossRef]
- Semilitsch, B.; Mihăescu, M. Evaluation of injection strategies in supersonic nozzle flow. Aerospace 2021, 8, 369. [Google Scholar] [CrossRef]
- Horner, C.N.; Sescu, A.; Afsar, M.; Collins, E. Numerical investigation of a rectangular jet exhausting over a flat plate with periodic surface deformations at the trailing edge. Aerospace 2021, 8, 314. [Google Scholar] [CrossRef]
- Abramovich, G.N. Applied Gas Dynamics; Nauka: Moscow, Russia, 1976. [Google Scholar]
- Landau, L.D.; Lifschitz, E.M. Hydrodynamics; Nauka: Moscow, Russia, 1986; ISBN 5-02-013850-9. [Google Scholar]
- Henderson, C.B. Drag coefficients of spheres in continuum and rarefied flows. AIAA J. 1967, 14, 707–708. [Google Scholar] [CrossRef]
- Dulov, V.G.; Luk’yanov, G.A. Gas Dynamics of Exhaustion Processes; Nauka: Moscow, Russia, 1984. [Google Scholar]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1983, 49, 357. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Kulikovskii, A.G.; Pogorelov, N.V.; Semenov, A.Y. Mathematical Aspects of Numerical Solution of Hyperbolic Systems; Fizmatlit: Moscow, Russia, 2012; ISBN 978-5-9221-1198-0. [Google Scholar]
- Lax, P.D.; Wendroff, B. Systems of coservation laws. Communs Pure Appl. Math. 1960, 13, 217–237. [Google Scholar] [CrossRef]
- Shu, C.W. High order ENO and WENO schemes for computational fluid dynamics in high-order methods for computational physics. In Lecture Notes in Computational Science and Engineering; Barth, T.J., Deconinck, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 9, pp. 439–582. [Google Scholar] [CrossRef]
- Anderson, D.A.; Tannehill, J.C.; Pletcher, R.H. Computional Fluid Mechanics and Heat Transfer; Hemisphere Publishing Corporation: London, UK, 1984. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiselev, S.; Kiselev, V.; Zaikovskii, V. Numerical Simulation of the Flow in Two-Phase Supersonic Underexpanded Gas–Particle Jets Exhausting into a Slotted Submerged Space. Aerospace 2022, 9, 432. https://doi.org/10.3390/aerospace9080432
Kiselev S, Kiselev V, Zaikovskii V. Numerical Simulation of the Flow in Two-Phase Supersonic Underexpanded Gas–Particle Jets Exhausting into a Slotted Submerged Space. Aerospace. 2022; 9(8):432. https://doi.org/10.3390/aerospace9080432
Chicago/Turabian StyleKiselev, Sergey, Vladimir Kiselev, and Viktor Zaikovskii. 2022. "Numerical Simulation of the Flow in Two-Phase Supersonic Underexpanded Gas–Particle Jets Exhausting into a Slotted Submerged Space" Aerospace 9, no. 8: 432. https://doi.org/10.3390/aerospace9080432
APA StyleKiselev, S., Kiselev, V., & Zaikovskii, V. (2022). Numerical Simulation of the Flow in Two-Phase Supersonic Underexpanded Gas–Particle Jets Exhausting into a Slotted Submerged Space. Aerospace, 9(8), 432. https://doi.org/10.3390/aerospace9080432





