Aircraft Autonomous Separation Assurance Based on Cooperative Game Theory
Abstract
1. Introduction
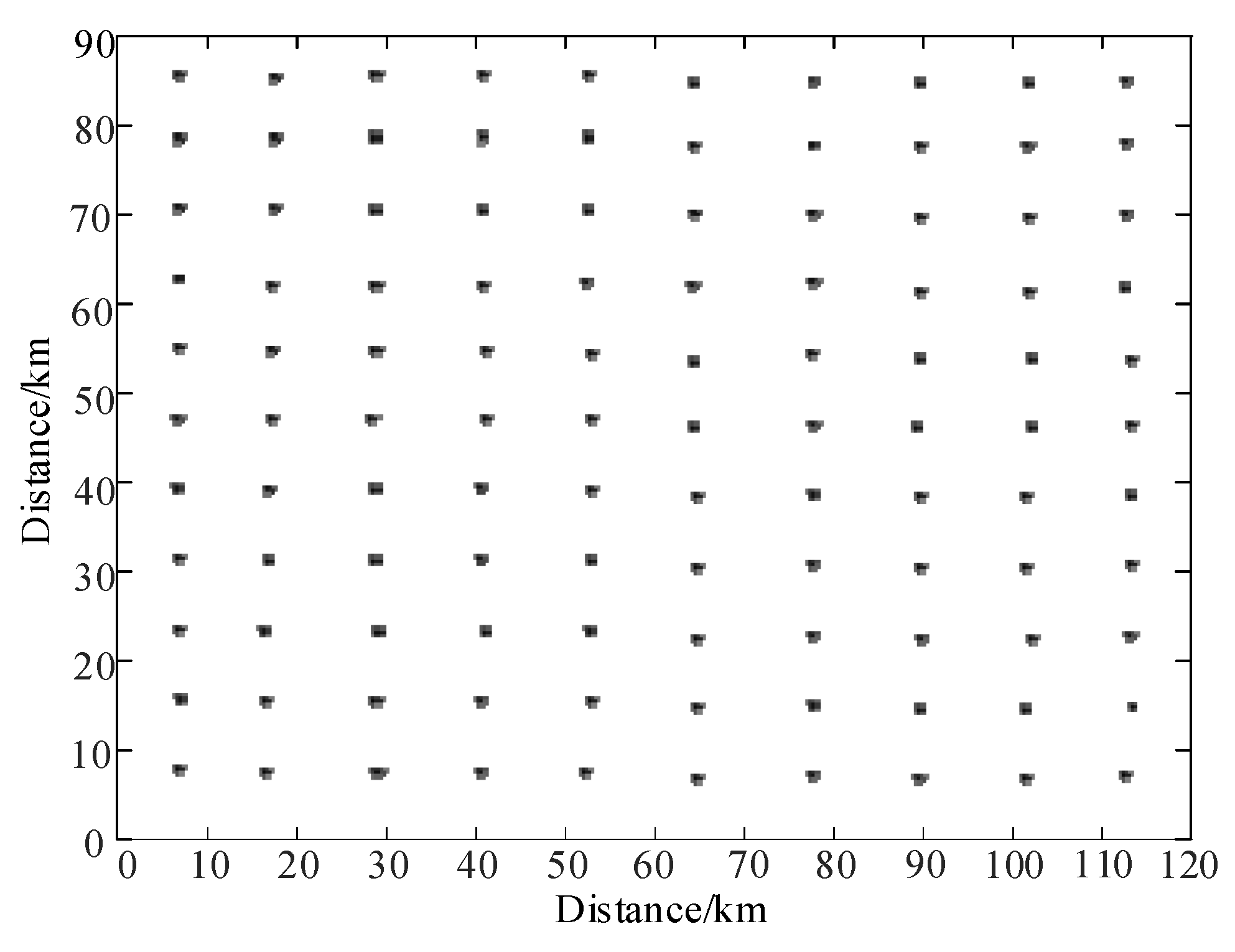
2. Instantaneous Wind Field Model
2.1. Aircraft Speed Triangle
2.2. Instantaneous Wind Field Model
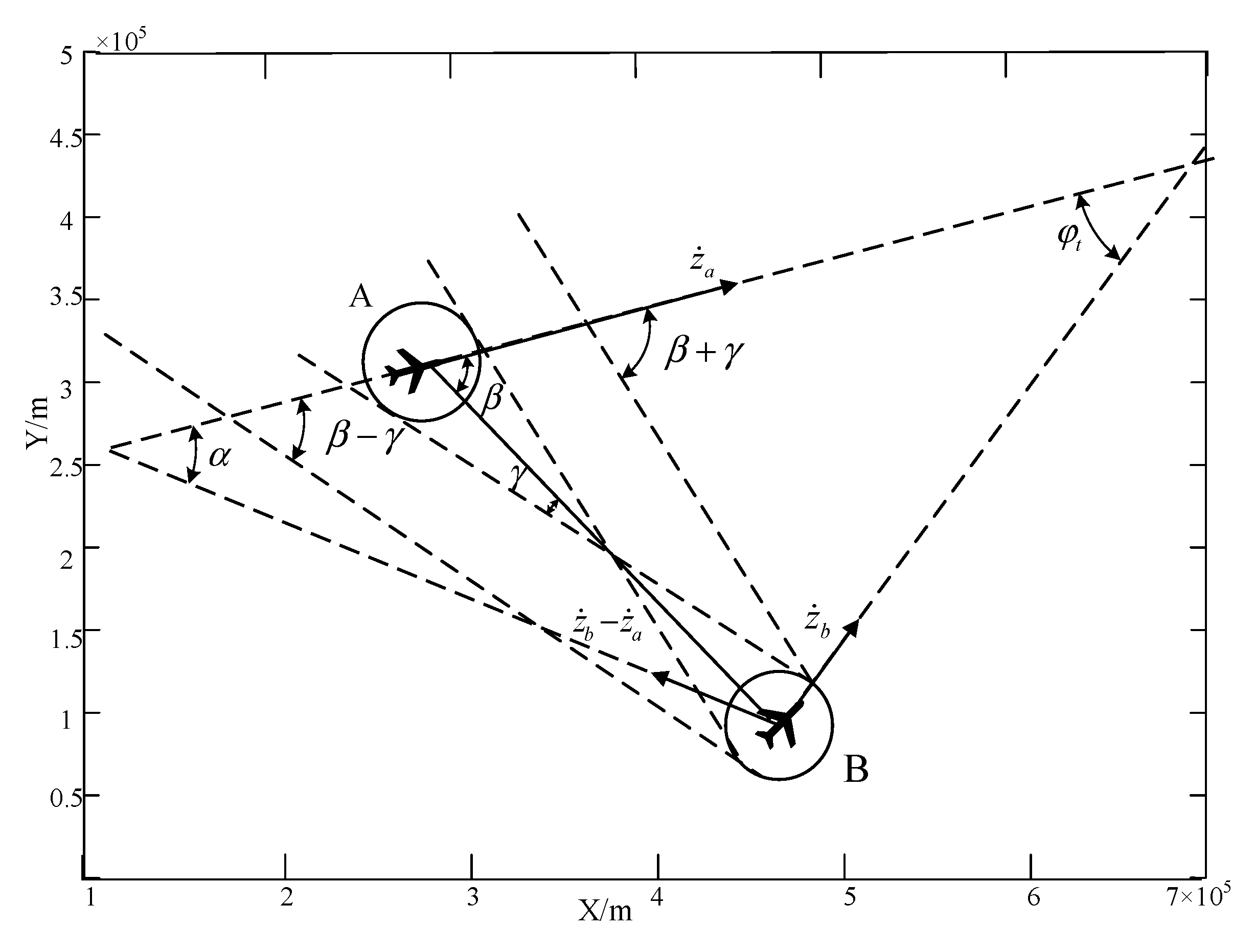
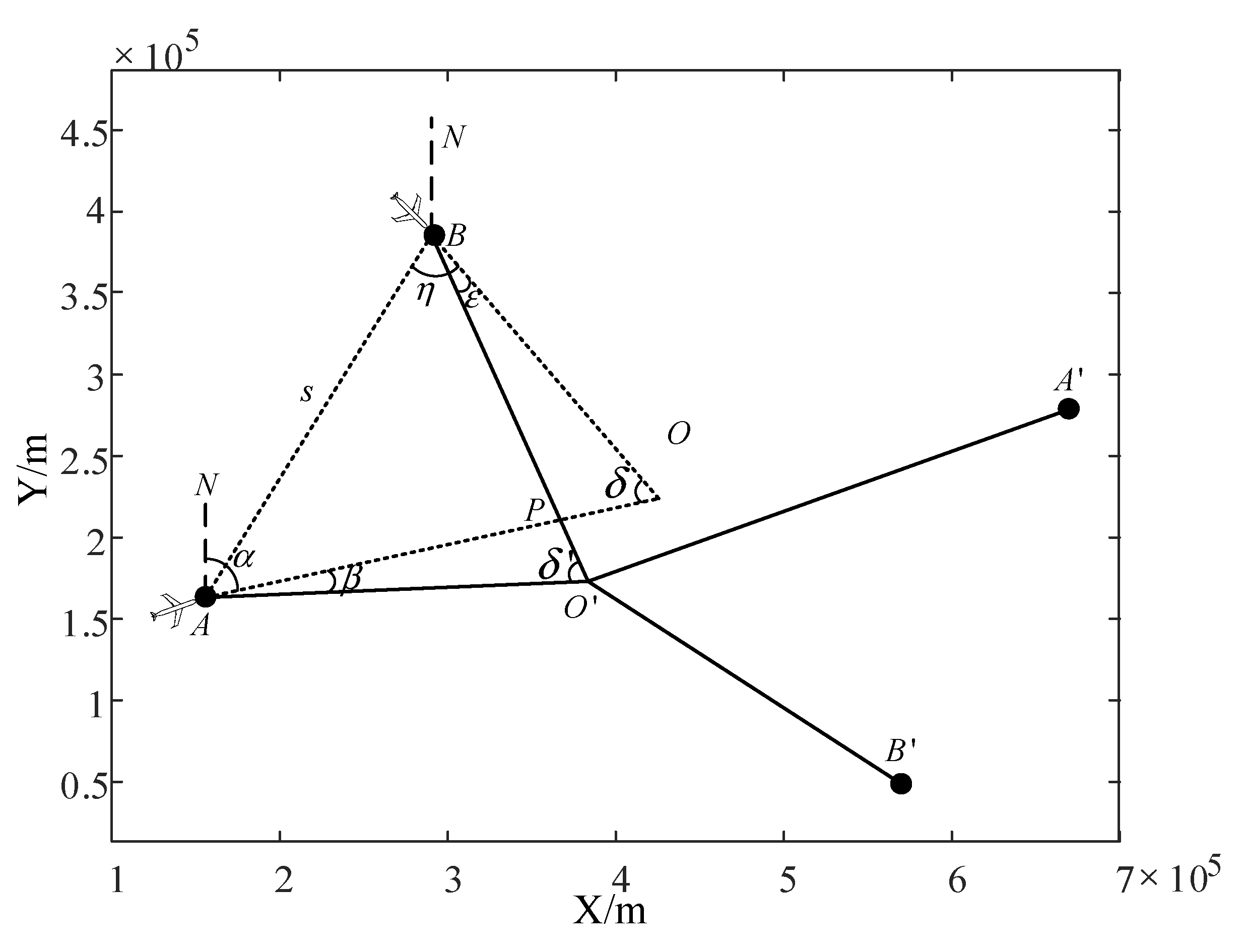
3. Conflict Detection Algorithm
4. Game Theory
4.1. Basics of Game Theory
- Player: a decision subject who independently chooses to act in the process of a game.
- Information: the knowledge possessed by a player in the process of a game that is useful for decision making, mainly including the rules of the system and the decisions of other players.
- Order: the order in which the game parties make their decisions.
- Strategies: the entire set of behaviors or strategies that game parties can choose.
- Payoff: the gain or loss that results from a decision made by a game party.
- Outcome: The set of elements that interest the gamer, including the chosen strategy, payoffs, and strategic paths.
4.2. Horizontal Cross-Conflict Scenario Model Based on Cooperative Game Theory
- Strategy space:
- 2.
- Utility function:
- 3.
- Priority:
- 4.
- Union welfare functions:
- 5.
- Conflict detection distance:
- 6.
- Safety separation:
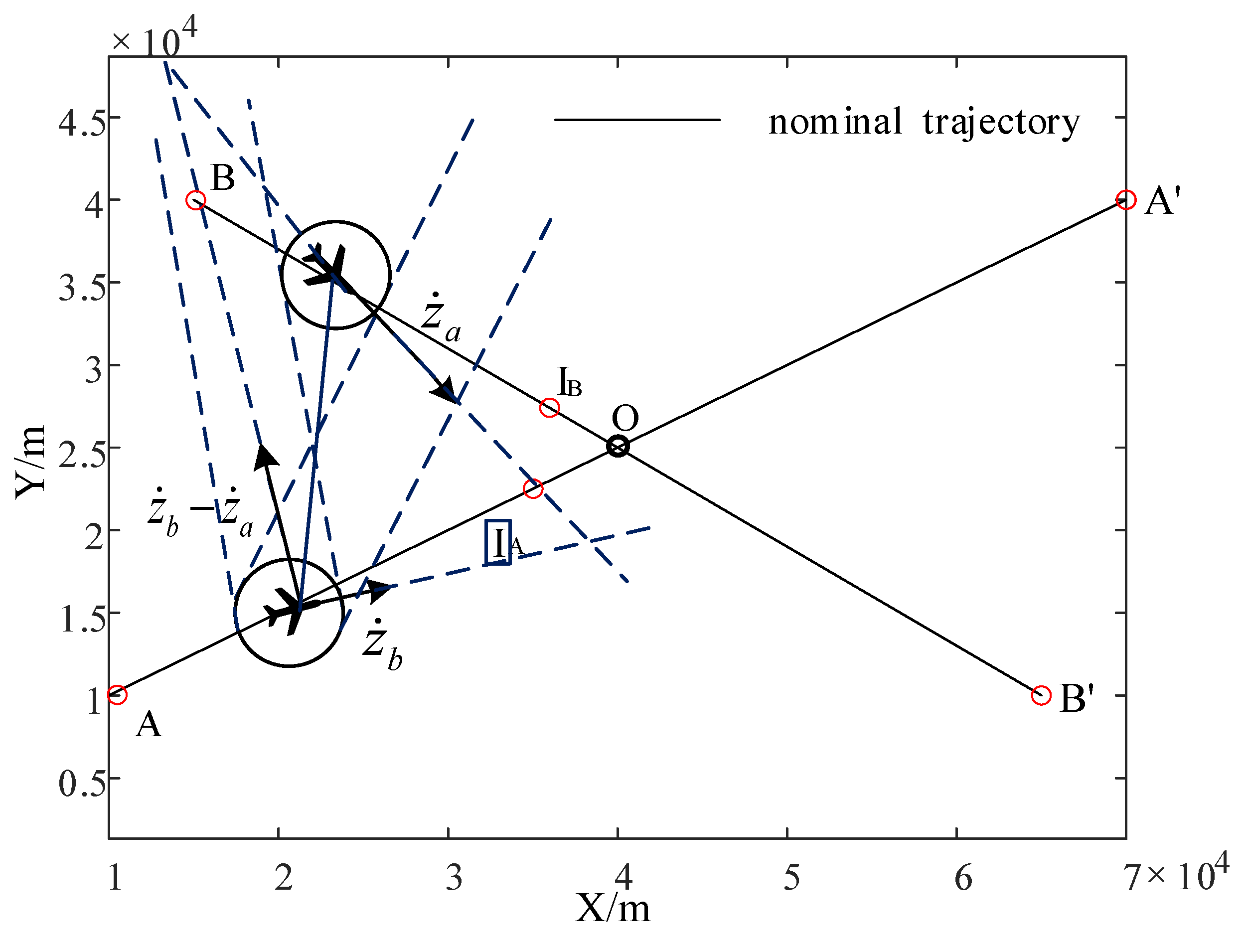
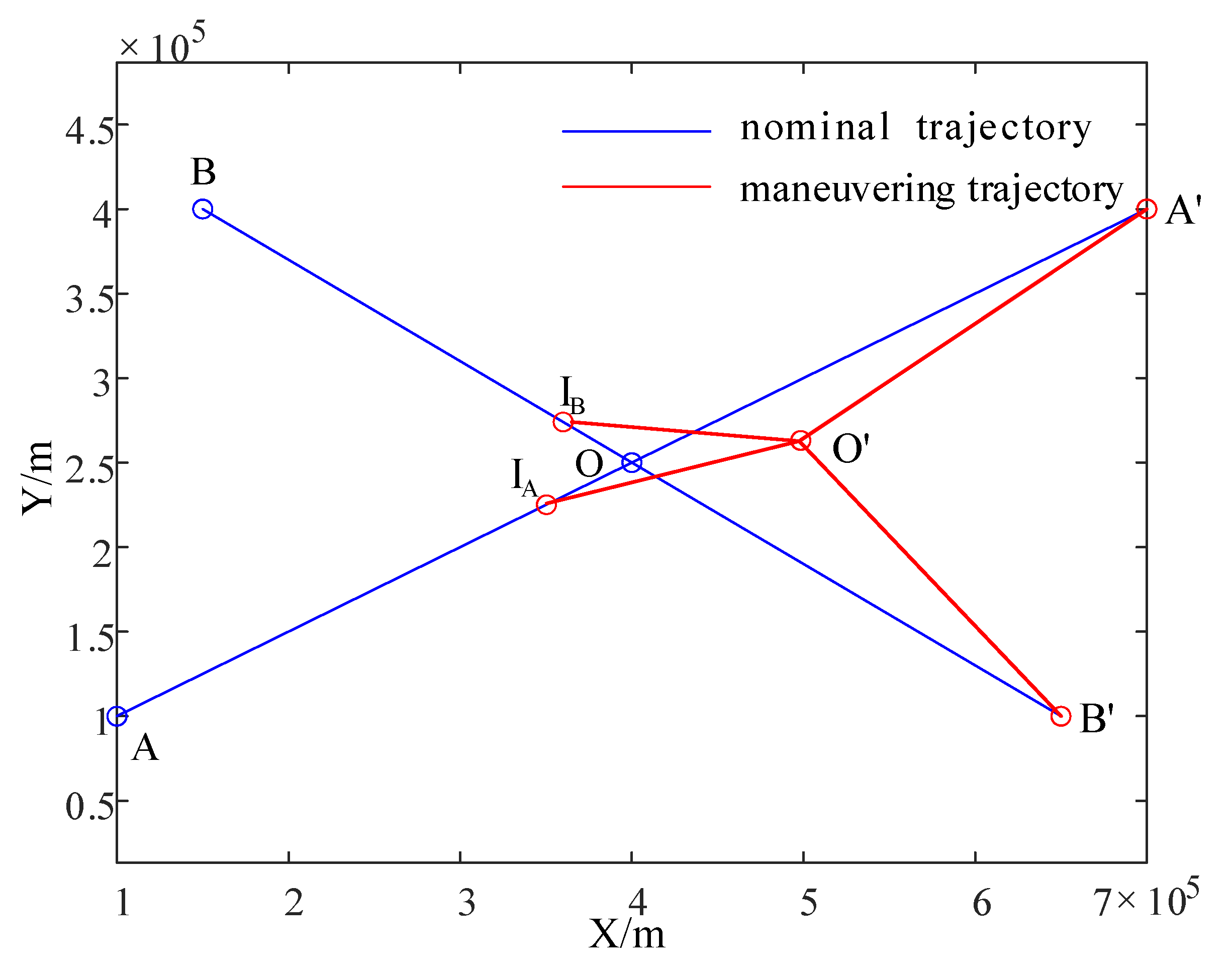
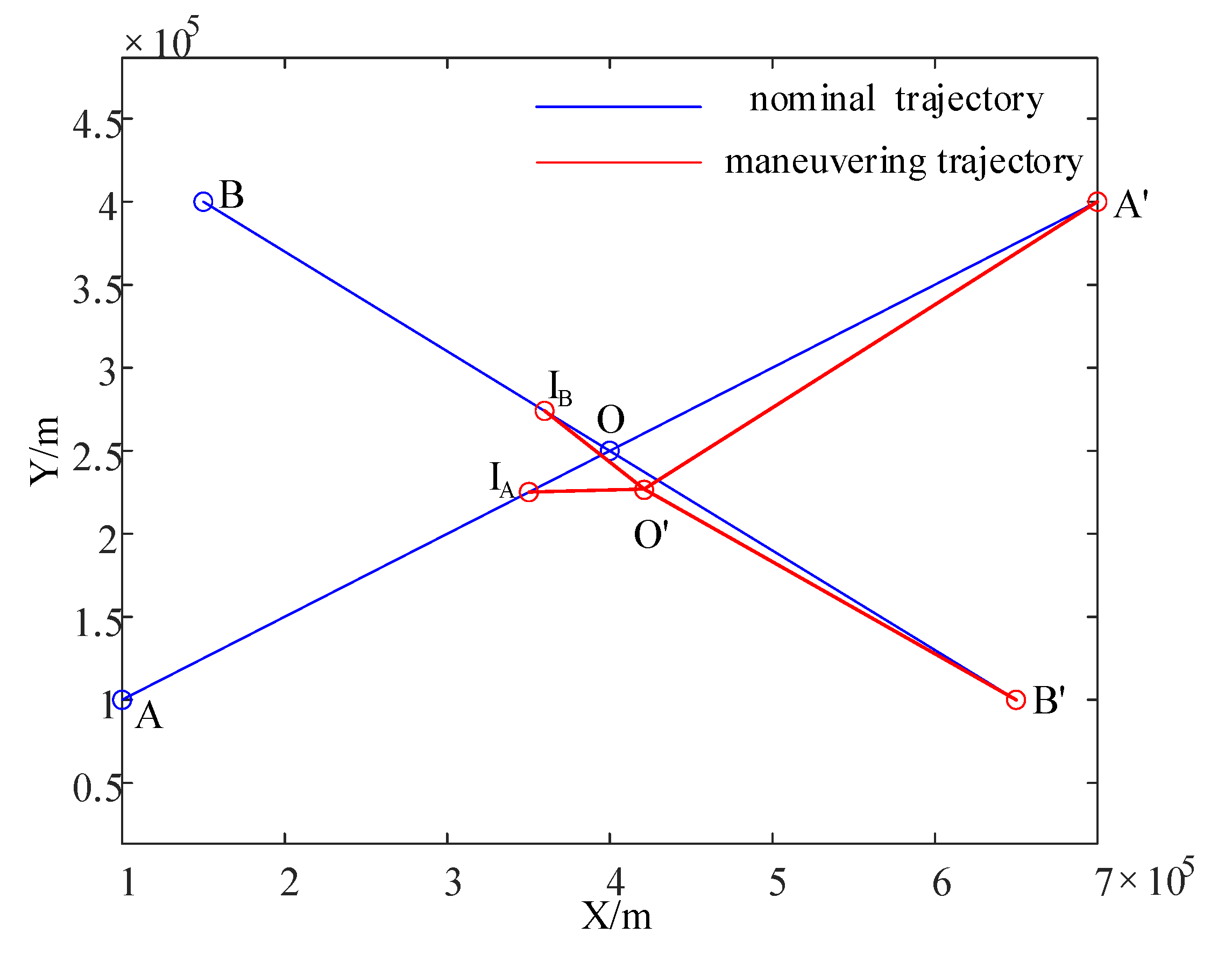
5. Simulation of Horizontal Cross-Conflict Scenarios
5.1. Horizontal Cross-Conflict Scenario
- 1.
- Utility function:
- 2.
- Priority
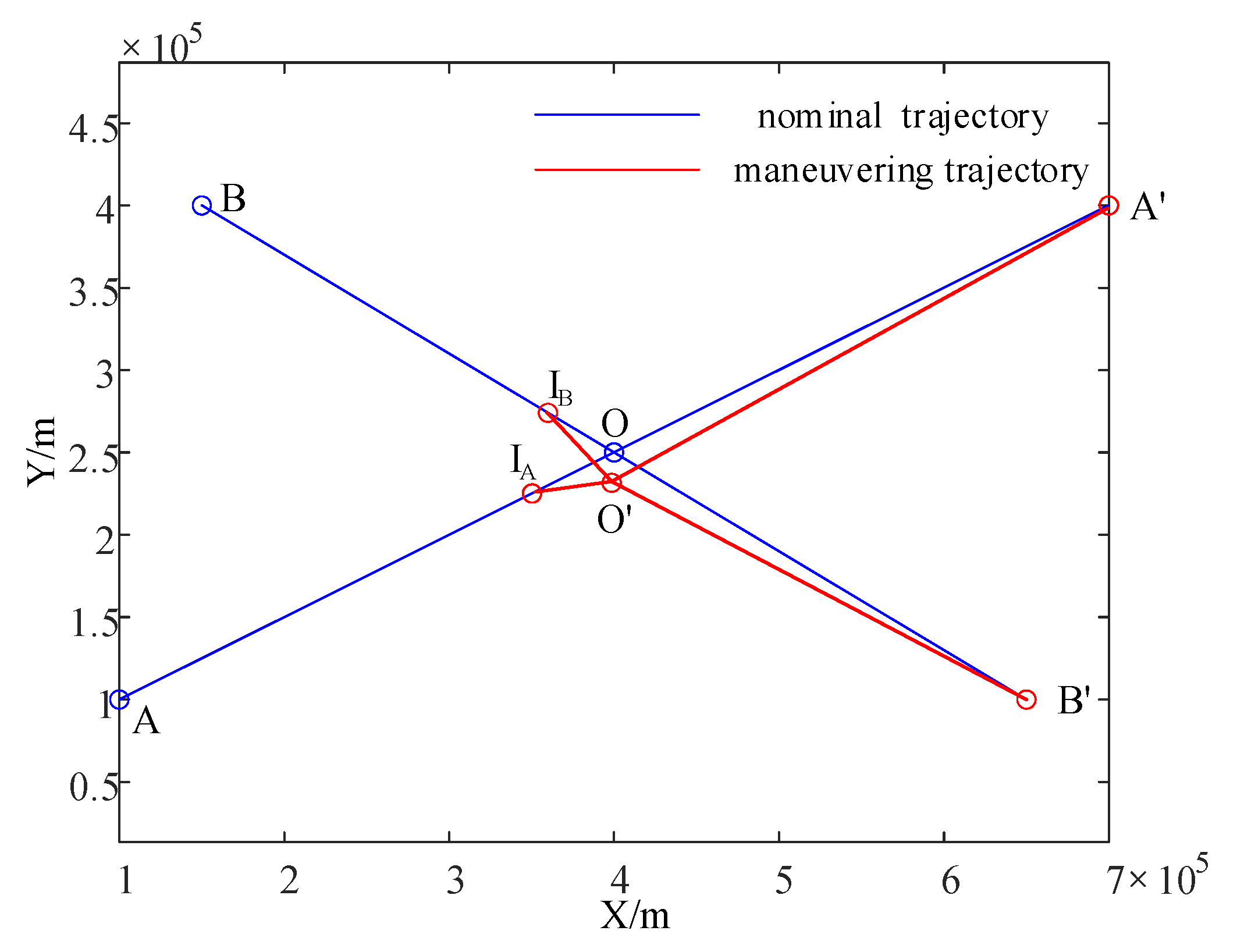
5.2. Comparison of Three Separation Assurance Strategies
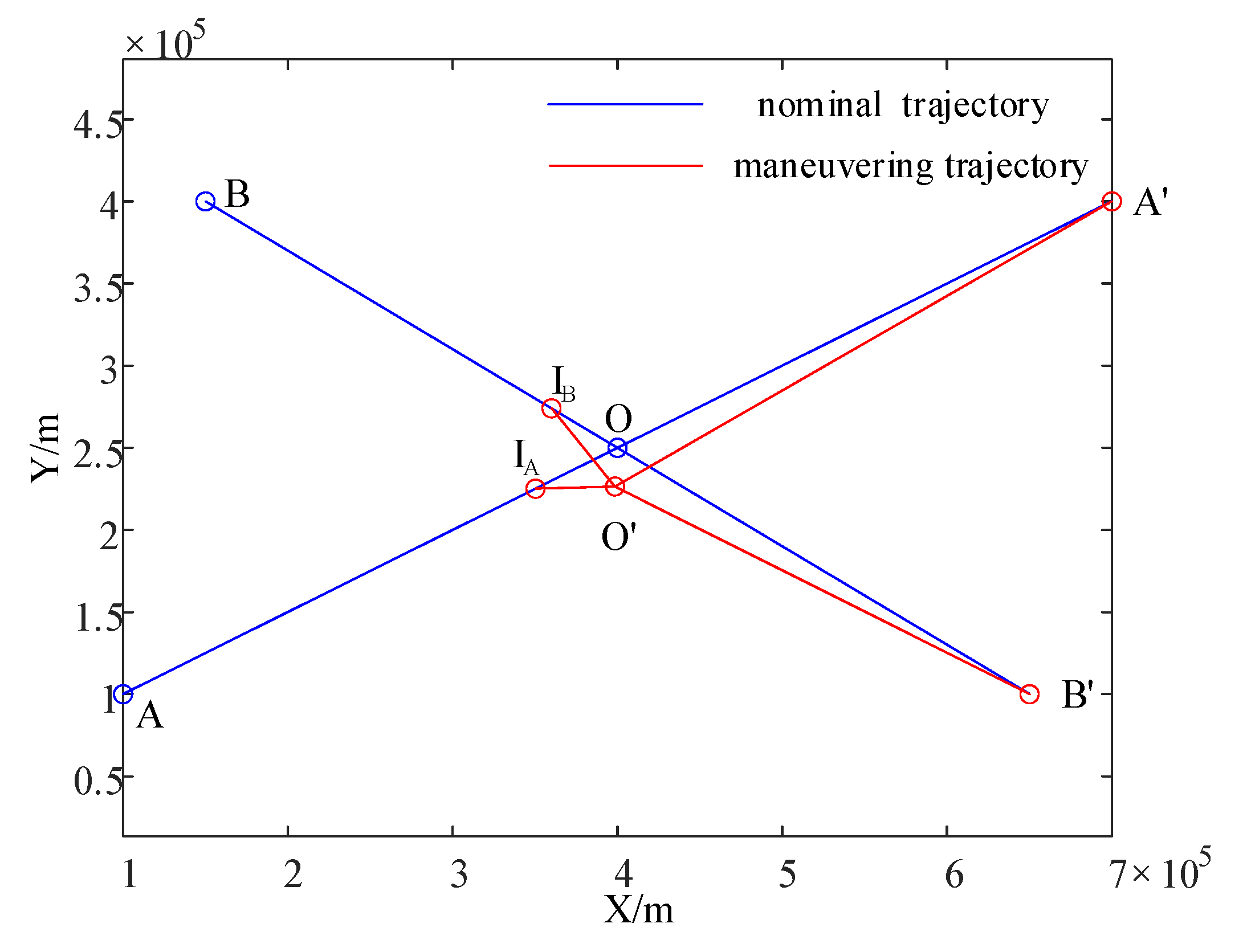
5.3. Effect of Priority on the Separation Assurance Control Law
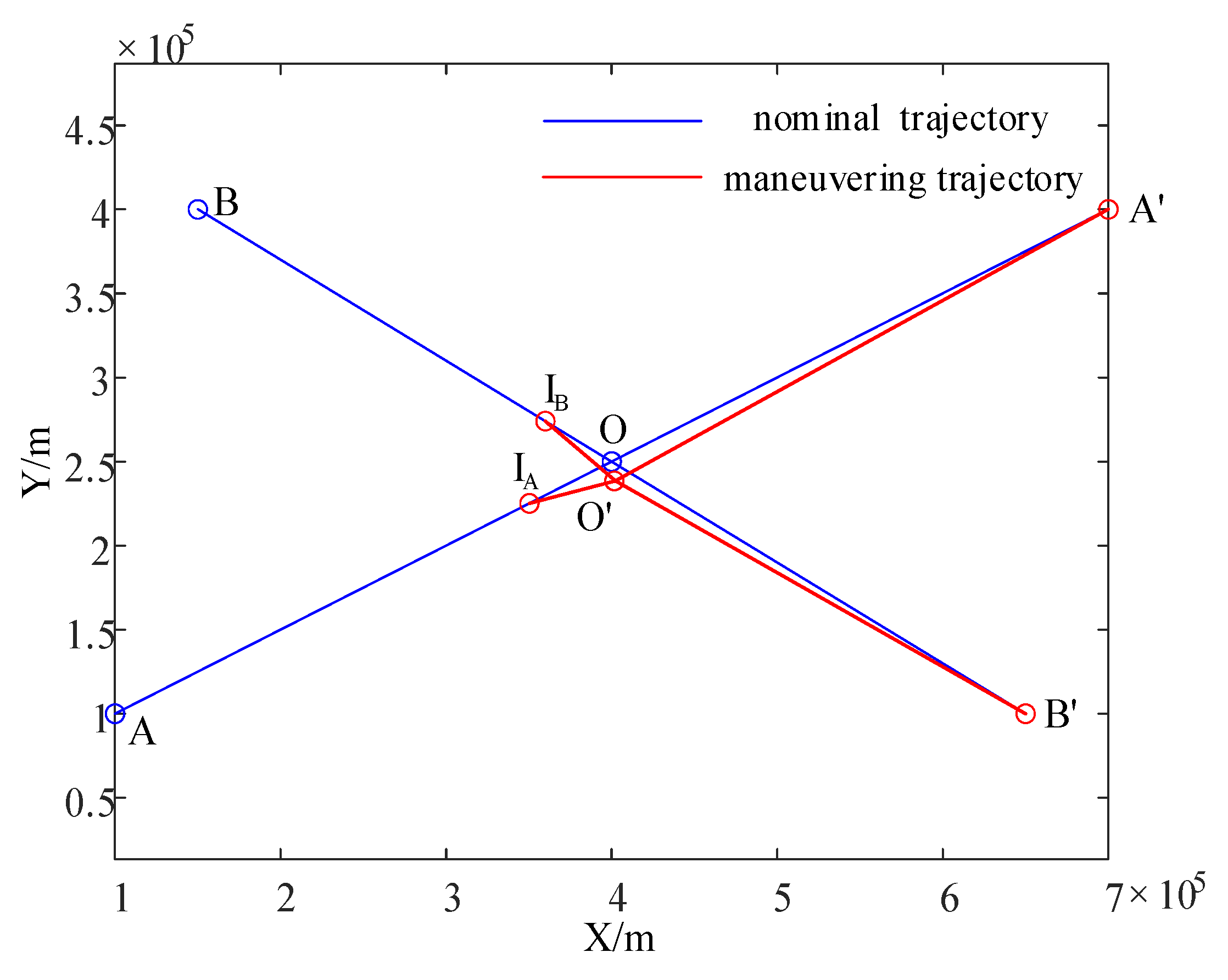
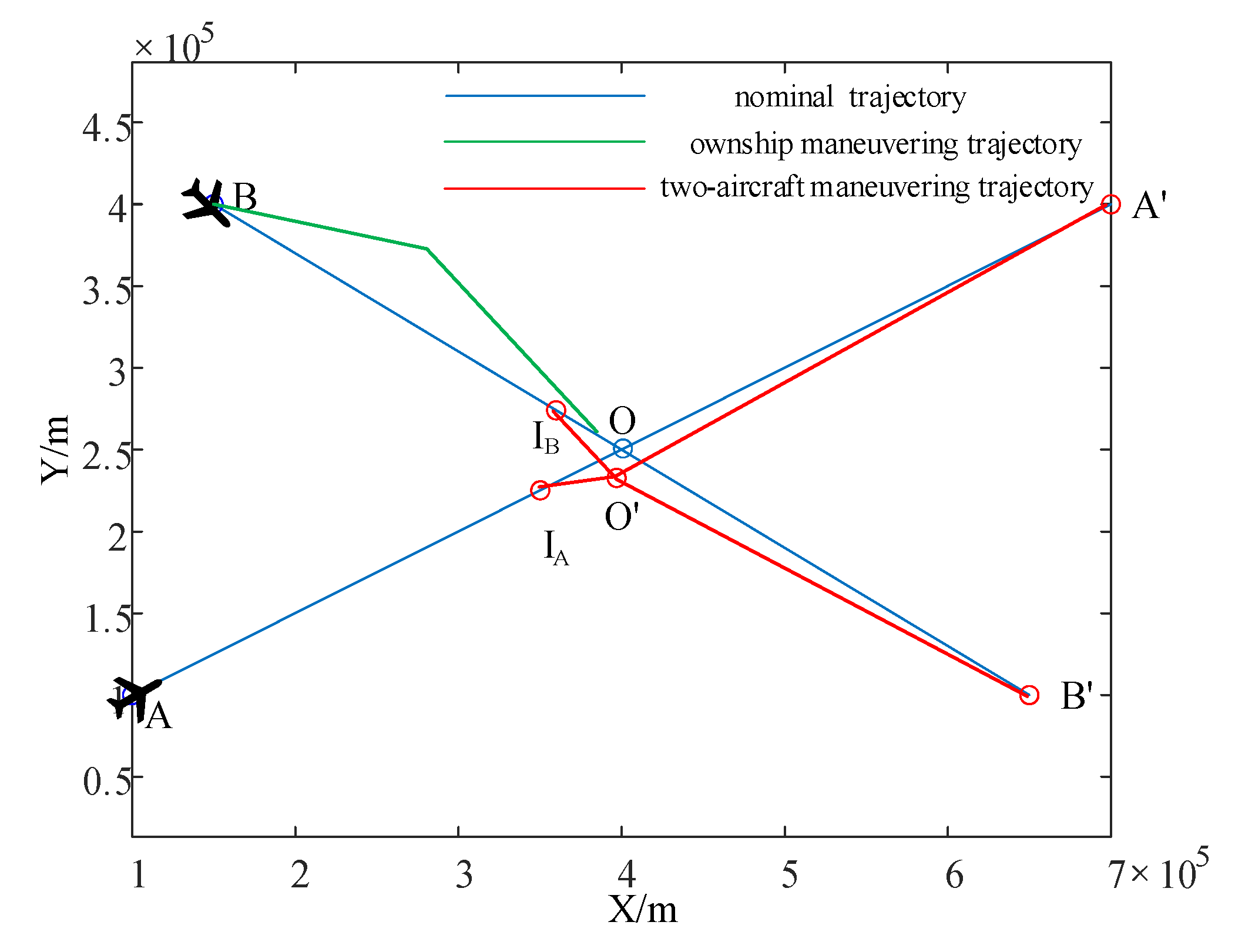
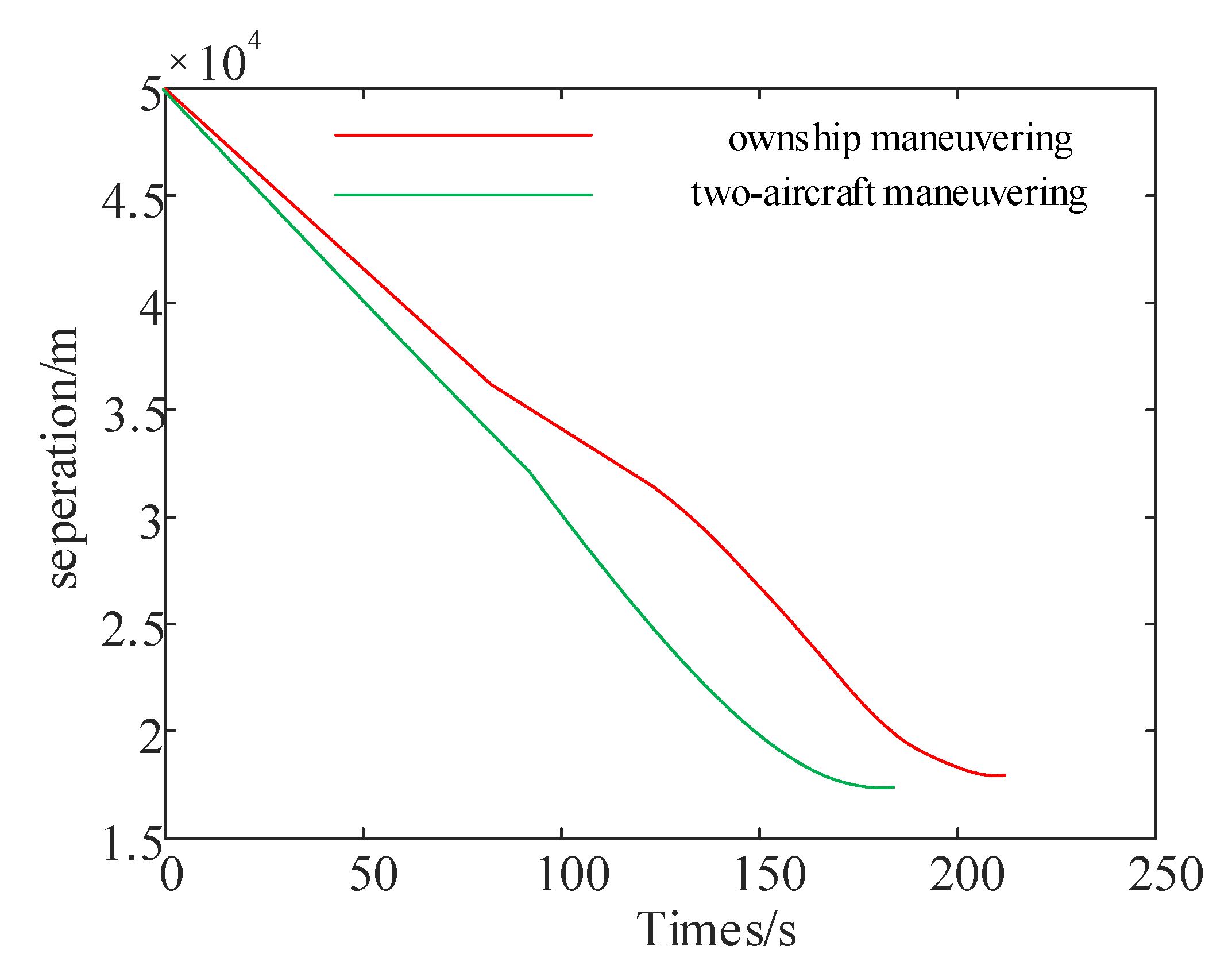
5.4. Comparison Experiments
6. Summary and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Di Stasi, L.L.; Marchitto, M.; Antolí, A.; Baccino, T.; Cañas, J.J. Approximation of on-line mental workload index in ATC simulated multitasks. J. Air Transp. Manag. 2010, 16, 330–333. [Google Scholar] [CrossRef]
- Zhang, M.; Hang, Y. Integrated evaluation of the safety controller’s workload based on improved extension evaluation model. J. Appl. Sci. 2013, 13, 2969–2973. [Google Scholar] [CrossRef][Green Version]
- Tomlin, C.; Pappas, G.J.; Sastry, S. Noncooperative conflict resolution [air traffic management]. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 10–12 December 1997; pp. 1816–1821. [Google Scholar]
- Tomlin, C.; Pappas, G.J.; Sastry, S. Conflict resolution for air traffic management: A study in multiagent hybrid systems. IEEE Trans. Autom. Control 1998, 43, 509–521. [Google Scholar] [CrossRef]
- Yang, M.; Wang, L.; Zhang, J. Coordination Method for Conflict Relief of Cooperative Vehicles in Convergence Zone Oriented to Smart High Speed. J. Transp. Eng. 2020, 20, 8. [Google Scholar]
- Cheng, Y.; Zhao, J.Y.; Wang, L. Conflict Resolution Model Based on Multi-vehicle Cooperative Optimization at Intersections. J. Transp. Syst. Eng. Inf. Technol. 2020, 20, 205–211. [Google Scholar]
- Erokhin, V.; Lezhankin, B.; Portnova, T. Bi-criteria Aircraft Trajectory Optimization in Implementing the Area Navigation Concept. Int. J. Aeronaut. Space Sci. 2021, 22, 948–962. [Google Scholar] [CrossRef]
- Xu, K.; Yin, H.; Zhang, L. Game Theory with Probabilistic Prediction for Conflict Resolution in Air Traffic Management. In Proceedings of the International Conference on Intelligent Systems & Knowledge Engineering, Coimbatore, India, 7–8 January 2016. [Google Scholar]
- Gang, S.P.; Menon, P.K. Game Theoretic Trajectory Negotiation Mechanism for Merging Air Traffic Management. In Proceedings of the AIAA Guidance, Navigation and Control Conference, Grapevine, TX, USA, 9–13 January 2017; pp. 3061–3074. [Google Scholar]
- Li, T.; Wan, Y. A fuel savings and benefit analysis of reducing separation standards in the oceanic airspace managed by the New York Air Route Traffic Control Center. Transp. Res. Part E-Logist. Transp. Rev. 2021, 152, 102407. [Google Scholar] [CrossRef]
- Baspinar, B.; Koyuncu, E. Assessment of Aerial Combat Game via Optimization-Based Receding Horizon Control. IEEE Access 2020, 8, 35853–35863. [Google Scholar] [CrossRef]
- Zhang, B.C.; Ye, Z.J.; Wang, L.L. Airport airside congestion pricing considering price discrimination between aircraft type under a Stackelberg game. Transp. Plan. Technol. 2020, 43, 48–61. [Google Scholar] [CrossRef]
- Garcia, E.; Von Moll, A.; Casbeer, D.W.; Pachter, M. Strategies for Defending a Coastline Against Multiple Attackers. In Proceedings of the 58th IEEE Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019. [Google Scholar]
- Sharma, M.G.; Singh, K.N. Modelling coopetition in aircraft spare part supply chain: Game-theoretic approach. Int. J. Procure. Manag. 2017, 10, 150–162. [Google Scholar] [CrossRef]
- Zhang, H. Flight law of aircraft in the wind. In Air Navigation, 3rd ed.; Southwest Jiao Tong University Press: Chengdu, China, 2016; p. 53. [Google Scholar]
- Lymperopoulos, L.; Lygeros, J. Sequential Monte Carlo methods for multi-aircraft trajectory prediction in air traffic management. Int. J. Adapt. Control. Signal Process. 2010, 24, 830–849. [Google Scholar] [CrossRef]
- Cole, R.E.; Richard, C.; Kim, S. Assessment of the 60 km Rapid Update Cycle (RUC) with Near Real-Time Aircraft Reports; Massachusetts Institute of Technology: Lexington, MA, USA, 1998. [Google Scholar]
- Tang, X.M.; Chen, P.; Li, B. Rolling time domain optimization of flight path conflict resolution strategy. J. Transp. Eng. 2016, 16, 74–82. [Google Scholar]
- Han, Y.X.; Tang, X.M.; Han, S.C. Optimal flight conflict resolution model for fixed routes. J. Transp. Eng. 2012, 12, 115–120. [Google Scholar]
- Fan, R. Game Theory; Wuhan University Press: Wuhan, China, 2019; pp. 1–3. [Google Scholar]
- Dong, B.; Wang, Y.; Guo, G. Cooperative Game Theory: Solution and Cost Allocation; Market Press: Beijing, China, 2008; p. 2. [Google Scholar]
- Jiang, X.; Wu, M.; Wen, X.; Tu, C.; Nie, D. Multi-aircraft Flight Conflict Relief Strategy Based on Cooperative Game. Syst. Eng. Electron. 2018, 40, 2482–2489. [Google Scholar]

| Notations | Concepts |
|---|---|
| vacuum velocity | |
| magnetic heading | |
| drift angle | |
| wind angle | |
| wind speed | |
| ground speed | |
| magnetic north |
| Variables | Concepts |
|---|---|
| vacuum velocity of the aircraft | |
| ground speed of the aircraft | |
| heading angle of the aircraft | |
| track angle of the aircraft | |
| , | lateral and longitudinal positions of the aircraft |
| , | lateral and longitudinal components of the aircraft velocity |
| lateral and longitudinal components of the wind speed |
| Separation Assurance Strategy | Aircraft one Priority: Aircraft Two Priority | |||||
|---|---|---|---|---|---|---|
| minimum yaw angle | 1:1 | 16.19 | 1876.54 | 1807.27 | 25 | −5 |
| minimum maneuver time | 1:1 | 15.84 | 1782.61 | 1767.26 | 20 | 15 |
| integrated optimal | 1:1 | 15.74 | 1785.98 | 1771.81 | 25 | 20 |
| Separation Assurance Strategy | Aircraft One Priority: Aircraft two Priority | |||||
|---|---|---|---|---|---|---|
| minimum maneuver time | 1:1 | 15.84 | 1782.61 | 1767.26 | 20 | 15 |
| minimum maneuver time | 2:1 | 16.01 | 1759.64 | 1771.84 | 15 | 25 |
| minimum maneuver time | 1:2 | 16.48 | 1821.17 | 1762.59 | 25 | 10 |
| Air Traffic Management Mode | Separation Assurance Strategy | |||||
|---|---|---|---|---|---|---|
| Distributed- two-aircraft cooperation | minimum maneuver time | 15.84 | 1782.61 | 1767.26 | 20 | 15 |
| Centralized- own ship maneuver | minimum maneuver time | 16.07 | 0 | 2279.64 | 0 | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Lu, X.; Zheng, P. Aircraft Autonomous Separation Assurance Based on Cooperative Game Theory. Aerospace 2022, 9, 421. https://doi.org/10.3390/aerospace9080421
Tang X, Lu X, Zheng P. Aircraft Autonomous Separation Assurance Based on Cooperative Game Theory. Aerospace. 2022; 9(8):421. https://doi.org/10.3390/aerospace9080421
Chicago/Turabian StyleTang, Xinmin, Xiaona Lu, and Pengcheng Zheng. 2022. "Aircraft Autonomous Separation Assurance Based on Cooperative Game Theory" Aerospace 9, no. 8: 421. https://doi.org/10.3390/aerospace9080421
APA StyleTang, X., Lu, X., & Zheng, P. (2022). Aircraft Autonomous Separation Assurance Based on Cooperative Game Theory. Aerospace, 9(8), 421. https://doi.org/10.3390/aerospace9080421





