Using Reinforcement Learning to Improve Airspace Structuring in an Urban Environment
Abstract
1. Introduction
2. Related Work
3. Layered Urban Airspace Design
4. Airspace Structure with Reinforcement Learning
4.1. Agent
4.2. Learning Algorithm
| Algorithm 1 Deep deterministic policy gradient. |
|
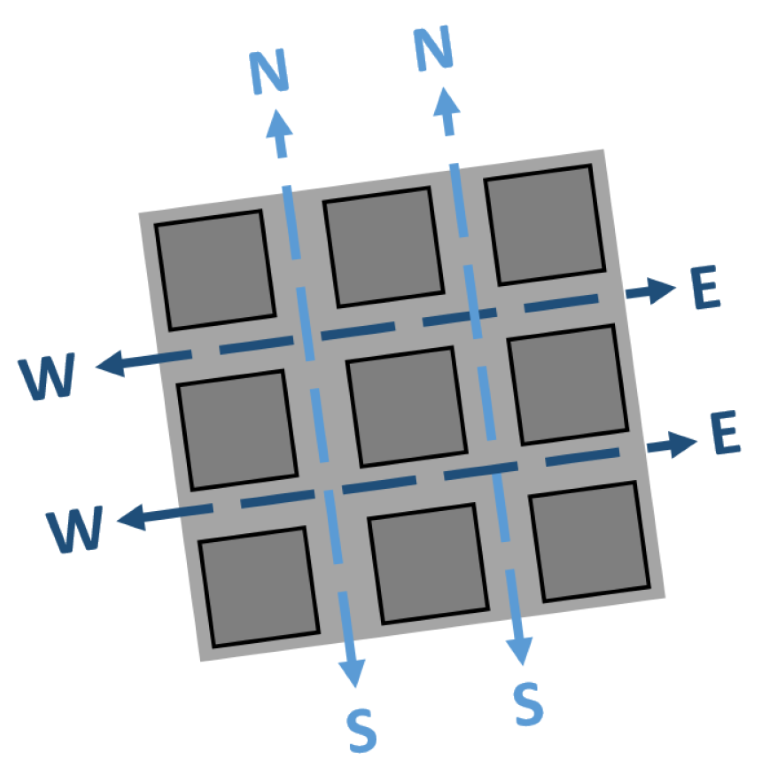
4.3. State
4.4. Action
- The number of layers for each direction: the RL agent may decide to select more layers for a direction adopted by the majority of aircraft. However, an important safeguard was implemented upon the airspace structure output by the RL agent. To make sure that all directions were allowed in the airspace, a final check was applied to the structure. If all possible directions were not yet allowed, the last layer was overwritten to allow for the missing directions. Note that it may occur that more than one flight direction is allowed in this layer.
- The order of the layers: the RL agent decides which directions are in adjacent layers. For a fixed structure, it is good practice to allow the left or right turning by just climbing or descending one layer. However, on purpose, the agent is free to choose the order of directions. It will be evaluated whether the structure output by the RL agent includes an understanding of perpendicular directions.
4.5. Reward
- The RL model receives a −1 for each conflict.
- The RL model receives a −1 for each loss of minimum separation.
5. Experiment: Safety-Optimized Airspace Structures
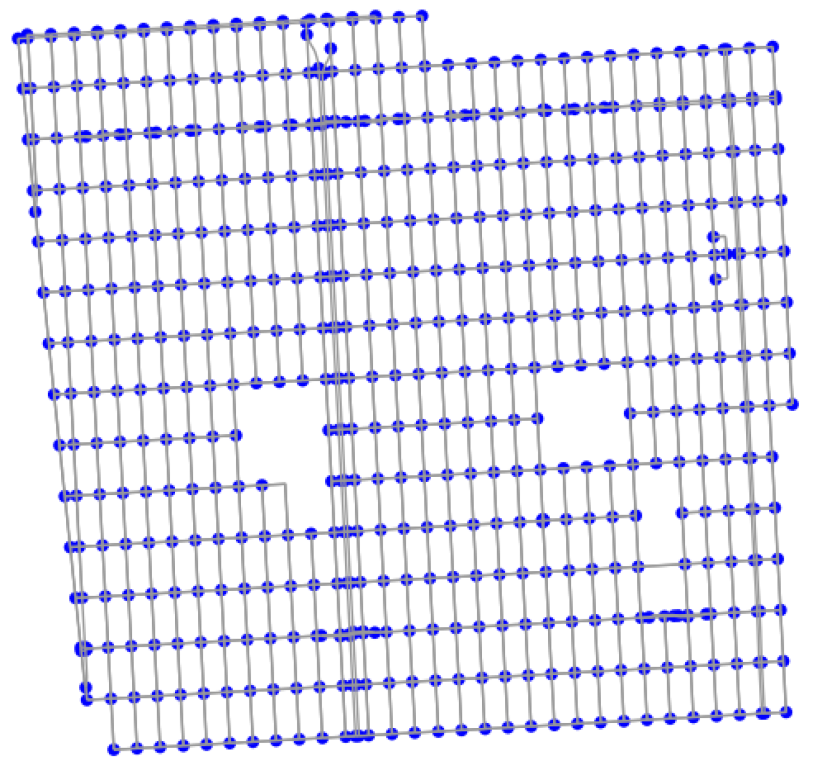
5.1. Simulated Environment
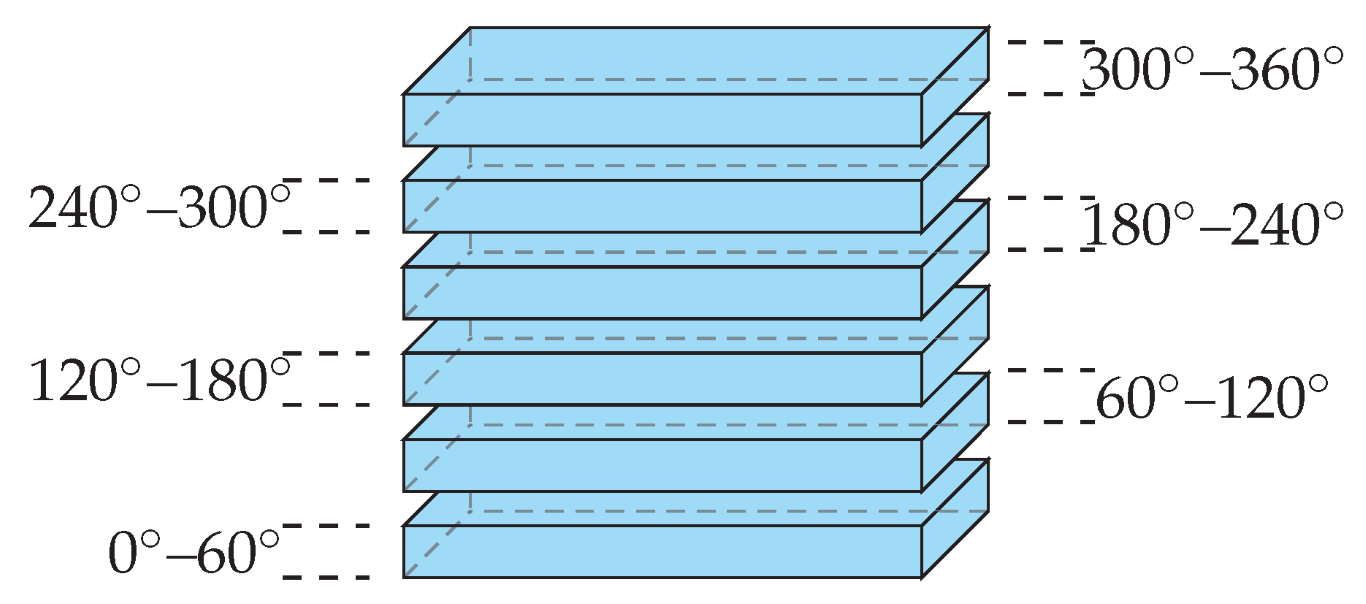
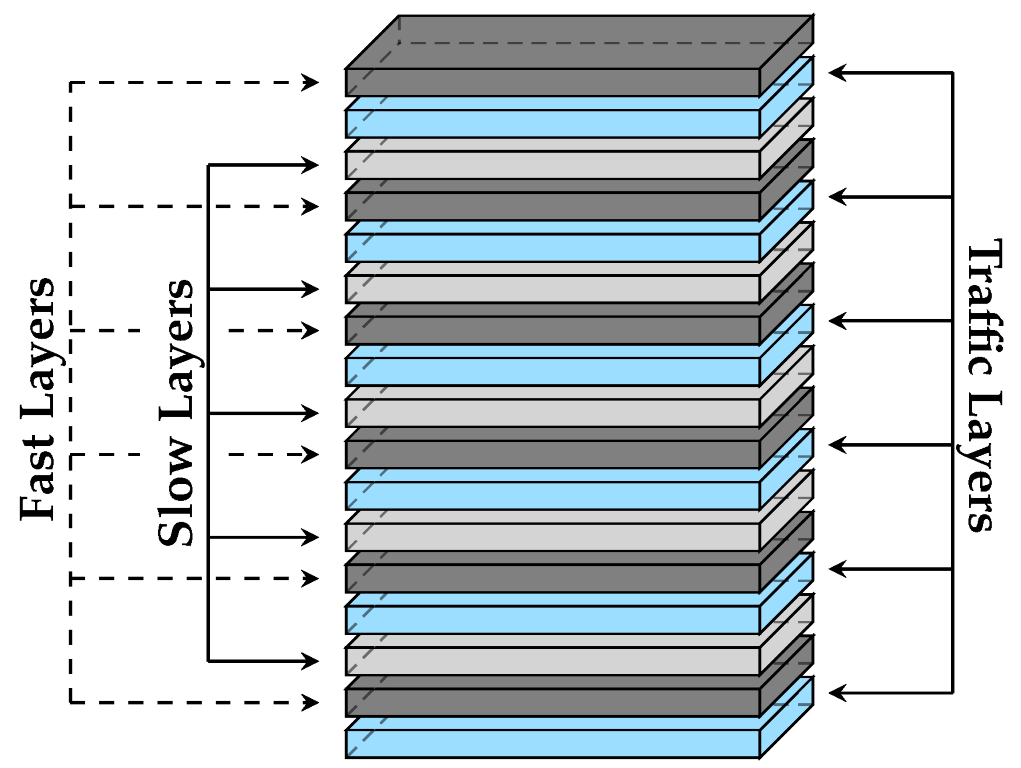
5.2. Transition Layers
- Six traffic layers (in blue): the main layers used by cruising traffic.
- Six slow transition layers (in light grey) were used for transitioning between traffic layers. This is a necessary mid-step prior to the aircraft entering different traffic layers. First, the aircraft exit the current traffic layer without modifying their speed, in order to not create conflict with other cruising aircraft, and they move toward the slow layer. Here, the aircraft decrease their speed to reach the speed required to comply with the turn radius. After turning, the aircraft start accelerating toward the desired cruising speed/moving to the destination traffic layer.
- Six fast transition layers (in dark grey) were used to perform vertical conflict avoidance when necessary. The overtaking aircraft resolve the conflict by moving into the fast layer; aircraft being overtaken have the right of way. Once the conflict is resolved, the aircraft move back into the traffic layer to guarantee that the fast layers are (mostly) depleted of other traffic when the aircraft need to perform vertical resolution.
5.3. Flight Routes
5.4. Apparatus and Aircraft Model
5.5. Minimum Separation
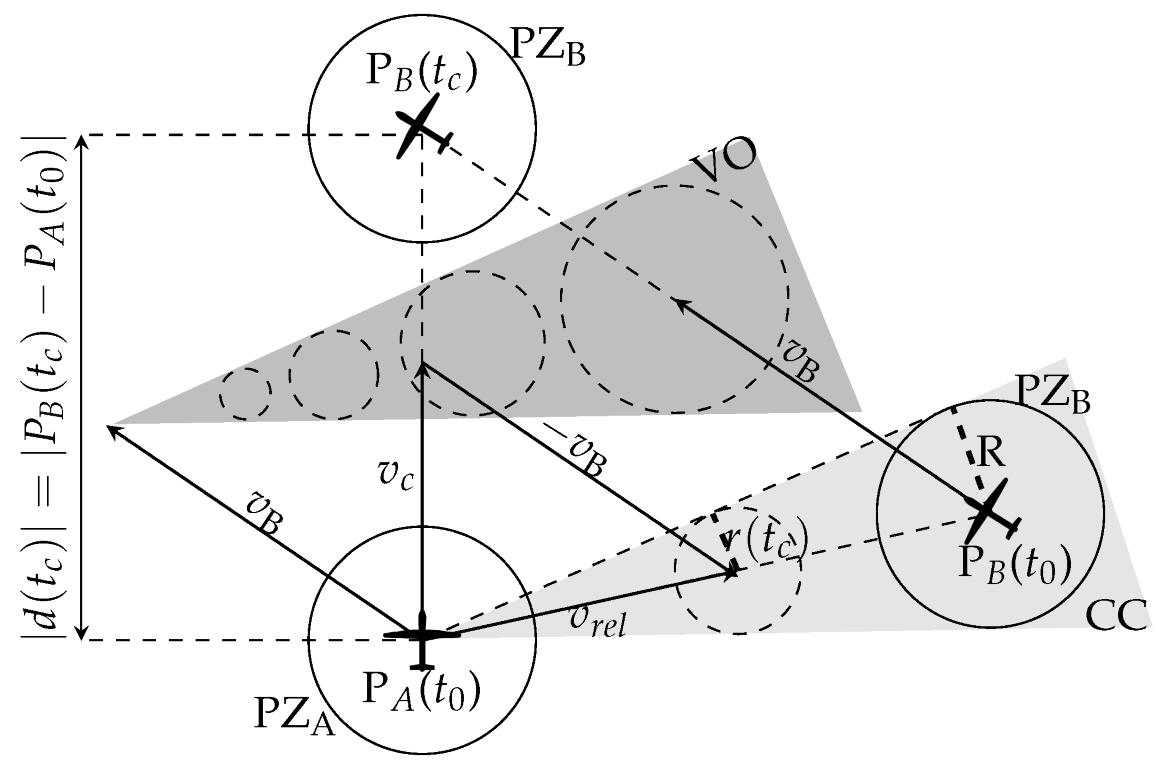
5.6. Conflict Detection
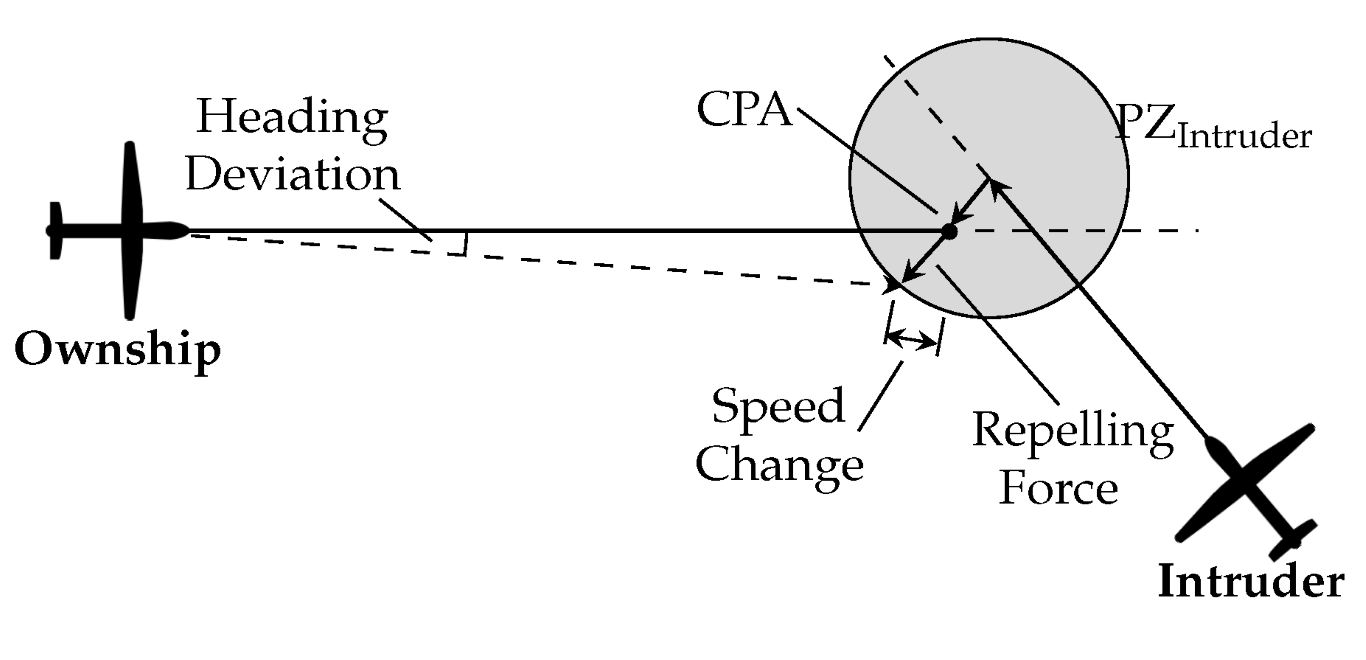
5.7. Conflict Resolution
5.8. Independent Variables
5.8.1. Reward Formulation
5.8.2. Conflict Resolution
5.8.3. Traffic Density
5.8.4. Airspace Structure
5.9. Dependent Variables
5.9.1. Safety Analysis
5.9.2. Stability Analysis
5.9.3. Efficiency Analysis
6. Experiment: Hypotheses
6.1. Simulated Traffic Scenarios
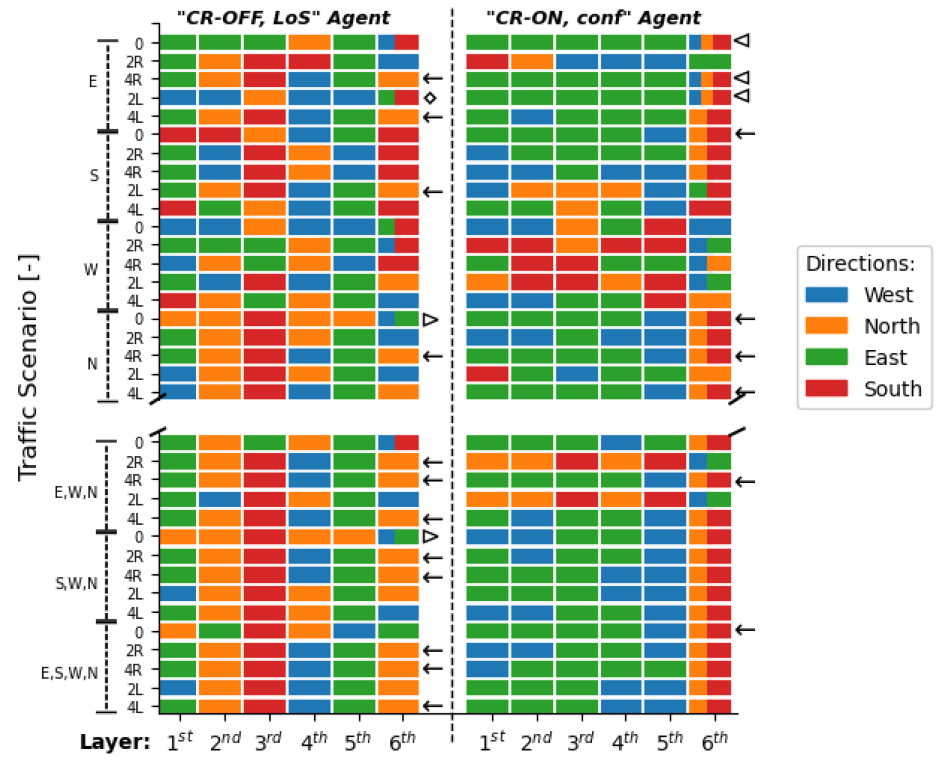
6.2. Dynamic Airspace Structuring
6.3. Training of the Reinforcement Learning Model
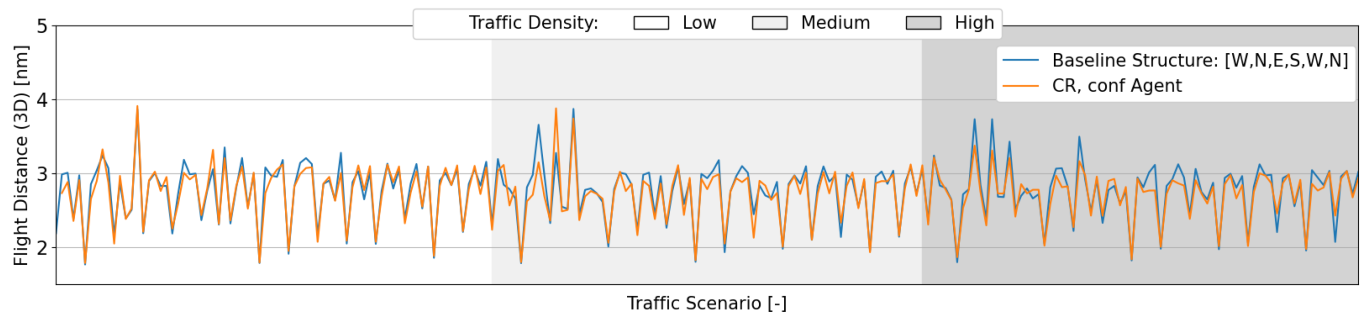
7. Experiment: Results
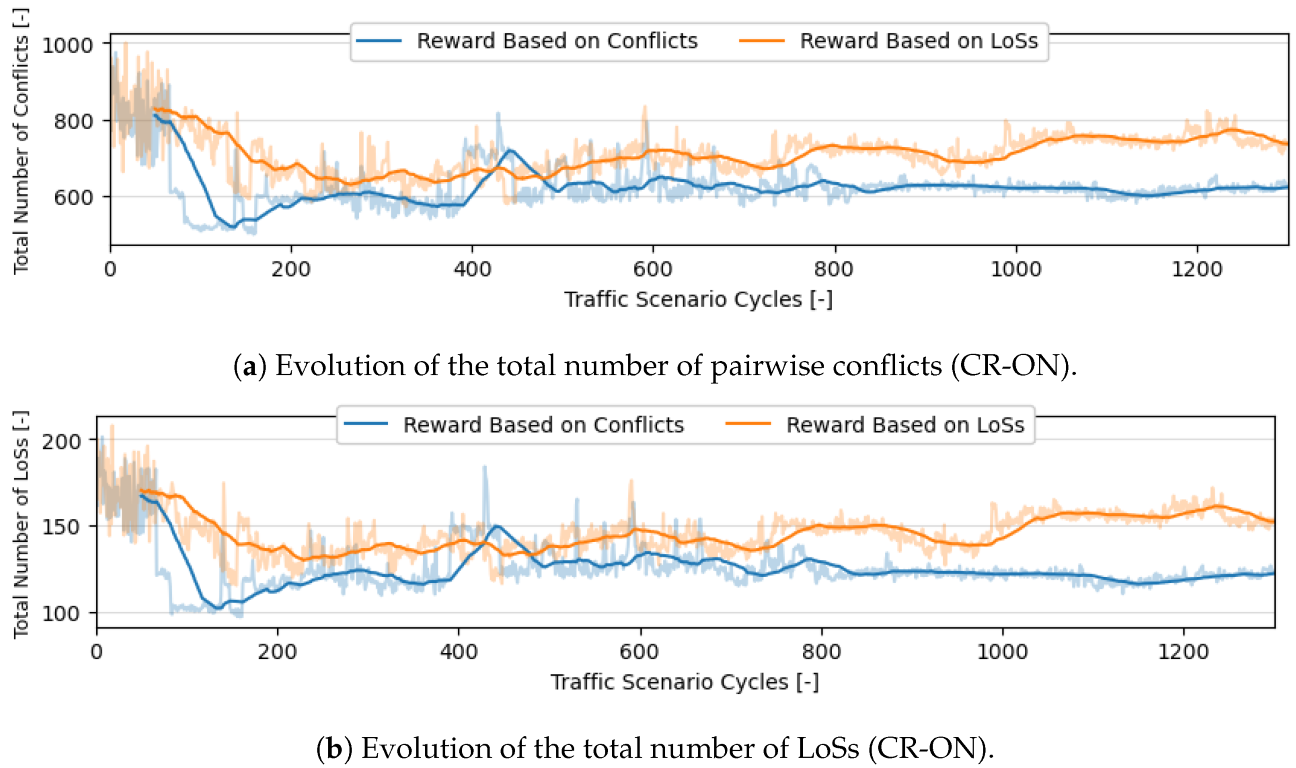
7.1. Training of the RL Agent for Safety-Optimized Airspace Structuring
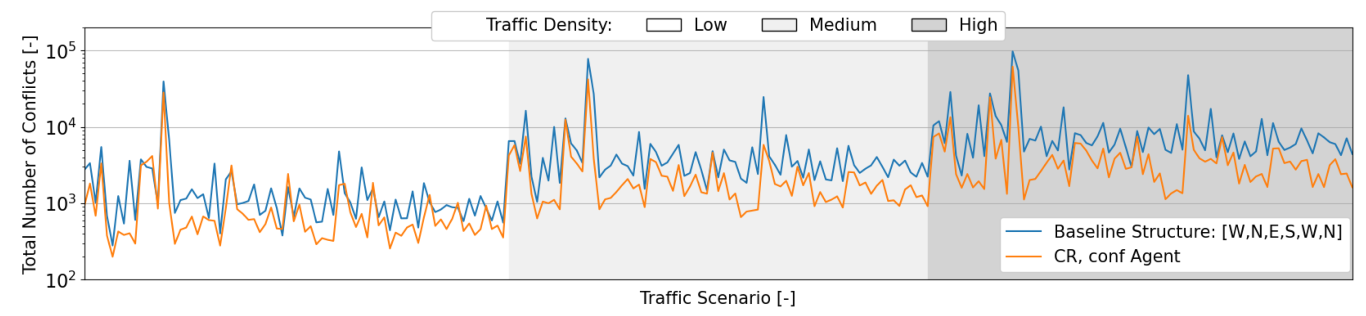
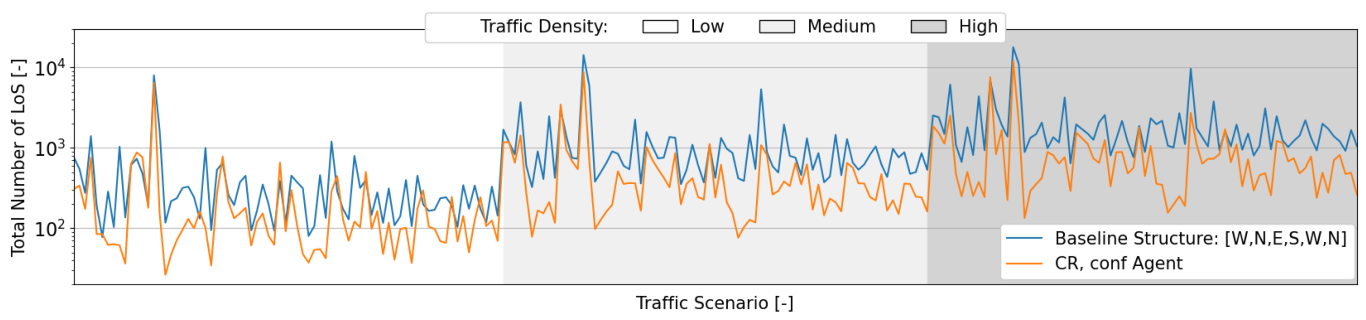
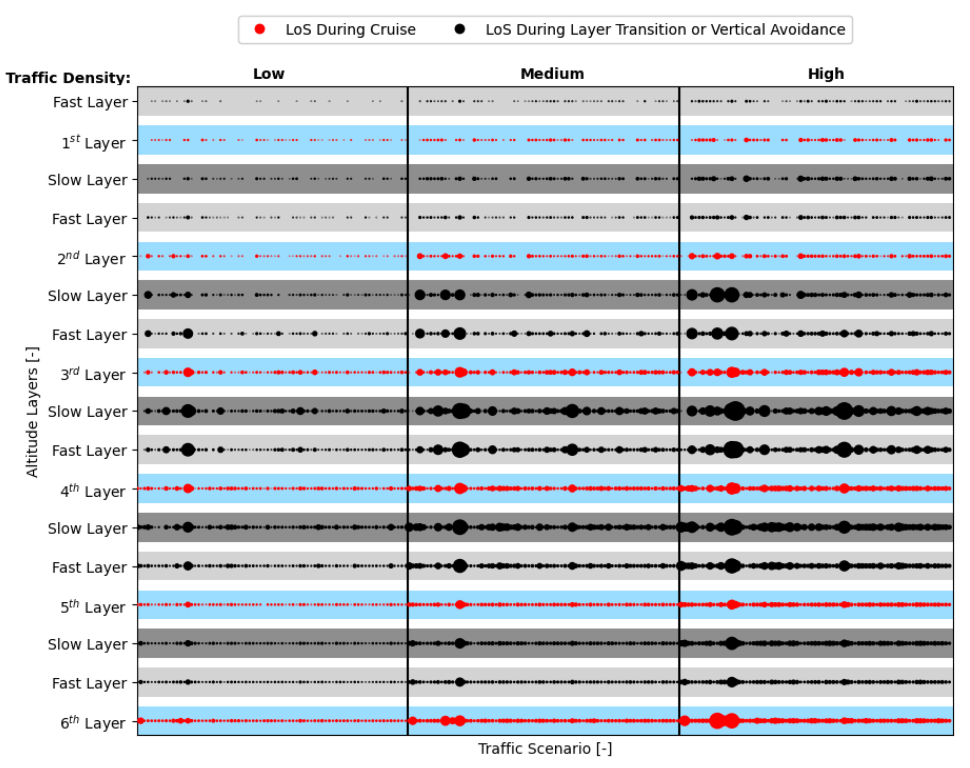
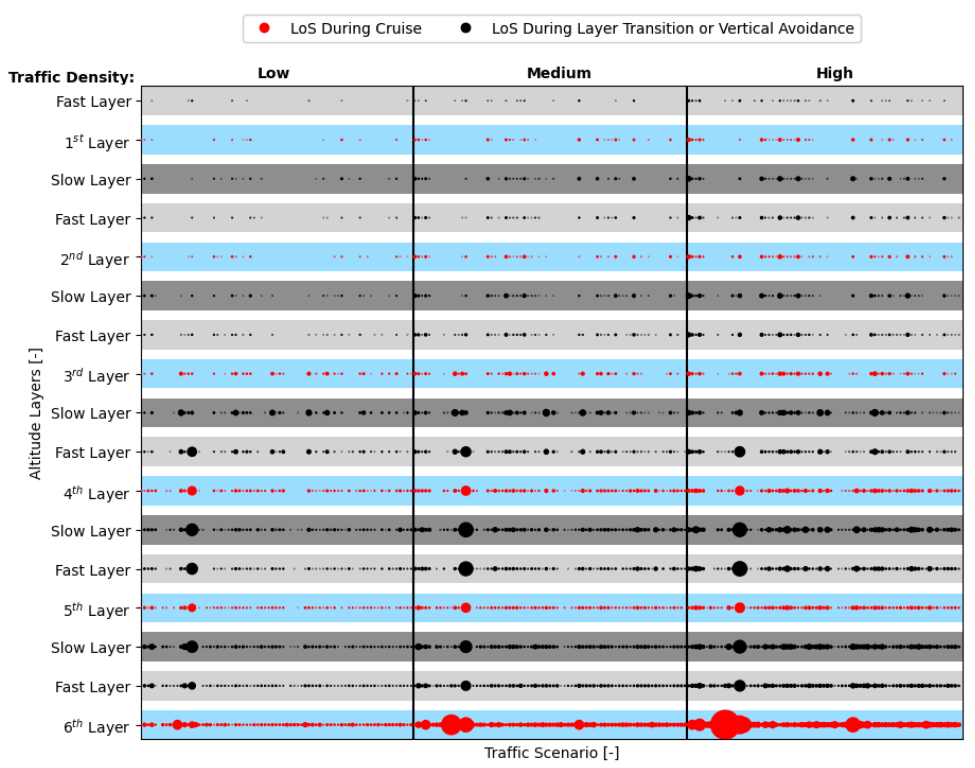
Safety Analysis
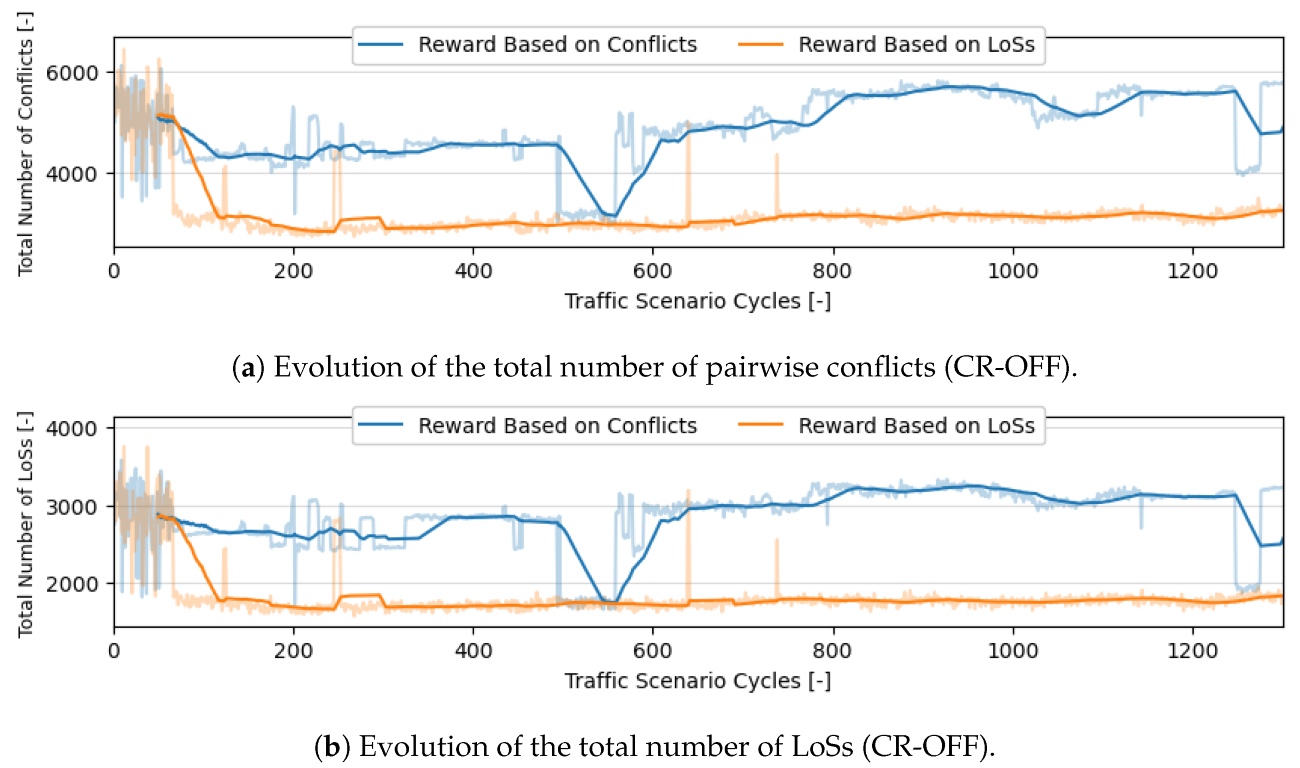
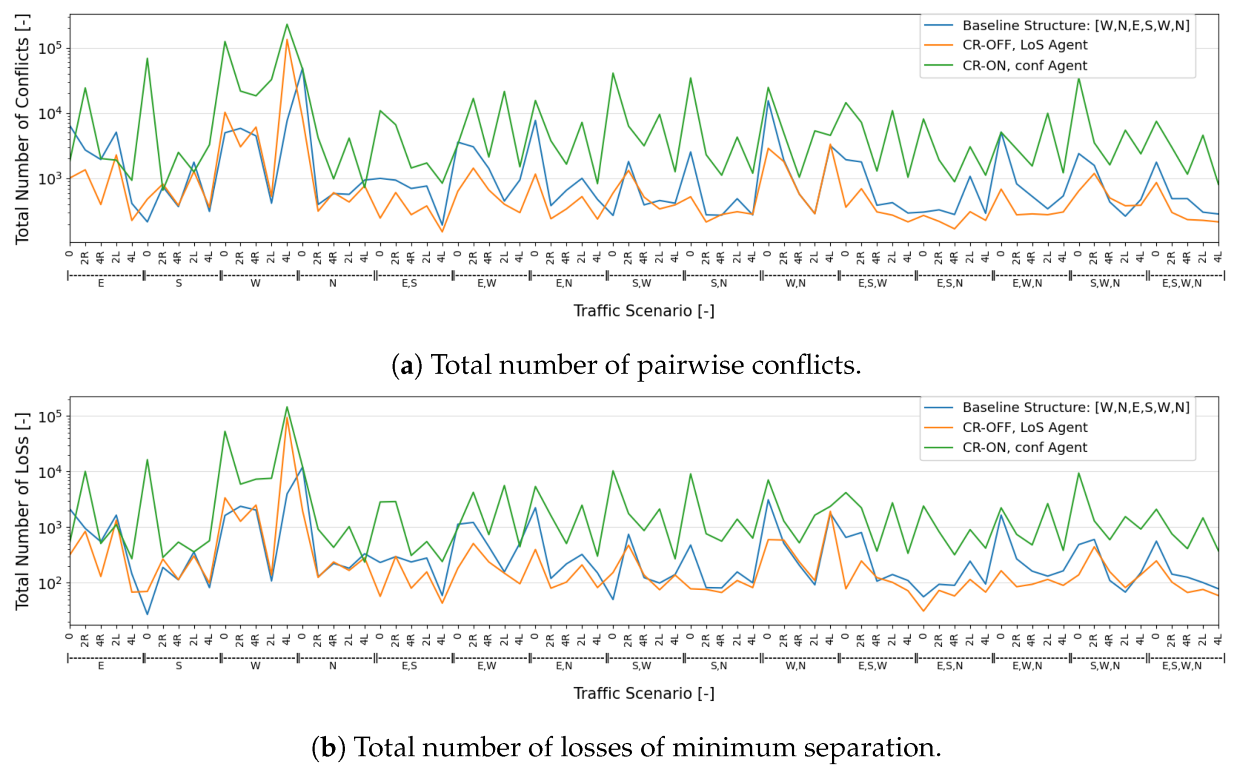
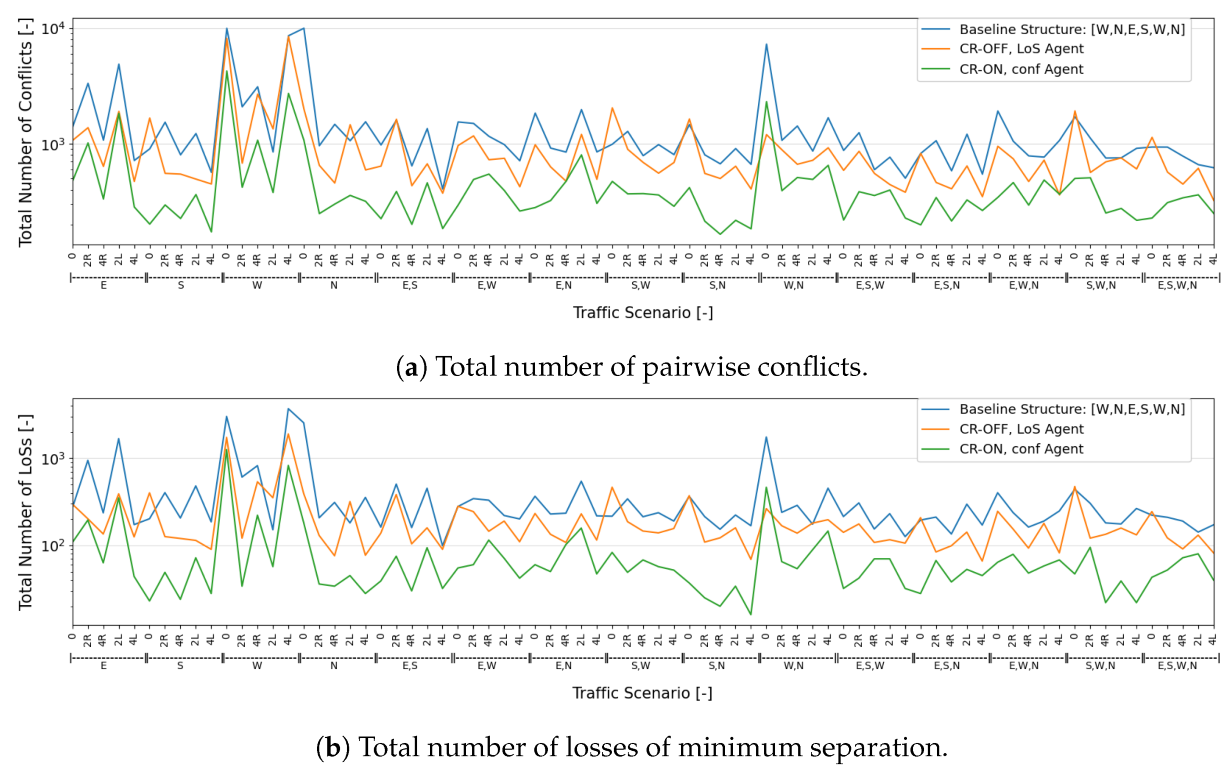
- Within traffic scenarios starting with a single direction, east and west stand out, resulting in considerably more conflicts. This justifies the emphasis by the ‘CR-ON, conf’ agent on these directions. Moreover, as expected, when aircraft are initially distributed through more directions, the consequent segmentation results in fewer conflicts and LoSs.
- It was hypothesized that increasing the number of turns would lead to a higher number of conflicts and LoSs. Turns lead to vertical deviations between cruising layers, and having aircraft enter and leave these layers lead to conflict situations [44]. However, within the experimental results, more turns sometimes result in fewer conflicts and LoSs. This is considered a result of additional segmentation created by vertical deviations. Aircraft become more distributed throughout the available airspace as now they also move within the transition layers. This effect appears to have had a positive impact on safety.
7.2. Testing of the RL Agent for Safety-Optimized Airspace Structuring
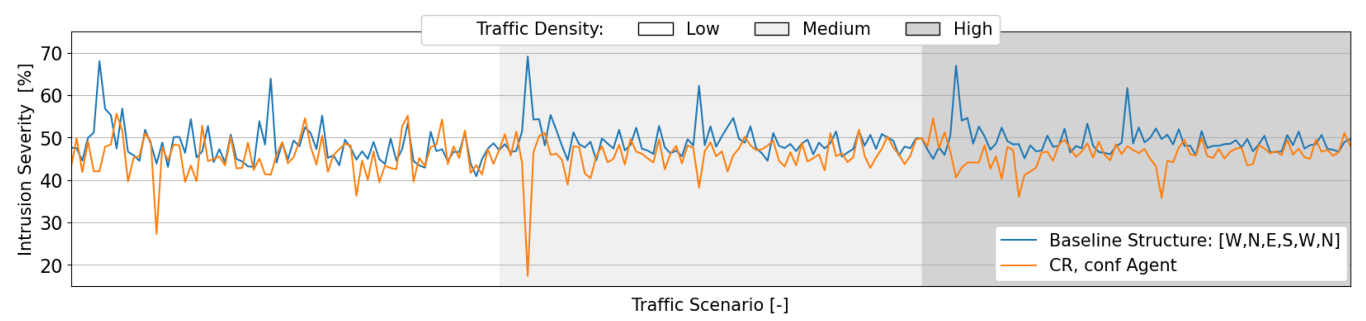
7.2.1. Safety Analysis
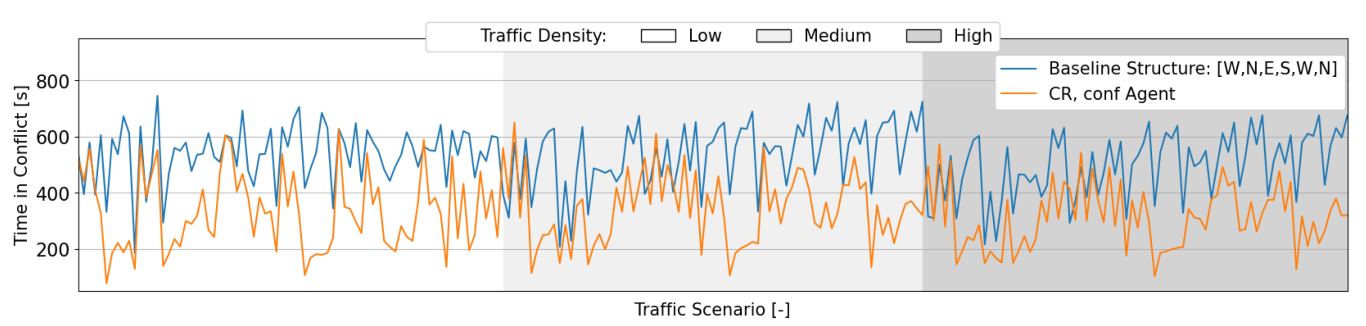
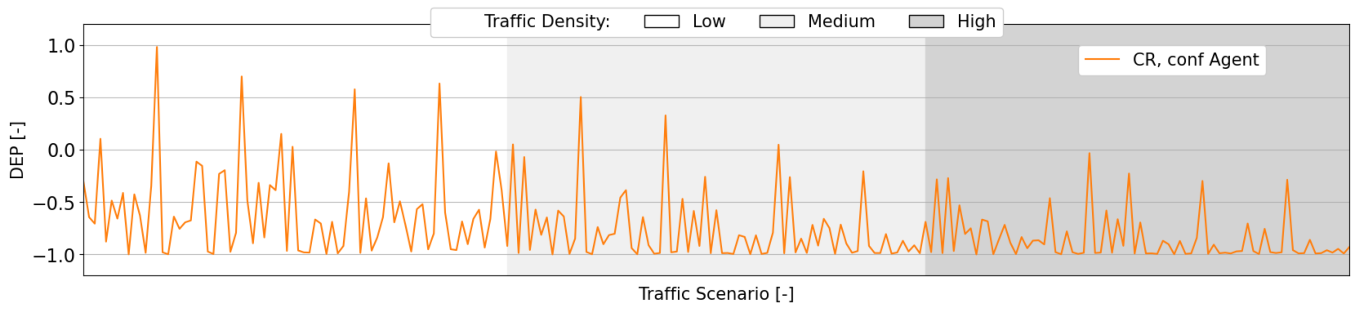
7.2.2. Stability Analysis
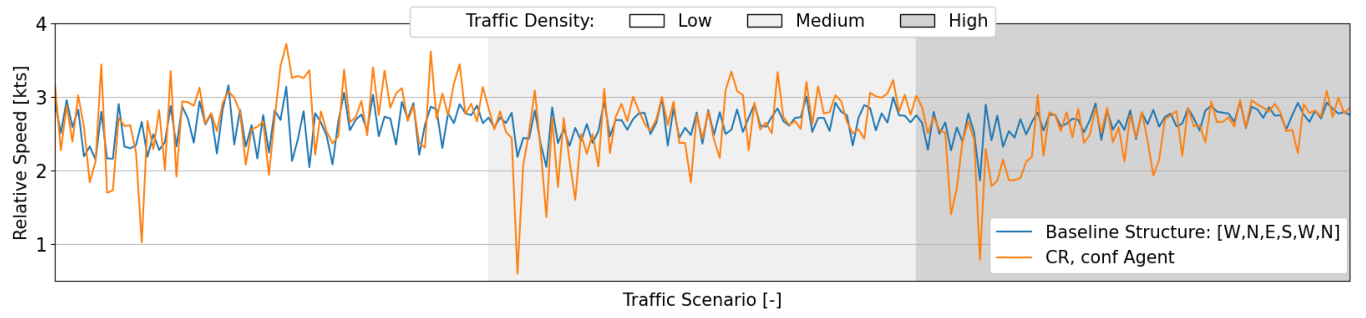
7.2.3. Efficiency Analysis
8. Discussion
8.1. Efficacy of Reinforcement Learning
8.2. Conflict Resolution
8.3. Advice for Future Work
- The exploration of more powerful states and reward formulations. For the state formulation, four ‘snapshots’ of the evolution of the traffic were considered. However, in fast-changing traffic scenarios, the RL agent may require more snapshots to fully understand the progression of traffic over time. Additionally, only safety factors were considered as the reward. Future implementations may also benefit from including efficiency elements, such as the flight path and flight time.
- In this work, the last traffic layer was used to allow directions that the RL did not allocate space for. However, this layer may become a ‘hotspot’ for conflicts when more than one direction is set. Other possibilities could be researched (e.g., distributing aircraft traveling within “missing directions” over layers with small heading differences).
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sesar Joint Undertaking. U–Space, Supporting Safe and Secure Drone Operations in Europe; Technical Report; Sesar Joint Undertaking: Brussels, Belgium, 2020. [Google Scholar]
- Galster, S.M.; Duley, J.A.; Masalonis, A.J.; Parasuraman, R. Air Traffic Controller Performance and Workload Under Mature Free Flight: Conflict Detection and Resolution of Aircraft Self-Separation. Int. J. Aviat. Psychol. 2001, 11, 71–93. [Google Scholar] [CrossRef]
- Sunil, E.; Ellerbroek, J.; Hoekstra, J.; Vidosavljevic, A.; Arntzen, M.; Bussink, F.; Nieuwenhuisen, D. Analysis of Airspace Structure and Capacity for Decentralized Separation Using Fast-Time Simulations. J. Guid. Control. Dyn. 2017, 40, 38–51. [Google Scholar] [CrossRef]
- Doole, M.; Ellerbroek, J.; Knoop, V.L.; Hoekstra, J.M. Constrained Urban Airspace Design for Large-Scale Drone-Based Delivery Traffic. Aerospace 2021, 8, 38. [Google Scholar] [CrossRef]
- Gunarathna, U.; Xie, H.; Tanin, E.; Karunasekara, S.; Borovica-Gajic, R. Real-Time Lane Configuration with Coordinated Reinforcement Learning. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: Applied Data Science Track, Ghent, Belgium, 14–18 September 2020; Dong, Y., Mladenić, D., Saunders, C., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 291–307. [Google Scholar]
- Chu, K.F.; Lam, A.Y.; Li, V.O. Dynamic lane reversal routing and scheduling for connected autonomous vehicles. In Proceedings of the 2017 International Smart Cities Conference (ISC2), Wuxi, China, 14–17 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Cai, M.; Xu, Q.; Chen, C.; Wang, J.; Li, K.; Wang, J.; Wu, X. Multi-Lane Unsignalized Intersection Cooperation with Flexible Lane Direction Based on Multi-Vehicle Formation Control. IEEE Trans. Veh. Technol. 2022, 71, 5787–5798. [Google Scholar] [CrossRef]
- Standfuß, T.; Gerdes, I.; Temme, A.; Schultz, M. Dynamic airspace optimisation. CEAS Aeronaut. J. 2018, 9, 517–531. [Google Scholar] [CrossRef]
- Schultz, M.; Reitmann, S. Machine learning approach to predict aircraft boarding. Transp. Res. Part Emerg. Technol. 2019, 98, 391–408. [Google Scholar] [CrossRef]
- Lee, H.; Malik, W.; Jung, Y.C. Taxi-Out Time Prediction for Departures at Charlotte Airport Using Machine Learning Techniques. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Rohacs, J.; Rohacs, D. Autonomous Flight Trajectory Control System for Drones in Smart City Traffic Management. ISPRS Int. J. Geo Inf. 2021, 10, 338. [Google Scholar] [CrossRef]
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Hoekstra, J.; Ellerbroek, J. BlueSky ATC Simulator Project: An Open Data and Open Source Approach. In Proceedings of the Conference: International Conference for Research on Air Transportation, Philadelphia, PA, USA, 20–24 June 2016. [Google Scholar]
- Hoekstra, J.; van Gent, R.; Ruigrok, R. Designing for safety: The ‘free flight’ air traffic management concept. Reliab. Eng. Syst. Saf. 2002, 75, 215–232. [Google Scholar] [CrossRef]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Review of conflict resolution methods for manned and unmanned aviation. Aerospace 2020, 7, 79. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016—Conference Track Proceedings. International Conference on Learning Representations, ICLR; San Juan, Puerto Rico, 2–4 May 2016. Available online: http://xxx.lanl.gov/abs/1509.02971 (accessed on 1 November 2021).
- Degas, A.; Islam, M.R.; Hurter, C.; Barua, S.; Rahman, H.; Poudel, M.; Ruscio, D.; Ahmed, M.U.; Begum, S.; Rahman, M.A.; et al. A Survey on Artificial Intelligence (AI) and eXplainable AI in Air Traffic Management: Current Trends and Development with Future Research Trajectory. Appl. Sci. 2022, 12, 1295. [Google Scholar] [CrossRef]
- Brito, I.R.; Murca, M.C.R.; d’Oliveira, M.; Oliveira, A.V. A Machine Learning-based Predictive Model of Airspace Sector Occupancy. In Proceedings of the AIAA Aviation 2021 Forum, Online, 2–6 August 2021. [Google Scholar] [CrossRef]
- Li, B.; Du, W.; Zhang, Y.; Chen, J.; Tang, K.; Cao, X. A Deep Unsupervised Learning Approach for Airspace Complexity Evaluation. IEEE Trans. Intell. Transp. Syst. 2021, 1–13. [Google Scholar] [CrossRef]
- Wieland, F.; Rebollo, J.; Gibbs, M.; Churchill, A. Predicting Sector Complexity Using Machine Learning. In Proceedings of the AIAA Aviation 2022 Forum, Las Vegas, NV, USA, 24–26 October 2022. [Google Scholar] [CrossRef]
- Xue, M. Airspace Sector Redesign Based on Voronoi Diagrams. J. Aerosp. Comput. Inf. Commun. 2009, 6, 624–634. [Google Scholar] [CrossRef]
- Kulkarni, S.; Ganesan, R.; Sherry, L. Static sectorization approach to dynamic airspace configuration using approximate dynamic programming. In Proceedings of the 2011 Integrated Communications, Navigation, and Surveillance Conference Proceedings, Herndon, VA, USA, 10–12 May 2011; pp. J2-1–J2-9. [Google Scholar] [CrossRef]
- Tang, J.; Alam, S.; Lokan, C.; Abbass, H.A. A multi-objective approach for Dynamic Airspace Sectorization using agent based and geometric models. Transp. Res. Part Emerg. Technol. 2012, 21, 89–121. [Google Scholar] [CrossRef]
- Irvine, R. The GEARS Conflict Resolution Algorithm; Technical Report; EUROCONTROL: Brussels, Belgium, 1997. [Google Scholar] [CrossRef]
- Tra, M.; Sunil, E.; Ellerbroek, J.; Hoekstra, J. Modeling the Intrinsic Safety of Unstructured and Layered Airspace Designs. In Proceedings of the Twelfth USA/Europe Air Traffic Management Research and Development Seminar, Seattle, WA, USA, 27–30 June 2017. [Google Scholar]
- Sunil, E.; Hoekstra, J.; Ellerbroek, J.; Bussink, F.; Nieuwenhuisen, D.; Vidosavljevic, A.; Kern, S. Metropolis: Relating Airspace Structure and Capacity for Extreme Traffic Densities. In Proceedings of the ATM Seminar 2015, 11th USA/EUROPE Air Traffic Management R&D Seminar, Baltimore, MD, USA, 27–30 June 2005. [Google Scholar]
- Samir Labib, N.; Danoy, G.; Musial, J.; Brust, M.R.; Bouvry, P. Internet of Unmanned Aerial Vehicles—A Multilayer Low-Altitude Airspace Model for Distributed UAV Traffic Management. Sensors 2019, 19, 4779. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.; Yoon, Y. Extraction and Interpretation of Geometrical and Topological Properties of Urban Airspace for UAS Operations. In Proceedings of the ATM Seminar 2019, 13th USA/EUROPE Air Traffic Management R&D Seminar, Vienna, Austria, 17–21 June 2019. [Google Scholar]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep Reinforcement Learning that Matters. In Proceedings of the Thirthy-Second AAAI Conference on Artificial Intelligence (AAAI-18); New Orleans, LA, USA, 2–7 February 2018. Available online: http://xxx.lanl.gov/abs/1709.06560 (accessed on 1 January 2021).
- Tang, C.; Lai, Y.C. Deep Reinforcement Learning Automatic Landing Control of Fixed-Wing Aircraft Using Deep Deterministic Policy Gradient. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Tsourdos, A.; Dharma Permana, I.A.; Budiarti, D.H.; Shin, H.S.; Lee, C.H. Developing Flight Control Policy Using Deep Deterministic Policy Gradient. In Proceedings of the 2019 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICARES), Yogyakarta, Indonesia, 17–18 October 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Wen, H.; Li, H.; Wang, Z.; Hou, X.; He, K. Application of DDPG-based Collision Avoidance Algorithm in Air Traffic Control. In Proceedings of the 2019 12th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 14–15 December 2019; Volume 1, pp. 130–133. [Google Scholar] [CrossRef]
- Duan, Y.; Chen, X.; Edu, C.X.B.; Schulman, J.; Abbeel, P.; Edu, P.B. Benchmarking Deep Reinforcement Learning for Continuous Control. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016. [Google Scholar] [CrossRef]
- Islam, R.; Henderson, P.; Gomrokchi, M.; Precup, D. Reproducibility of Benchmarked Deep Reinforcement Learning Tasks for Continuous Control. In Proceedings of the Reproducibility in Machine Learning Workshop, ICML’17, Sydney, Australia, 6–11 August 2017. [Google Scholar] [CrossRef]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- Boeing, G. OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef]
- Paielli, R.A. Tactical conflict resolution using vertical maneuvers in en route airspace. J. Aircr. 2008, 45, 2111–2119. [Google Scholar] [CrossRef]
- Alejo, D.; Conde, R.; Cobano, J.; Ollero, A. Multi-UAV collision avoidance with separation assurance under uncertainties. In Proceedings of the 2009 IEEE International Conference on Mechatronics, Malaga, Spain, 14–17 April 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Fiorini, P.; Shiller, Z. Motion Planning in Dynamic Environments Using Velocity Obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Chakravarthy, A.; Ghose, D. Obstacle avoidance in a dynamic environment: A collision cone approach. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 1998, 28, 562–574. [Google Scholar] [CrossRef]
- Velasco, G.; Borst, C.; Ellerbroek, J.; van Paassen, M.M.; Mulder, M. The Use of Intent Information in Conflict Detection and Resolution Models Based on Dynamic Velocity Obstacles. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2297–2302. [Google Scholar] [CrossRef]
- Hoekstra, J.M. Free Flight in a Crowded Airspace? Available online: https://www.semanticscholar.org/paper/Free-Flight-in-a-Crowded-Airspace-Hoekstra/9b85d3bd167044d479a11a98aa510e92b66af87b (accessed on 1 November 2021).
- Golding, R. Metrics to Characterize Dense Airspace Traffic; Technical Report 004; Altiscope: Beijing, China, 2018. [Google Scholar]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Velocity Obstacle Based Conflict Avoidance in Urban Environment with Variable Speed Limit. Aerospace 2021, 8, 93. [Google Scholar] [CrossRef]
- Bilimoria, K.; Sheth, K.; Lee, H.; Grabbe, S. Performance evaluation of airborne separation assurance for free flight. In Proceedings of the 18th Applied Aerodynamics Conference, Denver, CO, USA, 14–17 August 2000; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2000. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
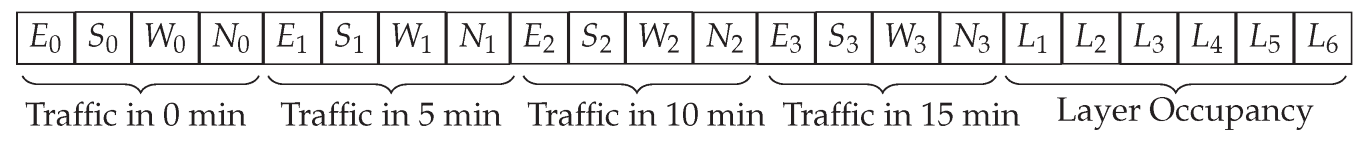


| Parameter | Value |
|---|---|
| TAU | 0.001 |
| Learning rate actor (LRA) | 0.0001 |
| Learning rate critic (LRC) | 0.001 |
| EPSILON | 0.1 |
| GAMMA | 0.99 |
| Buffer size | 1 M |
| Minibatch size | 256 |
| # Hidden layer-neural networks | 2 |
| # Neurons | 120 in each layer |
| Activation functions | Rectified linear unit (ReLU) in the hidden layers |
| Softmax in the last layer |
| Traffic Scenario: | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % A/C Initial Hdg Distribution | East (E): | 100 | 0 | 0 | 0 | 50 | 50 | 50 | 0 | 0 | 0 | 33 | 33 | 33 | 0 | 25 |
| South (S): | 0 | 100 | 0 | 0 | 50 | 0 | 0 | 50 | 50 | 0 | 33 | 33 | 0 | 33 | 25 | |
| West (W): | 0 | 0 | 100 | 0 | 0 | 50 | 0 | 50 | 0 | 50 | 33 | 0 | 33 | 33 | 25 | |
| North (N): | 0 | 0 | 0 | 100 | 0 | 0 | 50 | 0 | 50 | 50 | 0 | 33 | 33 | 33 | 25 | |
| Flight Path With Turns: | All traffic scenarios are repeated with: | •No Turns (0) •2 Turns to the Right (2R) •4 Turns to the Right (4R) •2 Turns to the Left (2L) •4 Turns to the Left (4L) | ||||||||||||||
| Low | Medium | High | |
|---|---|---|---|
| Traffic density [10,000 NM ] | 292,740 | 585,408 | 878,112 |
| Number of instantaneous aircraft [-] | 50 | 100 | 150 |
| Number of spawned aircraft [-] | 80–397 | 159–794 | 236–1189 |
| 1st Layer (W) | 2nd Layer (N) | 3rd Layer (E) | 4th Layer (S) | 5th Layer (W) | 6th Layer (N) |
|---|---|---|---|---|---|
 |  |  | 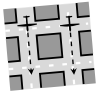 | 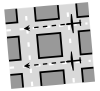 | 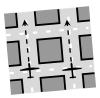 |
 | |||||
| Altitude | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Using Reinforcement Learning to Improve Airspace Structuring in an Urban Environment. Aerospace 2022, 9, 420. https://doi.org/10.3390/aerospace9080420
Ribeiro M, Ellerbroek J, Hoekstra J. Using Reinforcement Learning to Improve Airspace Structuring in an Urban Environment. Aerospace. 2022; 9(8):420. https://doi.org/10.3390/aerospace9080420
Chicago/Turabian StyleRibeiro, Marta, Joost Ellerbroek, and Jacco Hoekstra. 2022. "Using Reinforcement Learning to Improve Airspace Structuring in an Urban Environment" Aerospace 9, no. 8: 420. https://doi.org/10.3390/aerospace9080420
APA StyleRibeiro, M., Ellerbroek, J., & Hoekstra, J. (2022). Using Reinforcement Learning to Improve Airspace Structuring in an Urban Environment. Aerospace, 9(8), 420. https://doi.org/10.3390/aerospace9080420








