Review of Deep Reinforcement Learning Approaches for Conflict Resolution in Air Traffic Control
Abstract
1. Introduction
2. Background
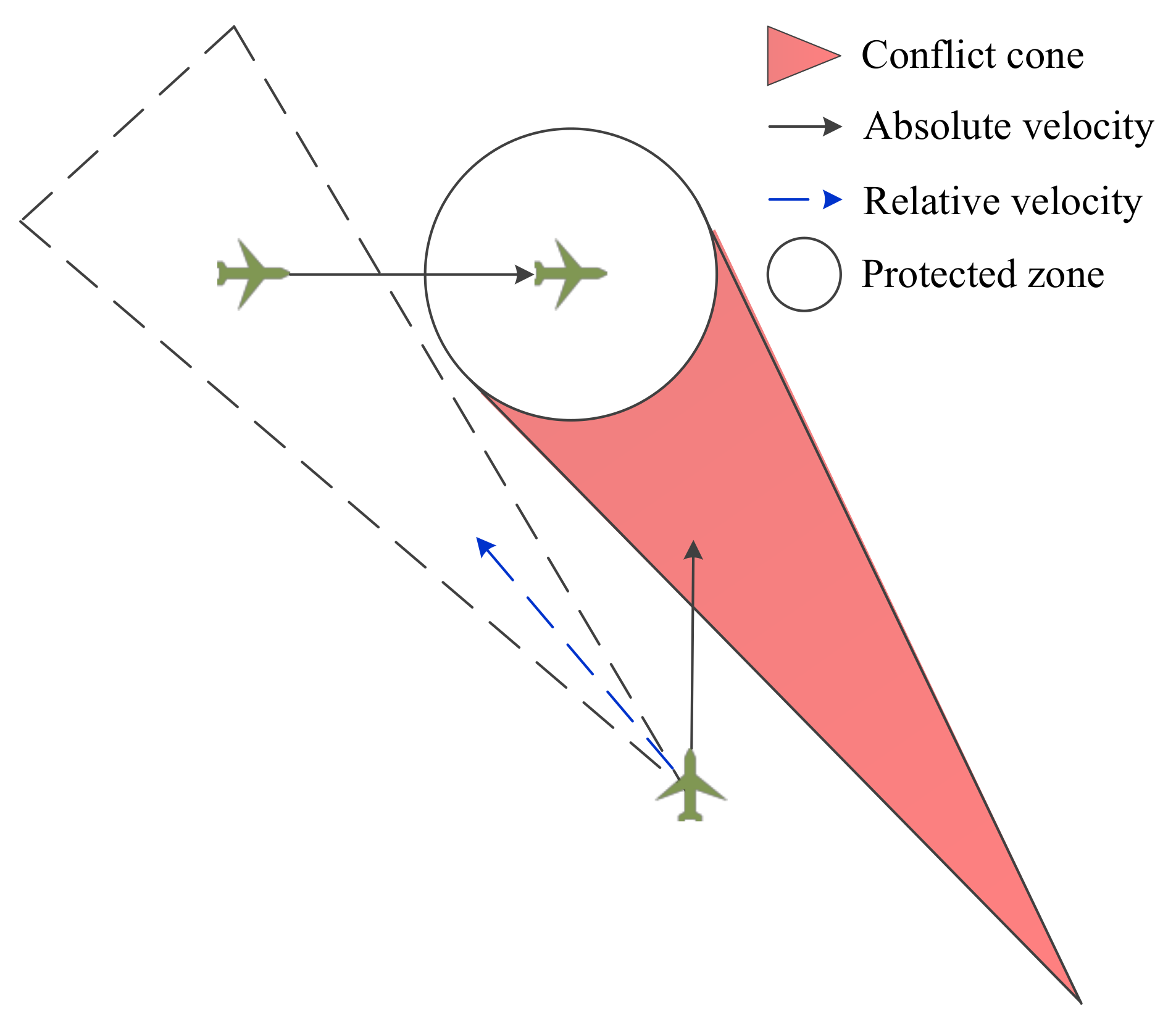
2.1. Conflict Resolution Process
- 1.
- Altitude adjustment. This is the most effective and frequently used method. The controller needs to abide by the flight level (FL) for altitude adjustment. Below FL 41, there is a flight level every 1000 ft, and above FL41, there is a flight level every 2000 ft.
- 2.
- Heading adjustment. This method can be used for conflict resolution intuitively, but it will change the aircraft route. There are two approaches for heading adjustment. One is heading angle change, which is to control an aircraft to turn left or right by an angle. The other is the offset method, which controls an aircraft to fly a certain distance to the left or right to maintain the lateral separation.
- 3.
- Speed adjustment. Aircraft usually fly at the cruising altitude according to the economic speed, and the speed change cannot be represented intuitively. Therefore, speed adjustment is not recommended and should be expressed in multiples of 0.01 Mach or 10 kt.
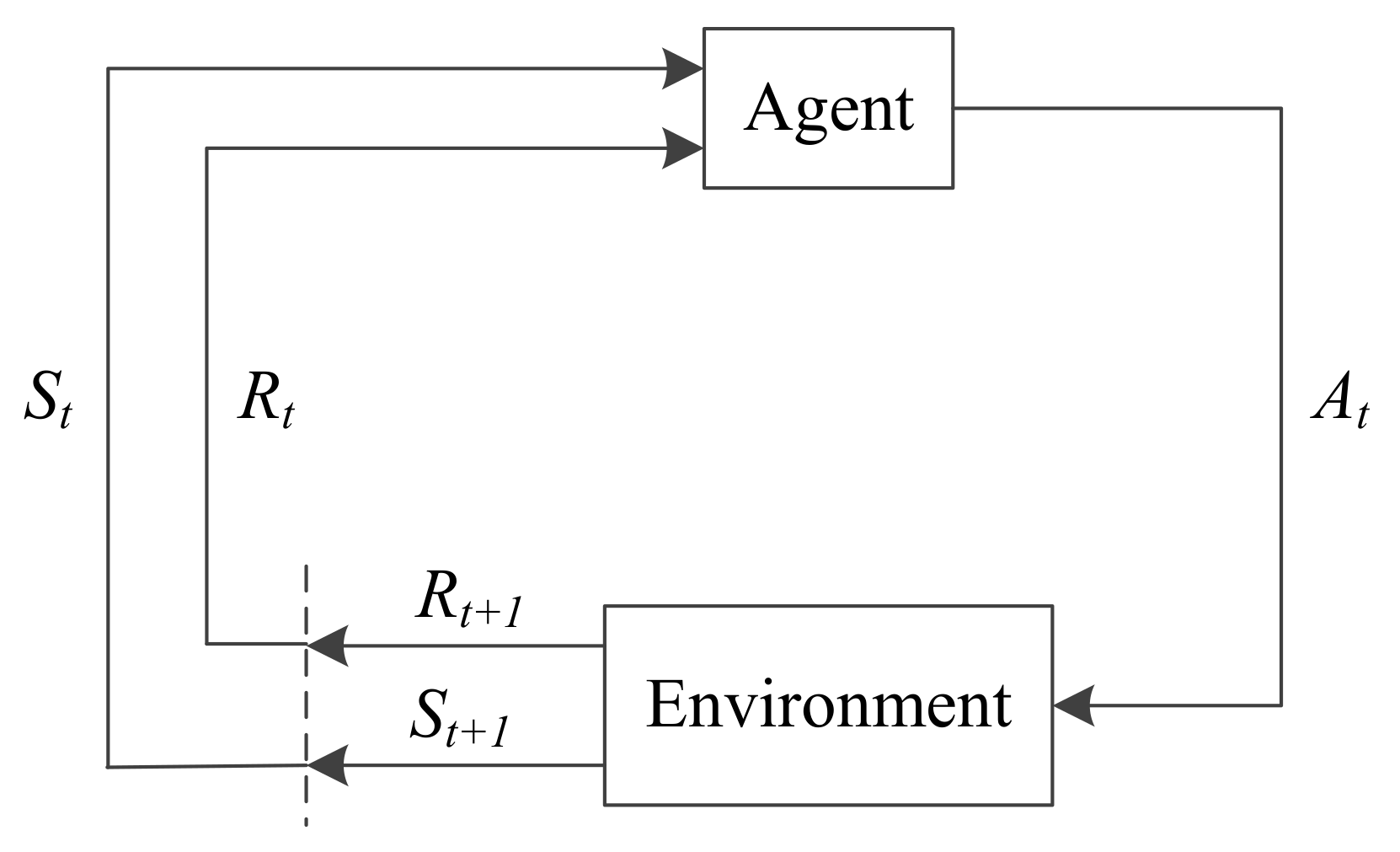
2.2. Deep Reinforcement Learning
3. Application
3.1. Overview
| Article | Algorithm | Authors | Year | Achievement |
|---|---|---|---|---|
| [22] | Heuristic Dyna-Q algorithm with Value Approximation | Yang et al. | 2014 | Similar to the principle of DRL |
| [23] | Strategic Conformal Automation | Regtuit et al. | 2018 | Training based on ATCos data |
| [24] | DDPG with Model Voltage Potential | Ribeiro et al. | 2020 | Combination with geometric method |
| [25] | Deep Q-Learning from Demonstrations | Hermans | 2021 | Explainability of the automation is contributed |
| [26] | Hierarchical DRL Framework | Brittain et al. | 2018 | Hierarchical agents are used |
| [27] | Deep Distributed Multi-Agent RL Framework | Brittain et al. | 2019 | Multi-agent RL is adopted |
| [28] | Deep Distributed Multi-Agent Variable | Brittain et al. | 2021 | LSTM network is used |
| [29] | Deep Distributed Multi-Agent Variable-Attention | Brittain et al. | 2020 | Attention network is added |
| [30] | Dropout and Data Augmentation Safety Module | Brittain et al. | 2021 | Can be used in uncertain environment |
| [31] | Single-Step DDPG | Pham et al. | 2019 | Continuous action space and non-fixed step |
| [32] | AI Agent with Interactive Conflict Solver | Tran et al. | 2019 | A conflict solver is developed |
| [33] | K-Control Actor-Critic | Wang et al. | 2019 | Decision-making is improved based on ATC process |
| [34] | Physics Informed DRL | Zhao et al. | 2021 | Prior physics understanding and model are integrated |
| [35] | Independent Deep Q Network | Sui et al. | 2021 | The DRL model closest to ATC process |
| [36] | DDPG | Wen et al. | 2019 | The efficiency of DRL method is proved |
| [37] | Corrected Collision Avoidance | Li et al. | 2019 | Correction network is added |
| [38] | Graph-Based DRL Framework | Mollinga et al. | 2020 | Graph neural network is added |
| [39] | Message Passing Neural Networks-Based Framework | Dalmau et al. | 2020 | Message passing neural network is added |
| [40] | Deep Ensemble Multi-Agent RL Architecture | Ghosh et al. | 2021 | Deep ensemble architecture is adopted |
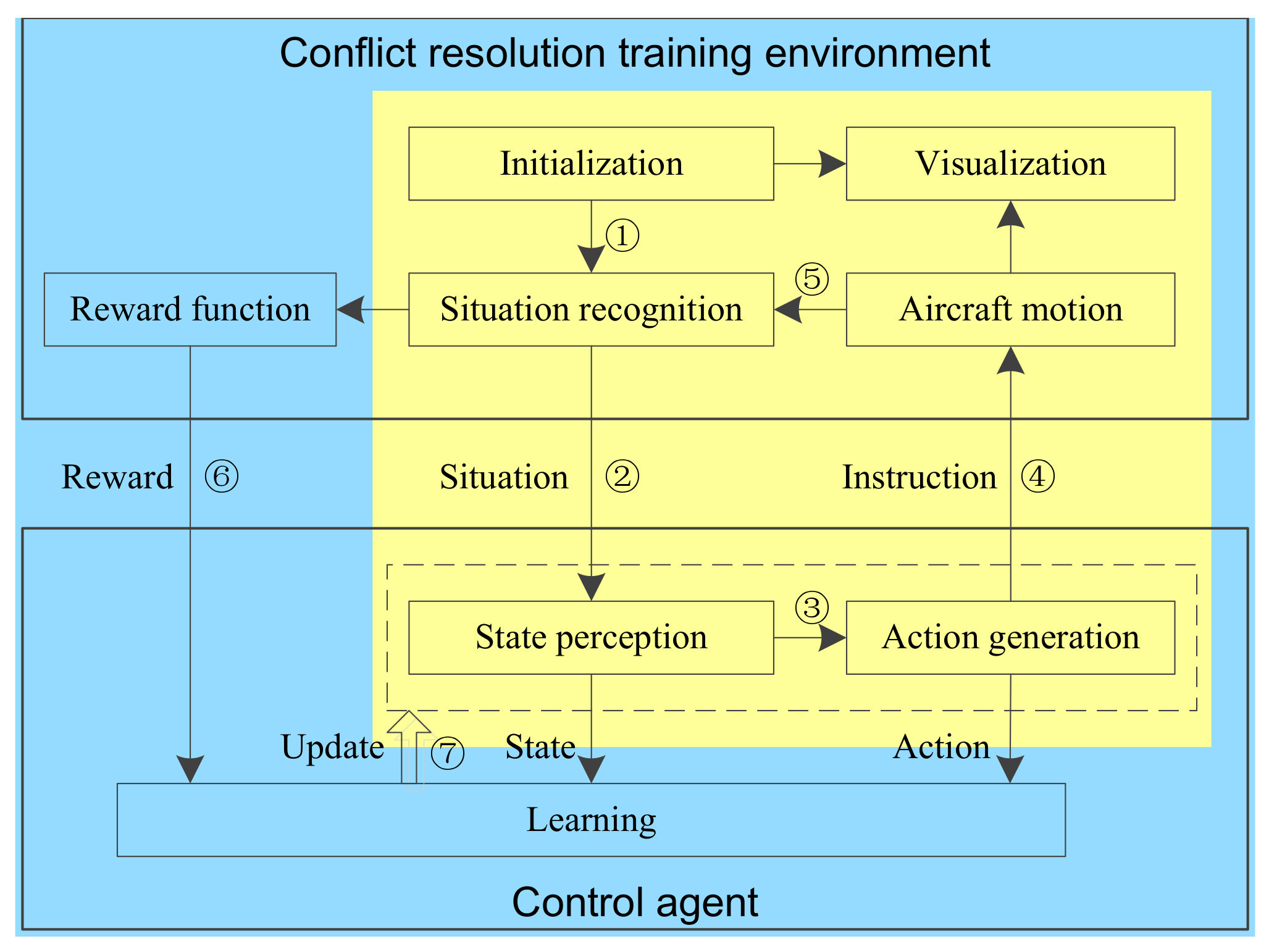
3.2. Environment
- 1.
- Geometric dimension. The current environment is either operating altitude, speed and heading in three-dimensional space, or operating speed or heading in a two-dimensional horizontal plane.
- 2.
- Operation mode. En-route is implemented in most airspace at present, and free flight, which has been implemented in some airspace in Europe, is the trend of operation mode in the future. Therefore, the DRL environment should be clear about whether to solve the problem of conflict resolution in en-route mode or free flight mode.
- 3.
- Aircraft number. It is necessary to specify the number of aircraft for conflict resolution, 2 or more generally, and multiple aircraft also include a fixed number and arbitrary numbers.
- 4.
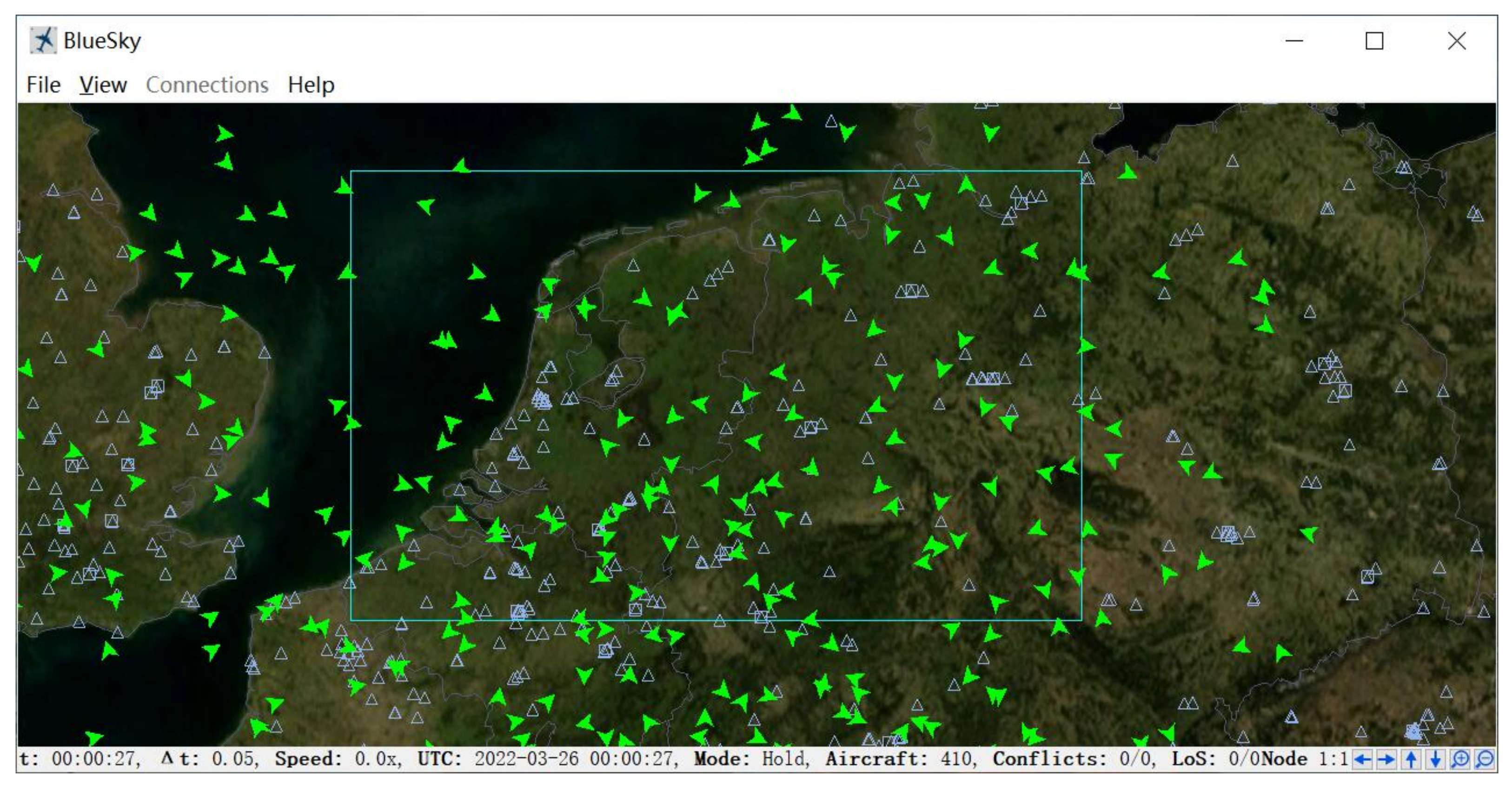
- Platform. DRL environment can be developed based on commercial or open-source ATC software, or independently.
| Article | Dimension | Operation Mode | Aircraft Number | Platform |
|---|---|---|---|---|
| [22] | 2D | Free Flight | Multiple, fixed | Independent development |
| [23] | 2D | Free Flight | 2 | Aircraft Data |
| [24] | 2D | En-route | Multiple, arbitrary | BlueSky |
| [25] | 2D | En-route | 2 | BlueSky |
| [26] | 2D | En-route | Multiple, fixed | NASA Sector 33 |
| [27] | 2D | En-route | Multiple, arbitrary | BlueSky |
| [28] | 2D | En-route | Multiple, arbitrary | BlueSky |
| [29] | 2D | En-route | Multiple, arbitrary | BlueSky |
| [30] | 2D | En-route | Multiple, arbitrary | BlueSky |
| [31] | 2D | Free Flight | 2 | Independent development |
| [32] | 2D | Free Flight | Multiple, fixed | Independent development |
| [33] | 2D | Free Flight | Multiple, fixed | Independent development |
| [34] | 2D | En-route | Multiple, arbitrary | PyGame |
| [35] | 3D | En-route | Multiple, arbitrary | ATOSS |
| [36] | 2D | Free Flight | Multiple, fixed | Independent development |
| [37] | 2D | Free Flight | Multiple, fixed | Independent development |
| [38] | 3D | En-route | Multiple, fixed | CSU Stanislaus |
| [39] | 2D | Free Flight | Multiple, arbitrary | Independent development |
| [40] | 2D | En-route | Multiple, arbitrary | ELSA-ABM |
3.3. Model
3.3.1. Action Space
| Article | Adjustment | Control Mode | Action Dimension | Decision Times |
|---|---|---|---|---|
| [22] | Heading | Discrete | Multi | Fixed step |
| [23] | Heading | Discrete | 3 | 1 |
| [24] | Heading, speed | Continuous | 2 | Non-fixed step |
| [25] | Heading | Discrete | 6 | Fixed step |
| [26] | Route, speed | Discrete | Multi | 1, fixed step |
| [27] | Speed | Discrete | 3 | Fixed step |
| [28] | Speed | Discrete | 3 | Fixed step |
| [29] | Speed | Discrete | 3 | Fixed step |
| [30] | Speed | Discrete | 3 | Fixed step |
| [31] | Heading | Continuous | 2 | Non-fixed step |
| [32] | Heading | Continuous | 2 | Non-fixed step |
| [33] | Heading | Continuous | 4 | Non-fixed step |
| [34] | Heading, speed | Both | 3 for Dis., 2 for Con. | Fixed step |
| [35] | Altitude, heading, speed | Discrete | 14 | Fixed step |
| [36] | Heading | Continuous | 1 | Non-fixed step |
| [37] | Heading | Discrete | 6 | Fixed step |
| [38] | Altitude, heading, speed | Discrete | Multi | Fixed step |
| [39] | Heading, speed, route | Discrete | Multi | Fixed step |
| [40] | Speed | Discrete | 3 | Fixed step |
3.3.2. State Space
| Article | Scope | Structure | Information | Pre-Processing | Aircraft Number |
|---|---|---|---|---|---|
| [22] | All aircraft | Data matrix | All information | No | Fixed |
| [23] | All aircraft | Data matrix | Relative information | Yes | Fixed |
| [24] | N-nearest | Data matrix | Relative information | Yes | Arbitrary |
| [25] | All aircraft | Raw pixels | All information | Yes | Fixed |
| [26] | All aircraft | Both | All information | No | Fixed |
| [27] | N-nearest | Data matrix | Self & relative information | Yes | Arbitrary |
| [28] | N-nearest | Data matrix | Self & relative information | Yes | Arbitrary |
| [29] | All aircraft | Data matrix | All & relative information | Yes | Arbitrary |
| [30] | N-nearest | Data matrix | Self & relative information | Yes | Arbitrary |
| [31] | All aircraft | Data matrix | Relative information | Yes | Fixed |
| [32] | All aircraft | Data matrix | Relative information | Yes | Fixed |
| [33] | All aircraft | Data matrix | All information | No | Fixed |
| [34] | All aircraft | Raw pixels | All & relative information | Yes | Arbitrary |
| [35] | Sub-airspace | Data matrix | All information | Yes | Arbitrary |
| [36] | All aircraft | Data matrix | All information | No | Fixed |
| [37] | All aircraft | Data matrix | All information | No | Fixed |
| [38] | All aircraft | Data matrix | All & relative information | Yes | Fixed |
| [39] | N-nearest | Data matrix | Self & relative information | Yes | Arbitrary |
| [40] | N-nearest | Data matrix | Self & relative information | Yes | Arbitrary |
3.3.3. Reward Function
| Article | Minimum Separation Maintenance | Additional Cost Penalty | Other Penalties |
|---|---|---|---|
| [22] | Termination step | / | Deviation from preset route |
| [23] | Termination step | / | Decision inconsistency, invalid action |
| [24] | Termination step | Heading angle, speed | / |
| [25] | Termination step | Heading angle | Deviation from preset route, invalid action |
| [26] | Termination step | Speed | / |
| [27] | Every step | / | Invalid action |
| [28] | Every step | / | / |
| [29] | Every step | / | / |
| [30] | Every step | / | Invalid action |
| [31] | Termination step | / | Deviation from preset route, illegal instruction |
| [32] | Termination step | / | Deviation from preset route, illegal instruction |
| [33] | Termination step | Heading angle | / |
| [34] | Termination step | / | Deviation from preset route |
| [35] | Every step | Heading angle, speed, altitude | Illegal instruction |
| [36] | Termination step | Heading angle | / |
| [37] | Every step | Heading angle | / |
| [38] | Every step | / | / |
| [39] | Every step | Heading angle, speed, delay | Deviation from preset route |
| [40] | Every step | Delay, fuel | / |
3.4. Algorithm
- 1.
- Agent number. The selection of a single agent or multi-agent mainly depends on the requirements for solving problems. The single agent has two advantages. One is in line with the actual ATC process, that is, one ATCo controlled all aircraft. The other is relatively simple in technology and easy to implement. However, its disadvantage is that it is difficult to deal with the changing number of aircraft. Multi-agent is opposite to a single agent, and communication between agents is needed.
- 2.
- Basic algorithm. The choice of the basic algorithm is closely related to the type of action space. DQN algorithm can only deal with discrete action space and is adopted in [25,26,35,37,38]. DDPG can only deal with continuous action space and is adopted in [24,31,32,36]. The standard actor-critic architecture can handle both continuous and discrete action spaces, which is improved in [33,39]. PPO is one of the best performing algorithms at present, which is used in [27,28,29,30,34].
- 3.
- Improved algorithm. Based on the basic algorithm, there are two improved approaches. One is to improve the structure of the agent according to the characteristics of ATC, including the improvement of neural network structure or agent structure. The other is the improvement of the DRL training method to improve the accuracy of selecting actions according to the situation.
| Article | Agent Number | Basic Algorithm | Improved Algorithm |
|---|---|---|---|
| [22] | Single | Dyna-Q | Training method improvement |
| [23] | Single | Q-learning | / |
| [24] | Single | DDPG | Training method improvement |
| [25] | Single | DQN/Double DQN | Training method improvement |
| [26] | Single | DQN | Agent structure improvement |
| [27] | Multi | PPO | Agent structure improvement |
| [28] | Multi | PPO | Agent structure improvement |
| [29] | Multi | PPO | Agent structure improvement |
| [30] | Multi | PPO | Agent structure improvement |
| [31] | Single | DDPG | / |
| [32] | Single | DDPG | / |
| [33] | Single | Actor-critic | Training method improvement |
| [34] | Single/Multi | PPO | Training method improvement |
| [35] | Multi | DQN | Training method improvement |
| [36] | Single | DDPG | / |
| [37] | Single | DQN | Agent structure improvement |
| [38] | Single | DQN | Agent structure improvement |
| [39] | Multi | Actor-critic | Agent structure improvement |
| [40] | Multi | Model-based | Agent structure improvement |
3.4.1. Agent Structure Improvement



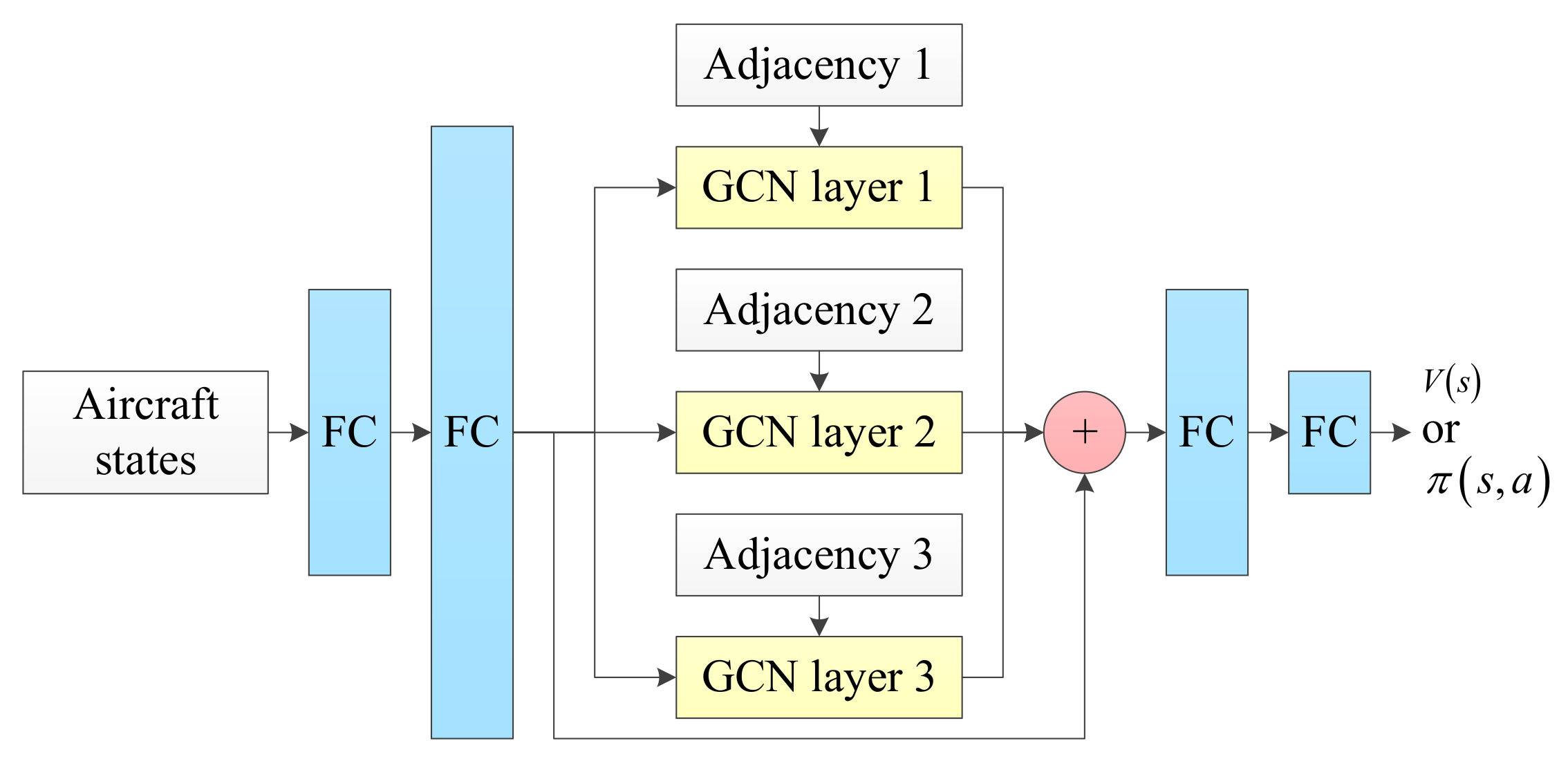


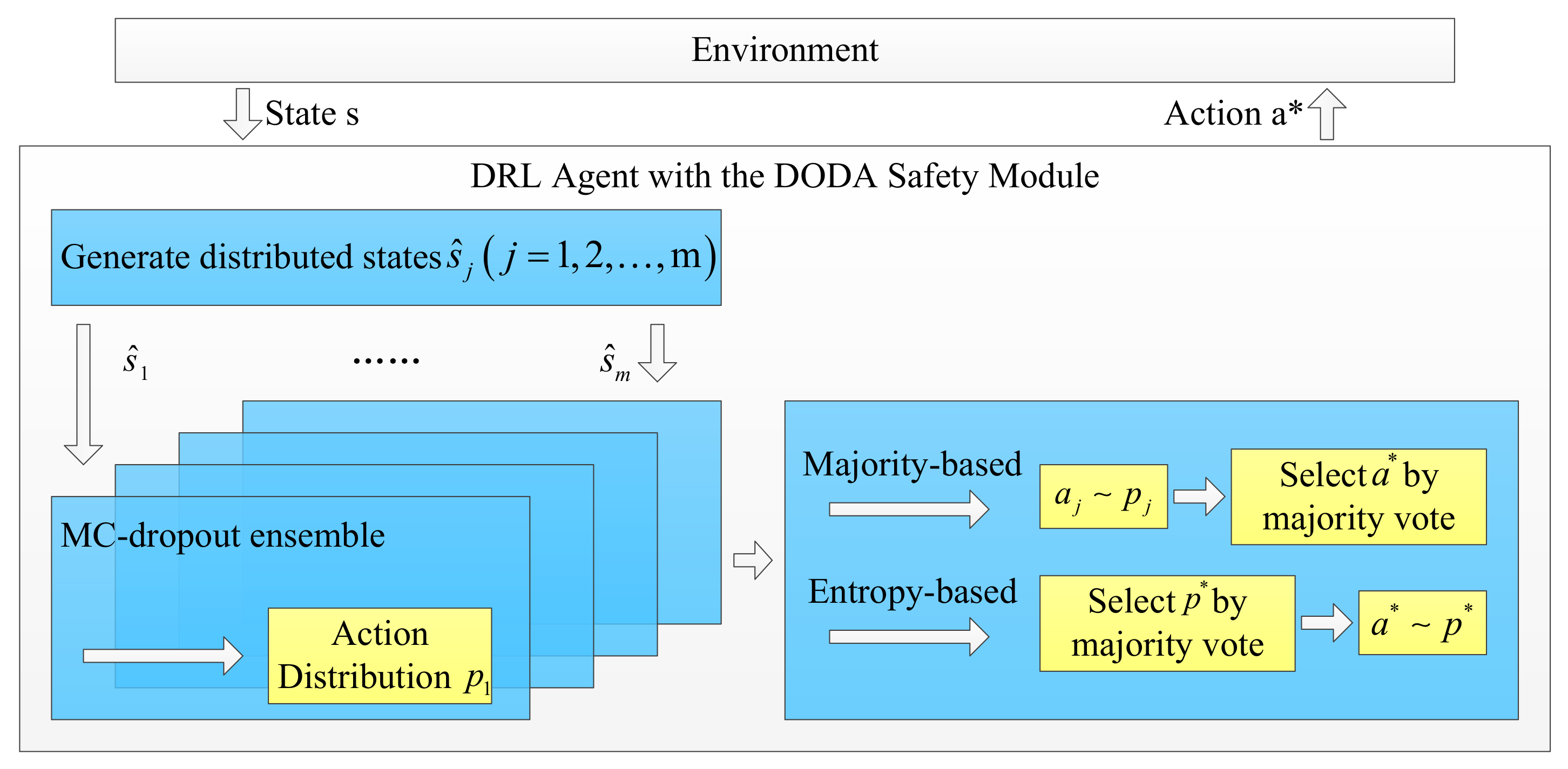
3.4.2. Training Method Improvement

| Algorithm 1: Deep Q-Learning from Demonstrations [60] used in [25] |
| Require: • : initialized with demonstration data set; |
| • : weights for initial behavior network; |
| • : weights for target network; |
| • : frequency at which to update target net; |
| • k: number of pre-training gradient updates; |
| • : learning rate; |
| • : number of epochs for training. |
| 1: for step {pre-training phase} do |
| 2: sample a mini-batch of n transitions from with prioritization |
| 3: calculate loss using target network |
| 4: perform a gradient descent step to update |
| 5: if t mod then |
| 6: {update target network} |
| 7: end if |
| 8: |
| 9: end for |
| 10: for step {normal training phase} do |
| 11: sample action from behavior policy |
| 12: play action a and observe |
| 13: store into , overwriting oldest self-generated transition if over capacity occurs |
| 14: sample a mini-batch of n transitions from with prioritization |
| 15: calculate loss using target network |
| 16: perform a gradient descent step to update |
| 17: if t mod then |
| 18: {update target network} |
| 19: end if |
| 20: |
| 21: end for |

| Algorithm 2: K-Control Actor-Critic. Reprint with permission from [33]. 2019, John Wiley and Sons. |
| Require: • and are polar radius and angle, forming a two-dimensional polar coordinate, which can be used to describe a position in the sector; |
| •actor and critic neural networks. |
| 1: if is training mode then |
| 2: for each episode do |
| 3: initialize random environment parameters |
| 4: for each step in range K do |
| 5: if is the Kth step then |
| 6: set the destination as the action |
| 7: run environment |
| 8: update parameters of critic network |
| 9: else |
| 10: obtain action by |
| 11: update parameters of critic network |
| 12: update parameters of actor network |
| 13: if conflict then |
| 14: break |
| 15: end if |
| 16: end if |
| 17: end for |
| 18: end for |
| 19: else |
| 20: for each testing episode or application situation do |
| 21: for each step in range K do |
| 22: if is the Kth step then |
| 23: set the destination as the action |
| 24: run environment |
| 25: else |
| 26: obtain action by |
| 27: if conflict then |
| 28: break |
| 29: end if |
| 30: end if |
| 31: end for |
| 32: end for |
| 33: end if |
| Algorithm 3: IDQN algorithm for the conflict resolution model [35] |
| 1: initialize the experience replay pool of each agent with a capacity of D |
| 2: initialize the action state value function Qi and randomly generate the weights |
| 3: initialize the target Q network with weight |
| 4: for each episode do |
| 5: randomly select the conflict scenario and initialize the state |
| 6: for each step do |
| 7: each aircraft adopts an -greedy strategy to select instruction actions from the action space to form joint actions |
| 8: execute the joint instruction action according to the reward received and the new state of the aircraft |
| 9: save the conflict samples into the experience playback pool D |
| 10: randomly select a conflict sample from the experience pool D |
| 11: if the step is final then |
| 12: set |
| 13: else |
| 14: set |
| 15: calculate the loss function |
| 16: update in using gradient descent |
| 17: update the target Q network for each C step, |
| 18: end if |
| 19: end for |
| 20: end for |
| Algorithm 4: Meta controller [34] |
| Require: v: velocity of next step |
| 1: while run do |
| 2: obs.← observe airspace |
| 3: states ← SSDProcess(obs.) |
| 4: velocity for resolution: vr ← Policy(states) |
| 5: velocity for return: vi ← intention velocity |
| 6: conflict detection for vi |
| 7: if conflict then |
| 8: v ← vr |
| 9: else |
| 10: v ← vi |
| 11: end if |
| 12: end while |
3.5. Evaluating Indicator
4. Discussion
4.1. A Guideline for the Application of DRL to Solve Conflict Resolution Problems
- 1.
- Build a conflict resolution environment, which not only provides current or future conflict resolution scenarios, but also supports the training of agents.
- 2.
- Define the control object, whether it is one aircraft or multiple aircraft.
- 3.
- Define the input and output of the control process, that is, the state space and action space of the agent.
- 4.
- Construct the research goal in the form of a reward function, to make the agent meet the expected evaluation requirements.
- 5.
- Design appropriate agent structure and training algorithm.
4.2. Open Issues of DRL in Conflict Resolution
- 1.
- Need a unified DRL framework. Some researchers have simplified the models in different directions according to their actual demands, and then many types of DRL models have been established. Some studies have also carried out personalized designs of state space or action space, which are inconsistent with the actual ATC scene, so they can not provide enough reference. Therefore, a challenge is that a DRL framework should be provided, and research should be carried out based on this to solve their respective problems.
- 2.
- Lack of a baseline. Compared with the fields with excellent DRL performance such as video games and robot control, the current application of DRL in the field of conflict resolution lacks a baseline. Firstly, an environment accepted by the research community is necessary. However, the environment is developed by each researcher independently and there is no unified version support. Secondly, there is also a lack of unified ATC scenarios. All studies design scenarios according to their practical problems and needs. Finally, the open-source baseline algorithm is also lacking. Of course, with the support of the environment and scenarios, the algorithm will be developed gradually.
- 3.
- New conflicts caused by multiple aircraft. For two aircraft, adjusting one or both aircraft can solve the conflict and will not bring new conflict. However, when the number of aircraft increases and the conflict between two aircraft is solved, the conflict between the original non-conflict aircraft pair may be caused. The current DRL conflict resolution strategies, including adjusting one aircraft or all aircraft, may bring new conflicts. This problem is mainly solved through the design of the reward function, which can not be solved perfectly.
- 4.
- Incomplete/uncertain information. Actual maneuver of the aircraft is always deviated from the controller’s command due to some noise. However, in current researches, it is assumed that the information is complete and unbiased, which is inconsistent with that of the actual situation. How to capture the errors that exist in the real world and have an impact on the conflict resolution process and reflect them in the model is also one of the important challenges.
- 5.
- Look-forward time. In actual ATC, ATCos make predictions according to the flight plan, flight route, and current aircraft position. However, for the DRL model, there is no unified standard for the length of look-forward time. Look-forward for a long time, on the one hand, wastes time and consumes resources, on the other hand, it is easy to generate a false alarm. Look-forward for a short time is not enough to detect potential conflicts. Therefore, adding an appropriate prediction of the future time into the model, whether autonomous or auxiliary ATCos decision-making, can be of great help.
- 6.
- Meteorological conditions are not considered. Meteorological conditions have a great impact on ATC. In bad weather, the aircraft needs to change the flight plan or route temporarily, which will bring potential conflicts. However, the influence of weather is not considered in current research. Therefore, it is necessary to consider the impact of meteorological conditions affecting flight and establish a model in the environment.
4.3. Future Research Suggestions
- 1.
- Representation of state and action space. In view of the inconsistency of MDP model in various studies, the representation methods of state space and action space need to be studied. By comparing the performance of agents with different state space and action space in typical ATC scenarios, effective combination points of actual conflict resolution and DRL model should be established.
- 2.
- Optimization of reward function. The agent learns according to the feedback of the reward function, and its role in DRL is equivalent to the label in supervised learning. Reward function is the main way to reflect the evaluation indicators of conflict resolution, including safety and efficiency. The agent should be guided to establish a better track by optimizing the reward function, so as to improve the performance.
- 3.
- Utilization of prior knowledge. In the short term, agents cannot work independently, and it is difficult to generate instructions beyond human controllers. Therefore, the prior knowledge of human controllers should be fully utilized to make the instructions of agents comply with the operation of ATCos and provide efficient auxiliary decision-making.
- 4.
- Combination with traditional approaches. The advantages of DRL are model-free and efficient decision-making. At present, its decision-making performance is not as good as traditional algorithms, such as geometric algorithms and optimization algorithms. Therefore, traditional algorithms can be combined with DRL to solve the problems that DRL is not good at.
- 5.
- Pre-training. Due to exploration, reinforcement learning often takes more time in the early phase of training. Pre-training can be carried out by using ATC data or in scenarios that are similar and easy to train. Retraining based on the pre-trained agent can significantly improve the training efficiency.
- 6.
- Improvement of evaluating indicators. The research on the evaluating indicator architecture of agents is also an important direction. Measure the safety and efficiency of conflict resolution and the evaluating indicators of DRL agents to establish a unified and reasonable evaluation system. On the one hand, it can form a more scientific evaluation, which is conducive to improvement. On the other hand, it can also guide the design of reward function.
- 7.
- Altitude adjustment agent. In a 3D scenario, both state space and action space are complex. Altitude adjustment is the most commonly used operation of ATCos, and its mechanism is different from that of adjustment in the horizontal plane. In the future, two agents can be trained, one to adjust the altitude and the other to adjust in the horizontal plane, and the coordination mechanism can be studied to use two agents together in practice.
- 8.
- Aircraft selection agent. For the scenario of multiple aircraft, it is necessary to select a conflicting aircraft for adjustment. However, the existing conflict resolution agents do not have this ability. An aircraft selection agent can be first trained, and be used to select one or more aircraft to be adjusted. Then the conflict resolution agent is adopted to generate maneuver decisions.
- 9.
- Returning to intention. There are flight routes in en-route mode, and pre-set routes and exit point in free flight mode. The current conflict resolution agent is only responsible for resolution while returning to intention still adopts the traditional method. Therefore, the research on the approach of intelligent return to intention is also one of the important research directions.
- 10.
- Distinguish between manned and unmanned aircraft. With the wide application of UAVs, the research on conflict resolution of UAVs is a hotspot. Different from manned aircraft, multi UAVs are mainly distributed, and the actions generated by an agent do not need to be smoothed.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Federal Aviation Administration. FAA Aerospace Forecast: Fiscal Years 2020–2040; U.S. Department of Transportation: Washington, DC, USA, 2020.
- Kuchar, J.; Yang, L. A review of conflict detection and resolution modeling methods. IEEE Trans. Intell. Transp. Syst. 2000, 1, 179–189. [Google Scholar] [CrossRef]
- Jenie, Y.I.; Van Kampen, E.J.; Ellerbroek, J.; Hoekstra, J.M. Taxonomy of conflict detection and resolution approaches for unmanned aerial vehicle in an integrated airspace. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1–10. [Google Scholar] [CrossRef]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Review of conflict resolution methods for manned and unmanned aviation. Aerospace 2020, 7, 79. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: London, UK, 2018. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T. A general reinforcement learning algorithm that masters chess, shogi, and go through self-play. Science 2018, 362, 1140–1144. [Google Scholar] [CrossRef]
- Hwangbo, J.; Lee, J.; Dosovitskiy, A.; Bellicoso, D.; Tsounis, V.; Koltun, V.; Hutter, M. Learning agile and dynamic motor skills for legged robots. Sci. Robot. 2019, 4, 1–20. [Google Scholar] [CrossRef]
- Degrave, J.; Felici, F.; Buchli, J.; Neunert, M.; Tracey, B.; Carpanese, F.; Ewalds, T.; Hafner, R.; Abdolmaleki, A.; de Las Casas, D. Magnetic control of tokamak plasmas through deep reinforcement learning. Nature 2022, 602, 414–419. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjel, A.K.; Ostrovski, G. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- International Civil Aviation Association. Doc 4444: Air Traffic Management - Procedures for Air Navigation Services, 16th ed.; ICAO: Montreal, QC, Canada, 2016. [Google Scholar]
- Watkins, C.J.; Dayan, P. Technical note: Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-learning. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling network architectures for deep reinforcement learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Busoniu, L.; Babuska, R.; Schutter, B. A comprehensive survey of multiagent reinforcement learning. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 2008, 38, 156–172. [Google Scholar] [CrossRef]
- Hernandez-Leal, P.; Kartal, B.; Taylor, M.E. A survey and critique of multiagent deep reinforcement learning. arXiv 2018, arXiv:1810.05587v3. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yin, D.; Xie, H. A reinforcement learning based UAVS air collision avoidance. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- Regtuit, R.; Borst, C.; Van Kampen, E.J. Building strategic conformal automation for air traffic control using machine learning. In Proceedings of the 2018 AIAA Information Systems-AIAA Infotech @ Aerospace, Kissimmee, FA, USA, 8–12 January 2018. [Google Scholar]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Improvement of conflict detection and resolution at high densities through reinforcement learning. In Proceedings of the 9th International Conference on Research in Air Transportation, Virtual, 15 September 2020. [Google Scholar]
- Hermans, M.C. Towards Explainable Automation for Air Traffic Control Using Deep Q-Learning from Demonstrations and Reward Decomposition. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, May 2020. [Google Scholar]
- Brittain, M.; Wei, P. Autonomous aircraft sequencing and separation with hierarchical deep reinforcement learning. In Proceedings of the 8th International Conference on Research in Air Transportation, Barcelona, Spain, 26–29 June 2018. [Google Scholar]
- Brittain, M.; Wei, P. Autonomous separation assurance in a high-density en route sector: A deep multi-agent reinforcement learning approach. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference, Auckland, New Zealand, 27–30 October 2019. [Google Scholar]
- Brittain, M.; Wei, P. One to any: Distributed conflict resolution with deep multi-agent reinforcement learning and long short-term memory. In Proceedings of the 2021 AIAA Science and Technology Forum and Exposition, Nashville, TN, USA, 11–15 January 2021. [Google Scholar]
- Brittain, M.; Yang, X.; Wei, P. A deep multi-agent reinforcement learning approach to autonomous separation assurance. arXiv 2020, arXiv:2003.08353. [Google Scholar]
- Guo, W.; Brittain, M.; Wei, P. Safety enhancement for deep reinforcement learning in autonomous separation assurance. arXiv 2021, arXiv:2105.02331. [Google Scholar]
- Pham, D.T.; Tran, N.P.; Goh, S.K.; Alam, S.; Duong, V. Reinforcement learning for two-aircraft conflict resolution in the presence of uncertainty. In Proceedings of the 2019 IEEE-RIVF International Conference on Computing and Communication Technologies, Danang, Vietnam, 20–22 March 2019. [Google Scholar]
- Tran, N.P.; Pham, D.T.; Goh, S.K.; Alam, S.; Duong, V. An intelligent interactive conflict solver incorporating air traffic controllers’ preferences using reinforcement learning. In Proceedings of the 2019 Integrated Communications, Navigation and Surveillance Conference, Herndon, VA, USA, 9–11 April 2019. [Google Scholar]
- Wang, Z.; Li, H.; Wang, J.; Shen, F. Deep reinforcement learning based conflict detection and resolution in air traffic control. IET Intell. Transp. Syst. 2019, 13, 1041–1047. [Google Scholar] [CrossRef]
- Zhao, P.; Liu, Y. Physics informed deep reinforcement learning for aircraft conflict resolution. IEEE Trans. Intell. Transp. Syst. 2021, 1, 1–14. [Google Scholar] [CrossRef]
- Sui, D.; Xu, W.; Zhang, K. Study on the resolution of multi-aircraft flight conflicts based on an IDQN. Chin. J. Aeronaut. 2021, 35, 195–213. [Google Scholar] [CrossRef]
- Wen, H.; Li, H.; Wang, Z. Application of DDPG-based collision avoidance algorithm in air traffic control. In Proceedings of the 12nd International Symposium on Computational Intelligence and Design, Hangzhou, China, 14–15 December 2019. [Google Scholar]
- Li, S.; Egorov, H.; Kochenderfer, M.J. Optimizing collision avoidance in dense airspace using deep reinforcement learning. In Proceedings of the 13th USA/Europe Air Traffic Management Research and Development Seminar, Vienna, Austria, 17–21 June 2019. [Google Scholar]
- Mollinga, J.; Hoof, H. An autonomous free airspace en-route controller using deep reinforcement learning techniques. In Proceedings of the 9th International Conference on Research in Air Transportation, Virtual, 15 September 2020. [Google Scholar]
- Dalmau, R.; Allard, E. Air traffic control using message passing neural networks and multi-agent reinforcement learning. In Proceedings of the 10th SESAR Innovation Days, Budapest, Hungary, 7–10 December 2020. [Google Scholar]
- Ghosh, S.; Laguna, S.; Lim, S.H.; Wynter, L.; Poonawala, H. A deep ensemble method for multi-agent reinforcement learning: A case study on air traffic control. In Proceedings of the 31st International Conference on Automated Planning and Scheduling, Guangzhou, China, 2–13 August 2021. [Google Scholar]
- Bellemare, M.G.; Naddaf, Y.; Veness, J.; Bowling, M. The arcade learning environment: An evaluation platform for general agents. J. Artif. Intell. Res. 2013, 47, 253–279. [Google Scholar] [CrossRef]
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 December 2012. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Kelly, S. Basic introduction to PyGame. In Python, PyGame and Raspberry Pi Game Development; Apress: Berkeley, CA, USA, 2019; pp. 87–97. [Google Scholar]
- Flight Control Exercise. Available online: https://github.com/devries/flight-control-exercise (accessed on 26 March 2022).
- ELSA Air Traffic Simulator. Available online: https://github.com/ELSA-Project/ELSA-ABM (accessed on 26 March 2022).
- Hoekstra, J.; Ellerbroek, J. BlueSky ATC simulator project: An open data and open source approach. In Proceedings of the 7th International Conference on Research in Air Transportation, Philadelphia, PA, USA, 20–24 June 2016. [Google Scholar]
- BlueSky-The Open Air Traffic Simulator. Available online: https://github.com/TUDelft-CNS-ATM/bluesky (accessed on 26 March 2022).
- Ng, A.; Harada, D.; Russell, S. Policy invariance under reward transformations: Theory and application to reward shaping. In Proceedings of the 16th International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999. [Google Scholar]
- Kanervisto, A.; Scheller, C.; Hautamäki, V. Action space shaping in deep reinforcement learning. In Proceedings of the 2020 IEEE Conference on Games, Osaka, Japan, 24–27 October 2020; pp. 479–486. [Google Scholar]
- Hermes, P.; Mulder, M.; Paassen, M.M.; Boering, J.H.L.; Huisman, H. Solution-space-based complexity analysis of the difficulty of aircraft merging tasks. J. Aircr. 2009, 46, 1995–2015. [Google Scholar] [CrossRef]
- Ellerbroek, J.; Brantegem, K.C.R.; Paassen, M.M.; Mulder, M. Design of a coplanar airborne separation display. IEEE Trans. Hum. Mach. Syst. 2013, 43, 277–289. [Google Scholar] [CrossRef][Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 34th Advances in Neural Information Processing Systems, Long Beach, CA, USA, 6–12 December 2017. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, J.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Patrick, S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Ormoneit, D.; Sen, Ś. Kernel-based reinforcement learning. Mach. Learn. 2002, 49, 161–178. [Google Scholar] [CrossRef]
- Bouton, M.; Julian, K.; Nakhaei, A.; Fujimura, K.; Kochenderfer, M.J. Utility decomposition with deep corrections for scalable planning under uncertainty. In Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Hoekstra, J.; Gent, R.; Ruigrok, R. Designing for safety: The ‘free flight’ air traffic management concept. Reliab. Eng. Syst. Saf. 2002, 75, 215–232. [Google Scholar] [CrossRef]
- Hester, T.; Vecerik, M.; Pietquin, O.; Lanctot, M.; Schaul, T.; Piot, B.; Horgan, D.; Quan, J.; Sendonaris, A.; Osband, I.; et al. Deep Q-learning from demonstrations. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–9 February 2018. [Google Scholar]
- Hong, Y.; Kim, Y.; Lee, K. Application of complexity map to reduce air traffic complexity in a sector. In Proceedings of the 2014 AIAA Guidance, Navigation, and Control Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Pan, W.; Li, H.; Wang, X.; Zuo, Q. Review of Deep Reinforcement Learning Approaches for Conflict Resolution in Air Traffic Control. Aerospace 2022, 9, 294. https://doi.org/10.3390/aerospace9060294
Wang Z, Pan W, Li H, Wang X, Zuo Q. Review of Deep Reinforcement Learning Approaches for Conflict Resolution in Air Traffic Control. Aerospace. 2022; 9(6):294. https://doi.org/10.3390/aerospace9060294
Chicago/Turabian StyleWang, Zhuang, Weijun Pan, Hui Li, Xuan Wang, and Qinghai Zuo. 2022. "Review of Deep Reinforcement Learning Approaches for Conflict Resolution in Air Traffic Control" Aerospace 9, no. 6: 294. https://doi.org/10.3390/aerospace9060294
APA StyleWang, Z., Pan, W., Li, H., Wang, X., & Zuo, Q. (2022). Review of Deep Reinforcement Learning Approaches for Conflict Resolution in Air Traffic Control. Aerospace, 9(6), 294. https://doi.org/10.3390/aerospace9060294






