Aircraft-Type-Specific Impact of Speed Brakes on Lift and Drag
Abstract
:1. Introduction
1.1. State of the Art
1.2. Paper Structure
2. Flight Performance Calculation
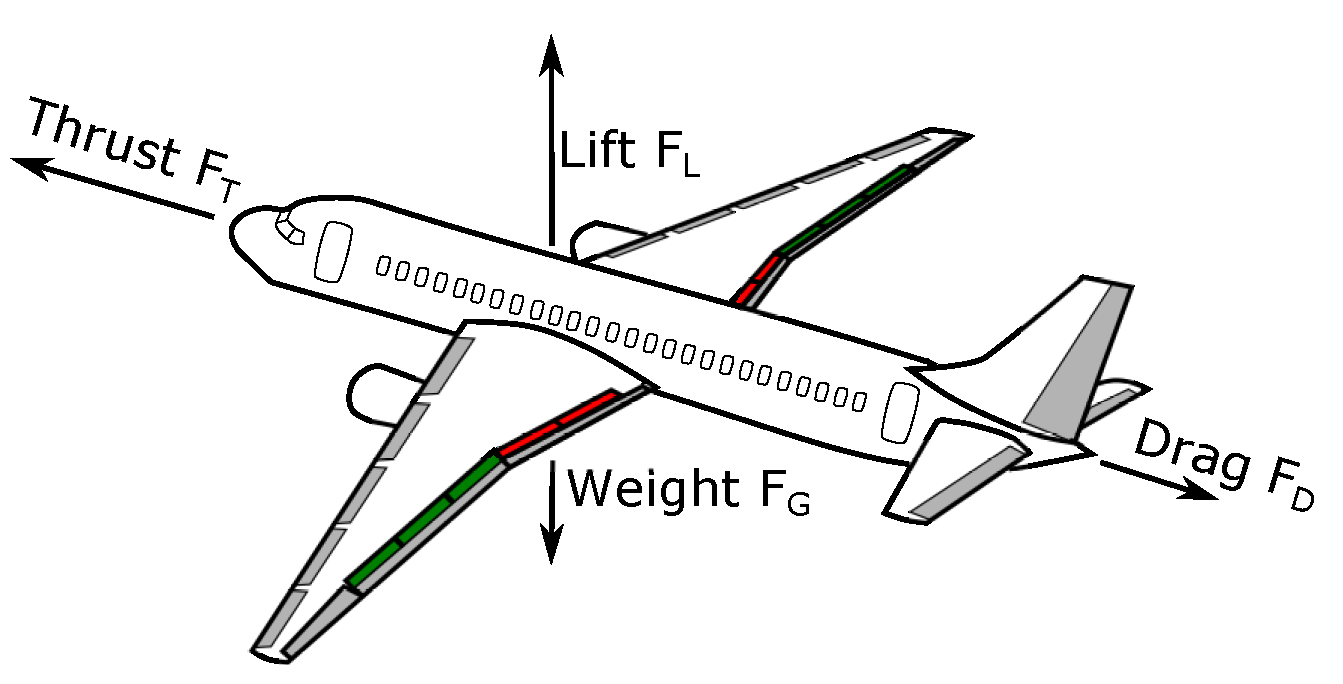
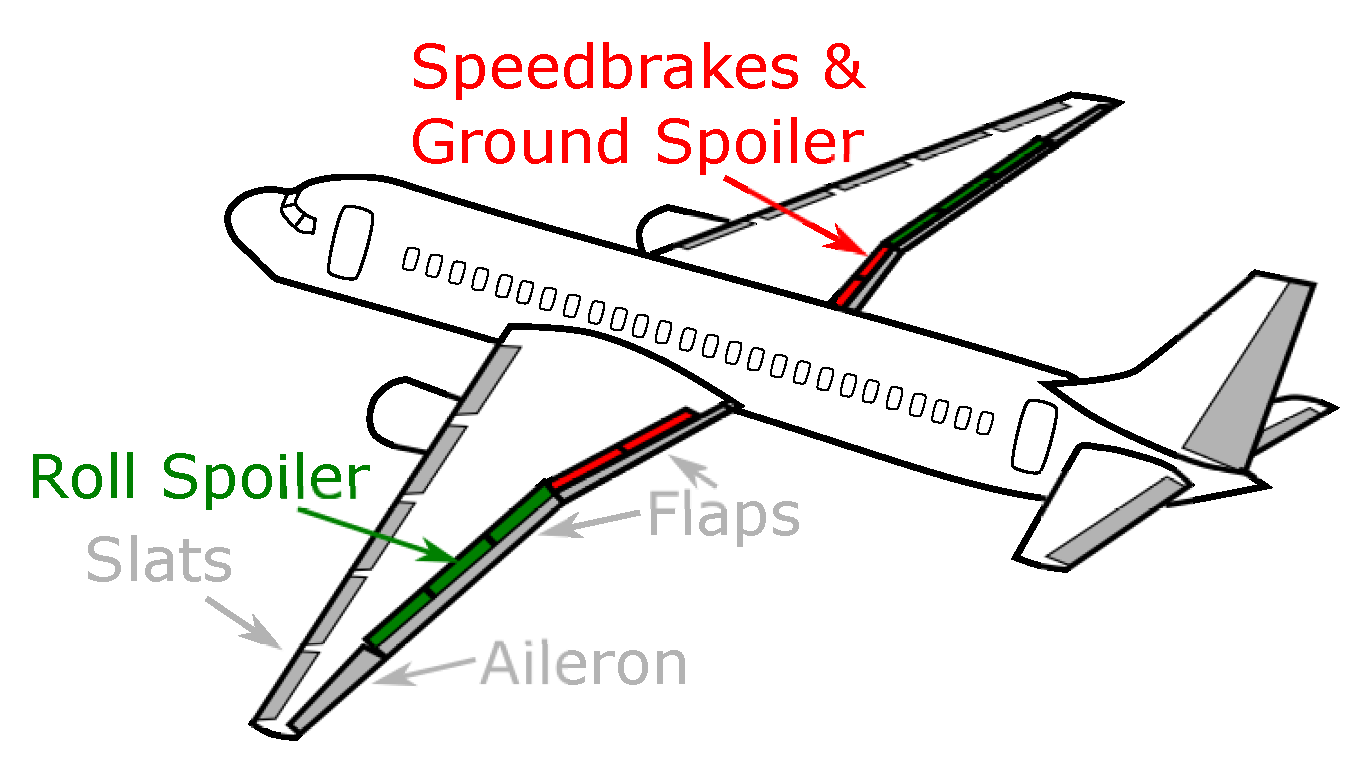
Preliminary Considerations of Speed Brakes
3. Methodology
3.1. Speed Brakes on NASA Model B747
3.2. Geometric Data of NASA Model B747
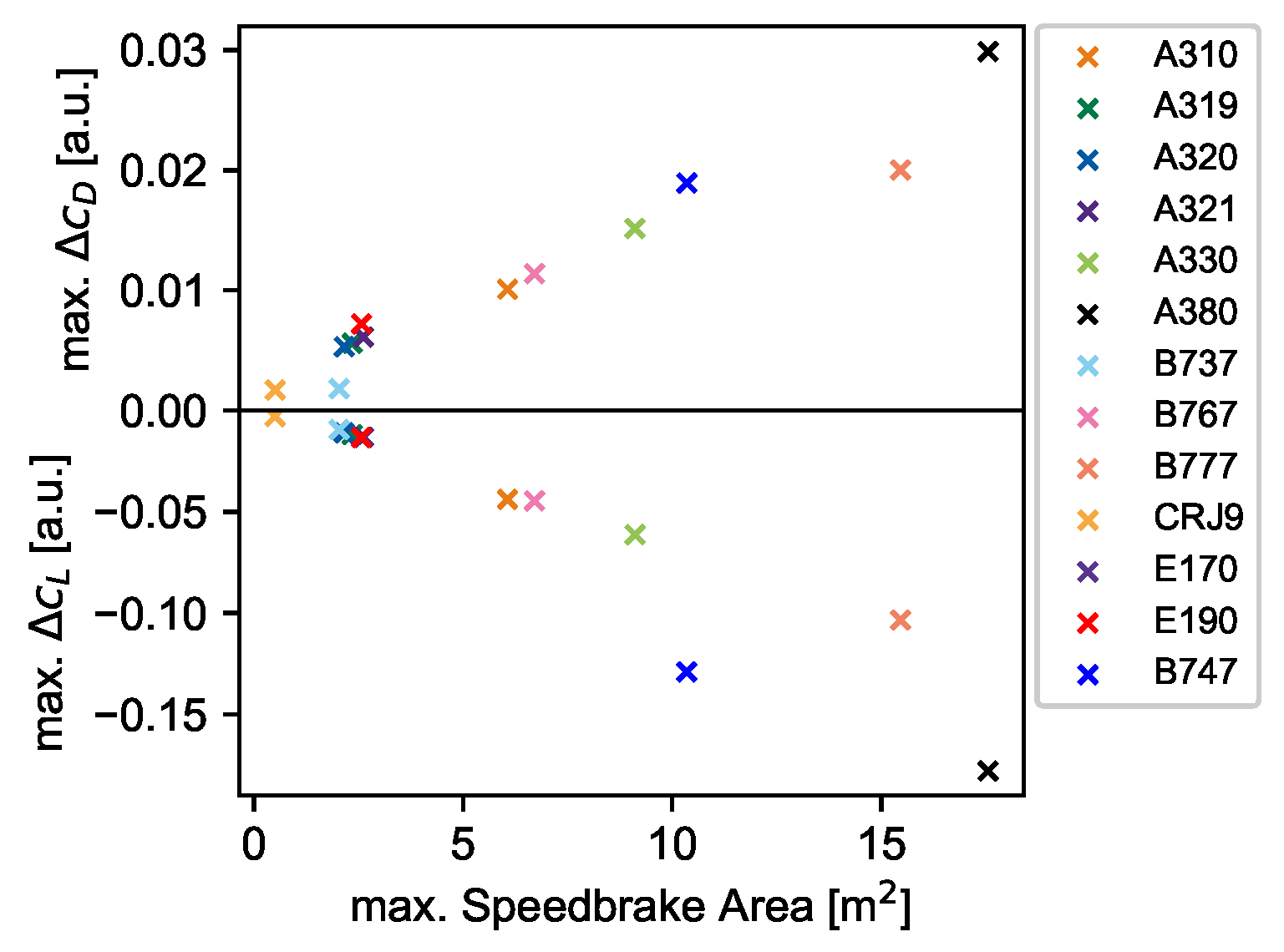
3.3. Transfer of the B747 Model to Other Aircraft Types
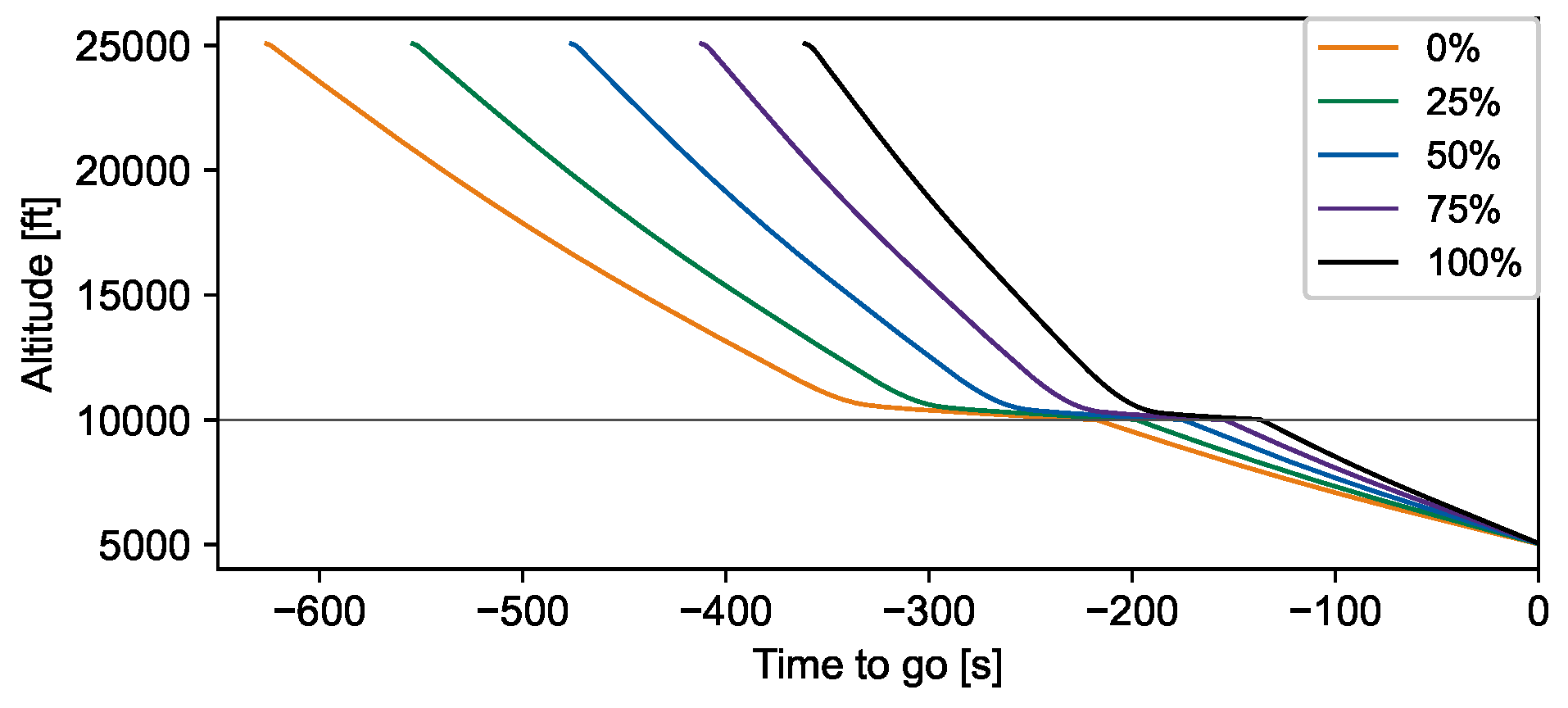
4. Trajectory Modelling with Speed Brakes
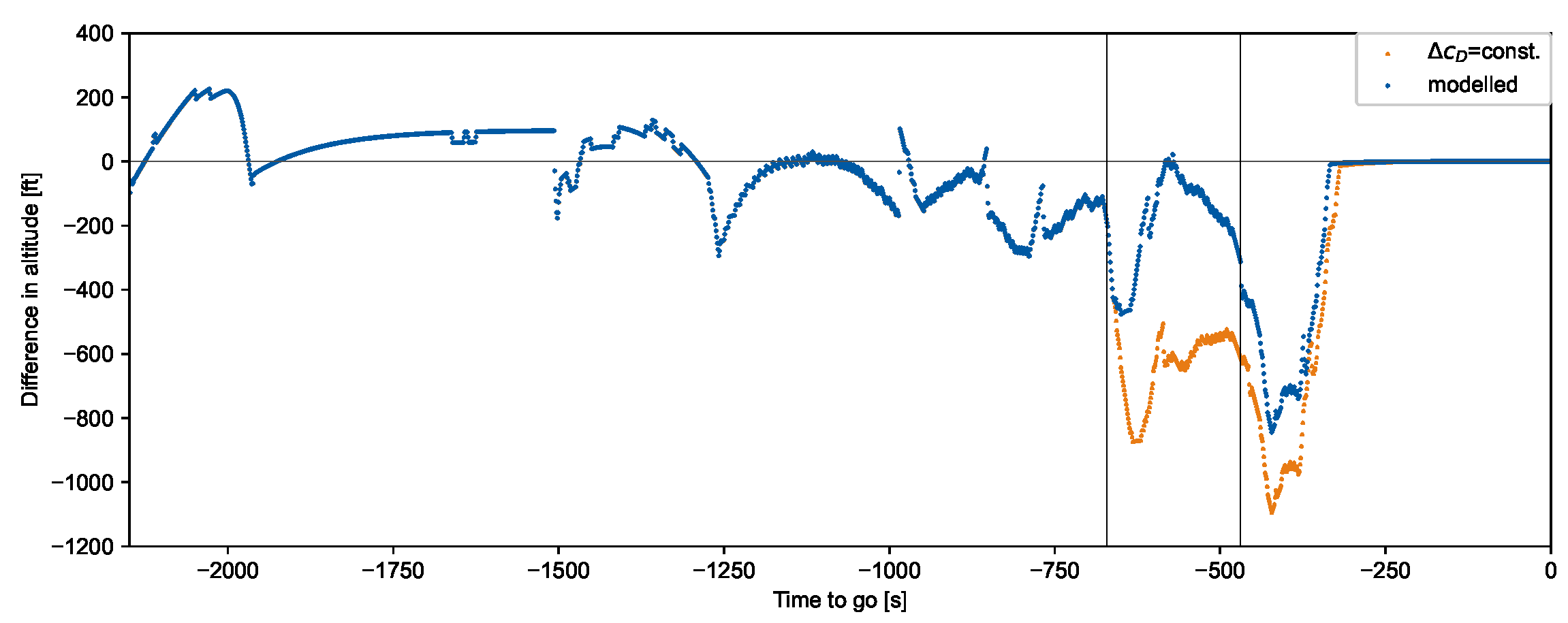
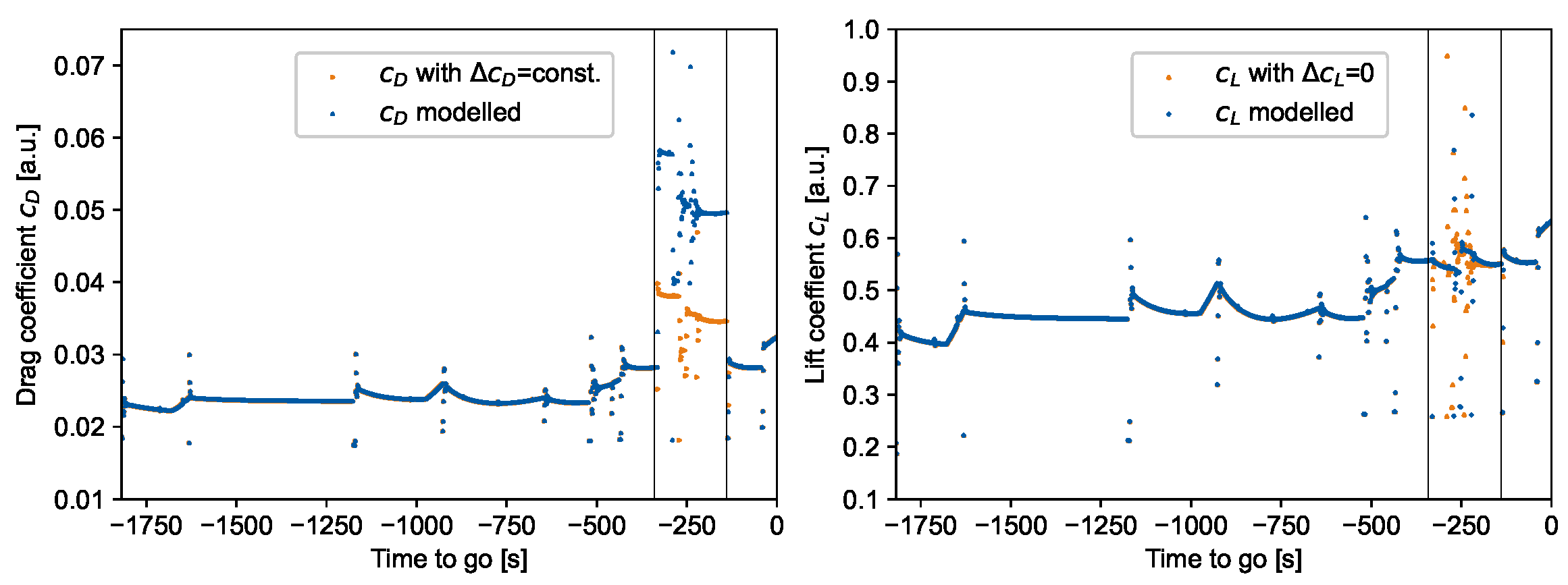
Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ICAO. Continuous Descent Operations (CDO) Manual—Doc 9931/AN/476; ICAO: Montreal, QC, Canada, 2010; Volume 1. [Google Scholar]
- Rosenow, J.; Förster, S.; Lindner, M.; Fricke, H. Multicriteria-Optimized Trajectories Impacting Today’s Air Traffic Density, Efficiency, and Environmental Compatibility. J. Air Transp. 2018, 27, 8–15. [Google Scholar] [CrossRef]
- Sun, J.; Hoekstra, J.M.; Ellerbroek, J. OpenAP: An Open-Source Aircraft Performance Model for Air Transportation Studies and Simulations. Aerospace 2020, 7, 104. [Google Scholar] [CrossRef]
- Kamo, S.; Rosenow, J.; Fricke, H.; Soler, M. Robust CDO trajectory planning under uncertainties in weather prediction. In Proceedings of the 14th USA/Europe Air Traffic Management Research and Development Seminar (ATM Seminar), Virtual Event, 20–23 September 2021. [Google Scholar]
- Kaiser, M.; Rosenow, J.; Fricke, H.; Schultz, M. Tradeoff between optimum altitude and contrail layer to ensure maximum ecological en-route performance using the Enhanced Trajectory Prediction Model (ETPM). In Proceedings of the 2nd International Conference on Application and Theory of Automation in Command and Control Systems (ATACCS), London, UK, 29–31 May 2012. [Google Scholar]
- Serafino, G. Multi-objective Aircraft trajectory optimization for weather avoidance and emissions reduction. In Proceedings of the Modelling and Simulation for Autonomous Systems, Prague, Czech Republic, 29–30 April 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 226–239. [Google Scholar]
- Ng, H.K.; Sridhar, B.; Grabbe, S.; Chen, N. Cross-polar aircraft trajectory optimization and the potential climate impact. In Proceedings of the 2011 IEEE/AIAA 30th Digital Avionics Systems Conference (DASC), Seattle, WA, USA, 16–20 October 2011; pp. 3D4-1–3D4-15. [Google Scholar]
- Wickramasinghe, N.K.; Miyamoto, Y.; Harada, A.; Kozuka, T.; Shigetomi, S.; Miyazawa, Y.; Brown, M.; Fukuda, Y. Flight Trajectory Optimization for Operational Performance Analysis of Jet Passenger Aircraft. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2014, 12, a17–a25. [Google Scholar] [CrossRef] [Green Version]
- Matthes, S.; Grewe, V.; Lee, D.; Linke, F.; Shine, K.; Stromatas, S. ATM4E: A concept for environmentally-optimized aircraft trajectories. In Proceedings of the Greener Aviation, Brussels, Belgium, 11–13 October 2016. [Google Scholar]
- Ye, B.; Wang, Z.; Tian, Y.; Wan, L. Aircraft-specific trajectory optimization of continuous descent approach for fuel savings. In Proceedings of the SII 2017—2017 IEEE/SICE International Symposium on System Integration, Taipei, Taiwan, 11–14 December 2017; pp. 751–756. [Google Scholar] [CrossRef]
- Luchinskiy, D.G.; Schuet, S.; Brenton, J.; Timucin, D.; Smith, D.; Kaneshige, J. Fast optimization for aircraft descent and approach trajectory. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, PHM, St. Petersburg, FL, USA, 2–5 October 2017; pp. 80–90. [Google Scholar]
- Lim, Y.; Gardi, A.; Sabatini, R. Energy efficient 4D trajectories for terminal descent operations. In Proceedings of the International Symposium on Sustainable Aviation (ISSA) 2018, Rome, Italy, 1 July 2018. [Google Scholar]
- Jia, Y.; Cai, K. The trade-off between trajectory predictability and potential fuel savings for continuous descent operations. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–6. [Google Scholar]
- Sáez, R.; Prats, X. Comparison of fuel consumption of continuous descent operations with required times of arrival: Path stretching vs. powered descents. In Proceedings of the 9th International Conference on Research in Air Transportation (ICRAT 2020), Tampa, FL, USA, 23–26 June 2020. [Google Scholar]
- Mclachlan, B.G.; Karamcheti, K. An Experimental Study of Airfoil-Spoiler Aerodynamics; National Aeronautics and Space Administration, NASA Ames Research Center: Washington, DC, USA, 1985. [Google Scholar]
- Stuckey, R. Identification of Nonlinear Aircraft Spoiler Parameters. IFAC Proc. Vol. 1993, 26, 809–814. [Google Scholar] [CrossRef]
- Abdelrahman, M.; Al-Bahi, A.; Ghazi, M.; Olwi, I. Aircraft spoiler effects under wind shear. J. Aircr. 1994, 31, 154–160. [Google Scholar] [CrossRef]
- Lindsay, S.; Walsh, P. Experimental Investigation of Spoiler Deployment on Wing Stall. Open J. Fluid Dyn. 2018, 8, 308–320. [Google Scholar] [CrossRef] [Green Version]
- Geisbauer, S. Numerical simulation and validation of the aerodynamics of static and dynamic spoilers. In Proceedings of the Virtual AIAA Aviation Forum 2020, Online, 15–19 June 2020. [Google Scholar]
- Omori, Y. Spoiler. J. Jpn. Soc. Aeronaut. Space Sci. 1963, 11, 108. [Google Scholar]
- Barnes, C.S. A Developed Theory of Spoilers on Aerofoils; Ministry of Aviation Aeronautical Research Council: London, UK, 1966. [Google Scholar]
- Kalligas, K. The Dynamic Characteristics of Two-Dimensional Spoilers at Low Speeds. Ph.D. Thesis, Department of Aeronautical Engineering, University of Bristol, Bristol, UK, 1986. [Google Scholar]
- Lee, C.S.; Bodapati, S. Experimental Investigations of the Flowfield of an Airfoil with Spoiler. AIAA J. 1987, 25, 1411–1416. [Google Scholar] [CrossRef]
- Consigny, H.; Gravelle, A.; Molinaro, R. Aerodynamic Characteristics of a Moving Two-Dimensional Spoiler in Subsonic and Transonic Flow. J. Aircr. 1984, 21, 687–693. [Google Scholar] [CrossRef]
- Costes, M.; Gravelle, A.; Philippe, J.J.; Vogel, S.; Triebstein, H. Investigation of Unsteady Subsonic Spoiler and Flap Aerodynamics. J. Aircr. 1987, 24, 629–637. [Google Scholar] [CrossRef]
- Nelson, C.F.; Koga, D.J.; Eaton, J.K. Unsteady, Separated Flow Behind an Oscillating, Two-Dimensional Spoiler. AIAA J. 1990, 28, 845–852. [Google Scholar] [CrossRef]
- Yeung, W.W.H.; Xu, C.; Gu, W. Reduction of Transient Adverse Spoiler Effects. J. Aircr. 1997, 34, 479–484. [Google Scholar] [CrossRef]
- Jordan, F., Jr.; Gato, W.; Masiello, M.F.; O’Rourke, M.J.; White, E.R. Experimental investigation of unsteady aerodynamics on a flap element induced by rapid spoiler deflection. In Proceedings of the 12th AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 1994. [Google Scholar]
- Scott, R.C.; Hoadley, S.T.; Wieseman, C.D.; Durham, M.H. The benchmark active controls technology model aerodynamic data. In Proceedings of the 35th AIAA Aerospace Sciences and Meeting Exhibit, Reno, NV, USA, 6–9 January 1997. [Google Scholar]
- Hanke, C. The Simulation of a Jumbo Jet Transport Aircraft—Volume I: Mathematical Model; National Aeronautics and Space Administration: Washington, DC, USA, 1971; pp. 1–65. [Google Scholar]
- Scheiderer, J. Angewandte Flugleistung; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Rossow, C.C.; Wolf, K.; Horst, P. Handbuch der Luftfahrzeugtechnik; Carl Hanser Verlag: München, Germany, 2014. [Google Scholar]
- Kundu, A.K. Aircraft Design. Aeronaut. J. 2011, 115, 66. [Google Scholar] [CrossRef]
- Bombardier Inc. Bombardier CRJ200 CBT—Flight Controls—Ailerons and Spoilerons; Bombardier Inc.: Montreal, QC, Canada, 2000. [Google Scholar]
- AIRBUS S.A.S. A310—Flight Crew Training Manual; REV 0398; AIRBUS S.A.S.: Leiden, The Netherlands, 2008. [Google Scholar]
- Boeing Commercial Airplane Company. 777-200 Flight Crew Operations Manual; The Boeing Company: Renton, WA, USA, 1999. [Google Scholar]
- Embraer S.A. Embraer 170 FCOM Part B—Volume 2; Embraer S.A.: Sao Paulo, Brazil, 2005. [Google Scholar]
- Anderson, G.; Clough, S.; Kneizys, F.; Chetwynd, J.; Shettle, E. AFGL Atmospheric Constituent Profiles (0–120 km); Technical Report Afgl-tr-86-0110; Air Force Geophys. Lab.: Hanscom Air Force Base, MA, USA, 1986. [Google Scholar]
- Roskam, J.; Lan, C.T.E. Airplane Aerodynamics and Performance; DARcorporation: Lawrence, KS, USA, 1997. [Google Scholar]
- Lord, D.; Czarnecki, K.R. Pressure Distributions and Aerodynamic Characteristics of several Spoiler-Type Controls on a Trapezoidal Wing at Mach Numbers of 1.61 and 2.01; National Advisory Committee for Aeronautics: Washington, DC, USA, 1956. [Google Scholar]
- Wentz, W.H. Wind Tunnel Tests of the GA-(W)-2 Airfoil with 20% Aileron, 25% Slotted Flap, 30% Fowler Flap and 10% Slot-Lip Spoiler; National Technical Information Service: Wichita, KS, USA, 1976. [Google Scholar]
- Mineck, R. Reynolds Number Effects on the Performance of Ailerons and Spoilers; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar]
- Boeing Commercial Airplane Company. CAD 3-View Drawing for Airport Planning Purposes; Boeing Commercial Airplane Company: Chicago, IL, USA, 2021. [Google Scholar]
- AIRBUS S.A.S. Airport Operataions—AutoCAD 3 View Aircraft Drawings; AIRBUS S.A.S.: Leiden, The Netherlands, 2012. [Google Scholar]
- AIRBUS S.A.S. A319, A320, A321—Flight Crew Operating Manual 1; System Description; AIRBUS S.A.S.: Leiden, The Netherlands, 2008. [Google Scholar]
- AIRBUS S.A.S. A330—Flight Crew Operating Manual 1; System Description; AIRBUS S.A.S.: Leiden, The Netherlands, 2003. [Google Scholar]
- AIRBUS S.A.S. A380—Flight Crew Operating Manual 1; Airbus S.A.S.: Blagnac Cedex, France, 2011. [Google Scholar]
- Bulfer, B. 737 Cockpit Companion (-300/-400/-500/-600/-700/-800/-900/BBJ/BBJ 2); Leading Edge Libraries: Kingwood, TX, USA, 2003. [Google Scholar]
- Bowers, P.M. Boeing Aircraft Since 1916; Naval Institute Press: Annapolis, MD, USA, 1989. [Google Scholar]
- The Boeing Company. B767 Student Book ATA 27—Flight Controls; TechOps Training: Chicago, IL, USA, 2013. [Google Scholar]
- The Boeing Company. Boeing 777 Specs, What Makes This Giant Twin Work? The Boeing Company: Chicago, IL, USA, 2020. [Google Scholar]
- Eitel, J.M. Flight Standardization Board Report, BOEING B-777-200/-200ER/-200LR/-200F, B-777-300/-300ER; U.S. Department of Transportation Federal Aviation Administration: Washington, DC, USA, 1998.
- Petitt, K. Flight to Success. Available online: https://karlenepetitt.blogspot.com/2017/10/b777-roll-control.html (accessed on 5 March 2022).
- CRJ Regional Jet. Title: Flight Crew Operating Manual CSP C–013–067. Available online: https://www.smartcockpit.com/docs/CRJ-00_and_00-Flight_Controls.pdf (accessed on 17 March 2022).
- Bombardier Inc. Airport Planning Manual CRJ900; Bombardier Inc.: Montreal, QC, Canada, 2015. [Google Scholar]
- Embraer S.A. Embraer 190 FCOM—Flight Controls; Embraer S.A.: Sao Paulo, Brazil, 2003. [Google Scholar]
- Buisson, A. Aircraft energy management in descent phase using FMS, Airbus fleet performance. In Proceedings of the 3rd Eurocontrol CDO Workshop, Brussels, Belgium, 18 March 2013; pp. 1–20. [Google Scholar]
- Snyder, C.; Snyder, C.A.; Sankar, C. Use of information Technologies in the process of building the Boeing 777. J. Inf. Technol. Manag. 1998, 9, 31–42. [Google Scholar] [CrossRef]
- Kamo, S.; Rosenow, J.; Fricke, H.; Soler, M. Fundamental Framework to Plan 4D Robust Descent Trajectories for Uncertainties in Weather Prediction. Aerospace 2022, 9, 109. [Google Scholar] [CrossRef]


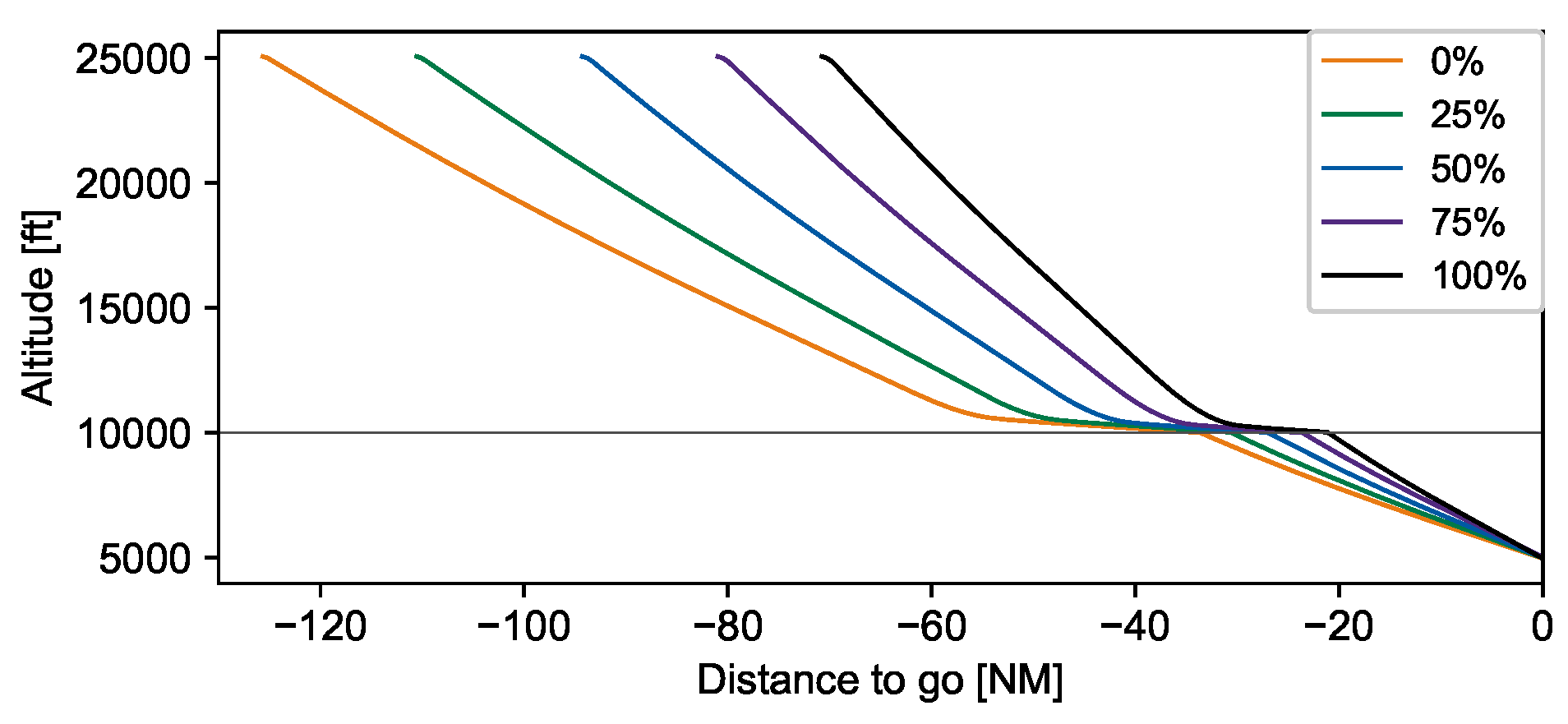
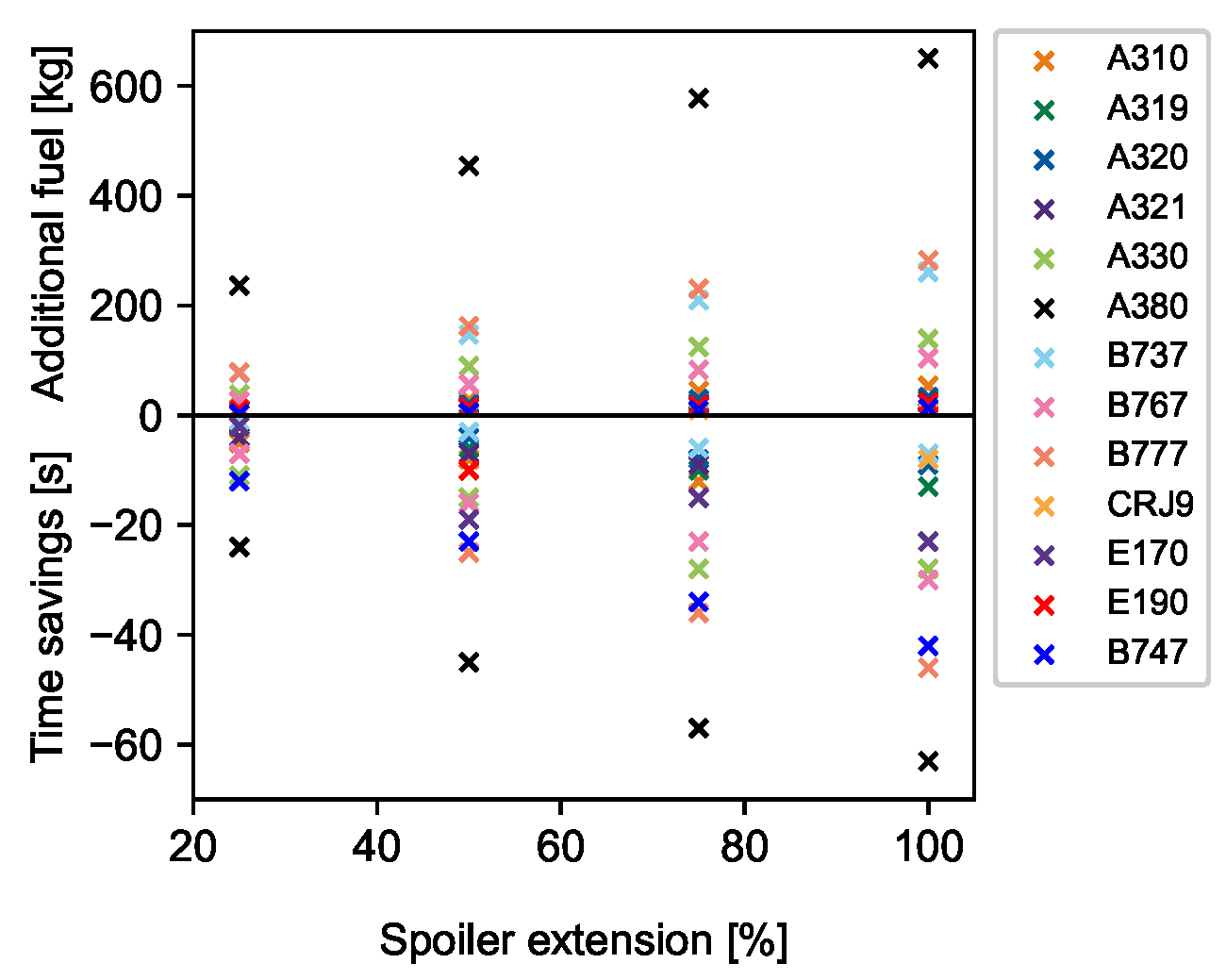
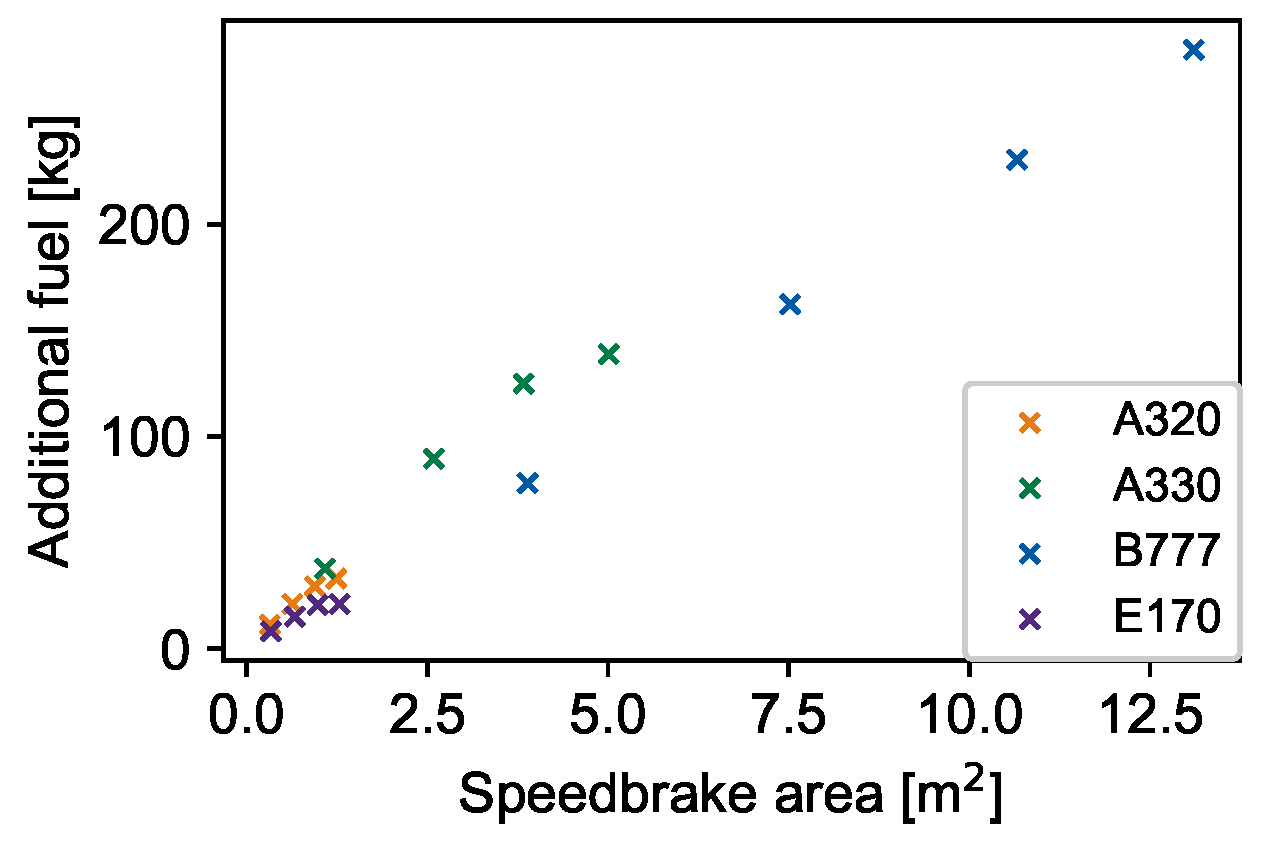
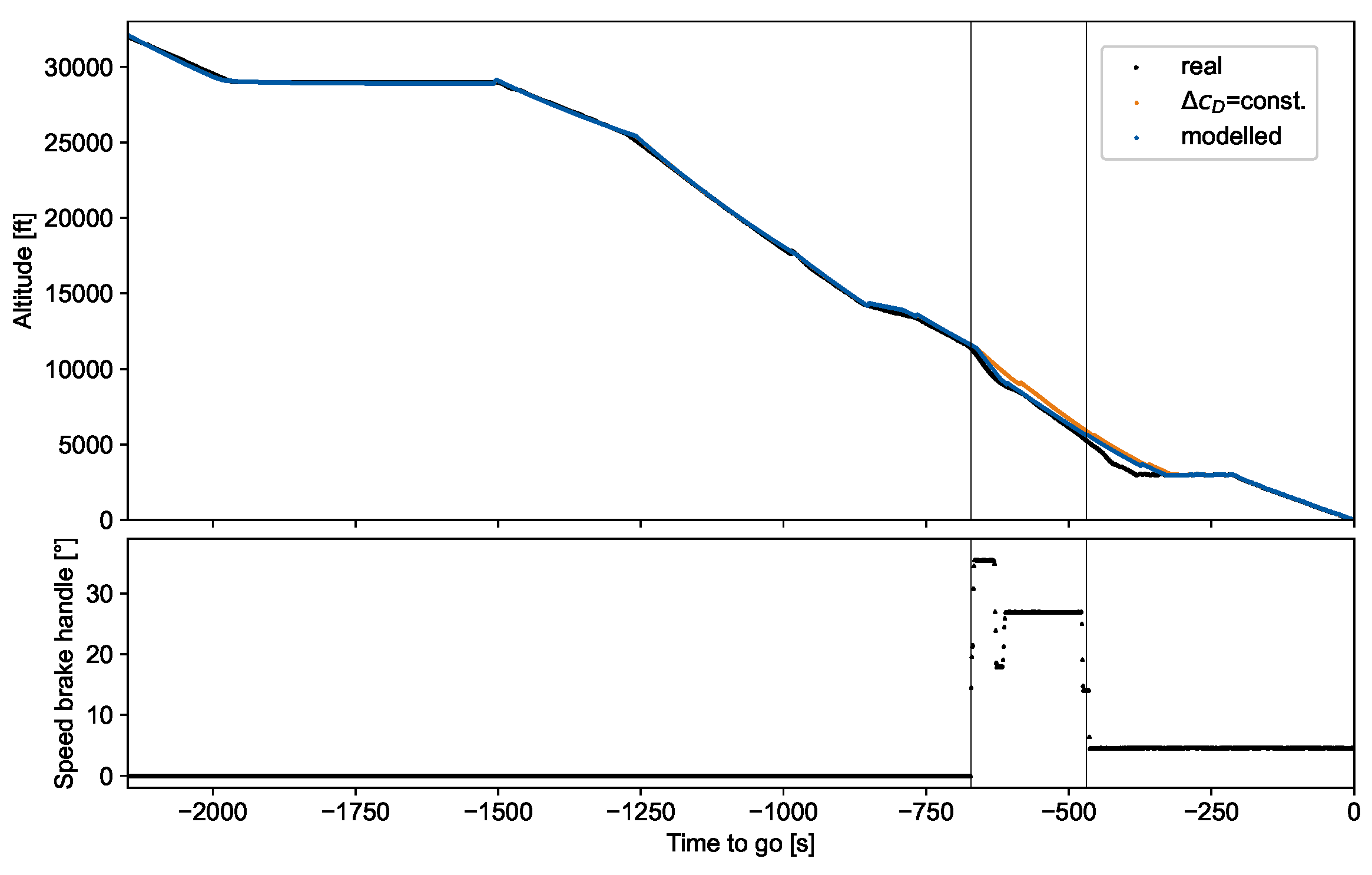
| Panel | Length | Width | Max. Angle | Max. Area | Mean Wing Depth |
|---|---|---|---|---|---|
| Number | [m] | [m] | [°] | [m] | [m] |
| 1 | 1.109 | 1.905 | 45 | 1.495 | 0.37 |
| 2 | 1.109 | 1.905 | 45 | 1.495 | 0.377 |
| 3 | 1.109 | 1.905 | 45 | 1.495 | 0.488 |
| 4 | 1.109 | 1.905 | 45 | 1.495 | 0.559 |
| 5 | 1.397 | 2.286 | 20 | 1.092 | 0.936 |
| 6 | 1.397 | 2.286 | 20 | 1.092 | 1.187 |
| Panel | No | ||||||
|---|---|---|---|---|---|---|---|
| max | max | B747 | B747 | ||||
| [m] | [m] | [°] | [°] | [m] | [°] | ||
| A310 | |||||||
| 1 | 1.62 | 0.743 | 35 | 0.69 | 5 | 1.006 | 12.485 |
| 2 | 1.69 | 0.904 | 35 | 0.876 | 4 | 0.746 | 24.488 |
| 3 | 1.87 | 0.684 | 35 | 0.734 | 2 | 0.428 | 20.31 |
| 4 | 1.862 | 0.684 | 35 | 0.731 | 2 | 0.41 | 20.277 |
| 5 | 1.526 | 0.549 | 0 | 0.286 | 2 | 0.388 | 7.786 |
| 6 | 1.529 | 0.549 | 0 | 0.287 | 1 | 0.377 | 7.805 |
| 7 | 1.478 | 0.549 | 0 | 0.277 | 1 | 0.289 | 7.542 |
| A319 | |||||||
| 1 | 1.763 | 0.626 | 17.5 | 0.633 | 2 | 0.381 | 17.434 |
| 2 | 1.661 | 0.625 | 25 | 0.596 | 1 | 0.297 | 16.37 |
| 3 | 1.528 | 0.625 | 25 | 0.548 | 1 | 0.343 | 15.016 |
| 4 | 1.531 | 0.627 | 0 | 0.55 | 1 | 0.251 | 15.096 |
| A320 | |||||||
| 1 | 1.763 | 0.626 | 12.5 | 0.633 | 2 | 0.381 | 17.434 |
| 2 | 1.661 | 0.625 | 25 | 0.596 | 1 | 0.343 | 16.37 |
| 3 | 1.528 | 0.625 | 25 | 0.548 | 1 | 0.297 | 15.016 |
| 4 | 1.531 | 0.627 | 0 | 0.55 | 1 | 0.251 | 15.096 |
| A321 | |||||||
| 1 | 1.763 | 0.626 | 25 | 0.633 | 2 | 0.381 | 17.434 |
| 2 | 1.661 | 0.625 | 25 | 0.438 | 1 | 0.343 | 11.986 |
| 3 | 1.528 | 0.625 | 25 | 0.548 | 1 | 0.297 | 15.016 |
| 4 | 1.531 | 0.627 | 0 | 0.55 | 1 | 0.251 | 15.096 |
| A330 | |||||||
| 1 | 2.43 | 0.693 | 25 | 0.711 | 5 | 1.054 | 12.871 |
| 2 | 2.12 | 0.705 | 30 | 0.857 | 4 | 0.682 | 23.913 |
| 3 | 2.163 | 0.707 | 30 | 0.878 | 4 | 0.597 | 24.531 |
| 4 | 2.165 | 0.709 | 30 | 0.88 | 3 | 0.541 | 24.614 |
| 5 | 2.193 | 0.71 | 30 | 0.893 | 3 | 0.49 | 24.998 |
| 6 | 2.209 | 0.712 | 30 | 0.902 | 2 | 0.445 | 25.254 |
| A380 | |||||||
| 1 | 2.43 | 1.296 | 20 | 1.077 | 6 | 1.655 | 19.713 |
| 2 | 2.374 | 1.229 | 20 | 0.998 | 6 | 1.34 | 18.211 |
| 3 | 1.972 | 1.117 | 20 | 0.754 | 5 | 1.154 | 13.649 |
| 4 | 2.195 | 1.095 | 20 | 0.882 | 5 | 1.042 | 14.919 |
| 5 | 2.084 | 1.056 | 20 | 0.752 | 5 | 0.985 | 13.629 |
| 6 | 2.782 | 0.883 | 45 | 1.736 | 4 | 0.907 | 55.241 |
| 7 | 2.503 | 0.737 | 45 | 1.305 | 4 | 0.878 | 38.13 |
| 8 | 2.35 | 0.581 | 45 | 1.329 | 4 | 0.788 | 38.956 |
| Panel | No | ||||||
|---|---|---|---|---|---|---|---|
| max | max | B747 | B747 | ||||
| [m] | [m] | [°] | [°] | [m] | [°] | ||
| B737 | |||||||
| 2 | 1.05 | 0.567 | 19.5 | 0.199 | 3 | 0.499 | 4.495 |
| 3 | 1.5 | 0.594 | 19.5 | 0.297 | 3 | 0.509 | 6.732 |
| 4 | 1.012 | 0.612 | 24.5 | 0.257 | 3 | 0.538 | 5.807 |
| 5 | 1.008 | 0.632 | 24.5 | 0.264 | 3 | 0.529 | 5.973 |
| B767 | |||||||
| 1 | 1.532 | 0.736 | 45 | 0.797 | 3 | 0.489 | 18.318 |
| 2 | 1.532 | 0.736 | 45 | 0.797 | 3 | 0.537 | 18.318 |
| 3 | 1.532 | 0.736 | 45 | 0.797 | 4 | 0.58 | 18.318 |
| 5 | 1.768 | 0.952 | 17 | 0.492 | 4 | 0.93 | 11.192 |
| 6 | 1.684 | 0.952 | 17 | 0.496 | 5 | 1.059 | 8.04 |
| B777 | |||||||
| 1 | 2.032 | 0.642 | 60 | 1.13 | 4 | 0.559 | 32.329 |
| 2 | 1.95 | 0.641 | 60 | 1.082 | 4 | 0.62 | 30.795 |
| 3 | 1.992 | 0.655 | 60 | 1.13 | 4 | 0.681 | 32.305 |
| 4 | 1.91 | 0.661 | 45 | 0.893 | 4 | 0.729 | 24.991 |
| 5 | 1.958 | 0.667 | 0 | 1.131 | 4 | 0.802 | 32.347 |
| 6 | 1.995 | 1.011 | 60 | 1.747 | 6 | 1.252 | 33.172 |
| 7 | 1.995 | 1.011 | 60 | 1.747 | 6 | 1.562 | 33.172 |
| CRJ900 | |||||||
| 1 | 0.815 | 0.199 | 50 | 0.124 | 1 | 0.3 | 3.373 |
| 2 | 0.85 | 0.199 | 50 | 0.13 | 1 | 0.268 | 3.519 |
| E170/E190 | |||||||
| 3 | 1.433 | 0.712 | 30 | 0.521 | 1 | 0.34 | 9.864 |
| 4 | 1.309 | 0.655 | 30 | 0.439 | 1 | 0.317 | 8.291 |
| 5 | 1.122 | 0.616 | 30 | 0.353 | 1 | 0.274 | 6.658 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosenow, J.; Sachwitz, T.; Kamo, S.; Chen, G.; Fricke, H. Aircraft-Type-Specific Impact of Speed Brakes on Lift and Drag. Aerospace 2022, 9, 263. https://doi.org/10.3390/aerospace9050263
Rosenow J, Sachwitz T, Kamo S, Chen G, Fricke H. Aircraft-Type-Specific Impact of Speed Brakes on Lift and Drag. Aerospace. 2022; 9(5):263. https://doi.org/10.3390/aerospace9050263
Chicago/Turabian StyleRosenow, Judith, Thomas Sachwitz, Shumpei Kamo, Gong Chen, and Hartmut Fricke. 2022. "Aircraft-Type-Specific Impact of Speed Brakes on Lift and Drag" Aerospace 9, no. 5: 263. https://doi.org/10.3390/aerospace9050263
APA StyleRosenow, J., Sachwitz, T., Kamo, S., Chen, G., & Fricke, H. (2022). Aircraft-Type-Specific Impact of Speed Brakes on Lift and Drag. Aerospace, 9(5), 263. https://doi.org/10.3390/aerospace9050263








