Correlated Bayesian Model of Aircraft Encounters in the Terminal Area Given a Straight Takeoff or Landing
Abstract
:1. Introduction
1.1. Motivation
1.2. Scope
1.3. Objectives and Contributions
2. Materials and Methods
2.1. Materials and Datasets
2.2. Assumptions
- An encounter is when ownship and intruder are within 4 nautical miles laterally and 2000 feet vertically of each other for at least one second over at least a thirty second duration;
- Ownship is on a straight-in takeoff or approach;
- Intruder aircraft may be landing, taking off, or transiting the area;
- Intruder aircraft may not be landing or taking off from a nearby airport;
- Sampled trajectories are constrained to within 8 NM of the airfield and 5000 ft above airfield elevation (minimum altitude is 200 ft above airport elevation); and
- Sampled trajectories are a maximum of 300 s in length.
2.3. Prior Art
2.4. Methods Overview
- Download and pre-process (i.e., interpolate, outlier detection, etc.) training data;
- Coarsely spatially filter training data to terminal airspace;
- Classify track intent (e.g., landing, taking off, transiting) for training data within terminal airspace;
- Given classified tracks, identify encounters between aircraft;
- Train model using identified encounters;
- Sample model to create representative encounters.
3. Track Filtering and Encounter Identification
3.1. Initial Spatial Filtering
3.2. Track Intent and Runway Identification
3.2.1. Clustering Using Airport Boundaries
3.2.2. Clustering Using Runway Corridors
3.2.3. Vertical Rate, Altitude, and Relative Heading
3.2.4. Transiting Aircraft
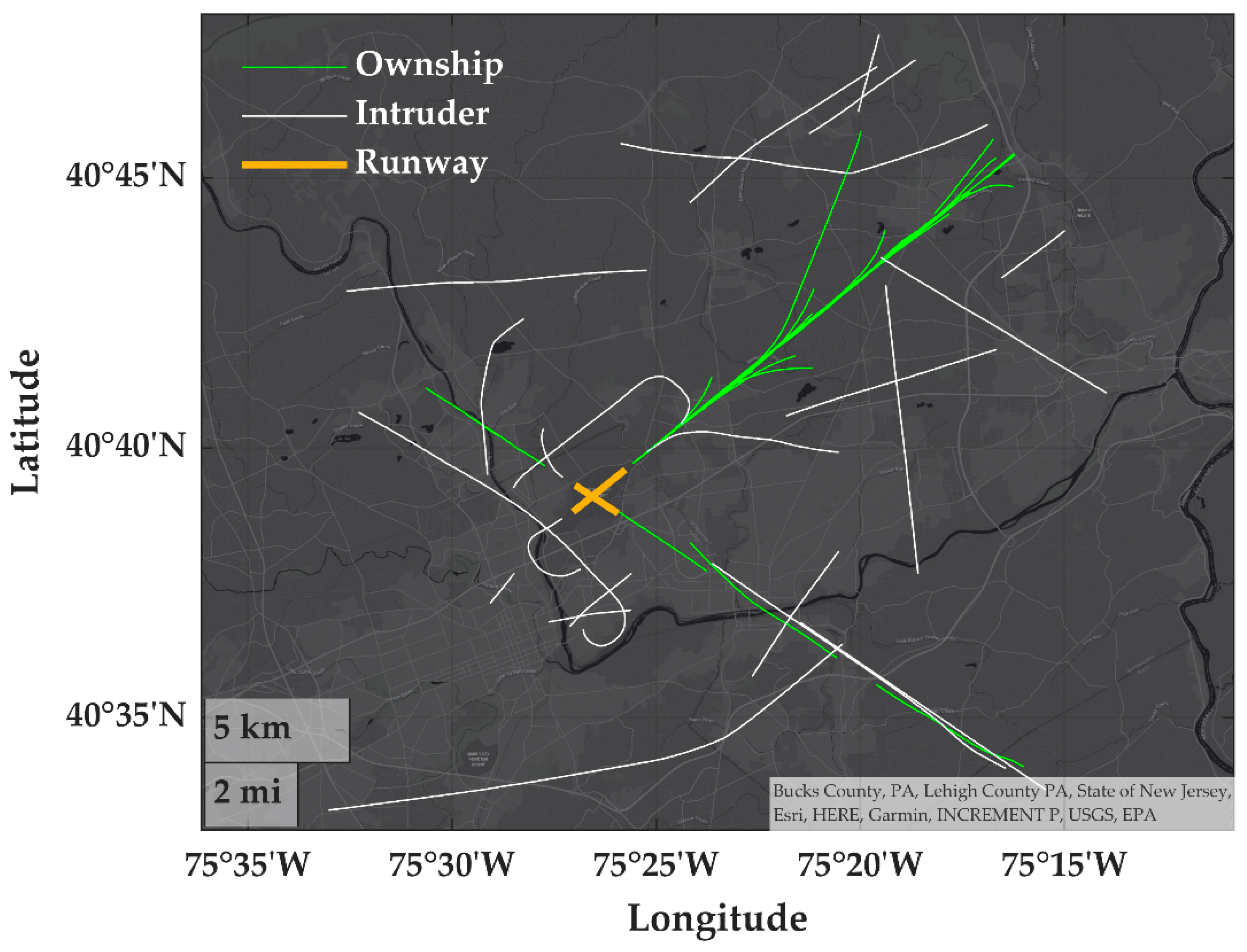
3.3. Encounter Identification
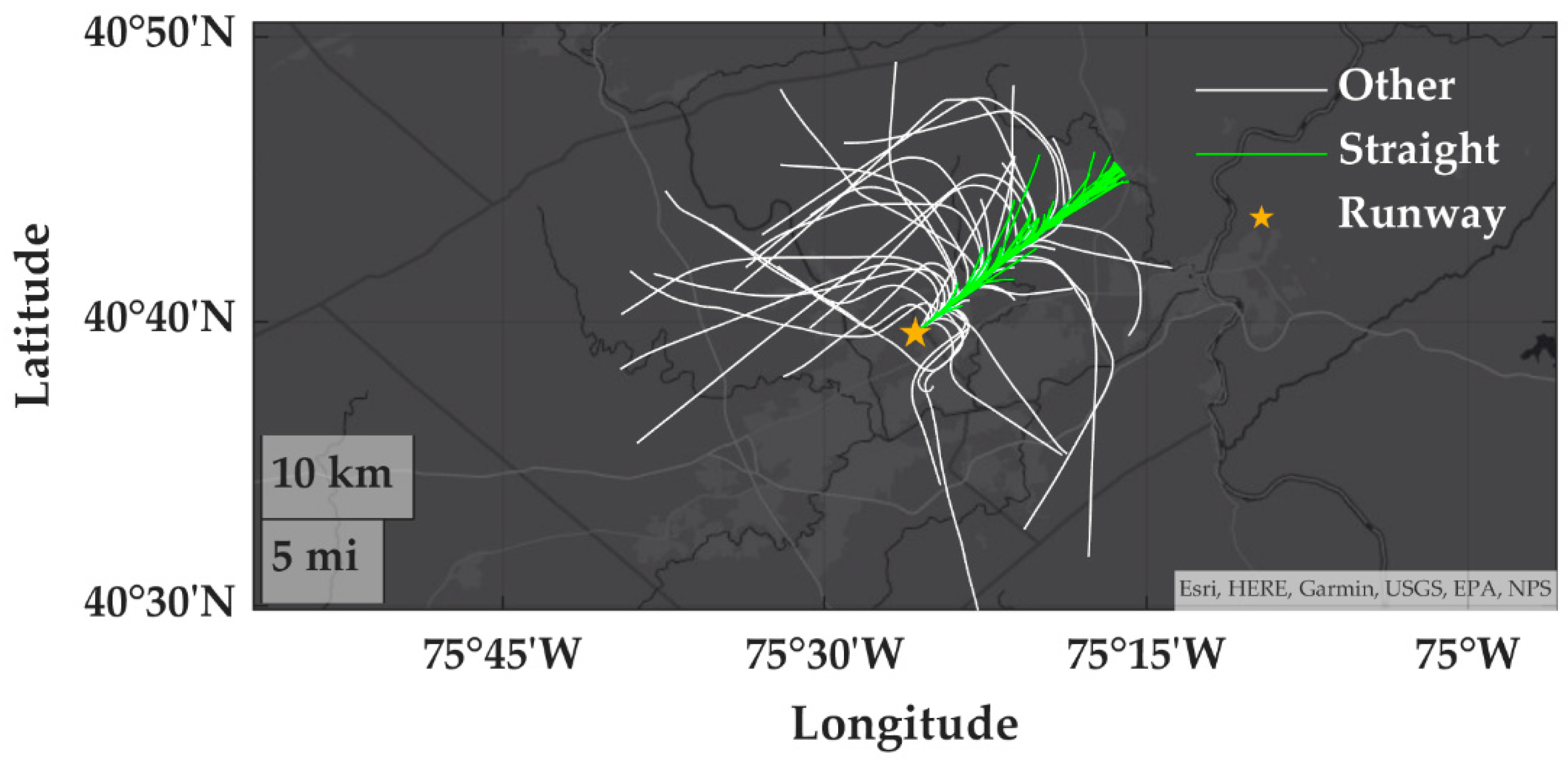
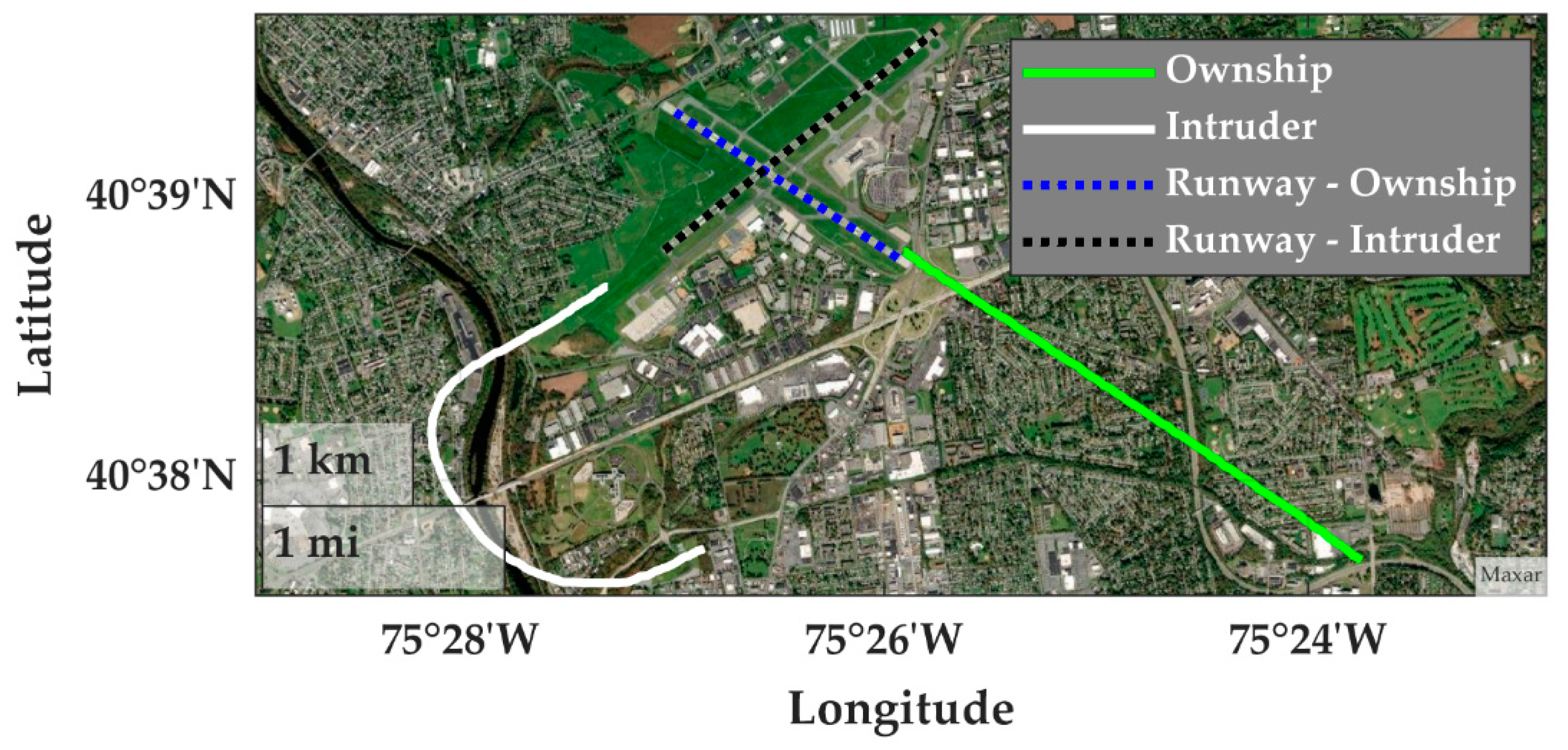
3.3.1. Example Training Encounters
3.3.2. Encounter Quantities
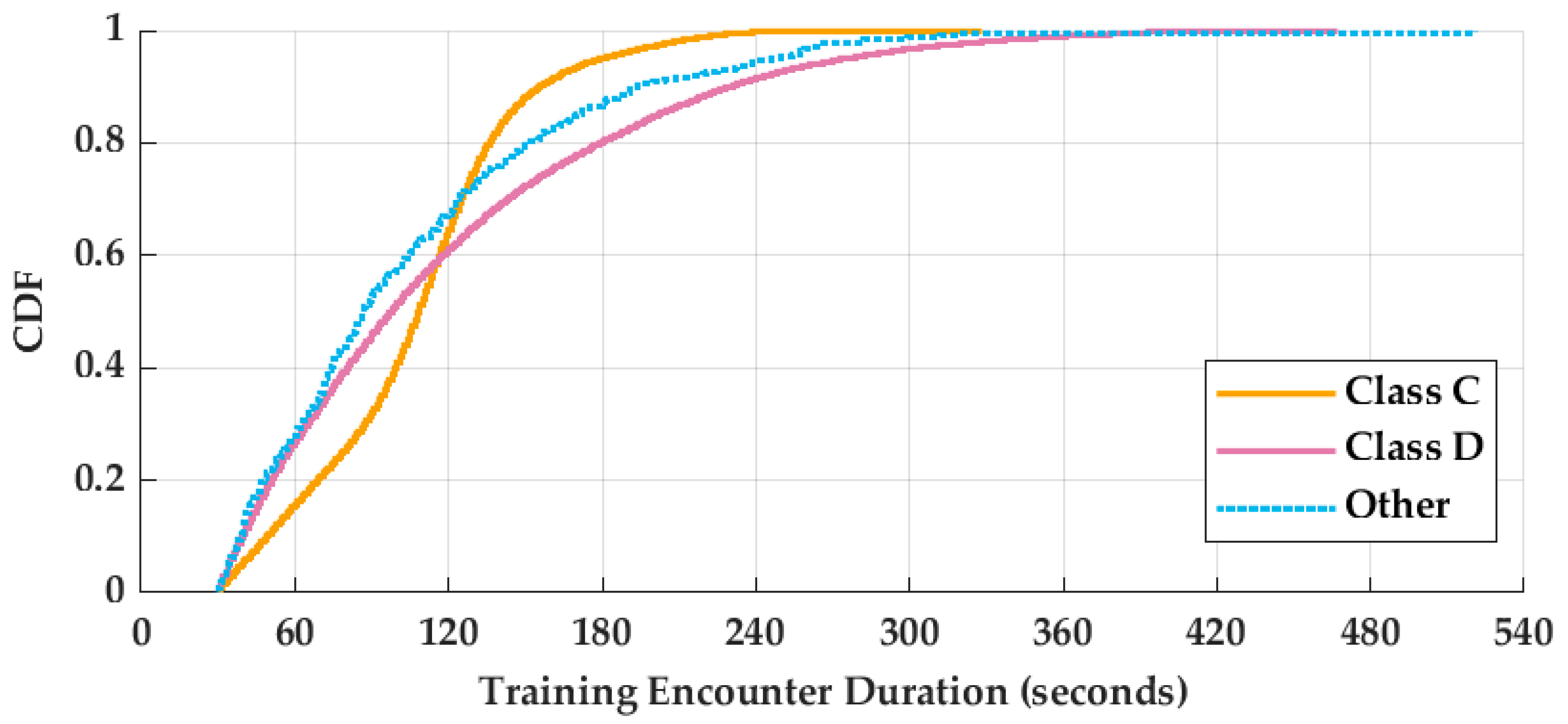
3.3.3. Encounter Duration
4. Training the Dynamic Bayesian Network
4.1. Model Training and Structure
Relative Local Coordinate System
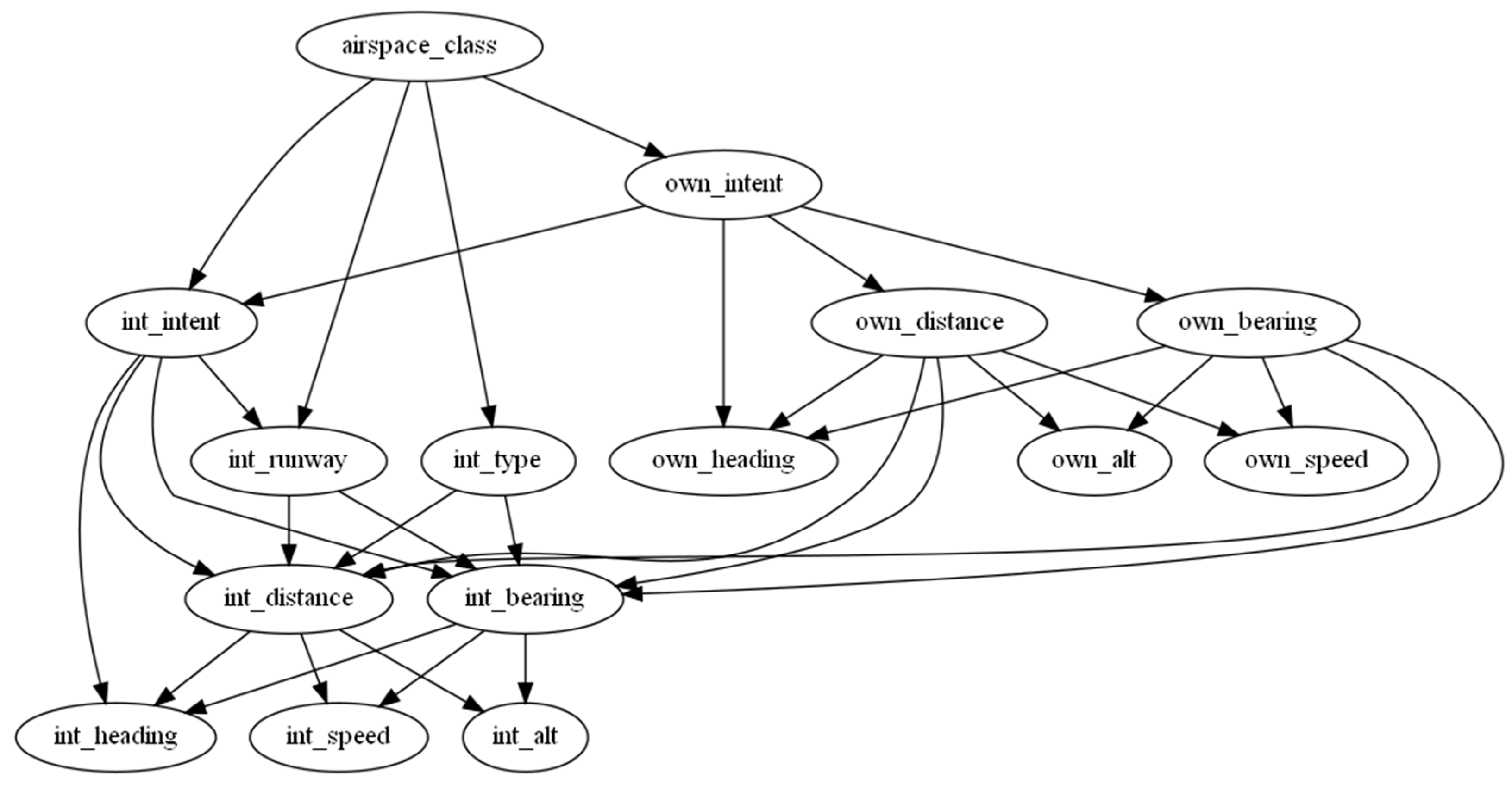
4.2. Encounter Geometry Model
- Airspace class: Airspace class of the airport.
- Ownship intent: The intent of the ownship of either a straight landing or take off.
- Intruder intent: The intent of the intruder of either landing, taking off, or transiting. Unlike the ownship, the intruder’s intent is not assumed to be straight.
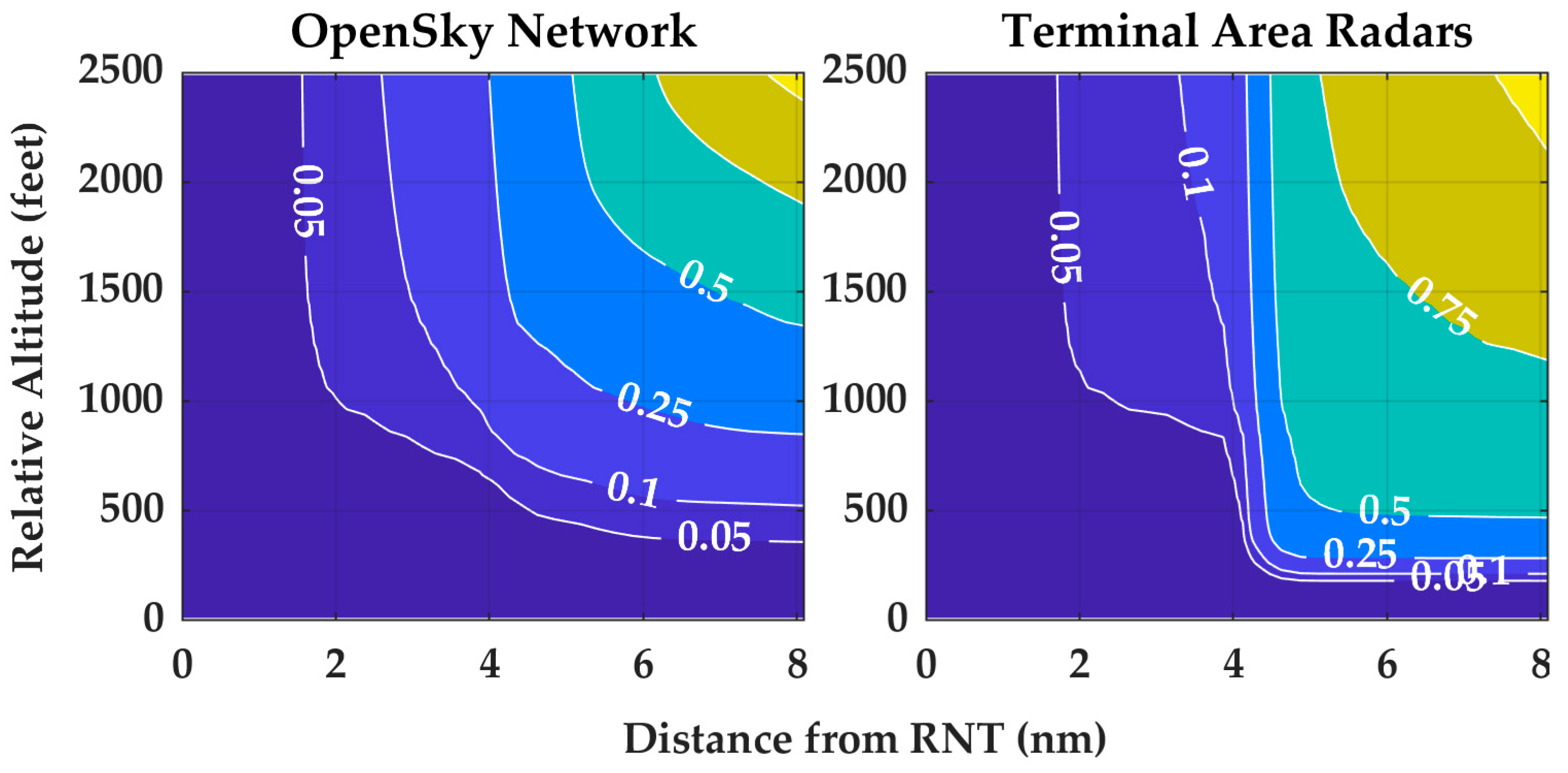
- Intruder type: The type of aircraft of the intruder: can either be fixed-wing or rotorcraft. Note that while the OpenSky Network-based uncorrelated models are individually organized by aircraft type [7], aircraft type is an explicit model variable here.
- Intruder runway: The runway the intruder was leveraging relative to the ownship. Designated as “same” if both aircraft were operating from the same runway; parallel” if the intruder was operating from a runway that did not intersect the ownship’s runway; as “crossing” if the intruder was operating from a runway that intersected the ownship’s runway; and “none” if the intruder intent was transiting.
- Ownship distance from runway: The horizontal distance between the ownship position at CPA and the runway mean position.
- Ownship bearing from runway: The polar angle of the ownship’s position at CPA.
- Ownship altitude: The altitude of the ownship relative to the runway elevation at CPA.
- Ownship speed: The smoothed speed of the ownship at CPA as estimated by a finite difference of the trajectory position data.
- Ownship heading: The direction of flight of the ownship at CPA.
- Intruder distance from runway: The horizontal distance between the intruder position at CPA and the runway mean position.
- Intruder bearing from runway: The polar angle of the intruder’s position at CPA.
- Intruder altitude: The altitude of the intruder relative to the runway elevation at CPA.
- Intruder speed: The smoothed speed of the intruder at CPA as estimated by a finite difference of the trajectory position data.
- Intruder heading: The direction of flight of the intruder at CPA.
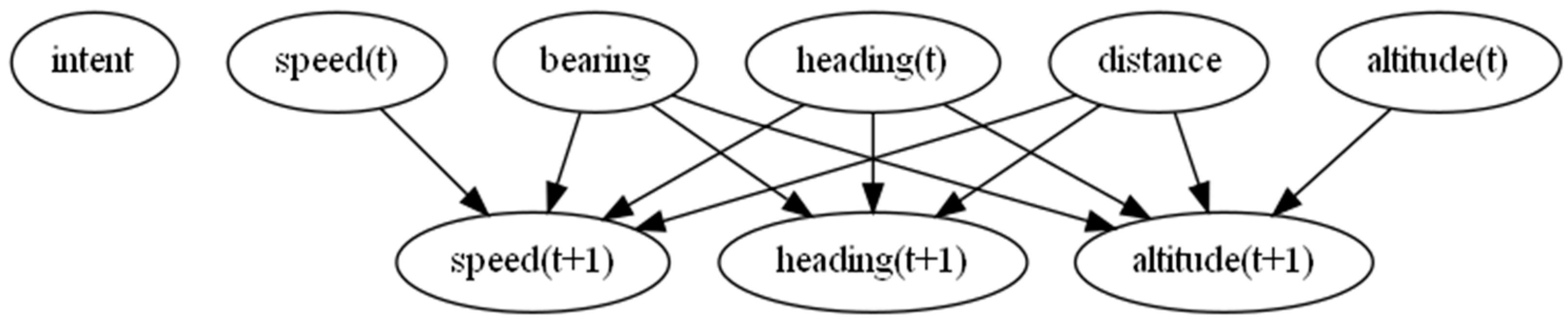
4.3. Trajectory Propagation Model
- Intent: The aircraft’s intent, same as defined for the encounter geometry model;
- Distance from runway: The horizontal distance between the aircraft position and the runway mean position over time;
- Bearing angle from runway: The polar angle of the aircraft’s position;
- Heading angle: The direction of flight of the aircraft;
- Altitude: The altitude of the aircraft relative to the runway elevation over time;
- Speed: The smoothed speed of the aircraft over time as estimated by a finite difference of the trajectory position.
4.4. Model Sampling and Encounter Generation
4.4.1. Sampling the Encounter Geometry Model
4.4.2. Sampling the Trajectory Models to Propagate Tracks
4.4.3. Rejection Sampling
- Encounter CPA must occur within 5 s of the sampled CPA;
- Tracks must overlap at least 30 s in time;
- If taking off or landing, a track must have at least one track update within 2.5 nautical miles of the runway mean position;
- For track updates within 2.5 nautical miles of the runway mean position, at least one point must have an altitude of 750 feet or less;
- A track must have sufficient quantity of updates with a vertical rate magnitude of 300 feet per minute or greater. If landing, the rate must be negative and if taking off, the rate must be positive;
- A track ends if it is within 0.25 nautical miles or more than 8 nautical miles away from the runway.
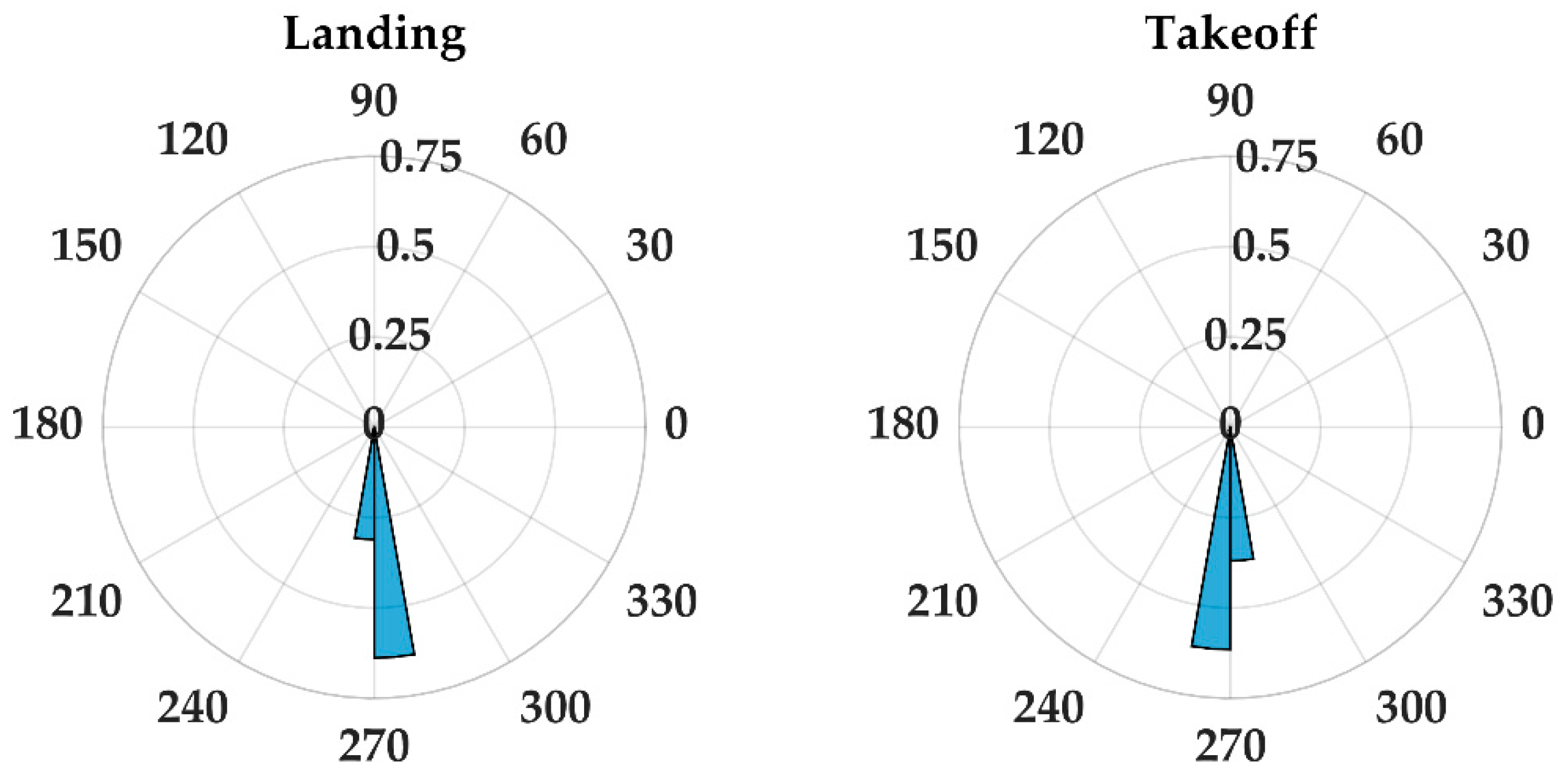
- If landing, at least 95% of heading updates need to be 90 ± 30 degrees;
- If taking off, at least 95% of heading updates need to be 270 ± 30 degrees.
4.5. Example Nominal Encounters
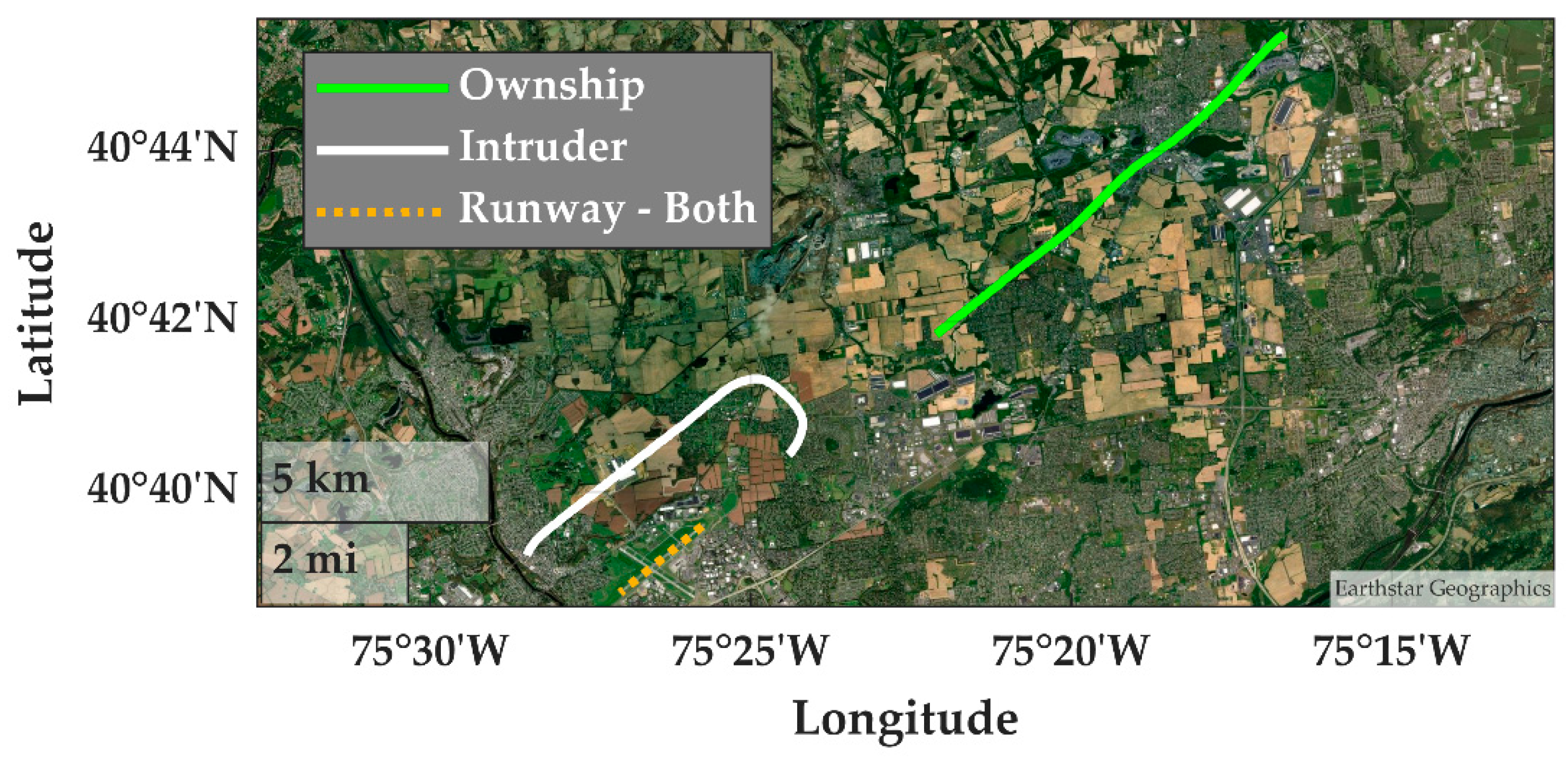
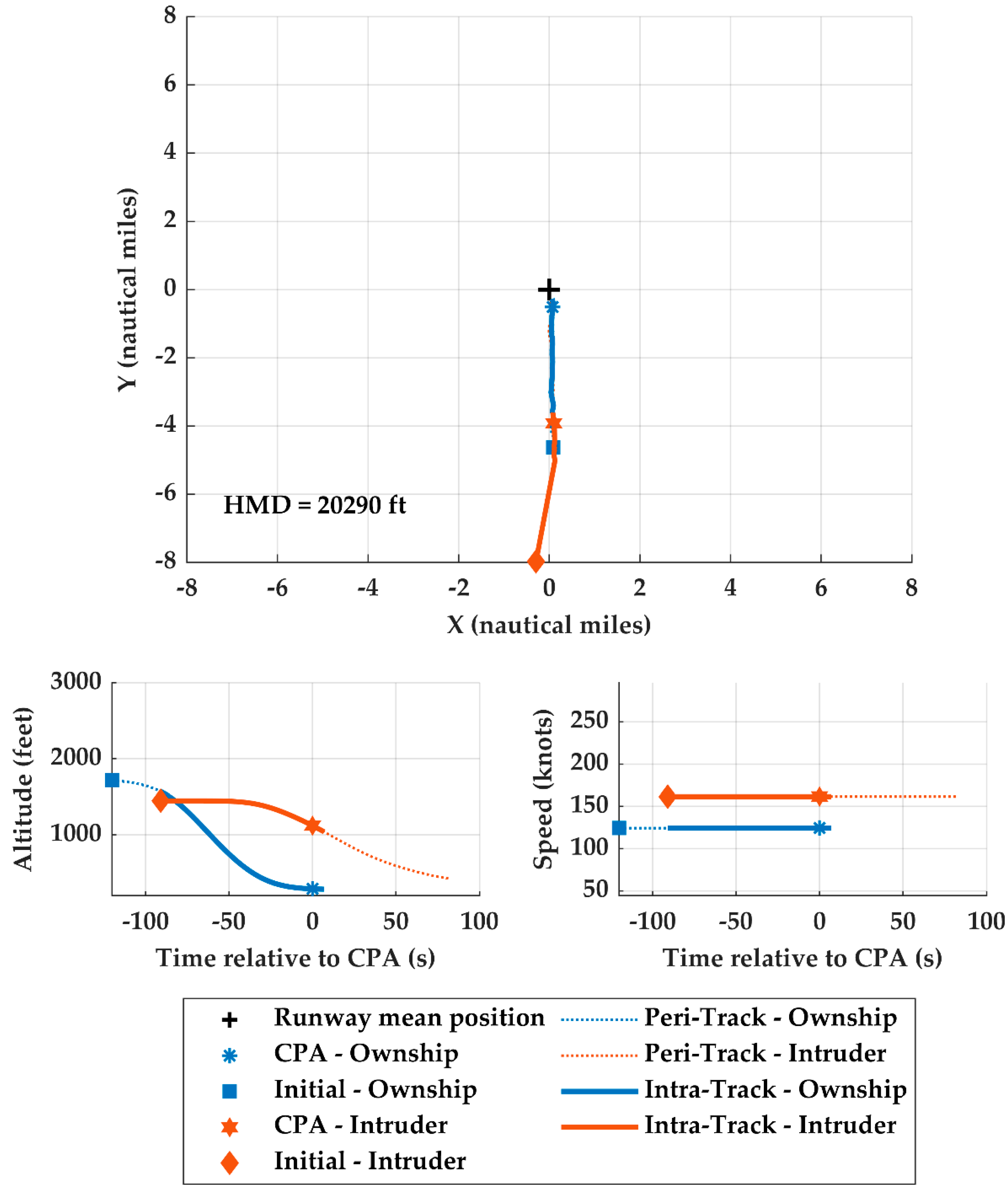
4.5.1. Sampled Nominal Landing Encounter
4.5.2. Sampled Encounter with Transiting Intruders
4.5.3. Sampled Encounter Idiosyncrasies
5. Sampled Encounter Dataset
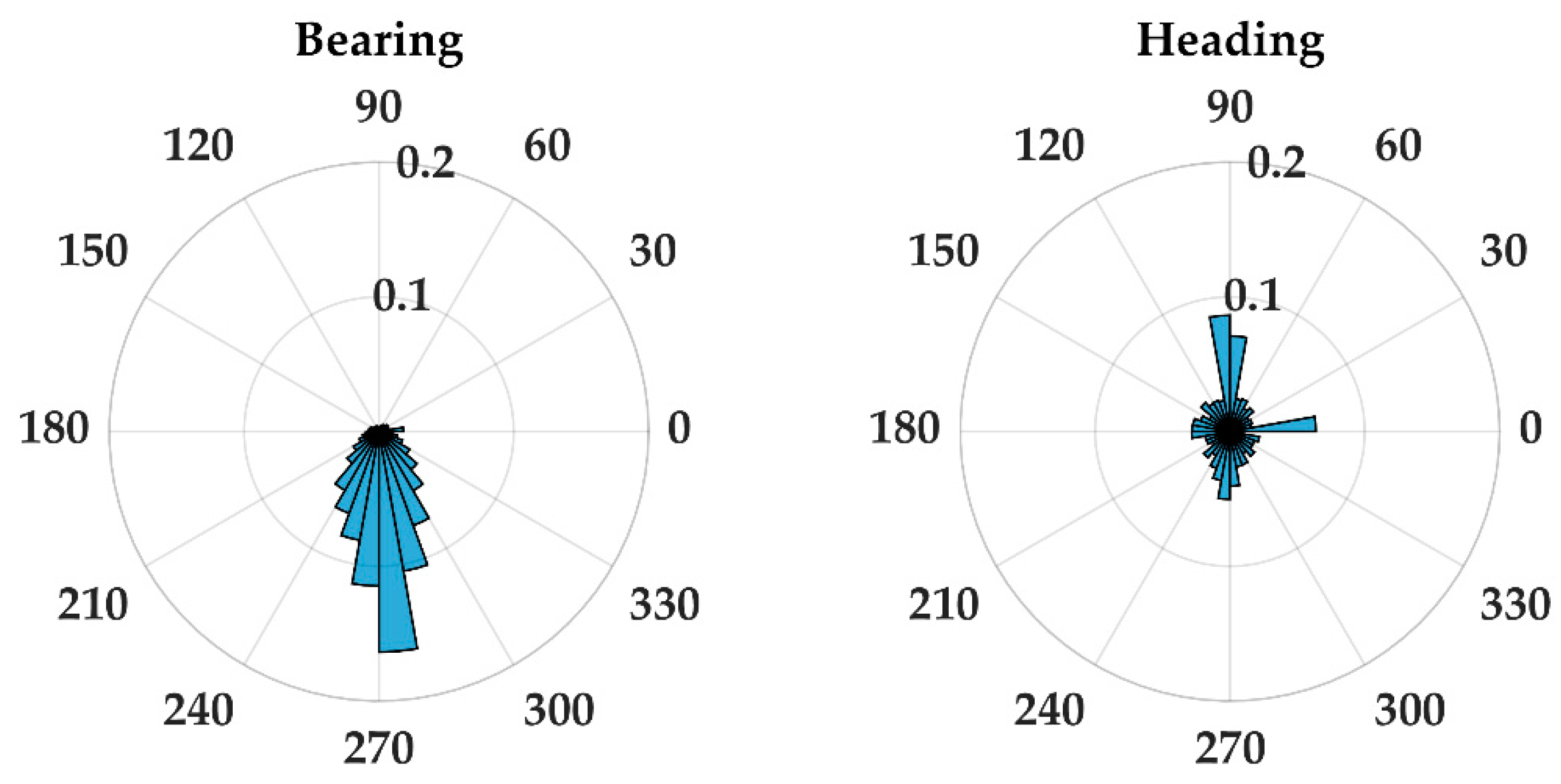
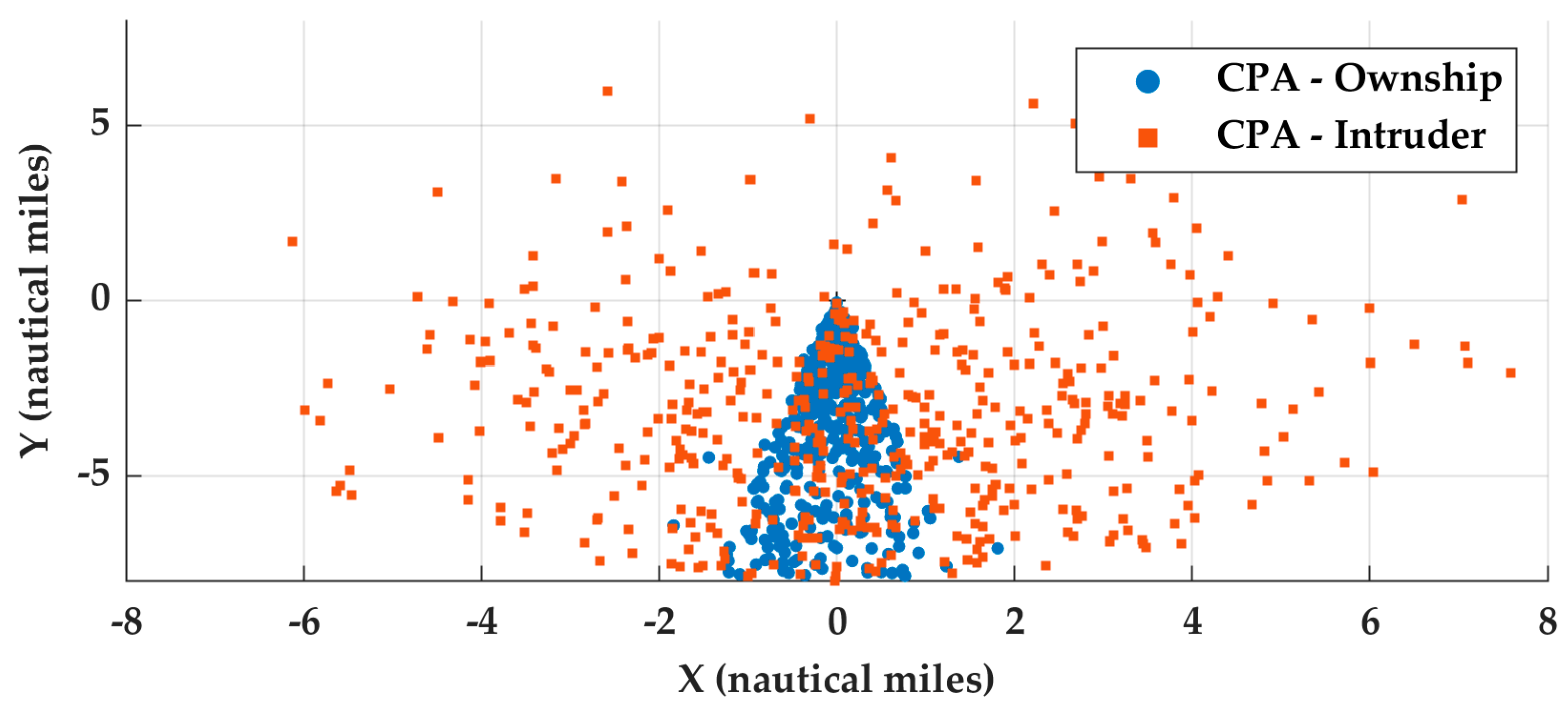
5.1. Kinematic Distributions at CPA
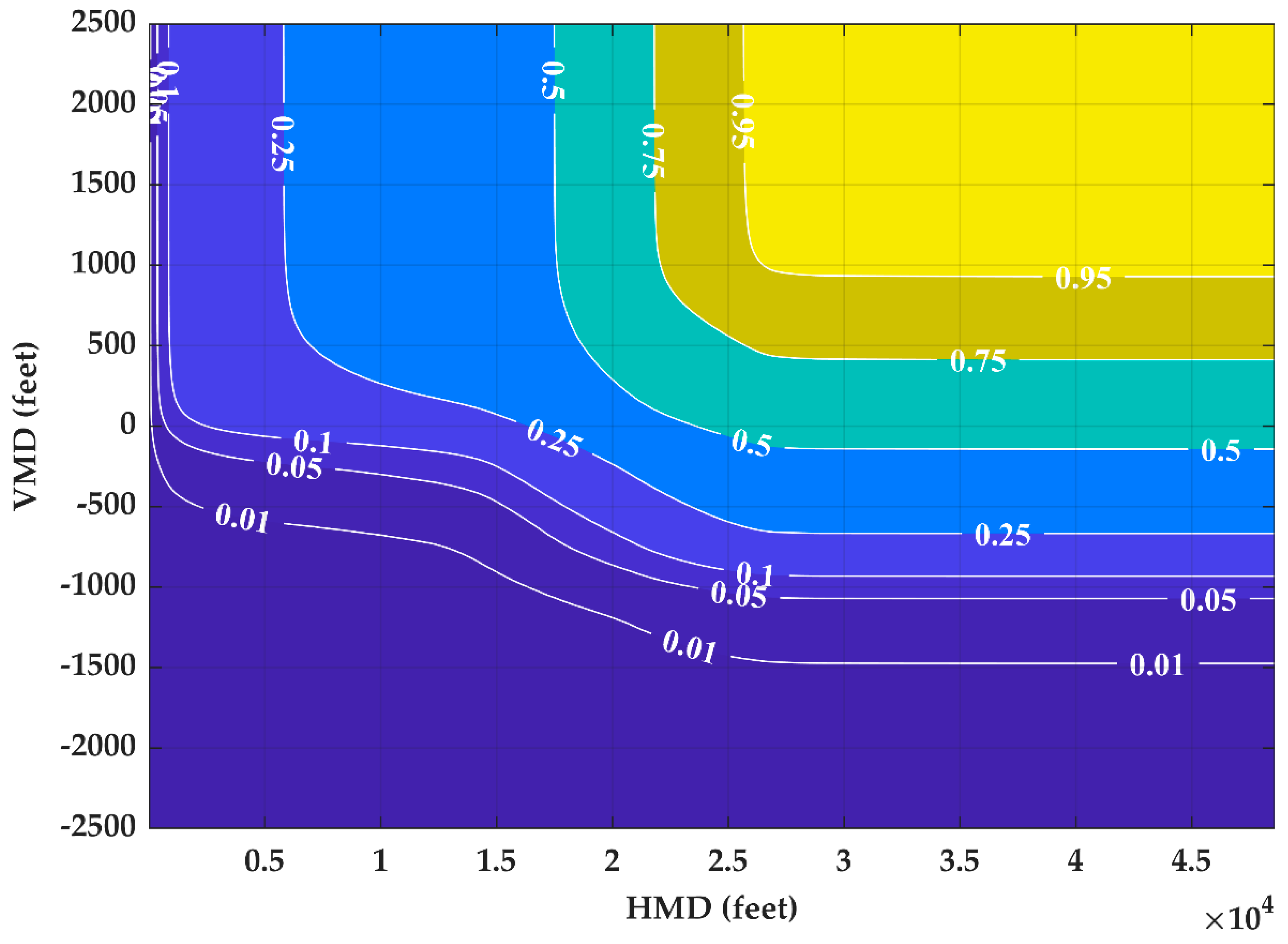
5.2. Horizontal and Vertical Miss Distance Distributions
6. Discussion
6.1. Accomplishments
6.2. Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
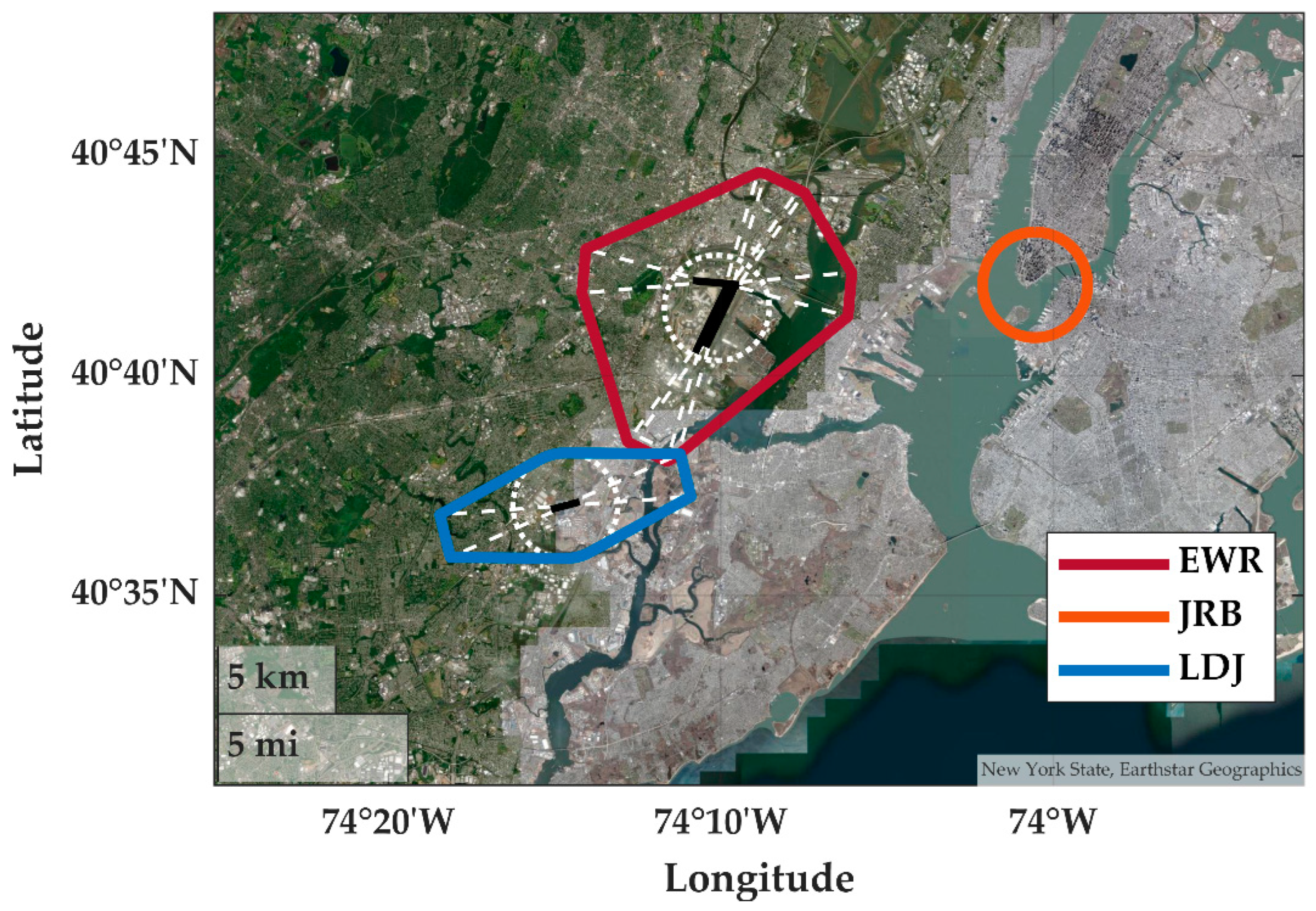
Appendix A. Datasets of Aircraft Tracks
Appendix A.1. OpenSky Network
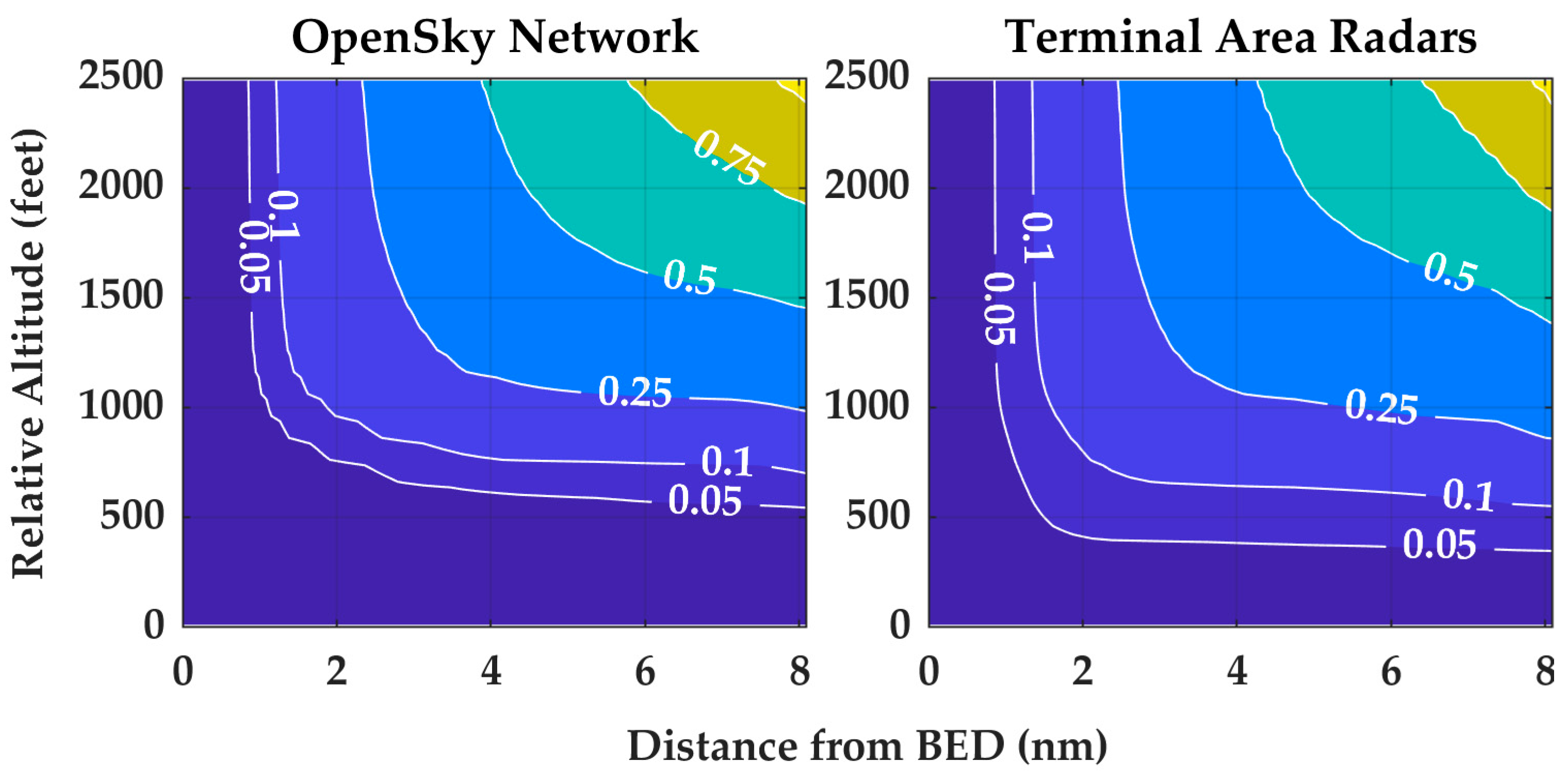
Appendix A.2. Terminal Area Radars
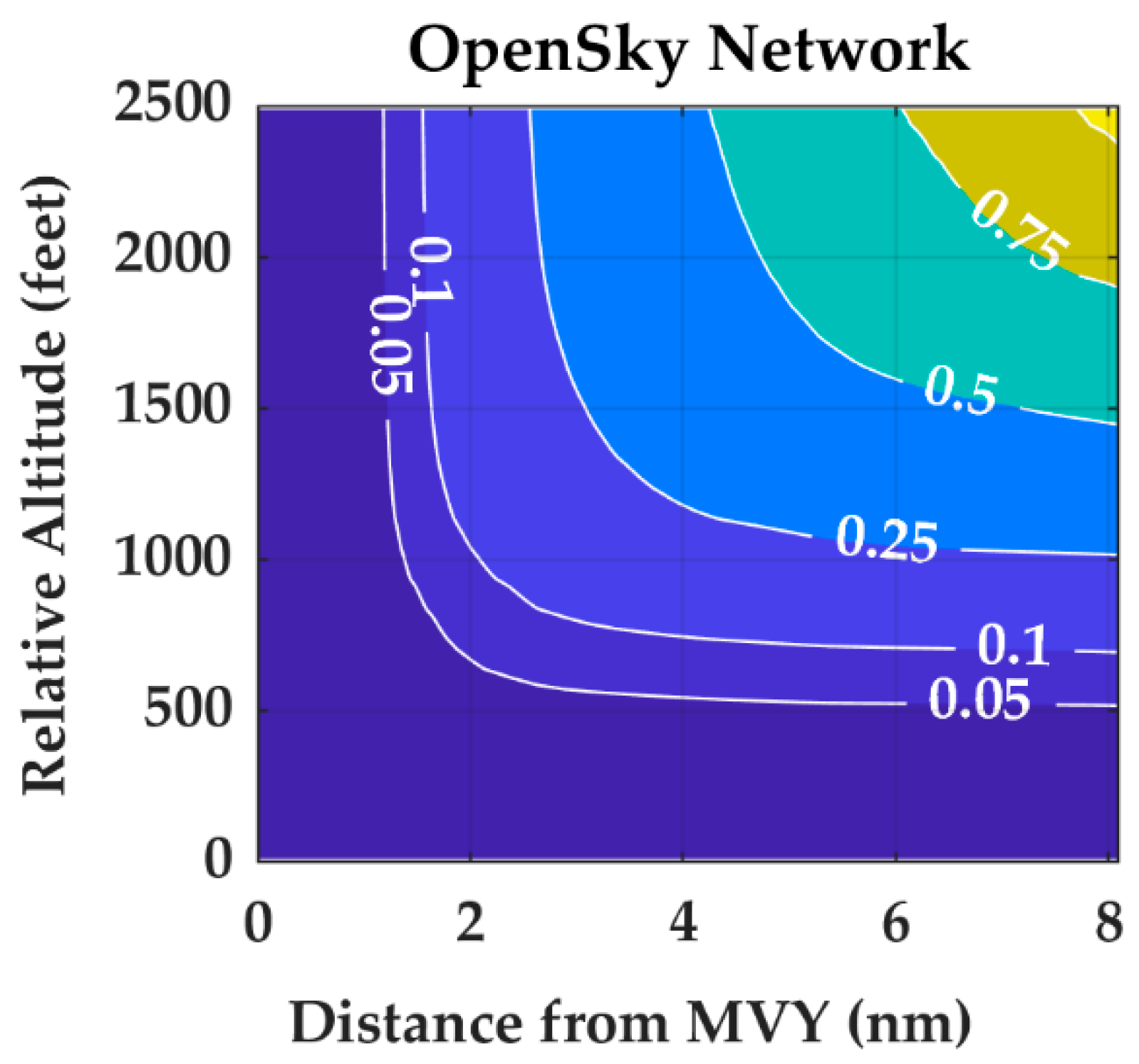
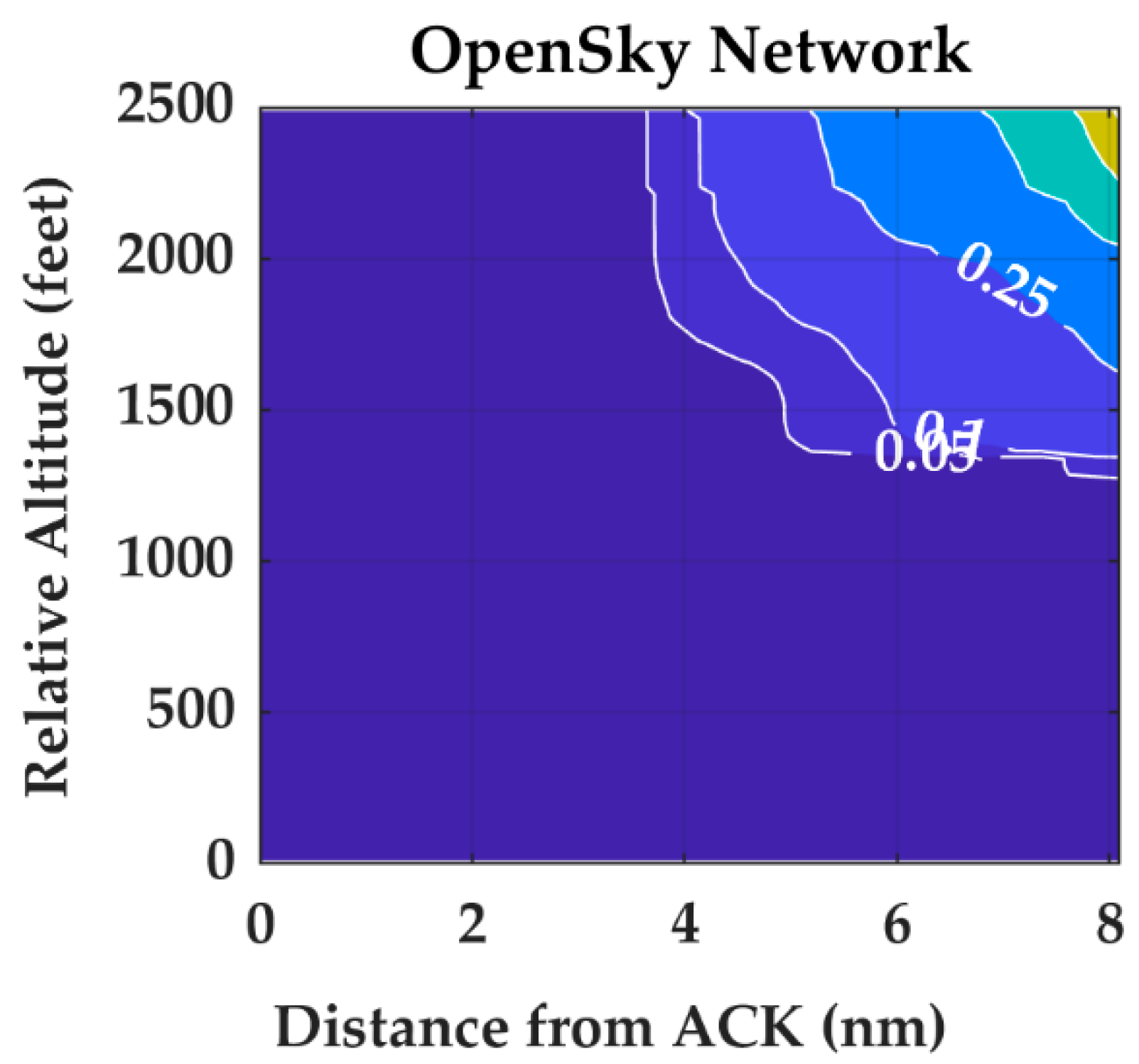
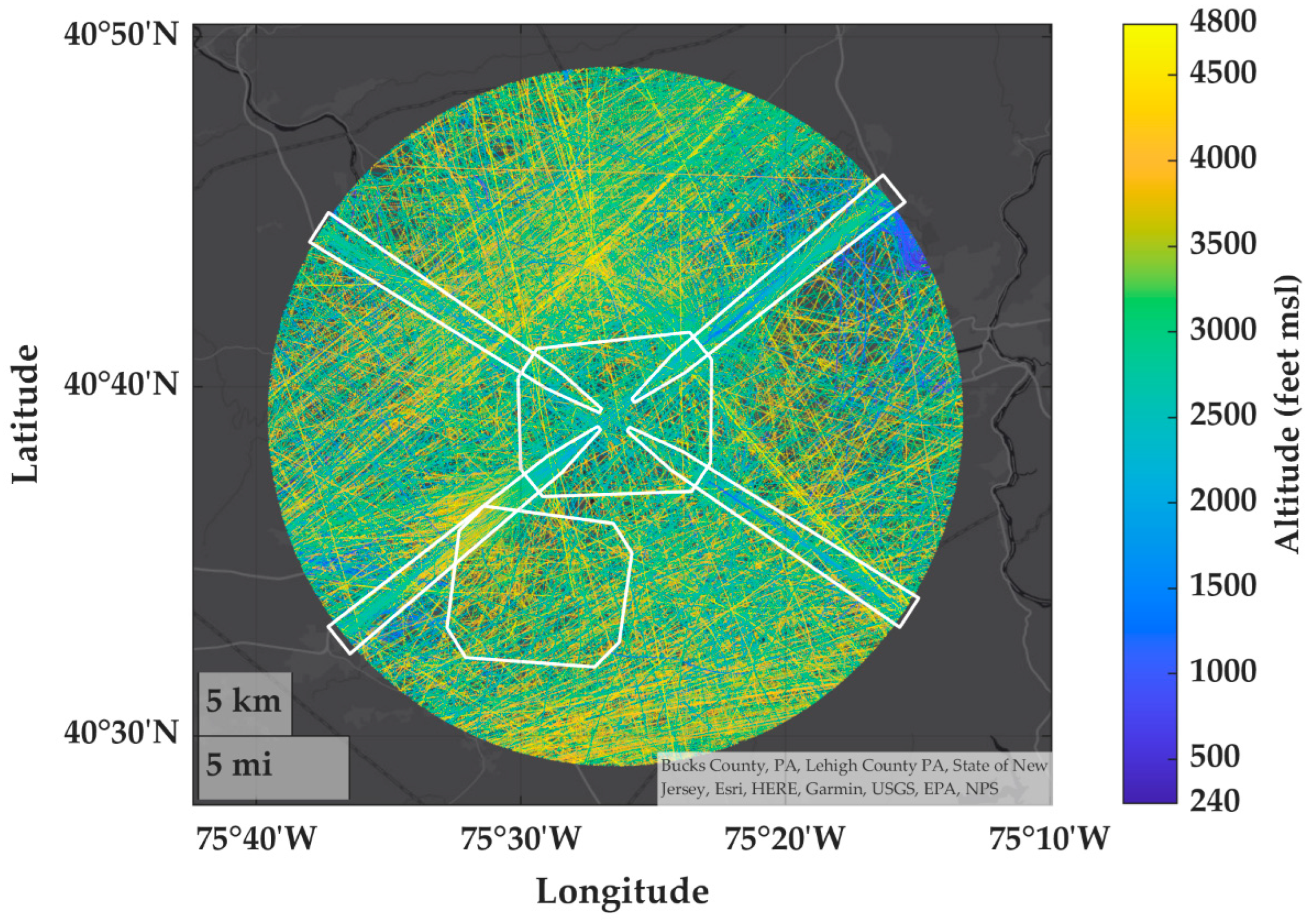
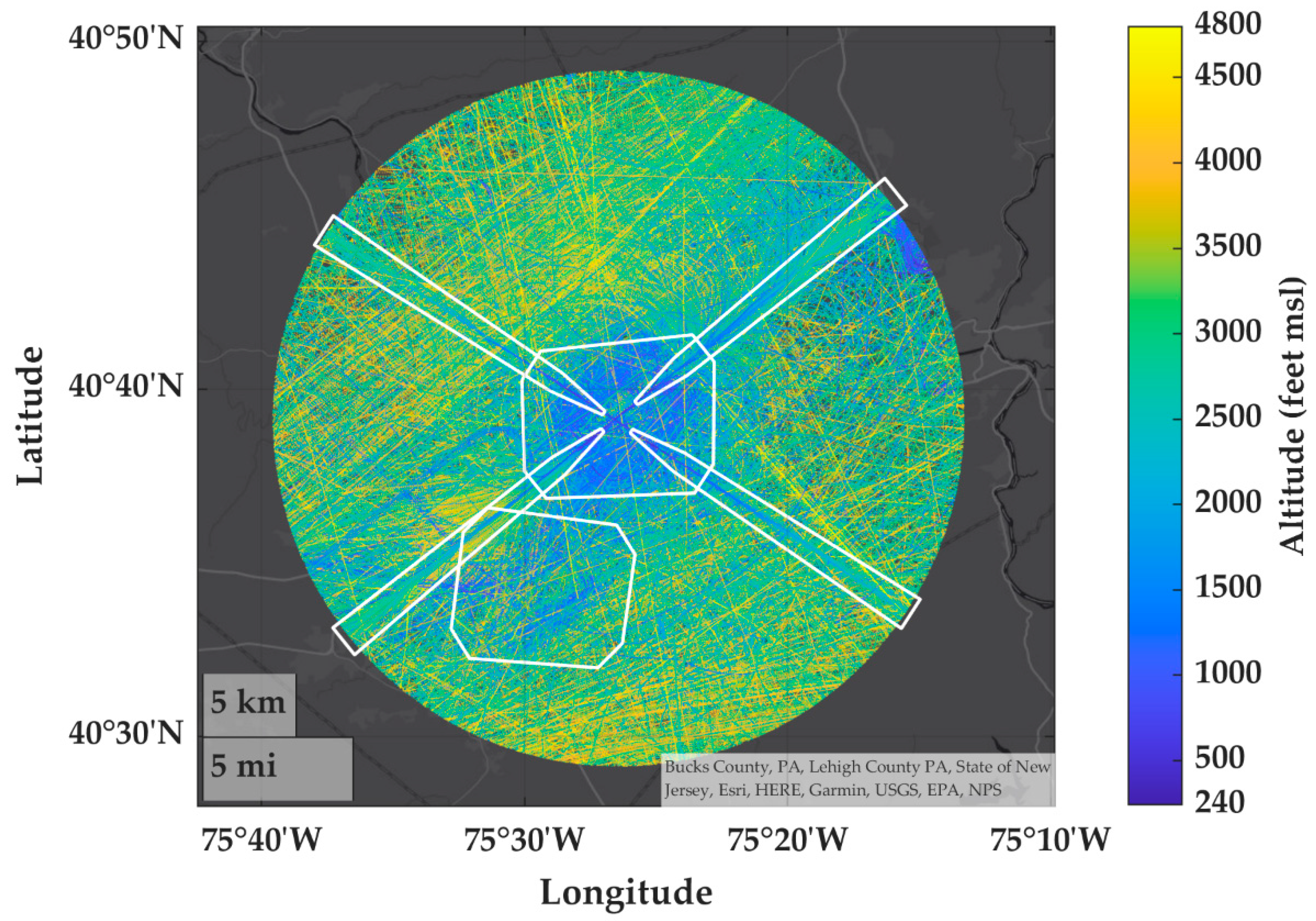
Appendix A.3. Altitude and Airspace Class Characterization
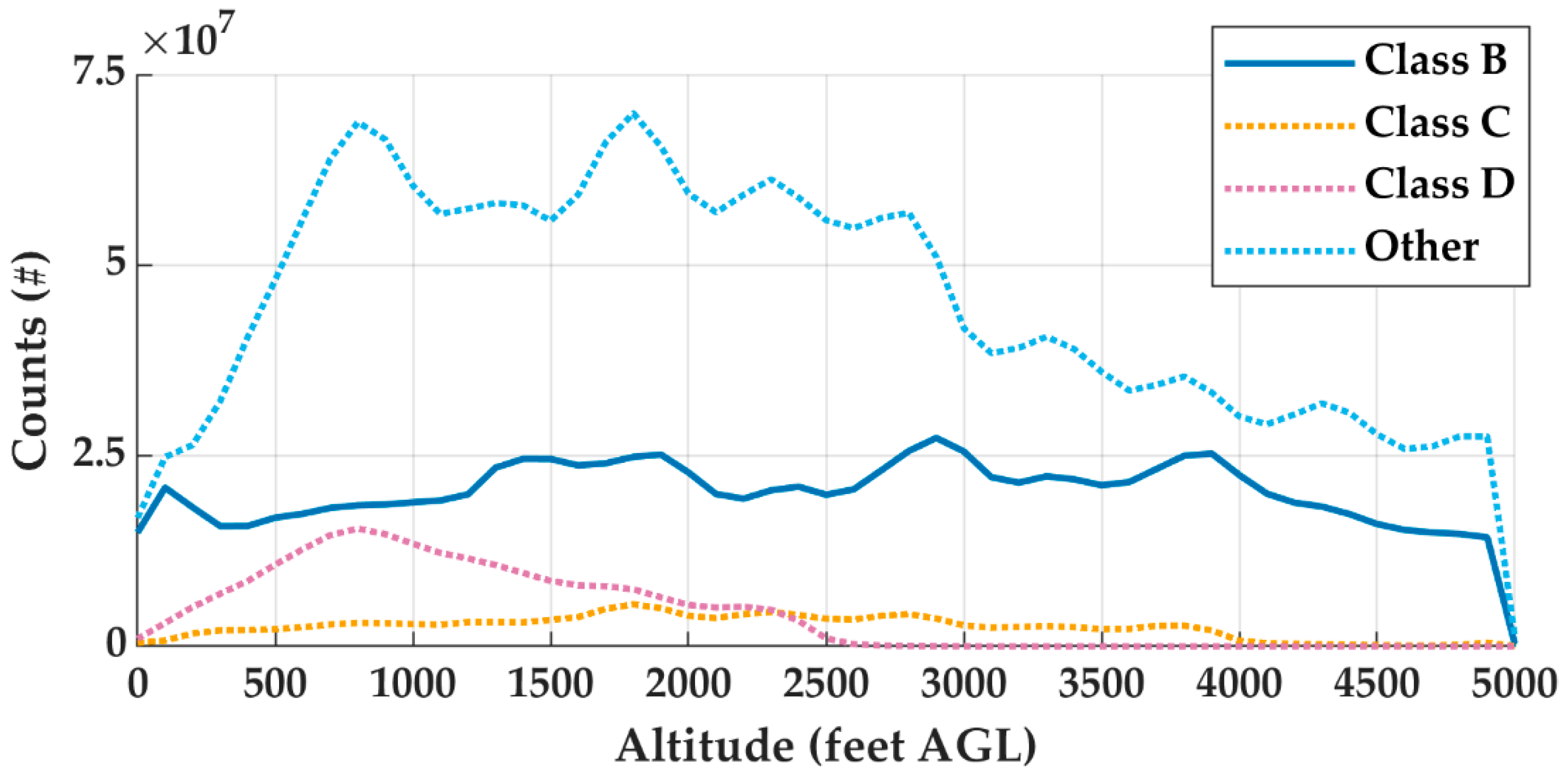
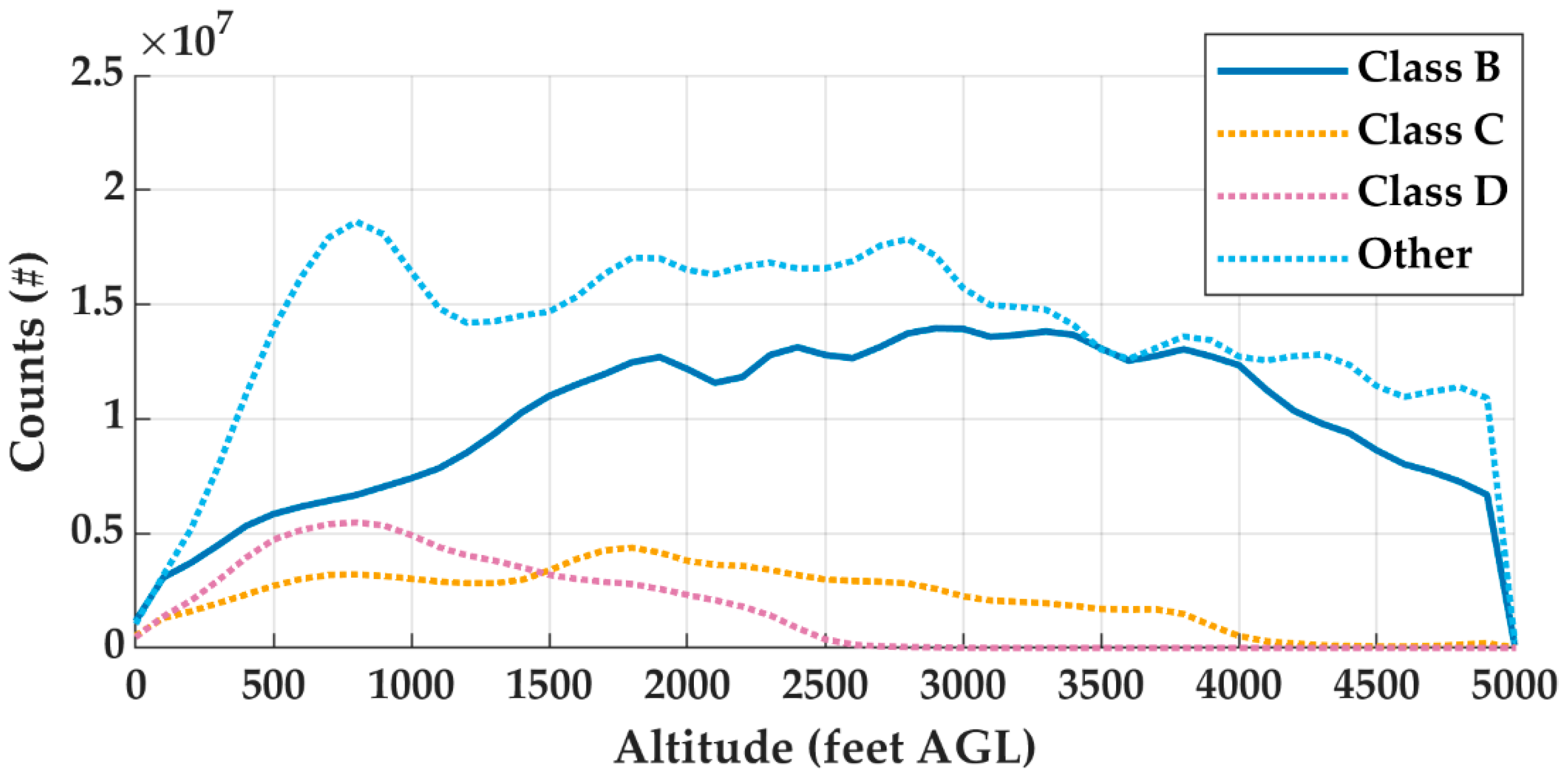
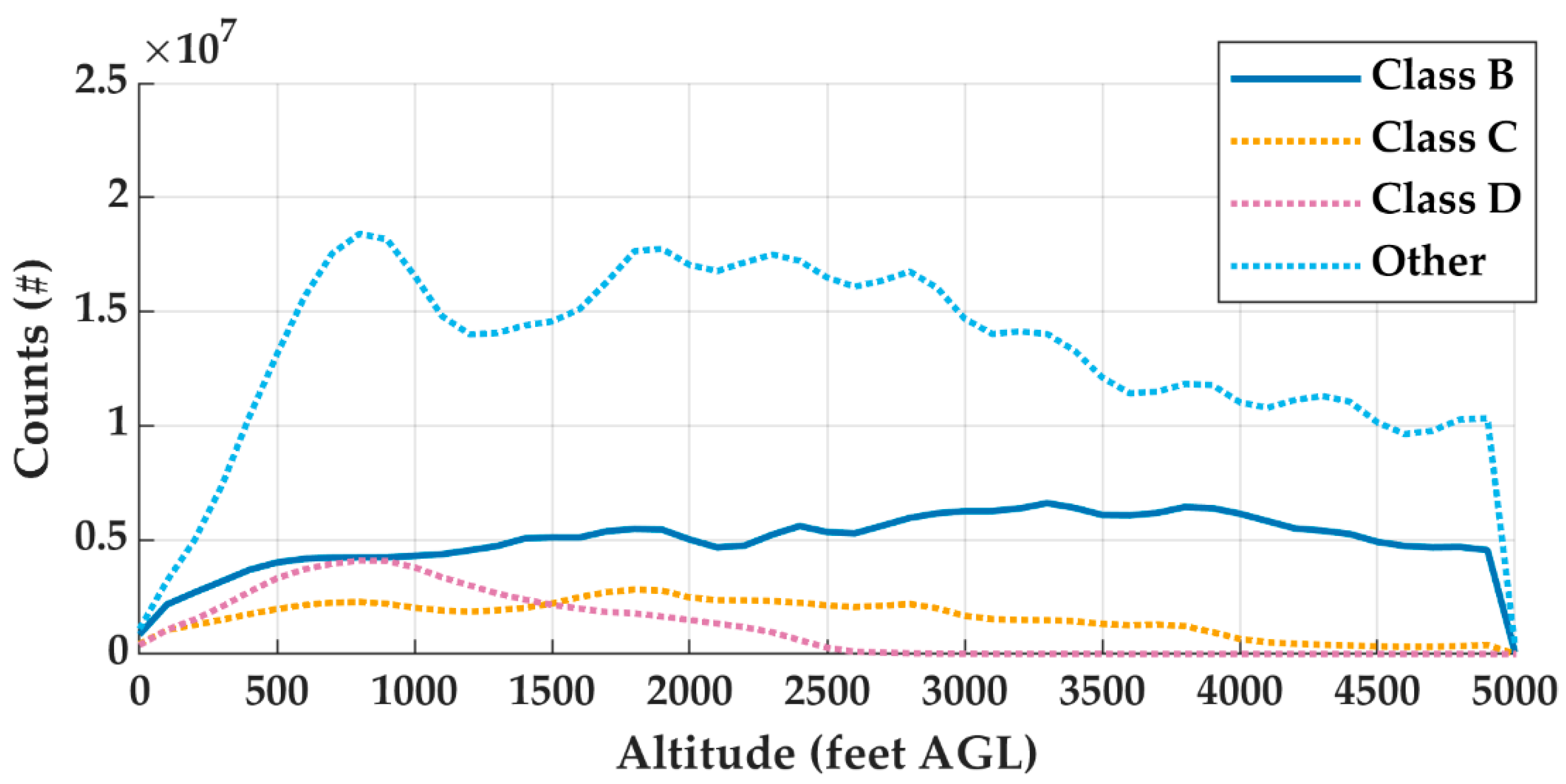
Appendix A.4. Data per National Plan of Integrated Airport Systems
| FAA ID | Class | Hub | OpenSky Network | Terminal Area Radar |
|---|---|---|---|---|
| BOS | B | L | 10,881,938 | 13,270,494 |
| ABE | C | N | 1,816,670 | 2,285,593 |
| BUR | C | M | 16,789,410 | 29,748,003 |
| FLL | C | L | 10,342,130 | 50,856,891 |
| SMF | C | M | 6,876,029 | 0 |
| XNA | C | S | 1,466,794 | 0 |
| ACK | D | N | 21,934 | 0 |
| ADS | D | - | 20,954,315 | 68,151,579 |
| BED | D | N | 2,740,664 | 6,220,588 |
| EYW | D | S | 0 | 0 |
| MVY | D | N | 820,654 | 0 |
| RNT | D | - | 21,892,547 | 46,653,226 |
| TTD | D | - | 5,360,106 | 14,106,809 |
| 7N7 | E/G | - | 7,968,295 | 18,523,179 |
| 17N | E/G | - | 2,252,995 | 13,006,900 |
| 19N | E/G | - | 5,818,462 | 18,784,328 |
| DDH | E/G | - | 0 | 0 |
Appendix B
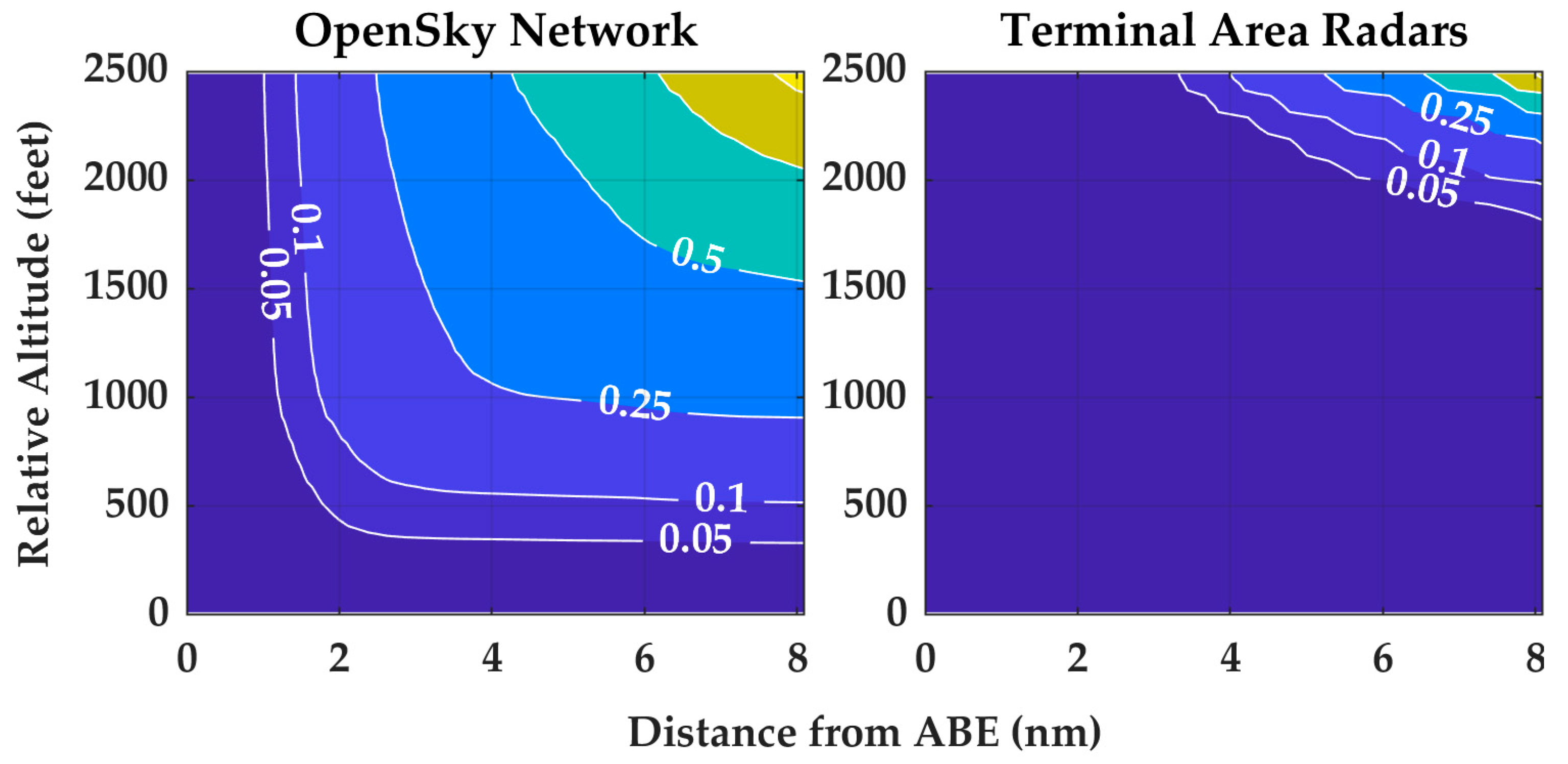
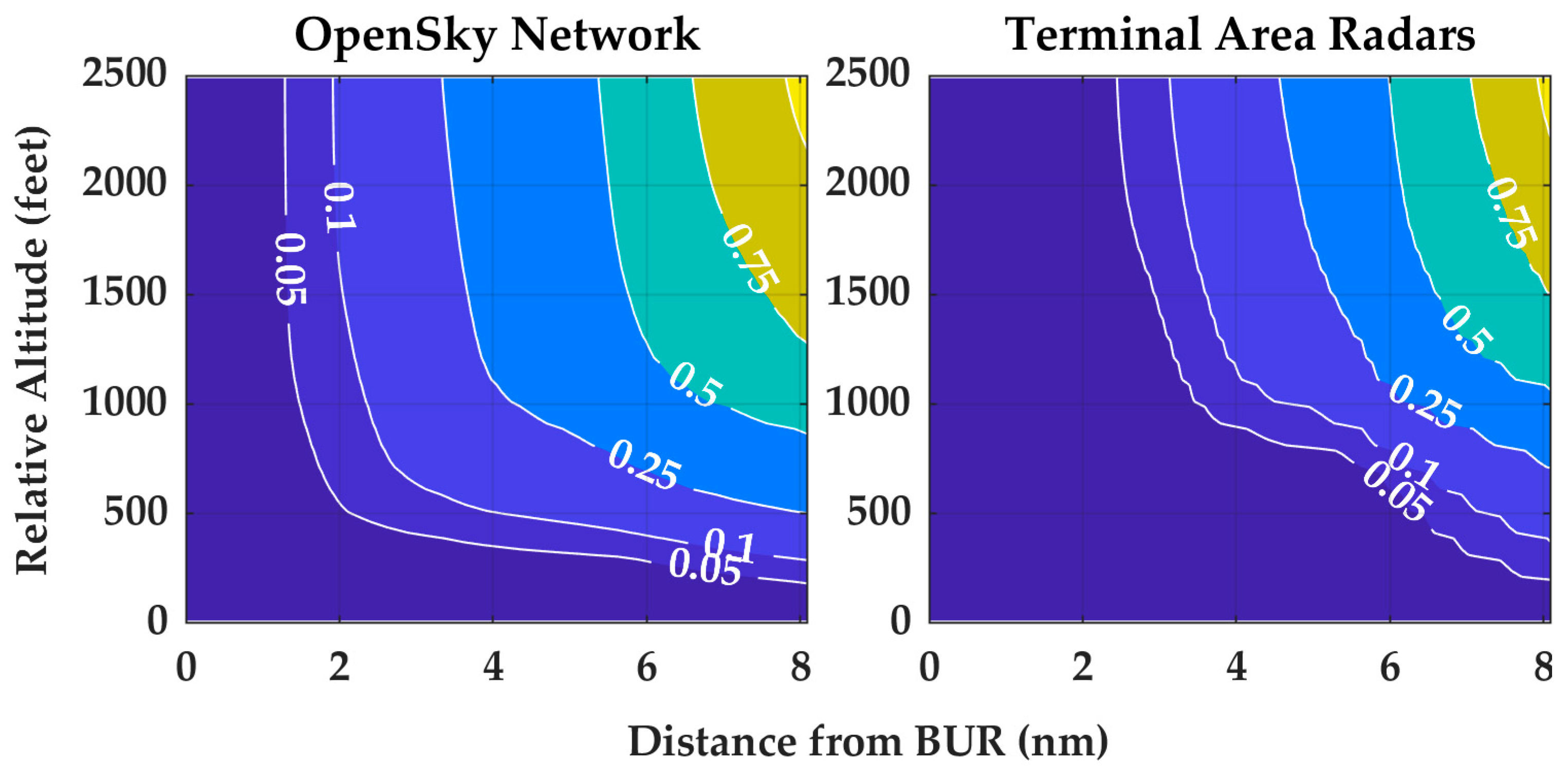
Appendix C
| Code | Purpose |
|---|---|
| 1206 | VFR law enforcement, first responder by L.A., may not be in contact with ATC |
| 1255 | Firefighting aircraft |
| 1273–1275 | Calibration and performance monitoring equipment |
| 1276 | Air defense identification zone penetration (when unable to contact ATC or aeronautical facility) |
| 4401–4433, 4466–4477 | Special aircraft—sensitive unclassified |
| 4434–4437 | Weather reconnaissance |
| 4447–4452 | Special flight support codes |
| 5000–5057, 5063–5077, 5400, 6100, 6400, 7501–7577 | DOD reserved codes only to be assigned by NORAD |
| 5100–5300 | More DOD aircraft |
| 7400 | Reserved for uncrewed aircraft with a lost link |
| 7500 | Hijack |
| 7600 | Radio failure |
| 7601–7607, 7701–7707 | Allocated by the FAA for special use by law enforcement agencies |
| 7700 | Emergency |
| 7777 | DOD interceptor aircraft on active air defense missions -operating without ATC clearance |
Appendix D
Appendix E
| Variable (Units) | Generic | RTCA228-A1 | RTCA228-A2 | RTCA228-A3 |
|---|---|---|---|---|
| Minimum speed (feet per second) | 50 | 169 | 68 | 68 |
| Maximum speed (feet per second) | 506 | 491 | 338 | 186 |
| Acceleration (feet per second2) | 50 | 50 | 50 | 50 |
| Maximum vertical rate (feet per second) | 100.00 | 41.67 | 25.00 | 8.34 |
| Maximum turn rate (degrees per second) | 12 | 1.5 | 3 | 7 |
| Maximum pitch (degrees) | ∞ | 15 | 15 | 15 |
Appendix G
- Trajectory segment include altitude below 1500 feet (relative to runway elevation);
- The segment is generally increasing in altitude;
- The ground track is aligned within 45° of the runway; and
- The segment includes positive points on the along-runway axis that are within 4000 feet of the runway laterally.
- Includes altitudes below 1500 feet (relative to runway elevation);
- Ground track is aligned within 35° of runway; and
- Includes negative points on the along-runway ways that are within 4000 feet of the runway laterally.
References
- RTCA. DO-365—Minimum Operational Performance Standards (MOPS) for Detect and Avoid (DAA) Systems; RTCA: Washington, DC, USA, 2017. [Google Scholar]
- International Civil Aviation Organization. Global Air Traffic Management Operational Concept; International Civil Aviation Organization: Montreal, QC, Canada, 2005. [Google Scholar]
- Espindle, L.P.; Griffith, J.D.; Kuchar, J.K. Safety Analysis of Upgrading to TCAS Version 7.1 Using the 2008 U.S. Correlated Encounter Model; Massachusetts Institute of Technology, Lincoln Laboratory: Lexington, MA, USA, 2009. [Google Scholar]
- Edwards, M.W.; Kochendedrfer, M.J.; Kuchar, J.K.; Espindle, L.P. Encounter Models for Unconventional Aircraft, Version 1.0; Project Report ATC-348; Massachusetts Institute of Technology, Lincoln Laboratory: Lexington, MA, USA, 2009. [Google Scholar]
- Kochenderfer, M.J.; Edwards, M.W.M.; Espindle, L.P.; Kuchar, J.K.; Griffith, J.D. Airspace Encounter Models for Estimating Collision Risk. J. Guid. Control Dyn. 2010, 33, 487–499. [Google Scholar] [CrossRef]
- Weinert, A.J.; Harkleroad, E.P.; Griffith, J.D.; Edwards, M.W.; Kochenderfer, M.J. Uncorrelated Encounter Model of the National Airspace System Version 2.0; Project Report ATC-404; Massachusetts Institute of Technology, Lincoln Laboratory: Lexington, MA, USA, 2013. [Google Scholar]
- Underhill, N.; Weinert, A. Applicability and Surrogacy of Uncorrelated Airspace Encounter Models at Low Altitudes. J. Air Transp. 2021, 29, 1–5. [Google Scholar] [CrossRef]
- Weinert, A. Airspace-Encounter-Models/Em-Model-Manned-Bayes: October 2021; Zenodo: 2021. Available online: https://doi.org/10.5281/zenodo.5544340 (accessed on 5 November 2020).
- Kochenderfer, M.J.; Espindle, L.P.; Kuchar, J.K.; Griffith, J.D. Correlated Encounter Model for Cooperative Aircraft in the National Airspace System; Project Report ATC-344; Massachusetts Institute of Technology, Lincoln Laboratory: Lexington, MA, USA, 2008. [Google Scholar]
- Underhill, N.; Harkleroad, E.; Guendel, R.; Weinert, A.; Maki, D.; Edwards, M. Correlated Encounter Model for Cooperative Aircraft in the National Airspace System; Version 2.0; Project Report ATC-440; Massachusetts Institute Technology Lincoln Laboratory: Lexington, MA, USA, 2018; Available online: https://apps.dtic.mil/docs/citations/AD1051496 (accessed on 16 January 2019).
- RTCA. Terms of Reference RTCA Special Committee 228: Minimum Performance Standards for Unmanned Aircraft Systems (Rev 10); RTCA: Washington, DC, USA, 2020. [Google Scholar]
- Ghatas, R.W.; Jack, D.P.; Tsakpinis, D.; Vincent, M.J.; Sturdy, J.L.; Munoz, C.A.; Hoffler, K.D.; Dutle, A.M.; Myer, R.R.; Dehaven, A.M.; et al. Unmanned Aircraft Systems Minimum Operations Performance Standards End-to-End Verification and Validation (E2-V2) Simulation; Technical Report NASA/TM-2017-219598; NASA Langley Research Center: Hampton, VA, USA, 2017. Available online: https://ntrs.nasa.gov/search.jsp?R=20170004506 (accessed on 5 November 2020).
- Weinert, A.; Underhill, N.; Wicks, A. Developing a Low Altitude Manned Encounter Model Using ADS-B Observations. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Weinert, A.; Kochenderfer, M.; Edwards, M.W.M.; Gill, B.; Guendel, R.; Underhill, N. Airspace-Encounter-Models/Em-Model-Manned-Bayes: July 2021—Terminal Model and Improved Performance. Zenodo. 2021. Available online: https://zenodo.org/record/5113936#.YellRfgRVPY (accessed on 5 November 2020).
- Schäfer, M.; Strohmeier, M.; Lenders, V.; Martinovic, I.; Wilhelm, M. Bringing up OpenSky: A large-scale ADS-B sensor network for research. In Proceedings of the IPSN-14 Proceedings of the 13th International Symposium on Information Processing in Sensor Networks, Berlin, Germany, 15–17 April 2014; pp. 83–94. [Google Scholar] [CrossRef]
- Weinert, A.; Brittain, M.; Serres, C.; Guendel, R. Benchmarking the Processing of Aircraft Tracks with Triples Mode and Self-Scheduling. In Proceedings of the 2021 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 20–24 September 2021; pp. 1–8. [Google Scholar]
- Gariel, M.; Srivastava, A.N.; Feron, E. Trajectory Clustering and an Application to Airspace Monitoring. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1511–1524. [Google Scholar] [CrossRef] [Green Version]
- Mahboubi, Z.; Kochenderfer, M.J. Learning Traffic Patterns at Small Airports from Flight Tracks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 917–926. [Google Scholar] [CrossRef]
- Barratt, S.T.; Kochenderfer, M.J.; Boyd, S.P. Learning Probabilistic Trajectory Models of Aircraft in Terminal Airspace From Position Data. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3536–3545. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Gariel, M.; Hansman, R.J.; Palacios, R. Anomaly detection in onboard-recorded flight data using cluster analysis. In Proceedings of the 2011 IEEE/AIAA 30th Digital Avionics Systems Conference, Seattle, WA, USA, 16–20 October 2011; pp. 4A4-1–4A4-11. [Google Scholar] [CrossRef]
- Li, L.; Hansman, R.J.; Palacios, R.; Welsch, R. Anomaly detection via a Gaussian Mixture Model for flight operation and safety monitoring. Transp. Res. Part C Emerg. Technol. 2016, 64, 45–57. [Google Scholar] [CrossRef]
- Krozel, J. Intelligent Tracking of Aircraft in the National Airspace System. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2002. [Google Scholar] [CrossRef]
- Georgiou, H.; Pelekis, N.; Sideridis, S.; Scarlatti, D.; Theodoridis, Y. Semantic-aware aircraft trajectory prediction using flight plans. Int. J. Data Sci. Anal. 2020, 9, 215–228. [Google Scholar] [CrossRef]
- Churchill, A.M.; Bloem, M. Clustering Aircraft Trajectories on the Airport Surface. In Proceedings of the 13th USA/Europe Air Traffic Management Research and Development Seminar, Chicago, IL, USA, 10–13 June 2019; pp. 10–13. [Google Scholar]
- Airplane Flying Handbook. Federal Aviation Administration, FAA-H-8083-3B. 2016. Available online: https://www.faa.gov/regulations_policies/handbooks_manuals/aviation/airplane_handbook/ (accessed on 5 November 2020).
- Serres, C.; Gill, B.; Reheis, P.; Edwards, M.; Guendel, R.; Weinert, A.; Williams, R.; Klaus, R. Mit-Ll/Degas-Core: Initial Release. Zenodo. 2020. Available online: https://doi.org/10.5281/zenodo.4323620 (accessed on 5 November 2020).
- Wu, M.G.; Lee, S.; Serres, C.C.; Gill, B.; Edwards, M.W.M.; Smearcheck, S.; Adami, T.; Calhoun, S. Detect-and-Avoid Closed-Loop Evaluation of Noncooperative Well Clear Definitions. J. Air Transp. 2020, 28, 195–206. [Google Scholar] [CrossRef]
- Chen, C.; Edwards, M.W.; Gill, B.; Smearcheck, S.; Adami, T.; Calhoun, S.; Wu, M.G.; Cone, A.; Lee, S.M. Defining Well Clear Separation for Unmanned Aircraft Systems Operating with Noncooperative Aircraft. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; pp. 1–14. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.G.; Cone, A.C.; Lee, S.; Chen, C.; Edwards, M.W.; Jack, D.P. Well Clear Trade Study for Unmanned Aircraft System Detect and Avoid with Non-Cooperative Aircraft. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar] [CrossRef] [Green Version]
- ASTM International. F3442/F3442M-20 Standard Specification for Detect and Avoid System Performance Requirements; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar] [CrossRef]
- Weinert, A.; Campbell, S.; Vela, A.; Schuldt, D.; Kurucar, J. Well-Clear Recommendation for Small Unmanned Aircraft Systems Based on Unmitigated Collision Risk. J. Air Transp. 2018, 26, 113–122. [Google Scholar] [CrossRef] [Green Version]
- Weinert, A.J. An information Theoretic Approach for Generating an Aircraft Avoidance Markov Decision Process; Boston University: Boston, MA, USA, 2015; Available online: https://open.bu.edu/handle/2144/15208 (accessed on 11 September 2019).
- Alvarez, L.E.; Jones, J.C.; Bryan, A.; Weinert, A.J. Demand and Capacity Modeling for Advanced Air Mobility. In Proceedings of the AIAA AVIATION 2021 FORUM, Online, 2–6 August 2021; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2021. [Google Scholar] [CrossRef]
- Wang, L.; Lucic, P.; Campbell, K.; Wanke, C. Helicopter Track Identification with Autoencoder. In Proceedings of the 2021 Integrated Communications Navigation and Surveillance Conference (ICNS), Dulles, VA, USA, 19–23 April 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Huang, H.; Huang, J.; Feng, Y.; Liu, Z.; Wang, T.; Chen, L.; Zhou, Y. Aircraft Type Recognition Based on Target Track. J. Phys. Conf. Ser. 2018, 1061, 012015. [Google Scholar] [CrossRef]
- Bertsimas, D.; Patterson, S.S. The air traffic flow management problem with enroute capacities. Oper. Res. 1998, 46, 406–422. [Google Scholar] [CrossRef]
- Weinert, A.; Brittain, M.; Serres, C.; Underhill, N. Mit-Ll/Em-Download-Opensky: Initial Release. Zenodo, 2020. [Google Scholar] [CrossRef]
- Dube, K.; Nhamo, G.; Chikodzi, D. COVID-19 pandemic and prospects for recovery of the global aviation industry. J. Air Transp. Manag. 2021, 92, 102022. [Google Scholar] [CrossRef]
- Weinert, A.; Underhill, N.; Gill, B.; Wicks, A. Processing of Crowdsourced Observations of Aircraft in a High Performance Computing Environment. In Proceedings of the 2020 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 22–24 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Olson, W.A.; Olszta, J.E. TCAS Operational Performance Assessment in the U.S. National Airspace. In Proceedings of the 29th Digital Avionics Systems Conference, Salt Lake City, UT, USA, 2–7 October 2010; pp. 4.A.2-1–4.A.2-11. [Google Scholar] [CrossRef]
- Weinert, A.; Brittain, M.; Guendel, R. Frequency of ADS-B Equipped Manned Aircraft Observed by the OpenSky Network. Proceedings 2020, 59, 15. [Google Scholar] [CrossRef]
- National Plan of Integrated Airport Systems (NPIAS), 2015–2019; Report to Congress; Federal Aviation Adminstration: Washington, DC, USA, 2014.
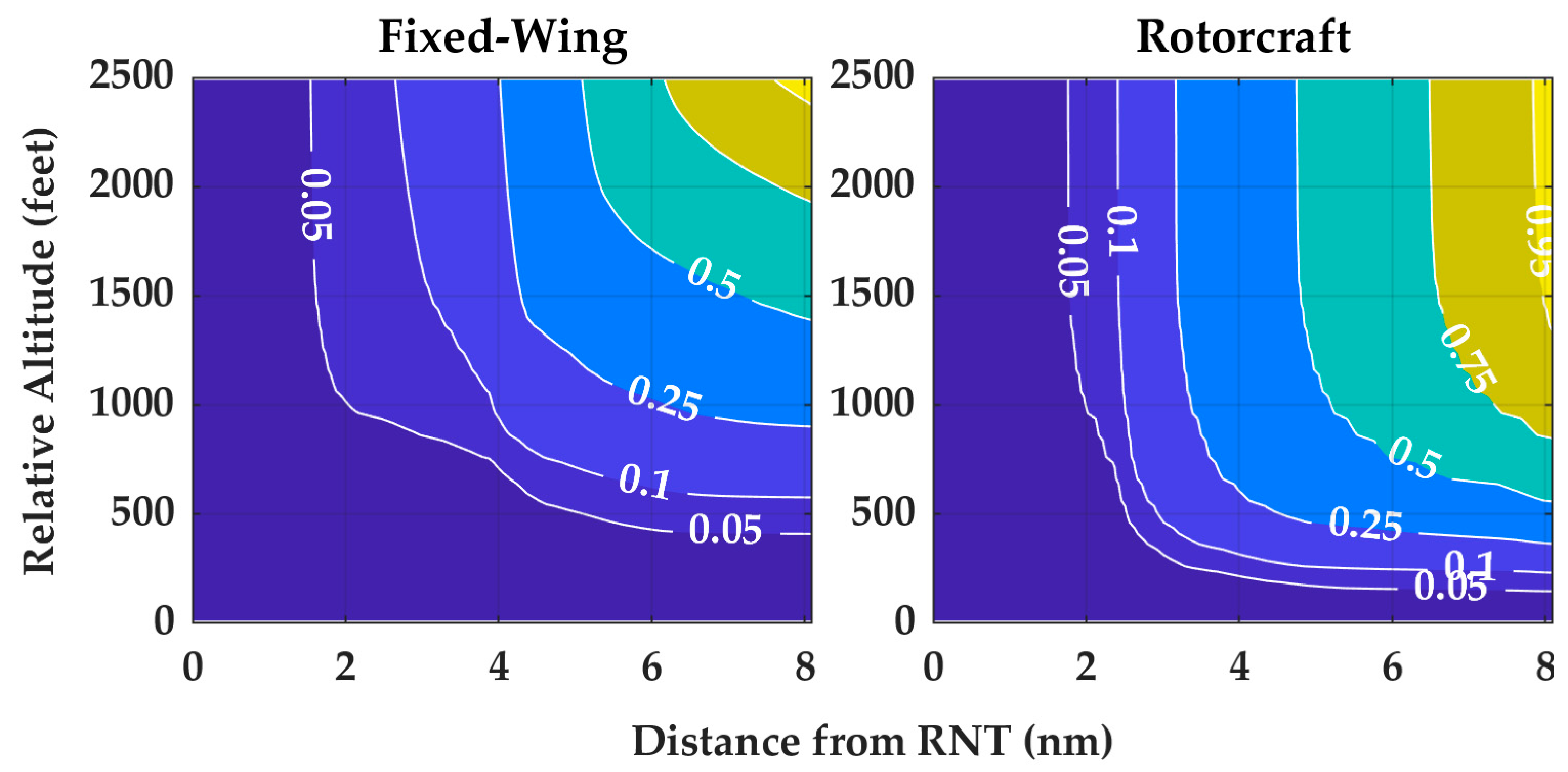






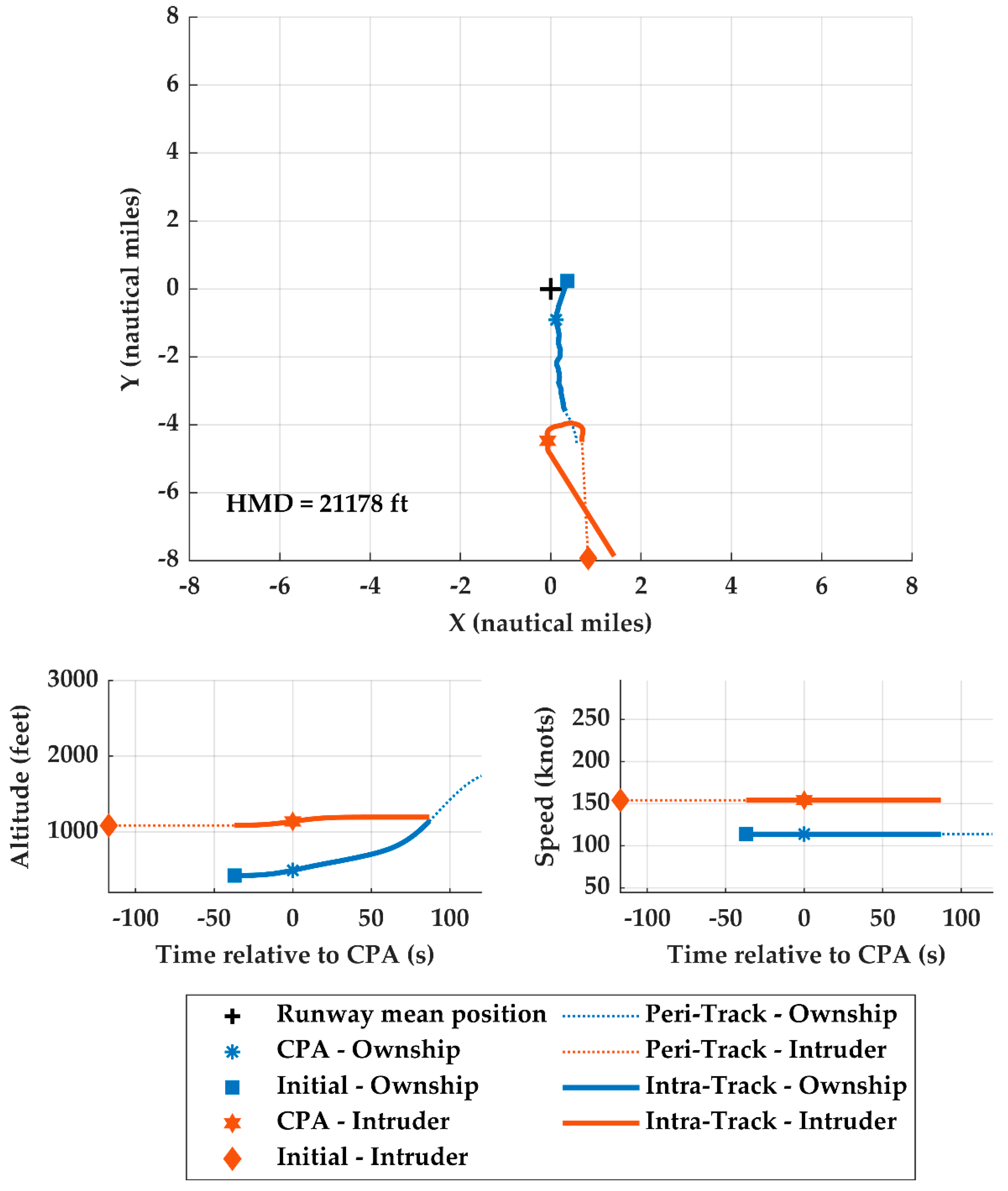
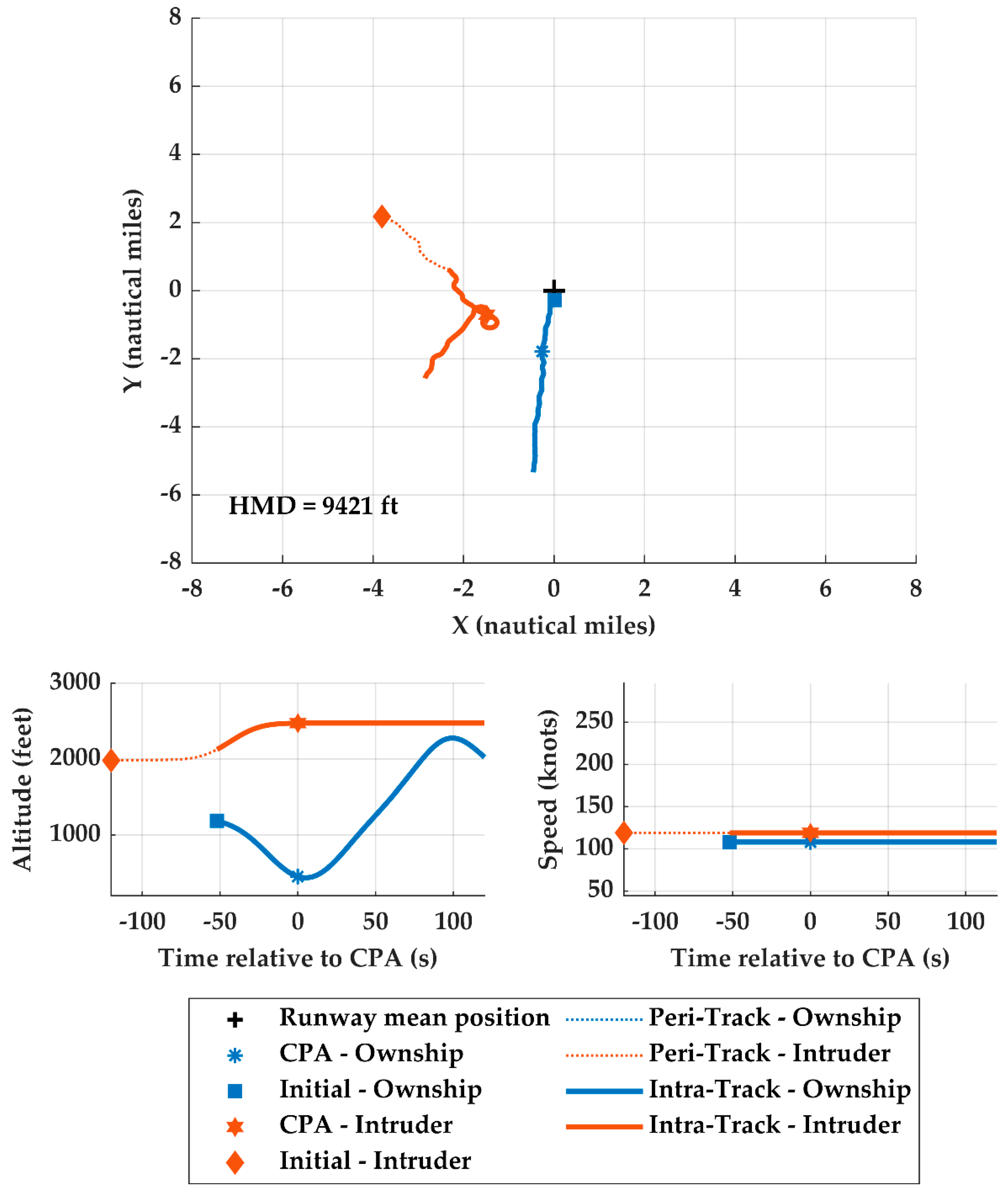
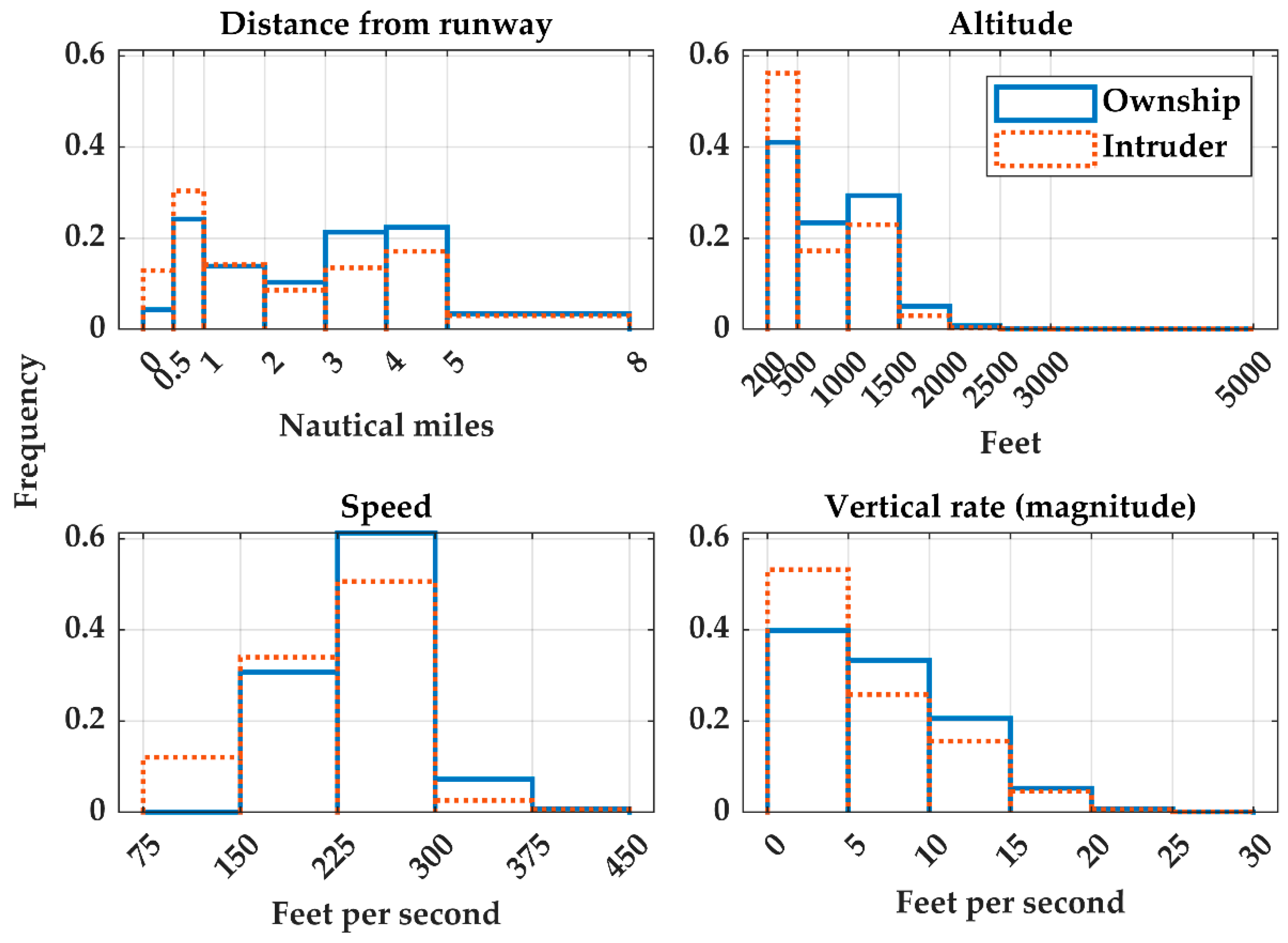
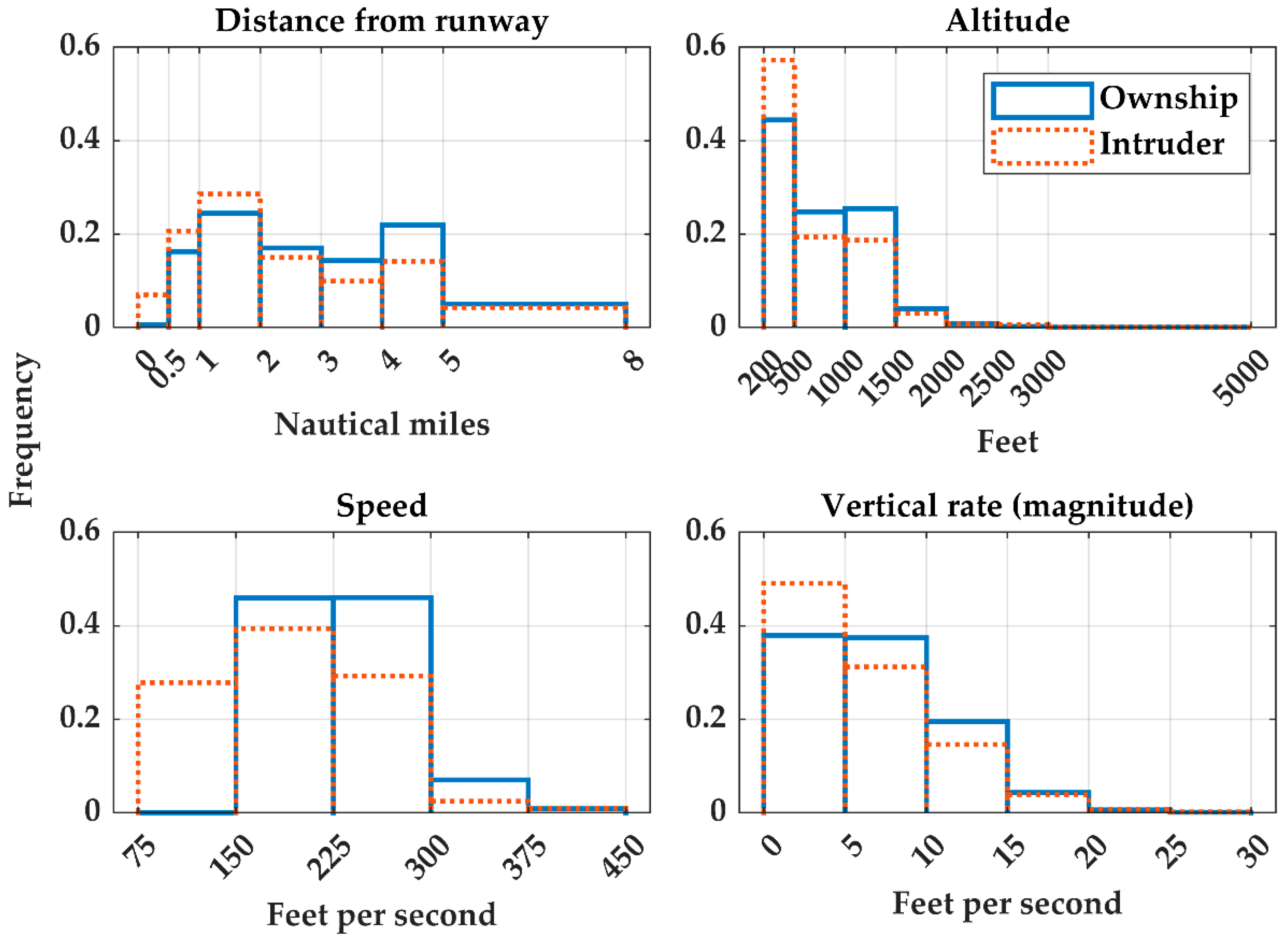

| Airspace | Mondays | Aerodromes | Terminal Area Radars |
|---|---|---|---|
| Class B | 251,671,725 | 505,322,452 | 1,026,076,842 |
| Class C | 79,874,269 | 108,969,262 | 126,863,443 |
| Class D | 57,887,219 | 81,304,346 | 214,349,345 |
| Other | 667,255,320 | 696,368,992 | 2,282,086,215 |
| Total | 1,056,688,533 | 1,391,965,052 | 3,649,375,845 |
| Count | ABE | ADS | LBJ |
|---|---|---|---|
| Points after initial spatial filtering | 1,816,670 | 20,954,315 | 14,538,290 |
| Takeoffs or landings (any) | 877 | 2913 | 3 |
| Transiting intruders | 4522 | 38,917 | 71,881 |
| Potential encounters based on intent and time | 28,174 | 753,067 | 23,889 |
| Final identified encounters for training | 22 | 402 | 0 |
| Airspace Class | Terminal Radar | Aerodromes |
|---|---|---|
| B | 2,396,048 | 1,038,390 |
| C | 103,566 | 81,253 |
| D | 85,514 | 45,066 |
| Other (E/G) | 1209 | 432 |
| Airspace Class | Dataset | 0 | (0, 10) | [10, 100) | [100, ∞) | Total |
|---|---|---|---|---|---|---|
| C | Aerodromes | 29 | 9 | 12 | 24 | 74 |
| C | Terminal Radars | 5 | 0 | 2 | 9 | 16 |
| D | Aerodromes | 139 | 40 | 45 | 44 | 268 |
| D | Terminal Radars | 43 | 6 | 25 | 44 | 118 |
| Other | Aerodromes | 829 | 37 | 13 | 0 | 879 |
| Other | Terminal Radars | 371 | 24 | 19 | 4 | 418 |
| Variable | Node Label | Values |
|---|---|---|
| Airspace Class | class | [1—B, 2—C, 3—D, 4—Other] |
| Ownship Intent | Ownship_intent | [1—Land, 2—Takeoff] |
| Intruder Intent | int_intent | [1—Land, 2—Takeoff, 3—Transit] |
| Intruder Type | int_type | [1—Fixed-Wing, 2—Rotorcraft] |
| Intruder Runway | int_runway | [1—Same, 2—Parallel, 3—Crossing, 4—None (Transit)] |
| Variable (Units) | Node Label | Cutpoints |
|---|---|---|
| Ownship Altitude (feet) | own_alt | [200, 500, 1000, …, 3000, 5000] |
| Ownship Bearing (degrees) | own_bearing | [0, 15, 30, …, 165, 175, 185, 195, 210, 225, …, 360] |
| Ownship Distance (nautical miles) | own_distance | [0, 0.5, 1, 2, 3, 4, 5, 8] |
| Ownship Speed (feet per second) | own_speed | [75, 150, 225, 300, 375, 450] |
| Ownship Track (degrees) | own_trk_angle | [−180, −175, −165, …, 175, 180] |
| Intruder Altitude (feet) | int_alt | [200, 500, 1000, …, 3000, 5000] |
| Intruder Bearing (degrees) | int_bearing | [0, 15, 30, …, 165, 175, 185, 195, 210, 225, …, 360] |
| Intruder Distance (nautical miles) | int_distance | [0, 0.5, 1, 2, 3, 4, 5, 8] |
| Intruder Speed (feet per second) | int_speed | [75, 150, 225, 300, 375, 450] |
| Intruder Track (degrees) | int_trk_angle | [−180, −175, −165, …, 175, 180] |
| Variable (Units) | Node Label | Cutpoints |
|---|---|---|
| Intent | intent | [1—Land, 2—Takeoff, 3—Transit] |
| Distance (nautical miles) | distance | [0, 0.5, 1, 2, 3, 4, 5, 8] |
| Bearing (degrees) | bearing | [0, 5, 15, 25, …, 355, 360] |
| Altitude (feet) | altitude | [200, 300, …, 2000, 2500, 3000, 5000] |
| Speed (feet per second) | speed | [75, 100, 150, 200, …, 350, 450] |
| Track (degrees) | trk_angle | [−180, −175, −165, …, 175, 180] |
| HMD (Feet) | VMD (Feet) | Terminal Area Radars | OpenSky Network Aerodromes |
|---|---|---|---|
| 2200 | 450 | 0.17 | 0.25 |
| 2500 | 0 | 0.10 | 0.15 |
| 2500 | 250 | 0.16 | 0.25 |
| 7000 | 500 | 0.25 | 0.40 |
| 16,400 | 0 | 0.25 | 0.34 |
| 23,600 | 0 | 0.50 | 0.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weinert, A.; Underhill, N.; Serres, C.; Guendel, R. Correlated Bayesian Model of Aircraft Encounters in the Terminal Area Given a Straight Takeoff or Landing. Aerospace 2022, 9, 58. https://doi.org/10.3390/aerospace9020058
Weinert A, Underhill N, Serres C, Guendel R. Correlated Bayesian Model of Aircraft Encounters in the Terminal Area Given a Straight Takeoff or Landing. Aerospace. 2022; 9(2):58. https://doi.org/10.3390/aerospace9020058
Chicago/Turabian StyleWeinert, Andrew, Ngaire Underhill, Christine Serres, and Randal Guendel. 2022. "Correlated Bayesian Model of Aircraft Encounters in the Terminal Area Given a Straight Takeoff or Landing" Aerospace 9, no. 2: 58. https://doi.org/10.3390/aerospace9020058
APA StyleWeinert, A., Underhill, N., Serres, C., & Guendel, R. (2022). Correlated Bayesian Model of Aircraft Encounters in the Terminal Area Given a Straight Takeoff or Landing. Aerospace, 9(2), 58. https://doi.org/10.3390/aerospace9020058








