1. Introduction
The path planning of planetary rovers is crucial for improving exploration benefits and system safety in extraterrestrial exploration. The existing lunar and Mars rovers mainly rely on man-involved local planning for path determination due to the limited local perception ability and surface mobility. For instance, the Yutu and Yutu-2 rovers move towards an object of interest for exploration through a series of waypoints and segmented paths that are terrestrially planned [
1,
2]. The present path planning systems seem to be reliable, but they are less efficient, and they can only plan as far as a rover can see. Orbital imageries of extraterrestrial planets can be provided at an effectively unlimited distance, which provides the possibility, as well as the basis, for long-range global path planning for extraterrestrial surface robotic activities [
3,
4]. High-precision orbital images can be further processed into digital elevation models (DEMs) carrying vivid three-dimensional topographical data, such as the CE2TMap2015 [
5,
6] for the Moon and the HiRISE [
7] data for Mars.
Generally, global path planning for planetary roving is divided into two stages, namely, map construction and path searching. First, the original orbital images are interpreted into computable configuration spaces in which free space and obstacle space are identified. Then, the right path can be identified by some path searching algorithms, such as the A* [
8,
9], the rapidly exploring random trees (RRT) [
10,
11], the ant colony algorithm [
12], and the genetic algorithm [
13], etc. These methods are operable in most instances, but may suffer from the exponential explosion of computation time when it comes to wide-range or high-resolution maps. Learning methods, such as deep learning and deep reinforcement learning (DRL), have been applied to the global path planning of planetary rovers in pursuit of improving computing efficiency [
14] and reducing dependence on human experience [
15,
16,
17]. However, there are still some questions that remain unsolved in learning-based methods. For the artificial neural network (ANN)-based planners, one very important issue is the difficulty of adapting to maps with various sizes due to their specific network structures.
In this paper, we propose a novel learning-based planning method for the global path planning of planetary roving, which can significantly improve the planning speed for long-range roving and which, meanwhile, can adapt to arbitrarily sized maps. First, a kind of binary feature map is obtained from the original extraterrestrial DEM through topography and illumination analysis. The feature map is designed to provide more distinguishable information for learning and planning. Then, a hierarchical planning framework is designed to resolve the issue into two hierarchies, namely, step iteration and block iteration. For the planning within step iteration, an end-to-end step planner named SP-ResNet is constructed using DRL. The planner employs double branches of residual networks for feature reasoning and action value estimation, and is trained over a simulated extraterrestrial DEM collection. In the results, comparative large-range planning tests with A*, RRT, and goal-biasing RRT (Gb-RRT) [
18] are conducted, demonstrating the prominent advantage of the proposed method in terms of planning efficiency. Furthermore, the effectiveness and the feasibility of the method are validated on real lunar terrains from CE2TMap2015.
The main contributions of this paper can be summarized as follows:
- (1)
A novel learning-based method combining a hierarchical planning framework and an end-to-end step planner improves the computational efficiency for long-range path planning.
- (2)
The step planner learns and conducts path planning on binary feature maps without relying on any label supervision or imitation.
- (3)
The hierarchical planning framework solves the problem that a single ANN-based planner only adapts to specifically sized maps.
The remainder of this paper is organized as follows. The related work is reviewed in
Section 2.
Section 3 formulates the path planning problem in an end-to-end style.
Section 4 presents the learning-based planning methodology in detail, including the feature map, the hierarchical planning framework, and the SP-ResNet planner.
Section 5 explains the planning application of the method.
Section 6 illustrates the numerical results and analysis, and this is followed by an overall conclusion in
Section 7.
2. Related Work
Global path planning methods for long-range planetary roving can be generally divided into two categories, namely, the conventional searching-based methods as well as the learning-based methods.
Conventionally, given computable configuration spaces, such as the Voronoi diagrams or grid maps, the right path from the start point to the target can be solved by a wide range of searching algorithms, such as the A* [
8,
9], the SD*lite [
1], the RRT [
10,
11], and the ant colony algorithm [
12], etc. Various improvements have been made to these methods. For instance, surface constraints, such as the terrain slope, roughness, and illumination over the original DEM, were considered in the cost function of the A* algorithm, which improved the feasibility and usability of the planned paths [
19,
20]. YU X Q et al. [
21] introduced a safety heuristic function for the A* algorithm to raise the overall security of the planned paths in large-range lunar areas. Sutoh M et al. [
22] discussed the influence of rover motion forms and isolation conditions on the planned paths with Dijkstra’s algorithm. However, there are some shortcomings in the conventional path planning methods. For one thing, the path planning performance depends on configuration space interpretation, which partly relies on human experience. For another, these path planning methods are usually searching-based, meaning that the computation time increases exponentially with the increase in the size of the solution space and it, thus, cannot meet the requirements of long-range roving and complex obstacles, or when some time-varying factors, such as illumination, temperature, or communication, must be considered.
Learning-based methods have also been explored by the researchers for the global path planning of planetary roving. Wang J. et al. [
14] trained a deep learning-based path predictor using label paths generated by A* that could directly generate a probability distribution of the optimal path on an obstacle map. The distribution was used for the guidance of RRT-based final path planning, which significantly improved the path planning speed. In addition, the value iteration network (VIN) was applied to end-to-end path planning for the Mars remote images [
15]. Furthermore, a soft action policy was applied to generate a soft VIN that outperformed the standard VIN in terms of the path planning accuracy [
16]. Zhang J. et al. [
17] proposed an end-to-end planner based on deep reinforcement learning (DRL) that could directly solve the sequenced nodes of a safety path for Mars remote sensing imageries through the iterative application of the planner. It can be concluded that learning-based methods are preferable alternatives that can not only provide end-to-end planning directly from pixel images without the need for artificial computable configuration space representation, but they can also get rid of the problem that the planning time increases exponentially with the problem space size. Nevertheless, the current learning-based methods mainly employ artificial neural networks (ANNs) to build the planning policy, and hence have difficulty adapting to planning tasks on maps with various sizes due to the limitations of the specific network structures. It is really not advisable to plan on reshaped maps, since this may lead to a serious loss of accuracy and the impracticability of the planned path.
This work is devoted to proposing a novel learning-based planning method, which can remarkably improve the computing speed of global path planning for long-range planetary roving and, meanwhile, improve the previous learning-based methods’ poor adaptability to the maps of various sizes. An DRL-based path planner, employing double branches of residual networks, is built to directly plan on binary feature maps. Furthermore, a hierarchical planning framework is designed in pursuit of high planning speed and adaptability to arbitrarily sized maps. The method is able to plan faster than the baselines and is validated to be effective in planning tasks with real lunar terrain maps.
3. Problem Formulation
Generally, path planning is intended to solve a finite path from a start point to a target point on a map, with no collision with obstacles. For the development of a learning-based planning system, we further arranged the elements into the input and output of a step planner. For the global path planning based on the planetary DEM, the input consists of the current rover position, the target point, and the global map containing some form of environment information, which we call the feature map. The output refers to the best moving direction suggested by the planner at each step. For ease of understanding, some related elements should be further explicitly defined, as follows:
Step planner: An end-to-end planner designed based on ANNs, which suggests an optimal action for one step according to the rover position, the target position, and a specifically sized feature map.
Feature map: , an image representing distinguishable obstacle information.
Block: , a feature map with a specific size, e.g., , which is intercepted or deformed from , to be directly fed to the step planner for planning. Due to the fixed network architecture of the planner, the planner can only plan on a specifically sized map, which is why the block is introduced. The next section addresses the role that the block plays in adapting the end-to-end planner to maps with arbitrary sizes.
Start point: , the initial position of a planning task.
Target point: , the target position of a planning task.
Rover position: , rover position at the current step. is the step index.
Action: , one of the eight directions pointing to the surrounding grid points suggested by the step planner, based on which is updated.
Path: , the sequenced nodes determined by the planner. If is used to represent the obstacle area of the map, a safe path is attributed to .
4. Learning-Based Path Planning Methodology
4.1. Feature Map
The planetary DEM data include 3D elevation information for extraterrestrial surfaces that is not suitable for learning and planning with the ANNs. For feature reasoning and planning by the end-to-end planner, a kind of binary feature map with more distinguishable characteristics is constructed based on the local traversability analysis, including the terrain amplitude, slope, and illumination.
4.1.1. Traversability Analysis
(1) Terrain amplitude
The terrain amplitude, essentially referring to the local relative elevation, directly reflects the locations and shapes of the craters and highlands in the DEM. The terrain amplitude can be calculated with . represents the pixel coordinates, represents the elevation, and represents the local level. A terrain amplitude traversability map can be filled by if , and if . On the traversability map, 1 represents the traversable area, and 0 represents the untraversable area. represents the safety threshold of the terrain amplitude.
(2) Slope
It is preferable for planetary rovers to move on areas with gentle slopes. A 3 × 3 grid rolling window around
is created to determine the local slope, which can be calculated with:
where
represents the slope along the eight directions around
, and
,
, and
. A slope traversability map
can be constituted using
if
, and
if
.
is the safety threshold for the slopes, and
represents the DEM resolution.
(3) Illumination
Illumination is an essential condition for the rovers to maintain warmth and ample solar power. The accessibility of sunlight depends on the angle between the solar ray vector
and the normal vector of the local surface
. The angle can be quantitatively expressed with
The illumination is determined to be accessible only if
is larger than some threshold. An illumination traversability map
can be filled using
if
, and by
if
.
represents the safety threshold of
, and
.
can be calculated based on the 3 × 3 grid rolling window with:
4.1.2. Feature Map Calculation
Based on the traversability maps, operations are conducted with pixels, and a comprehensive feature map
is constructed; that is,
can be obtained with:
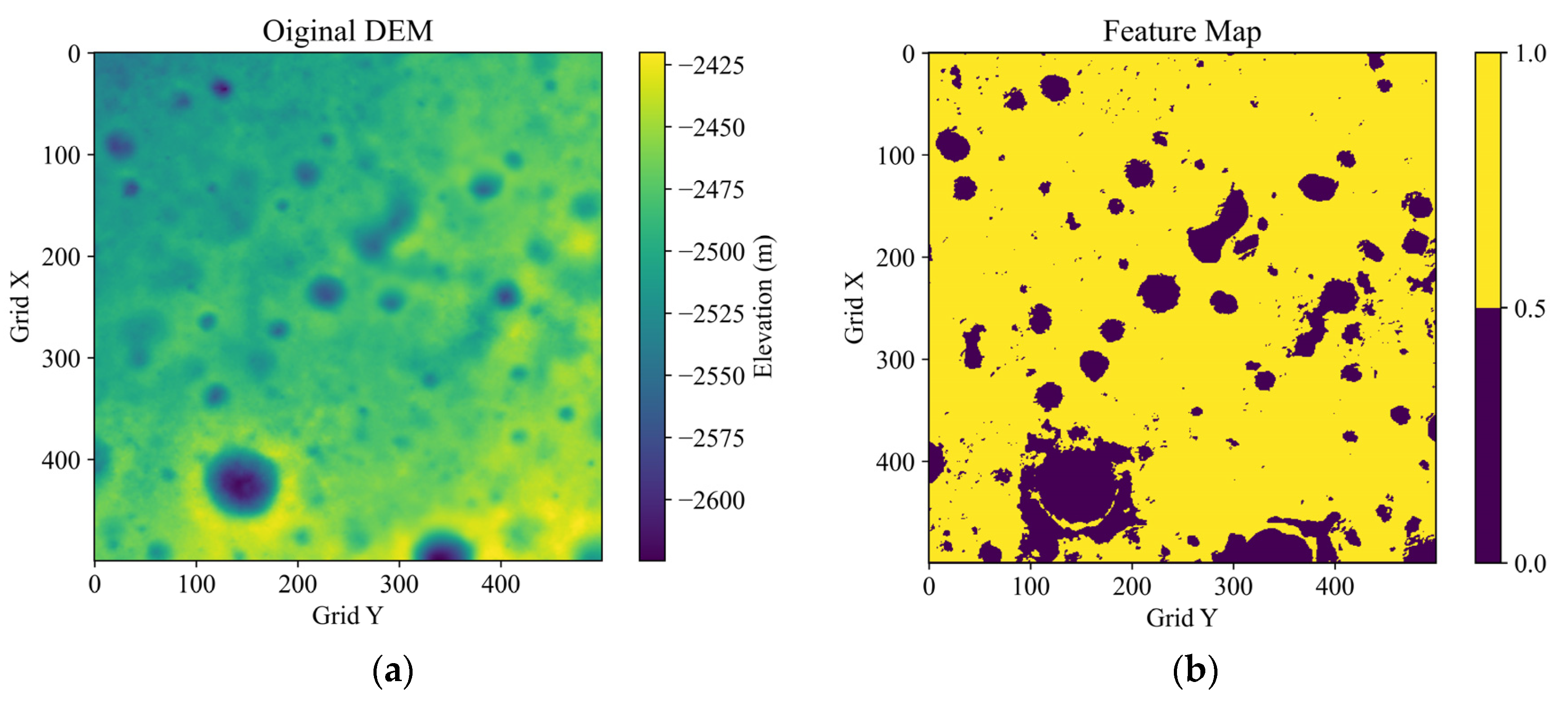
Figure 1 shows an example of the traversability maps and the added comprehensive feature map, which is based on a 10 × 10 km
2 DEM at the bottom of a crater near the south lunar pole from the CE2TMap2015. The thresholds are set as:
,
,
, and
. It can be seen that the feature map, with consideration of the topography and illumination traversability, conveys the obstacle areas in a more distinguishable way than the original DEM.
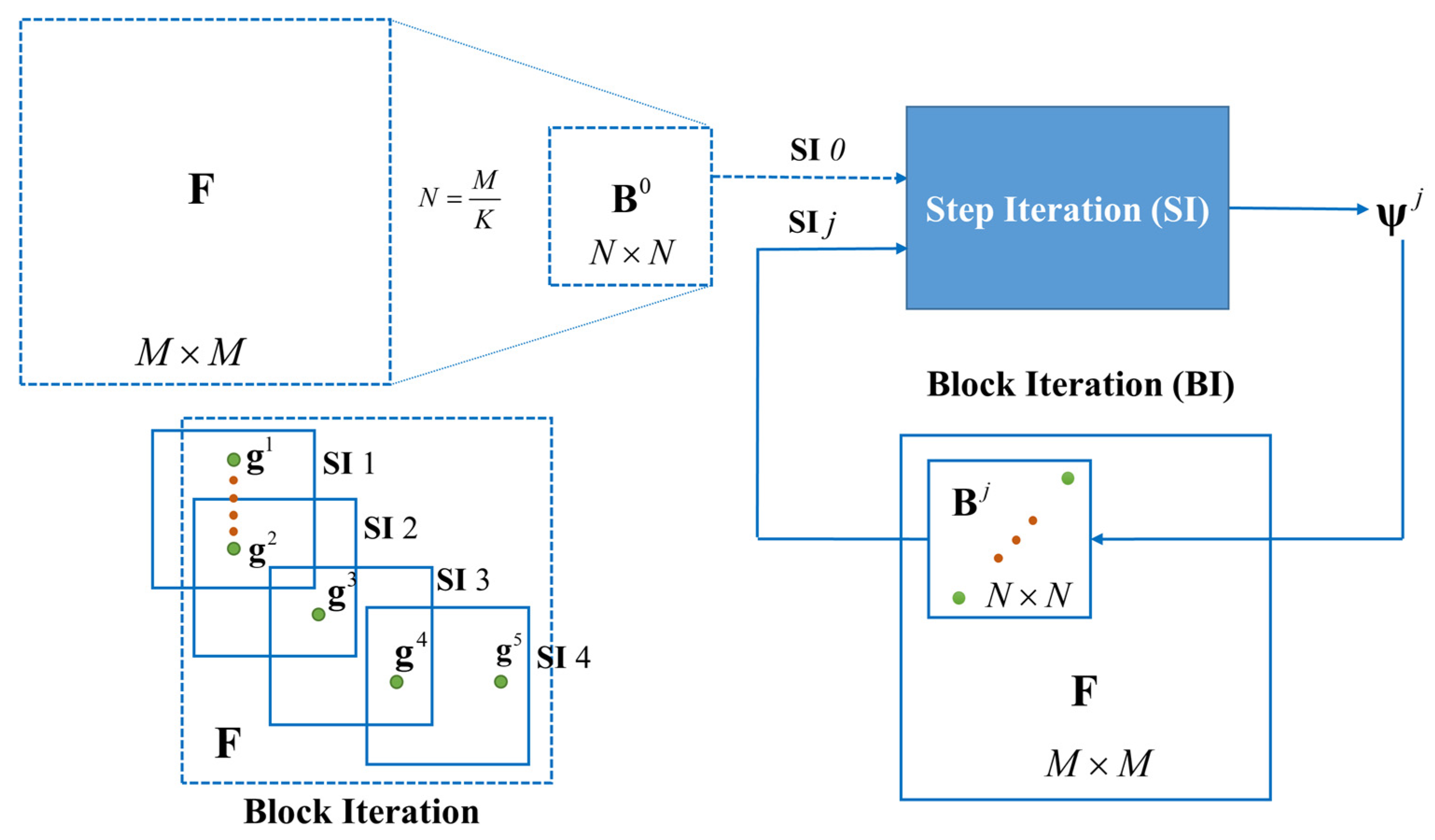
4.2. Hierarchical Planning Framework
Trying to cope with a planning task on a feature map with an arbitrary size directly based on an end-to-end planner does not work due to the defects of fixed network architectures. Even if the feature map could be deformed to match the planner input, a serious loss of accuracy and feasibility might occur. A hierarchical planning framework is designed to break through this defect, which divides the issue into two levels of iteration, namely, step iteration and block iteration. It should be noted that step iteration is carried out on the block with a size of , which matches the input of the end-to-end planner, while the block iteration is carried out on the original feature map with an arbitrary shape of .
4.2.1. Step Iteration
An end-to-end step planner is designed to solve the optimal moving action for the rover at the current step according to the input rover position , the target position , and the block map . Through the iterative application of the step planner, a complete path from the start point to the target point can be worked out, which is known as step iteration, or SI for short.
4.2.2. Block Iteration
Block iteration employs
SI to plan a segmented path using blocks on the original map along a rough initial path; that is to say, the planning is divided into two phases, including the initial rough planning and the accurate block planning, as shown by
Si and
SI in
Figure 2, respectively. The final path on a feature map with an arbitrary size is usually obtained by splicing the segmented paths that are planned on multiple blocks.
Given an original feature map
with a size of
, the map is first deformed into an
block
, for which an initial rough path is planned through
SI 0. The initial path is denoted by
, which can be calculated with:
where
represents the transformation ratio, and
indicates the initial path length. We use
to indicate the variables solved by
SI , and we use
to distinguish the variable for the block coordinate system.
Along
, a series of guide nodes
are determined that serve as the endpoints of the precise block planning of the second phase. The guide nodes are illustrated by
in
Figure 2.
is up to the length of the initial path by
. The guide nodes can be determined by:
Each block
is located using a pair of adjacent guide nodes
and
as follows:
where
indicates the center position of
. The segmented path on the block is then planned with
SI . The path coordinates for block
and the original feature map
F can be converted using the following formula:
4.3. SP-ResNet Planner
4.3.1. DRL Model
Step planning is based on DRL, which can be essentially modeled by the Markov decision process. At the
time step, the navigator observes a state
and selects an action
from the action set
. This decision is guided by the policy
, in which
represents the weights in the Q-network [
23]. Afterward, the agent reaches the next state
and obtains an instant reward
. The state-action value
is introduced as
and used to evaluate the current policy
, where
represents the expected cumulative sum of rewards, and
is a discount factor. The best action choice for the current policy is determined by
, according to:
As the agent learns from interacting experiences within the environment,
can be optimized using the Bellman equation:
The Q-network can then be trained by minimizing the loss function, which can be expressed as follows:
where
represents the weights in a target Q-network that are only updated for a specific number of steps [
24].
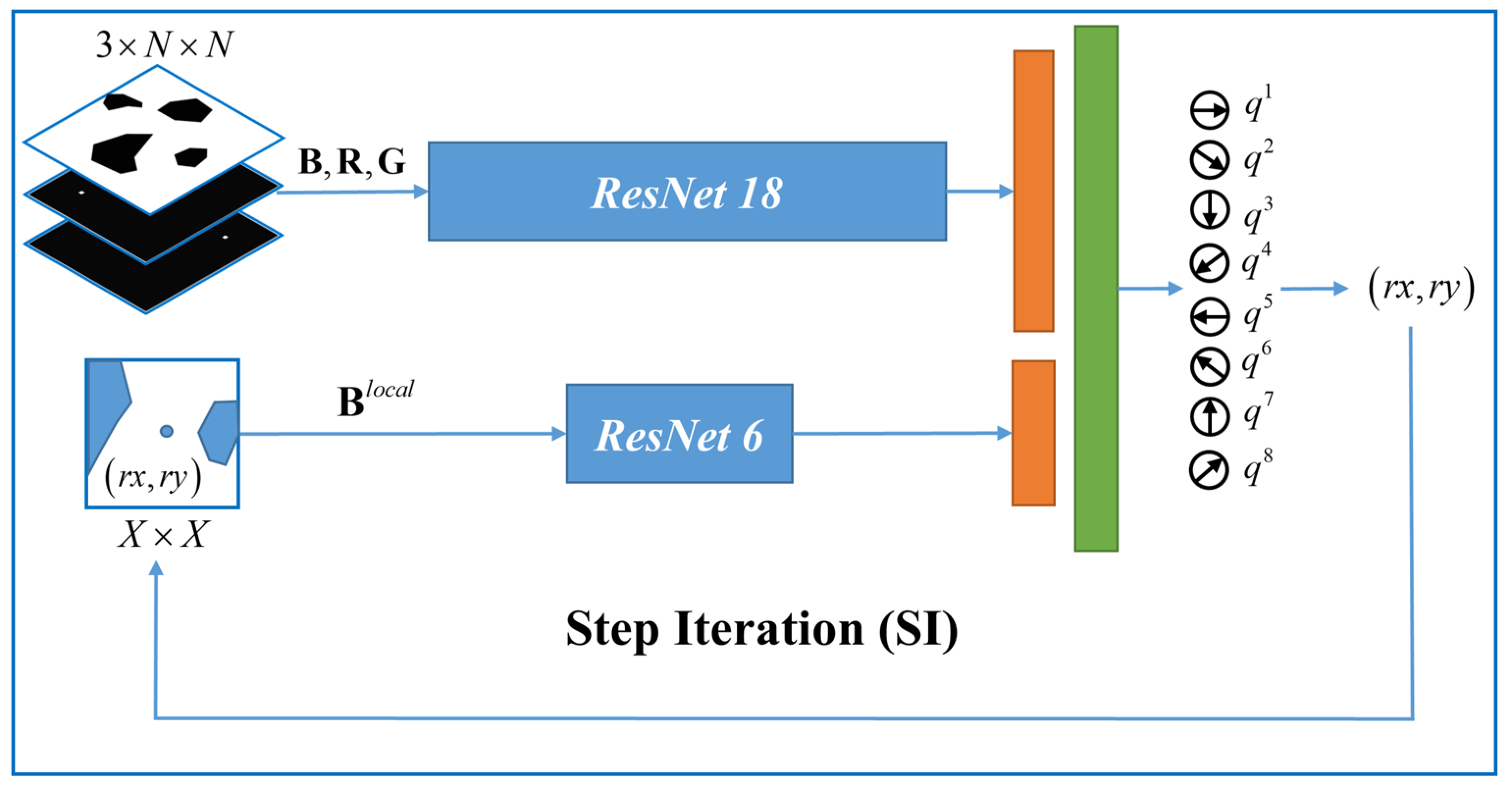
4.3.2. SP-ResNet Planner
The Q-network is the predominant learner as well as the planner for step planning, which determines features and holds the planning policy. We designed a novel Q-network consisting of double branches of residual networks [
25] for global and local obstacle abstraction, as shown in
Figure 3. The planner is named “the step planner based on ResNet”, or “SP-ResNet” for short.
The global branch employs ResNet18 to extract the global information, including
,
, and
. The block size is denoted by
. To provide a more direct spatial relationship for the rover position and the target position for the branch,
and
are marked on an
blank layer as a bright pixel. The added layers are denoted as
and
, individually. Therefore, the input of the global branch is arranged as a three-layered state cube with dimensions of
. The local branch employs ResNet6 to work on a local area around
on
, which contains three BasicBlocks. The local area is a matrix denoted as
, whose size is denoted by
.
can be obtained with:
The outputs of the two branches are fused through two fully connected layers for the value estimation of eight actions , which denote the motions in the eight directions. The optimal motion at each step can be planned using Equation (9).
4.3.3. Step Planning Iteration
It is important to specify how the SP-ResNet works in the step planning iteration. For each step,
,
R, and
are updated according to the current
, while the action selection is achieved by the one-time reasoning of the Q-network. The operation flow of the step iteration is summarized in
Table 1.
5. Training and Planning
5.1. Rewards for Training
In fact, it is hard work to train an ANN to learn image-based path planning without supervision or imitation [
18,
21]. A comprehensive reward strategy is designed for our SP-ResNet planner to help it to efficiently learn the behaviors required to approach the target, avoid obstacles, optimize the accumulated length, and smooth the path.
The reward for arrival is denoted as
. If the rover arrives at the target position,
, and the current episode is ended, while at other moments,
. The reward for a hazard is denoted by
. If the rover enters any hazard area, a penalty of −1 is given to
, and the current episode is ended; else,
. The hazard area can be classified by
. The reward for approaching
is designed as a linear function of the distance variance between
and
, denoted as
. If the rover approaches the target,
takes a positive value, while if the rover leaves the target, the value is negative. The reward for the energy cost
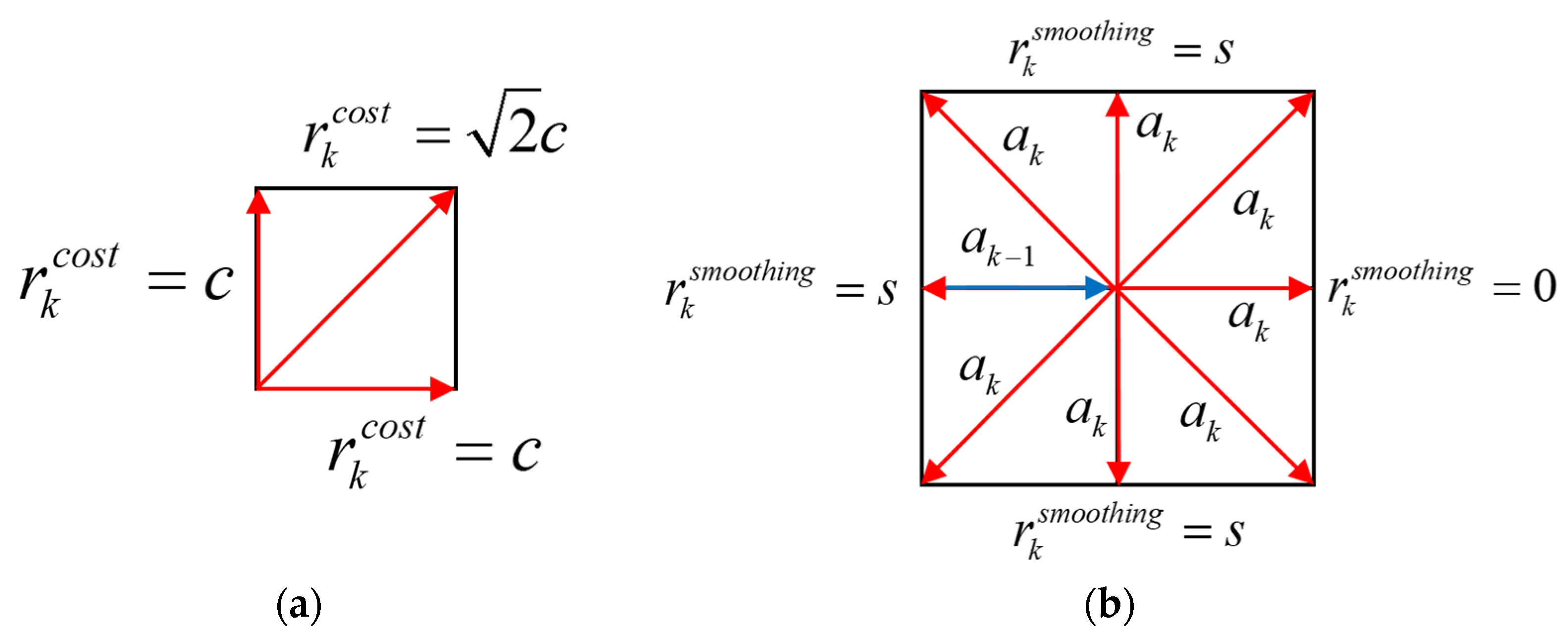
is introduced for the path length optimization, whose value is based on
. If
goes along the grid edge,
, but if
goes along the diagonal,
, where
stands for the energy cost per unit length. The reward for smoothing
can also be considered to be a turning cost for the rover whose value relies on the actions taken in adjacent moments. If
is along the same direction with
,
; else,
. The schematics of
and
are illustrated in
Figure 4. The final reward at the
step is obtained with the sum of the above rewards:
5.2. Planning Application
This sub-section introduces the application of our hierarchical framework to the SP-ResNet planner for path planning according to the specific operation flow, which is presented in
Table 2 in brief.
Task initialization: The start position , the target position , the original DEM for planning, and the map resolution are given;
Feature map acquisition: The feature map is constructed using traversability analysis;
Deformation: The original feature map is deformed into , and the transformation ratio can be determined with ;
Initial rough planning: The initial rough path on the size-reduced map is solved with SI 0, according to Equation (6);
Guide node determination: Along the initial path, a series of guide nodes is determined by Equation (7);
Precise planning: Precise block planning based on the guide nodes is conducted. First, the blocks are determined according to Equation (8); then, SI
is called to plan a fine path on
until
. The input of SI
j can be obtained with:
After this, the path on the block should be back-calculated into the original F coordinate system with Equation (8);
Path splicing: The segmented paths
. are spliced in sequence to form the final path on the original map, which can be expressed as follows:
6. Numerical Results and Analysis
6.1. Planner Training and Evaluation
6.1.1. Training Settings
Without loss of generality, an SP-ResNet planner is instantiated by
. and
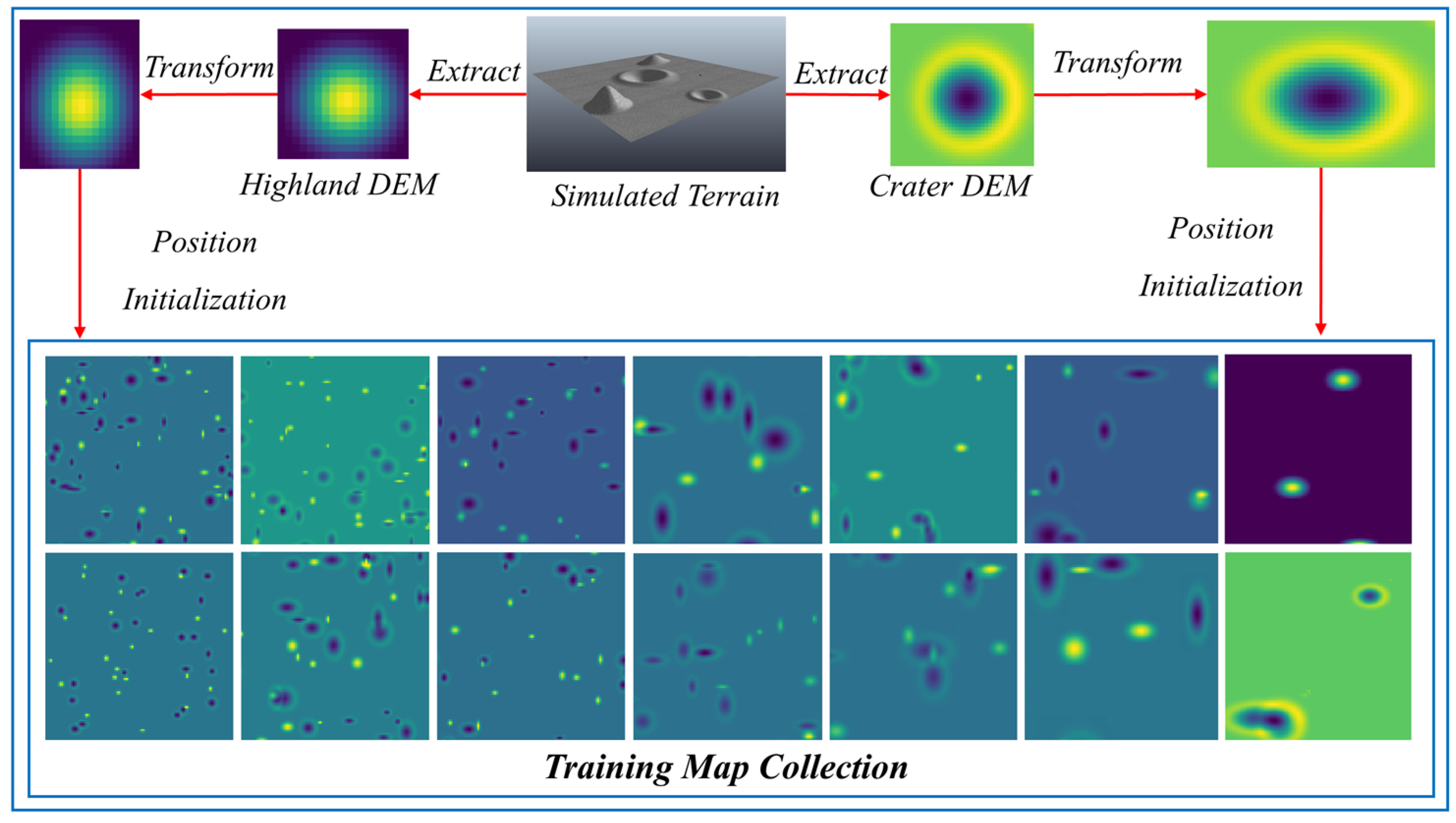
, which means that the planner plans on the 100 × 100 block and has a 10 × 10 input for the local branch. To meet the application of block iteration, the planner needs to adapt to various scaled obstacles, although the block size is unified. The planner is trained on a map collection containing 10,000 frames of 100 × 100 blocks, each of which contains obstacles with random quantities and various scales.
Figure 5 illustrates the constitution of the training map collection based on the simulated DEMs of craters and highlands.
At the beginning of each training episode, the start position and the target position are randomly initialized. Experiences in the form of
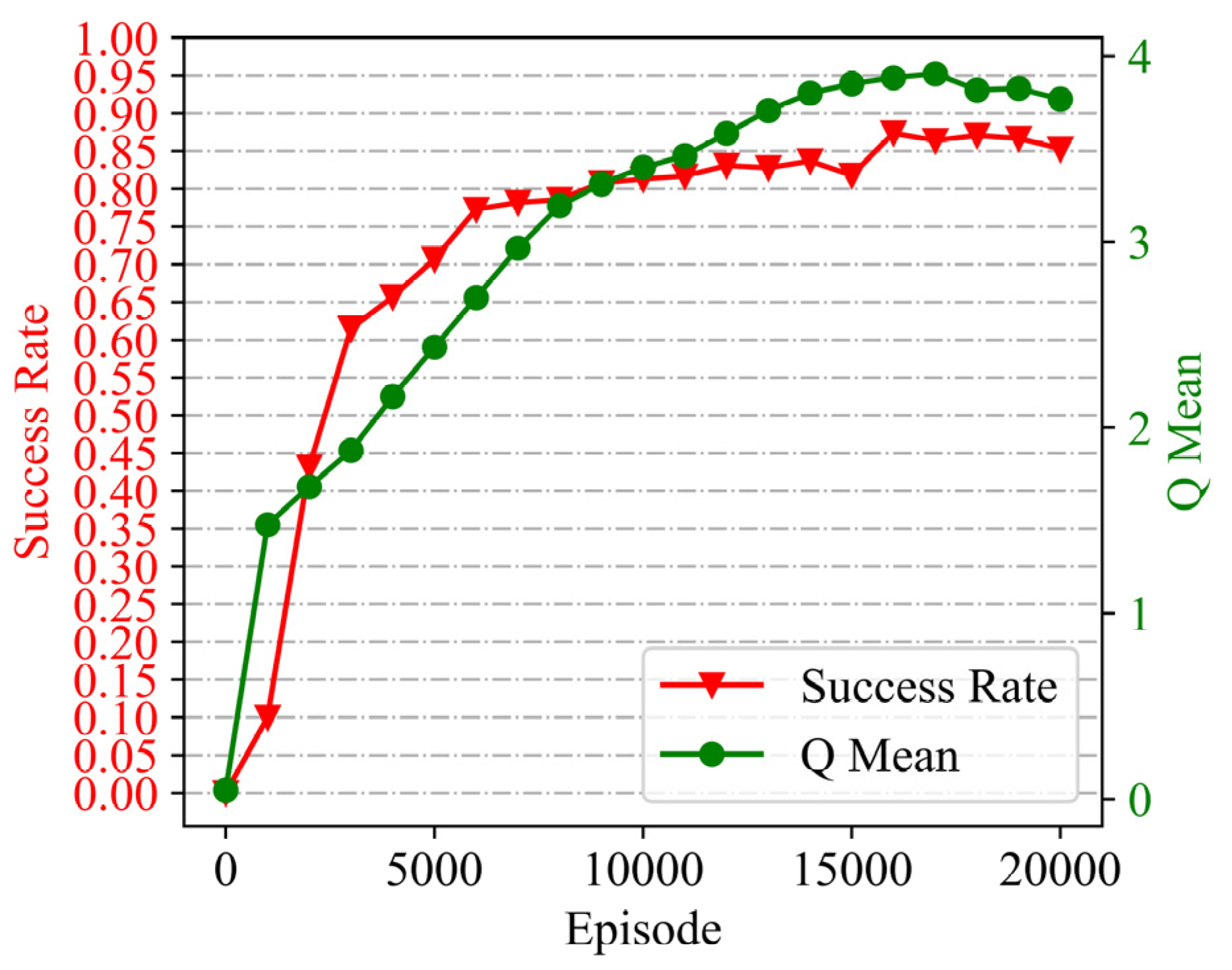
are collected according to Equation (9) for each step, and the loss function in Equation (11) is optimized by an Adam optimizer. Finally, we managed to train the planner with a final planning success rate of 85% for the map collection (over 20,000 episodes for about 48 h), as shown by the training curves in
Figure 6.
6.1.2. Visualized Evaluation of the Block Planner
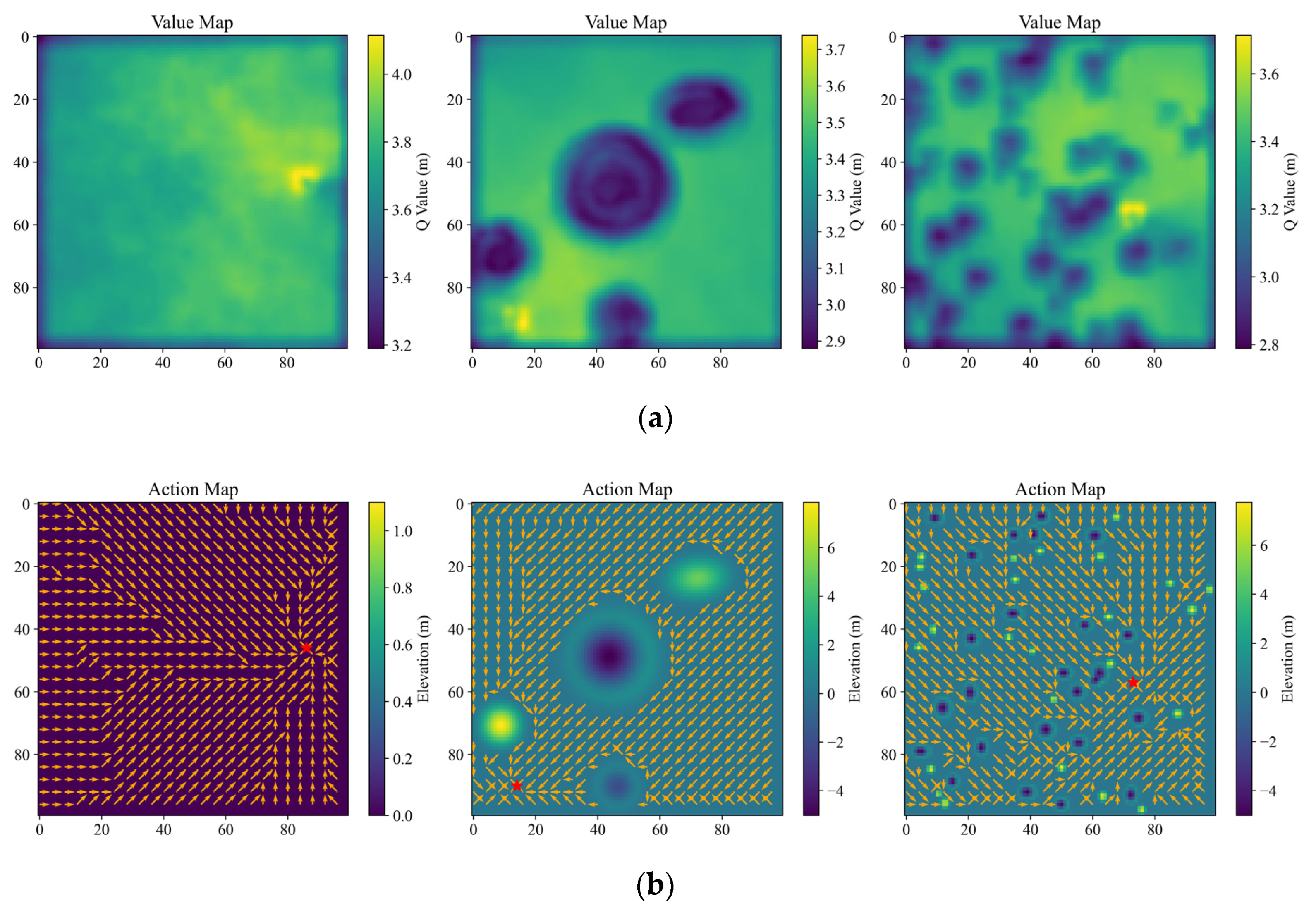
(1) Value map
A value map displaying the state value of the pixels all over the map in color mapping is an effective way to visually evaluate the learning-based planning methods [
19,
21]. With the trained SP-ResNet, the value maps in three cases are plotted, as shown in
Figure 7a, including a map with flat terrain, a local perspective map with large-scale obstacles, and a global perspective map with small-scale obstacles. It should be noted that the SP-ResNet planner can clearly distinguish between the obstacles, safety areas, and target positions in all three cases.
(2) Action map
Furthermore, a type of action map is drawn to directly look over the planned motion all around the original map. On the action map, for a given target position, the best motion direction at each pixel is planned and marked by arrows.
Figure 7b depicts the action maps of the previous three cases. The figure shows that the SP-ResNet can identify the optimal motion direction at almost all traversable positions, though for some minor areas, the planned results are suboptimal, indicating that the training is effective and reliable. It should be noted that the original maps for visualized evaluation in the three cases are beyond the training collection. With the end-to-end mechanism, the value map and the action map can be solved by one instance of network reasoning in a batch.
6.2. Comparative Analysis with Baselines
This section compares the learning-based method with the baselines, namely A*, RRT, and Gb-RRT, for the metrics of planning time consumption and path length. A* has been provided with complete theoretical proofs to find the optimal path, if it exists [
8], which serves as the basic basis for the comparative analysis. Gb-RRT is an efficient method based on the heuristic mechanism of goal-biasing growth, which greatly improves the planning speed of RRT [
18]. The planning methods involved are tested on several 500 × 500 m
2 maps. The SP-ResNet is applied following the hierarchical planning framework. A* adopts an action space of eight motions toward eight directions, which is the same as the SP-ResNet planner. The RRT and Gb-RRT methods take a constant step size of one grid (1.0 m), and the Gb-RRT adopts a classical target biasing probability of 0.05.
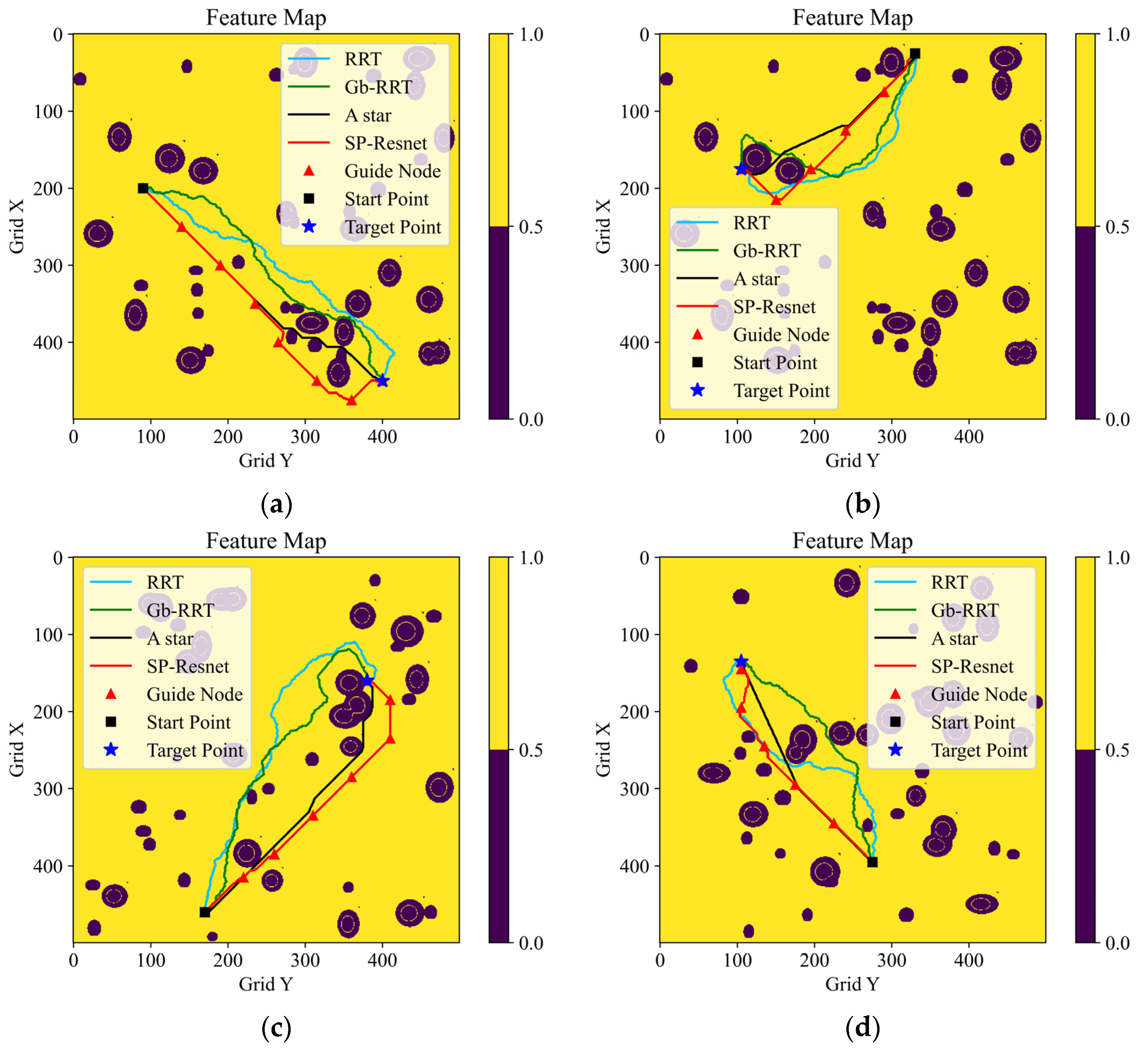
Figure 8 depicts the results of four planning tests, in which the planning methods are distinguished by color. Intuitively, the quality of the path planned with our method is close to the quality of the A* algorithm, and is apparently better than that of the RRT series algorithms.
The planning time costs and the final path lengths of the four methods are presented in
Table 3. It can be seen that our learning-based method performs the best in terms of the planning speed among the baselines, whose planning time consumptions are less than half of the A*. Moreover, longitudinal comparisons demonstrate that the longer the path is, the greater the advantage of computational efficiency our end-to-end method has. As we expected, however, the final paths generated by the learning-based method are always partly greater than those by A*. Due to the strong randomness of the RRT series algorithm, the time costs and the path lengths of RRT and Gb-RRT are statistically averaged over 20 repeated planning instances. It can be noted that the Gb-RRT’s planning speed is very unstable, although on some occasions it can nearly match that of our method. In addition, the paths created by the RRT series algorithm are significantly longer than those of the end-to-end algorithm. It can be concluded that the method based on the hierarchical planning framework and the SP-ResNet planner has the advantages of a rapid planning speed and robust stability, which makes it better suited for scenarios with long-range maneuvers and complex environments. The above planning tests are run on a platform of Intel Core i9 with a CPU @2.40 GHz (32 GB) and NVIDIA GeForce RTX 2080 Super with Max-Q Design (8G).
6.3. Tests with CE2TMap2015
The feasibility and the effect of our planning method were evaluated using the real lunar terrain data in CE2TMap2015 [
5]. Two 20 m/pixel areas were selected as the test maps, as shown in
Figure 9. For each of these maps, several path planning tests were conducted to validate our SP-ResNet planner and the hierarchical planning framework, as shown in
Figure 10. Map 1 is a 10 × 10 km
2 area in the east of the Sinus Iridum area that is relatively flat overall, and there are a few craters. Map 2 is a 10 × 10 km
2 area at the bottom of a crater near the south pole that is covered by dense craters and highlands.
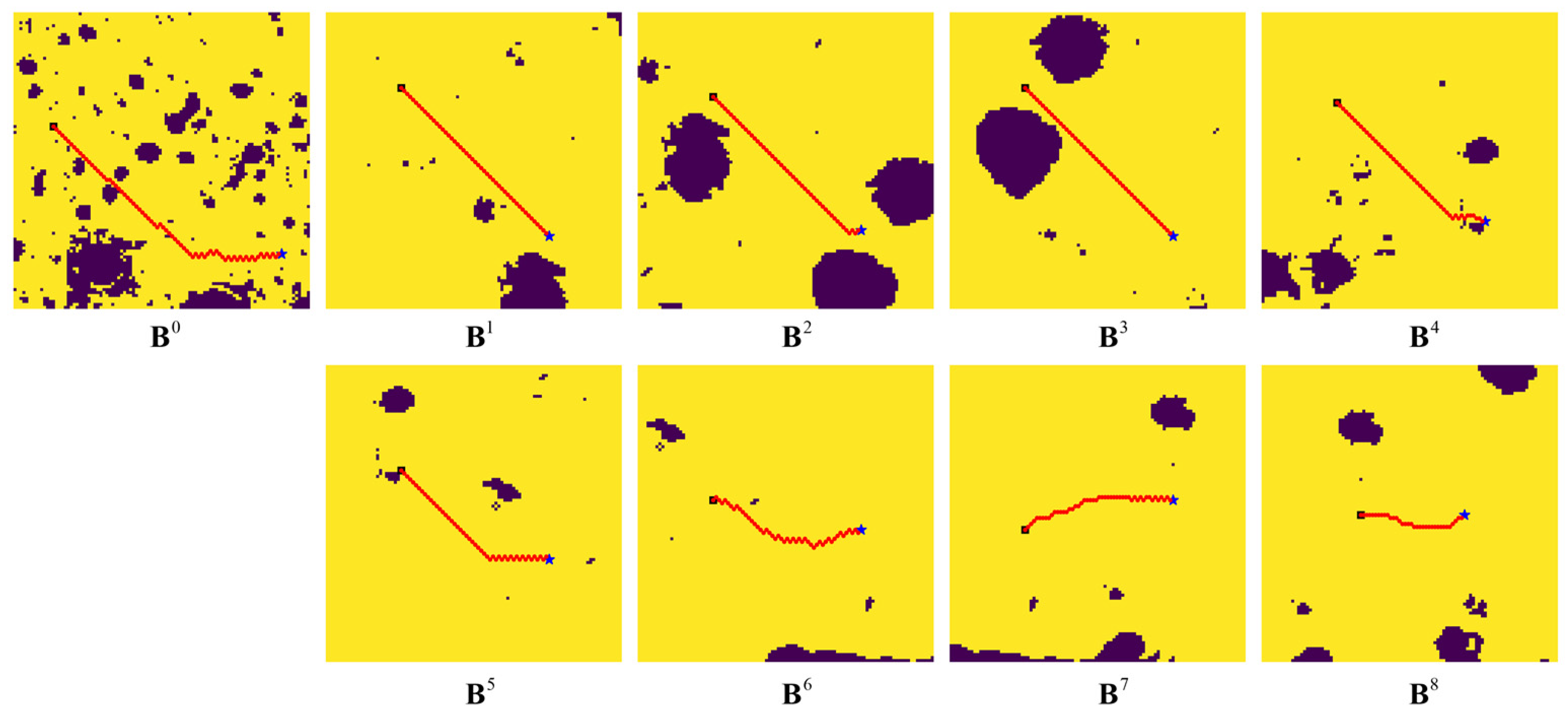
Figure 11 depicts the results planned by blocks during the implementation process of a planning task on Map 2, in which
shows the initial rough path on the size-reduced map, and
–
shows the path planning results for the blocks along the initial path. In the visualized results in
Figure 10 and
Figure 11, the blue stars indicate the start points, the black cube indicates the target points, and the guide points are marked by red triangles.
It can be seen from the above test results that the SP-ResNet planner performs well for the real lunar natural terrain, whether it is deformed from an original feature map with small-scale obstacles or from a precise block with large-scale obstacles, though the planner is trained using a map collection of simulated terrains. It can also be concluded that the hierarchical planning framework is effective for long-range path planning on lunar surfaces.
7. Conclusions
It is of great significance to improve the computational efficiency of planetary roving path planning, especially for the cases of long-range maneuvers or obstacle constraints that are time-varied, such as illumination. This research is devoted to investigating a novel learning-based global path planning method that can plan a safe path directly using a binary feature map in a fast and stable way. A binary feature map is constructed based on topography and illumination traversability analyses. A hierarchical planning framework containing step iteration and block iteration is designed that not only breaks through the defect of the poor adaptability of ANN-based methods, but also improves the planning speed. A step planner is constituted based on DRL, which determines features and plans paths through a double-branch ResNet. The step planner is trained with a map collection based on simulated terrains, achieving a final planning success rate of 85%. Then, both a value map and an action map are generated to validate the step planner’s ability of feature abstracting and path planning. Comparative analyses with A*, RRT, and Gb-RRT for long-range planning tasks demonstrate the prominent planning speed and stability of our method. Finally, the proposed learning-based planning system is verified to be effective on real lunar terrains using CE2TMap2015.
The study is an important attempt to improve the path planning efficiency in long-range extraterrestrial roving based on a learning method. The performance of the involved planning system may be further improved in several ways. In fact, the reward and sampling mechanisms need further investigation to improve the optimality of the SP-ResNet planner, which seems to still have a certain gap from A*. In addition, DRL algorithms for continuous action space can be introduced into the planner constitution to produce smoother paths.