Abstract
We study noise generation at the blade tips of propellers designed for future electric aircraft propulsion and, furthermore, analyze the interrelationship between noise mitigation and aerodynamics improvement in terms of propeller geometric designs. Classical propellers with three or six blades and a conceptual propeller with three joined dual-blades are compared to understand the effects of blade tip vortices on the noise generation and aerodynamics. The dual blade of the conceptual propeller is constructed by joining the tips of two sub-blades. These propellers are designed to operate under the same freestream flow conditions and similar electric power consumption. The Improved Delayed Detached Eddy Simulation (IDDES) is adopted for the flow simulation to identify high-resolution time-dependent noise sources around the blade tips. The acoustic computations use a time-domain method based on the convective Ffowcs Williams–Hawkings (FW-H) equation. The thrust of the 3-blade conceptual propeller is larger than the 3-blade classical propeller and more than the 6-blade one, given that they have similar efficiencies. Blade tip vortices are found emitting broadband noise. Since the classical and conceptual 3-blade propellers have different geometries, especially at the blade tips, they introduce deviations in the vortex development. However, the differences are small regarding the broadband noise generation. As compared to the 6-blade classical propeller, both 3-blade propellers produce much larger noise. The reason is that the increased number of blades leads to the reduced strength of tip vortices. The findings indicate that the noise mitigation through the modification of the blade design and number can be traded-off by the changed aerodynamic performance.
1. Introduction
In order to meet more stringent requirements on fuel consumption and pollution emissions [,], electrification has increasingly attracted attention across the aeronautical industry. In particular, the tremendous success of electric cars has greatly enhanced public confidence in extensive applications of the electrification concept to aviation, which recently led to the advent of massive electric airplanes. The usages of electrified propulsion architectures enable electric aircraft to achieve zero emissions, additionally lowering the operation costs []. On top of that, electrification also allows innovative concepts of airplanes being infeasible due to some intrinsic limitations of conventional propulsion architectures. Needless to say, the move to more electric propulsion systems would ultimately spark a revolution in the aeronautical industry.
Currently, the development of electric aircraft is mainly focused on short-haul flights. In this category, propellers connected to electric motors have been regarded as the most effective propulsion systems, just as turboprop-driven aircraft widely used in regional airliners. Moreover, the rotational motion of propellers to generate thrust is naturally aligned with electric motors to output power. This has further expanded the popularization of propellers for electric aircraft. Consequently, advanced propeller design has become one of the core technologies to be explored for electric aircraft in order to achieve excellent overall performance.
Among various design factors for an advanced propeller, the low-noise requirement is of great importance. Nowadays the expectations of more comfortable travel and low impacts on ground communities are increased for enter-into-service aircraft, particularly future electric airplanes operating at relatively low altitudes. For a propeller-driven electric aircraft, the propeller noise becomes relatively dominant in the absence of the primary perceived noise from turbomachinery, combustion chamber and high-speed jet existing in conventional gas turbo engines. Apparently, the mitigation of the radiated noise from propellers is the premise to design quieter electric aircraft [].
For a classical rotating blade, the associated aerodynamic noise sources can be found in Figure 1. As can be seen, the overall aerodynamic noise is classified as discrete frequency (tonal) and broadband noise. The tonal noise is mainly associated with periodic aerodynamic loading that is imposed on blade surfaces, whereas the broadband noise is primarily generated from turbulence. The sources of the loading and thickness noise are formulated from surface pressure fluctuations and surface normal velocity [,]. Although a noticeable part of the loading and thickness noise is tonal, another part is broadband noise, the sources of which are flow separation and turbulence near the blade surface []. Moreover, tip vortices can also generate tonal noise at specific conditions, for example, blade–vortex interaction (BVI) [] or gap turbulence and blade interaction []. A dual-blade concept, termed Boxprop was proposed by Richard and Lundbladh [] and has recently been studied in terms of its aerodynamics and noise generation []. The dual-blade is designed by joining the tips of two sub-blades. The blade tip of this concept is apparently different from classical single blade tips. On the other hand, the effects of the new tip geometry on the noise generation have not yet been clear in terms of possible differences compared to classical propellers.

Figure 1.
Sources of the aerodynamic noise from a rotating blade, reproduced from []. The sources in the colorful boxes are usually predominant, and the one in the red box is the focus in this paper. Note that the loading and thickness noise can also be related to part of the broadband noise if flow separation or turbulence near the blade exists. Moreover, tip vortices can generate tonal noise under certain conditions, e.g., BVI.
The noise generation caused by tip vortices was also found for counter-rotating propellers []. The mechanisms are that tip vortices shed from the blades of the upstream propeller interact with the blades of the downstream propeller and the interaction is essentially the source of the tonal noise. In that study, the effects of the spiral tip vortices were modelled in two ways and the direct modelling of the vortices was found more accurate. In the study of Elson [], the tip vortex noise is divided into two parts, namely the pure rotor noise and the interaction noise. Different rotor blade geometries were investigated using the Reynolds-Averaged Navier–Stokes equations (RANS) and Particle Image Velocimetry (PIV). The tip vortex effects were parameterized to analyze the effects on the noise generation.
A major contributor to the helicopter BVI noise is blade-tip vortices []. Based on the vorticity computed using RANS, Zhao et al. modelled the spiral tip vortices using a viscous wake model. The vortices were then treated as noise sources and input into the Ffowcs Williams and Hawkings (FW-H) equation [] to predict the noise. More specifically, one of the formulations from the family of the FW-H equation, Formulation 1A of Farassat [], was used. It was found that the interaction angle is important in determining the noise intensity and propagation direction.
The spiral blade-tip vortex development was studied for a typical multicopter drone propeller subjected to inflow angles from 0 to 180 []. The isolated propeller has two blades and the diameter is 0.46 m. The numerical methods such as a blade element momentum theoretical approach, free wake method and unsteady RANS were compared to evaluate their accuracy in the aerodynamics evaluation. Moreover, PIV measurements were conducted to validate the numerical results. The effects of the non-axial inflow (the angle above 0) on the aerodynamics were addressed. A DJI Phantom 2 stock propeller with two blades was modified by notching the trailing edge near the blade tips []. Noise measurements in an anechoic chamber showed that the modified propeller produced similar noise levels in the far field, while a tone at 50 Hz was present due to the notch.
Reduction of propeller tonal noise can be achieved by improving the blade geometric parameters (e.g., chord length and pitch angle distribution), tip speed and blade number, as the forces on the blade surface contributing to the noise generation are adjusted [,]. Spacing blades asymmetrically in the circumferential direction has been shown to reduce the tonal noise over a wide range of frequencies []. This effect has been confirmed, for example, by experiments []. The blade tip speed determines the optimal spacing angle, according to a theoretical approach and experiments by Dobrzynski []. In recent developments for drone propellers, the noise has been reduced with additional bio-inspired micro structures. In the work by Noda et al. [], a serrated Gurney flap consisting of an array of small cylinders was attached onto the blade trailing edge. Inspired by owl feathers, a comb-shaped serrated structure was added to the blade leading edge []. A variety of shapes and geometric parameters of the leading edge serration were discussed by Wei et al. [].
This paper aims at investigating the noise generated from the vortices that are developed at the blade tips of three different propellers for short-range electric aircraft. The analysis will focus on the blade tip geometry and the number of blades, that is, three- and six-blade propellers. The interrelations between tip vortex development and noise generation will be exploited. The aerodynamic performance and noise emission will be addressed with respect to the propeller geometry differences, to understand the trade-off between the aerodynamic benefits and noise mitigation.
2. Numerical Methodology
2.1. Genetic Algorithm-Based Optimization Platform
In order to evaluate the effects of the blade geometry on tip-vortex generation and induced broadband noise, three propellers are designed and then optimized using a optimization platform that is developed based on the genetic algorithm []. It is worth noting that this optimization platform is a generic propeller design program, so it is applicable to both conceptual and classical propeller design. The initial geometries of the classical propellers are input from our previous study [].
Figure 2 illustrates the implementation process for optimizing the propeller on the optimization platform. First of all, a set of initial samples of parameterized blades are generated using the Latin Hypercube Sampling technique. The sampling goes through the variation range of each design parameter, including the stacking line and sectional airfoil parameters. Afterwards, the optimization loop iterates until a Pareto Front of the objective functions (i.e., the thrust and efficiency) is established. Finally, the optimized blade is down-selected from the established Pareto Front for a given thrust with optimal efficiency in general.
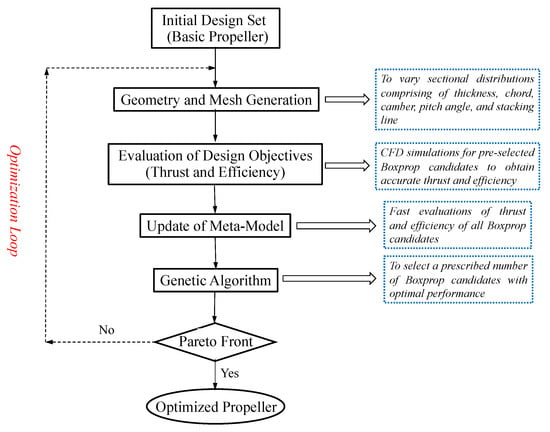
Figure 2.
The flow chart of the optimization platform [].
During every loop, a Meta-Model is constructed and updated to build the implicit links between the design parameters and the objective functions. The Meta-Model serves to quickly evaluate the objective functions for the newly generated configurations. A prescribed percentage of the total number of new candidates is selected on the basis of the genetic algorithm. Then, the candidates are simulated using the computational fluid dynamics (CFD) method, the Reynolds-averaged Navier–Stokes equations (RANS), to obtain more accurate objective functions at every loop. The data from CFD are used to establish the Pareto Front and update the Meta-Model. Detailed descriptions of the functions of the individual modules of the optimization platform can be found in [,].
2.2. Hybrid Computational Aeroacoustics
To perform aeroacoustic analysis, a hybrid computational aeroacoustics (CAA) method is applied. This numerical method consists of two steps: the first one is to identify noise sources through experiments or CFD simulations; an acoustic solver is then executed to compute sound propagation and acoustic levels in the field far away from the known noise sources. The hybrid CAA has neglected the effects of sound on flow. In the present study, the acoustic solver is developed based on the convected FW-H equation reported in [], described as
In the above equation, we have
and
where denotes the surface of a rigid body or a permeable surface with the unit outward normal . The coefficient is the subsonic constant freestream Mach number and is the acoustic pressure perceived at the location and the time instant t. The variables p and represent the local flow pressure and density. In addition, , and stand for the normal velocities of the local flow, the free-stream flow and the integral surface of , respectively. The coefficients and are the density and sound of speed in the free stream. The variable denotes the compressible stress tensor. and are the Dirac delta function and the Heaviside function, respectively.
The propagation of the sound from sources with arbitrary motions in subsonic constant free-stream flow is expressed in Equation (1). By adopting a permeable surface away from the solid body walls, this equation is capable of including the contributions of dominant quadruple sources that are located within this permeable surface []. The quadruple sources outside the permeable surface are neglected due to their minor contributions. The usage of the permeable surface enables one to account for all the noise sources by means of pure surface integration, which increases the computational efficiency. Furthermore, the convention effects of the free-stream flow in an arbitrary direction are explicitly taken into account. The analytical solution of Equation (1) in the time domain derived by Ghorbaniasl and Lacor in [] is numerically implemented in this study.
3. Design and Optimization of Propellers
The optimization platform mentioned above is applied to designing the classical propellers with 3 or 6 blades, termed Conprop-3 and Conprop-6 and the conceptual propeller with 3 dual-blades, termed Boxprop. The 3D geometries of these propellers are illustrated in Figure 3. Table 1 outlines the primary geometrical and operational parameters that are set to design these propellers. The thrust coefficient is the objective variable of the optimization. To avoid repetition, the elaborate derivation of the thrust coefficient refers to [].

Figure 3.
From left to right: Conprop-6, Conprop-3 and Boxprop.

Table 1.
The primary parameters targeted to achieve in the design of the propellers.
To execute the optimization program, the propeller blade geometry needs to be first parameterized. The parameterization is performed in terms of the stacking line and the airfoil geometric parameters. Figure 4 shows the sectional distributions of the parameters for the two classical propellers, Conprop-3 and -6. Here the ideal lift coefficient is defined at the angle of attack with the minimum drag coefficient. The distributions are defined based on Bézier’s curves.
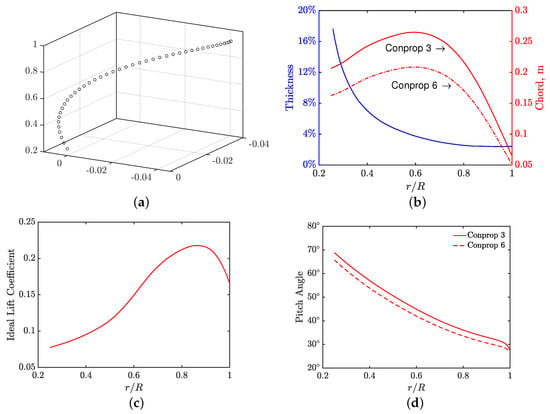
Figure 4.
The sectional distributions of the classical propellers, Conprop-3 and Conprop-6: (a) the stacking line, (b) the chord and thickness, (c) the ideal lift coefficient and (d) the pitch angle.
The underlying motivation to choose two classical propellers with 3 and 6 blades is that quantifying the equivalence between the dual-blade and the single blade is not obvious in terms of the number of blades. In fact, a dual-blade is composed of 2 sub-blades with their tips joined. This means that the present Boxprop propeller possessing 3-dual blades contains 6 sub-blades in total. We therefore believe that Boxprop should be assessed in comparison with classical propellers with either 3 or 6 blades. In Figure 4, the difference of the chord distribution between Conprop-3 and -6 is attributed to the activity factor and mechanical safety. In the initial settings for the propeller generation, the same activity factor is defined for both propellers. However, this leads to a too large chord length distribution for a propeller with 3 blades, which exceeds the limits prescribed to ensure structure mechanical safety. The chord length distribution for the 3-blade propeller is therefore reduced and, meanwhile, the pitch angle distribution is increased to achieve the required thrust (see Figure 4b). The camber distribution is quantified using the ideal lift coefficient.
Using the same design method for Conprop-3 and -6, the Boxprop blade geometry is also parameterized in terms of the stacking line and sectional airfoil parameters, as shown in Figure 5. Each dual-blade consists of leading and trailing sub-blades. The stacking lines of the sub-blades are defined with 3D Bézier’s curves. The NACA 16 airfoil is utilized in the sectional geometry. The airfoil parameters are the thickness, chord, camber and angle of attack (AOA). These parameters are represented by 4th-order 2D Bézier curves varying with respect to the radius of the leading or trailing sub-blade. The camber is expressed as the function of the lift coefficient.
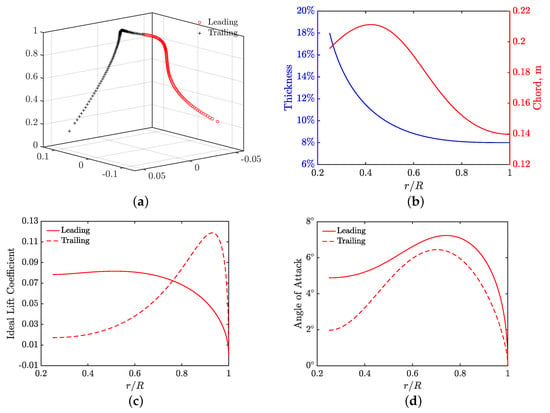
Figure 5.
The sectional distributions of the parameters of the Boxprop dual-blade consisting of the leading and trailing sub-blades: (a) the stacking line, (b) the chord and thickness, (c) the ideal lift coefficient and (d) AOA as the sum of the pitch and helix angles.
Note that in the parameterization of the Boxprop blade, AOA instead of the pitch angle is considered. The pitch angle is the sum of the AOA and helix angle. The helix angle is dependent on the cruise Mach number and rotation speed and presents a linear decrease against the radial distance. Therefore, it is equivalent in the adjustments between the AOA and pitch angle. The parameterization of Conprop-3 and -6 chooses the pitch angle, whereas Boxprop selects the AOA. This difference is inherited from the definition of the initial geometries at the start of the optimization.
It should be added that all the geometrical parameters mentioned above can be chosen as design variables on the optimization platform. However, in the present study, only the pitch angle and AOA have been selected for Conprop-3/6 and Boxprop in consideration of the computational costs and the scope of the present study.
In the process of the optimization, the technique of Multiple Reference Frame (MRF) is employed to perform steady flow simulations using the Reynolds-averaged Navier–Stokes equations (RANS). The SST turbulence model is applied. Figure 6 displays the computational domain set for the MRF. The domain consists of two zones, i.e., stationary and rotating. The radius of the propeller is denoted by R. Only one single passage is considered in the simulation in light of the periodic flow in the circumferential direction.
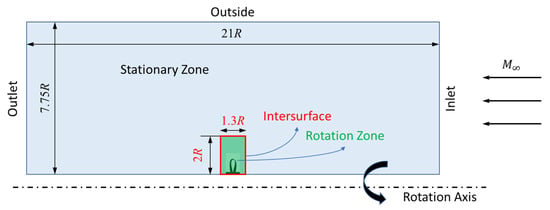
Figure 6.
The computational domain in the simulation of the configuration samples in the optimization, where R stands for the radius of the propeller.
Regarding the boundary conditions, the total pressure, total temperature, turbulence intensity and the flow speed normal to the boundary are prescribed at the inlet. The static pressure boundary condition is set at the outlet. The free-stream boundary condition is imposed at the side boundary. The no-slip condition is set on the propeller blade surface. The periodic boundary condition is set at the boundaries encasing the flow passage. Between the rotating and stationary zones, an interface is set to communicate flow quantities.
Figure 7 shows surface and volume cells of the meshes generated for Conprop-6 and Boxprop. As the blade geometries of Conprop-3 and -6 are overall similar, the meshes for them are comparable. The mesh for Conprop-3 is not shown for brevity. The mesh generation method and mesh cell parameters are the same as the previous study []. There are million cells in the meshes for Conprop-3 and Conprop-6 and million for Boxprop. A specific refinement of cell sizes is made near the blade tip to resolve well vortices developed from the tip, as shown in Figure 7c,d. A mesh indecency study was conducted to validate the current mesh resolution, which is not presented here for brevity.
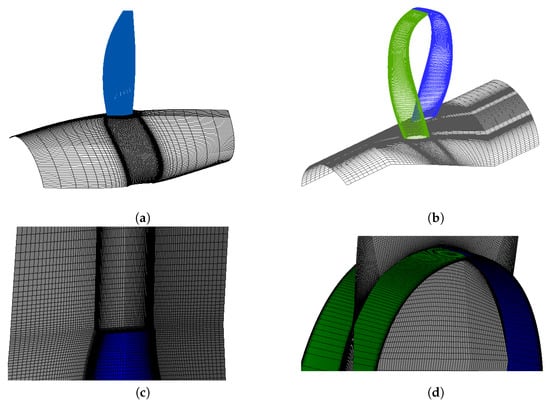
Figure 7.
Surface cells of the meshes for (a) Conprop-6 and (b) Boxprop. Volume and surface cells near the blade tip for (c) Conprop-6 and (d) Boxprop.
As introduced in Section 2.1, the Pareto Front is established based on the objective variables, i.e., the thrust coefficient and propeller efficiency that are obtained from the CFD simulations, after executing the optimization platform. Figure 8 shows the respective Pareto Front of the propellers. Then, the optimized propellers are extracted, corresponding to the optimal efficiencies at the targeted thrust coefficient of (see the blue stars in the figure).
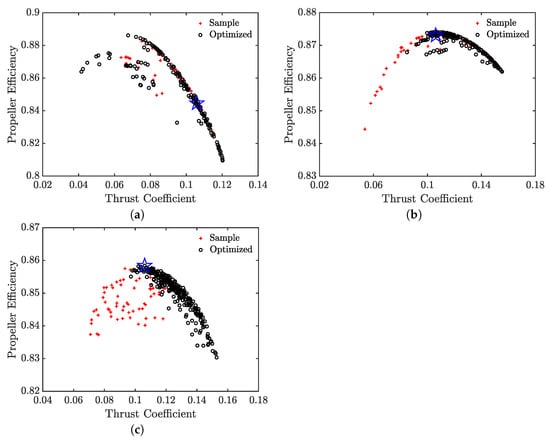
Figure 8.
The Pareto Fronts obtained from the optimization of (a) Conprop-3, (b) Conprop-6 and (c) Boxprop. Here the blue stars mark the points where the optimal configurations are extracted.
The aerodynamic performance parameters of the final selected optimal propellers, which are obtained from the RANS simulations during the optimization, are listed in Table 2. The thrust coefficient of Conprop-3 is . It is slightly smaller than of both Conprop-6 and Boxprop. The propeller efficiency of Conprop-3 is , which is smallest amongst the three optimal propellers. Despite that Conprop-6 and Boxprop possess the same thrust coefficient, the efficiency of Conprop-6 (0.873) is much larger than that of Boxprop (0.858). Nonetheless, these aerodynamic parameters are computed using RANS. It is known that RANS is relatively less accurate in comparison to advanced turbulence-resolved CFD methods such as the improved delayed detached eddy simulation (IDDES) or large eddy simulation. Moreover, accurate noise prediction based on the hybrid CAA methods also requires transient noise source data that need to be resolved in time. IDDES is therefore chosen in the subsequent sections for the further high-fidelity validation of the propeller performance and the prediction of the noise, especially for vortices developed from the blade tip.

Table 2.
The aerodynamic performance of the down-selected optimal propellers, obtained from the preliminary prediction using RANS in the optimization.
4. Transient Flow Simulation
4.1. Computational Setup
In order to obtain a turbulence-resolved flow field around the blade tip, IDDES is utilized in the current study. Figure 9 illustrates the new computational domain for the CAA simulation. Unlike the partial domain with the period boundary condition used to simulate or of the propeller for the optimization purpose, the CAA domain is set with a complete cylindrical shape to include the entire propeller. Furthermore, the rotation region is split into two parts, Zones 1 and 2. The inner part Zone 1 contains the propeller and the outer part Zone 2 is extended towards downstream for . The cells in both rotation zones are refined. In addition, cells near each individual blade tip are refined. This setup is to better resolve the evolution of blade-tip vortices in the wake. The boundary conditions at the inlet, outlet and side boundary are the same as those prescribed for the simulations in the optimization.
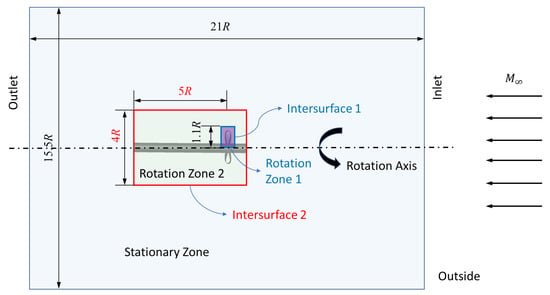
Figure 9.
The computational domain used for the CAA simulations.
In the IDDES simulations, the Sliding Mesh Method (SMM) instead of the MRF is employed to compute the transient flow with the blade-tip vortex shedding. The time step is prescribed to be 2 s , which is the time taken to rotate with 0.186. The transient simulations are initialized using the steady flow fields obtained with RANS, to reduce the time needed to develop the flows.
4.2. Mesh Independence Study and Aerodynamics Validation
A study on the grid independence for the IDDES simulations is first conducted. Table 3 lists the thrust coefficients and the total number of nodes inside Zone 1 (see Figure 9) with coarse, medium and fine resolution. Cell sizes in Zone 2 and the stationary zone are also adjusted accordingly when the cell sizes in Zone 2 are changed. However, the adjustment is only made near the interface between Zones 1 and 2, to make sure that the cell sizes of the two zones are compatible at the interface. The relative differences of the thrust coefficients among the three propellers are less than . In addition, as the total number of nodes increases, the absolute difference of the thrust coefficients among the coarse, medium and fine mesh resolution gradually decreases by –, which is acceptable for the mesh resolution convergence. The fine meshes are used for the IDDES simulations hereafter.

Table 3.
The total number of nodes in Zone 1 and the aerodynamic parameters in the mesh independence study.
Based on the results obtained from the fine meshes for the three optimal propellers, the thrust of the 3-blade conceptual propeller is larger than the 3-blade classical propeller and more than the 6-blade one.
5. Tip-Vortex Noise Simulations
This section is dedicated to investigating the noise emitted from blade-tip vortices and analyzing how the blade tip geometry and the number of blades affect the noise level. The flows are first simulated using advanced CFD solvers, to identify noise sources within the flows. Afterwards, the CAA method presented in Section 2.2 is applied to predicting the noise emitted from the sources.
5.1. Noise Source Identification
Figure 10 displays the transient thrust coefficients with respect to the normalized physical time that is expressed in revolution. As can be seen, the results are fluctuating and overall stationary, indicating that the flow fields are developed.
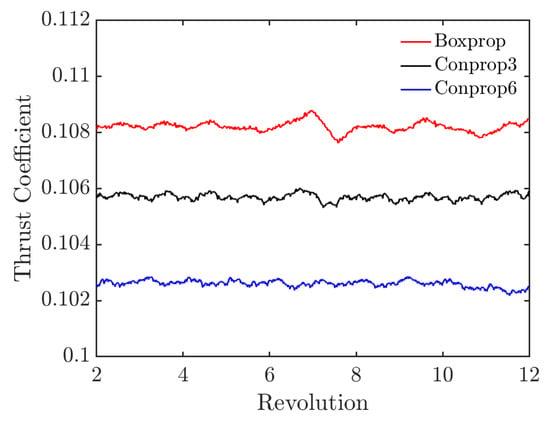
Figure 10.
The transient thrust coefficients with respect to the normalized physical time in revolutions.
To visualize vortices developed from the propeller tips, the Q-criterion is used []. The quantity Q represents the local balance between the shear strain and the vorticity magnitude. It defines vertices in regions where the vorticity magnitude is larger than the magnitude of the rate of strain. Figure 11 presents the iso-surfaces of the Q-criterion colored by the velocity magnitude. Spiral vortex shedding detached from the blade tips is observed. The tip vortices are convected downstream by the main flow. The dual blades of Boxprop with the joined tips introduce similar vortices, as compared to Conprop-3 with the individual blades, regarding the vortex shedding shapes and the vorticity magnitudes on the iso-surfaces. Although each blade of Boxprop consists of two sub-blades, there is only one shedding detached from the joined blade tip. This is apparently different from Conprop-6, which has six individual blades inducing shedding separately.
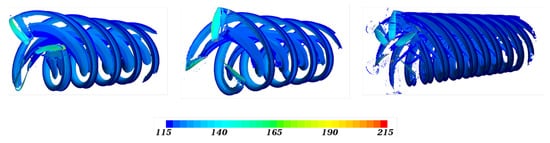
Figure 11.
Iso-surfaces of the Q-criterion, colored by the velocity magnitude. From left to right: Boxprop, Conprop-3 and Conprop-6.
To analyze the strength of tip vortices, the contours of the instantaneous vorticity magnitudes on the cutting surface at the radial position of are shown in Figure 12. The snapshots are at the times , and T, where T is the propeller resolution period. As can be seen, obvious spiral vortices are shed from the tip and developed in the wake. Amongst the three propellers, Conprop-6 has the weakest vortices, whereas Conprop-3 and Boxprop exhibit similar vortices. Every sub-blade of the Boxprop dual blade is observed to induce vortices near the joined tip, but these vortices merge into one after a short distance. As a consequence, Boxprop presents three spiral vortex structures, which are similar to those of Conprop-3.
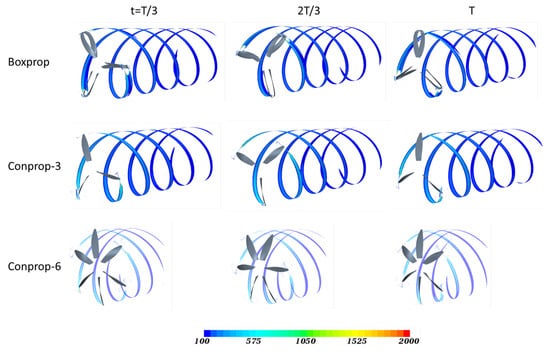
Figure 12.
Contours of the instantaneous vorticity magnitudes at the radial position of , where R is the propeller radius. The snapshots from left to right: , and T. T denotes the propeller revolution period. Note that the contour levels outside the range between 100 and 2000 are clipped off here.
The contours of the transient vorticity magnitudes at the blade tips are shown in an array of cutting planes in Figure 13. The same range of the vorticity magnitudes is visualized for the three propellers. The regions with large vorticity magnitudes indicate the process of the tip-vortex development. For the dual blade, small vortices are developed along the joined tip surface. This phenomenon is consistent with the observation in Figure 12, where two vortices are found being induced from the sub-blades near the tip rather than directly from the tip. Thus, the dual-blade tip presents the smallest vortices that directly evolve from the tip, compared to Conprop-3 and -6. On the other hand, according to Figure 12, the dual-blade finally results in vortices similar to the Conprop-3 blade, even though the dual-blade vortices are originally from two sub-blades instead of from the joined blade tip. It is worth noting that there are no streamwise long vortex tubes formed along the joined round blade tip. This effect is apparently different from a classical blade tip [] or airfoil side edge [], where vortex tubes are induced from the blade pressure and suction sides and merge in the downstream wake. Such streamwise vortex tubes are also observed for Conprop-3 and -6. Recalling Figure 11 and Figure 12, however, the structures of the dominant spiral vortices in the wake are rather similar among these propellers. It is therefore deduced that the joined blade tip has limited effects on influencing the final formation of the spiral vortices in both structures and vorticity magnitudes.
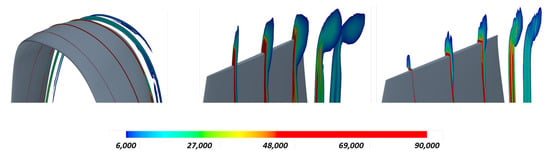
Figure 13.
Contours of the transient vorticity magnitudes in the cutting planes arranged along the propeller axial direction. From left to right: Boxprop, Conprop-3 and Conprop-6.
As shown in Figure 13, the tip vortices of Conprop-3 and -6 are similar, but the high vorticity region of Conprop-3 is larger than Conprop-6. This phenomenon is associated with the surface pressure distribution, i.e., the aerodynamic performance. The blade of Conprop-3 produces double the thrust compared to that of Conprop-6, leading to stronger shedding of tip vortices. Since the tip vortices of Conprop-6 are obviously weaker, they fade away in a short distance (see Figure 12).
5.2. Aeroacoustic Analysis
Prior to performing the aeroacoustic analysis, the flows are simulated for six propeller revolutions in the IDDES simulations, to achieve fully developed fields. Afterwards, the transient flow data including the pressure, density and velocity vector on the interface between Zones 1 and 2 (as illustrated in Figure 9) are collected in the permeable surfaces. Given the focus of this work is the noise emitted from blade-tip vortices instead of the whole blade, the permeable surfaces are cylindrical and enclose only the blade tips, as illustrated in Figure 14. The cylinders are aligned along the blade in the radial direction from to , where R is the propeller radius. The bottom surfaces of the cylinders that intersect with the blades are removed. A similar setup of permeable surfaces was also presented in a previous study on the blade-tip vortex noise for wind turbines []. Nevertheless, we admit that the present method has no theoretical flaws. First, the tip vortices can pass through the permeable surfaces when they are swept downstream (see Figure 12). The passing process leads to artificial noise. Second, sound waves propagate spherically and uniformly in all directions, so the open permeable surfaces miss to capture part of the sound waves. Finally, there are no criteria to quantify the dimension of the permeable surfaces such as the cylinder radius and length. A typical way of examining the position and dimension of the permeable surfaces is to set up several surfaces with different sizes [], while this method does not perfectly justify the current scenario because the spiral vortices can penetrate the permeable surfaces anyway. On the other hand, since the vortex penetration should possess the same characteristic frequencies of the vortices, the noise contaminated with the artificial noise tends to be comparable with the real noise.
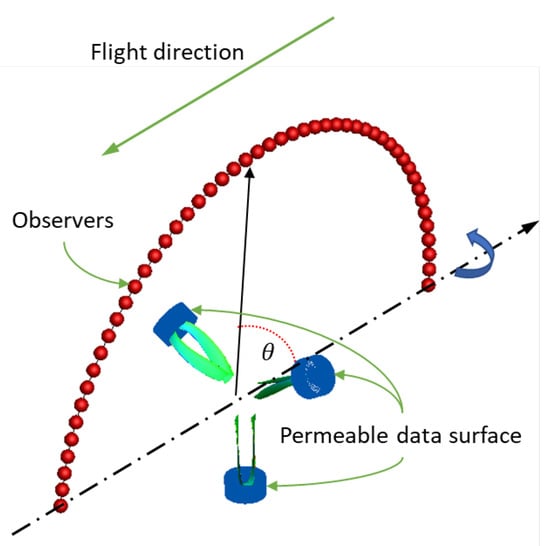
Figure 14.
The placement of the permeable surfaces and the observers in the CAA computation. Boxprop is shown as an example.
The data on the permeable surfaces are collected every three time steps, i.e., the propeller rotating for 0.558. The total physical time of the data collection is three periods for Boxprop and Conprop-3 and six periods for Conprop-6, to obtain the same resolution of the sampling frequency.
By inputting the noise source data in the permeable surfaces, the overall sound pressure levels (OASPLs) are computed using an in-house acoustic solver introduced in Section 2.2. Figure 15 presents a comparison of the OASPL directivity of the three propellers as regards the tip-vortex noise. The observer locations are seen in Figure 14, which are distributed over a half circle with a radius of in the x-y plane parallel to the propeller axial axis. Conprop-6 emits the lowest tip-vortex noise among all propellers. The noise mitigation of Conprop-6 reaches a maximum of 15 dB. This can be explained on the basis of its least intensive vorticity magnitudes identified in Figure 12 and Figure 13. Conprop-3 and Boxprop have nearly the same OASPLs over all directions and the maximum difference is around 1 dB in the downstream directions ranging between and . This phenomenon is associated with the similar blade-tip vortices from these two propellers, as indicated in Figure 12 and Figure 13.
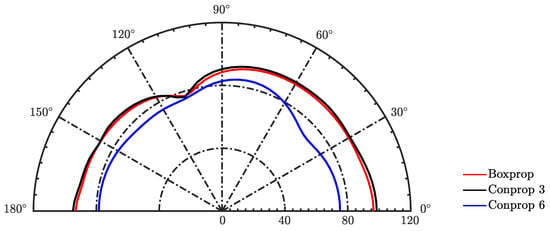
Figure 15.
The OASPL directivity of the blade-tip vortex noise.
Figure 16 displays the SPLs of the blade-tip vortex noise at the polar angles of and . The noise of Conprop-6 is the smallest and it has obvious tones at the blade passing frequency (BPF) at Hz, which is calculated based on RPM and the blade number and at its harmonics such as 310 Hz and 465 Hz. The overall smallest noise levels of Conprop-6 from 40 to 4000 Hz result in the smallest OASPLs shown in Figure 15. Compared to Conprop-3, Boxprop produces smaller broadband noise at all the frequencies. This indicates that the dual-blade behaves more similar to the classical blade given the number of blades are the same, i.e., the propellers of three blades in the current study. However, considering the differences between Boxprop and Conprop-6, the dual-blade is not equivalent to two classical blades.
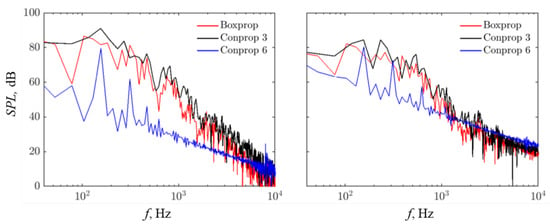
Figure 16.
The SPL spectra of the noise from the blade-tip vortices, compared at the far-field microphone positions located at (left) and (right).
As can be seen in Figure 16, in contrast to Conprop-6 producing the tonal noise, the noise of Conprop-3 and Boxprop are mainly broadband and no extraordinary tonal peaks present although some peaks are observed. The finding for Conprop-6 is opposed to the blade noise classification in Figure 1 reported in []. This indicates that the noise from tip vortices can be either tonal or broadband, even though the vortices are in the form of simple spiral tubes which are identified in Figure 11 and Figure 12. According to the illustration in Figure 13, the blade tip geometries of Conprop-3 and -6 are similar, but the characteristics of the noise spectra are disparate. To explain this phenomenon, we propose a hypothesis that the local flow separation at the blade tip prominently affects the noise spectral characteristics. Since the tips of the Concept-3 blade as well as the Boxprop sub-blade have larger pitch angles than that of Conprop-6, the position and region of the local flow separation is different. The vortex detachment is affected and tends to become turbulent at the larger pitch angles, but to be regularly coherent at the small pitch angle. The turbulent vortex detachment gives rise to the broadband noise generation, whereas the periodic mode of the regular coherence related to BPF generates the tonal noise. Another of our hypotheses is that the regular coherent vortices exist at all pitch angles, whilst turbulent vortices commence when the pitch angle is above a critical AOA. As a result, although the tonal noise from the regular coherence still exists at large pitch angles, it is masked by the significant broadband noise from the turbulence. The tonal noise can be noticed once the turbulence broadband noise becomes insignificant at small pitch angles. Nevertheless, both hypotheses cannot be simply proven based on the current study owing to the limited data, operation conditions and propeller geometry samples. A comprehensive analysis of a large database, systematically covering most representative propellers in practical operation conditions, is demanded in order to demonstrate the validity and universality of the hypotheses. This will need efforts from the whole community of this field, including the present authors in the future.
6. Conclusions
The noise emitted from vortices induced by the blade tip is investigated for three propellers: a classical propeller with three blades (Conprop-3), another classical propeller with six blades (Conprop-6) and a conceptual propeller with three dual-blades (Boxprop). These propellers are designed to target the same diameter, RPM, flight altitude, cruise Mach number of and thrust coefficient. The optimization of the propellers adopts the genetic algorithm and RANS. The IDDES coupled with the FW-H formulation is then used to compute the aerodynamic performance and blade-tip vortex noise of the selected optimal propellers.
The thrust coefficients of Conprop-6, Conprop-3 and Boxprop are , and . The dual blade consists of two sub-blades whose tips are joined in a round shape. This blade-tip geometry is disparate from the classical ones of Conprop-3 and -6. By means of a sophisticated visualization of the vorticity magnitudes, the joined round blade tip exhibits the vortex development surrounding its surface, with no formation of streamwise vortex tubes that are commonly found for the classical blades. However, the tip vortices shed from the joined blade tip are quickly developed into a dominant spiral vortex in the wake. The spiral vortex is the same as those vortices shed from the classical blade tips, even though there are obvious differences between the joined tip and the classical tip in terms of the initialization of the vortices. In addition, the spiral vortices from Conprop-6 are much weaker than those from the three-blade propellers such as Conprop-3 and Boxprop. Up to this point, it infers that the dual-blade of Boxprop is not equivalent to two single classical blades of Conprop-6. Instead, given the same number of blades (three) in Boxprop and Conprop-3, the aerodynamics of the dual-blade is more similar to the single classical blade.
Given there is the same number of blades in the conceptual propeller Boxprop and the classical propeller Conprop-3, the noise from the blade-tip vortices of the dual-blade is only slightly smaller than the classical blade in all directions and the maximum reduction is approximately 1 dB. Conprop-6 with six classical blades produces significantly smaller blade-tip vortex noise than the other propellers. Thus, with the premise of the same propeller parameters such as the diameter, thrust coefficient and RPM, the blade-tip noise is mitigated with the increased blade number.
The blade-tip vortex noise of Conprop-6 features the tones at BPF and the harmonic frequencies, whereas the noise of Conprop-3 and Boxprop is broadband. Two hypotheses are proposed to explain these distinct effects, considering that the blades of the 3-blade propellers have larger pitch angles than that of the 6-blade propeller. The tones might be generated from the periodic mode of coherent vortices and the broadband noise is from turbulence. The first hypothesis assumes that the periodic mode fades and that the turbulence commences due to the flow separation at the large pitch angles. Consequently, the tones are extinct and the broadband noise appears. In the other hypothesis, the periodic mode still exists at the large pitch angle, but its tonal noise is smaller than the broadband noise from the turbulence. The tonal noise is masked by the broadband noise. The data and results of the current study are not sufficient to justify these hypotheses. Instead, the hypotheses are presented to humbly request more systematic studies by the entire community in the future.
Since the propellers are designed by constraining a group of primary geometric and operational parameters, a question is whether aerodynamic performance can be further improved if other constraints are selected, for example, the distribution of the chord length and camber. The broadband noise of the 3-blade propellers infers the important role of the turbulence. It would be interesting to develop modelling methods for the quick prediction of the broadband noise such as the stochastic noise generation and radiation (SNGR) method []. The method has been applied to the optimization of flap side-edge noise [].
Author Contributions
Conceptualization, H.-D.Y. and Z.H.; methodology, Z.H.; software, Z.H.; validation, H.-D.Y. and Z.H.; formal analysis, H.-D.Y., Z.H., J.N. and Z.-W.C.; investigation, H.-D.Y., Z.H., L.D., J.N. and Z.-W.C.; resources, L.D.; data curation, H.-D.Y.; writing—original draft preparation, H.-D.Y. and Z.H.; writing—review and editing, L.D., J.N. and Z.-W.C.; visualization, Z.H.; supervision, L.D. and H.-D.Y.; project administration, L.D.; funding acquisition, L.D. and H.-D.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Transport Area of Advance at Chalmers University of Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would also like to appreciate the Swedish National Infrastructure for Computing (SNIC) for providing computer resources at the Chalmers Centre for Computational Science and Engineering (C3SE). The authors appreciate Anders Lundbladh for the Boxprop data input from the previous study.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AOA | Angle of attack |
| BPF | Blade passing frequency |
| BVI | Blade votex interaction |
| CAA | Computaional aeroacoustics |
| CFD | Computational fluid dynamics |
| FW-H | Ffowcs Williams and Hawkings |
| IDDES | Improved delayed detached eddy simulation |
| MRF | Multiple reference frame |
| OASPL | Overall sound pressure level |
| RPM | Revolutions per minute |
| SMM | Sliding Mesh Method |
| SPL | Sound pressure level |
| RANS | Reynolds-averaged Navier–Stokes equations |
References
- Follen, G.J.; Del Rosario, R.; Wahls, R.; Madavan, N. NASA’s Fundamental Aeronautics Subsonic Fixed Wing Project: Generation N+3 Technology Portfolio. In Proceedings of the Aerospace Technology Conference and Exposition, Toulouse, France, 18–20 September 2011. [Google Scholar] [CrossRef]
- Krein, A.; Williams, G. FlightPath 2050: Europe Vision 2020 for Aviation. In Innovation for Sustainable Aviation in a Global Environment, Proceedings of the Sixth European Aeronautics Days, Madrid, Spain, 30 March–1 April 2011; IOS Press: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Pornet, C.; Isikveren, A.T. Conceptual Design of Hybrid-Electric Transport Aircraft. Prog. Aerosp. Sci. 2015, 79, 114–135. [Google Scholar] [CrossRef]
- Huang, Z.J.; Yao, H.D.; Sjögren, O.; Lundbladh, A.; Davidson, L. Aeroacoustic analysis of aerodynamically optimized joined-blade propeller for future electric aircraft at cruise and take-off. Aerosp. Sci. Technol. 2020, 107, 106336. [Google Scholar] [CrossRef]
- Ffowcs Williams, J.E.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Farassat, F.; Succi, G. A review of propeller discrete frequency noise prediction technology with emphasis on two current methods for time domain calculations. J. Sound Vib. 1980, 71, 399–419. [Google Scholar] [CrossRef]
- Zhao, Y.; Shi, Y.; Xu, G. Helicopter Blade-Vortex Interaction Airload and Noise Prediction Using Coupling CFD/VWM Method. Appl. Sci. 2017, 7, 381. [Google Scholar] [CrossRef]
- Ottersten, M.; Yao, H.D.; Davidson, L. Tonal noise of voluteless centrifugal fan generated by turbulence stemming from upstream inlet gap. Phys. Fluids 2021, 33, 075110. [Google Scholar] [CrossRef]
- Richard, A.; Lundbladh, A. Air Propeller Arrangement and Aircraft. U.S. Patent 2012/0288374, 15 November 2012. [Google Scholar]
- Marte, J.E.; Kurtz, D.W. A Review of Aerodyanmic Noise from Propellers, Rotors and Lift Fans; Technical Report; California Institute of Technology: Pasadena, CA, USA, 1970. [Google Scholar]
- Kingan, M.; Self, R. Counter-Rotation Propeller Tip Vortex Interaction Noise. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, FL, USA, 11–13 May 2009; AIAA: Miami, FL, USA, 2009. AIAA 2009-3135. [Google Scholar]
- Elson, T. Computational Aerodynamics for Open Rotor Tip Vortex Interaction Noise Prediction. Ph.D. Thesis, Cranfield University, Cranfield, UK, 2015. [Google Scholar]
- Farassat, F. Derivation of Formulations 1 and 1A of Farassat; Technical Report; NASA Technical Reports Server (NTRS): Hampton, VA, USA, 2007.
- Černý, M.; Herzog, N.; Faust, J.; Stuhlpfarrer, M.; Breitsamter, C. Systematic Investigation of a Fixed-Pitch Small-Scale Propeller Under Non-Axial Inflow Conditions. In Proceedings of the Deutscher Luft- und Raumfahrtkongress, Friedrichshafen, Germany, 4–6 September 2018. [Google Scholar] [CrossRef]
- Sanchez, R.D. Aerodynamic and Aeroacoustic Design of Small Unmanned Aircraft System Propellers at Low Reynolds Numbers. Ph.D. Thesis, Baylor University, Waco, TX, USA, 2020. [Google Scholar]
- Wilson, C.E. Noise Control: Measurement, Analysis and Control of Sound and Vibration; Krieger Publishing Company: Malabar, FL, USA, 2005. [Google Scholar]
- Mellin, R.C.; Sovran, G. Controlling the tonal characteristics of the aerodynamic noise generated by fan rotors. J. Basic Eng. 1970, 92, 143–154. [Google Scholar] [CrossRef]
- Kim, T. Reduction of Tonal Propeller Noise by Means of Uneven Blade Spacing. Ph.D. Thesis, University of California, Irvine, CA, USA, 2016. [Google Scholar]
- Dobrzynski, W. Propeller noise reduction by means of unsymmetrical blade-spacing. J. Sound Vib. 1993, 163, 123–136. [Google Scholar] [CrossRef]
- Noda, R.; Ikeda, T.; Nakata, T.; Liu, H. Characterization of the low-noise drone propeller with serrated Gurney flap. Front. Aerosp. Eng. 2022, 1, 1004828. [Google Scholar] [CrossRef]
- Callender, M. UAS Propeller/Rotor Sound Pressure Level Reduction through Leading Edge Modification. J. Appl. Mech. Eng. 2017, 6, 254. [Google Scholar]
- Wei, Y.; Xu, F.; Bian, S.; Kong, D. Noise Reduction of UAV Using Biomimetic Propellers with Varied Morphologies Leading-Edge Serration. J. Bionic Eng. 2020, 17, 767–779. [Google Scholar] [CrossRef]
- Patrao, A.C.; Villar, G.M.; Tomita, J.T.; Bringhenti, C.; Avellan, R.; Lundbladh, A.; Grönstedt, T. An Optimization Platform for High Speed Propellers. In Proceedings of the Aerospace Technology Congress, Toyama, Japan, 25–27 October 2016. [Google Scholar]
- Ghorbaniasl, G.; Lacor, C. A Moving Medium Formulation for Prediction of Propeller Noise at Incidence. J. Sound Vib. 2012, 331, 117–137. [Google Scholar] [CrossRef]
- Yao, H.D.; Davidson, L.; Eriksson, L.E.; Grundestam, O.; Peng, S.H.; Eliasson, P.E. Surface integral analogy approaches to computing noise generated by a 3D high-lift wing configuration. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. AIAA 2012-0386. [Google Scholar]
- Haller, G. An objective definition of a vortex. J. Fluid Mech. 2005, 525, 1–26. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Eitelberg, G. An investigation of tip vortices unsteady interaction for Fokker 29 propeller with swirl recovery vane. Chin. J. Aeronaut. 2016, 29, 117–128. [Google Scholar] [CrossRef]
- Joulain, A.; Desvigne, D.; Alfano, D.; Leweke, T. Numerical investigation of the vortex roll-up from a helicopter blade tip using a novel fixed-wing adaptation method. CEAS Aeronaut. J. 2017, 8, 245–260. [Google Scholar] [CrossRef][Green Version]
- Arakawa, C.; Fleig, O.; Iida, M.; Shimooka, M. Numerical approach for noise reduction of wind turbine blade tip with earth simulator. J. Earth Simulator 2005, 2, 11–33. [Google Scholar]
- Yao, H.D.; Davidson, L.; Peng, S.H.; Eriksson, L.E. Assessment of flap side-edge fence noise using SNGR method. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Zhou, B.Y.; Gauger, N.R.; Yao, H.D.; Peng, S.H.; Davidson, L. Towards Adjoint-Based Broadband Noise Minimization Using Stochastic Noise Generation; AIAA 2019-0002; AIAA: Reston, VI, USA, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).