Abstract
Ground thermal tests are always mandatory before any space mission is flown into space. The collected results of these tests are mainly temperatures of the different parts of the spacecraft (nodes) for different mission scenarios. The measured temperatures always show differences with the expected values coming from the computer thermal mathematical models. The origin of these differences is partially related to the inherent error coming from physical measurements. The thermal parameters that compose the computer thermal mathematical models must always be correlated with the results coming from tests. This paper studies, through three thermal models, the difficulties that are found in the correlation process when the measured temperatures reach a certain level of error. Thermal parameters become more difficult to be identified when the measurement error level increases. However, the temperature fields obtained with these poor thermal parameters are good enough for the mission thermal analysis. Several error levels, different load cases and correlation for steady-state and transient cases are studied to probe these findings.
1. Introduction
The Thermal Control Subsystem is a fundamental component of the engineering design work of any spacecraft. Its purpose is clear: to maintain all the components of the spacecraft and payloads inside the safe range of temperatures devised for the mission. The design task requires to know the temperatures distributions expected for the spacecraft for any mission scenario (cold case, hot case, transport, experimentation, etc.) [1,2,3,4,5]. This task requires defining the heat inputs that the spacecraft undergoes from external sources (solar, infrared, albedo, etc.) as well as the heat produced inside the spacecraft (electronics, heaters, etc.).
To be able to predict these temperatures distributions, Thermal Mathematical Models (TMM) are built, considering the geometry, the materials thermal properties, the presence of thermal insulation (Multi-Layer Insulation, MLI), thermostats, heaters, etc. The temperature of each node, in which the TMM is discretized, is given by Equation (1), where n is the number of nodes of the TMM, GL(i, j) is the conductive conductance (W/m) between nodes i and j, is the Stefan–Boltzmann constant (5.67⋅× 10−8 W/(m2⋅K4)), GR(i, j) is the radiative conductance (m2) between nodes i and j, Ti and Tj are the temperatures (K) of nodes i and j, is the product of the i node mass (kg) times the heat capacity (J/(kg⋅K)) and qi is the power (W) that enters into node i. The subscripts i and j go from 1 to n. It is usual to call thermal inertia to the product as it describes the “opposition” to change the temperature of i node when subjected to a power input. Therefore, the solution of the set of nonlinear equations corresponding to the nodes solves the TMM. This process is called the Thermal Lumped Parameter method (TLP) and provides the temperature distribution of the different parts of the spacecraft (nodes), as well as the heat flows (W) between the nodes [6,7]. The TMM is solved for the different load cases and scenarios, in order to predict the thermal behavior in every situation expected during the mission.
As any mathematical model, the TMM represents reality in an approximate way. The temperatures predicted by the TLP method will be correct if the simplifying assumptions made to build the TMM were appropriate and reasonable. Otherwise, predicted results will be poor. For this reason, the TMMs must be validated.
Considering the ideas mentioned in the previous paragraphs, the need of thermal tests on ground is clear. Their purpose is to reproduce on ground the thermal scenarios that the spacecraft will find in orbit. These tests at the laboratory scale will produce a set of measured temperatures that could be compared with the predicted temperatures calculated with the TMMs. If the temperatures measured and the temperatures predicted are close enough, the TMM represents well the reality, and the thermal engineers have a tool to predict with reliability other thermal scenarios that could not be tested in the laboratory.
However, there is always differences between the measured temperatures in the laboratory and the calculated ones with the TMMs. These differences could be attributed to two different sources. On the one hand, the TMMs construction is an approximate process and simplifying assumptions or even errors could be done. On the other hand, measurement devices and, in general, measurement techniques are, by themselves, an imperfect process, which implies uncertainties and errors.
Therefore, the TMMs must be correlated. That is, the thermal parameters that compose the TMM (GLs, GRs and MCs) must be modified in order to predict temperatures as close as possible to the measured ones. Much work has already been devoted to this task by researchers and different methods and approaches have been used, but a fully operational semiautomatic solution of the problem has not been achieved yet. For instance, Klement [8] used quasi-Newton algorithms of the class defined by C. G. Broyden and stated that his approach reduces the number of iterations by several orders of magnitude. Further work by Klement, Anglada and Garmendia [9] compared the quasi-Newton approach with the genetic algorithm solutions, showing a better performance of quasi-Newton algorithms. In reference [10], Garmendia and Anglada presented their initial work on correlation, based on genetic algorithms. In the Ph.D. work of I. Torralbo [11], a complete mathematical development of the correlation problem was tackled based on a Jacobian matrix formulation and a Moore–Penrose pseudo-inversion on the non square matrix. Finally, Anglada, Martínez-Jiménez and Garmendia [12] analyzed the work of M.J.D. Powell on optimization and compared results based on gradient-based algorithms with results obtained with genetic algorithms.
The method that is presented in this paper deals with the correlation problem in a semiautomated, mathematical way, instead of doing it in a manual way, based on the experience of thermal engineers. Other approaches, like statistical or even machine learning, are out of the scope of this study.
The TMM correlation procedure is basically an inverse thermal problem where the values of the model parameters are estimated based on the temperature data. The main drawback of this approximation is that the problem is ill-posed due to the absence of a unique solution. That is, different combinations of the TMM parameters could provide the correct temperatures, being the main risk, the loss of the physical sense due to the values mathematically assigned to these parameters. One option to attenuate this problem is to include several load cases in the correlation as was stated in previous works of the authors [13,14].
An additional difficulty of inverse thermal problems is that the effect of changes in boundary conditions are usually dumped, causing a change in system temperature of lower magnitude than those changes in boundary conditions. Therefore, during the inverse problem resolution, small changes in the system temperature caused, for example, by measurement uncertainties, can originate from big changes in the adjusted parameters.
For this reason, the objective of this paper is to study the influence of the measurement uncertainties and errors, in the process of correlating the TMM against the measured temperatures.
2. Correlation Methodology and Handling of Measurements Uncertainties
Previous works by the authors have shown the possibility of doing an adequate correlation of thermal parameters, both in the steady state and transient situations, for small size TMMs using minimization algorithms [13,14]. These works were developed using the same three small TMMs used in the work presented hereafter, composed by 4 nodes, 7 nodes and 16 nodes, respectively. The last two models were derived from the TMM of the Tribolab instrument, a space tribometer that was flown on board the International Space Station [15].
The correlation methodology followed could be summarized saying that the objective is to minimize the differences between the temperatures measured in the tests and the temperatures predicted by the TMMs. For doing this, the TMM thermal parameters (GLs, GRs, MCs) are changed through a gradient-based set of minimization subroutines (TOLMIN), developed by Professor M. J. D. Powell [16,17].
In an ideal case, temperatures predicted for each node would be compared with the corresponding measured value. However, the number of measurement points in the thermal test are usually lower than the number of nodes of the TMMs.
In this case, instead of using real test temperatures as reference values, the next procedure has been followed. For each model, a reference TMM was set up and solved. The GLs, GRs and MCs used in that model are considered the reference parameters (the correct parameters) and the temperatures provided the reference temperatures. Then, this model has been modified (GLs, GRs and MCs have been randomly altered) and has been called the base model. The temperatures obtained with this base model are the predicted temperatures (or base temperatures), which should match the reference (correct) ones. That is, the base model represents the model that thermal engineers would produce with CAD tools, material properties, etc., and that must be correlated against reference temperatures. The main advantage of using this procedure in this study instead of the temperatures measured in thermal tests is that in this way, we have available the correct temperature values in every node of the model, and we have also available the correct values of the model parameters (GLs, GRs and MCs). Therefore, we can evaluate not only the error level in the predicted temperatures but also the error in the values assigned to the TMM parameters (GLs, GRs and MCs) during the correlation.
What has been explained as far as now does not take into account possible error measurements, instead it is assumed that temperatures would be “perfectly” measured. In order to study the effect of having some degree of error in the measurement of the temperatures, the reference temperatures have been modified following Equation (2) (see reference [18]).
where is a random variable with normal (Gaussian) distribution, zero mean, and unitary standard deviation. is the standard deviation of the measurement errors.
Real precision of temperature measurements is difficult to estimate, as the information given by the measurement devices suppliers is not complete. To add more uncertainty, different types of thermocouples or thermistors are used for the temperature measurements. The scenario complicates further if we take into account the fact that thermal tests equipment is always built on an individual client basis (there are no standard thermal vacuum chambers). Consequently, we will try to resume these facts in a unique parameter, the standard deviation , and we will use different values of it ranging from to to see the influence it has on the results’ accuracy. Assuming 99% confidence for the measured temperature, lies in the range shown in Equation (3).
To generate values of in the mentioned range, the random_seed and random_number subroutines of the Fortran language have been used. The pseudorandom number returned, , is a real value between 0 and 1, so a linear transformation is used to obtain the values of in the adequate range following Equation (4).
A graphical description of the methodology can be seen in Figure 1.
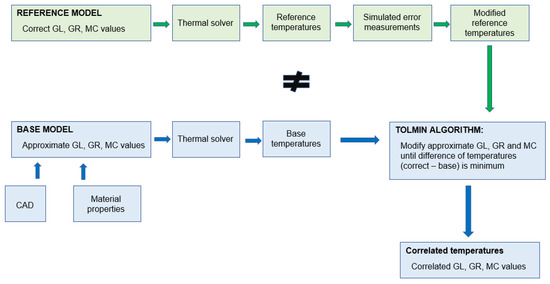
Figure 1.
Graphical description of the methodology.
3. Results Obtained for Different Case Studies and Discussion
Now, the results obtained for the three different case studies (4, 7 and 16 nodes TMMs) will be presented. The number of calculations done is very high, therefore, the tables that follow will try to resume the most important points needed to evaluate the correlation process when measurement errors are present. The employed cases will be those presented previously elsewhere (see references [13,14]), to allow the interested reader to have a complete idea of the process of correlation, its possibilities and the difficulties present.
For the sake of clarity, before displaying the tables with results, it is interesting to note that there are two table types: those showing results for thermal parameters and those showing results for temperatures.
Results corresponding to thermal parameters represent the arithmetic mean of the differences between the reference thermal parameters and the values assigned to them by the minimization algorithm. If we call NPAR, the number of unknown parameters that must be correlated (GLs, GRs and MCs), and each one of these parameters, the error would be calculated following Equation (5).
In the case of temperature results, the values correspond to the arithmetic mean between the reference temperatures and the temperatures obtained with the TMM once correlated, that is, using the thermal parameters obtained from the correlation. If we call NNOD, the number of nodes of the model, NSTEP, the number of time steps used in the solution of the thermal case and NCASE, the number of load cases taken into account in the calculation, we can see that NTEMP, the number of temperatures present in the correlation, is given by Equation (6). Further, the error would be calculated following Equation (7) (calling each one of these temperatures).
3.1. 4 Nodes Model
As a first simple model, a theoretical 4 nodes model (nodes 1 to 4) has been used. The thermal model, which can be seen in Figure 2, has three linear conductances (GLs), three radiative conductances (GRs) and three thermal inertias (MCs). Power is applied in node number 1 and a constant temperature of 20 °C is maintained in sink node 4, for all the load cases. The transient case extends 7200 s (2 h), and the initial temperature for all the nodes is 20 °C. The time step used is 600 s (10 min). The behavior and correlation of this model was studied in depth in references [13,14], which can be consulted for more detailed information. Now, different error levels have been introduced for the reference temperatures, as can be seen in the different values assigned to the standard deviation (SD) in the tables included in next sections. Their influence has been studied for steady state cases and for transient analysis.
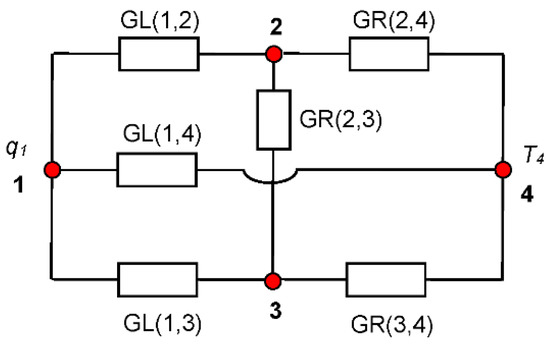
Figure 2.
The 4 nodes model.
3.1.1. 4 Nodes Model: Correlation for Steady State Cases
Table 1 shows the errors in the TMM parameters both at the initial state and after the correlation, for different levels of measurement errors (different standard deviation values). The analysis has been done including different load cases in the correlation. Three load cases results (hot, stay alive and cold) were available for the correlations. Correlation 2(a) was done using hot and stay alive cases, correlation 2(b) was done using hot and cold cases and correlation 2(c) was done using stay alive and cold cases.

Table 1.
Errors obtained for the TMM thermal parameters. Steady state 4 nodes model.
The mean initial error in the parameters (67.92%) can be reduced if the standard deviation error in the measurements is 0.0001 or lower.
After obtaining the correlated thermal parameters with the different SD error levels, TMMs were re-built using the correlated parameters. Then, these correlated models were run and new predicted temperatures were obtained. Table 2 collects the absolute temperature error level for these models.

Table 2.
Errors obtained for predicted temperatures for steady state 4 nodes model.
The mean initial error for predicted temperatures goes clearly down if the standard deviation SD in the measured temperatures is equal or lower than 0.001.
As it can be seen, the smaller the standard deviation of the error in the temperatures measurements, the better the results both for the thermal parameters and for temperatures.
3.1.2. 4 Nodes Model: Correlation for Transient Cases
The simple 4 nodes model has been also studied for transient cases. The number of temperatures is now much higher, as values in each time step are available for each node. Again, different levels of standard deviation SD were considered in the correlation of the thermal parameters. Table 3 collects the results for transient cases for the thermal parameters, when two load cases or one load case are considered. As expected, the lower the standard error in the measurement of temperatures, the better the thermal parameters correlation. Additionally, when two load cases are used instead of one, improved results are obtained.

Table 3.
Errors obtained for the TMM thermal parameters. Correlation of transient 4 nodes model.
Once the correlated thermal parameters were obtained, a calculation of predicted temperatures was done for the different load cases considered. Results are collected in Table 4, which shows the mean error value of the temperatures predicted versus the correct temperatures.

Table 4.
Errors obtained for predicted temperatures for transient 4 nodes model.
It is worth to note that, even for the highest levels of standard deviation error, the temperature values match very well with the correct temperature values. This happens even for the TMMs whose thermal parameters show bigger errors.
Finally, the effect of the measurement errors has been also studied in the situation when the temperature of one node is unknown (node 2), which implies a higher difficulty to achieve a good correlation. Thermal parameters results obtained in this case are collected in Table 5. As it could be expected, results are worse than those shown in Table 3. Only the three load cases with a minimum standard deviation (SD = 0.00001) show a good match between the correlated parameters and the real ones.

Table 5.
Errors obtained for the TMM thermal parameters. Correlation of transient 4 nodes model with 1 unknown temperature.
Once again, the new sets of predicted temperatures were obtained with the new correlated thermal parameters. The results are shown in Table 6, where the mean absolute temperature errors are collected.

Table 6.
Errors obtained for predicted temperatures for transient 4 nodes model, 1 unknown temperature.
Close examination of the new predicted temperatures in Table 6 shows a dramatic improvement of the predicted values versus the initial error. Even for the poorest thermal parameters correlation (those with the highest standard deviation), the new set of temperatures match well with the correct temperatures. However, results when considering three load cases instead of two load cases for the correlation are worse, which is an unexpected result. The authors have no clear explanation for this fact.
3.2. 7 Nodes Model
The previous 4 nodes model showed the trends and limitations of the correlation method when applied to a theoretical small thermal model. It is interesting to make an equivalent study for a bigger model, which corresponds to a real device. In this section, we study a reduced 7 nodes model of the Tribolab instrument, a space tribometer that was flown on board the International Space Station [15]. Three of the nodes are sink nodes: two radiation sink nodes (nodes 99,241 and 99,271) and one conduction sink node (node 10,000). The model consists of four linear conductances, two radiation conductances and four thermal inertias, for the transient cases, which can be seen in Figure 3. In the transient cases, the calculations run for 86.400 s (that is, one day) and time step . This makes a total of 144 time steps. The initial temperature considered for t = 0 is T = 20 °C.
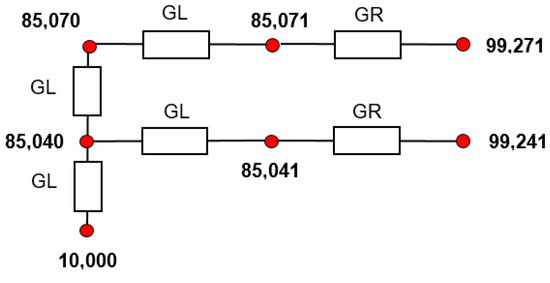
Figure 3.
The 7 nodes model.
Powers are applied in no sink nodes (85,040, 85,041, 85,070 and 85,071) and sink temperatures are known. For this 7 nodes model, both steady state and transient results have been used in the parameter correlation.
3.2.1. 7 Nodes Model: Correlation for Steady State Cases
The results obtained for the parameters correlation in the steady state cases are collected in Table 7. Two different situations are considered in these results: All the temperatures are known (first row) or two temperatures (those of nodes 85,040 and 85,050) are unknown (rows 2 and 3). For the correlation, the temperatures of two load cases were used (first row), three load cases (second row) or four load cases (third row).

Table 7.
Errors obtained for the TMM thermal parameters. Steady state 7 nodes model.
As expected, a smaller standard deviation in the temperatures measurements implies a better correlation of the parameters. The presence of unknown temperatures on some of the nodes makes it more difficult (or even impossible) to obtain a correct thermal parameters correlation. However, the use of more load cases balances the added difficulty and results, for the thermal parameters are quite satisfactory if SD is equal or lower than 0.001. It is also interesting to note that the results for SD = 0.1 behave in some unexpected way (they are worse than the initial error) but the use of smaller values of SD improves the results clearly.
Once the thermal parameters have been obtained from the correlation, all the thermal steady state cases have been calculated again using them. Results are collected in this case in Table 8.

Table 8.
Errors obtained for predicted temperatures for steady state 7 nodes model.
Once again, a dramatic improvement of the temperatures predicted is achieved, even for big standard deviations. The presence of unknown temperatures is well balanced with the effect of taking into account more load cases for the correlation.
3.2.2. 7 Nodes Model: Correlation for Transient Cases
The simple 7 nodes case of the Tribolab instrument is also used in the transient version of the correlation algorithm. The measured temperatures have been used in three different situations, when all the temperatures are known, when one temperature is missed (that of node 85,040) and when two temperatures are missed (those of nodes 85,040 and 85,070). For each of these situations, two load cases, two load cases and four load cases have been used, respectively. Errors with different standard deviation values were added to the reference temperatures for each time step considered.
The results obtained for the thermal parameters can be seen in Table 9.

Table 9.
Errors obtained for the thermal parameters for transient 7 nodes model.
With 0 and 2 unknowns and using two or four load cases, the results of the correlation are good: smaller temperature deviations and enough load cases considered lead to a better correlation, also for this transient case. However, behavior is somehow erratic when one temperature is unknown and two load cases are used. There is not a clear explanation of this fact. A possible human error in the model or a non convergence situations are possible explanations of the unexpected behavior.
Results for the temperatures calculated with the thermal parameters obtained from the correlation, can be seen in Table 10.

Table 10.
Errors for predicted temperatures for transient 7 nodes model.
The results for the temperatures are good, for zero and two unknowns, even if the thermal parameters correlated were not that exact. The error in the temperatures is small, even for high standard deviations. However, the one unknown case does not behave well, which is consistent with the poor results obtained for the thermal parameters
3.3. 16 Nodes Model
After the two previous small models, with limited number of nodes and thermal parameters, a 16 nodes model was devised. It is called the Tribolab compact model, because the model represents in a more accurate way the real geometry and thermal behavior of Tribolab. The number of nodes is N = 16 and, between them, there are 22 linear conductances and 25 radiative conductances. There is also one conductive sink node (node 10,000, the ISS) and one radiative sink node (node 99,292, the Space). The total number of thermal parameters to be correlated is 58, as also the thermal inertias are considered in the transient cases.
The model is shown in Figure 4, where the red dots represent the nodes, the dash lines the radiative conductances (GRs), the solid thin lines the conductive conductances (GLs) and the solid thick lines represent the presence of conductive and radiative conductances (GLs and GRs) between the nodes.
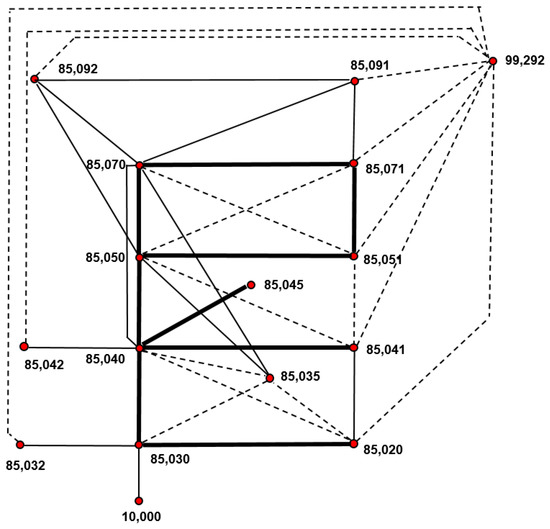
Figure 4.
The 16 nodes model.
3.3.1. 16 Nodes Model: Correlation for Steady State Cases
Results for the thermal parameters correlation are shown in Table 11. All the temperatures of the nodes have been considered known and different standard deviation levels have been considered. The four, five and six load cases results were taken into account for the correlations.

Table 11.
Errors obtained for thermal parameters correlation for steady state 16 nodes model.
Results seem to be poor, even if a high number of load cases are considered. Only for a small value of SD = 0.0001, the thermal parameters have improved. However, as can be seen in Table 12, temperature results are good for all the error standard deviation values, also with four, five or six load cases.

Table 12.
Errors obtained for predicted temperatures for steady state 16 nodes model.
3.3.2. 16 Nodes Model: Correlation for Transient Cases
Table 13 collects the results for the thermal parameters correlation when using two load cases or four load cases and when the reference temperatures have different error levels (standard deviation going from 0.0001 to 0.1).

Table 13.
Errors obtained for thermal parameters for transient 16 nodes model.
Results show a poor behavior of the correlation methodology for the thermal parameters and results only improve if SD = 0.0001 or lower.
However, the results for the temperatures field for the correspondent cases are better than expected, as can be seen in Table 14. When using four load cases, all the results obtained with the correlated parameters are better than the initial error of temperatures.

Table 14.
Errors obtained for predicted temperatures for transient 16 nodes model.
Finally, the correlation of this model done with transient results permits us to study the possibility of trying the correlation even if some nodes temperatures are unknown. This could be the case when thermocouples cannot physically reach the position of the node or recording problems are experienced when testing. It is worth to be noted that this situation makes it more difficult to obtain sensible results.
Table 15 collects the results obtained for the thermal parameters, when different number of unknown temperatures are present and when different number of load cases were used for the correlation.

Table 15.
Errors obtained for thermal parameters for transient 16 nodes model.
The results show a poor behavior of the correlation algorithm when looking for the correct thermal parameters. In general terms, the higher the number of unknown temperatures, the higher the error when identifying thermal parameters.
However, the correlation algorithm makes its job minimizing the error function or at least sending a set of thermal parameters that decreases the differences between measured temperatures and predicted temperatures. This can be seen in Table 16, where almost all the predicted temperatures are better values than the initial ones if the SD = 0.01 or lower. This happens even for the cases where the number of unknown temperatures is high.

Table 16.
Errors obtained for predicted temperatures for transient 16 nodes model.
4. Conclusions
Results have been previously discussed when they were presented in Section 3 of this paper. For this reason, in this final conclusions section, only the most remarkable and general trends of the results will be highlighted.
The first idea is that the higher the error level in the measured temperatures, the more difficult to reach convergence for the thermal parameters and, consequently, the higher the error of these thermal parameter values. This fact can be observed in almost all the analyzed cases.
A second point that must be underlined is that, in general, even if the values obtained for the thermal parameters are poor, the temperatures obtained with models using these correlated parameters are better than the initial estimations before the correlation. This fact is related to the absence of a unique solution to the correlation problem.
The third conclusion is that smaller models (4 or 7 nodes, with less than 10 thermal parameters) obtain better results for the correlation than bigger ones. At the same time, the presence of more load cases (measured temperatures) helps the correlation, as more information is available for the minimization algorithm.
As a fourth conclusion, it can be said that a higher amount of data present in the transient cases (data for different time steps) helps in the optimization if unknown node temperatures are present in the process.
As a general conclusion, it can be stated that when measurement errors are present, the correlation methodology based on the minimization set of subroutines TOLMIN cannot guarantee good results in the correct thermal parameters identification, but almost always reaches significantly better results than initial estimates for the temperature fields.
Author Contributions
Conceptualization, methodology and investigation I.G. and E.A.; writing, review and editing, I.G. and E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gilmore, D.G. (Ed.) Spacecraft Thermal Control Handbook, 2nd ed.; American Institute of Aeronautics and Astronautics: El Segundo, CA, USA, 2002; Volume 1, ISBN 1-884989-11-X. [Google Scholar]
- Meseguer, J.; Pérez-Grande, I.; Sanz-Andrés, A. Spacecraft Thermal Control; Woodhead Publishing: Cambridge, UK, 2012; ISBN 978-0-84569-996-3. [Google Scholar]
- Karam, R.D. Satellite Thermal Control for Systems Engineers. In Progress in Astronautics and Aeronautics; Zarchan, P., Ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1998; Volume 181, ISBN 1-56347-276-7. [Google Scholar]
- Silk, E.A. Introduction to Spacecraft Thermal Design; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Miao, J.; Zhong, Q.; Zhao, Q.; Zhao, X. Spacecraft Thermal Control Technologies; Springer: Singapore, 2021; ISBN 978-981-15-4983-0. [Google Scholar]
- Redor, J.F. Introduction to Spacecraft Thermal Control; ESA Publications Division: Noordwijk, The Netherlands, 1995; ESA-EWP1599. [Google Scholar]
- K&K Associates (Ed.) K&K Associates Thermal Network Modeling Handbook; K&K Associates: Westminster, CO, USA, 2002. [Google Scholar]
- Klement, J. Quality Assessment for Parameters Obtained with Model Correlation. In Proceedings of the 31st European Space Thermal Analysis Workshop, Noordwijk, The Netherlands, 24–25 October 2017; pp. 177–178. [Google Scholar]
- Klement, J.; Anglada, E.; Garmendia, I. Advances in Automatic Thermal Model to Test Correlation in Space Industry. In Proceedings of the 46th International Conference on Environmental Systems, ICES 2016, Wien, Österreich, 10–14 July 2016; Texas Tech University: Lubbock, TX, USA, 2016; pp. 1–11. [Google Scholar]
- Garmendia, I.; Anglada, E. Thermal Mathematical Model Correlation through Genetic Algorithms of an Experiment Conducted on Board the International Space Station. Acta Astronaut. 2016, 122, 63–75. [Google Scholar] [CrossRef]
- Torralbo, I. Correlation of Spacecraft Thermal Mathematical Models to Reference Data. Acta Astronaut. 2018, 144, 305–319. [Google Scholar] [CrossRef]
- Anglada, E.; Martinez-Jimenez, L.; Garmendia, I. Performance of Gradient-Based Solutions versus Genetic Algorithms in the Correlation of Thermal Mathematical Models of Spacecrafts. Int. J. Aerosp. Eng. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Garmendia, I.; Anglada, E. Thermal Parameters Identification in the Correlation of Spacecraft Thermal Models against Thermal Test Results. Acta Astronaut. 2022, 191, 270–278. [Google Scholar] [CrossRef]
- Garmendia, I.; Anglada, E. Transient Thermal Parameters Correlation of Spacecraft Thermal Models against Test Results. Acta Astronaut. 2022, 199, 49–57. [Google Scholar] [CrossRef]
- Garmendia, I.; Anglada, E. Thermal Control of Tribolab, a Materials Experiment on Board the International Space Station. In Advances in Materials Science Research; Wythers, M.C., Ed.; Advances in Materials Science Research; Nova Science Publishers: New York, NY, USA, 2018; Volume 32, pp. 65–142. ISBN 978-1-53613-329-5. [Google Scholar]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math Program 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Zhang, Z. Software by Professor M. J. D. Powell. Available online: https://www.zhangzk.net/software.html (accessed on 1 May 2021).
- Mohebbi, F.; Sellier, M. Estimation of Functional Form of Time-Dependent Heat Transfer Coefficient Using an Accurate and Robust Parameter Estimation Approach: An Inverse Analysis. Energy 2021, 14, 5073. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).