1. Introduction
Unmanned Aerial Vehicles (UAVs) have drawn growing applications in many scenarios, such as search and rescue, logistic delivery, and aerial photography. Such aerial vehicles usually have the advantages of fast movement, wide field of view (FOV), and imperviousness to terrain. On the other hand, UAVs are severely limited by the fuel or battery, which affects their payload capacity and mission performance accordingly. Combining the UAV with a ground support platform can extend the endurance and assist its flight capacity.
Autonomous approaching and landing of UAVs play an important role in the aforementioned air–ground cooperation, especially for long-term missions. To accomplish this task, real-time pose and velocity of the ground platform need to be estimated accurately. For UAVs, attitude and position feedback are essential for flight control. Global Positioning System (GPS) can provide general position feedback. Attitude state can be obtained from the onboard IMU. To date, a considerable amount of studies rely on GPS–IMU guided autonomous flight. Nevertheless, such a sensor combination presents difficulties in precisely controlling UAV approaches and landings on a ground platform [
1]. When approaching the ground, ground effects cause the inertial sensor to vibrate, and the near-ground environment easily blocks GPS and induces position feedback deterioration. Some scenarios even deny GPS information totally.
In addition to IMU and GPS, visual sensors provide a favorable alternative in UAV approaches and landings, especially in GPS-denied areas. The key factor in vision-based sensing is identifying and tracking ground objects, such as landmarks, on the mobile platform. To improve the robustness of the vision-based tracking, the self-designed visual cooperation logo has been widely used to solve the problem of the autonomous landing of UAVs. Following this topic, scholars in various countries have achieved remarkable results. In terms of designing visual cooperation signs, more and more open-source libraries for state estimation have been launched, including ARTag [
2], Apriltag [
3,
4,
5], ArUco [
6,
7,
8,
9], and other open-source libraries. The visual cooperation sign in the form of a fiducial marker based on black and white blocks has gradually become the mainstream method for vision-based autonomous landing state estimation of UAVs. Based on these open-source libraries, many scholars have conducted research and proposed a series of methods to improve the accuracy and stability of state estimation [
10,
11].
In real-world applications, a single fiducial marker meets the challenge that it cannot be tracked when the UAV is too close to the mobile platform, due to the limited FOV of the onboard camera. So, many kinds of landing pads with a combination of different size markers were designed and employed. Ref. [
12] designed a new type of landing pad, which includes several ArUco signs of different sizes which can ensure that the UAV can detect the signs at all heights, and the relative pose information estimated by each sign is also the same. To solve the low detection rate of the landmark, Ref. [
13] designed a landing platform containing Apriltag signs of different sizes, and took the fusion of inertial measurement data and visual attitude estimation data into consideration, thereby ensuring a high sampling rate, improving the ability of the UAVs to deal with short-term target occlusion and false detection, and improving the maneuverability of the UAVs. In most mark tracking algorithms, the position and speed of the ground vehicle were estimated by an extended Kalman filter (EKF) to improve the accuracy of relative pose estimation and the speed range of relative pose estimation. However, although the EKF can provide short-term state estimation and prediction, autonomous maneuvering in the case of complete loss of visual information is not considered. Ref. [
14] proposed a vision-based autonomous landing system for UAV mobile platforms using visual information to locate and track the mobile platform and established a finite state machine to complete the entire autonomous landing process, enabling the system to have the ability to relocate the mobile platform after vision information is lost.
When the UAV is far from the landing platform, other sensors are usually used to guide the approach. To accommodate such limitations, Ultra Wide-Band (UWB) technology provides a favorable alternative to localize the relative position between the UAV and the ground platform. By leveraging the high sampling rate of the IMU, a sensor fusion of UWB and the IMU can offer high-frequency reliable position feedback, which is promising to address the open challenge of navigating the UAV to approach the target ground platform. The integration of UWB-IMU will expand the related air–ground collaborative applications in GPS-denied environments. A large amount of work has been conducted on UWB and vision-guided landing in recent years. A UWB-vision combined autonomous landing framework [
15,
16,
17] was developed that uses UWB technology to provide relative localization and vision localization to guide the final precision landing, but it is hard to provide high-frequency and real-time localization information due to the low update rate of the UWB system. To improve reliability and consistency, a UWB-IMU fusion relative location algorithm was implemented in autonomous landing [
18]; however, without guided vision in the final descending stage, the landing precision is hard to guarantee. For autonomous landing on a moving platform without custom-designed marks, a deep-learning object detection algorithm and UWB were adopted to estimate the location of the moving platform [
19]. All of above research are location oriented relying on the magnetometer, which is badly affected by the electromagnetic environment.
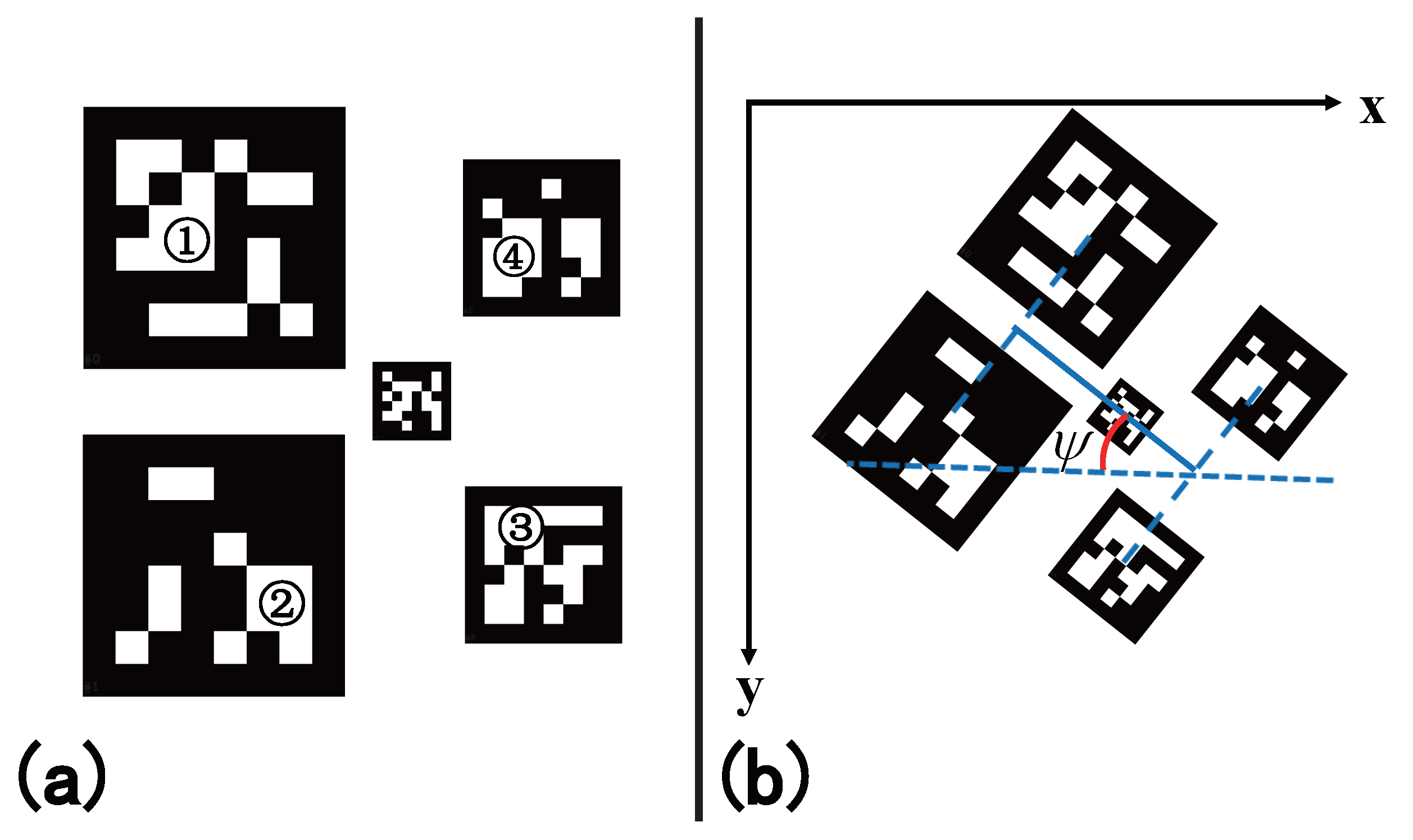
In this paper, a cooperative landing scheme integrating multiple sensor fusion relative localization is proposed for UAVs to perform autonomous landings. The proposed scheme is composed of two stages depending on the availability of different sensors. When no landmark is detected, the UAV is guided to approach the mobile platform using the relative position estimated by the UWB-IMU localization subsystem. In this case, a UWB-IMU fusion framework is proposed to integrate these two sensors’ data, aiming to leverage both the high sampling rate of the inertial feedback and the accuracy of the UWB feedback to enhance the computational efficiency and compensate for the sensing delay. Once the landmark is detected, the navigation law switches to the UWB-IMU and vision-guided landing stage. A real-time landmark detector and vision-based landmark pose estimation are designed to provide reliable vision pose estimation during the landing stage. In order to improve the accuracy of pose perception, a customized landmark with high accuracy orientation estimation algorithm is built by an aggregation of squared ArUco markers with different sizes. The proposed state estimation framework is validated in both simulations and real-world experiments. As a result, the proposed UWB-IMU-Vision framework can guide UAV landing on the desired platform with a deviation < 10 cm.
The main contributions of this paper can be summarized as follows:
A UWB-IMU based localization algorithm is designed to provide onboard relative pose between a UAV and a landing platform with high frequency and consistency;
A detection and pose extraction algorithm of a landing pad with a customized ArUco marker bundle is designed for a UAV to estimate the relative orientation of the landing platform with high accuracy in real time;
A systematic landing scheme with integrated UWB-IMU-vision localization is proposed for UAVs to achieve autonomous approaching and landing on a moving platform. Flight experiments in both simulation and real-world are conducted to validate the robustness and reliability of the proposed multi-sensor framework.
The rest of the article is organized as follows.
Section 2 formulates the autonomous landing problem and introduces the framework and workflow of the proposed landing scheme.
Section 3 specifies the algorithm of the UWB-IMU-based position estimation algorithm.
Section 4 details the detection of the landmark and orientation extraction.
Section 5 presents the evaluation of the proposed UWB-IMU position estimation and the vision orientation estimation algorithm.
Section 6 presents the experimental validation of the proposed landing scheme.
Section 7 summarizes this work.
2. System Overview
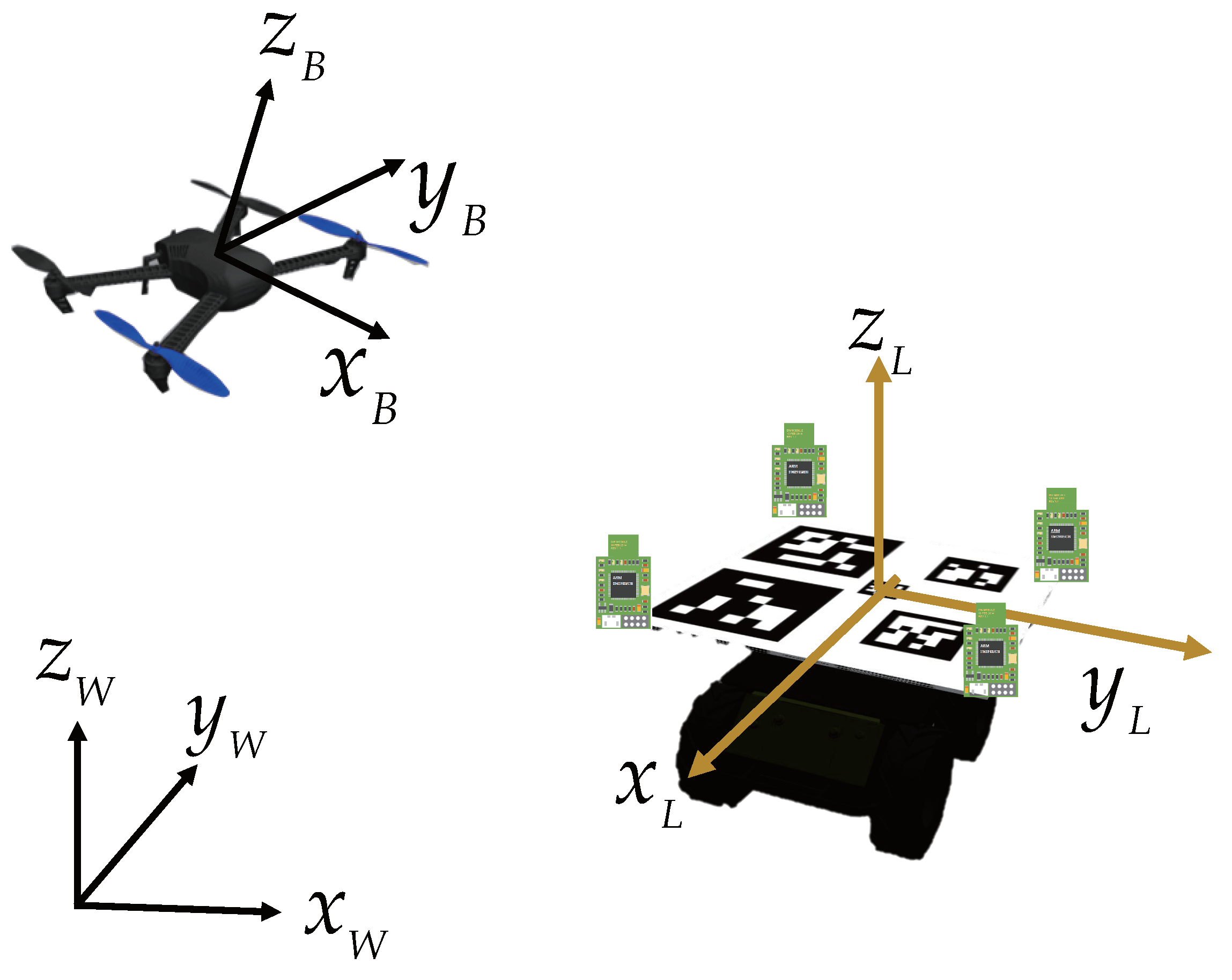
This study integrates a variety of sensors. Their respective coordinates are shown in
Figure 1. In particular, the UAV body frame is fixed with the aerial vehicle. The landmark frame is fixed with the mobile platform which carries the custom designed markers and UWB station. Both of them are defined in forward-left-up(FLU) format, i.e., the
x-axis is aligned with the forward moving direction, the
y-axis is aligned left, and the
z-axis is determined by the right-hand rule. An East-North-Up (ENU) coordinate is defined as the world frame.
2.1. Problem Formulation
During autonomous landing, the UAV can be guided to the landmark by position and velocity control. A flight controller is designed to precisely track the control references. The UAV locomotion can be modeled by
where
is the position of the UAV in the world frame,
T is the control period, and
is the velocity control input.
Similar to the UAV, the motion of the ground platform can be modeled as:
where
is the position of the ground mobile platform in the world frame, and
is the velocity of the ground mobile platform. Since the mobile platform is moving on the ground, its height variation is assumed as constant, and the velocity on the
z-axis is zero.
The velocity control input of the UAV in the
x-
y plane can be obtained by a feed-forward proportional-integral-derivative (PID) controller:
where
,
are the control gains. According to the latter experimental results, with the fine-tuned control gains, the proposed PID law matches the accuracy requirements of approaching and landing control.
2.2. UWB-IMU-Vision-Based Pose Estimation
The accuracy of position and velocity estimation of the ground platform is essential for the UAV landing. The position of the ground platform in the world coordinate can be obtained by
where
is the rotation matrix from the world frame to the landmark frame which can be obtained by the onboard IMU of the mobile platform, and
is the relative position of the UAV in the landmark frame which can be obtained from vision estimation and the UWB measurements. As the state of the UAV in the world frame can be obtained by the onboard sensors (GPS and IMU), the state of the ground mobile platform can be estimated by measuring the relative motion state between the air and ground vehicles.
In such cases, the UWB can provide the X-Y position estimation under a relatively low sampling rate with some occasional outliers. A typical example is shown in
Section 3.1. To address the shortcomings of UWB, relative acceleration was taken into consideration to provide high-frequency motion estimation. Under the assumption of the constant moving velocity of the ground platform, the relative acceleration of the UAV can be obtained accordingly by the projection of the acceleration of the UAV in the body frame to the mobile platform, which is given by
where
is the acceleration of UAV in the mobile platform,
is the rotation matrix from the UAV body coordinate to the mobile platform coordinate, and
is the acceleration measured by the IMU of the UAV.
The attitude of the UAV in world coordinates can be estimated by the onboard IMU. In addition, the roll and pitch angle of the ground mobile platform is nearly zero. Then, is the function of the orientation of the ground platform. The IMU can also be applied on ground platforms for orientation estimation. In addition, extracting relative orientation using a custom-defined landmark from the UAV’s vision sensor is a reliable alternative, which can avoid the disturbances of electromagnetic interference.
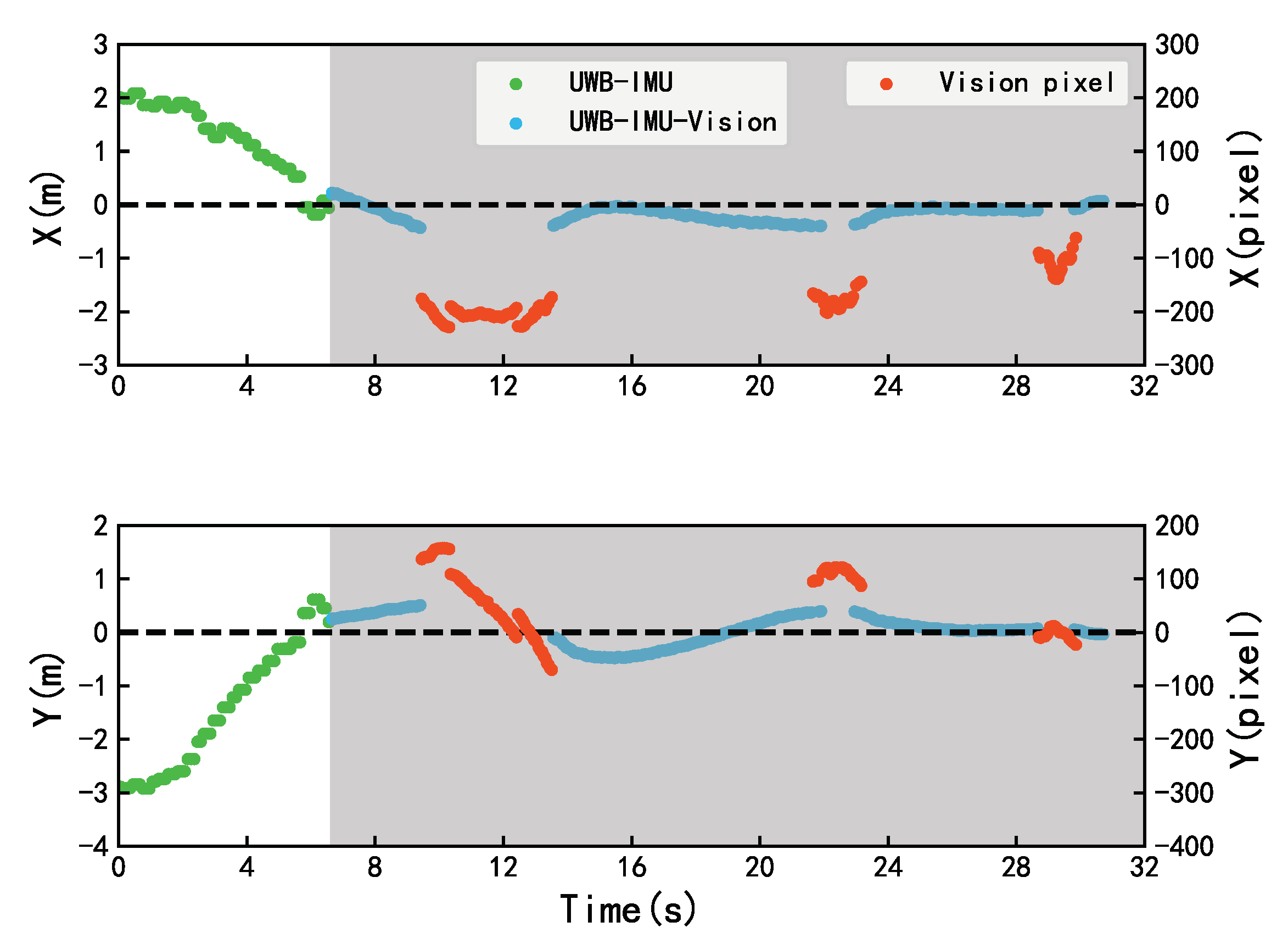
From the above discussion, in order to improve the effectiveness, reliability, and stability of the autonomous landing system and ensure continuous and stable tracking of the landing platform throughout the landing mission, relative pose estimation was provided by using three kinds of sensors - UWB, IMU, and vision location. The UWB-IMU was integrated to provide real-time relative position estimation, and the vision sensor was adopted to provide reliable relative pose estimation.
2.3. Landing Scheme Work Flow
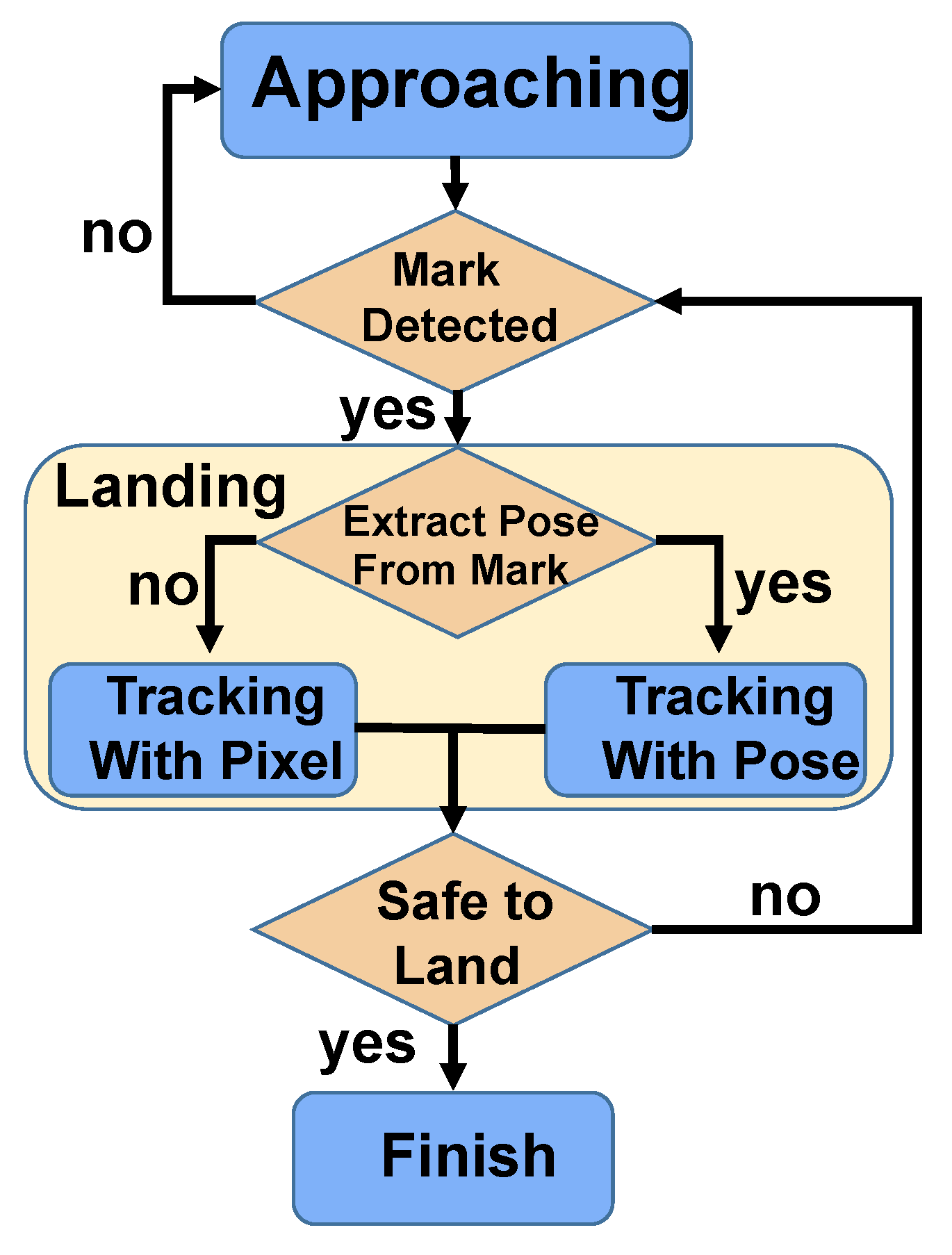
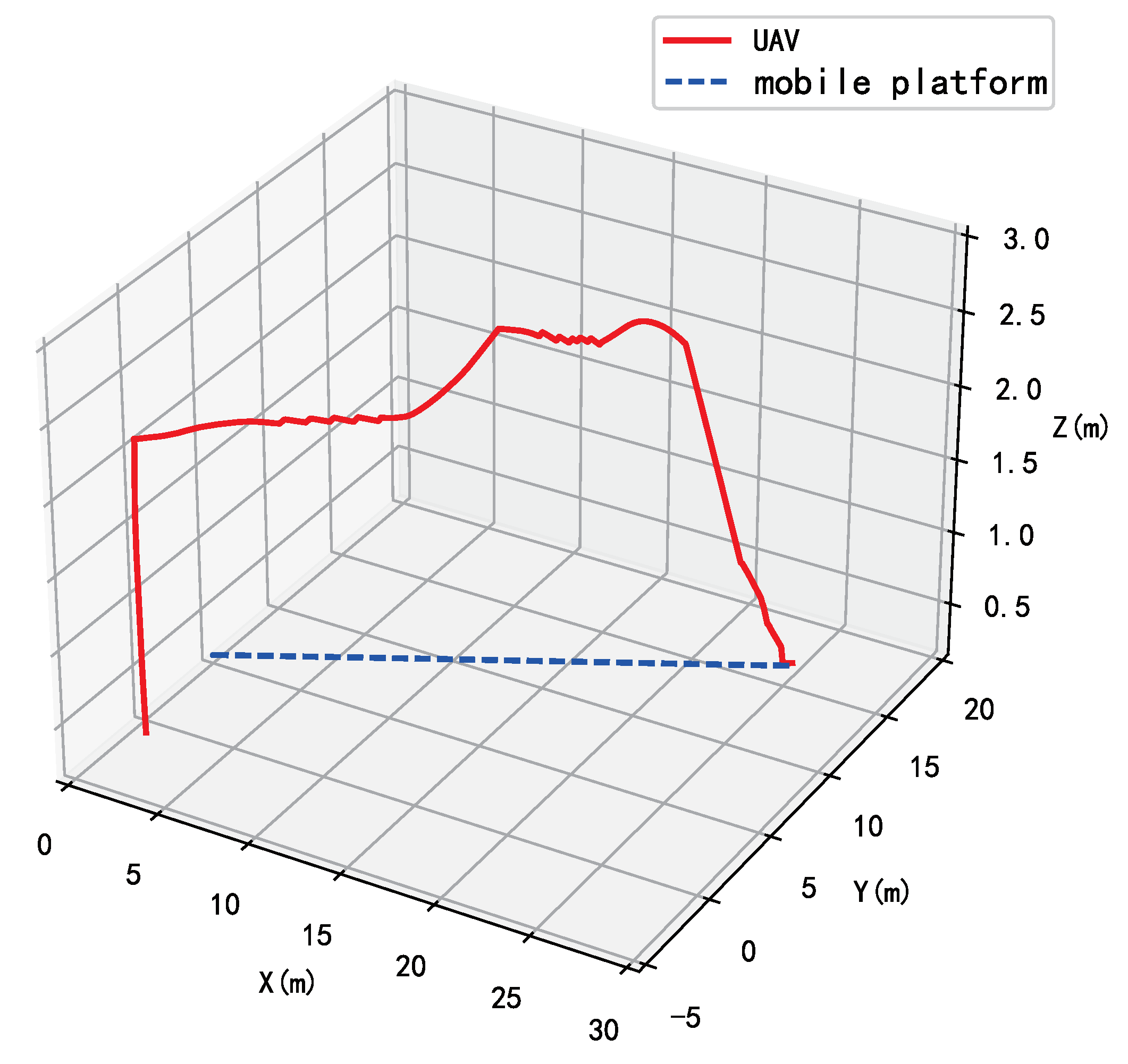
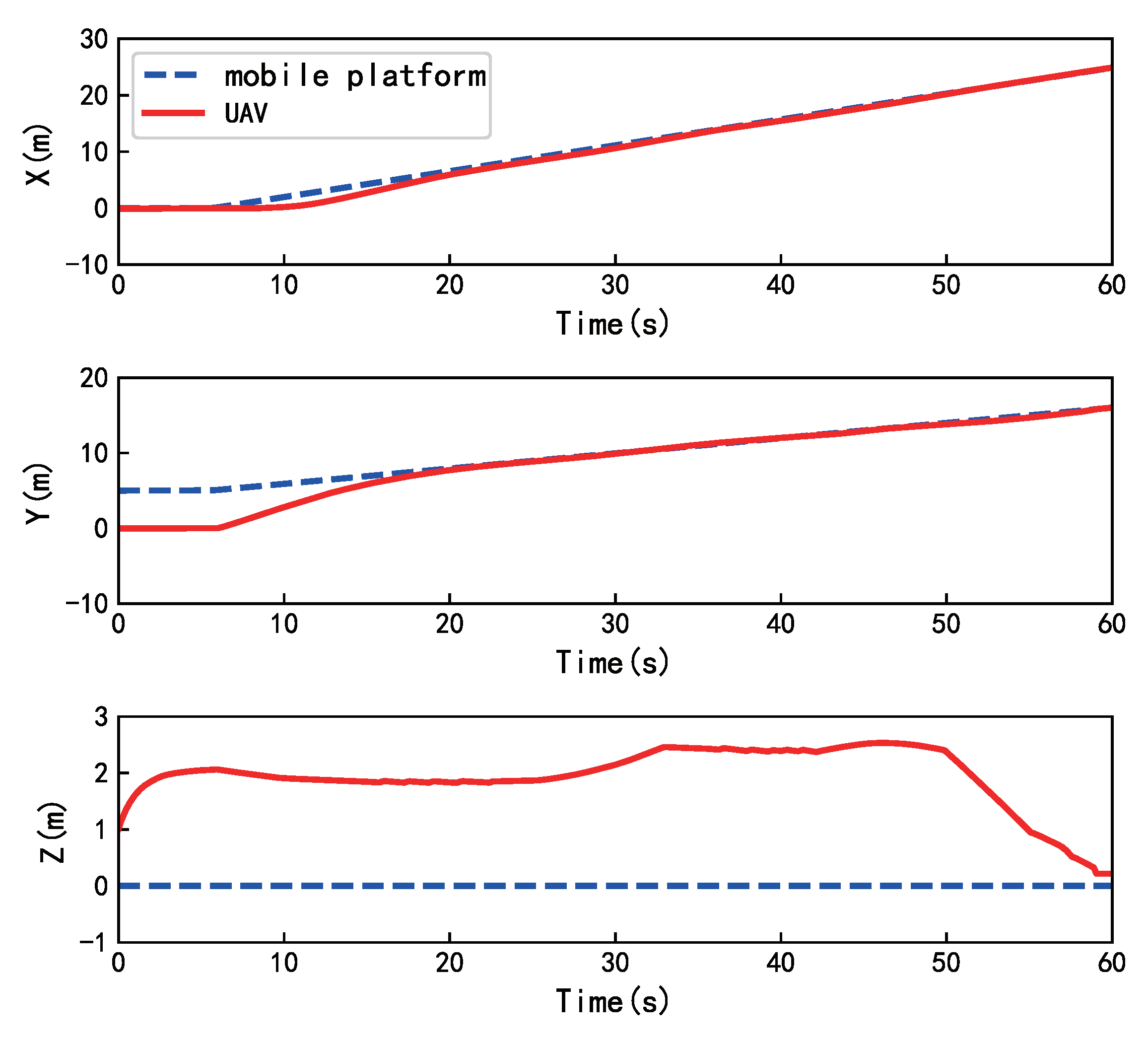
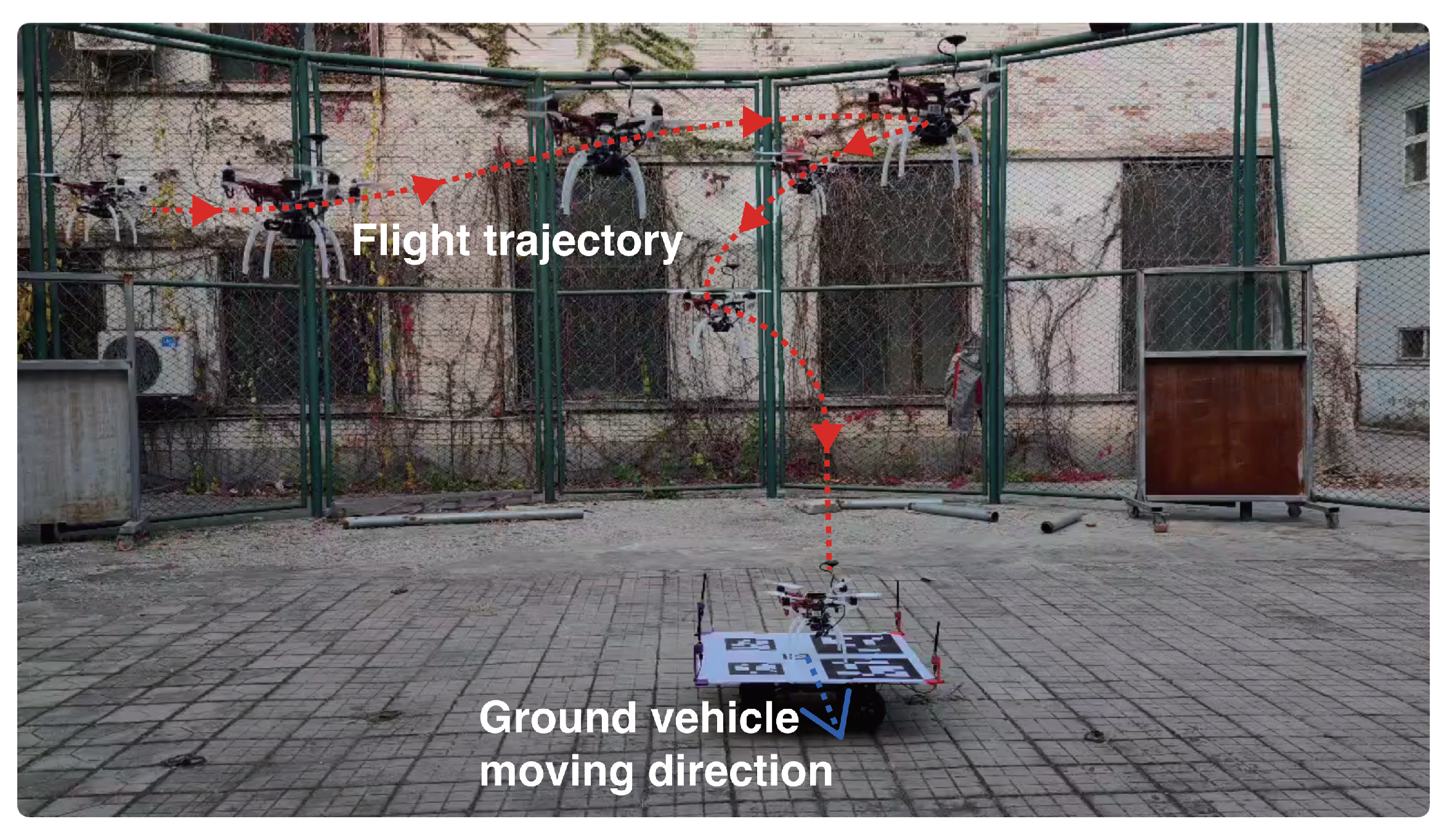
The overall configuration of the proposed landing scheme is composed of a moving ground vehicle carrying a custom-designed landmark with four UWB stations fixed in the corner of the landing pad. The UAV carries a downward camera to capture the landmark and a UWB label to estimate the relative position between the UAV and the moving vehicle. As shown in
Figure 2, The autonomous landing scheme is mainly divided into two stages: the approaching stage and the landing stage. In the approaching stage, when the autonomous landing mission starts, the UAV is far from the landing platform, the visual information is unreachable, and the pose estimation from vision cannot be provided. Therefore, the UAV obtains the relative position between the UAV and the ground mobile platform mainly relying on the UWB-IMU fusion positioning system, and the relative orientation is estimated by their onboard IMU. In addition, the UAV will remain at a certain height at this stage to have a wide field of vision for detecting the landmark. When the UAV is close to the landing platform and the visual information is captured, the UAV enters the landing stage based on the pose provided by both visual information and the UWB-IMU location system. At this stage, the UAV relies on UWB-IMU fusion positioning information to provide the relative position and velocity estimation of the mobile platform. The relative orientation is precisely tracked based on the visual information.
3. UWB-IMU-Based Localization in Approaching Stage
3.1. The Limitation of UWB-Based Position Estimation
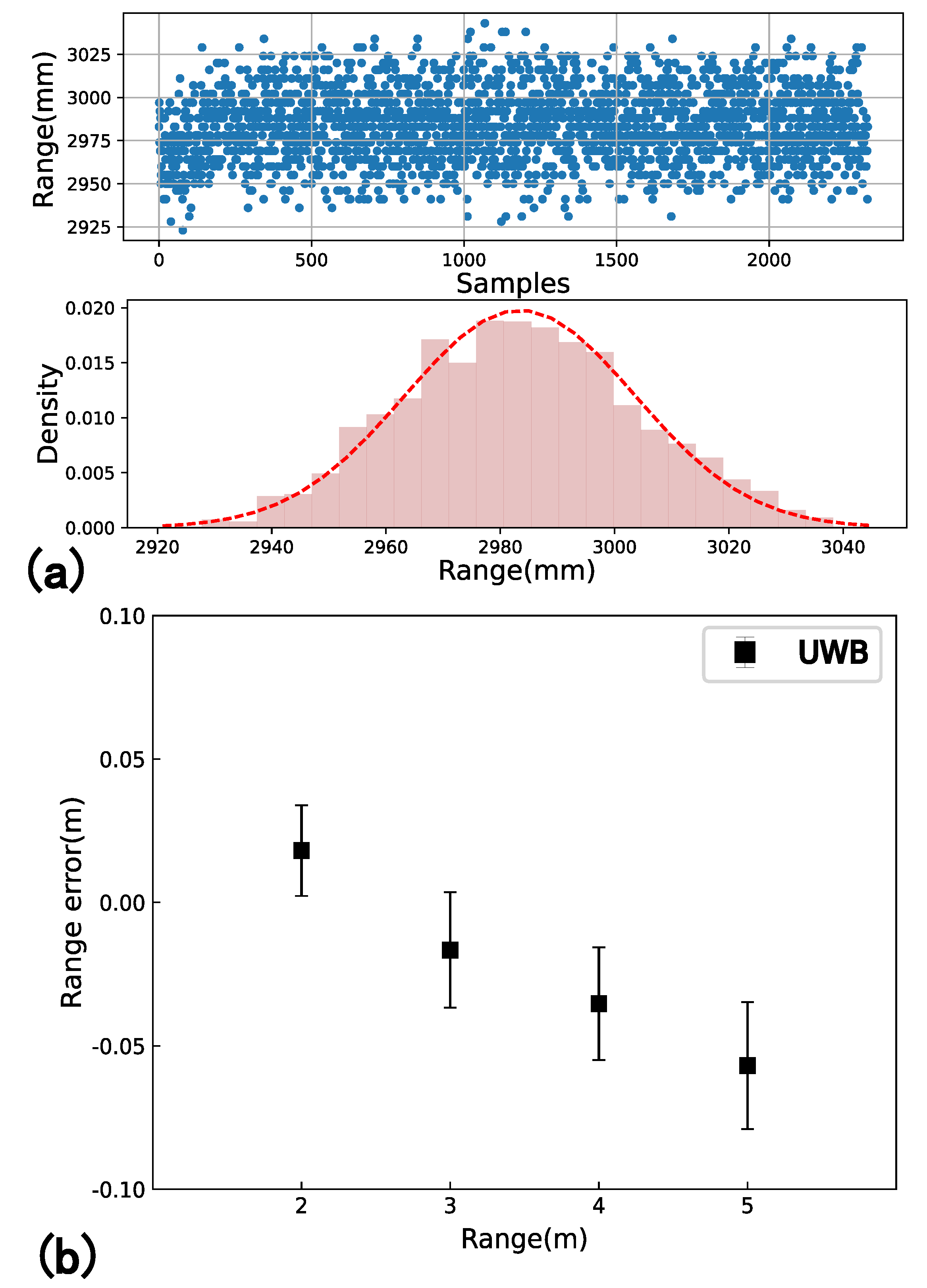
UWB is a sensor that can provide range measurement information between each UWB anchor. In most cases, the UWB positioning method has higher positioning accuracy in the X-Y plane, while it can only provide position measurement with a low frequency (about 3–4 Hz). In addition, the location accuracy is affected by a non-line-of-sight error (NLOS), i.e., the object occlusion between UWB modules. Such errors induce outliers in UWB readings.
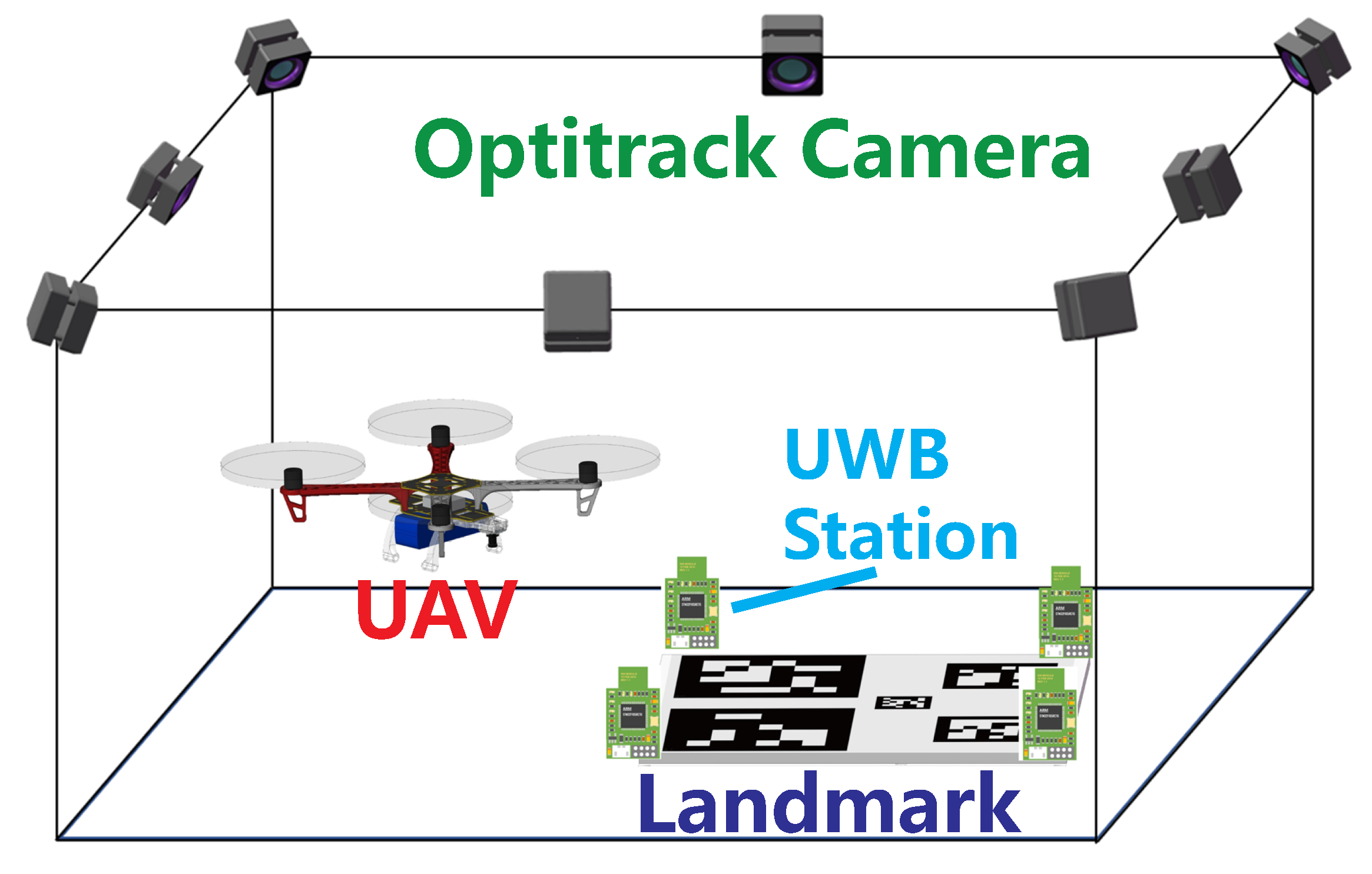
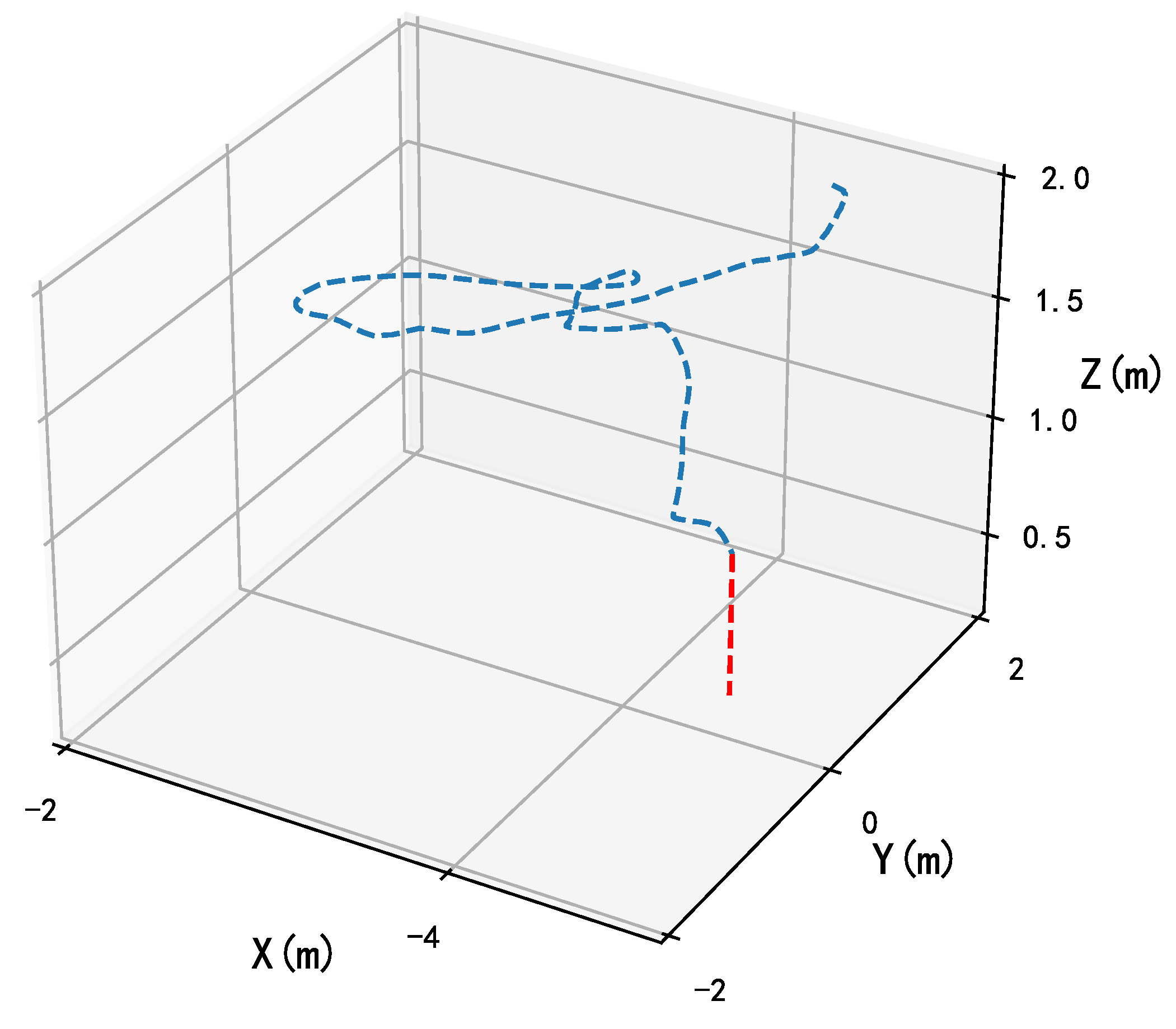
An experiment was conducted to evaluate the performance of UWB-based relative position estimation. As shown in
Figure 3, four UWB anchors were placed on the corner of the landing pad, and a UWB label was carried by the flying UAV for localization. To validate the reliability of the UWB readings, we used a motion capture system—Optitrack—to provide ground truth. Optitrack is widely used to track objects with the accuracy up to sub-millimeter resolution at high sensing frequency. Camera-mounted strobes illuminate small, retro-reflective markers, which are identified and processed to extract the high precision position and attitude of the objects. The Optitrack cameras tracked reflective markers on the UAV to obtain precise position data, which was then compared to the UWB result for validation.
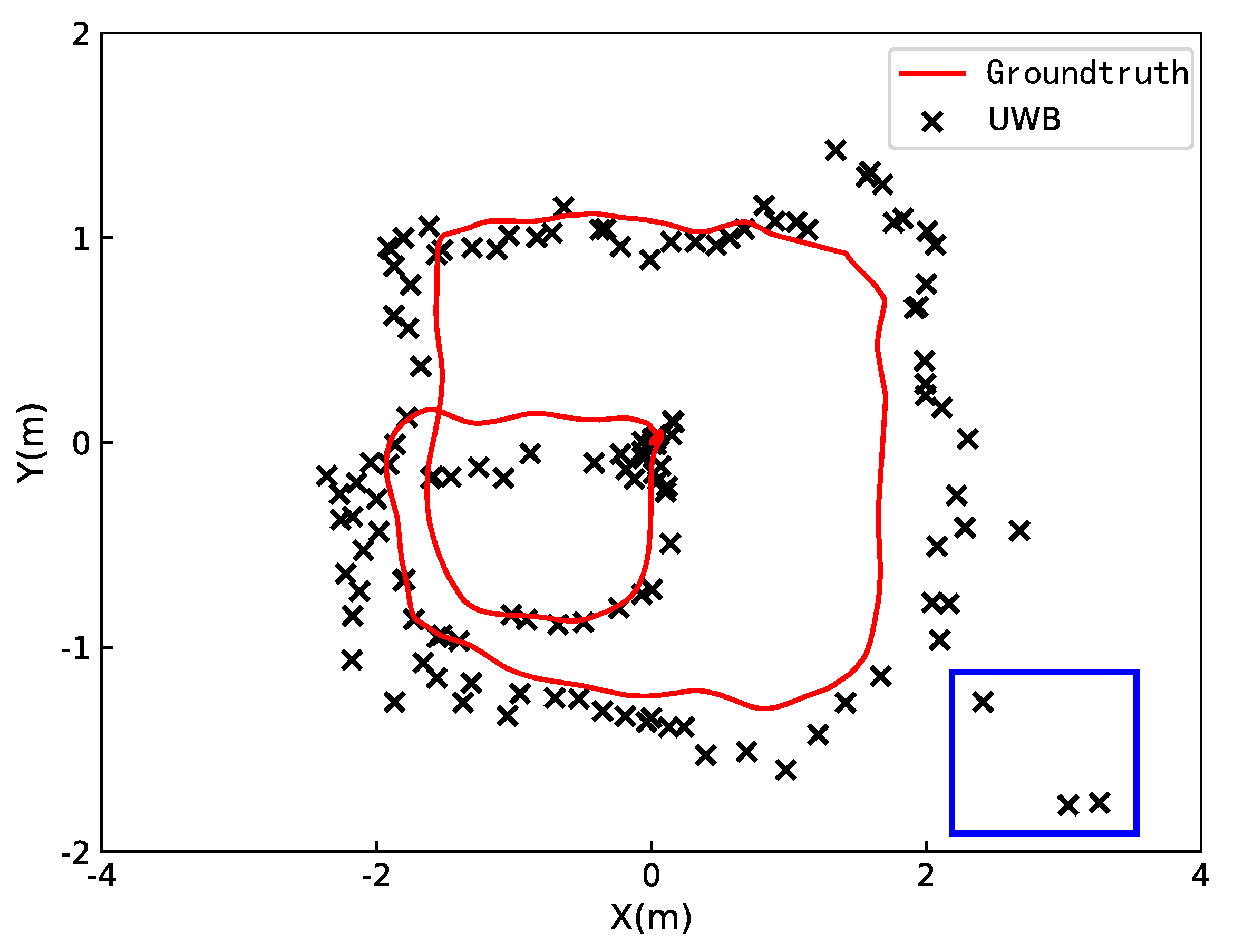
A typical localization result of UWB is shown in
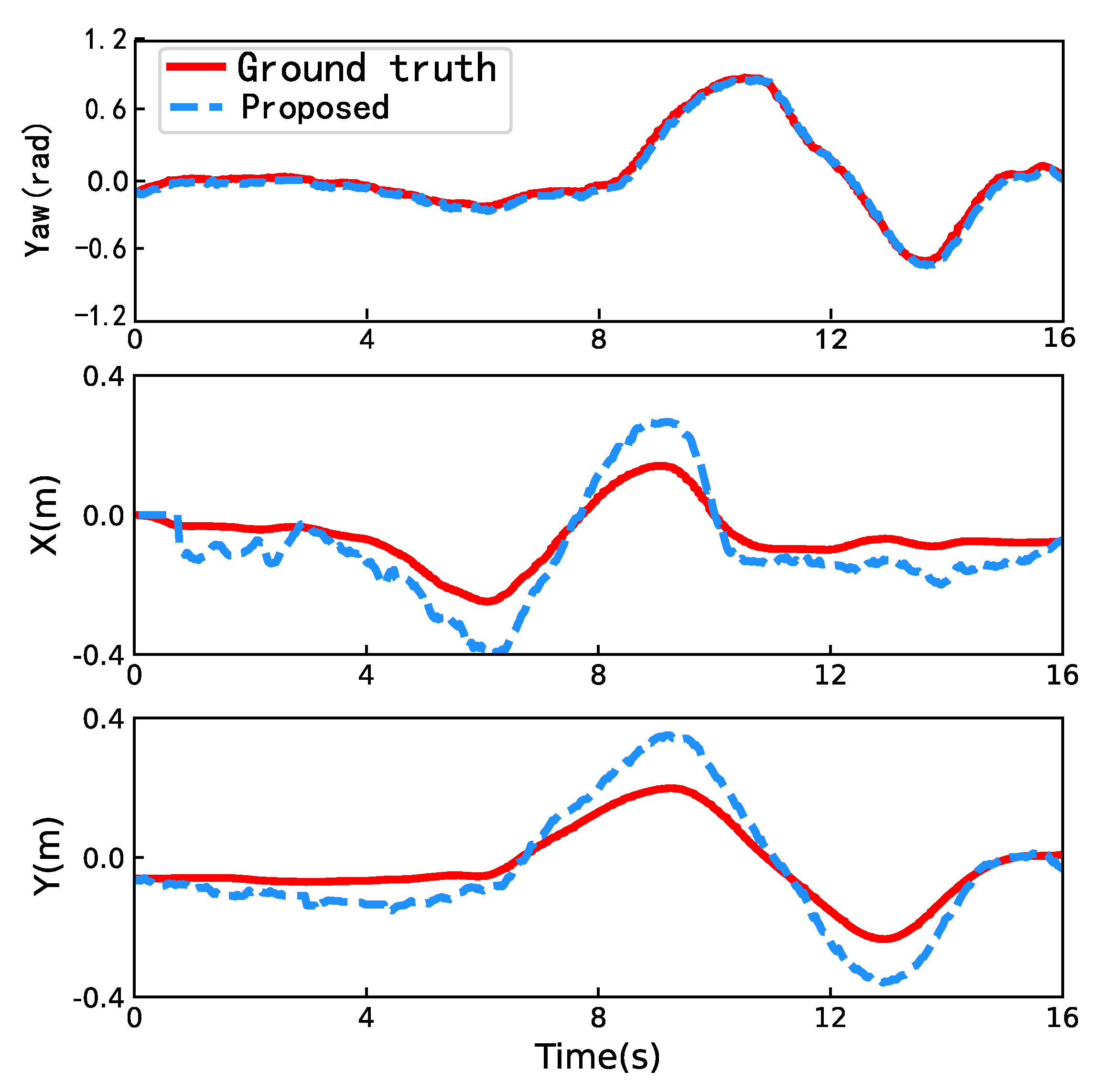
Figure 4. Based on
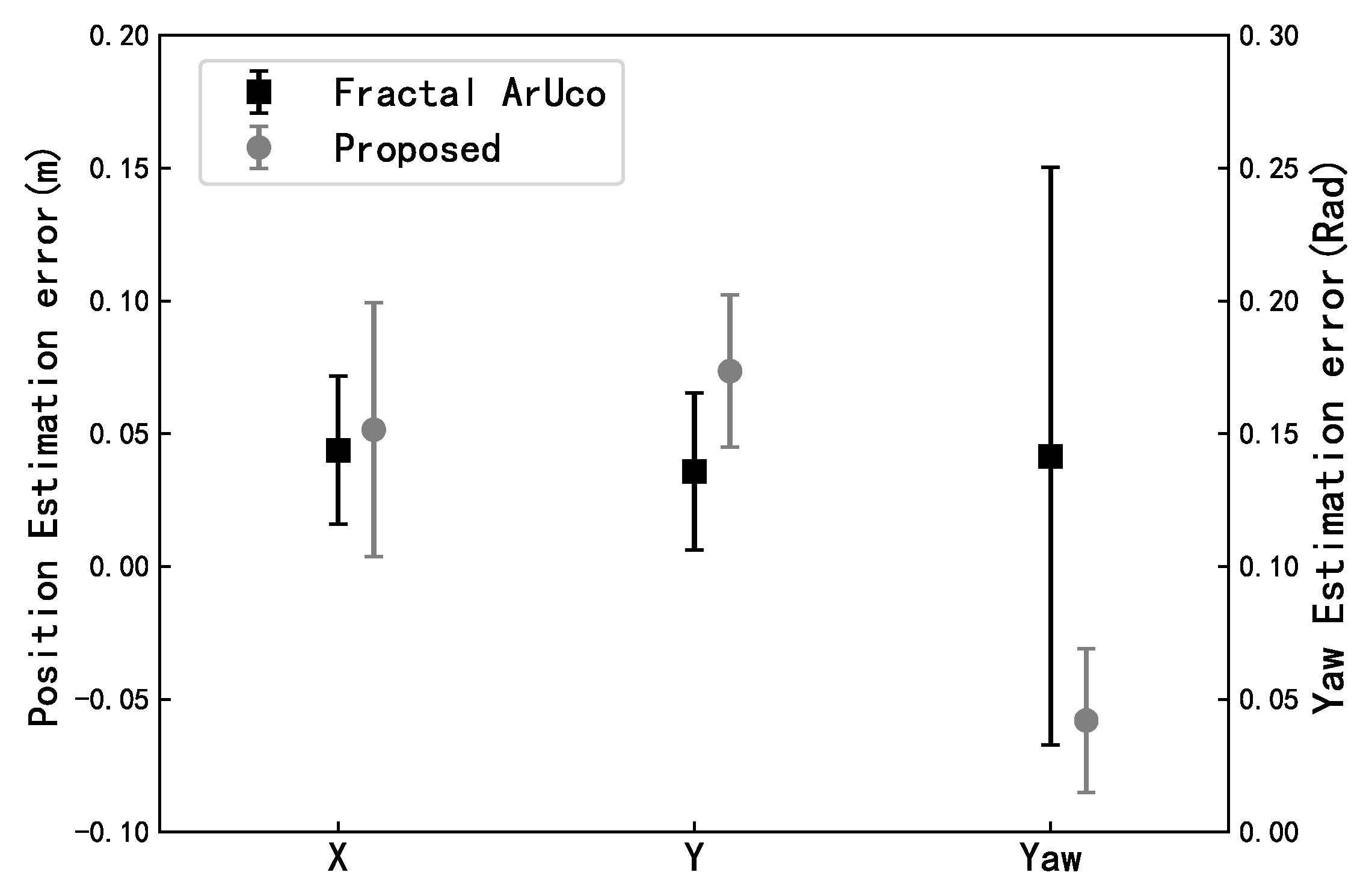
Figure 4, although the UWB measurement is barely consistent with the real flight trajectory, it demonstrates low consistency performance and unsmooth sensing results. Moreover, the outliers, as labeled in the blue square, increase the flight risk greatly and are not conducive to the completion of the flight mission. In this experiment, the mean localization error of UWB is 1.020 m and 0.617 m along the
x-axis and
y-axis, respectively. As a result, using UWB alone is unreliable for vehicle localization, and its precision is severely affected by the outliers of the UWB system.
3.2. UWB-IMU Position Estimation
As discussed above, due to the low update rate and outliers of UWB sensing, the position estimated by UWB is difficult for guaranteeing the smoothness and consistency. Therefore, the acceleration information provided by the IMU was taken into account. An EKF-based UWB-IMU sensor fusion algorithm is proposed to improve the sensing accuracy and boost the sampling frequency. Particularly, the proposed UWB-IMU sensory system was applied to estimate the relative position between the air and ground platforms in the mobile platform coordinate.
In the proposed EKF-based UWB-IMU localization algorithm, the acceleration from the IMU of the UAV
is taken as the input vector of the state equation. The state vector of the EKF state equation is composed of the three-dimensional relative positions and velocities of the UAV in the mobile platform coordinate. What is more, the noise of the IMU is relatively large in the practical application, and the acceleration bias is affected by various factors, such as temperature and mechanical vibration, leading to a serious drift for integration directly from the measurement of the IMU accelerometer. In order to solve the position drift, the acceleration deviations are considered into state vectors:
where
and
are the three-dimensional relative positions and velocities of the UAV in the mobile platform coordinate, and
is the bias of the acceleration of the UAV in the mobile platform coordinate.
Since the acceleration information from the IMU of the UAV is the acceleration measurements of the UAV in its body coordinate system, it is essential to estimate the relative orientation between the UAV and the landmark and project the acceleration of the body frame to the landmark coordinate system as we discussed in
Section 2.2. In the approaching stage, the relative orientation is obtained by the IMU measurement of the UAV and the IMU measurement from the mobile platform. In the landing stage, a more accurate yaw estimation is provided by the vision pose extraction described in
Section 4. With the estimated relative orientation, the relative acceleration of the UAV can be projected according to the attitude angle of the UAV in the platform coordinate system, and the rotation matrix is set as
. The state equation can be obtained as:
In order to construct the observation matrix of the EKF estimator, the distances between each anchor on the landing pad and the onboard UWB label of the UAV are measured as observations. The observed variable of the observation equation is the error between the measured distance of UWB and the predicted distance estimated from the state equation. The relative position of the UAVs is set as
. Then, the distance between the UAV and the
i-th UWB station is:
At the same time, based on the state equation, Equation (
7), the posterior estimated value of the position of the UAV in the platform coordinate system is
, and the distance information between the UAV and the
i-th UWB base station installed on the landing platform should be:
Here, first-order Taylor expansion was applied to Equation (
8) at
, and we obtain:
Subtracting the distance estimated from the equation of state from the measured distance:
Then, the observation equation is:
Here n is the number of the UWB stations, and N is the dimension of the state vector.
Due to the instability of the readings of the UWB sensor, even the measured distance can be accurate to the centimeter level in most cases, while occasionally, the measured distance is completely wrong due to the influence of the complex environment, which will lead to a sharp increase in estimate errors. At the same time, the IMU readings are also quite noisy, especially when the micro UAV is moving slowly, which means that it is impractical to rely too much on the IMU. Therefore, when adjusting the covariance matrices Q and R, the choice tends to rely more on UWB readings. In order to alleviate the abrupt outlier measurements from UWB, the distance estimated according to the state equation is used to compare with the measured value of the UWB sensors in the update stage of EKF. If the error exceeds a certain threshold, the current measurement of UWB is discarded, and the position continues to be predicted according to the state equation until the next UWB range measurement is updated.
With the IMU-based prediction step and the UWB-based update step, the proposed method can eliminate the shortage of the IMU integral cumulative error and the occasional jump out of the UWB range measurements, making the positioning result smoother and more reliable. In addition, the EKF can also increase the localization frequency to make up for the low frequency of UWB measurements. As shown in
Figure 5, the red line represents the UWB measurement information, and the black one is IMU information. When the UWB range measurement is available, normal prediction and update steps are performed based on the EKF. When UWB range measurement is unavailable, IMU information is used for forecasting the position estimation. Due to the high frequency of IMU measurement release, the fusion positioning algorithm can improve the positioning frequency while maintaining accuracy so that the UAV can obtain real-time perception information when maneuvering quickly.