Compression and Deformation Behaviors of Hierarchical Circular-Cell Lattice Structure with Enhanced Mechanical Properties and Energy Absorption Capacity
Abstract
1. Introduction
2. The Novel Circular-Base Configuration of Unit Cell with Structural Hierarchy
3. Experiment and Simulation
3.1. Fabrication of the Lattice Samples Using the 3D Printing Technique
3.2. Compression Experiment
3.3. Finite Element Models
4. Results and Discussion
4.1. Compression Behaviors and Mechanical Properties
4.2. Deformation Mechanism and Failure Behaviors
4.3. Energy Absorption Capacity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fernandes, M.C.; Aizenberg, J.; Weaver, J.C.; Bertoldi, K. Mechanically robust lattices inspired by deep-sea glass sponges. Nat. Mater. 2021, 20, 237–241. [Google Scholar] [CrossRef] [PubMed]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef]
- Obadimu, S.O.; Kourousis, K.I. Compressive Behaviour of Additively Manufactured Lattice Structures: A Review. Aerospace 2021, 8, 207. [Google Scholar] [CrossRef]
- Di Caprio, F.; Acanfora, V.; Franchitti, S.; Sellitto, A.; Riccio, A. Hybrid Metal/Composite Lattice Structures: Design for Additive Manufacturing. Aerospace 2019, 6, 71. [Google Scholar] [CrossRef]
- Li, C.; Lei, H.; Liu, Y.; Zhang, X.; Xiong, J.; Zhou, H.; Fang, D. Crushing behavior of multi-layer metal lattice panel fabricated by selective laser melting. Int. J. Mech. Sci. 2018, 145, 389–399. [Google Scholar] [CrossRef]
- Sun, Z.P.; Guo, Y.B.; Shim, V.P.W. Characterisation and modeling of additively-manufactured polymeric hybrid lattice structures for energy absorption. Int. J. Mech. Sci. 2021, 191, 106101. [Google Scholar] [CrossRef]
- Tan, C.; Zou, J.; Li, S.; Jamshidi, P.; Abena, A.; Forsey, A.; Moat, R.J.; Essa, K.; Wang, M.; Zhou, K.; et al. Additive manufacturing of bio-inspired multi-scale hierarchically strengthened lattice structures. Int. J. Mach. Tools Manuf. 2021, 167, 103764. [Google Scholar] [CrossRef]
- Refai, K.; Montemurro, M.; Brugger, C.; Saintier, N. Determination of the effective elastic properties of titanium lattice structures. Mech. Adv. Mater. Struct. 2019, 27, 1966–1982. [Google Scholar] [CrossRef]
- Goh, G.D.; Agarwala, S.; Goh, G.L.; Dikshit, V.; Sing, S.L.; Yeong, W.Y. Additive manufacturing in unmanned aerial vehicles (UAVs): Challenges and potential. Aerosp. Sci. Technol. 2017, 63, 140–151. [Google Scholar] [CrossRef]
- Bici, M.; Brischetto, S.; Campana, F.; Ferro, C.G.; Seclì, C.; Varetti, S.; Maggiore, P.; Mazza, A. Development of a multifunctional panel for aerospace use through SLM additive manufacturing. Procedia CIRP 2018, 67, 215–220. [Google Scholar] [CrossRef]
- Alsaidi, B.; Joe, W.Y.; Akbar, M. Computational Analysis of 3D Lattice Structures for Skin in Real-Scale Camber Morphing Aircraft. Aerospace 2019, 6, 79. [Google Scholar] [CrossRef]
- Deng, H.; Zhao, J.; Wang, C. Leaf Vein-Inspired Bionic Design Method for Heat Exchanger Infilled with Graded Lattice Structure. Aerospace 2021, 8, 237. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and specific energy absorption of additively-manufactured metallic BCC metamaterials composed of tapered beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Bai, L.; Gong, C.; Chen, X.; Sun, Y.; Xin, L.; Pu, H.; Peng, Y.; Luo, J. Mechanical properties and energy absorption capabilities of functionally graded lattice structures: Experiments and simulations. Int. J. Mech. Sci. 2020, 182, 105735. [Google Scholar] [CrossRef]
- Bonatti, C.; Mohr, D. Large deformation response of additively-manufactured FCC metamaterials: From octet truss lattices towards continuous shell mesostructures. Int. J. Plast. 2017, 92, 122–147. [Google Scholar] [CrossRef]
- Gorguluarslan, R.M.; Gungor, O.U.; Yıldız, S.; Erem, E. Energy absorption behavior of stiffness optimized graded lattice structures fabricated by material extrusion. Meccanica 2021, 56, 2825–2841. [Google Scholar] [CrossRef]
- Sun, Z.P.; Guo, Y.B.; Shim, V.P.W. Deformation and energy absorption characteristics of additively-manufactured polymeric lattice structures—Effects of cell topology and material anisotropy. Thin-Walled Struct. 2021, 169, 108420. [Google Scholar] [CrossRef]
- Osman, M.M.; Shazly, M.; El-Danaf, E.A.; Jamshidi, P.; Attallah, M.M. Compressive behavior of stretched and composite microlattice metamaterial for energy absorption applications. Compos. Part B Eng. 2020, 184, 107715. [Google Scholar] [CrossRef]
- Chen, X.Y.; Tan, H.F. An effective length model for octet lattice. Int. J. Mech. Sci. 2018, 140, 279–287. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical behaviors of SLM additive manufactured octet-truss and truncated-octahedron lattice structures with uniform and taper beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef]
- Chen, X.; Ji, Q.; Wei, J.; Tan, H.; Yu, J.; Zhang, P.; Laude, V.; Kadic, M. Light-weight shell-lattice metamaterials for mechanical shock absorption. Int. J. Mech. Sci. 2020, 169, 105288. [Google Scholar] [CrossRef]
- Li, P.; Yang, F.; Bian, Y.; Zhang, S.; Wang, L. Deformation pattern classification and energy absorption optimization of the eccentric body centered cubic lattice structures. Int. J. Mech. Sci. 2021, 212, 106813. [Google Scholar] [CrossRef]
- White, B.C.; Garland, A.; Alberdi, R.; Boyce, B.L. Interpenetrating lattices with enhanced mechanical functionality. Addit. Manuf. 2021, 38, 101741. [Google Scholar] [CrossRef]
- Zhou, H.; Cao, X.; Li, C.; Zhang, X.; Fan, H.; Lei, H.; Fang, D. Design of self-supporting lattices for additive manufacturing. J. Mech. Phys. Solids 2021, 148, 104298. [Google Scholar] [CrossRef]
- Alomar, Z.; Concli, F. Compressive behavior assessment of a newly developed circular cell-based lattice structure. Mater. Des. 2021, 205, 109716. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Meng, J.; Zhou, H.; Liu, Y.; Zhang, X.; Wang, P.; Fang, D. Evaluation of compressive properties of SLM-fabricated multi-layer lattice structures by experimental test and μ-CT-based finite element analysis. Mater. Des. 2019, 169, 107685. [Google Scholar] [CrossRef]
- Bai, L.; Xu, Y.; Chen, X.; Xin, L.; Zhang, J.; Li, K.; Sun, Y. Improved mechanical properties and energy absorption of Ti6Al4V laser powder bed fusion lattice structures using curving lattice struts. Mater. Des. 2021, 211, 110140. [Google Scholar] [CrossRef]
- Novak, N.; Al-Ketan, O.; Krstulović-Opara, L.; Rowshan, R.; Abu Al-Rub, R.K.; Vesenjak, M.; Ren, Z. Quasi-static and dynamic compressive behaviour of sheet TPMS cellular structures. Compos. Struct. 2021, 266, 113801. [Google Scholar] [CrossRef]
- Sharma, D.; Hiremath, S.S. Additively manufactured mechanical metamaterials based on triply periodic minimal surfaces: Performance, challenges, and application. Mech. Adv. Mater. Struct. 2021, 1–31. [Google Scholar] [CrossRef]
- Ingrole, A.; Aguirre, T.G.; Fuller, L.; Donahue, S.W. Bioinspired energy absorbing material designs using additive manufacturing. J. Mech. Behav. Biomed. Mater. 2021, 119, 104518. [Google Scholar] [CrossRef]
- McKittrick, J.; Chen, P.Y.; Tombolato, L.; Novitskaya, E.E.; Trim, M.W.; Hirata, G.A.; Olevsky, E.A.; Horstemeyer, M.F.; Meyers, M.A. Energy absorbent natural materials and bioinspired design strategies: A review. Mater. Sci.Eng. C 2010, 30, 331–342. [Google Scholar] [CrossRef]
- Wegst, U.G.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Guo, W.; Wang, H.; Huang, Y.; Yang, R.; Hu, Z.; Chen, D.; Xu, J.; Ritchie, R.O. Strong and Tough Bioinspired Additive-Manufactured Dual-Phase Mechanical Metamaterial Composites. J. Mech. Phys. Solids 2021, 149, 104341. [Google Scholar] [CrossRef]
- Wang, P.; Yang, F.; Lu, G.; Bian, Y.; Zhang, S.; Zheng, B.; Fan, H. Anisotropic compression behaviors of bio-inspired modified body-centered cubic lattices validated by additive manufacturing. Compos. Part B Eng. 2022, 234, 109724. [Google Scholar] [CrossRef]
- He, M.; Li, Y.; Yin, J.; Sun, Q.; Xiong, W.; Li, S.; Yang, L.; Hao, L. Compressive performance and fracture mechanism of bio-inspired heterogeneous glass sponge lattice structures manufactured by selective laser melting. Mater. Des. 2022, 214, 110396. [Google Scholar] [CrossRef]
- Tsang, H.H.; Tse, K.M.; Chan, K.Y.; Lu, G.; Lau, A.K.T. Energy absorption of muscle-inspired hierarchical structure: Experimental investigation. Compos. Struct. 2019, 226, 111250. [Google Scholar] [CrossRef]
- Duan, S.; Wu, S.; Hua, M.; Wu, D.; Yan, Y.; Zhu, X.; He, X. Tendon-inspired Anti-Freezing Tough Gels. iScience 2021, 24, 102989. [Google Scholar] [CrossRef]
- Kong, E.; Liu, D.; Guo, X.; Yang, W.; Sun, J.; Li, X.; Zhan, K.; Cui, D.; Lin, J.; Zhang, A. Anatomical and chemical characteristics associated with lodging resistance in wheat. Crop J. 2013, 1, 43–49. [Google Scholar] [CrossRef]
- Ha, N.S.; Pham, T.M.; Hao, H.; Lu, G. Energy absorption characteristics of bio-inspired hierarchical multi-cell square tubes under axial crushing. Int. J. Mech. Sci. 2021, 201, 106464. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, Y.; Yin, Q.; Pan, F.; Cui, C.; Zhang, Z.; Liu, B. Advances in mechanics of hierarchical composite materials. Compos. Sci. Technol. 2021, 214, 108970. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, Z.; Wang, M.Y.; Feih, S. Hierarchical sheet triply periodic minimal surface lattices: Design, geometric and mechanical performance. Mater. Des. 2021, 209, 109931. [Google Scholar] [CrossRef]
- Chen, Y.; Li, T.; Jia, Z.; Scarpa, F.; Yao, C.-W.; Wang, L. 3D printed hierarchical honeycombs with shape integrity under large compressive deformations. Mater. Des. 2018, 137, 226–234. [Google Scholar] [CrossRef]
- Yin, S.; Li, J.; Chen, H.; Ritchie, R.O.; Xu, J. Design and strengthening mechanisms in hierarchical architected materials processed using additive manufacturing. Int. J. Mech. Sci. 2018, 149, 150–163. [Google Scholar] [CrossRef]
- Yin, S.; Chen, H.; Li, J.; Yu, T.X.; Xu, J. Effects of architecture level on mechanical properties of hierarchical lattice materials. Int. J. Mech. Sci. 2019, 157–158, 282–292. [Google Scholar] [CrossRef]
- Gong, C.; Bai, Z.; Wang, Y.; Zhang, L. On the crashworthiness performance of novel hierarchical multi-cell tubes under axial loading. Int. J. Mech. Sci. 2021, 206, 106599. [Google Scholar] [CrossRef]
- Tsang, H.H.; Raza, S. Impact energy absorption of bio-inspired tubular sections with structural hierarchy. Compos. Struct. 2018, 195, 199–210. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, Y.; Wang, X.; Wei, K. Compression behavior of strut-reinforced hierarchical lattice—Experiment and simulation. Int. J. Mech. Sci. 2021, 210, 106749. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Zhang, X.; Wang, P.; Zhou, H.; Zhao, Z.; Fang, D. Deformation behavior of heterogeneous multi-morphology lattice core hybrid structures. Addit. Manuf. 2021, 37, 101674. [Google Scholar] [CrossRef]
- Liu, C.; Lertthanasarn, J.; Pham, M.-S. The origin of the boundary strengthening in polycrystal-inspired architected materials. Nat. Commun. 2021, 12, 4600. [Google Scholar] [CrossRef]
- Yang, H.; Cao, X.; Liao, B.; Wang, G.; Huang, Z.; Li, Y. Mechanical properties of bio-molecular inspired MnL2n cage-lattices: Simulations & experiments. Mater. Sci.Eng. A 2021, 826, 141991. [Google Scholar] [CrossRef]
- ABAQUS. Analysis User’s Manual Version 6.9; Software for Finite Element Analysis and Computer-Aided Engineering; ABAQUS Inc.: Providence, RI, USA, 2009.
- Bai, L.; Gong, C.; Chen, X.; Zheng, J.; Yang, J.; Li, K.; Sun, Y. Heterogeneous compressive responses of additively manufactured Ti-6Al-4V lattice structures by varying geometric parameters of cells. Int. J. Mech. Sci. 2021, 214, 106922. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular solids: Structure & properties, Oxford: Pergamon Press. Adv. Polym. Technol. 1989, 9, 165–166. [Google Scholar]
- Wang, X.; Zhu, L.; Sun, L.; Li, N. Optimization of graded filleted lattice structures subject to yield and buckling constraints. Mater. Des. 2021, 206, 109746. [Google Scholar] [CrossRef]
- Li, Q.M.; Magkiriadis, I.; Harrigan, J.J. Compressive strain at the onset of densification of cellular solids. J. Cell. Plast. 2016, 42, 371–392. [Google Scholar] [CrossRef]



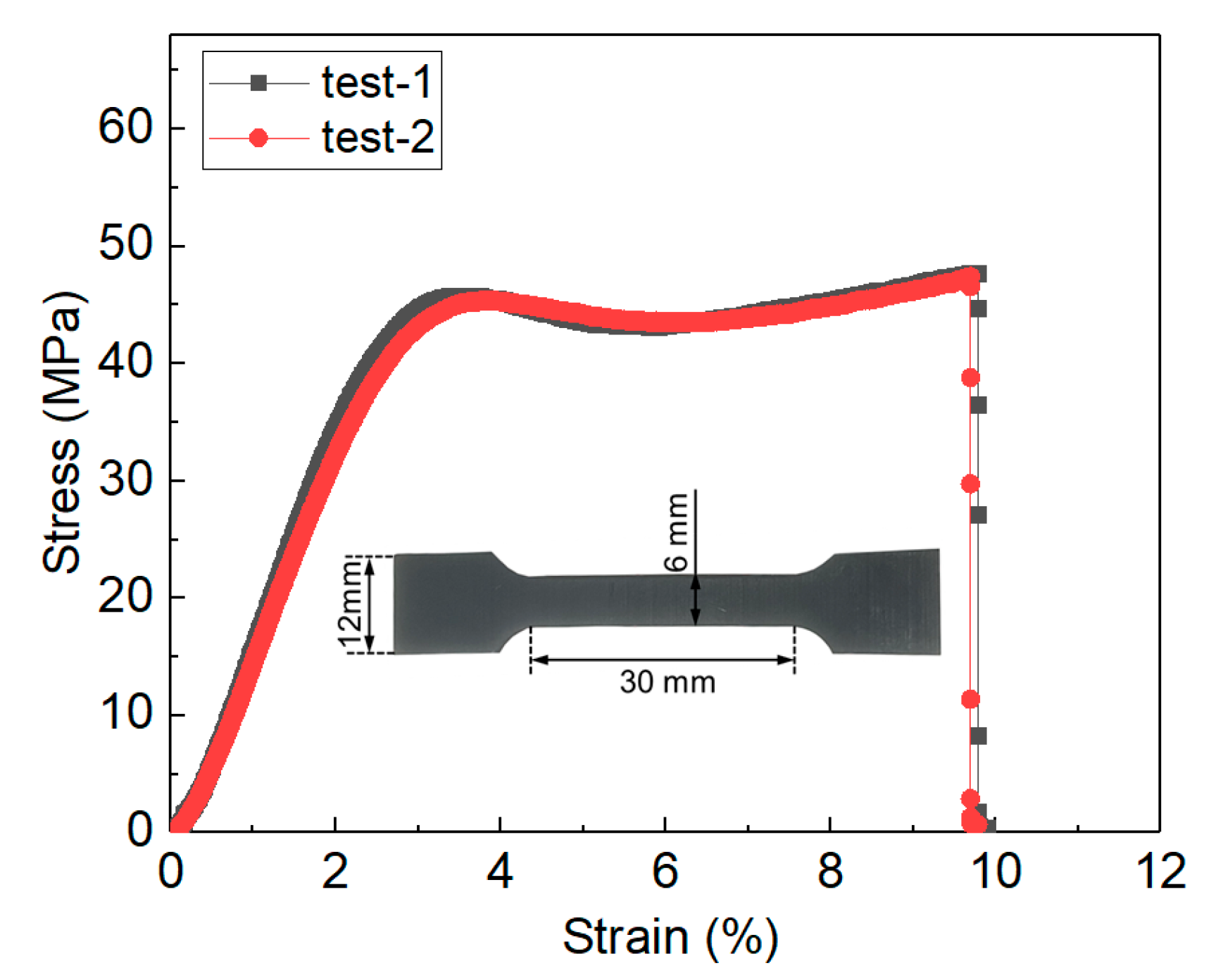
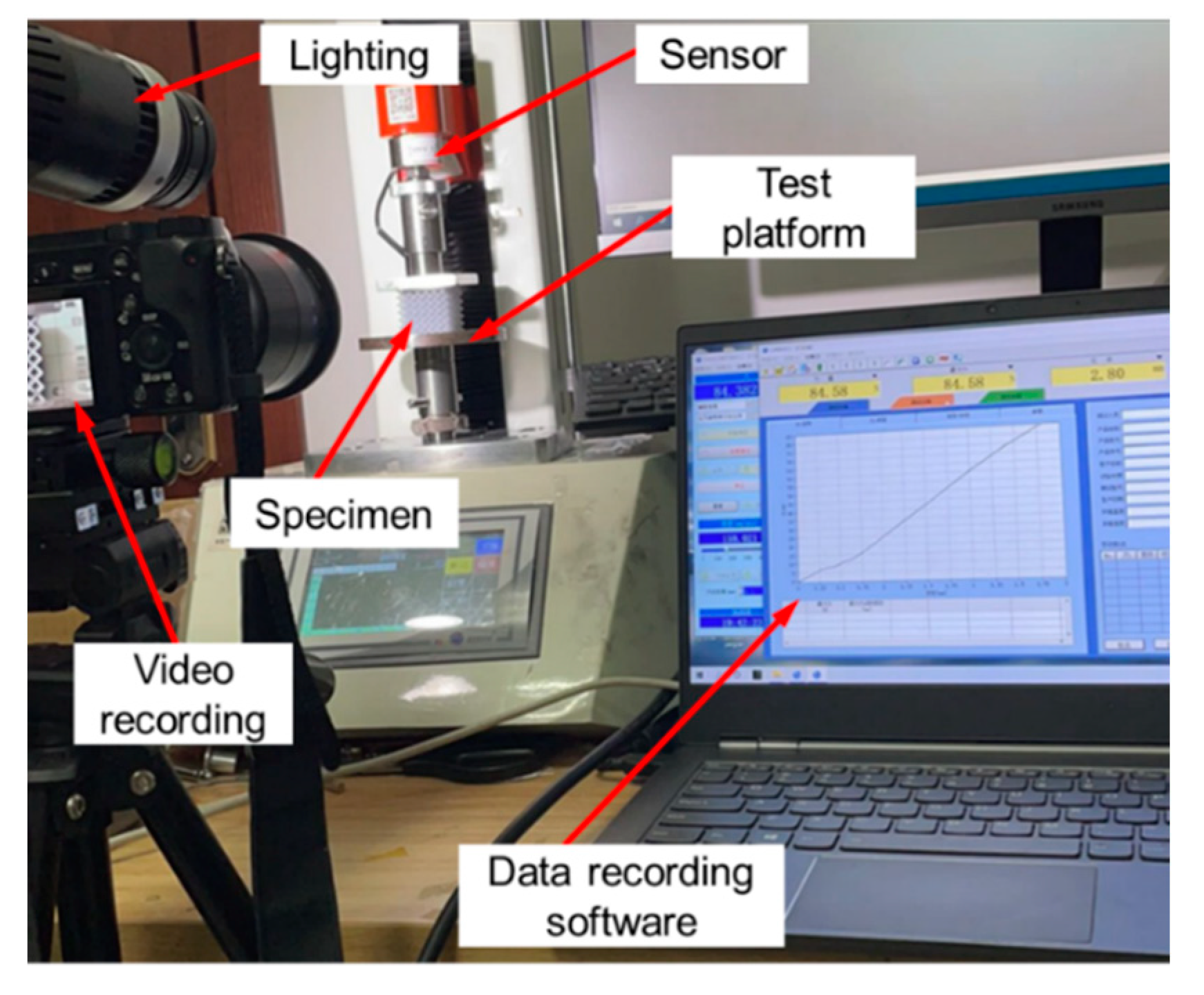

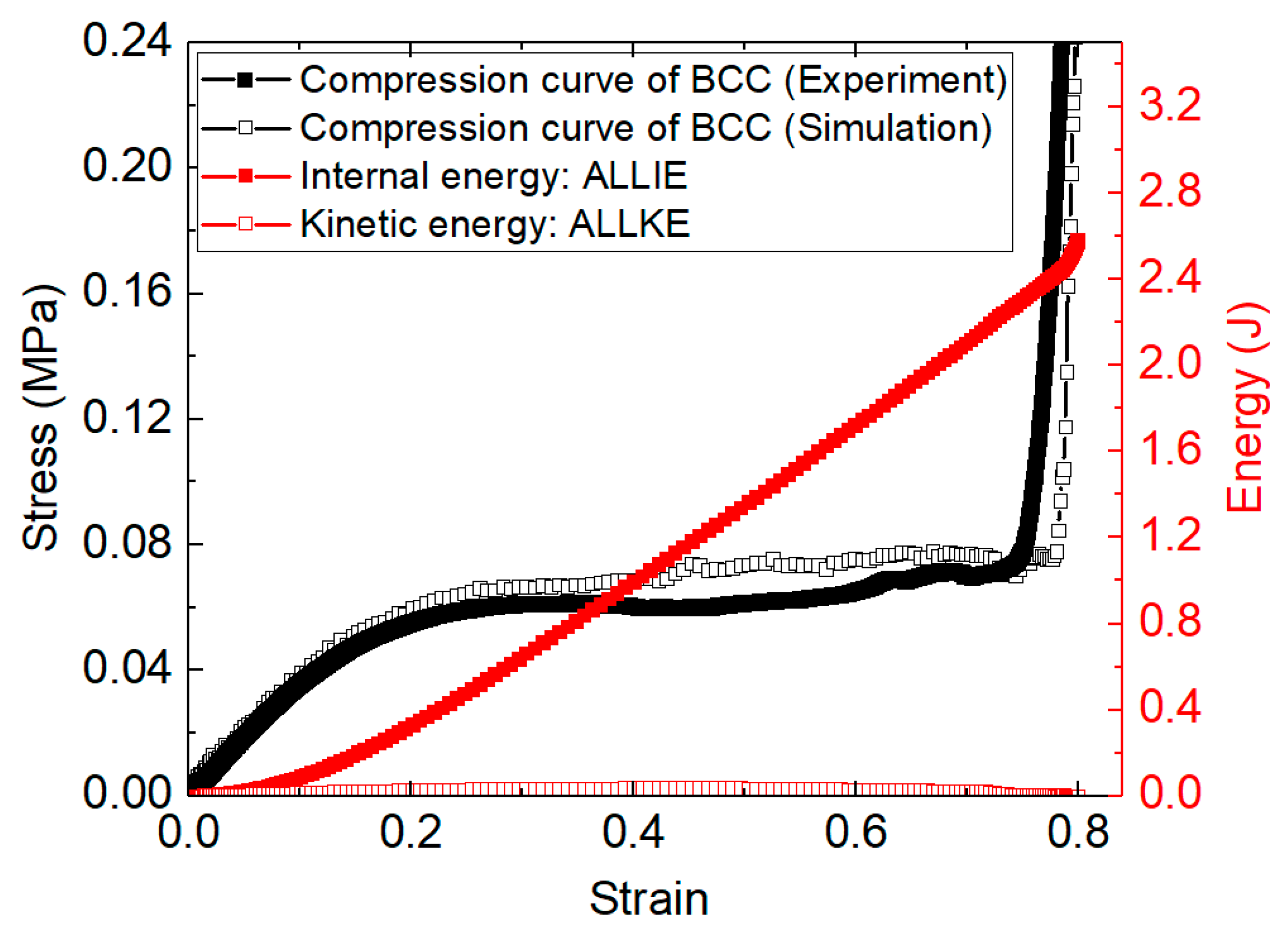




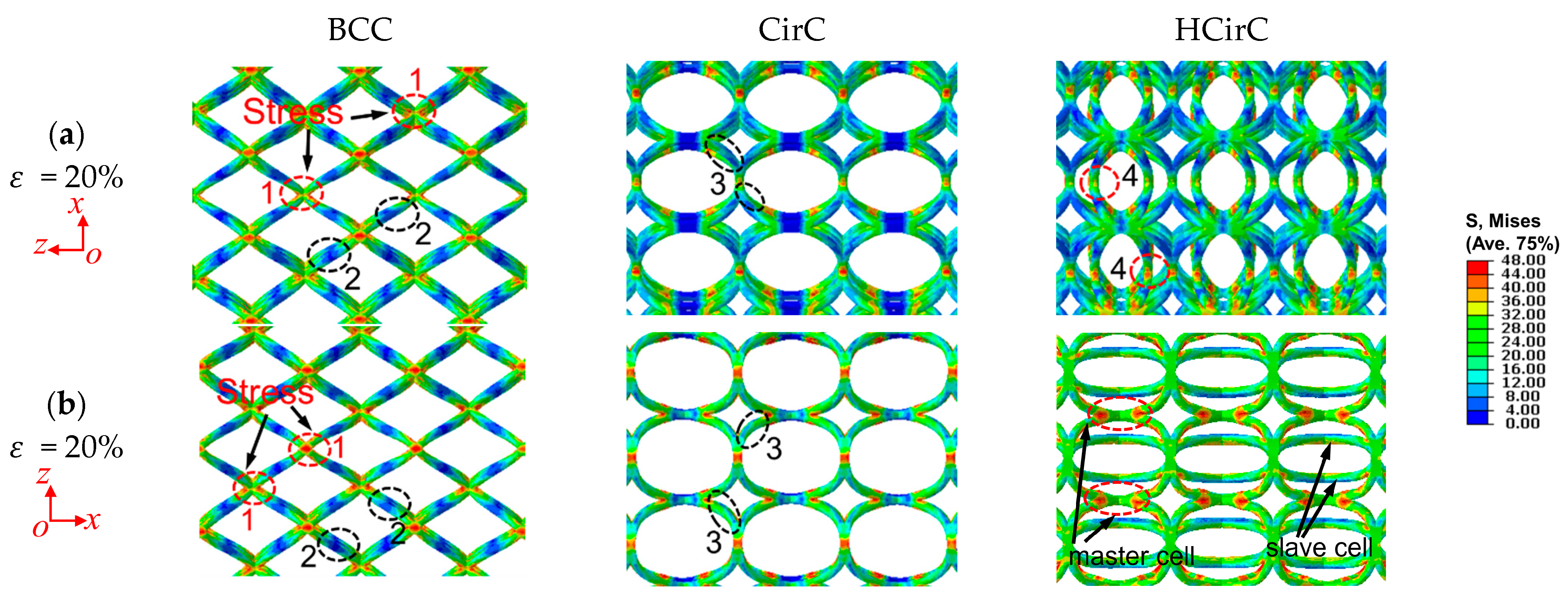
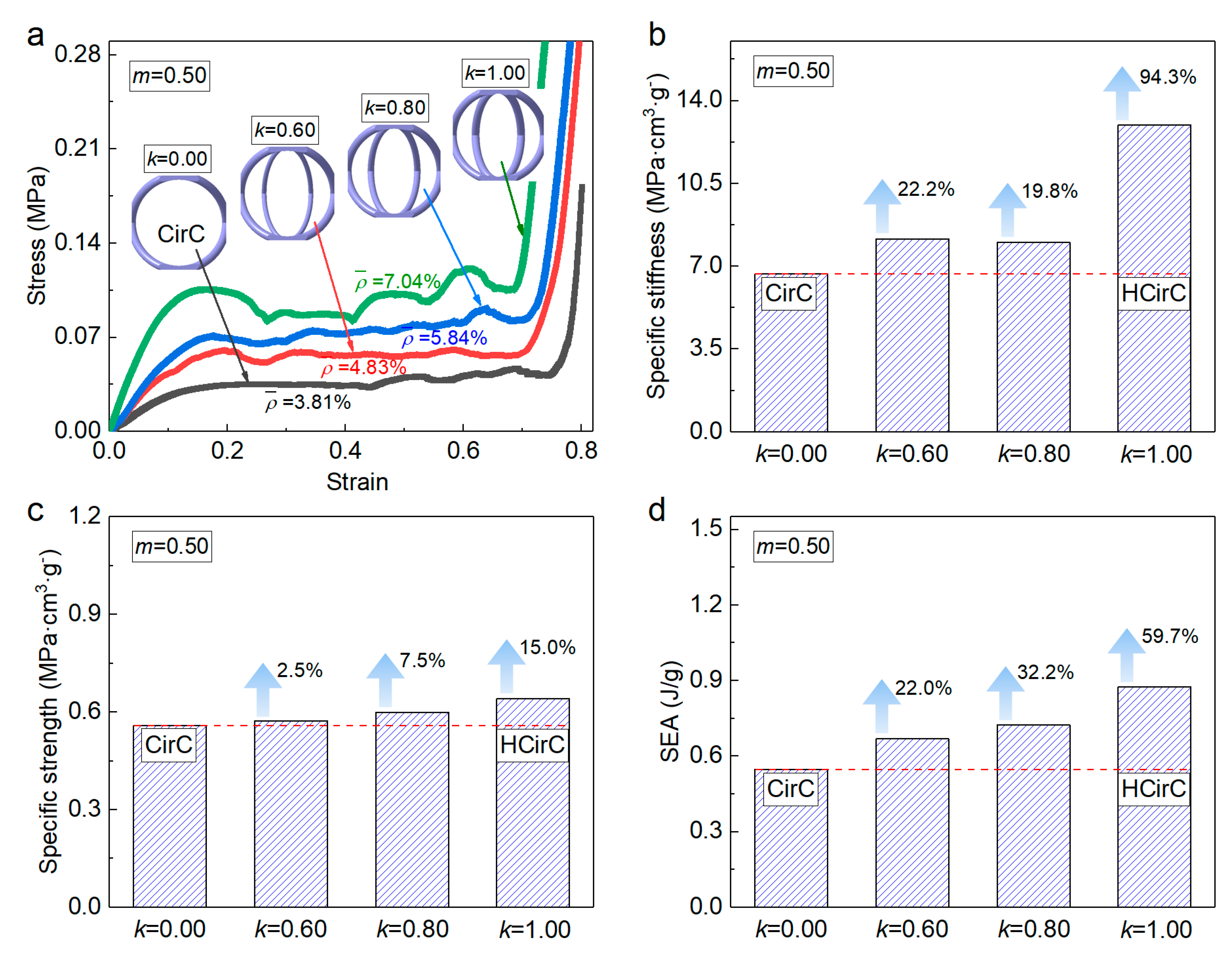
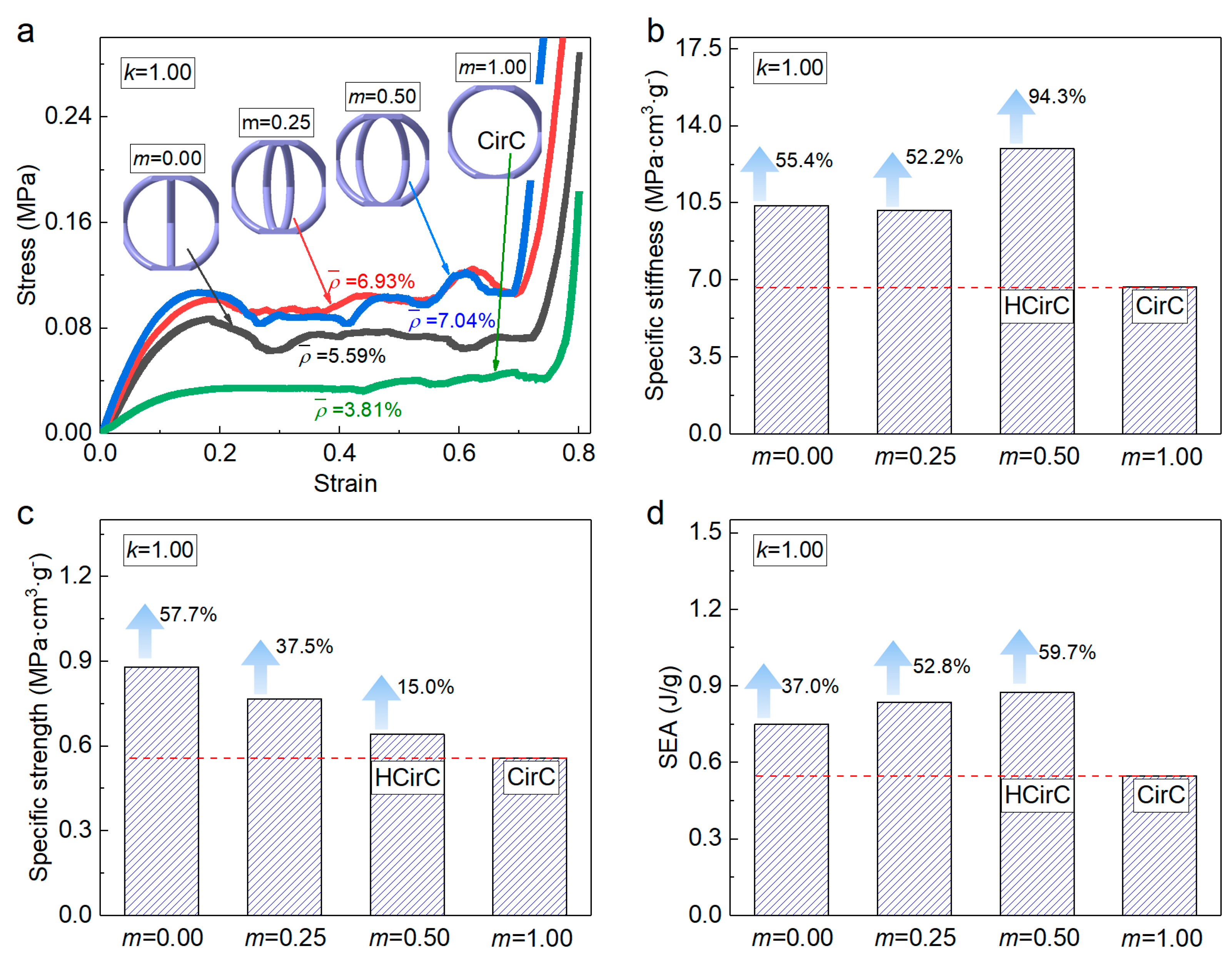

| Group Number | Specimen | Dimension | L (mm) | d (mm) | Relative Density | |
|---|---|---|---|---|---|---|
| Theoretical | Experiment | |||||
| 1 | BCC | 5 × 5 × 5 | 7.5 | 0.60 | 0.03482 | 0.03461 |
| CirC | 0.03444 | 0.03457 | ||||
| HCirC | 0.05982 | 0.06008 | ||||
| 2 | BCC | 5 × 5 × 5 | 7.5 | 0.65 | 0.04087 | 0.04035 |
| CirC | 0.03850 | 0.03811 | ||||
| HCirC | 0.07120 | 0.07037 | ||||
| 3 | BCC | 5 × 5 × 5 | 7.5 | 0.70 | 0.04740 | 0.04659 |
| CirC | 0.04336 | 0.04375 | ||||
| HCirC | 0.08220 | 0.08299 | ||||
| 4 | BCC | 5 × 5 × 5 | 7.5 | 0.75 | 0.05441 | 0.05267 |
| CirC | 0.04902 | 0.04889 | ||||
| HCirC | 0.09284 | 0.09255 | ||||
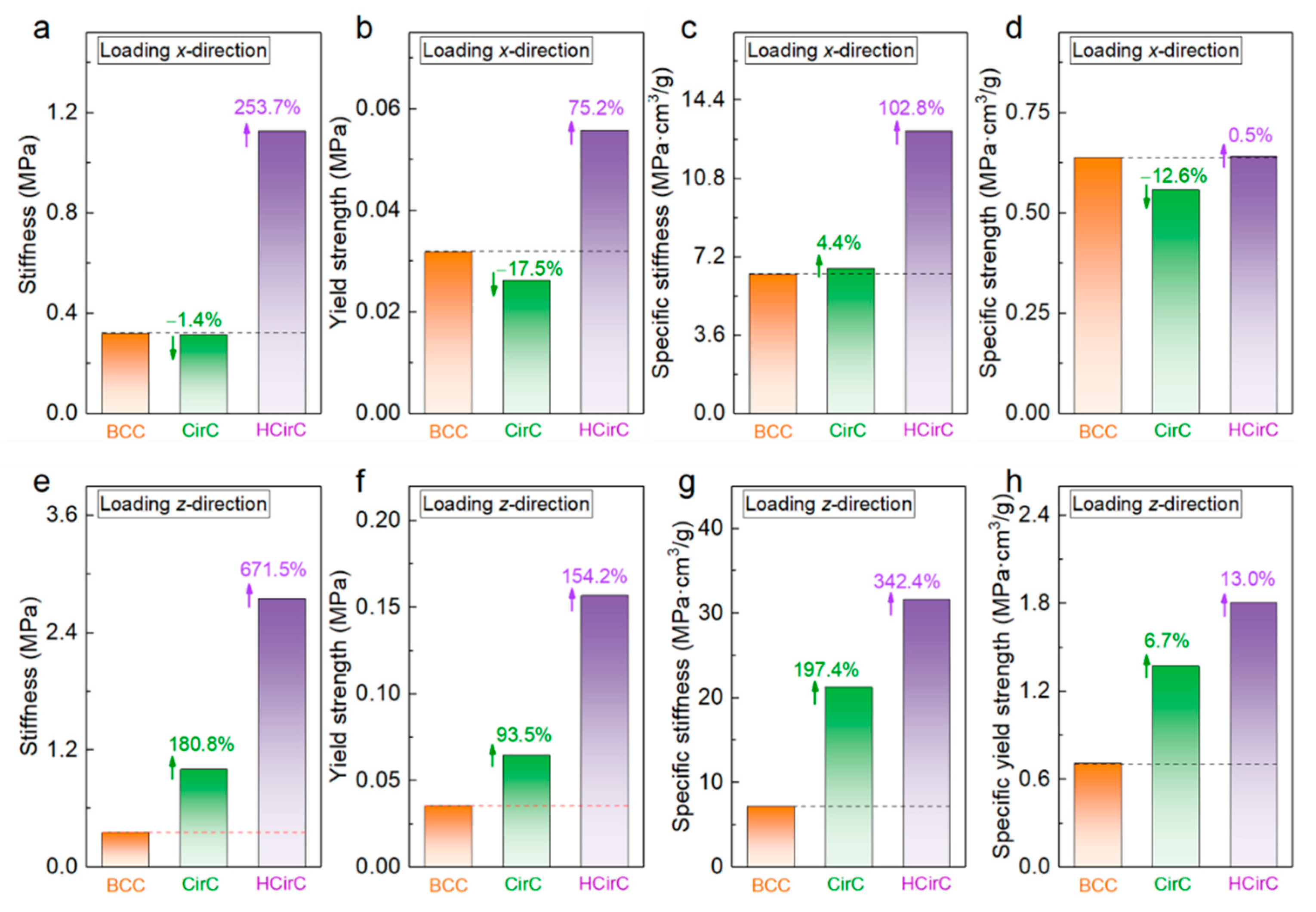
| Lattice Structures | Stiffness (MPa) | Strength (MPa) | Specific Stiffness (MPa·cm3/g) | Specific Strength (MPa·cm3/g) |
|---|---|---|---|---|
| BCC | 0.3190 | 0.03183 | 6.4018 | 0.6387 |
| Compression along x-direction | ||||
| CirC | 0.3145 | 0.02627 | 6.6821 | 0.5582 |
| HCirC | 1.1283 | 0.05577 | 12.9824 | 0.6417 |
| Compression along z-direction | ||||
| CirC | 1.0019 | 0.06469 | 21.2890 | 1.3746 |
| HCirC | 2.7526 | 0.1569 | 31.6732 | 1.8054 |
| Lattice Structures | ||||
|---|---|---|---|---|
| BCC | 0.198 | 2.120 | - | - |
| CirC | 0.837 | 2.537 | 7.842 | 2.909 |
| HCirC | 0.146 | 2.067 | 0.417 | 2.066 |
| Lattice Type | Dimension | L (mm) | Relative Density | |||
|---|---|---|---|---|---|---|
| HCirC | 0.50 | 0.00 | 5 | 7.5 | 0.65 | 0.03811 |
| 0.60 | 0.04833 | |||||
| 0.80 | 0.05836 | |||||
| 1.00 | 0.07037 | |||||
| HCirC | 0.00 | 1.00 | 5 | 7.5 | 0.65 | 0.05592 |
| 0.25 | 0.06931 | |||||
| 0.50 | 0.07037 | |||||
| 1.00 | 0.03811 |
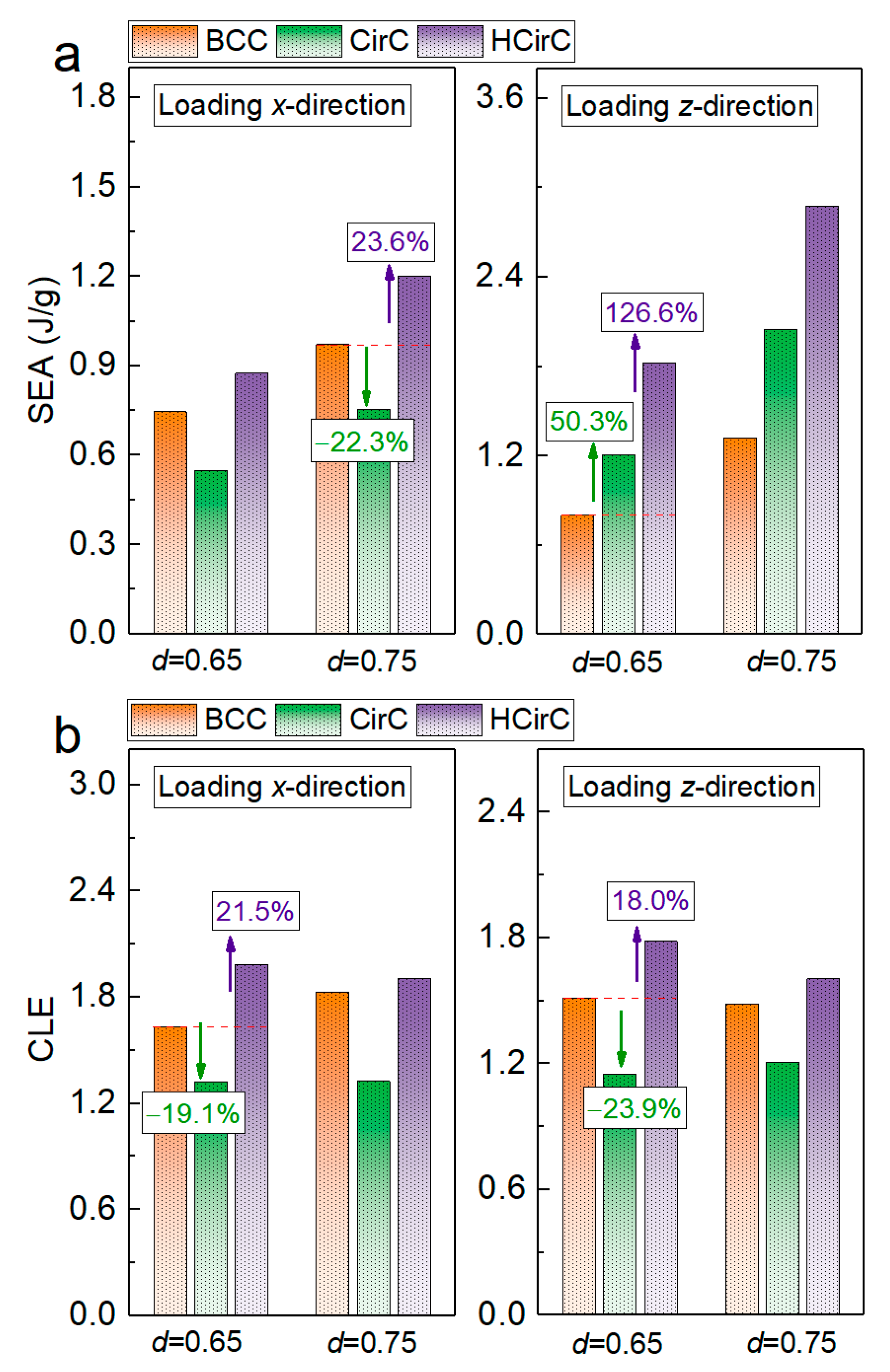
| Lattice Structures | = 0.65 | = 0.75 | |
|---|---|---|---|
| SEA (J/g) | BCC | 0.7462 | 0.9719 |
| Compression along x-direction | |||
| CirC | 0.5478 | 0.7555 | |
| HCirC | 0.8751 | 1.2015 | |
| Compression along z-direction | |||
| CirC | 1.2093 | 2.0497 | |
| HCirC | 1.8237 | 2.8788 | |
| CLE | BCC | 1.6341 | 1.8284 |
| Compression along x-direction | |||
| CirC | 1.3223 | 1.3246 | |
| HCirC | 1.9859 | 1.9052 | |
| Compression along z-direction | |||
| CirC | 1.1511 | 1.2087 | |
| HCirC | 1.7843 | 1.6051 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zhang, J.; Wang, W. Compression and Deformation Behaviors of Hierarchical Circular-Cell Lattice Structure with Enhanced Mechanical Properties and Energy Absorption Capacity. Aerospace 2022, 9, 786. https://doi.org/10.3390/aerospace9120786
Wang M, Zhang J, Wang W. Compression and Deformation Behaviors of Hierarchical Circular-Cell Lattice Structure with Enhanced Mechanical Properties and Energy Absorption Capacity. Aerospace. 2022; 9(12):786. https://doi.org/10.3390/aerospace9120786
Chicago/Turabian StyleWang, Mingzhi, Junchao Zhang, and Weidong Wang. 2022. "Compression and Deformation Behaviors of Hierarchical Circular-Cell Lattice Structure with Enhanced Mechanical Properties and Energy Absorption Capacity" Aerospace 9, no. 12: 786. https://doi.org/10.3390/aerospace9120786
APA StyleWang, M., Zhang, J., & Wang, W. (2022). Compression and Deformation Behaviors of Hierarchical Circular-Cell Lattice Structure with Enhanced Mechanical Properties and Energy Absorption Capacity. Aerospace, 9(12), 786. https://doi.org/10.3390/aerospace9120786








