Static and Dynamic Analysis of Re-Entry Vehicle Nose Structures Made of Different Functionally Graded Materials

Abstract

High-speed aerospace applications, such as re-entry vehicles, mostly involve thin-walled structural components with a high strength-to-weight ratio and high-temperature resistant. The present novel work comprises the structural and thermal analysis of re-entry vehicle nose structures made of four functionally graded materials (FGM). Four FGM shell structures made of aluminum/silicon carbide, aluminum/aluminum oxide, Ti-6Al-4V/silicon carbide and Ti-6Al-4V/aluminum oxide have been considered for the re-entry vehicle nose. The effect of various thermal environments, as well as the linear temperature rise from metal-rich to ceramic-rich on critical buckling temperature and natural frequency have been studied. The critical buckling temperature, as well as the natural frequency of the large, thin re-entry vehicle nose structures, decrease with an increase in a uniform thermal environment, as well as linear temperature rise. The effect of shell thickness on buckling and dynamic characteristics of an FGM shell is also studied, suiting the nose of the re-entry vehicle under various linear temperature rises. The critical buckling temperature and natural frequency are quantified for several cases, and it was observed that they are significantly influenced by the shell thickness. Thus, the research intends to determine the thickness required for such thin and large shells to withstand in the re-entry thermal conditions.

1. Introduction

Surviving extreme heating through the atmosphere during high-speed flight and guarding the crew and equipment until they safely reach Earth are the prime objectives of a re-entry vehicle. Although this technology has changed quite significantly in recent years, re-entry vehicles have used the same basic design concept. A re-entry capsule comprises two major components: a blunt front body succeeded by a conical aft body with a rounded or straight base. Re-entry vehicles are subjected to aerodynamic heating during the atmospheric descent. This generates excessive heat; subsequently, the external surface of the capsule gets heated. Hence, to protect the vehicle and its internal structure from such high temperatures, re-entry vehicles are furnished with ablative thermal protection systems. Thermal loads play a major role during the re-entry phase. High temperature change produces in-plane compressive loads, which causes the structure to deform and buckle. When the structure begins to deform from its equilibrium state due to thermal loads, thermal buckling occurs due to the critical buckling temperature, which is the in-plane thermal load. Thermal stresses and deflections will be produced, and the structure will eventually fail if the buckling temperature is further increased. Thin-walled structures, such as shells, undergo buckling when their membrane strain energy is converted to bending energy. Thermal stability characteristics of functionally graded shells are relevant areas of research and hence, in-depth studies are needed. Vibration analysis is also necessary to obtain natural frequency, the knowledge of which will help to prevent failure of structures due to the resonance condition.

Functionally graded materials (FGMs) are inhomogeneous in nature, comprised of two or more different components, and are designed in such a way that the material composition in the direction of thickness is varied gradually [1]. In the present work, FGMs are designed by varying material composition from metal-rich to ceramic-rich [2]. Their advantages include better thermal stress reduction, high heat and wear resistance, breakage resistance, etc. Since the variation is gradual, it eliminates stress concentration followed by delamination occurring from composition discontinuities. Various industries, such as automobile, aircraft, aerospace, biomedical, steel and nuclear reactor industries, have paid serious attention to FGMs as heat-protecting advanced materials. In the last decade, several studies emerged on FGM panels. Finite element formulation was developed to explore static structural characteristics of the FGM panels [3,4]. The impact of geometrical constraints and temperature fields on the buckling temperature of FGM plates has been examined in [5,6,7]. FGM plates have a higher critical thermal gradient under non-linear temperature distribution than linear distribution. Buckling, as well as dynamic characteristics of axisymmetric FGM circular panels [8] and elliptical panels [9] under a thermal environment, have been examined. Zhao et al. [10] and Kumar et al. [11] evaluated the dynamic characteristics for FGM panels and the influence of the thermal field in a dynamic analysis was presented in [12,13,14]. They highlighted the influence of boundary constraints, geometrical constraints, material compositions and temperature rise. Other works by Kim [15] and Huang and Shen [16] explored linear, as well as non-linear dynamic responses of FGM panels exposed to thermal field and parametric studies for the dynamic nature of the panels. The influence of temperature-reliant material properties on the structural behavior of a thin-walled box column assembled by FGM plates has been studied by Ramkumar and Ganesan [17].

Shell-type structures are commonly used in aerospace structures due to their free-form shape. Thin shells are highly preferred due to their efficient ways of achieving a greater strength-to-weight ratio. In comparison with other structure types, the most critical part of the shell is the strength of the material because shells tend to deform in buckling and, consequently, exhibit yielding. Rosario et al. [18] used ultra-high temperature ceramics for the nose of a re-entry vehicle and carried out FEM-based thermo-structural analysis. It has been noted that the studies on FGM shells for the nose structures of re-entry vehicles are highly significant. Buckling, as well as dynamic analysis of FGM shells [19,20], have been studied by employing classical thin shell theory, as well as meshless method, respectively. Neves et al. [21] evaluated the frequencies of clamped, as well as simply supported spherical and cylindrical FGM shells. Hajlaoui et al. [22] examined the thermal buckling of FGM shells by employing a modified FSDT-based shell element. The proposed formulation has a strong advantage compared to other shear deformation theories. Moita et al. [23] and Das et al. [24] inspected the buckling nature of FGM axisymmetric shells exposed to mechanical and thermal environments. Reddy and Chin [25] and Trabelsi et al. [26] analyzed the thermal buckling nature of FGM cylinder-shaped shells, as well as plates, by adopting a modified FSDT-based shell element. Sun et al. [27] derived a novel analytical formulation for the thermal buckling characteristics of FGM cylinder-shaped shells by using temperature-reliant properties. The findings indicate that there exists a critical power law exponent, above which the thermal buckling starts to occur. Torabi et al. [28] and Sofiyev [29] conducted buckling analysis of an FGM conical shell under non-linear temperature distribution. Kumar and Kumar [30] presented a new analytical model to examine the vibration features of FGM-stiffened shallow shells exposed to thermo-mechanical loads. Das and Karmakar [31] and Jooybar et al. [32] evaluated the thermal influences on the vibration behavior of an FGM conical shell using FEM and found that the natural frequency reduces because of the incremental increase in temperature, but it has higher circumferential modes. Thermal stresses and semi-vertex angle have a substantial effect on the frequency parameter.

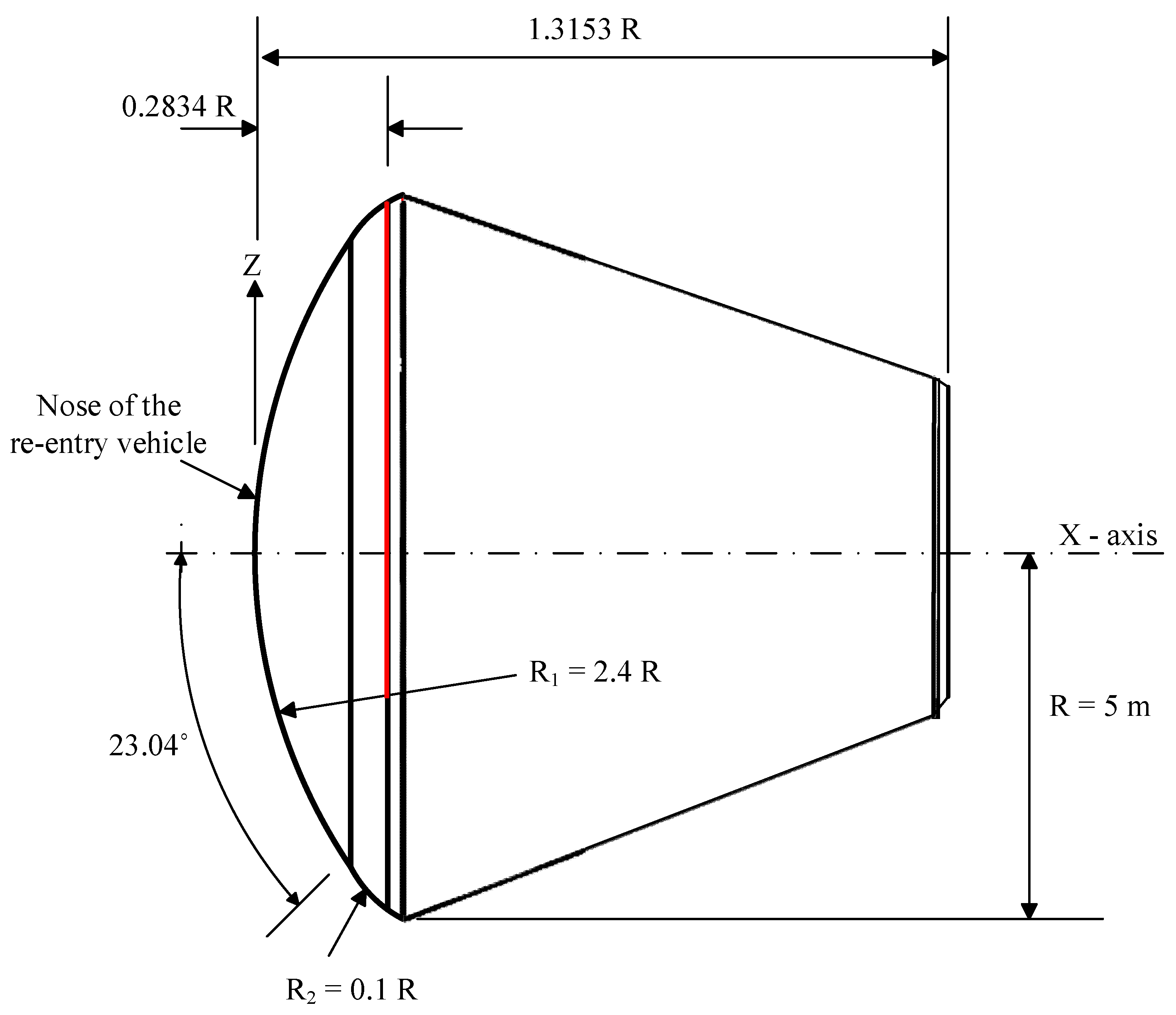
It is noted from the literature mentioned above that it is desirable to explore the application of FGM as nose structures in re-entry vehicles. The base re-entry vehicle model considered for the present study is the Orion model [33]. The rationale of the study is to understand the thermo-structural behaviour of different FGM shell structures, which are of the size suiting re-entry vehicles. The research intends to determine the thickness required for such thin and large shells to withstand in the re-entry thermal conditions. In the present work, large and thin FGM shell structures with 20 layers made of aluminum/silicon carbide, aluminum/aluminum oxide and Ti-6Al-4V/silicon carbide, as well as Ti-6Al-4V/aluminum oxide, are considered instead of ceramic tiles in Orion to perform the structural and thermal analysis. Thus, the objective of present research is to explore the static, as well as dynamic characteristics of the nose of the re-entry vehicle model made of four different FGM exposed to various temperature fields.

2. Numerical Simulation and Methodology

The structural analysis was carried out for the nose of re-entry vehicle, which is made of FGM. The model dimensions are given in Figure 1. A schematic representation of the FGM shell structure that forms the nose of re-entry vehicle is shown in Figure 2. The FGM nose shell consisting of 20 layers with an overall thickness of 0.01 m was modeled in ANSYS based on the estimated properties. It was clamped over the entire circumferential boundary. A 3D layered 4-node shell181 element was considered and the upper surface of the shell was loaded with a uniformly distributed pressure load of 10 kN/m². The results of central displacement and buckling load, as well as natural frequency were plotted against the power law index to understand the variations in structural characteristics for different FGM shell structures at different temperature cases.

2.1. Material Selection for Structural Analysis

To study the behaviour of the FGM shell, in the present work, a metallic component (aluminum or Ti-6Al-4V) was considered to bind with a ceramic component (silicon carbide or aluminum oxide) with a gradual variation of constituents along the thickness. Metal provides good structural integrity with good tensile strength; a ceramic component gives good temperature resistance under the high-temperature application. The properties of the FGM constituents are shown in

Table 1. Properties of the FGM constituents [1,10].

Constituents	E (GN/m2)	$\mathit{\rho }$ (kg/m3)	$\mathit{\nu }$
Aluminum	70	2707	0.30
Ti-6Al-4V	105.7	4429	0.298
Silicon carbide	410	3210	0.17
Aluminum oxide	320.2	3750	0.26

. Four different material combinations, including aluminum/silicon carbide, aluminum/aluminum oxide, Ti-6Al-4V/silicon carbide and Ti-6Al-4V/aluminum oxide were considered. FGM with 20 layers was considered and the ratio of ceramic and metal in each layer was estimated using the power law [3,34]. The power law includes the volumetric ratio of the ceramic ($V_c)$, the height of the layer from the central axis (z), the thickness of the shell (h), the power law index (k) and the volumetric ratio of the metal $(V_m)$. The analysis was performed by employing ANSYS software. The FGM shell properties were calculated for different compositions obtained from the power law for different values of k, such as 0, 0.1, 0.5, 1, 5, 10, 50 and 100. The volumetric ratio of the material constituents was calculated by Equations (1) and (2). The material properties, such as Young’s modulus ($E_z)$, Poisson’s ratio (${\nu }_z$) and the density (${\rho }_z)$ of each layer in the FGM shell were found using Equations (3)–(5).$(E_c, {\nu }_c, {\rho }_{c }) \mathrm{and} \left(E_m, {\nu }_m, {\rho }_m\right)$ correspond to Young’s modulus, Poisson’s ratio and the density of the ceramic, as well as metal. The material properties were assigned to each layer analogous to the power law index, which determines the constituents of the metal and the ceramic.

$$V_c={\left(\frac{Z}{h}+\frac{1}{2}\right)}^k;-\frac{h}{2} \le z \le \frac{h}{2}$$

(1)

$$V_c+V_m=1$$

(2)

$$E_z=\left(E_c-E_m\right)V_c+E_m$$

(3)

$${\nu }_z=\left({\nu }_c-{\nu }_m\right)V_c+{\nu }_m$$

(4)

$${\rho }_z=\left({\rho }_c-{\rho }_m\right)V_c+{\rho }_m$$

(5)

2.2. Material Selection for Thermal Analysis

Four different FGM compositions, such as aluminum/silicon carbide, aluminum/aluminum oxide, Ti-6Al-4V/Silicon carbide and Ti-6Al-4V/aluminum oxide were considered for thermal buckling, as well as vibration analysis. Initially, the material properties of metal and ceramic, P, where P is any property, for various thermal fields were estimated using Equation (6), where $P_{-1}$, $P_0$, $P_1,$ $P_2,$ $P_3$ are temperature-dependent coefficients. Temperature-dependent coefficients employed for aluminum, Ti-6Al-4V, silicon carbide and aluminum oxide were considered from [25,35]. Then, layer-wise material properties, including a thermal expansion coefficient (${\alpha }_z$) and thermal conductivity (${\overline{k}}_z)$, were calculated using Equation (1) and Equations (7)–(11), where the material properties rely on the temperature (T), as well as ceramic constituents in power law formulation [14].

$$P \left(T\right)=P_{0 } (P_{-1}{T}^{-1}+1+P_{1}T+ P_2{T}^2+P_3{T}^3)$$

(6)

$$E_z \left(V_c, T\right)=\left(E_c\left(T\right)-E_{m }\left(T\right)\right)V_c+E_m\left(T\right)$$

(7)

$${\rho }_z \left(V_c, T\right)=\left({\rho }_c\left(T\right)-{\rho }_m\left(T\right)\right)V_c+{\rho }_m\left(T\right)$$

(8)

$${\nu }_z=\left({\nu }_c\left(T\right)-{\nu }_m\left(T\right)\right)V_c+{\nu }_m\left(T\right)$$

(9)

$${\alpha }_z \left(V_c, T\right)=\left({\alpha }_c\left(T\right)-{\alpha }_{m }\left(T\right)\right)V_c+{\alpha }_m\left(T\right)$$

(10)

$$\overline{k}{ }_z \left(V_c, T\right)=\left(\overline{k}{ }_c\left(T\right)-\overline{k}{ }_{m }\left(T\right)\right)V_c+\overline{k}{ }_m\left(T\right)$$

(11)

The analysis was performed on the FGM shell for two different cases. The first case was under various thermal environments in which both the metal-rich and the ceramic-rich layers were exposed to a uniform temperature. The second case was under linear temperature rise in which the metal-rich layer (inner layer) was kept at a constant temperature, 300 K, and the ceramic-rich layer (outer layer) was exposed to various temperatures. A coupled thermo-structural analysis was carried out and the temperature-dependent material properties were assigned to each layer. The steady-state solution was solved to obtain the temperature distribution. Eigen buckling analysis with the first mode was carried out. The buckling analysis provides a load multiplier and the corresponding mode shape. Similarly, modal analysis with the first mode of natural frequency was carried out. The same methodology was applied for different power law indices and different temperatures for all material combinations of the FGM structure.

3. Results and Discussions

3.1. Structural Analysis

3.1.1. Convergence and Validation of Methodology

Initially, the convergence study was completed to calculate the optimum mesh size, and k = 1 was chosen for the convergence study, as it has linearly varying properties from metal-rich to ceramic-rich. The optimum mesh size in each segment of the shell was found and used for further analysis. To validate the present methodology, the model used by Zhao and Liew [20] was considered. As structural analysis of the re-entry nose with FGM are not often discussed in existing literature, the validation of the present methodology was confirmed by simulating a truncated cone panel, implementing the same procedures as Zhao and Liew [20]. The cone is made of Al/ZrO₂ FGM and the power law index is 1. The larger base part was clamped, and using modal analysis, the first mode of natural frequencies was determined. The fundamental natural frequency using the present methodology was 133.57 Hz and it was compared with Zhao and Liew [20]. A variation of only 1% was noted. Thus, the methodology is validated.

3.1.2. Bending Characteristics

The variation of the maximum central displacement with the material compositions (defined by the power law index) was compared for different material combinations as shown in Figure 3. It was observed that the FGM structure with k = 1 has low stress concentration due to the linearly varying spatial profile, which results in greater structural integrity. The displacement is greatest for the metallic shell (k = 100) and at its lowest for the ceramic shell (k = 0) in all material combination cases. Also, the central displacement reduces when the power law index drops due to a reduction in stiffness. Aluminum-rich material combinations have higher displacement because the modulus of elasticity for aluminum is lower as compared to Ti-Al-4V. A maximum displacement of 5.959 mm was observed for the aluminum/silicon carbide FGM shell and a displacement of 1.012 mm (minimum among the considered shells) was observed for the Ti-6Al-4V/silicon carbide FGM shell.

3.1.3. Buckling Characteristics

Buckling characteristics are described by the thickness, material properties, curvatures, imperfection, loading condition and membrane force. We intended to study the buckling characteristics for various power law index ‘k’ in the present work. The pressure load of 10 kN was employed over the upper surface. The buckling characteristics for different material compositions were found and the first mode of the buckling load with the power law index is plotted in Figure 4. Initially, the buckling load of the structure decreased steeply and finally, the variation became gradual from k = 5 to k = 100. The shell is isotropic with the highest possible hardness and compressive strength at k = 0. When k > 1, the percentage of metal is more prominent, which leads to a drop in compressive strength, thereby reducing the buckling strength.

The effect of the power law index on the buckling load was then quantified and compared as shown in Figure 4 for all material combinations. It was observed that other material combinations also show similar buckling characteristics as aluminum/silicon carbide. It was also observed that the buckling characteristics improved when Ti-6Al-4V was added instead of aluminum as metal. The buckling characteristics are improved for FGM with metal that has higher stiffness and modulus of elasticity.

3.1.4. Vibration Characteristics

Vibration characteristics were studied to understand the variation of the fundamental natural frequency of the re-entry vehicle nose structure for various power law index ‘k’. The analysis type was chosen as Modal and the analysis option was block Lanczos in APDL. It can be determined from Figure 5 and Figure 6 that the natural frequency of the structure reduces when the power law index increases. When k > 1, the structure becomes more metallic, hence the material will be able to withstand high vibration. Initially, the natural frequency decreased steeply, and the variation was quite gradual and it finally became linear from power law index k = 5 to k = 100. Other material combinations also show similar vibration characteristics as aluminum/silicon carbide. It was also observed that the vibration characteristics are superior for FGM with Ti-6Al-4V as metal because of higher stiffness as compared to aluminum.

3.2. Thermal Analysis

3.2.1. Validation Study

Initially, a validation study was performed for thermal analysis of the shell structure. For validation of the thermal buckling analysis, two different types of cylindrical shell—Type A (ceramic outer, metal inner) and Type B (metal outer, ceramic inner) made of stainless steel/silicon carbide—were considered, as in Moita et al. [23]. The critical buckling temperature for several power law indices was calculated at a thermal environment of 300 K, as shown in

Table 2. Variation of critical buckling temperatures (in K) of FGM cylindrical shells for different material composition.

Shell Configuration	k	0	0.5	1	2	5
Type A	Moita et al. [23]	394.13	415.93	429.41	445.16	464.87
	Present	397.44	414.35	426.69	444.13	469.11
Type B	Moita et al. [23]	492.94	441.95	427.09	416.04	406.7
	Present	499.57	448.75	433.10	421.15	410.95

. The results are perfectly matched with Moita et al. [23].

For the validation study of thermal vibration analysis, a clamped (CCCC) plate case from Li et al. [14] was considered. The square plate was made of Si₃N₄/SUS304 FGM with a size of 0.2 × 0.2 × 0.02 m. The natural frequency parameters under a thermal environment of 300 K are shown in

Table 3. Natural frequency parameters for clamped FGM square plates under a thermal environment of 300 K.

Mode	1	2	3	4	5	6	7
Li et al. [14]	4.16	7.94	7.94	11.12	13.10	13.22	15.36
Present	4.13	7.89	7.89	11.06	13.06	13.19	15.45

. The power law coefficient is considered as 2 and the analysis was carried out at 300 K, as in Li et al. [14]. The first 7 modes of the natural frequency parameters are perfectly matched with Li et al. [14]. Similarly, the natural frequency parameters of the same panel (with 4 edges simply supported) exposed to linear temperature variation along the thickness is shown in

Table 4. Natural frequency parameters for simply supported FGM square plates exposed to a linear temperature rise of 300 K across the thickness.

k	Mode	1	2	3	4	5	6	7
1	Li et al. [14]	2.65	6.37	6.37	8.96	8.96	9.79	11.94
	Present	2.64	6.32	6.32	9.05	9.05	9.71	11.88
2	Li et al. [14]	2.37	5.69	5.69	7.92	7.92	8.74	10.66
	Present	2.37	5.67	5.67	7.97	7.97	8.71	10.64
5	Li et al. [14]	2.14	5.14	5.14	7.08	7.08	7.89	9.63
	Present	2.16	5.15	5.15	7.09	7.09	7.89	9.63
10	Li et al. [14]	2.04	4.91	4.91	6.72	6.72	7.53	9.19
	Present	2.06	4.91	4.91	6.73	6.73	7.52	9.19

. The analysis was performed for k = 1, 2, 5 and 10. The temperature of the metal-rich layer is presumed to be at 300 K and the linear temperature growth of 300 K to the ceramic-rich layer. These results also show good agreement with Li et al. [14].

3.2.2. Buckling Characteristics under Thermal Environment

The clamped FGM shell was initially considered under a thermal field of 300 K throughout its structure and then the critical buckling temperature for such a case was evaluated. Then, the material properties for each layer corresponding to different thermal fields were calculated and assigned for calculating the critical buckling temperature to understand the impact of different thermal environments. The impact of various thermal environments on the critical buckling temperature for aluminum/silicon carbide, aluminum/aluminum oxide, Ti-6Al-4V/silicon carbide and Ti-6Al-4V/aluminum oxide are shown in

Table 5. Effect of a uniform thermal field on critical buckling temperatures (in K) of an aluminum/silicon carbide FGM shell for different material composition in re-entry vehicle nose structures.

Thermal Environment (in K)	Power Law Index (k)
	0	0.1	0.5	1	5	10	50	100
300	897.92	755.96	587.62	531.43	478.66	470.34	447.66	441.42
350	894.53	748.60	579.45	524.10	471.93	463.90	441.58	435.61
400	891.18	741.54	571.83	517.09	465.75	457.83	436.13	430.29
450	887.86	734.38	564.56	510.54	459.92	452.44	-	-
500	884.58	727.58	557.72	504.27	-	-	-	-
550	881.34	721.25	551.25	-	-	-	-	-
600	878.14	714.71	-	-	-	-	-	-

,

Table 6. Effect of a uniform thermal field on critical buckling temperatures (in K) of an aluminum/aluminum oxide FGM shell for different material composition in re-entry vehicle nose structures.

Thermal Environment (in K)	Power Law Index (k)
	0	0.1	0.5	1	5	10	50	100
300	744.40	669.62	561.76	520.42	478.11	469.34	446.64	441.12
350	740.12	663.74	554.88	513.63	471.57	462.92	440.69	435.32
400	736.52	657.76	548.39	507.21	465.41	456.93	435.26	429.96
450	732.97	652.02	542.04	501.04	459.89	451.53	-	-
500	729.49	646.47	535.92	-	-	-	-	-
550	725.49	641.31	-	-	-	-	-	-
600	722.12	636.26	-	-	-	-	-	-

,

Table 7. Effect of a uniform thermal field on critical buckling temperatures (in K) of a Ti-6Al-4V/silicon carbide FGM shell for different material composition in re-entry vehicle nose structures.

Thermal Environment (in K)	Power Law Index (k)
	0	0.1	0.5	1	5	10	50	100
300	897.92	853.39	766.22	725.32	694.08	688.13	659.63	651.31
350	894.53	847.98	757.83	715.68	682.66	676.57	647.92	639.50
400	891.18	842.56	749.54	706.36	671.46	665.23	636.95	628.43
450	887.86	837.10	741.30	697.07	660.55	653.97	625.32	616.98
500	884.58	831.78	733.16	688.22	650.79	644.63	616.43	608.15
550	881.34	826.32	725.22	679.12	640.03	633.68	605.61	597.12
600	878.14	821.00	717.02	670.37	630.36	623.78	-	-

and

Table 8. Effect of a uniform thermal field on critical buckling temperatures (in K) of a Ti-6Al-4V/aluminum oxide FGM shell for different material composition in re-entry vehicle nose structures.

Thermal Environment (in K)	Power Law Index (k)
	0	0.1	0.5	1	5	10	50	100
300	744.40	729.60	696.31	680.23	680.33	678.63	657.07	650.63
350	740.12	724.63	689.19	671.98	669.59	667.36	645.34	638.84
400	736.52	719.71	682.13	663.88	658.84	656.52	634.40	627.78
450	732.97	714.95	675.13	655.76	648.66	645.39	623.01	616.31
500	729.49	710.16	668.48	647.90	639.25	636.30	613.98	607.45
550	725.49	705.42	661.51	640.26	629.50	626.05	603.39	596.60
600	722.12	700.69	655.04	632.48	620.00	616.34	-	-

, respectively. The critical buckling temperature reduces gradually with a rise in the thermal field, as well as in the power law index. When k < 1, it causes the composition of the ceramic to be more dominant, which leads to an increase in the compressive strength and the critical buckling temperature. When k > 1, it makes the composition of metal more dominant, which leads to a decrease in the compressive strength and the critical buckling temperature. The same behavior was observed for all material combinations and quantified the values for all the different parametric studies. In some cases of the thermal field, the critical buckling temperature was less than the corresponding thermal field, which gives the buckling temperature limit for each k and the limit reduces when k increases, due to dominance in metallic properties. For example, the critical buckling temperature obtained corresponding to k = 50 for the aluminum/silicon carbide FG shell kept at a thermal environment of 450 K is 431.12 K, which is less than the applied temperature, hence the values exhibiting such behavior are not mentioned in Table 5, Table 6, Table 7 and Table 8.

The FGM shell with silicon carbide as a ceramic shows good buckling characteristics when compared to aluminum oxide as a ceramic. Similarly, the FGM shell with Ti-6Al-4V as a metal shows good buckling characteristics when compared to aluminum as a metal. Overall, the FGM shell with Ti-6Al-4V/silicon carbide has good buckling strength, and therefore a high critical buckling temperature in a thermal environment.

3.2.3. Buckling Characteristics under Linear Temperature Rise

Thermal buckling analysis was performed to understand the effect of a linear temperature rise from the metal-rich to the ceramic-rich layer. The metal-rich layer (inner) was kept at 300 K and the ceramic-rich layer (outer) was exposed to 300 K to 700 K, increasing by 100 K. Layer-wise material properties were calculated as discussed in the former section. The changes in critical buckling temperature with linear temperature rise for aluminum/silicon carbide, aluminum/aluminum oxide, Ti-6Al-4V/silicon carbide and Ti-6Al-4V/aluminum oxide are shown in

Table 9. Critical buckling temperature (in K) of an aluminum/silicon carbide FGM shell under linear temperature rise for different material composition in re-entry vehicle nose structures.

Temperature of Outer Layer (in K)	Power Law Index (k)
	0	0.1	0.5	1	5	10	50	100
300	897.92	755.96	587.62	531.43	478.66	470.34	447.66	441.42
400	894.31	750.74	581.28	524.85	471.88	463.84	-	-
500	891.07	745.56	575.23	518.83	-	-	-	-
600	887.81	740.72	-	-	-	-	-	-
700	884.74	735.57	-	-	-	-	-	-

,

Table 10. Critical buckling temperature (in K) of an aluminum/aluminum oxide FGM shell under linear temperature rise for different material composition in re-entry vehicle nose structures.

Temperature of Outer Layer (in K)	Power Law Index (k)
	0	0.1	0.5	1	5	10	50	100
300	744.40	669.62	561.76	520.42	478.11	469.34	446.64	441.12
400	740.40	664.67	556.02	514.32	471.52	462.90	440.84	435.53
500	736.71	660.29	550.62	508.57	-	-	-	-
600	733.18	655.70	-	-	-	-	-	-
700	729.63	-	-	-	-	-	-	-

,

Table 11. Critical buckling temperature (in K) of a Ti-6Al-4V/silicon carbide FGM shell under linear temperature rise for different material composition in re-entry vehicle nose structures.

Temperature of Outer Layer (in K)	Power Law Index (k)
	0	0.1	0.5	1	5	10	50	100
300	897.92	853.39	766.22	725.32	694.08	688.13	659.63	651.31
400	894.31	849.06	759.74	717.49	683.65	677.30	648.41	639.99
500	891.07	844.74	753.38	709.71	673.28	666.69	637.40	628.74
600	887.82	840.37	746.79	702.03	663.44	656.60	626.84	618.09
700	884.74	836.25	740.45	-	-	-	-	-

and

Table 12. Critical buckling temperature (in K) of a Ti-6Al-4V/aluminum oxide FGM shell under linear temperature rise for different material composition in re-entry vehicle nose structures.

Temperature of Outer Layer (in K)	Power Law Index (k)
	0	0.1	0.5	1	5	10	50	100
300	744.40	729.60	696.31	680.23	680.33	678.63	657.07	650.63
400	740.40	725.21	690.25	673.20	670.33	668.11	645.90	639.20
500	736.71	720.84	684.60	666.35	660.57	657.80	634.81	628.02
600	733.18	716.81	678.81	659.54	651.04	647.98	624.35	617.56
700	729.63	712.71	-	-	-	-	-	-

, respectively. The critical buckling temperature drops when the temperature of the outer layer, as well as the power law index increase. The increase in the power law coefficient dominates the metal constituents. In some cases, the critical buckling temperature is less than the corresponding outer temperature. It gives the buckling temperature limit for each k in the analysis and the limit reduces when k increases, due to dominance in metallic properties.

An effort has been made to explore the impact of the shell thickness on the critical buckling temperature. The shell thickness should be increased to withstand a high temperature. A Ti-6Al-4V/Silicon carbide FGM shell with various thicknesses, subjected to various linear temperature rises, was considered as shown in

Table 13. Critical buckling temperature (in K) of a Ti-6Al-4V/silicon carbide FGM shell under linear temperature rise for various shell thicknesses in re-entry vehicle nose structures.

Shell Thickness (in m)	Temperature of Outer Layer (in K)	Power Law Index (k)
		0	0.1	0.5	1	5	10	50	100
0.01	600	887.82	840.37	746.79	702.03	663.44	656.60	626.84	618.09
	900	-	-	-	-	-	-	-	-
0.02	600	1431.43	1340.06	1159.96	1073.60	998.28	984.62	927.16	910.11
	900	1413.48	1316.05	1123.45	1030.45	943.85	930.10	-	-
	1200	1395.92	1292.02	-	-	-	-	-	-
0.03	600	1958.72	1824.54	1559.94	1433.02	1320.94	1300.32	1216.22	1191.79
	900	1932.41	1789.35	1506.43	1369.81	1241.21	1220.46	1132.91	1107.82
	1200	1906.67	1754.11	1453.79	1308.43	-	-	-	-
	1500	1880.90	1718.03	-	-	-	-	-	-
	1800	1855.01	-	-	-	-	-	-	-
0.04	600	2474.44	2298.57	1950.65	1783.80	1634.01	1607.48	1495.61	1463.88
	900	2439.94	2252.37	1880.63	1701.13	1530.03	1502.71	1386.85	1354.25
	1200	2406.20	2206.14	1811.71	1620.82	1437.10	1408.58	1292.21	1257.32
	1500	2372.49	2158.87	1743.22	1544.18	-	-	-	-
	1800	2338.70	2112.41	-	-	-	-	-	-
	2100	2302.75	-	-	-	-	-	-	-
0.05	600	2976.82	2759.62	2331.05	2125.40	1938.13	1903.36	1767.85	1729.98
	900	2934.37	2702.83	2244.78	2023.53	1809.78	1774.82	1634.01	1595.21
	1200	2892.81	2645.97	2159.89	1924.61	1695.06	1660.06	1517.63	1476.27
	1500	2851.20	2587.72	2075.55	1830.19	1590.79	1560.39	-	-
	1800	2809.37	2530.38	1993.03	-	-	-	-	-
	2100	2764.79	2469.97	-	-	-	-	-	-

. Since the outer layer of the re-entry nose structure is exposed to very high temperature, the analysis was carried out by keeping the inner layer at 300 K and the outer layer at 300 K, 600 K, 900 K, 1200 K, 1500 K, 1800 K and 2100 K. It was observed that the critical buckling temperature rises when the shell thickness increases for a given thermal load of the outer layer and quantified the same. Even though the analysis was carried out from 300 K to 2100 K with a temperature rise of 300 K for all cases of shell thickness, the critical buckling temperature less than that of the applied temperature are not mentioned in the Table 13. The maximum value of 2764.79 K that was obtained corresponds to the applied temperature of 2100 K and the shell thickness of 0.05 m for the FGM shell with k = 0. Even though the FGM shell with k = 0 gives high temperature resistance, the shell is made of only ceramics. Since metal provides structural integrity and high energy absorbing capacity in the FGM shell, the FGM shell with k = 0.1 can be used for re-entry vehicle nose structures for high temperature resistance. For example, the impact resistance will be significantly high for FGM shells compared to pure ceramics [36].

3.2.4. Vibration Characteristics under Thermal Environment

Thermal analysis was performed to understand the impact of thermal environments on the vibration characteristics of FGM shells made of different material combinations. The clamped FGM shell was initially considered under a thermal field of 300 K throughout its structure and then the fundamental natural frequency for such a case was evaluated. Later, the clamped FGM shell was analyzed in different thermal field. The variation of the natural frequencies with different thermal environments for aluminum/silicon carbide, aluminum/aluminum oxide, Ti-6Al-4V/silicon carbide and Ti-6Al-4V/aluminum oxide are shown in Figure 7, Figure 8, Figure 9 and Figure 10 respectively. First mode of natural frequency reduces with an increase in the thermal field. It is also noted that the natural frequency is higher when k < 1, and the natural frequency is low when k > 1. The decrease in the power law index makes the FGM more dominant in ceramic and therefore, the natural frequency increases. The power law index rise makes the FGM more dominant in metal, which causes a decrease in the natural frequency. Overall, Ti-6Al-4V/silicon carbide shows good vibration characteristics in a thermal environment.

3.2.5. Vibration Characteristics under Linear Temperature Rise

Thermal analysis was performed to understand the effect of temperature rise from the metal-rich layer to the ceramic-rich layer. The temperature of the metal-rich layer (inner layer) was considered to be fixed at 300 K, and increased linearly to 400 K, 500 K, 600 K and 700 K on the ceramic-rich layer (outer layer). Initially, the natural frequency was evaluated at the outer layer temperature of 300 K. Then, the material properties corresponding to each outer layer temperature were calculated by using temperature-dependent coefficients and power law to evaluate the natural frequency. The variation of the natural frequency with the temperature of the outer layer for aluminum/silicon carbide, aluminum/aluminum oxide, Ti-6Al-4V/silicon carbide and Ti-6Al-4V/aluminum oxide are shown in Figure 11, Figure 12, Figure 13 and Figure 14, respectively. The natural frequency decreases when the temperature of the outer layer increases. The natural frequency increases if the power law index decreases. For k < 1, the shell was influenced with ceramic, hence the natural frequency increases. For k > 1, the FGM shell characteristics were influenced with metal, hence the natural frequency decreases.

The influence of the shell thickness on the natural frequency has also been studied. A Ti-6Al-4V/Silicon carbide FGM shell with various thicknesses, subjected to various linear temperature rises was considered. The natural frequency corresponding to each critical buckling temperature (as in Table 13) was evaluated and is presented in

Table 14. Natural frequency (in Hz) of a Ti-6Al-4V/silicon carbide FGM shell under a linear temperature rise for various shell thicknesses in re-entry vehicle nose structures.

Shell Thickness (in m)	Temperature of Outer Layer (in K)	Power Law Index (k)
		0	0.1	0.5	1	5	10	50	100
0.01	600	143.31	136.03	116.90	103.89	76.73	69.99	62.97	61.88
0.02	600	144.04	136.66	117.32	104.21	77.02	70.32	63.33	62.23
	900	143.03	135.64	116.13	102.83	75.04	68.03	-	-
	1200	142.09	134.63	-	-	-	-	-	-
0.03	600	145.04	137.54	117.93	104.70	77.48	70.81	63.82	62.71
	900	144.02	136.51	116.74	103.31	75.49	68.53	61.17	59.99
	1200	143.08	135.50	115.59	101.96	-	-	-	-
	1500	142.09	134.46	-	-	-	-	-	-
	1800	140.89	-	-	-	-	-	-	-
0.04	600	146.37	138.72	118.79	105.41	78.15	71.51	64.49	63.35
	900	145.34	137.68	117.59	104.02	76.16	69.22	61.82	60.61
	1200	144.39	136.67	116.44	102.66	74.12	66.89	59.04	57.73
	1500	143.39	135.62	115.18	101.26	-	-	-	-
	1800	142.18	134.35	-	-	-	-	-	-
	2100	140.65	-	-	-	-	-	-	-
0.05	600	148.02	140.21	119.91	106.35	79.02	72.40	65.32	64.15
	900	146.98	139.17	118.71	104.95	77.03	70.11	62.62	61.38
	1200	146.02	138.14	117.54	103.59	74.99	67.78	59.82	58.46
	1500	145.00	137.08	116.28	102.18	72.83	65.30	-	-
	1800	143.77	135.79	114.83	-	-	-	-	-
	2100	142.22	134.19	-	-	-	-	-	-

. The natural frequency increases when the shell thickness increases for a given thermal load of the outer layer.

4. Conclusions

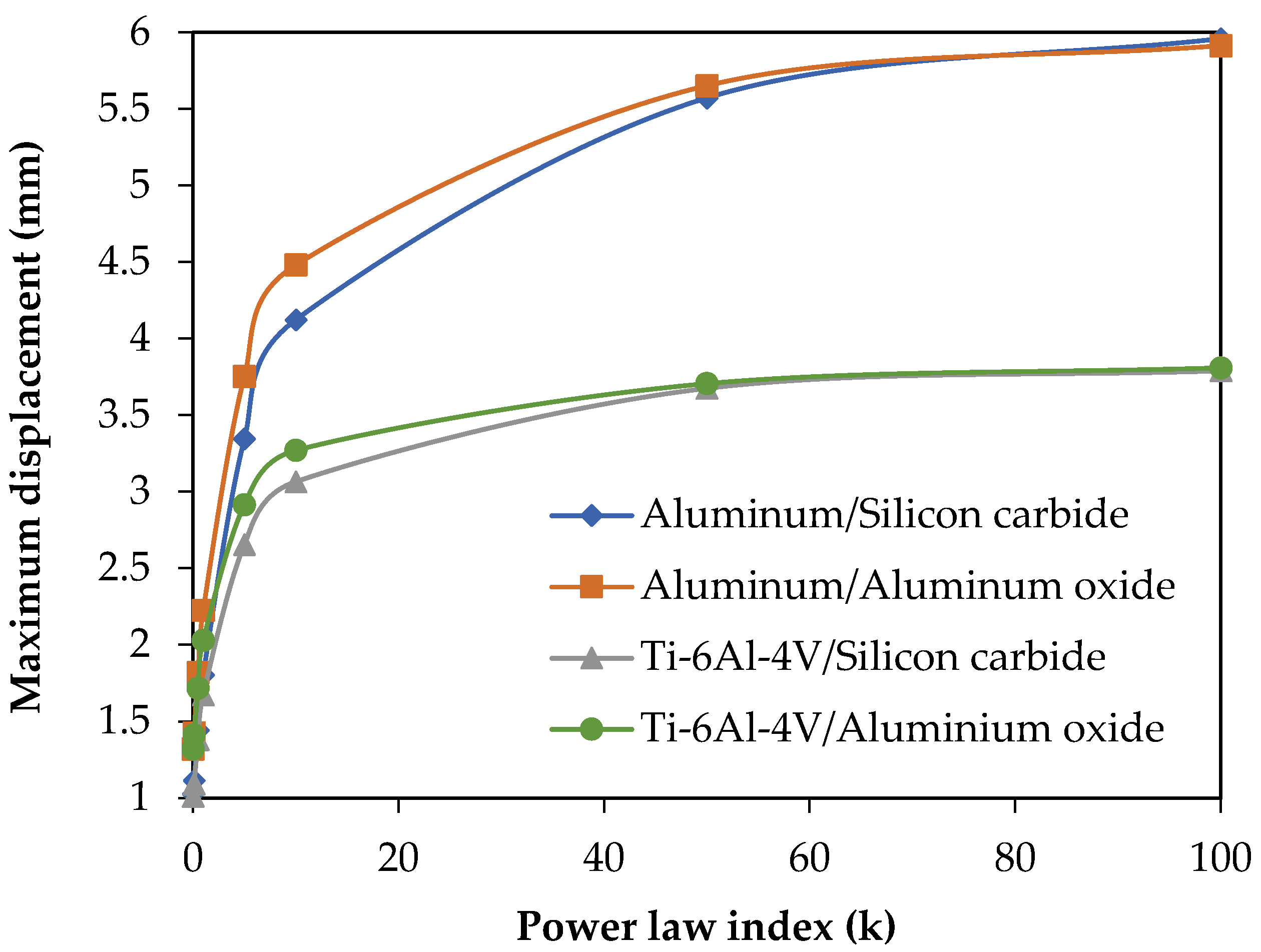
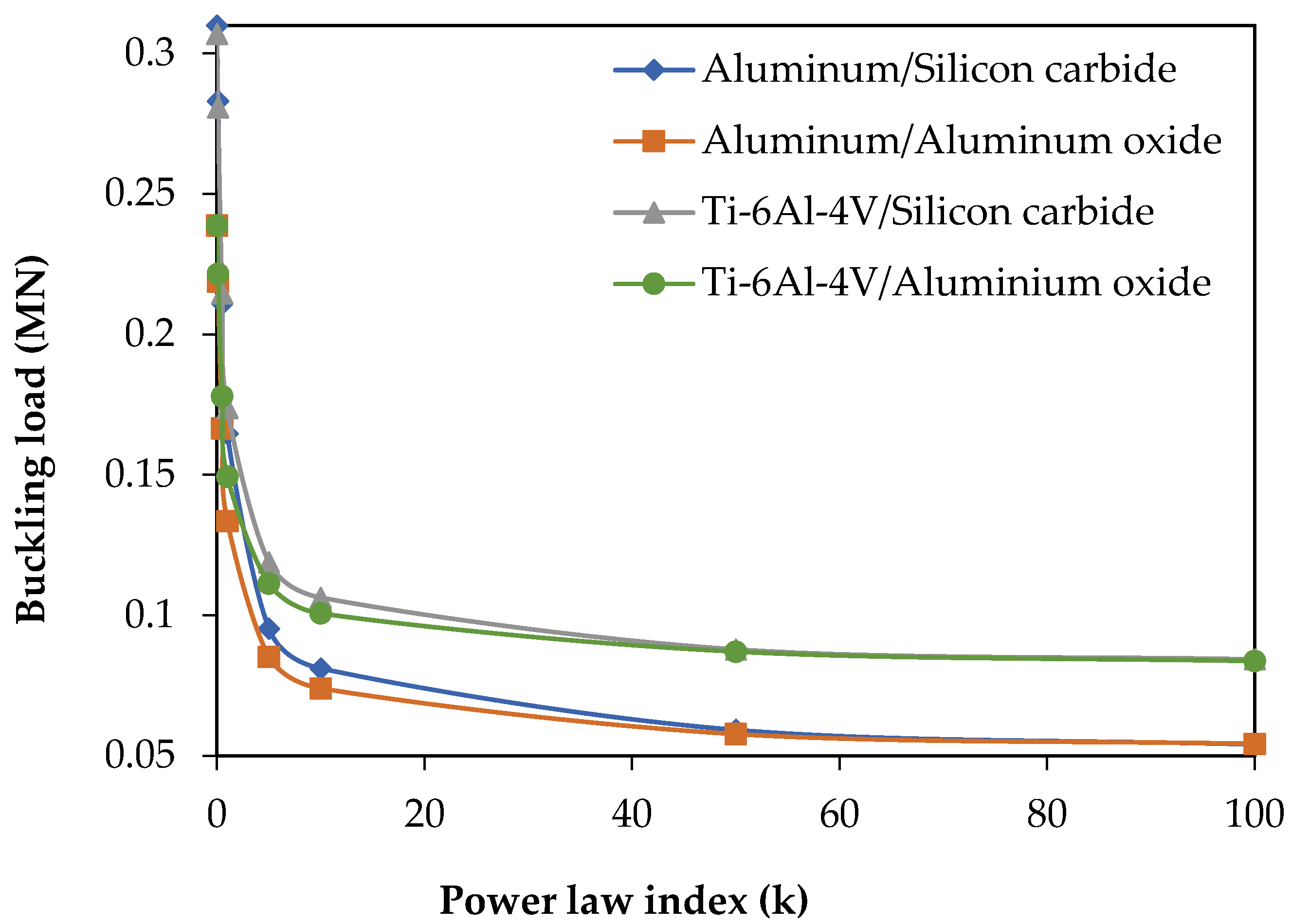
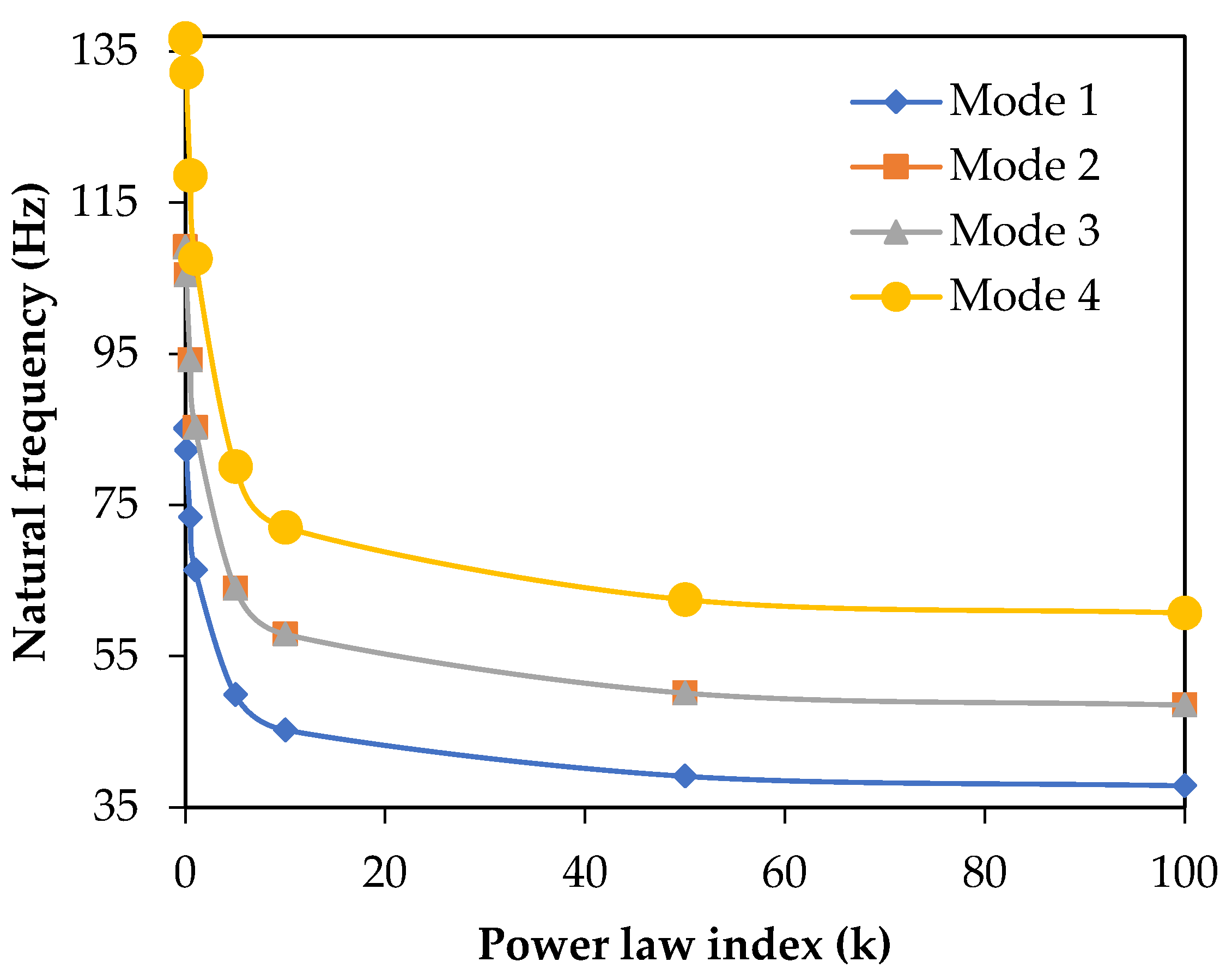
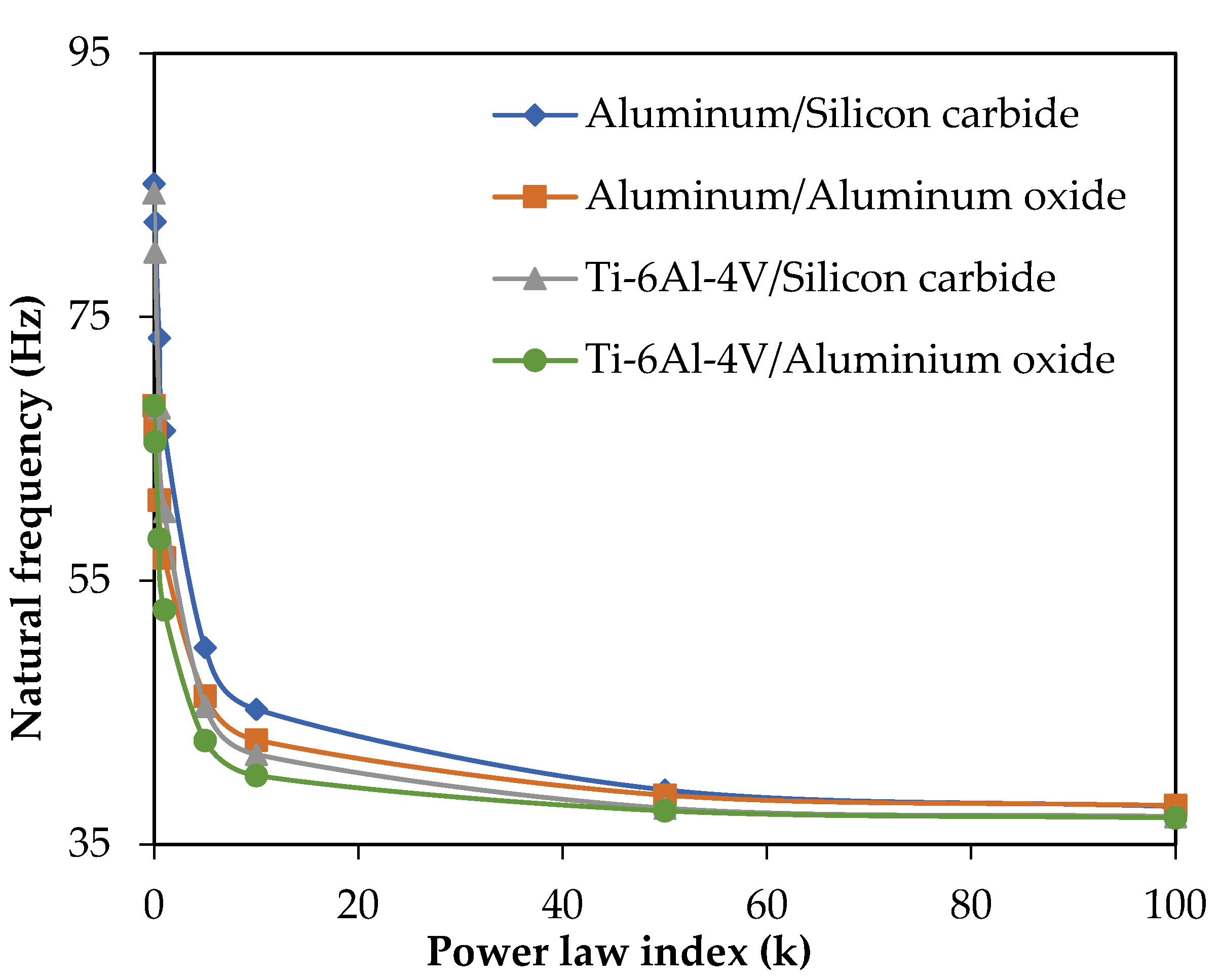
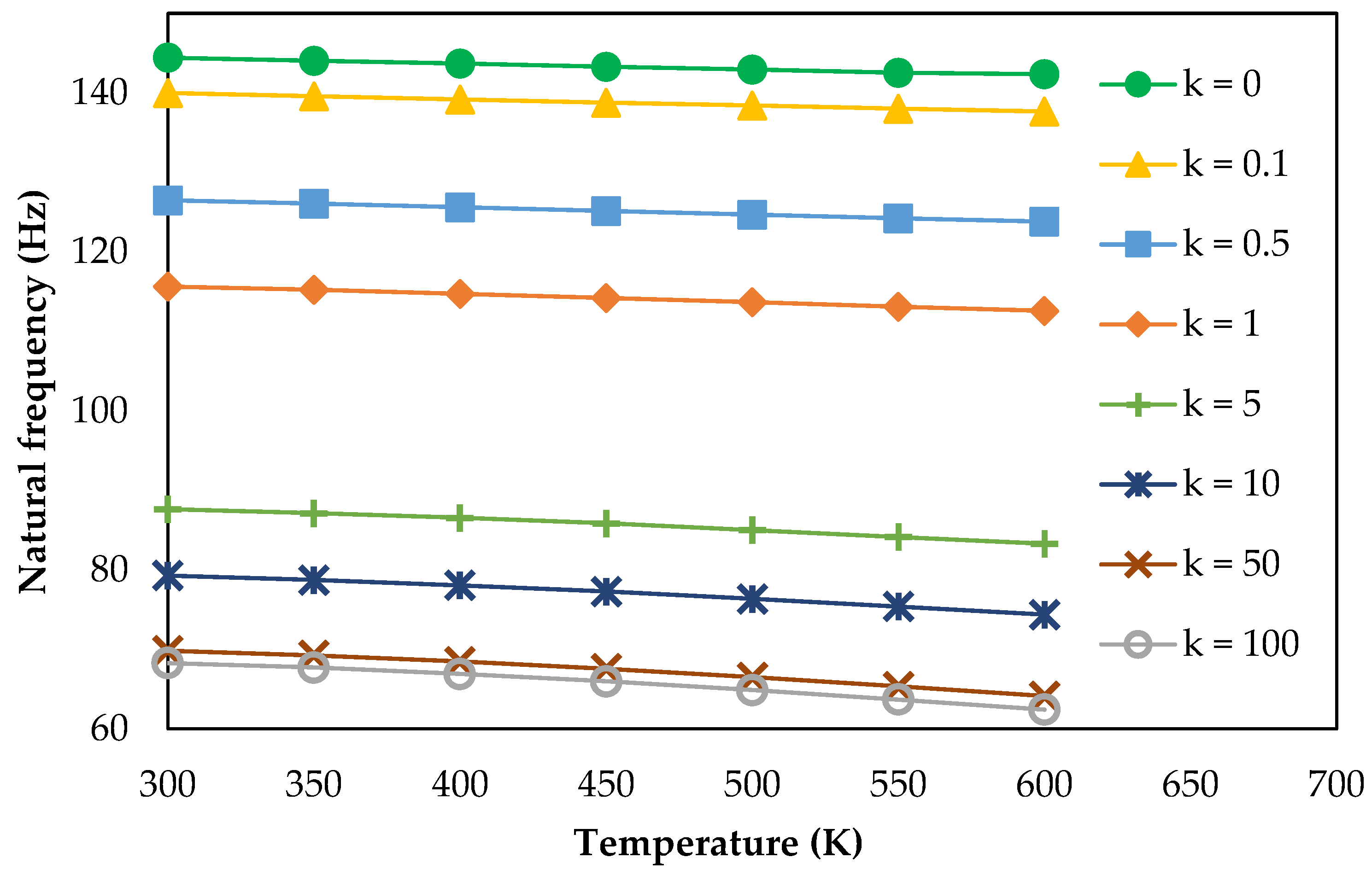
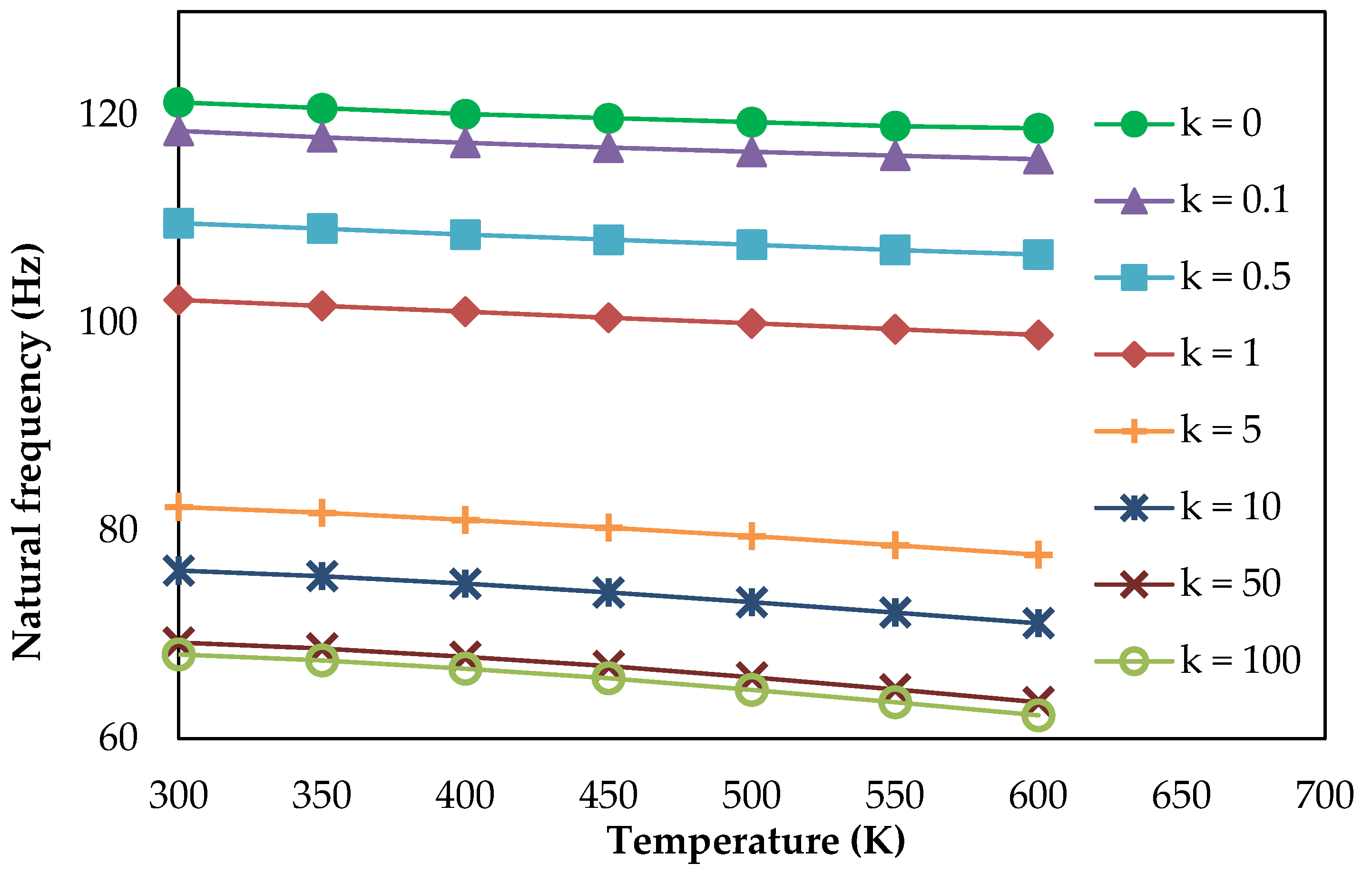
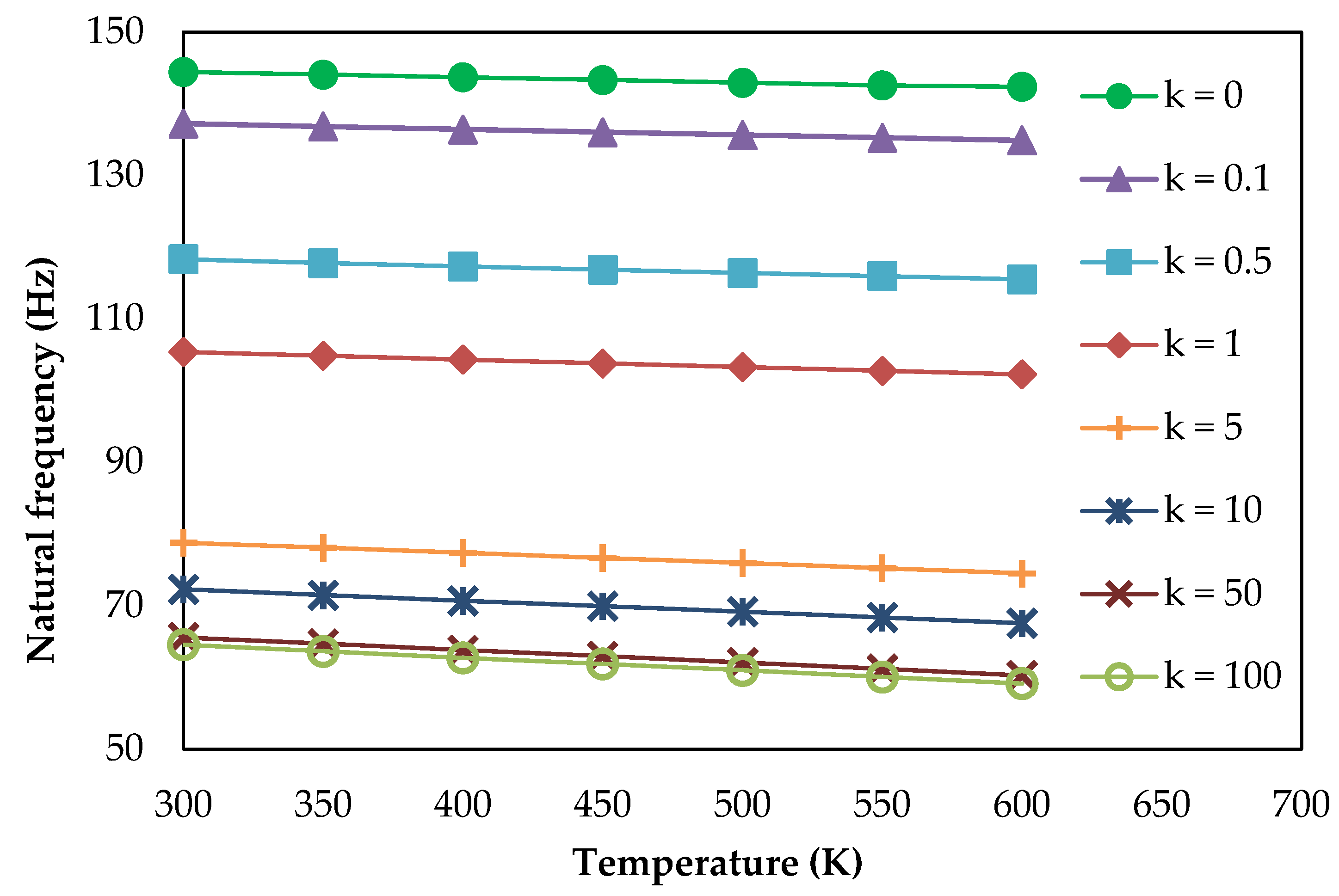
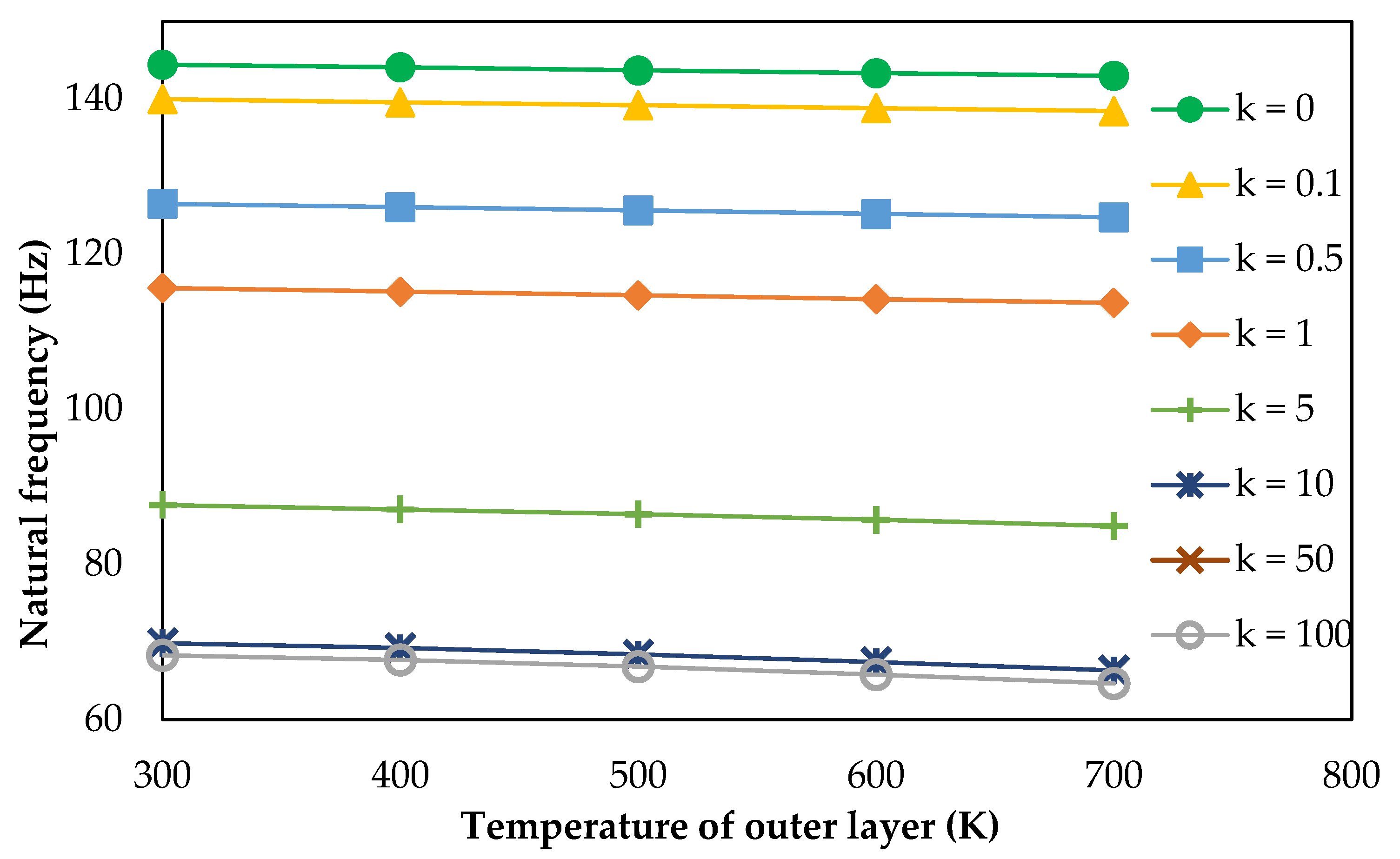
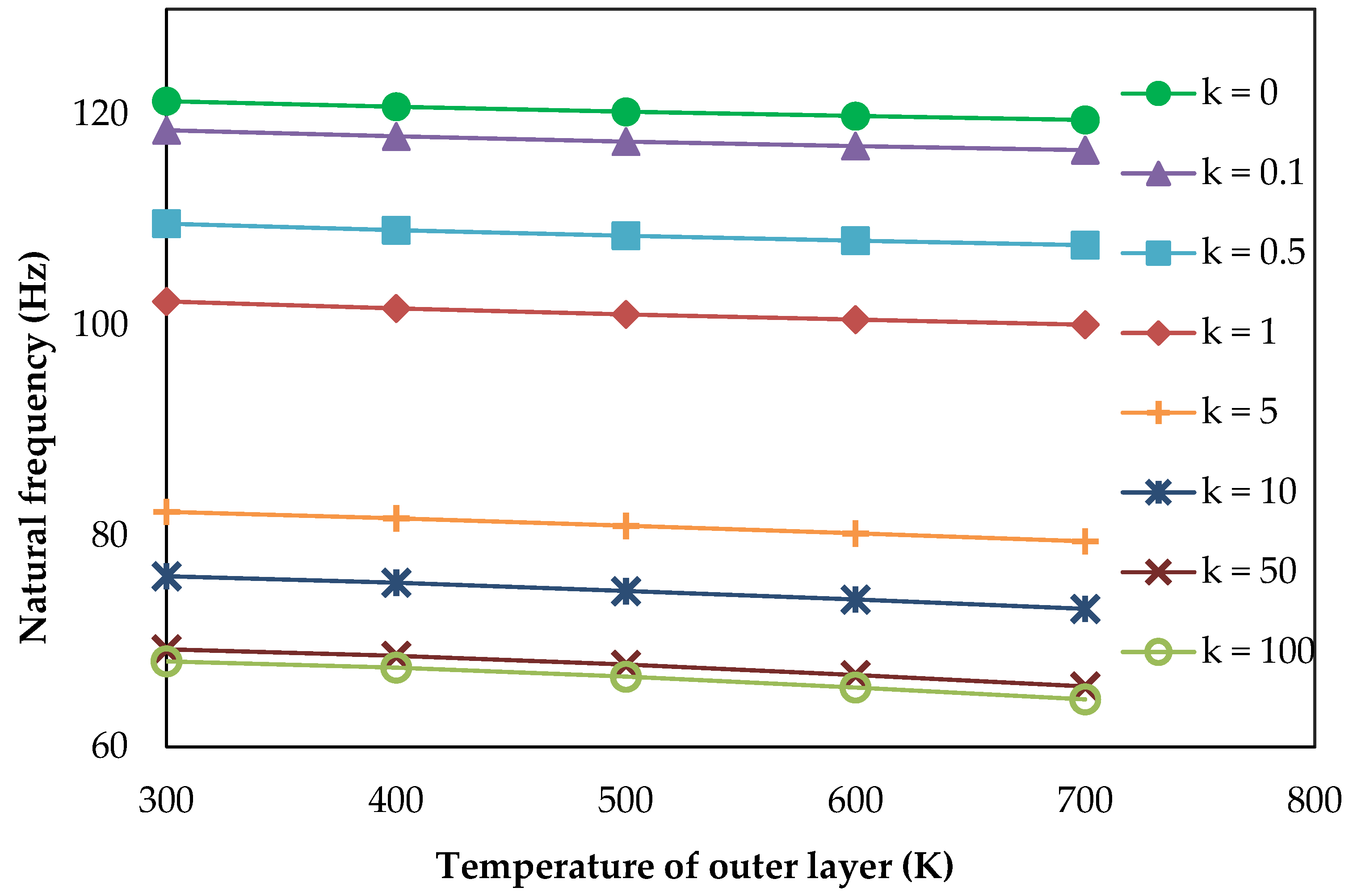
The structural and thermal analysis of the re-entry vehicle nose model made of FGM has been studied and the numerical results for the bending and buckling, as well as the vibration responses have been computed. Four FGM shell structures made of aluminum/silicon carbide, aluminum/aluminum oxide, Ti-6Al-4V/silicon carbide and Ti-6Al-4V/aluminum oxide were considered. Convergence and validation studies were performed to confirm the adopted methodology. The FGM shell with k = 1 gives uniform and linear distribution of material composition in the direction of thickness. Structural analysis of the re-entry vehicle nose model made of FGM shows that an increase in the maximum central displacement and a decrease in the critical buckling load and the natural frequency occurs due to the increase in the power law index. The bending, buckling and vibration characteristics of FGM shell are enhanced when Ti-6Al-4V is considered as a metal constituent due to the high modulus of elasticity and stiffness. Thermal buckling analysis shows that the critical buckling temperature drops with an increase in the thermal environment and the linear temperature rise of the outer layer. It was also observed that when k < 1, it causes the composition of ceramic to be more dominant, which leads to an increase in the compressive strength and the critical buckling temperature. An FGM shell with Ti-6Al-4V/silicon carbide shows good buckling characteristics in thermal applications. From vibration analysis under a thermal environment, it was concluded that the natural frequency reduces with a uniform increase in temperature, as well as in linear a temperature rise. Under various linear temperature rises of outer layer, it was concluded that the increase in shell thickness increases the critical buckling temperature and natural frequency. An FGM shell with a thickness of 0.05 m and k = 0.1 can be used for re-entry vehicle nose structures due to an enhanced critical buckling temperature. Thus, a detailed thermo-structural analysis on thin, large FGM shells for different material combinations was carried out and quantified several significant parametric results. Multiscale analysis can be performed in the future, including the wavelength and amplitude of the long strip inclusion.