Effects of Open-Hole and Reinforcement on the Bearing Performance of the Plain-Woven Fabric Composite I-Section Beams under Shear Load
Abstract
1. Introduction
2. Shear Experiments on the PWF Composite I-Section Beams
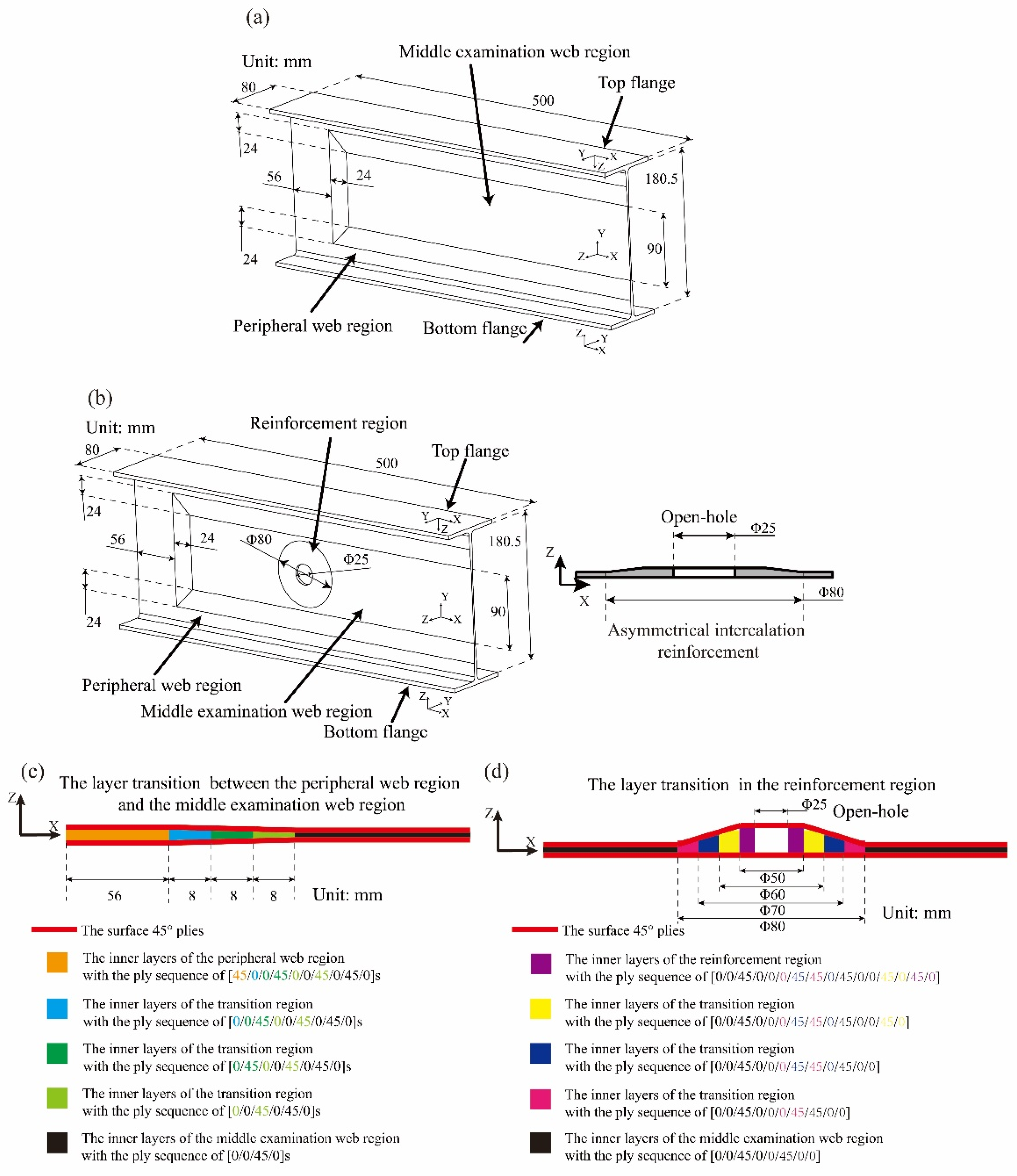
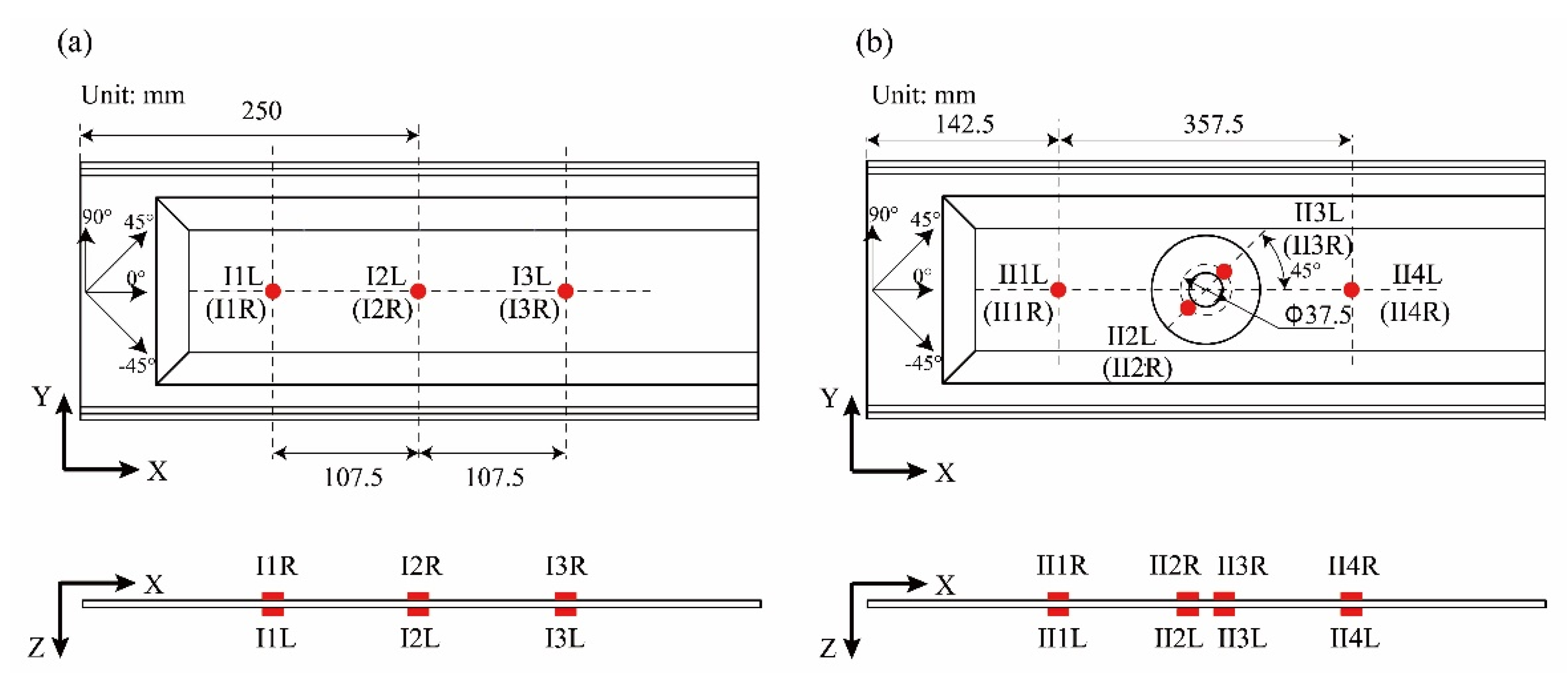
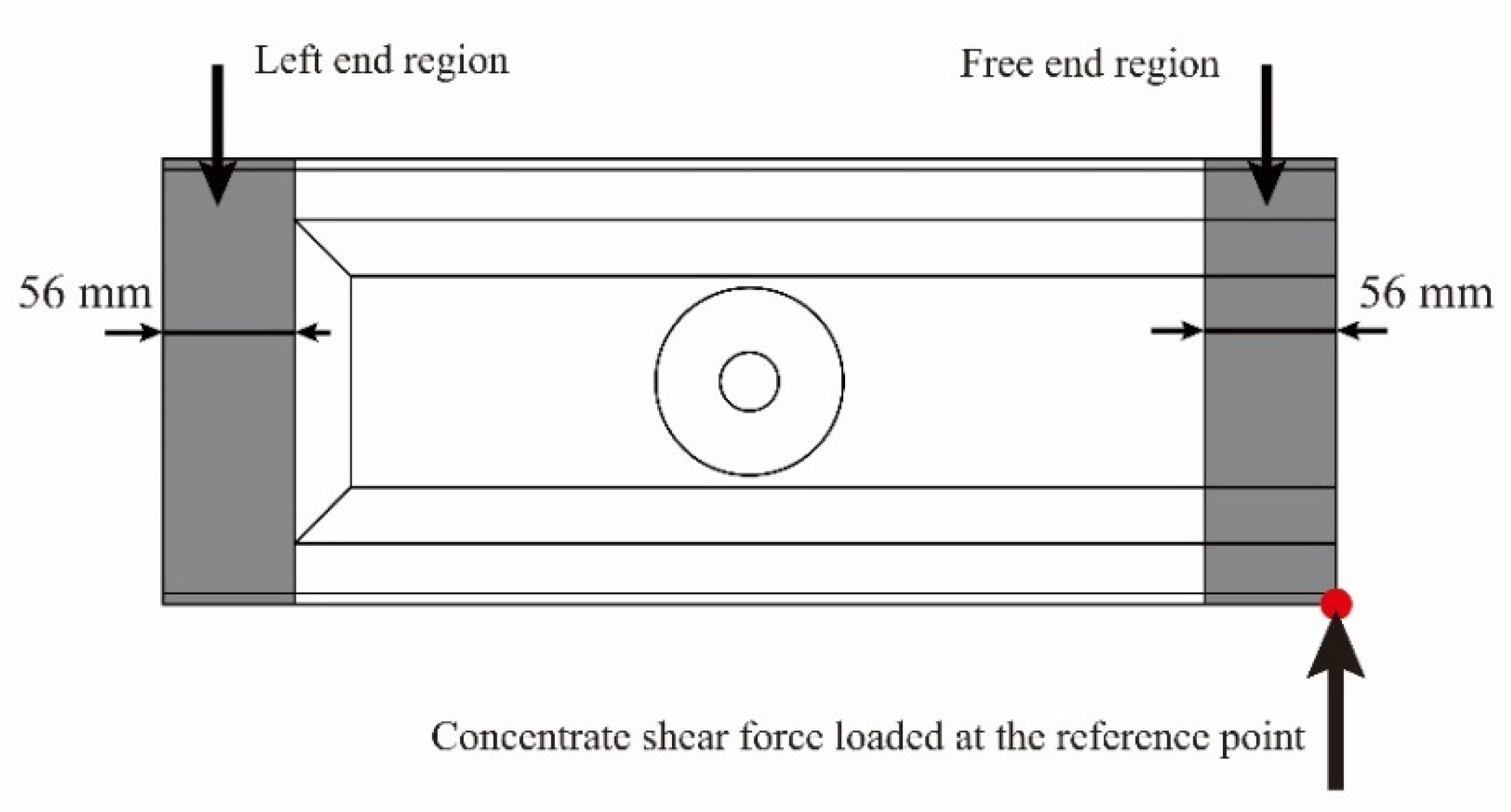
2.1. Specimens and Shear Loading
2.2. Experimental Results and Analysis
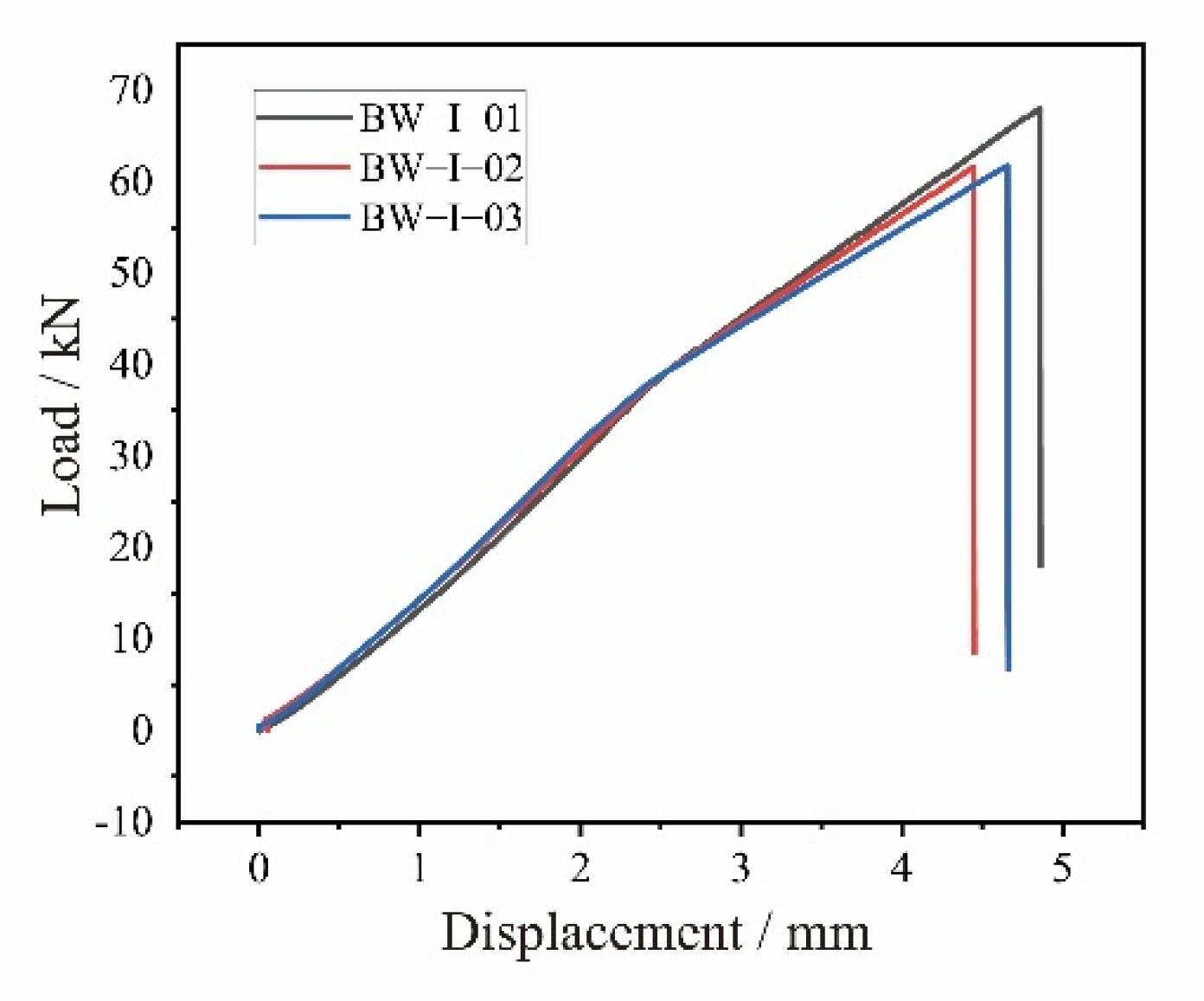
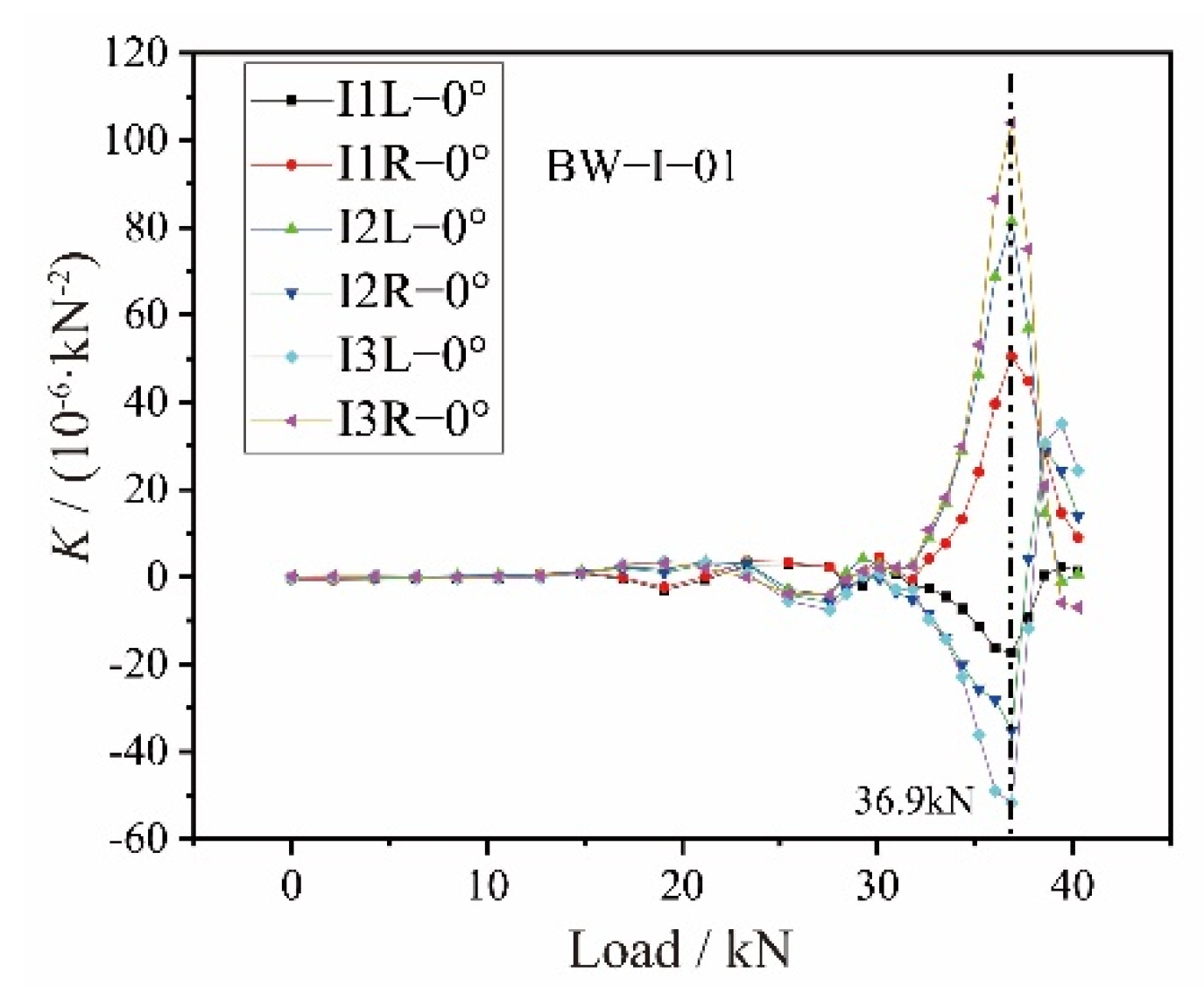
2.2.1. Experimental Results of the BW-I Composite Beams
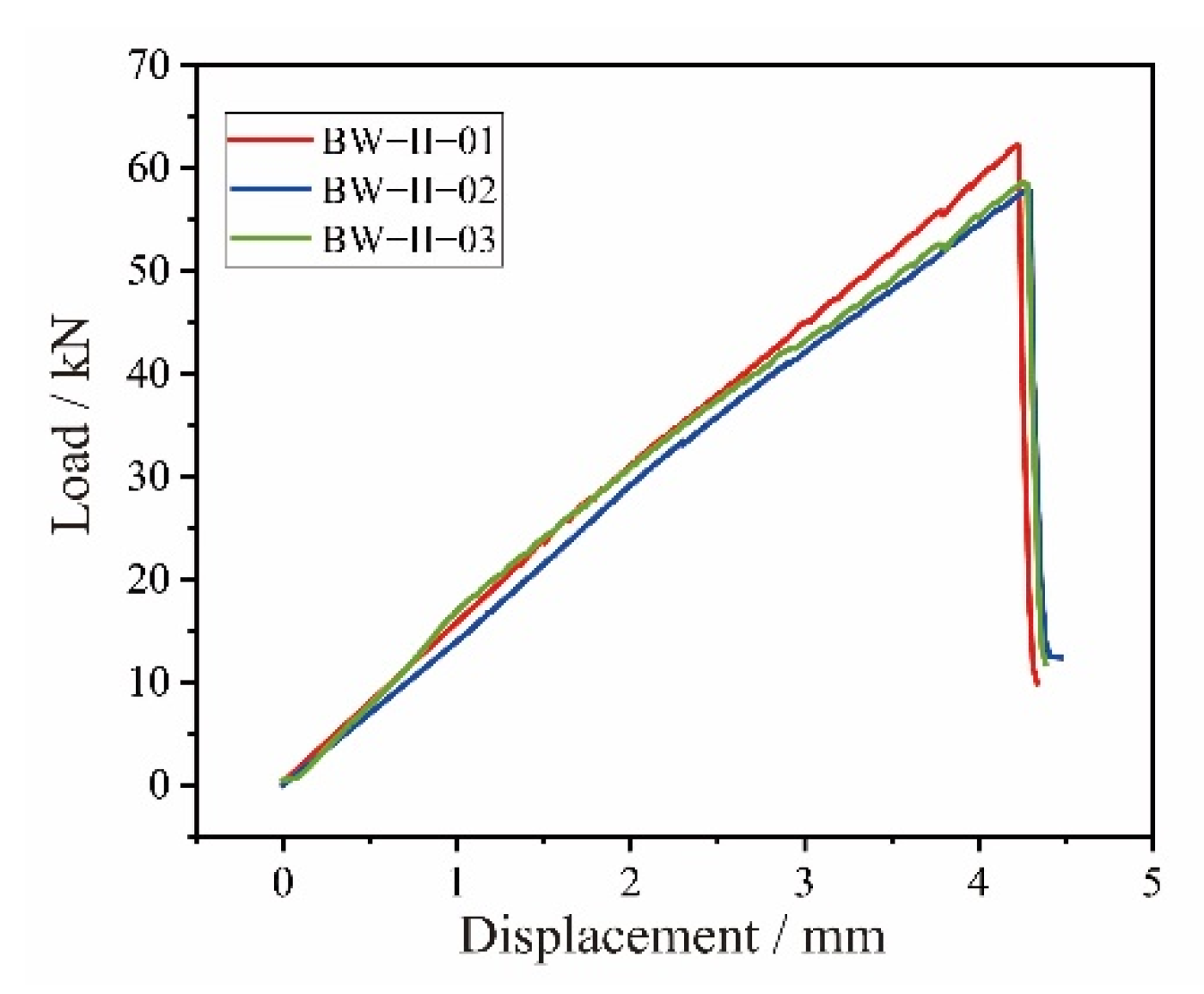
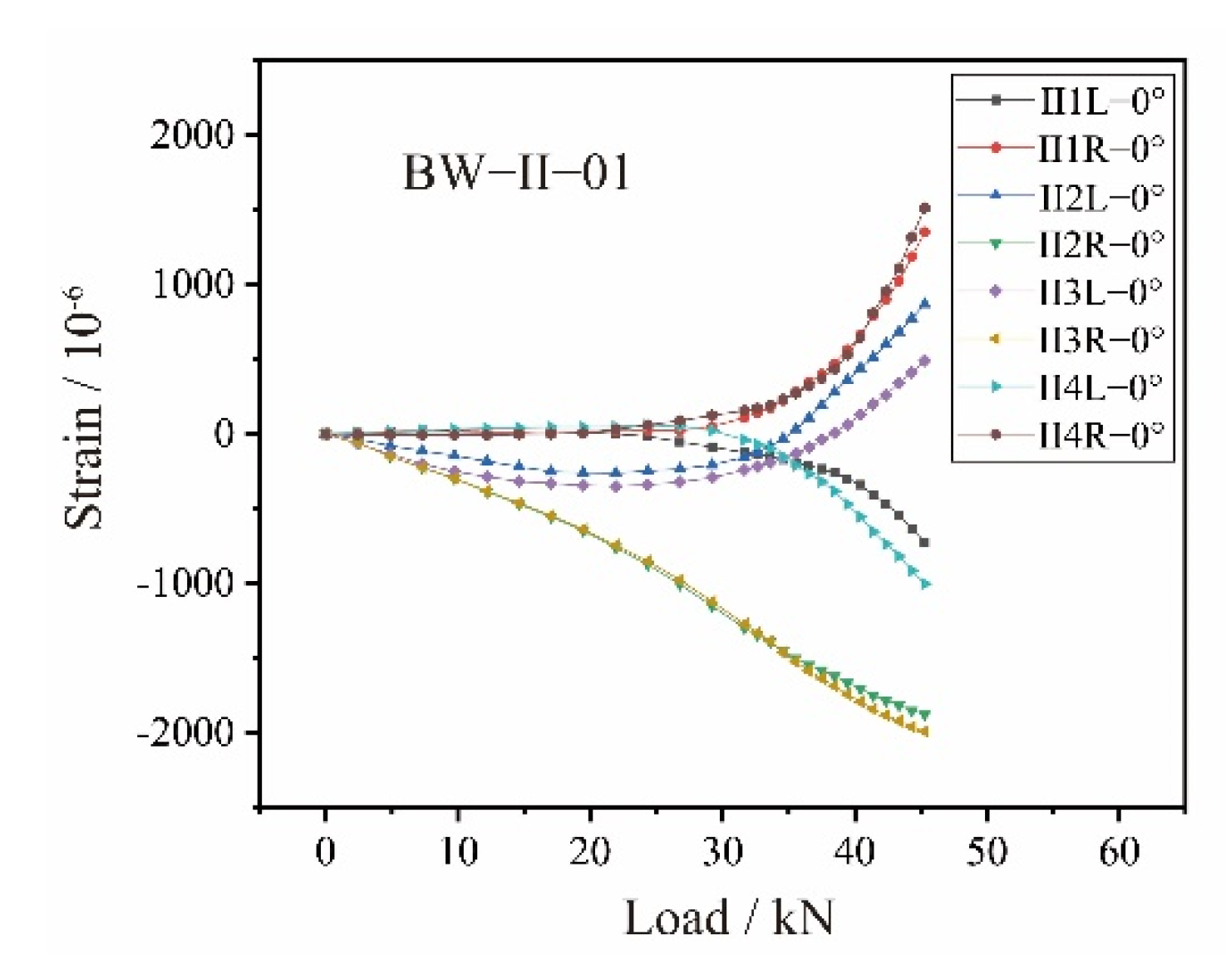
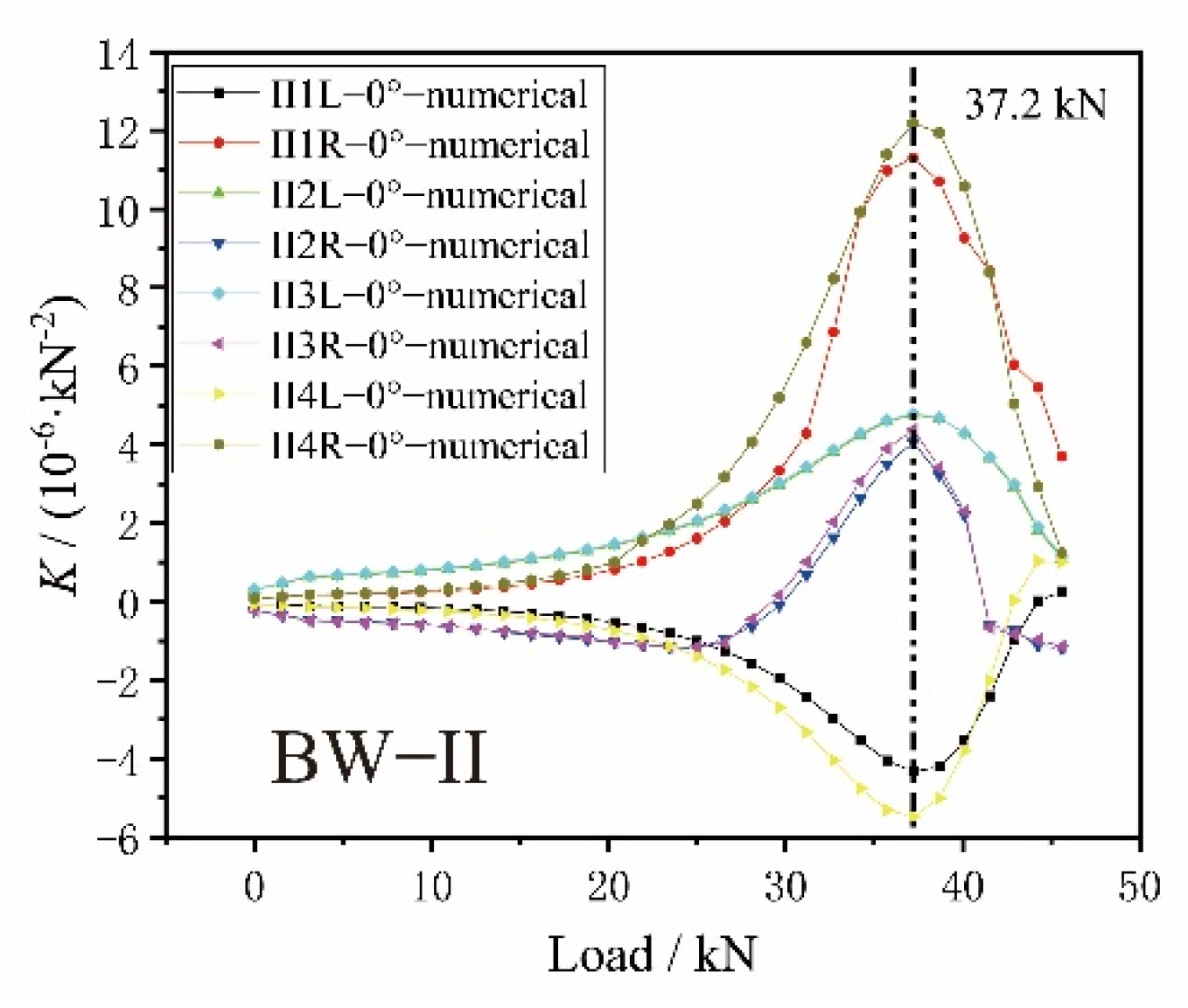
2.2.2. Experimental Results of the BW-II Composite Beams
3. FE Models and Method for the FE Analysis
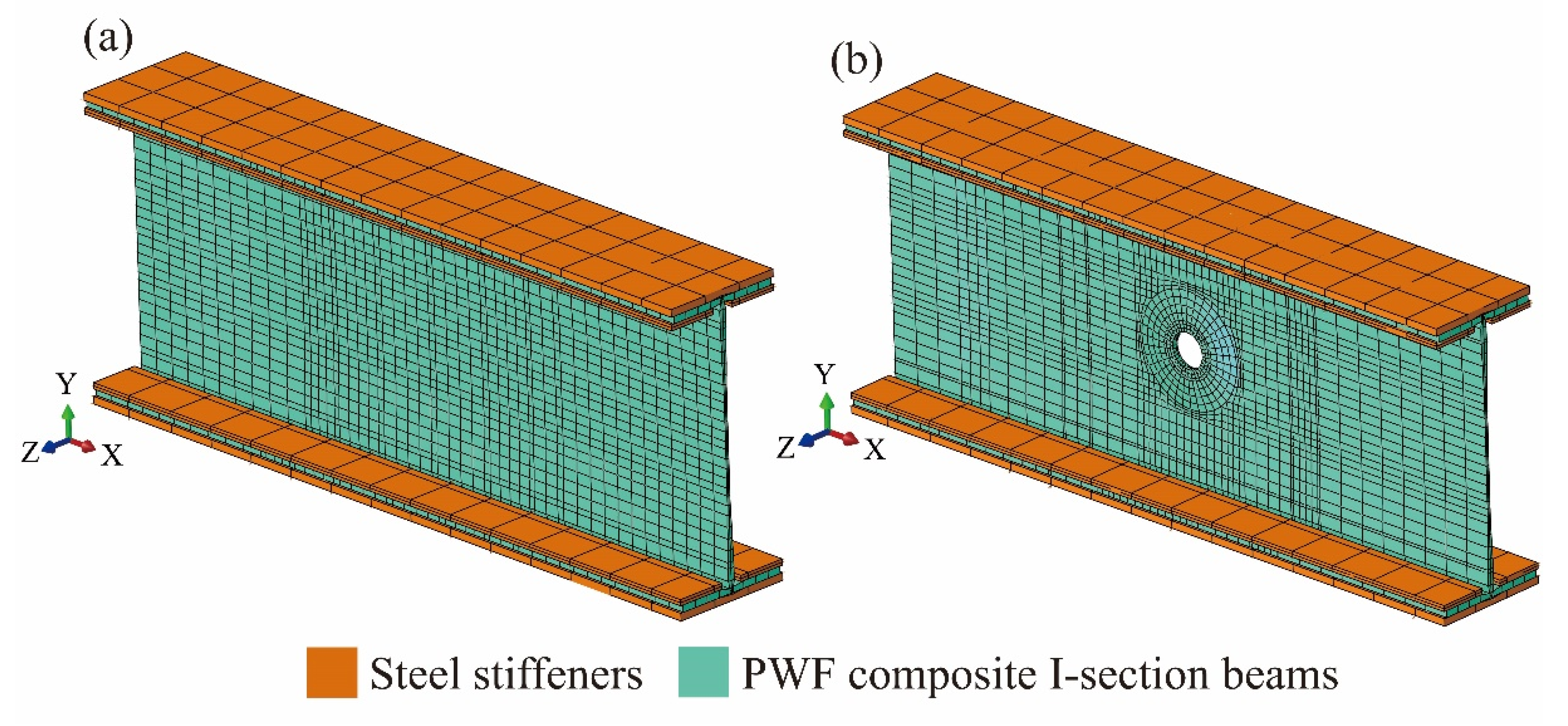
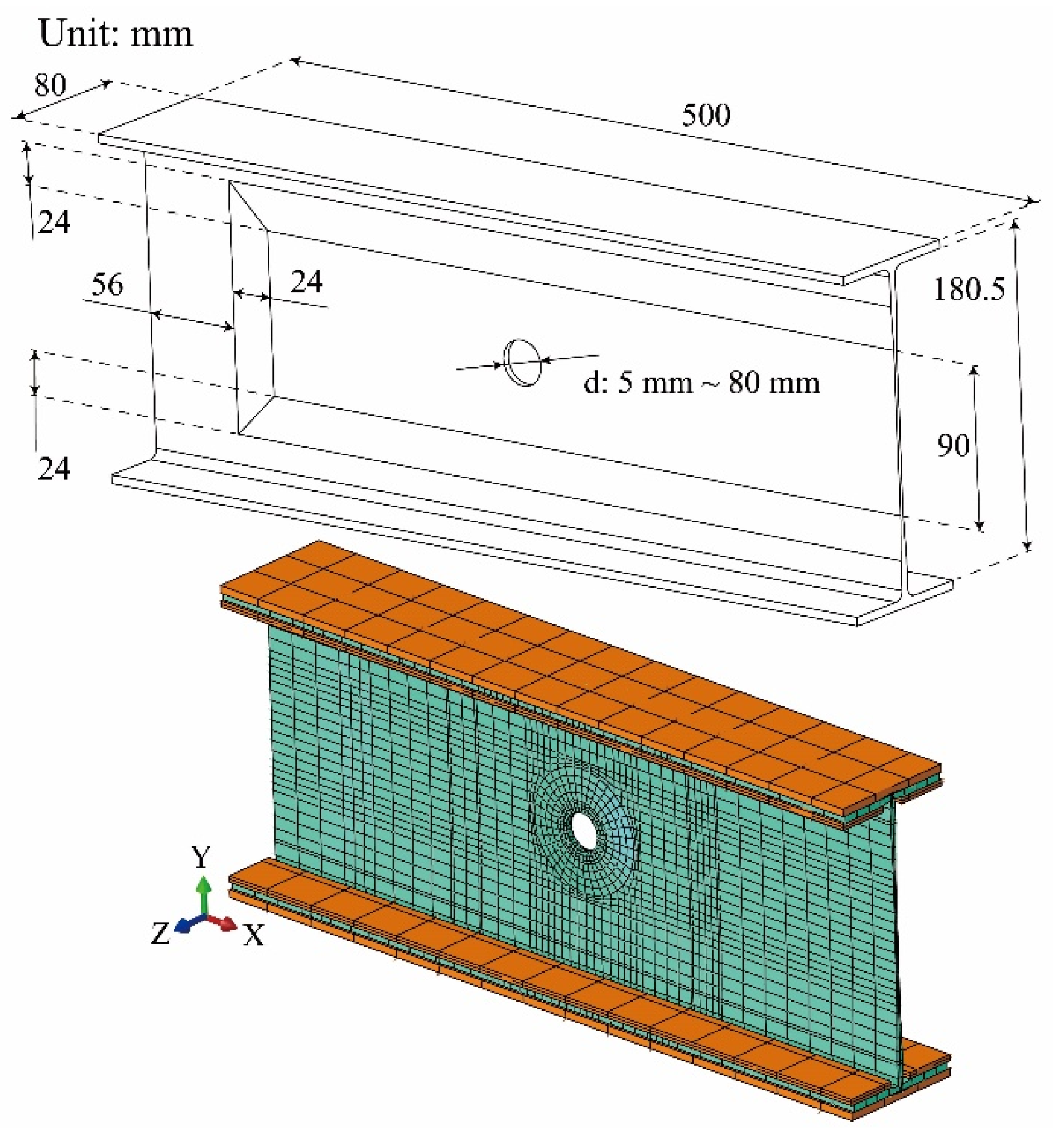
3.1. Finite Element Models
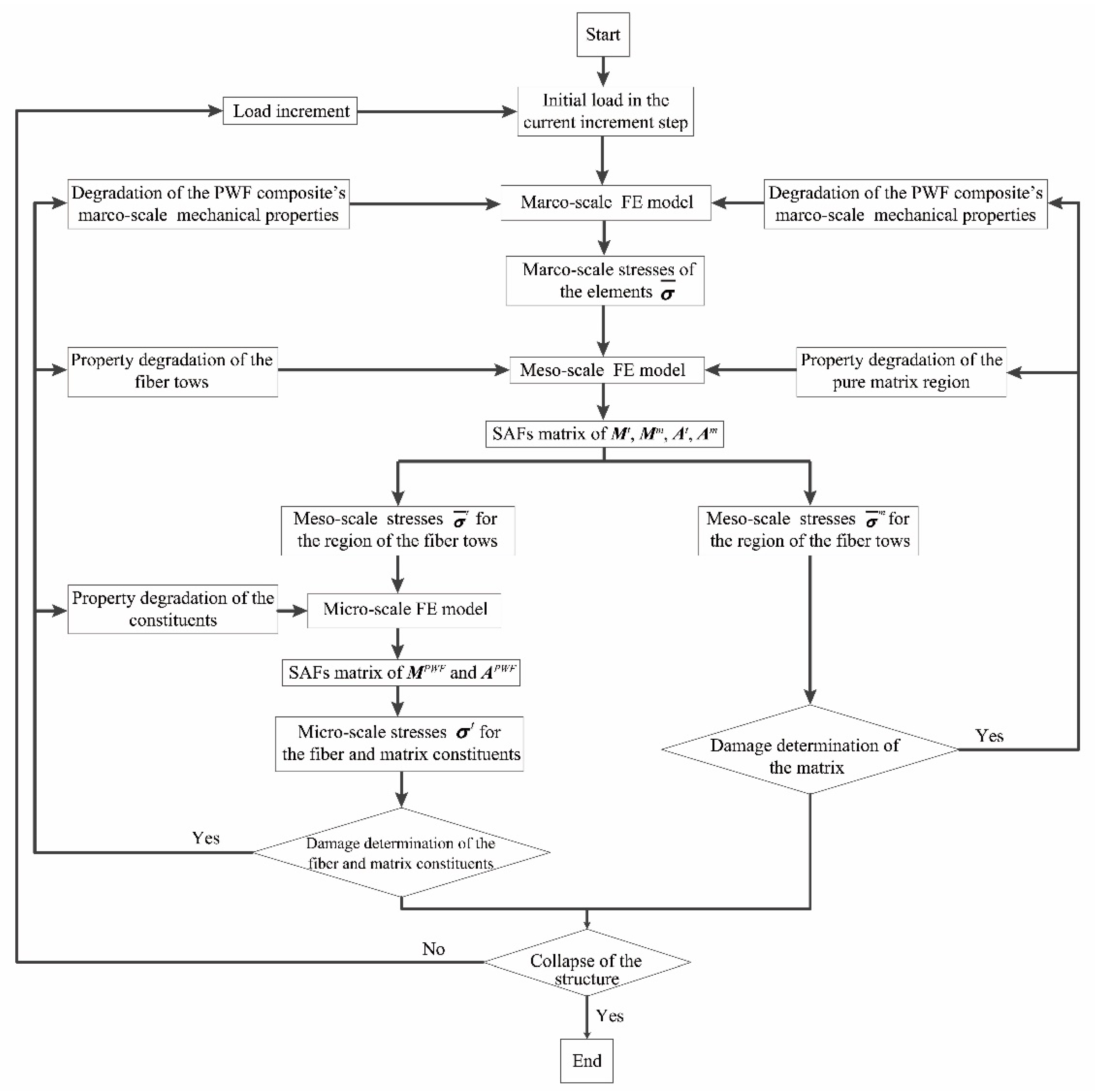
3.2. Multi-Scale FE Method for the PWF Composites’ Failure Analysis
3.2.1. Stress Transformation between Different Analyzing Scales
3.2.2. Damage Determination for the Composite’s Constituents
3.2.3. Degradation of the PWF Composite’s Mechanical Properties after Damage
3.2.4. Multi-Scale Method for the PWF Composite’s Failure Analysis
4. Model Validation and Parametric Analysis
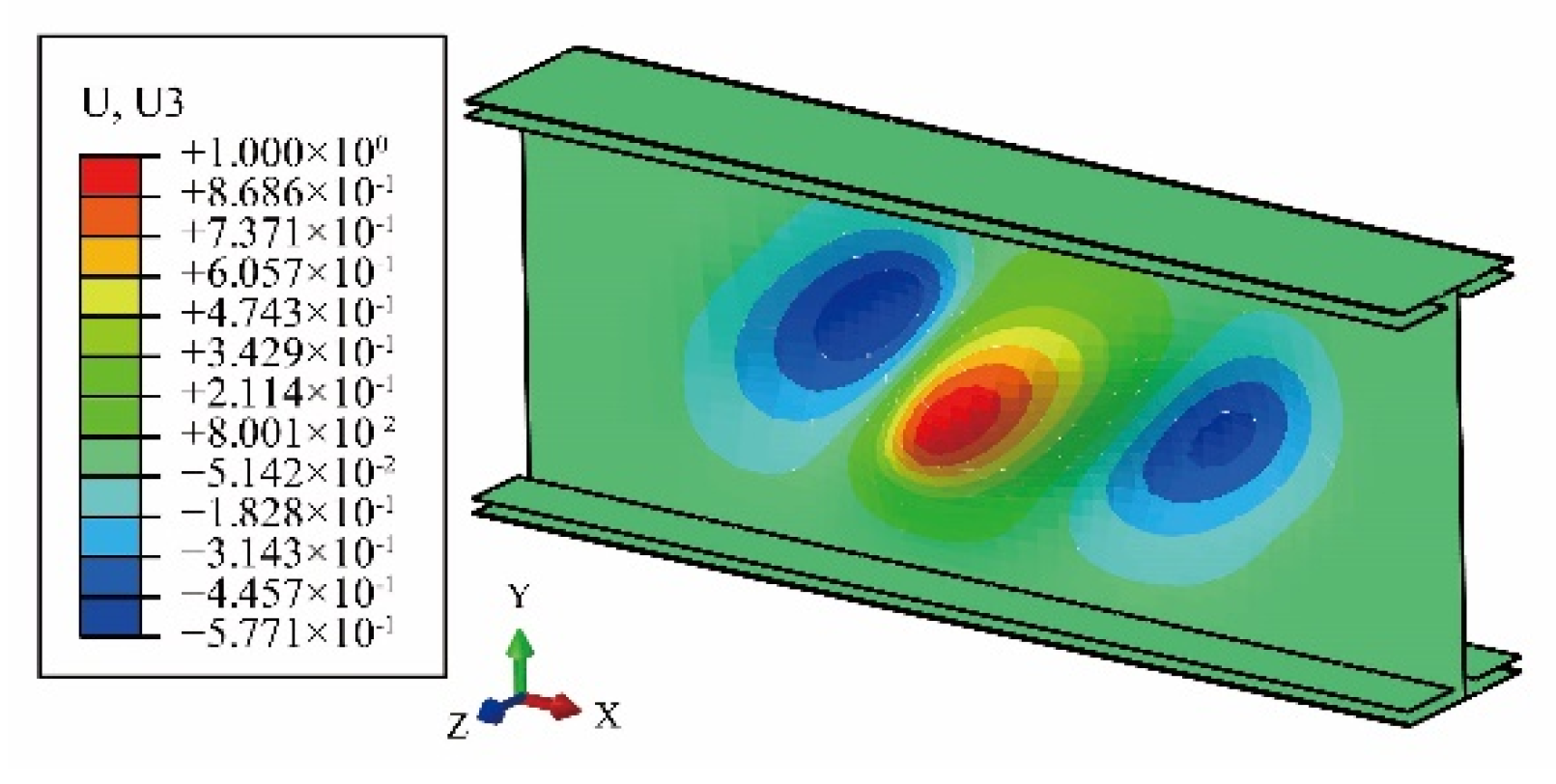
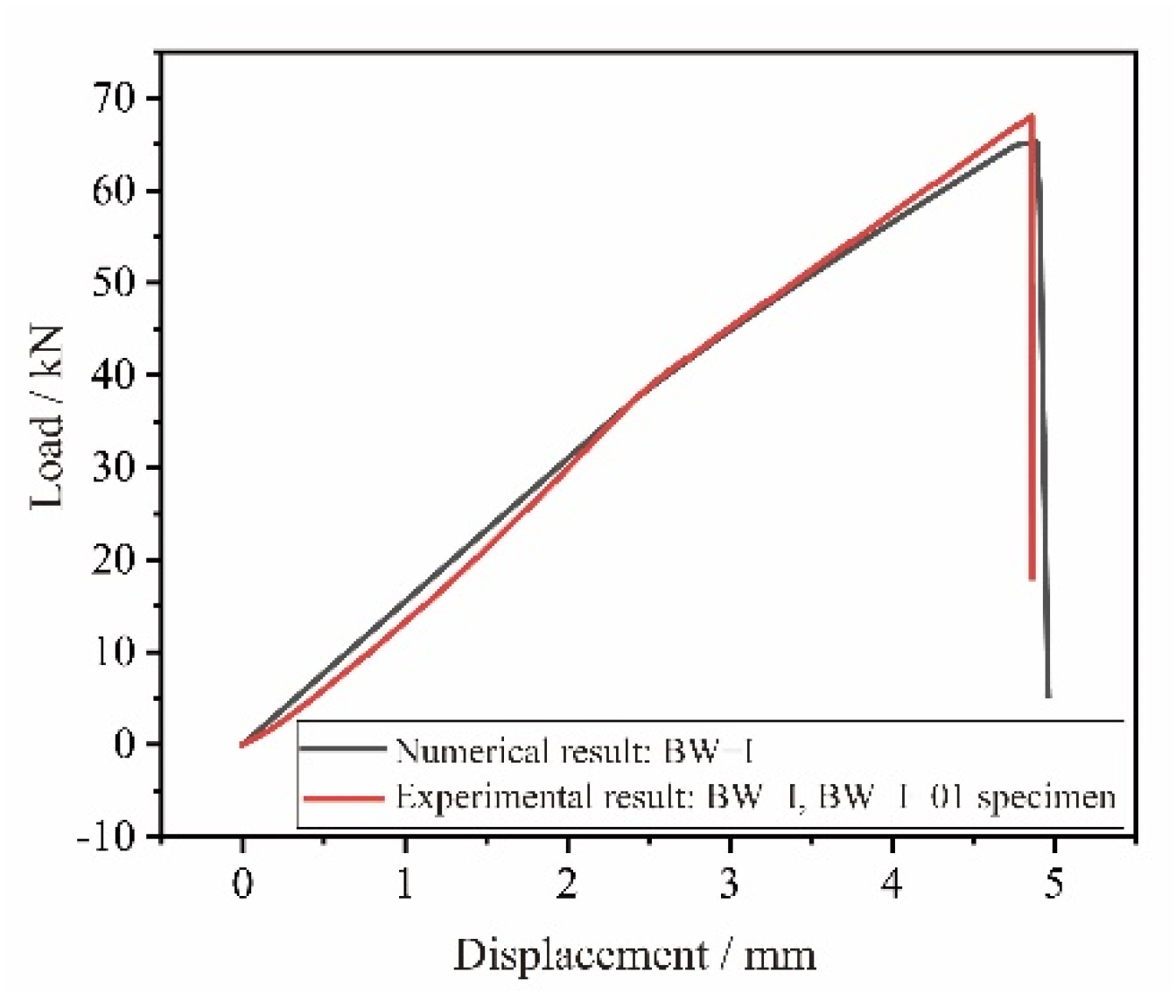
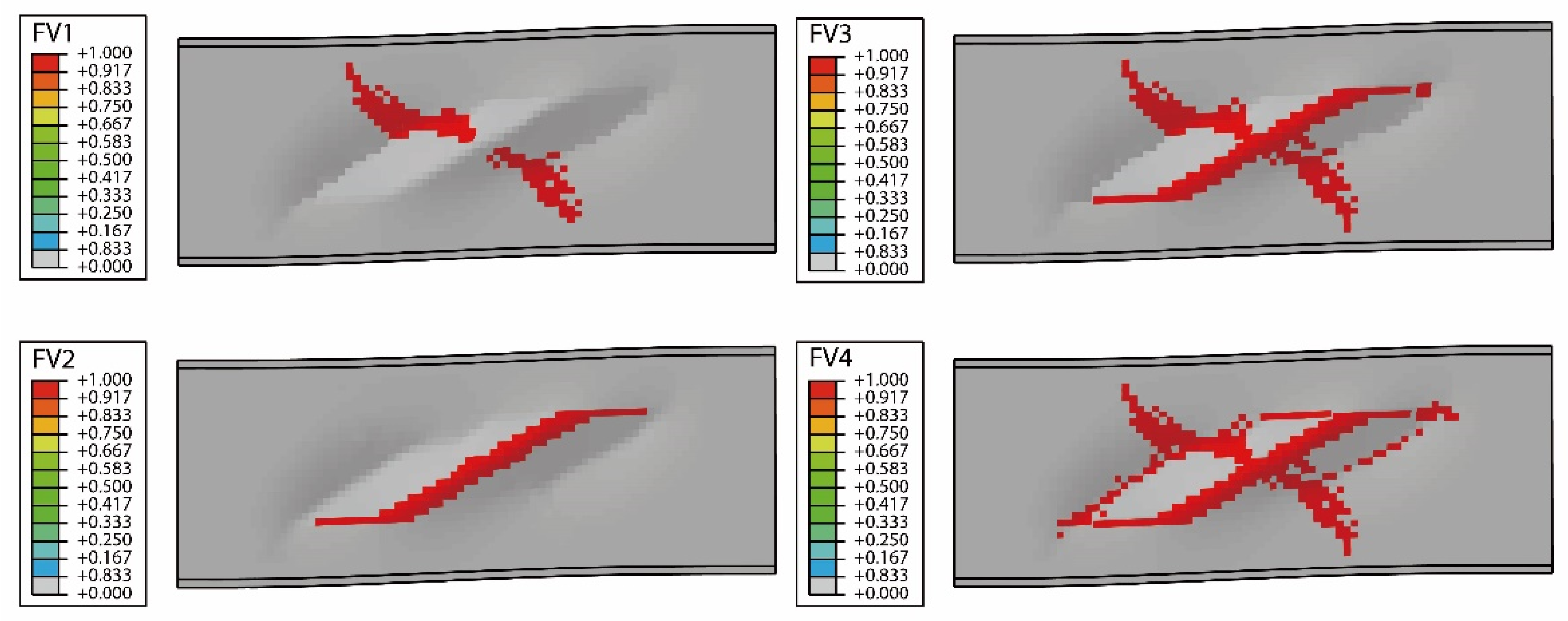
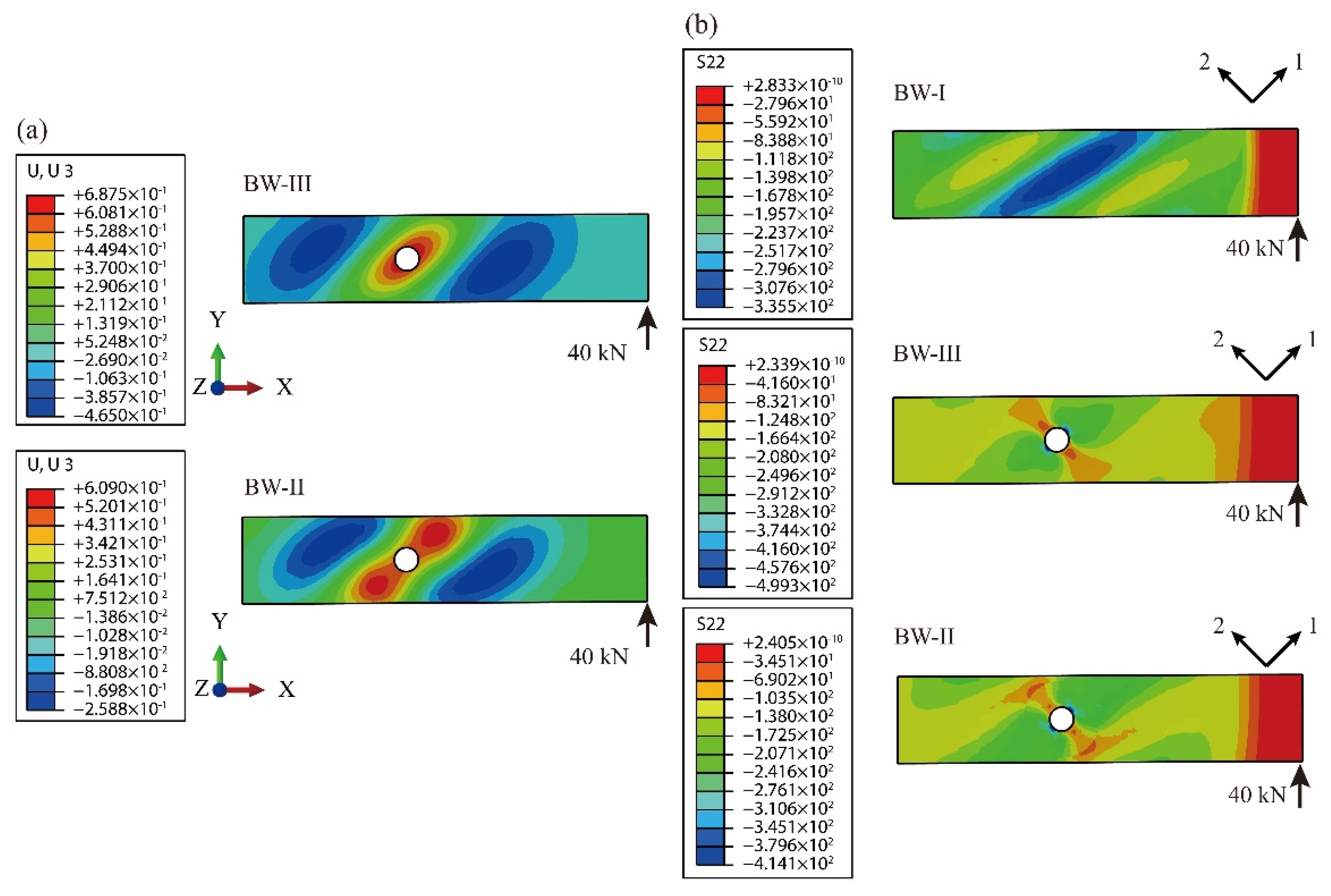
4.1. FE Analysis Results of the BW-I Composite Beams
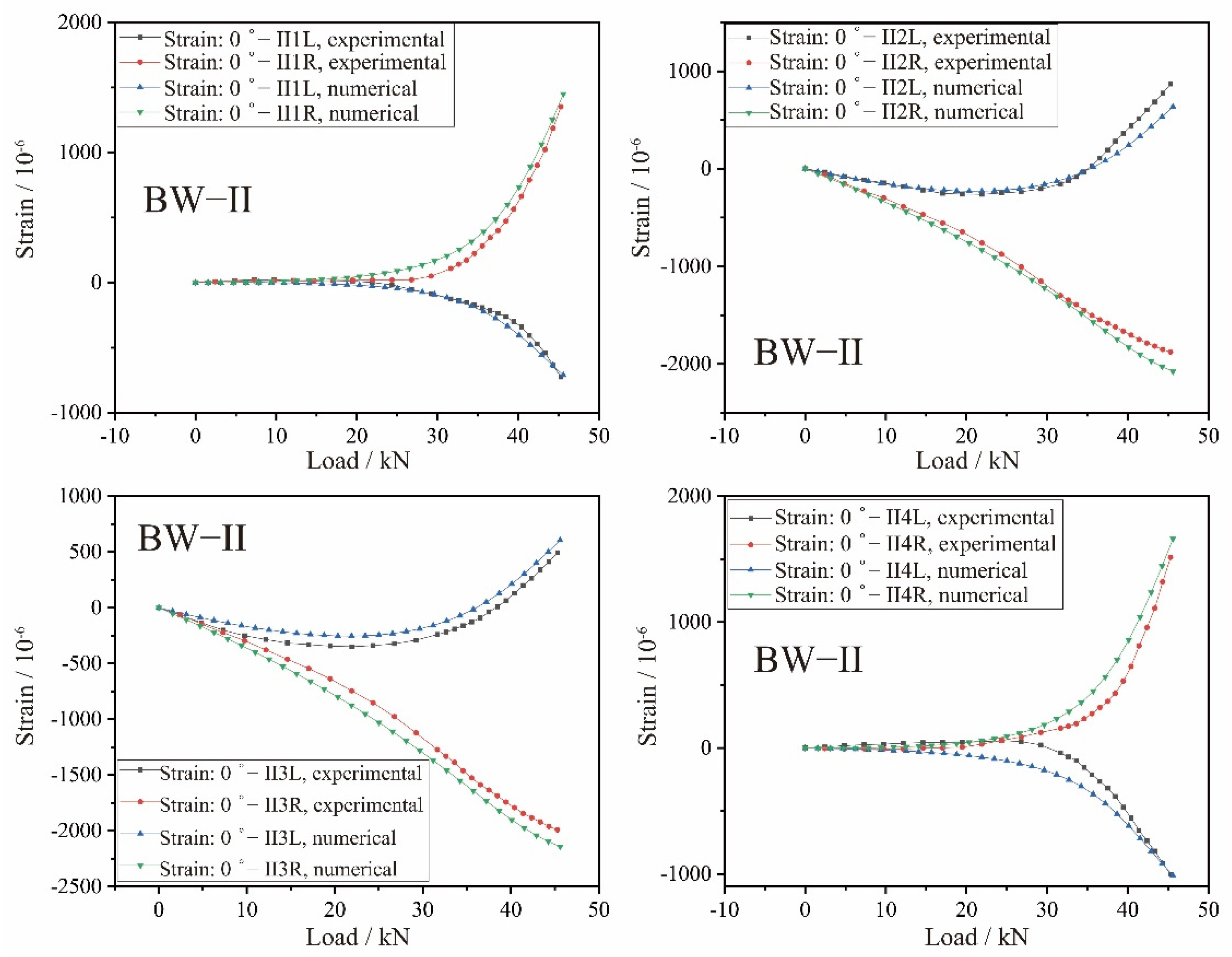
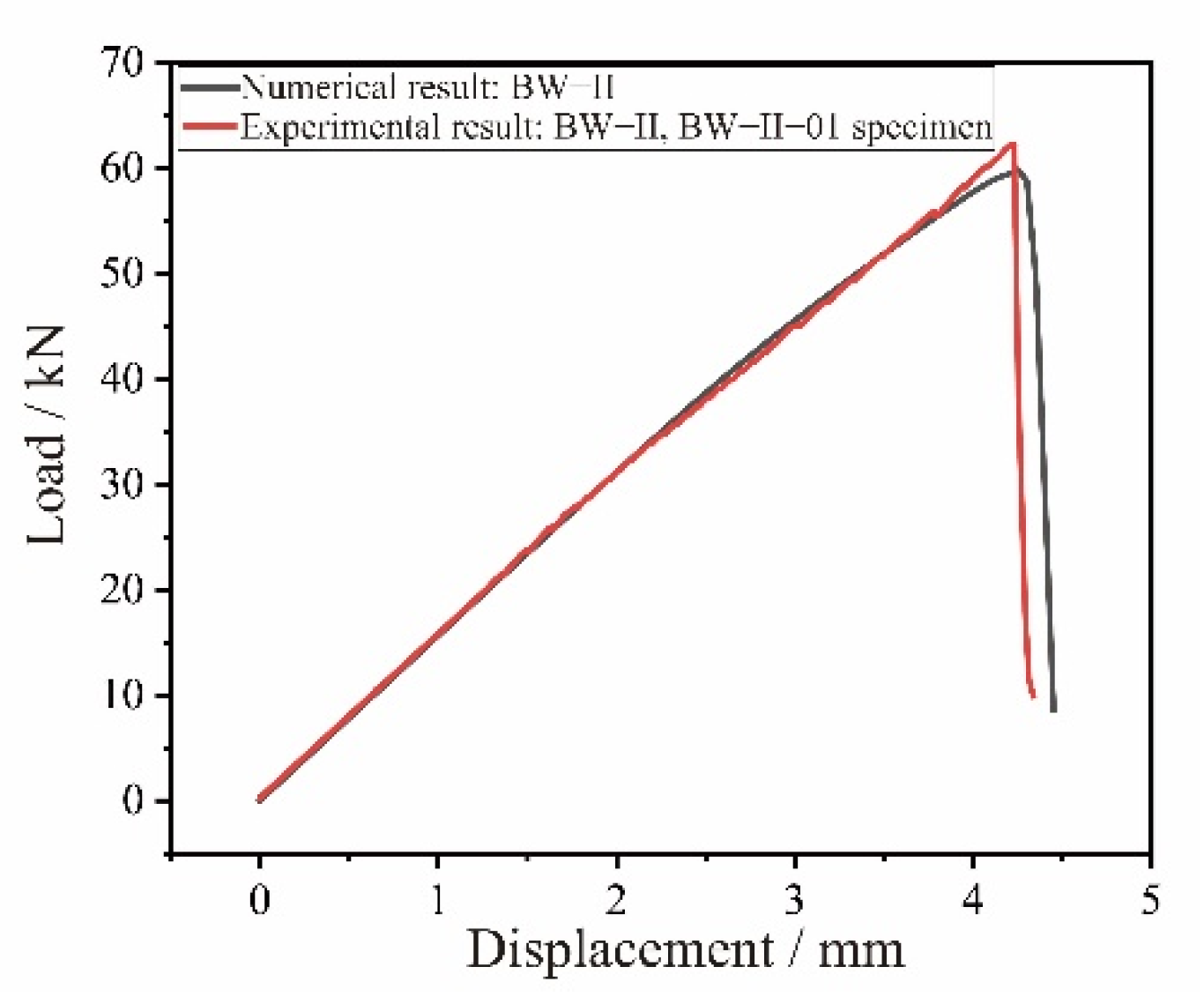
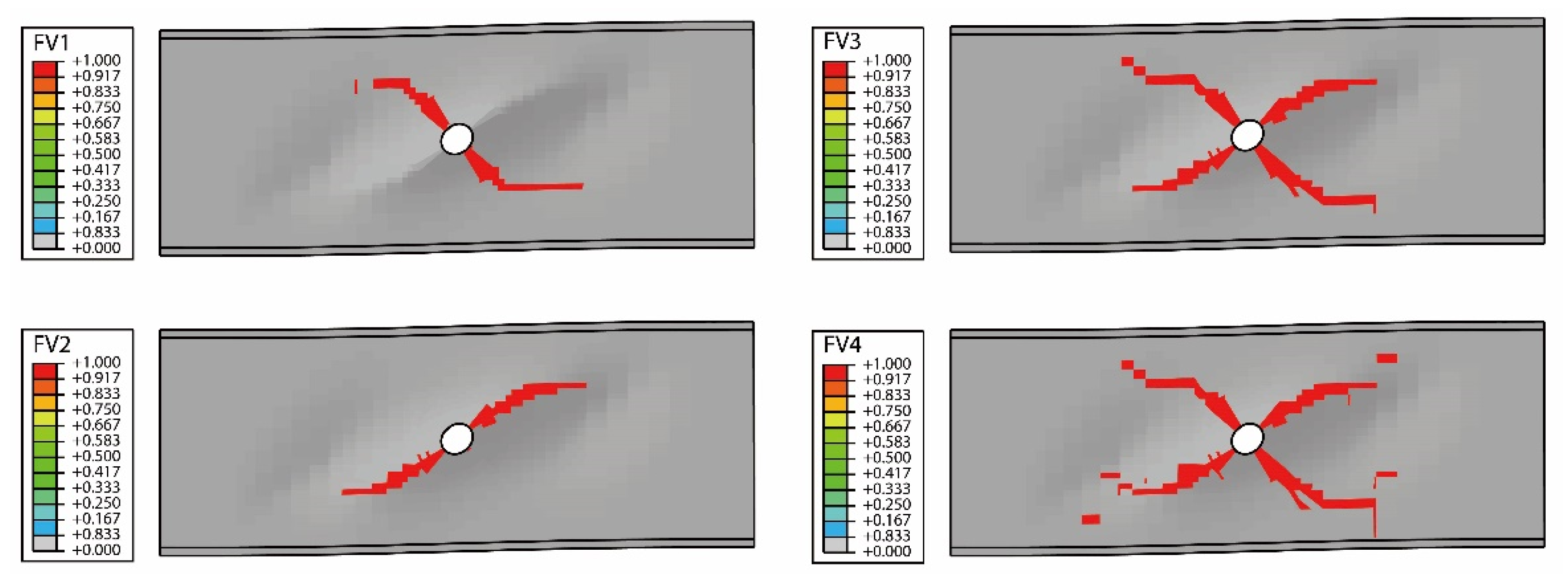
4.2. FE Analysis Results of the BW-II Composite Beams
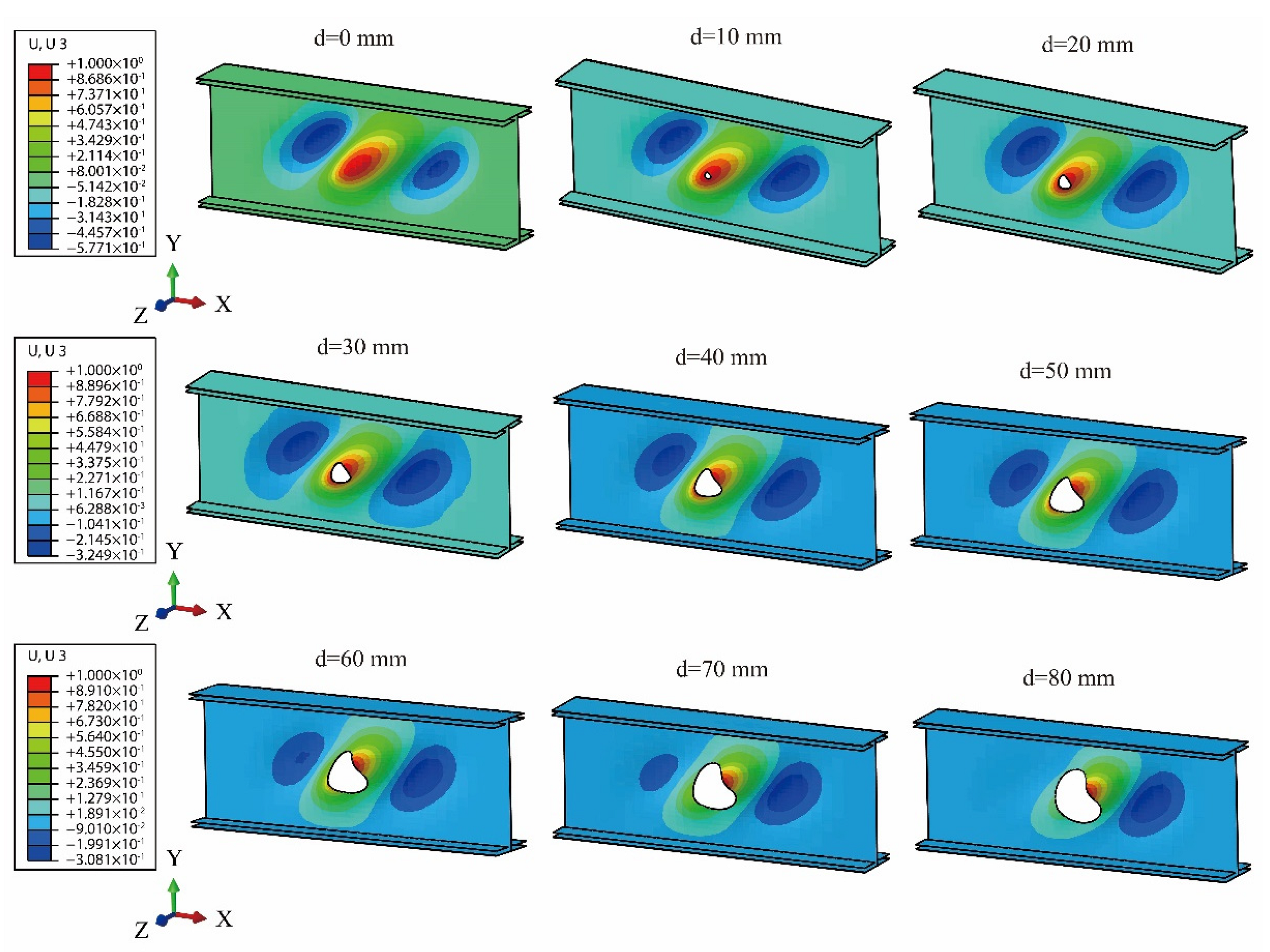
4.3. Parametric Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, O.; Librescu, L.; Jeong, N.-H. Static response of thin-walled composite I-beams loaded at their free-end cross-section: Analytical solution. Compos. Struct. 2001, 52, 55–65. [Google Scholar] [CrossRef]
- Lee, J.; Kin, S.-E.; Hong, K. Lateral buckling of I-section composite beams. Eng. Struct. 2002, 24, 955–964. [Google Scholar] [CrossRef]
- Mittelstedt, S.; Mittelstedt, C. Mixed-mode buckling of shear-deformable composite laminated I-beams. Int. J. Mech. Sci. 2020, 169, 105332. [Google Scholar] [CrossRef]
- Asadi, A.; Sheikh, A.H.; Thomsen, O.T. Buckling behavior of thin-walled laminated composite beams having open and closed sections subjected to axial and end moment loading. Thin Wall. Struct. 2019, 141, 85–96. [Google Scholar] [CrossRef]
- Guo, S.; Morishima, R.; Zhang, X.; Mills, A. Cutout shape and reinforcement design for composite C-section beams under shear load. Compos. Struct. 2009, 88, 179–187. [Google Scholar] [CrossRef]
- Guo, S.; Li, D.; Zhang, X.; Xiang, J. Buckling and post-buckling of a composite C-section with cutout and flange reinforcement. Compos. Part B Eng. 2014, 60, 119–124. [Google Scholar] [CrossRef]
- Orun, A.E.; Guler, M.A. Effect of hole reinforcement on the buckling behavior of thin-walled beams subjected to combined loading. Thin Wall. Struct. 2017, 118, 12–22. [Google Scholar] [CrossRef]
- Erklig, A.; Yeter, E.; Bulut, M. The effects of cut-outs on lateral buckling behavior of laminated composite beams. Compos. Struct. 2013, 104, 54–59. [Google Scholar] [CrossRef]
- Eryigit, E.; Zor, M.; Arman, Y. Hole effects on lateral buckling of laminated cantilever beams. Compos. Part B Eng. 2009, 40, 174–179. [Google Scholar] [CrossRef]
- Pasinli, A. Shape and position effects of double holes on lateral buckling of cantilever composite beams. Compos. Part B Eng. 2013, 55, 433–439. [Google Scholar] [CrossRef]
- Rezaeepazhand, J.; Jafari, M. Stress analysis of perforated composite plates. Compos. Struct. 2005, 71, 463–468. [Google Scholar] [CrossRef]
- Wu, H.-C.; Mu, B. On stress concentrations for isotropic/orthotropic plates and cylinders with a circular hole. Compos. Part B Eng. 2003, 34, 127–134. [Google Scholar] [CrossRef]
- Guo, S.J. Stress concentration and buckling behavior of shear loaded composite panels with reinforced cutouts. Compos. Struct. 2007, 80, 1–9. [Google Scholar] [CrossRef]
- Naouar, N.; Vidal-Salle, E.; Schneider, J.; Marie, E.; Boisse, P. Meso-scale FE analyses of textile composite reinforcement deformation based on X-ray computed tomography. Compos. Struct. 2014, 116, 165–176. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z. Statistical analysis of yarn feature parameters in C/Epoxy plain-weave composite using micro CT with high-resolution lens-coupled detector. Appl. Compos. Mater. 2016, 23, 601–622. [Google Scholar] [CrossRef]
- Nguyen, M.; Herszberg, I.; Paton, R. The shear properties of woven carbon fabric. Compos. Struct. 1999, 47, 767–779. [Google Scholar] [CrossRef]
- Doitrand, A.; Fagiano, C.; Irisarri, F.-X.; Hirsekorn, M. Comparison between voxel and consistent meso-scale models of woven composites. Compos. Part A Appl. S. 2015, 73, 143–154. [Google Scholar] [CrossRef]
- Goyal, D.; Tang, X.; Whitecomb, J.D.; Kelkar, A.-D. Effect of various parameters on effective engineering properties of 2 × 2 braided composites. Mech. Adv. Mater. Struct. 2005, 12, 113–128. [Google Scholar] [CrossRef]
- Mayes, J.S.; Hansen, A.C. Composite laminate failure analysis using multicontinuum theory. Compos. Sci. Technol. 2004, 64, 379–394. [Google Scholar] [CrossRef]
- Ha, S.K.; Jin, K.K.; Huang, Y. Micro-mechanics of failure (MMF) for continuous fiber reinforced composites. J. Compos. Mater. 2008, 42, 1873–1895. [Google Scholar]
- Li, X.; Guan, Z.; Li, Z.; Liu, L. A new stress-based multi-scale failure criterion of composites and its validation in open hole tension tests. Chin. J. Aeronaut. 2014, 27, 1430–1441. [Google Scholar] [CrossRef]
- Xu, L.; Huang, Y.C.; Zhao, C.; Ha, S.K. Progressive failure prediction of woven fabric composites using a multi-scale approach. Int. J. Damage Mech. 2018, 27, 97–119. [Google Scholar] [CrossRef]
- Xu, L.; Jin, C.Z.; Ha, S.K. Ultimate strength prediction of braided textile composites using a multi-scale approach. J. Compos. Mater. 2015, 49, 477–494. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, P.; Fei, Q.; Guo, F. Modified micro-mechanics based multiscale model for progressive failure prediction of 2D twill woven composites. Chin. J. Aeronaut. 2020, 33, 2070–2087. [Google Scholar] [CrossRef]
- Zhao, C.; Huang, Y.; Chen, Z.; Ha, S.K. Progressive failure prediction of a landing gear structure of braided composites. Compos. Struct. 2017, 161, 407–418. [Google Scholar] [CrossRef]
- Zhou, R.; Gao, W.; Liu, W.; Xu, J. An analytical model for the uniaxial tensile modulus of plain-woven fabric Composites and Its Experimental Validation. Aerospace 2022, 9, 26. [Google Scholar] [CrossRef]
- Torayca. T300 Standard Modulus Carbon Fiber; Toray Composite Materials America, Inc.: Tacoma, WA, USA, 2018. [Google Scholar]
- Solvay. Cycom 970 Epoxy Resin System Technical Data Sheet; Solvay Company: Tempe, AZ, USA, 2017. [Google Scholar]
- Zhou, R.; Gao, W.; Liu, W. An MMF3 criterion based multi-scale strategy for the failure analysis of plain-woven fabric composites and its validation in the open-hole compression tests. Materials 2021, 14, 4393. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Guan, Z.; Tan, R.; Xu, J.; Li, X. Multiscale analysis of CFRP laminates with MMF3 criterion under different off-axis loading conditions. Materials 2018, 11, 2255. [Google Scholar] [CrossRef]







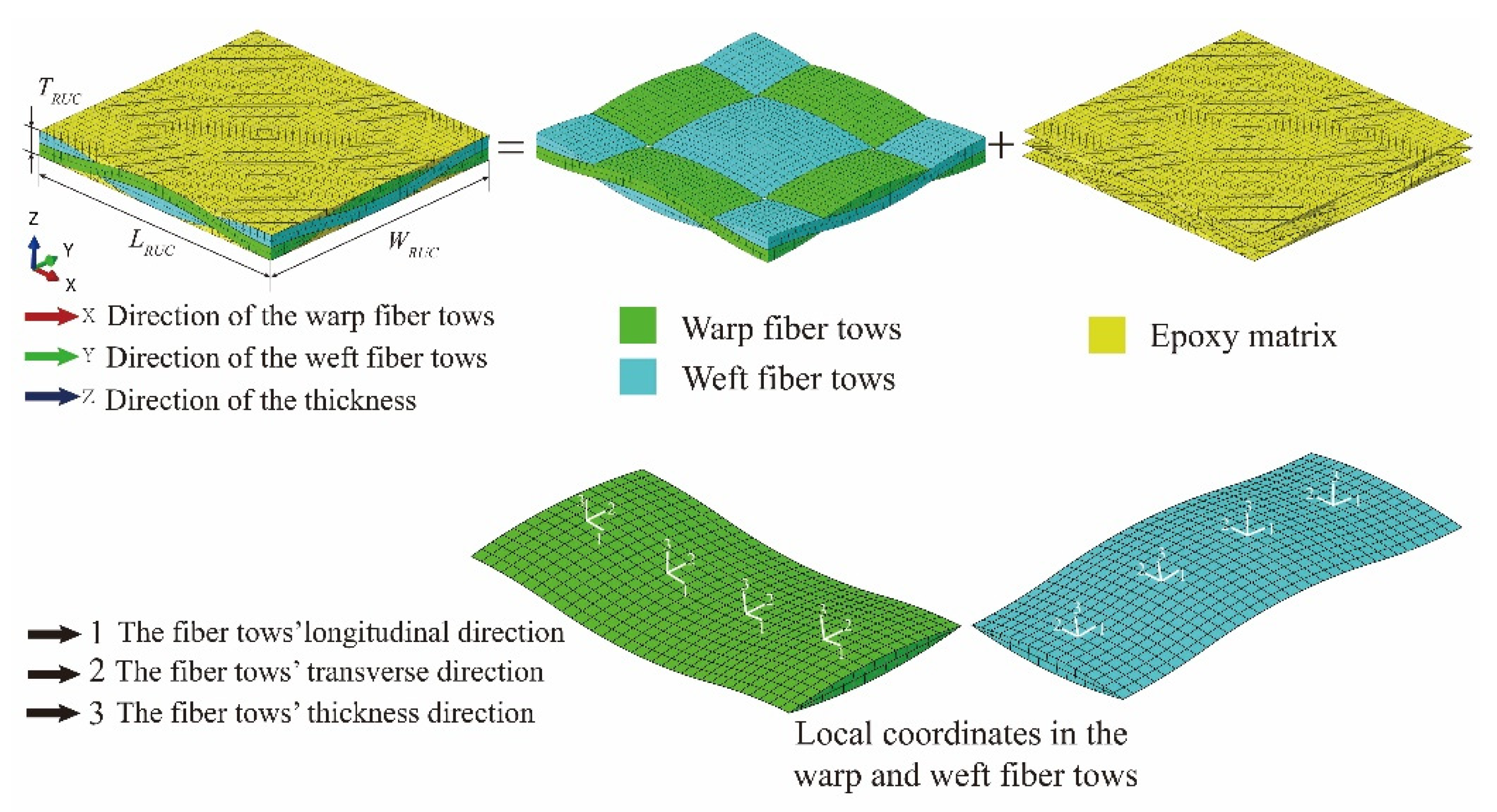
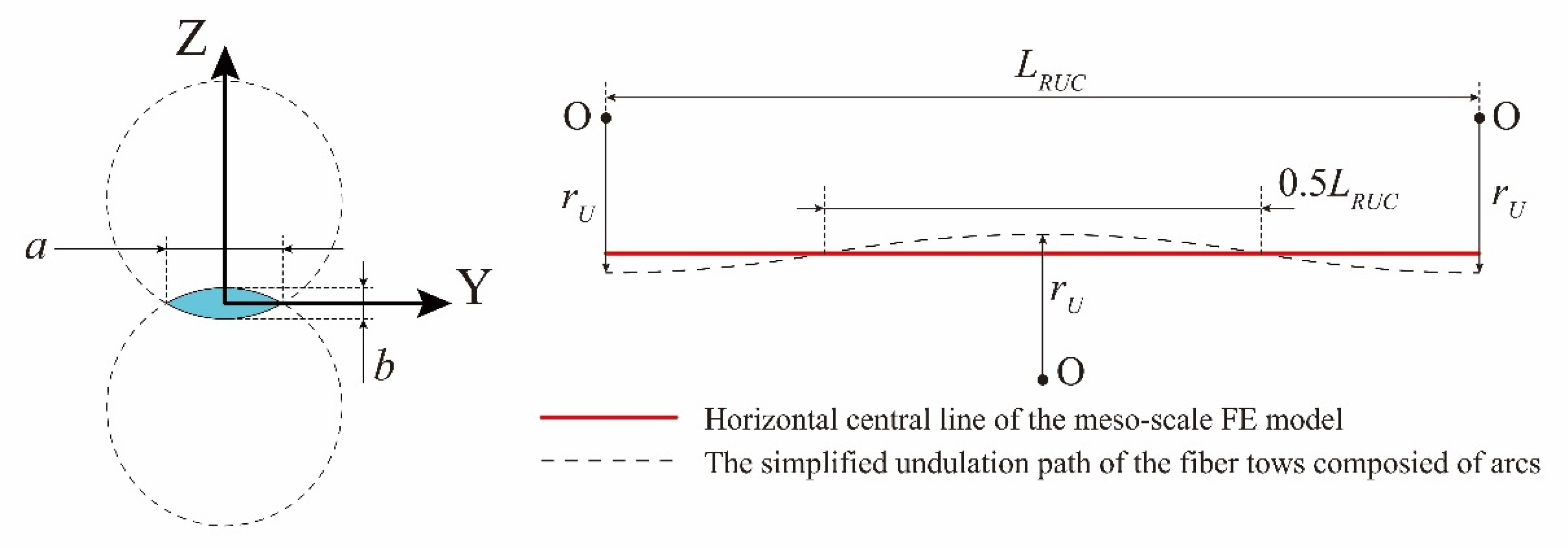
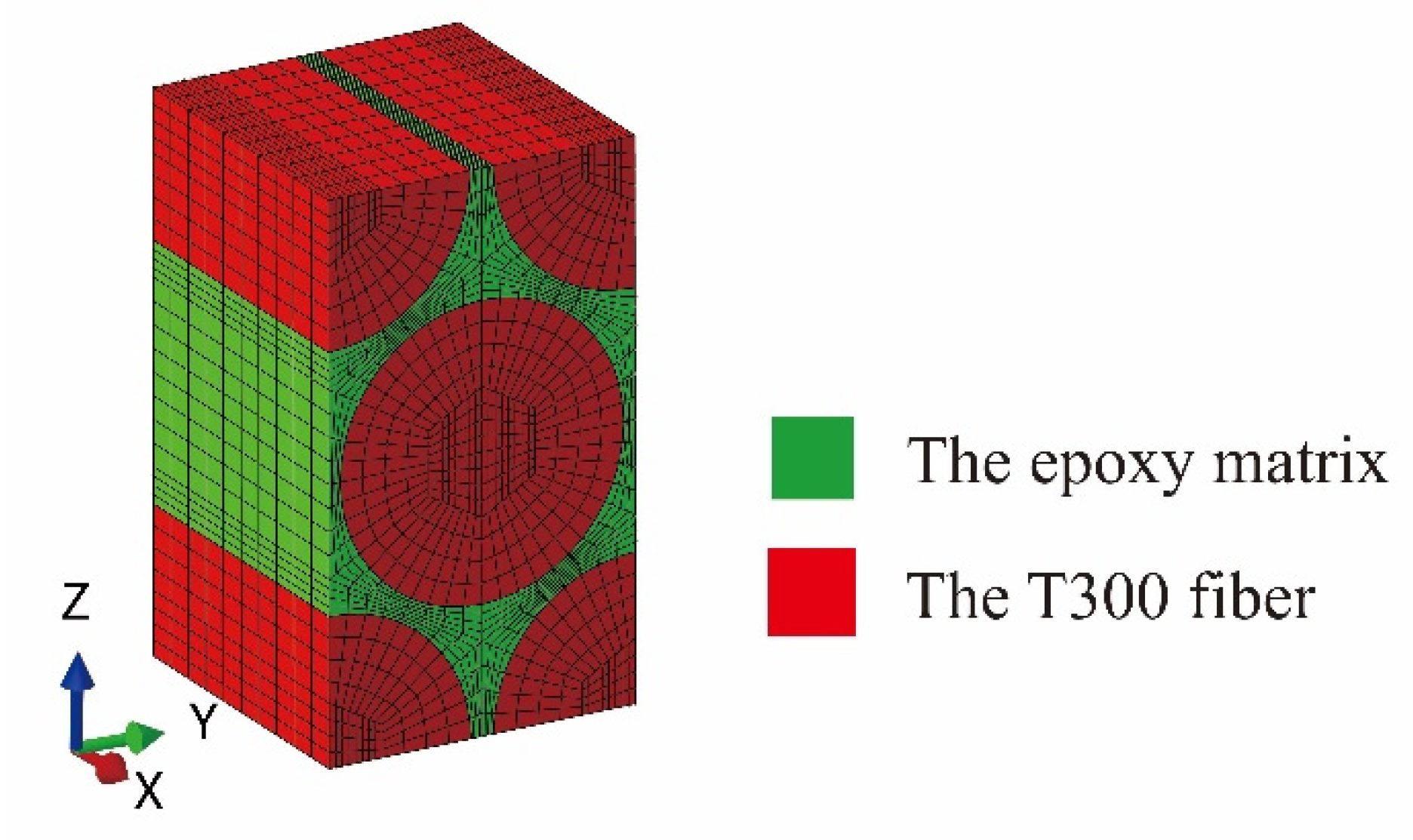

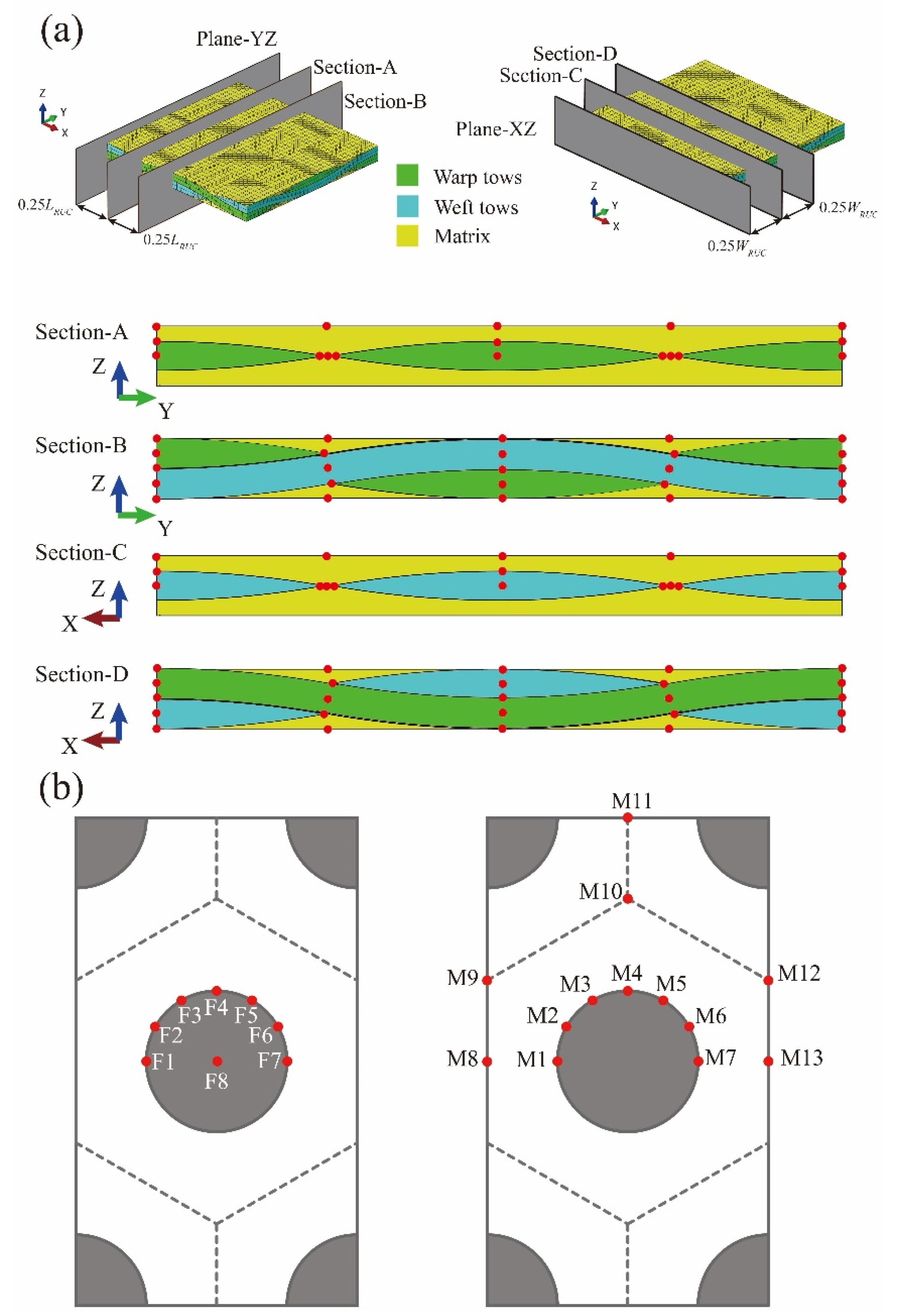
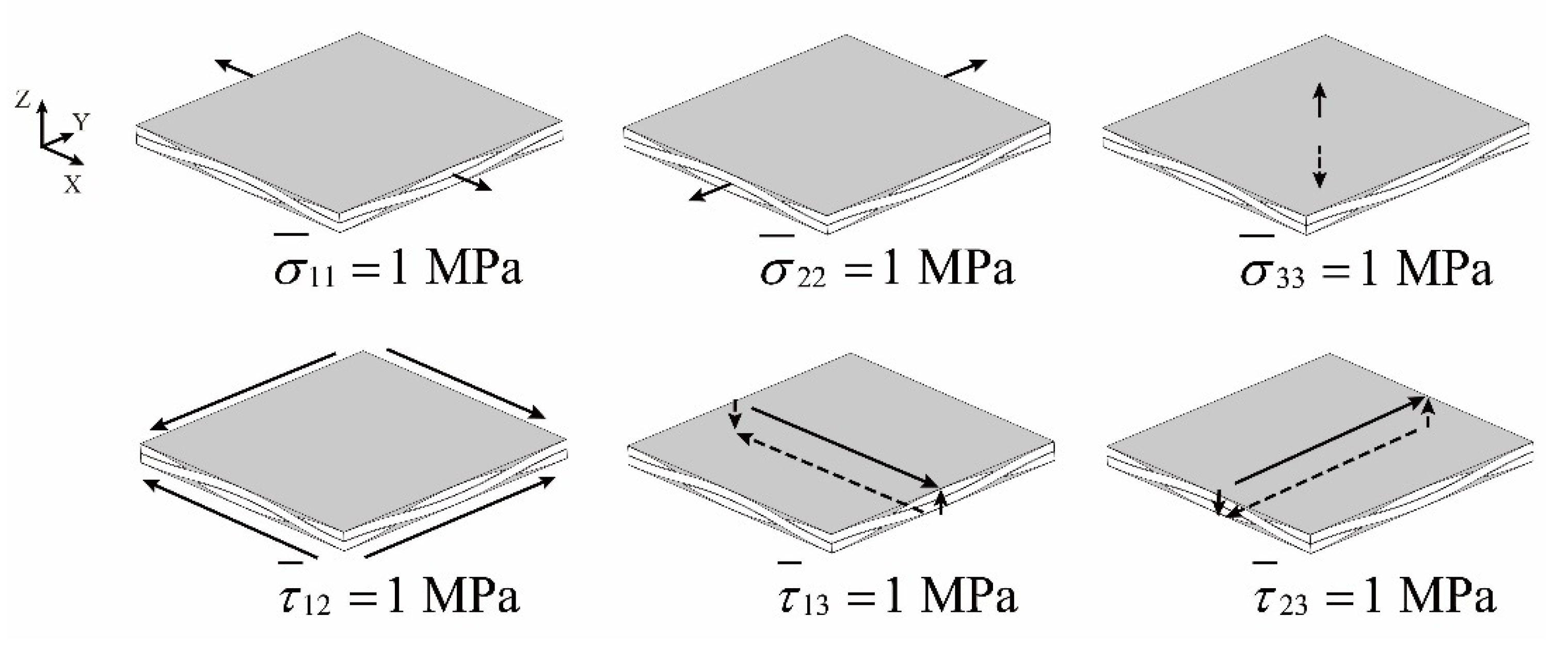

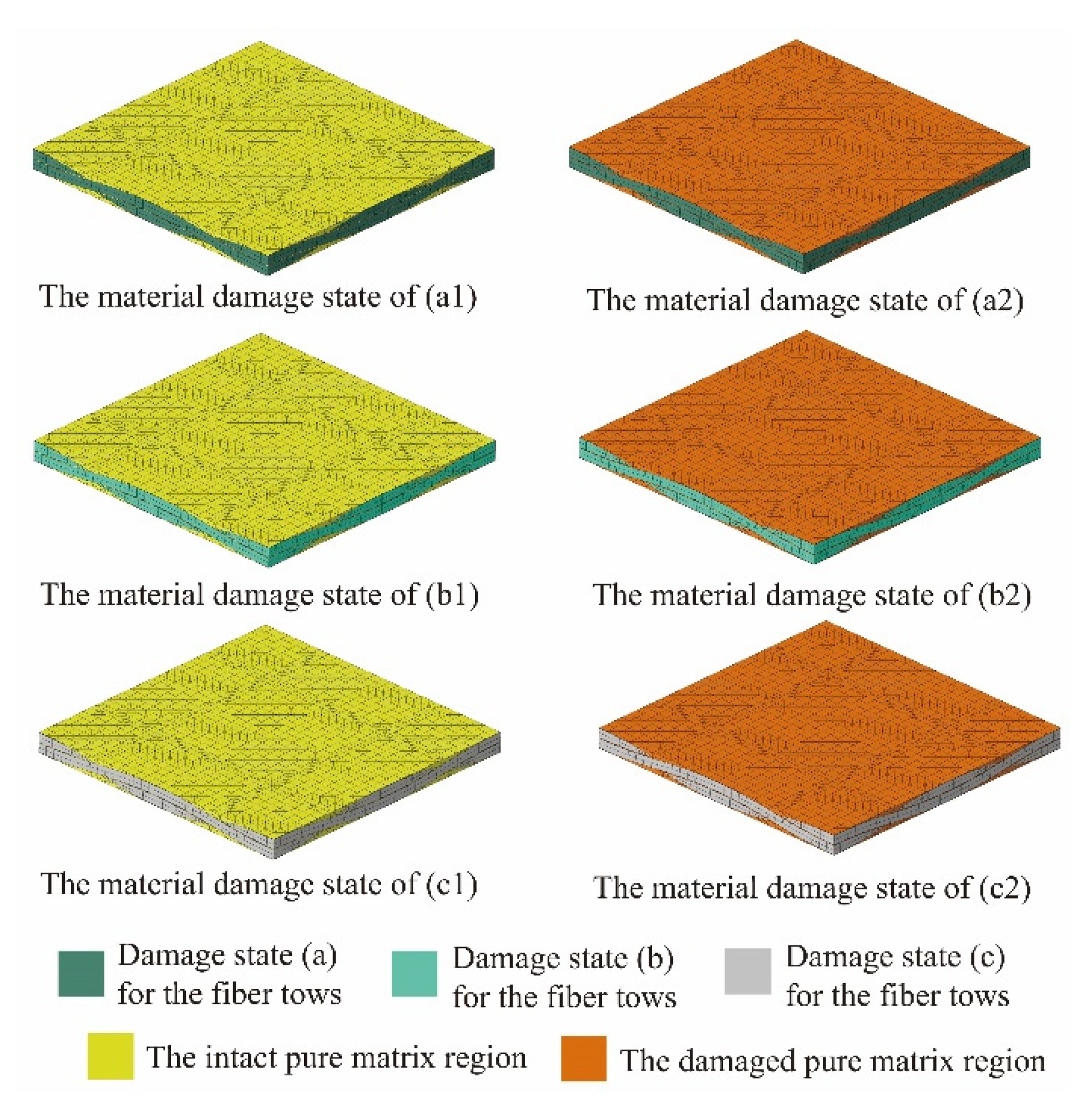



| Property | Value |
|---|---|
| Longitudinal modulus, (GPa) | 56.85 |
| Transverse modulus, (GPa) | 56.85 |
| In-plane shear modulus, (GPa) | 3.86 |
| In-plane Poisson’s ratio, | 0.042 |
| Longitudinal tensile strength, (MPa) | 717.0 |
| Longitudinal compressive strength, (MPa) | 597.0 |
| Transverse tensile strength, (MPa) | 717.0 |
| Transverse compressive strength, (MPa) | 597.0 |
| Region | Ply Sequence |
|---|---|
| Top flange | [45/45/0/0/45/0/0/45/0/45/0]s |
| Bottom flange | [45/45/0/0/45/0/0/45/0/45/0]s |
| Peripheral web region | [45/45/0/0/45/0/0/45/0/45/0]s |
| Middle examination web region | [45/0/0/45/0]s |
| Region | Ply Sequence |
|---|---|
| Top flange | [45/45/0/0/45/0/0/45/0/45/0]s |
| Bottom flange | [45/45/0/0/45/0/0/45/0/45/0]s |
| Peripheral web region | [45/45/0/0/45/0/0/45/0/45/0]s |
| Middle examination web region | [45/0/0/45/0]s |
| Reinforcement region | [45/0/0/45/0/0/0/45/45/0/45/0/0/45/0/45/0/45] |
| Specimen | Experimental Failure Load (kN) | Average Value (kN) | Experimental Critical Buckling Load (kN) | Average Value (kN) |
|---|---|---|---|---|
| BW-I-01 | 68.0 | 63.8 | 36.9 | 36.9 |
| BW-I-02 | 61.6 | 37.7 | ||
| BW-I-03 | 61.7 | 36.1 |
| Specimen | Experimental Failure Load (kN) | Average Value (kN) | Experimental Critical Buckling Load (kN) | Average Value (kN) |
|---|---|---|---|---|
| BW-II-01 | 62.1 | 59.2 | 37.5 | 36.8 |
| BW-II-02 | 57.9 | 36.5 | ||
| BW-II-03 | 58.6 | 36.5 |
| Geometric Parameter | Value |
|---|---|
| Width of the fiber tows’ cross-section, a (mm) | 1.82 |
| Thickness of the fiber tows’ cross-section, b (mm) | 0.13 |
| Radius of the arcs in the simplified undulation path of the fiber tows, rU (mm) | 7.18 |
| Length of the PWF composite’s meso-scale FE model, LRUC (mm) | 4.00 |
| Width of the PWF composite’s meso-scale FE model, WRUC (mm) | 4.00 |
| Thickness of the PWF composite’s meso-scale FE model, TRUC (mm) | 0.28 |
| Parameter | Value |
|---|---|
| Total fiber volume fraction, VfT | 0.56 |
| Fiber volume fraction in tows, Vf | 0.78 |
| Volume fraction of tows, Vt | 0.72 |
| Constituent | Material Property | Value |
|---|---|---|
| T300 fiber | Longitudinal modulus of the fiber, Ef11 (GPa) | 230.00 |
| Transverse modulus of the fiber, Ef22 = Ef33 (GPa) | 14.00 | |
| In-plane shear modulus of the fiber, Gf12 (GPa) | 94.00 | |
| Out-of-plane shear modulus of the fiber, Gf13 (GPa) | 94.00 | |
| Out-of-plane shear modulus of the fiber, Gf23 (GPa) | 5.20 | |
| In-plane Poisson’s ratio of the fiber, | 0.26 | |
| Out-of-plane Poisson’s ratio of the fiber, | 0.26 | |
| Out-of-plane Poisson’s ratio of the fiber, | 0.34 | |
| Longitudinal coefficient of thermal expansion of the fiber, (10−6/K) | −0.54 | |
| Transverse coefficient of thermal expansion of the fiber, (10−6/K) | 10.50 | |
| Epoxy matrix | Elastic modulus of the matrix, Em (GPa) | 3.35 |
| Elastic Poisson’s ratio of the matrix, | 0.35 | |
| Coefficient of thermal expansion of the matrix, (10−6/K) | 58.00 |
| Property | Value |
| Longitudinal modulus of the fiber tows, E11(tow) (GPa) | 174.67 |
| Transverse modulus of the fiber tows, E22(tow) = E33(tow) (GPa) | 9.51 |
| In-plane shear modulus of the fiber tows, G12(tow) (GPa) | 8.52 |
| Out-of-plane shear modulus of the fiber tows, G13(tow) (GPa) | 8.28 |
| Out-of-plane shear modulus of the fiber tows, G23(tow) (GPa) | 3.39 |
| In-plane Poisson’s ratio of the fiber tows, | 0.28 |
| Out-of-plane Poisson’s ratio of the fiber tows, | 0.28 |
| Out-of-plane Poisson’s ratio of the fiber tows, | 0.41 |
| Longitudinal coefficient of thermal expansion of the fiber tows, (10−6/K) | −0.22 |
| Transverse coefficient of thermal expansion of the fiber tows, (10−6/K) | 24.91 |
| Failure Type | Failure Criterion |
|---|---|
| Fiber failure | |
| Matrix failure |
| Micro-Scale Strength | Value |
|---|---|
| Tensile strength of fiber, Tf (MPa) | 3526.3 |
| Compressive strength of fiber, Cf (MPa) | 2942.9 |
| Tensile strength of matrix, Tm (MPa) | 126.6 |
| Compressive strength of matrix, Cm (MPa) | 238.3 |
| Constituent | Material Property | Value |
|---|---|---|
| T300 fiber | Longitudinal modulus of the fiber after damage, Ef11* (GPa) | 2.30 |
| Transverse modulus of the fiber after damage, Ef22* = Ef33 (GPa) | 14.00 | |
| In-plane shear modulus of the fiber after damage, Gf12* (GPa) | 0.94 | |
| Out-of-plane shear modulus of the fiber after damage, Gf13* (GPa) | 0.94 | |
| Out-of-plane shear modulus of the fiber after damage, Gf23* (GPa) | 5.20 | |
| In-plane Poisson’s ratio of the fiber after damage, * | 0.0026 | |
| Out-of-plane Poisson’s ratio of the fiber after damage, * | 0.0026 | |
| Out-of-plane Poisson’s ratio of the fiber after damage, * | 0.34 | |
| Epoxy matrix | Elastic modulus of the matrix after damage, Em* (GPa) | 0.1675 |
| Elastic Poisson’s ratio of the matrix after damage, * | 0.35 |
| Mechanical Property | Parameter and Value | ||
|---|---|---|---|
| Damage State (a) for the Fiber Tows | Damage State (b) for the Fiber Tows | Damage State (c) for the Fiber Tows | |
| Longitudinal modulus of the fiber tows after damage | 2.65 GPa | 173.88 GPa | 1.78 GPa |
| Transverse modulus of the fiber tows after damage | 9.28 GPa | 1.27 GPa | 1.26 GPa |
| Transverse modulus of the fiber tows after damage | 9.28 GPa | 1.27 GPa | 1.26 GPa |
| In-plane shear modulus of the fiber tows after damage | 1.74 GPa | 0.81 GPa | 0.54 GPa |
| Out-of-plane shear modulus of the fiber tows after damage | 1.01 GPa | 0.45 GPa | 0.31 GPa |
| Out-of-plane shear modulus of the fiber tows after damage | 3.38 GPa | 0.46 GPa | 0.46 GPa |
| In-plane Poisson’s ratio of the fiber tows after damage | 0.077 | 0.28 | 0.068 |
| Out-of-plane Poisson’s ratio of the fiber tows after damage | 0.077 | 0.28 | 0.068 |
| Out-of-plane Poisson’s ratio of the fiber tows after damage | 0.37 | 0.37 | 0.37 |
| Macro-Scale Mechanical Property | Parameter and Value | |||
| Damage State (a) for the Fiber Tows | Damage State (b) for the Fiber Tows | Damage State (c) for the Fiber Tows | ||
| Longitudinal modulus after damage | Pure matrix region remains intact | 4.71 GPa | 49.82 GPa | 2.31 GPa |
| Transverse modulus after damage | 4.71 GPa | 49.82 GPa | 2.31 GPa | |
| In-plane Poisson’s ratio after damage | 0.22 | 0.012 | 0.23 | |
| In-plane shear modulus after damage | 1.52 GPa | 0.99 GPa | 0.82 GPa | |
| Longitudinal modulus after damage | Pure matrix region damaged | 2.11 GPa | 47.17 GPa | 0.89 GPa |
| Transverse modulus after damage | 2.11 GPa | 47.17 GPa | 0.89 GPa | |
| In-plane Poisson’s ratio after damage | 0.12 | 0.011 | 0.093 | |
| In-plane shear modulus after damage | 0.75 GPa | 0.40 GPa | 0.28 GPa | |
| FE Model of the PWF Composite Beams | The Calculated Critical Buckling Load (kN) | The Calculated Collapse Load (kN) |
|---|---|---|
| BW-I | 38.0 | 65.2 |
| BW-III | 33.8 | 48.8 |
| BW-II | 37.2 | 59.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Gao, W.; Liu, W.; Xu, J. Effects of Open-Hole and Reinforcement on the Bearing Performance of the Plain-Woven Fabric Composite I-Section Beams under Shear Load. Aerospace 2022, 9, 537. https://doi.org/10.3390/aerospace9100537
Zhou R, Gao W, Liu W, Xu J. Effects of Open-Hole and Reinforcement on the Bearing Performance of the Plain-Woven Fabric Composite I-Section Beams under Shear Load. Aerospace. 2022; 9(10):537. https://doi.org/10.3390/aerospace9100537
Chicago/Turabian StyleZhou, Rui, Weicheng Gao, Wei Liu, and Jianxun Xu. 2022. "Effects of Open-Hole and Reinforcement on the Bearing Performance of the Plain-Woven Fabric Composite I-Section Beams under Shear Load" Aerospace 9, no. 10: 537. https://doi.org/10.3390/aerospace9100537
APA StyleZhou, R., Gao, W., Liu, W., & Xu, J. (2022). Effects of Open-Hole and Reinforcement on the Bearing Performance of the Plain-Woven Fabric Composite I-Section Beams under Shear Load. Aerospace, 9(10), 537. https://doi.org/10.3390/aerospace9100537






