Previous work by the authors described a Direct Eddy Simulation (DES) model of a Slingsby T67 aerobatic light aircraft and a series of flight tests, to validate the numerical model in the stall [
7,
8]. In this work, the in-flight data focused on surface flow visualization, accelerometer data, GPS data and cockpit instrument pressure data, and comparisons identified a significant buffet frequency, which in both the in-flight accelerometer and DES aerodynamic spectra. A separate ground test was also carried out, to identify the natural frequency of the wing, and showed this structural frequency could be discriminated from the aerodynamic buffet frequency.
Subsequent examination of the full DES flow field showed a substantial interaction of the wing wake with the tailplane during the stall [
7,
8]. Therefore, a further flight test was conducted, to see if this wake interaction was significant and to ensure a higher level of validation of the DES model. The following section presents details of this additional flight test, including a separate ground test, which was used to establish the structural frequencies of the tailplane.
2.1. Tailplane Ground Measurements
To measure the natural frequency of the tailplane, a Pixhawk4TM inertial reference unit, with a weight of 33 g and a sample rate of 250 Hz, was secured to the top surface of the tailplane using adhesive tape, near the tail tip. The tailplane, which is primarily constructed from fiberglass and fixed to a fiberglass fuselage, was then excited with an impulse impact in the vertical direction, within the stress limits of the tailplane structure.
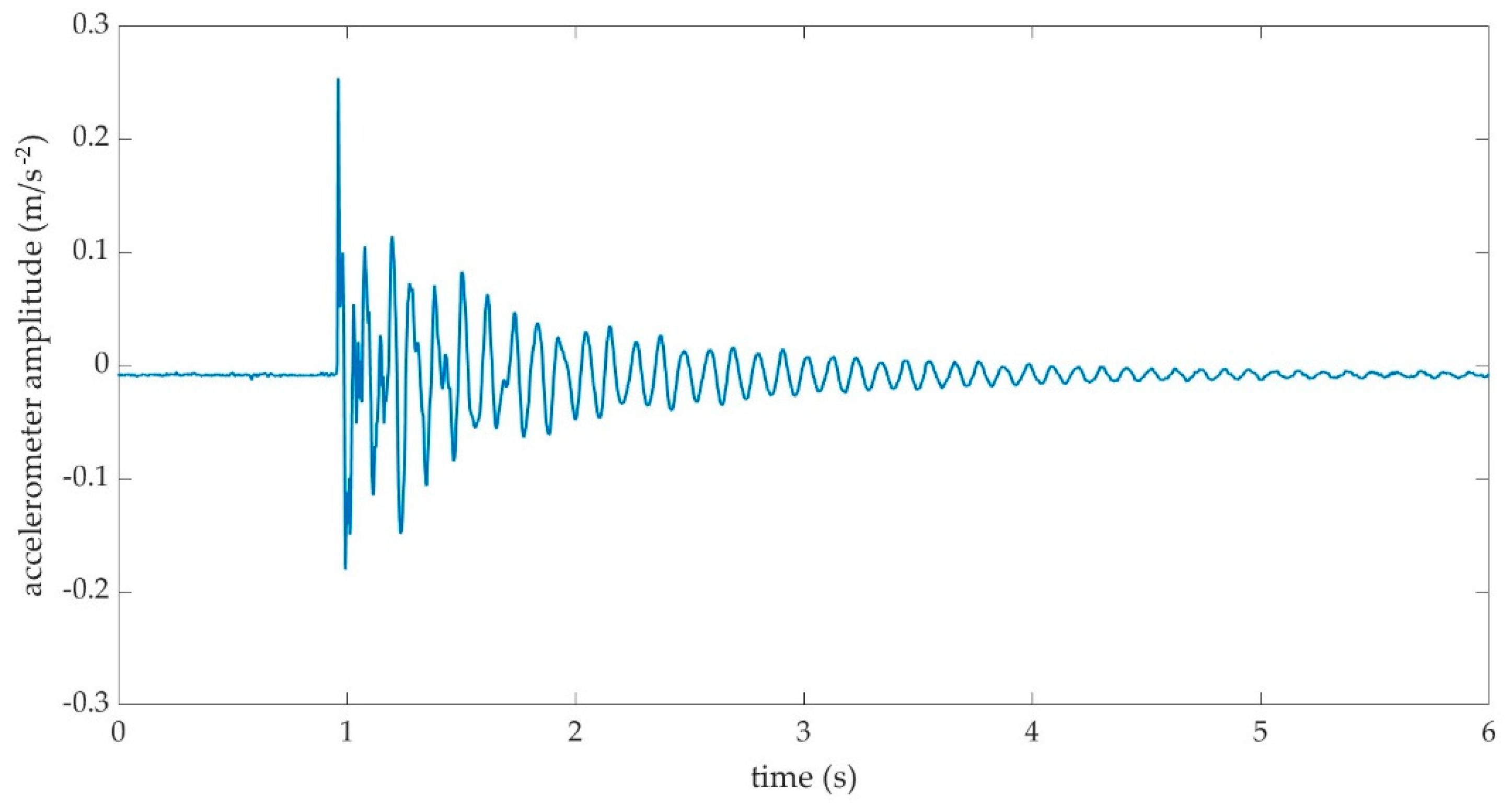
With the elevator fixed in a level position, the impact excited a resonance which was captured by the accelerometer. A typical response from the vertical axis accelerometer data is shown in
Figure 1 and the spectra for this response is shown in
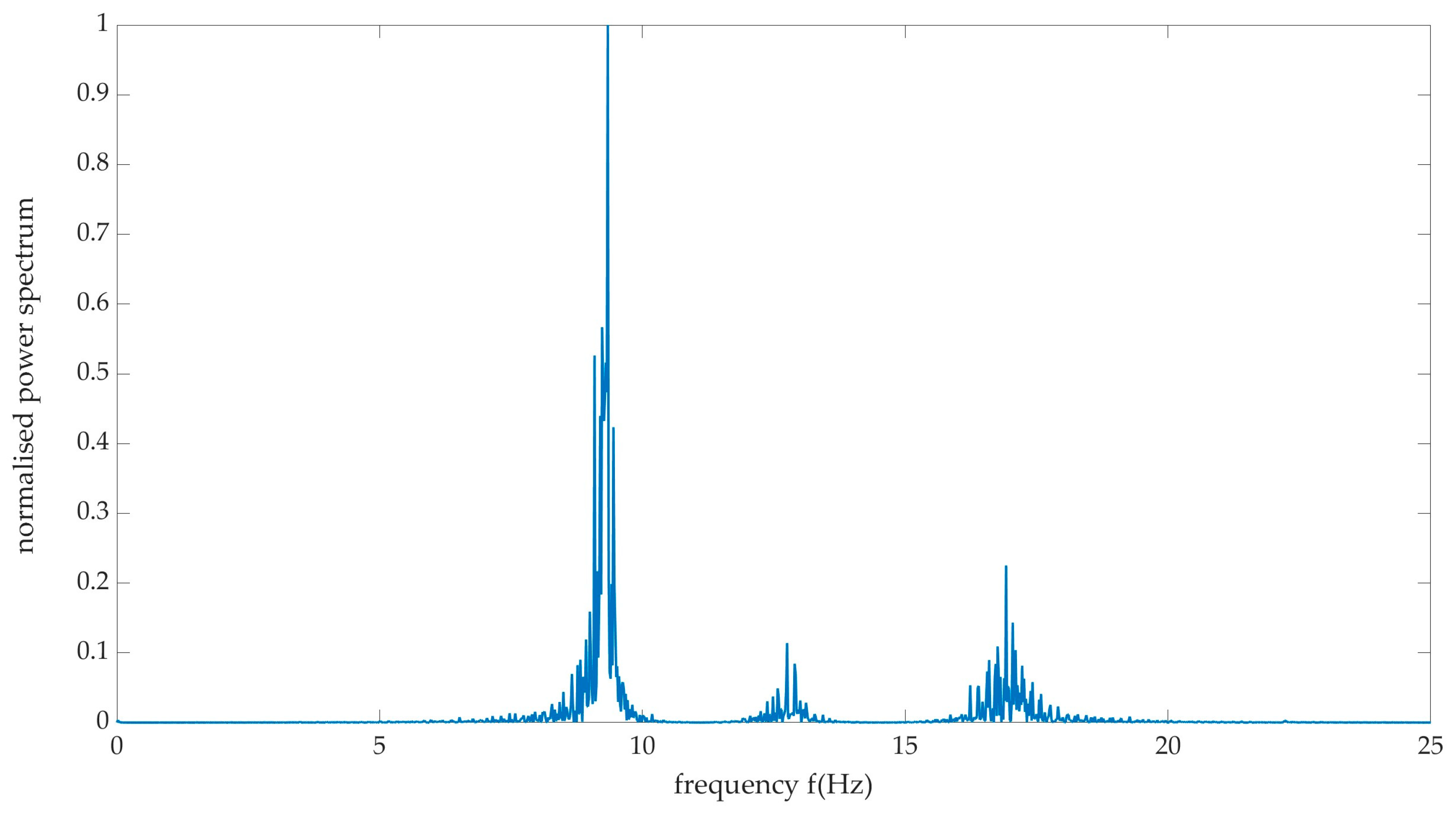
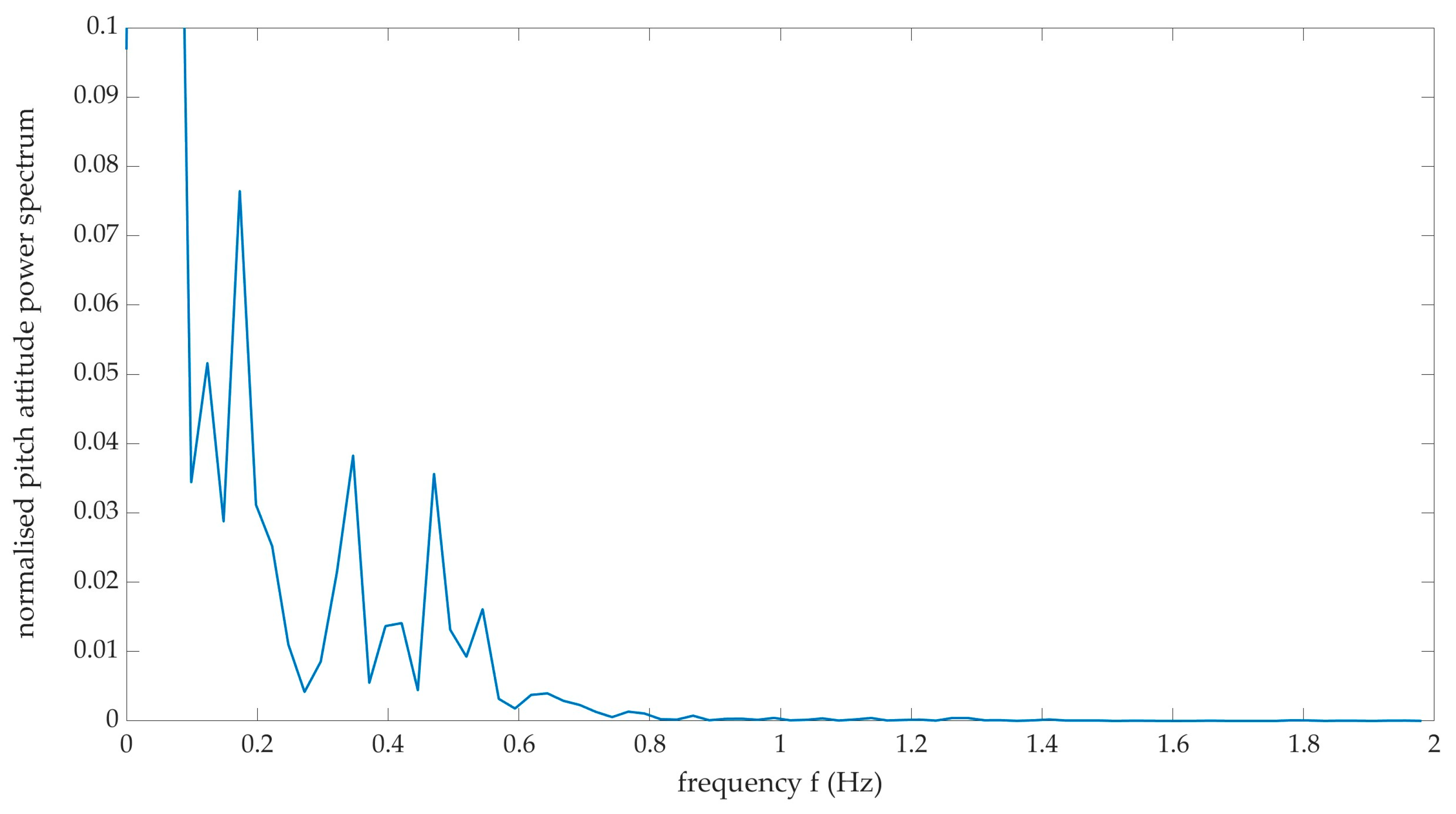
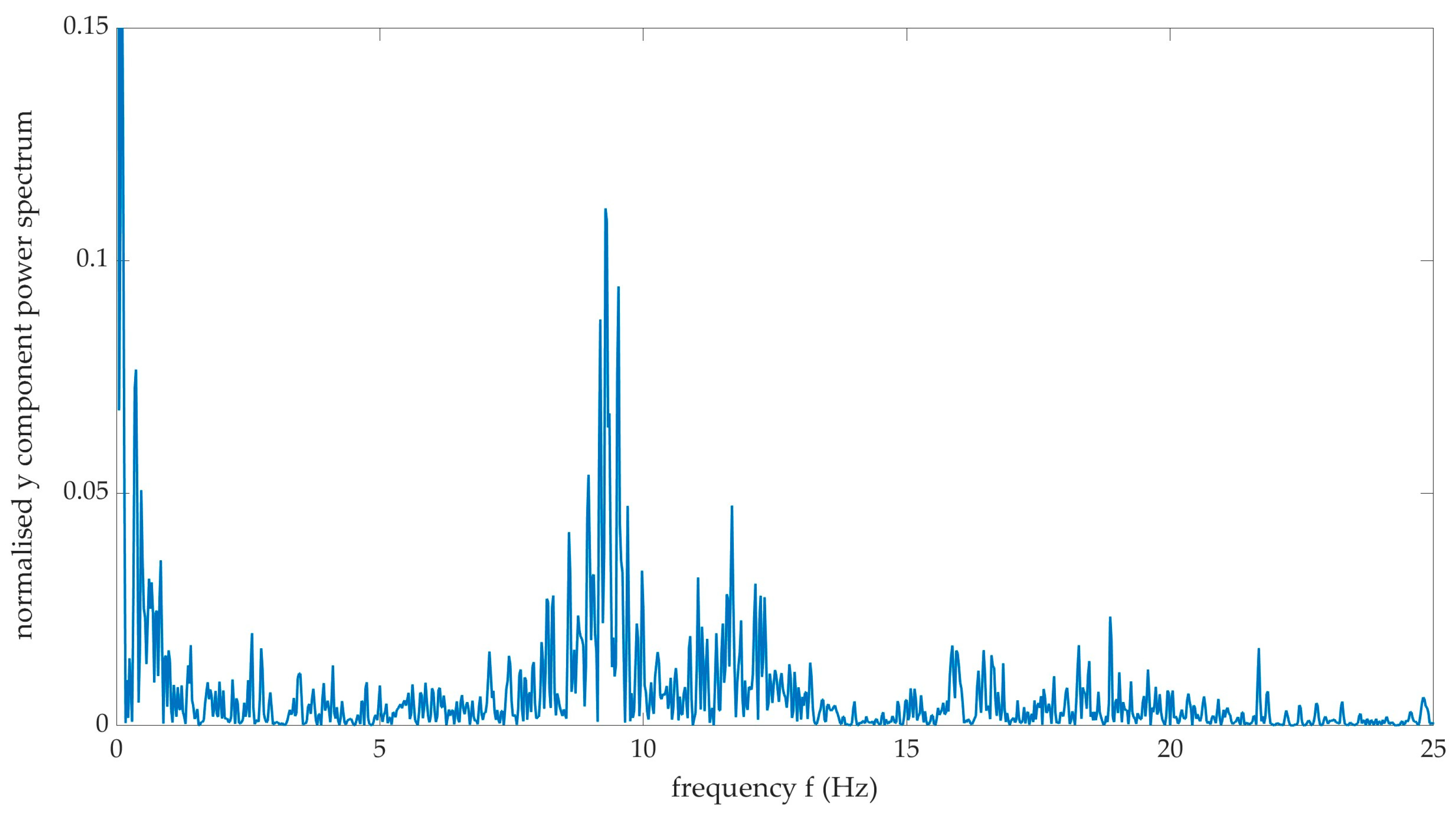
Figure 2. This excitation was repeated with the elevator at maximum deflection (trailing edge up). However, no significant changes were noted in the spectra. Errors in the spectra frequency, based on the sampling frequency of the Pixhawk and spectra resolution, are estimated to be ±0.01Hz. With reference to
Figure 2, the spectra contain characteristic frequencies at 9.34 Hz, 12.75 Hz and 16.92 Hz, with the former frequency the most dominant, based on amplitude. Previous work [
7] has shown the dominant shedding frequency during the stall to vary between 9 Hz to 12 Hz, indicating a potential aerodynamic excitation of the resonant frequency of the tailplane structure, during the stall.
2.2. Tailplane Airborne Measurements
To record the tailplane behavior during the stall, a GoPro Fusion 360 camera with a framerate of 50Hz and resolution of 1920 pixels × 1080 pixels (3k50 mode) was mounted to simultaneously record the front cockpit (see
Figure 3) and rear view in-flight (see
Figure 4). In the rear view, the tailplane, canopy rail and antenna are visible. The flight test conditions are also shown in
Table 1. On entering the aerodynamic stall, the pilot progressively moved the stick back to enter heavy buffet, continuing until experiencing significant ‘g-break’ and wing drop, before recovering to level flight again. Further data from similar stall tests are found in [
7,
8].
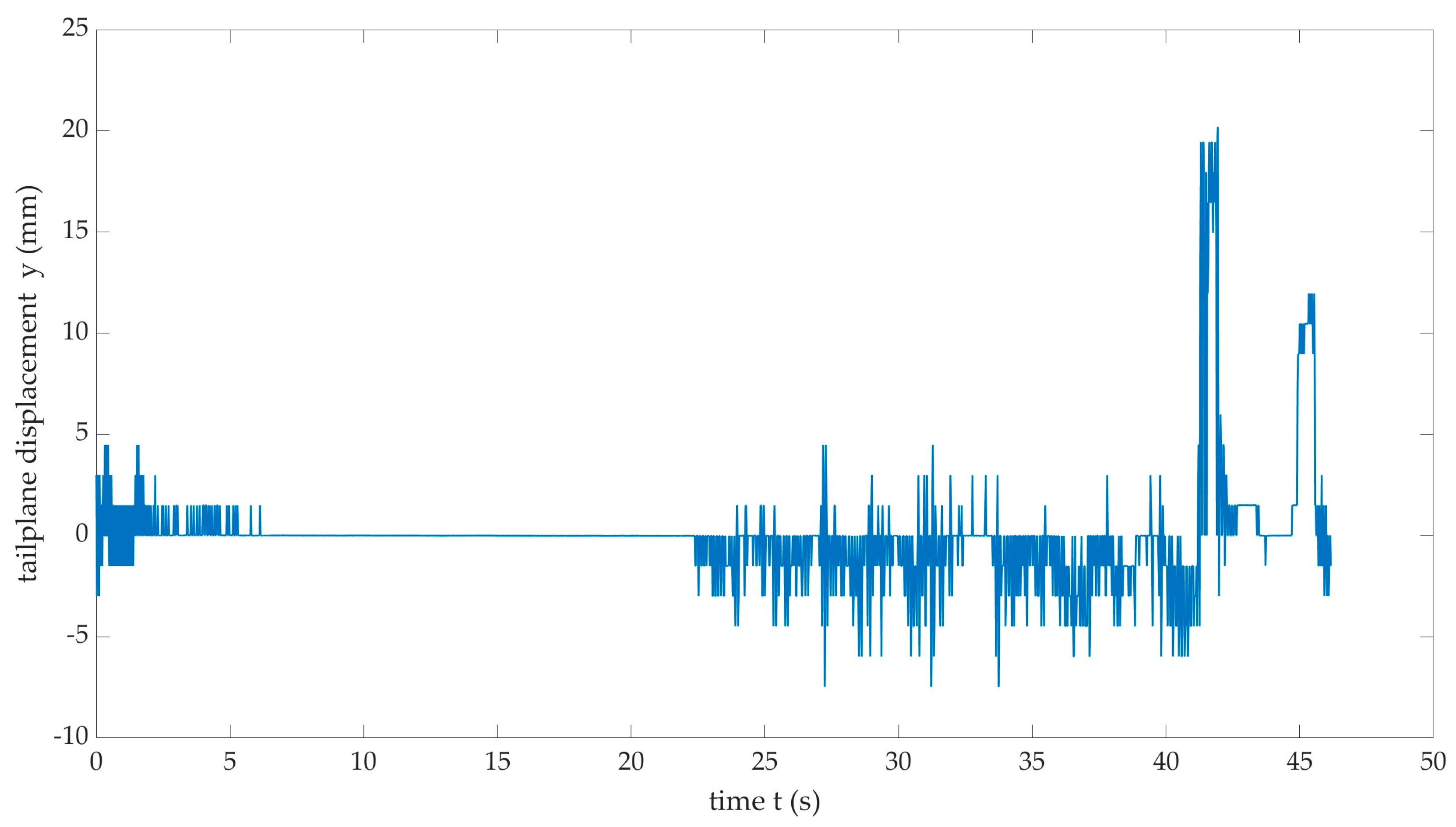
To calculate tailplane tip displacement data from the GoPro video recording, a frame-by-frame analysis process was developed, as shown in the schematic in
Figure 5. In the initial stage, the GoPro bitmap sequence of 2660 images in 24-bit format was extracted from the video. The 47s image sequence started from a wings level condition until stall recovery was commenced, and an 8-bit cropped sample of the tailplane tip area, with size 201 pixels × 221 pixels, was taken from the full image as shown in
Figure 4. This cropped image sequence was then processed using an in-house spatial cross-correlation code, ‘xpiv’ developed by the first author, written in X-Windows Motif and C-code. The code outputs pixel displacement, based on the spatial correlation of key image-to-image features and an initial image, at a selected number of grid points from a sequence of cropped bitmaps. In this case, each cropped image was sampled with 32 pixel × 32 pixel interrogation windows on a 3 × 3 grid, with centroid peak fit on the correlation peaks. A single grid point from the dataset was subsequently sampled into a time series of displacement data, at the center grid point of the sub-image.
In order to check for camera movement during the image sequence, a second correlation data set was also processed, from a separate canopy rail cropped image or sub-window (see
Figure 4) where the movement of the camera relative to the rail feature was monitored, with 5 × 3 grid points and 64 pixel × 64 pixel interrogation region sizes. This camera movement was less than 0.05 pixels for the image sequence, which was several orders of magnitude lower than the peak pixel movements from the tailplane tip.
Further xpiv processing of a third image sub-window, above the tailplane and to the left of the fin (see
Figure 4 and
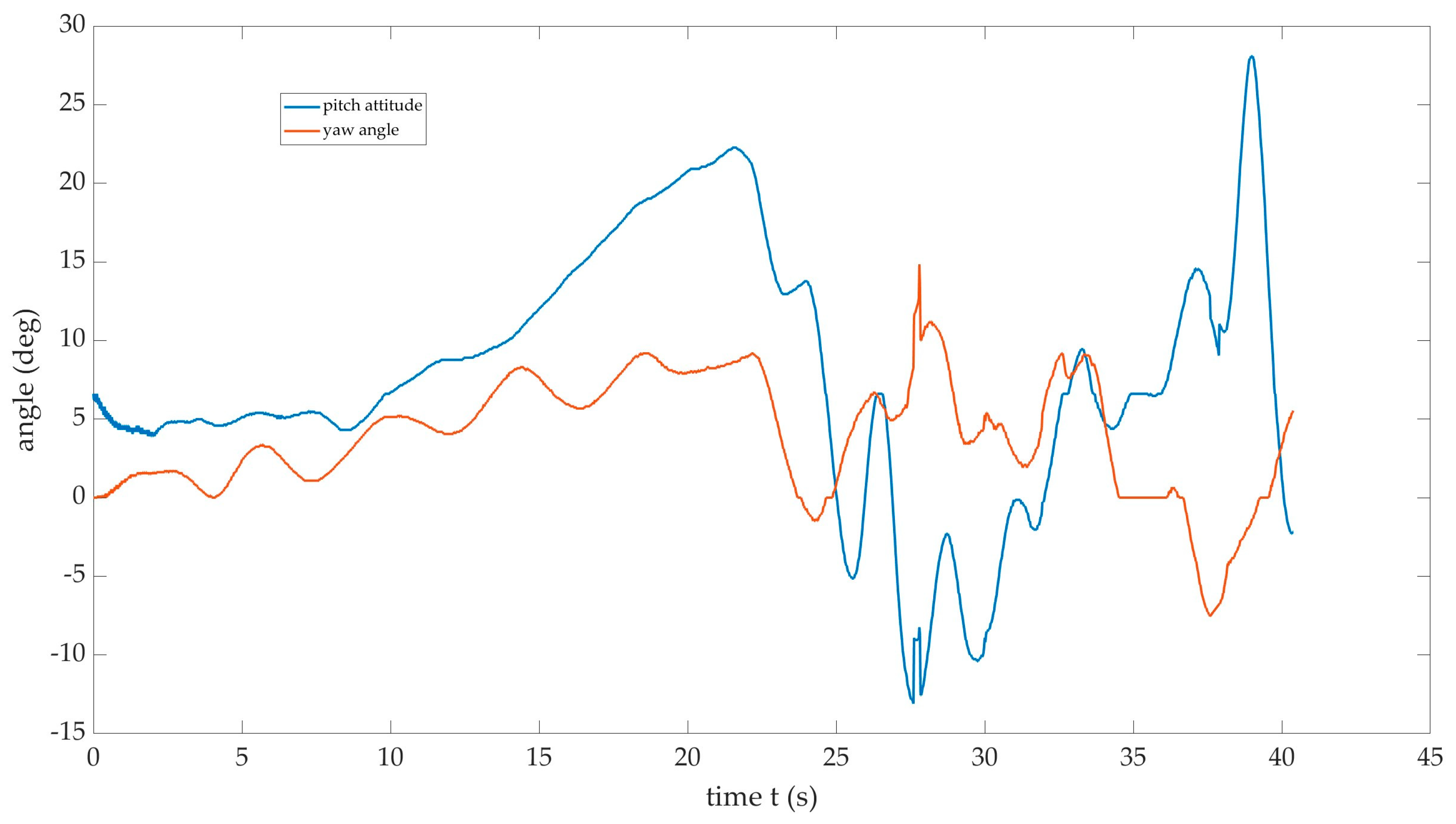
Figure 5), was used to estimate the pitch-attitude of the aircraft throughout the stall sequence, up to stall recovery. This approach assumed constant background features throughout the 43s sequence, including the clouds and horizon. In this case, to capture the gross features, a larger 512 × 512 interrogation region was used for the cross correlation with a 3 × 3 grid. Estimates of pitch attitude angle were then derived from previous aerodynamic data of the aircraft [
7] and the point at which the stall warner sounded in the cockpit, which is known to be 12° of pitch attitude. This data allowed deviations in oscillations in pitch to be monitored before recovery by the pilot, and the spectra of the oscillation frequency could also be calculated.
2.3. Data Processing Error Analysis
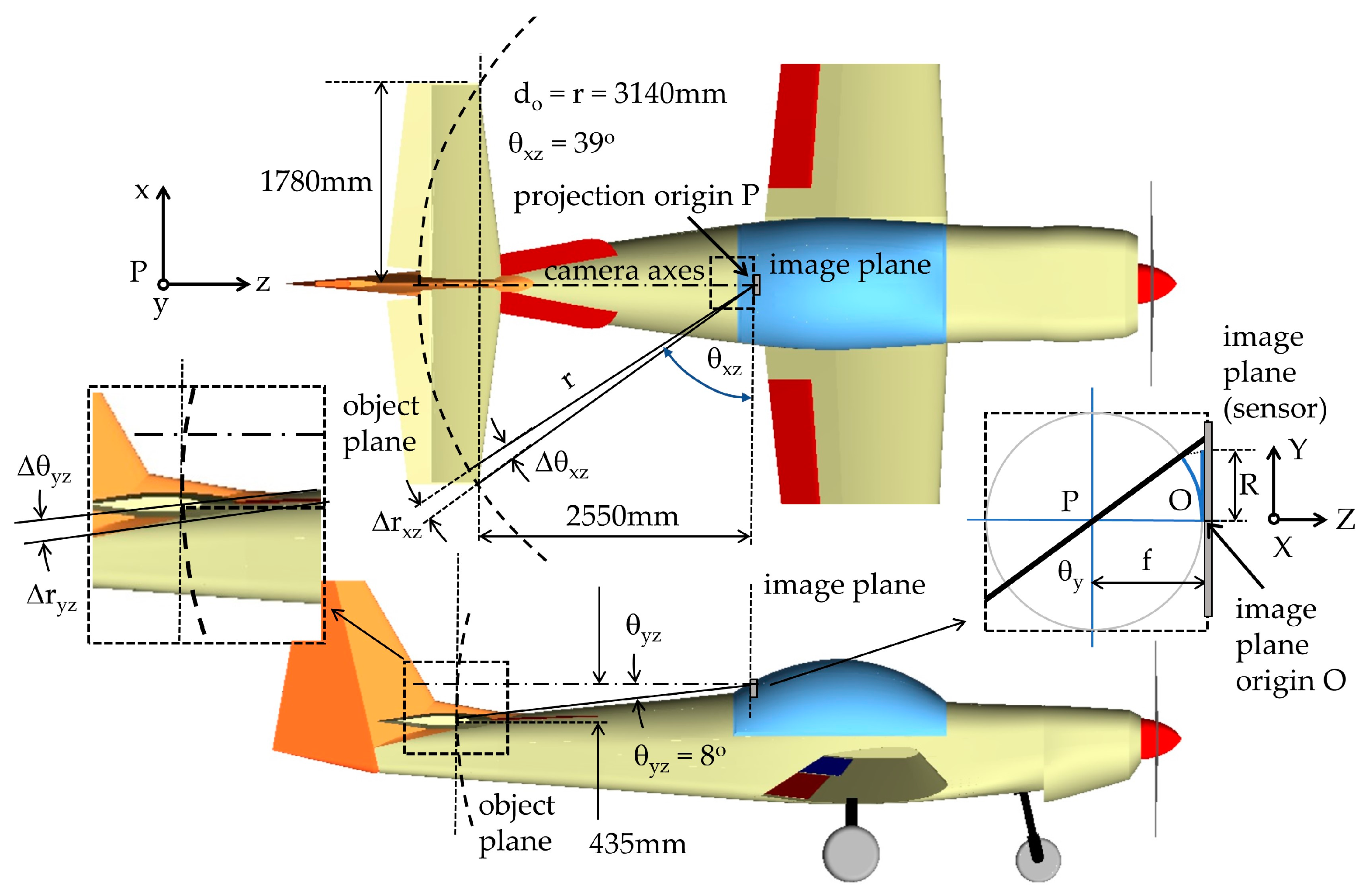
To estimate the error in measurement of the tailplane displacement, we need to consider a simplified model of the imaging system. The camera uses a fisheye lens with a field of view (FOV) of 180°. This prohibits the assumption of rectilinear (pinhole) projection, whereby straight lines from a flat object plane appear as straight lines in the image plane. Therefore, based on work by Hughes et al. [
9], who assessed a similar FOV fisheye lens camera, we shall assume an equidistant projection model. In equidistant projection, the radial distance on the image plane is directly proportional to the incidence ray angle. Hence, with reference to
Figure 6, with respect to the image plane origin
O, the radius of projection
R on the image plane is found from:
where
,
X and
Y are distances from the sensor origin,
f is the focal length of the imaging lens, and the incidence ray has an angle
θ to the camera axes. In this case, the object plane is a hemisphere defined by a radius
where
x,
y,
z are distances from the projection origin P of the lens, and the estimated object distance to the tailplane tip
do =
r = 3140 mm. Further, with respect to the
x–z and
y–z distance planes, the sub-angles
θxz and
θyz are defined by
θxz = tan
−1(
x/z) and
θyz = tan
−1(
y/z), given
.
In the object plane, a displacement of the tailplane tip at
do, can be estimated from the
x–
z and
y–
z radial components
rxz,
ryz such that:
where
and
, and given (1), the corresponding displacement in the imaging plane can be found from:
Hence, from the image plane data, if the cross-correlation produces an error in measurement of
δX and
δY, then at
do, the error
δr in measurement of the tailplane displacement is simply found from:
Thus, given a typical cross-correlation rms error is 0.05 pixel in
X and
Y [
10], with a pixel size of 1.8 microns, if
f = 3 mm and
do = 3140 mm, the rms displacement error in tailplane measurement is estimated to be
δr = ±0.09 mm, equivalent to 2 mrad. It should be noted that for a fisheye lens, this error may vary across the FOV due to manufacturing limitations, particularly near the edge of the FOV. In this case, as the tailplane tip is away from the edge of the field, this error variation should be minimal.
For the measurement of frequency, given a sample rate of fsample, based on the Nyquist criterion, using a fast Fourier transform (FFT), the resolution in frequency will be 2/fsample, equivalent to 1 pixel in the FFT frequency plane. Hence, with a camera frame rate of 50 Hz, the spectra resolution is estimated to be ±0.04 Hz.