Aerodisk Effect on Hypersonic Boundary Layer Transition and Heat Transfer of HIFiRE-5 Vehicle
Abstract
1. Introduction
2. Transition Model
3. Computational Details
3.1. HIFiRE-5 Configuration and Freestream Conditions
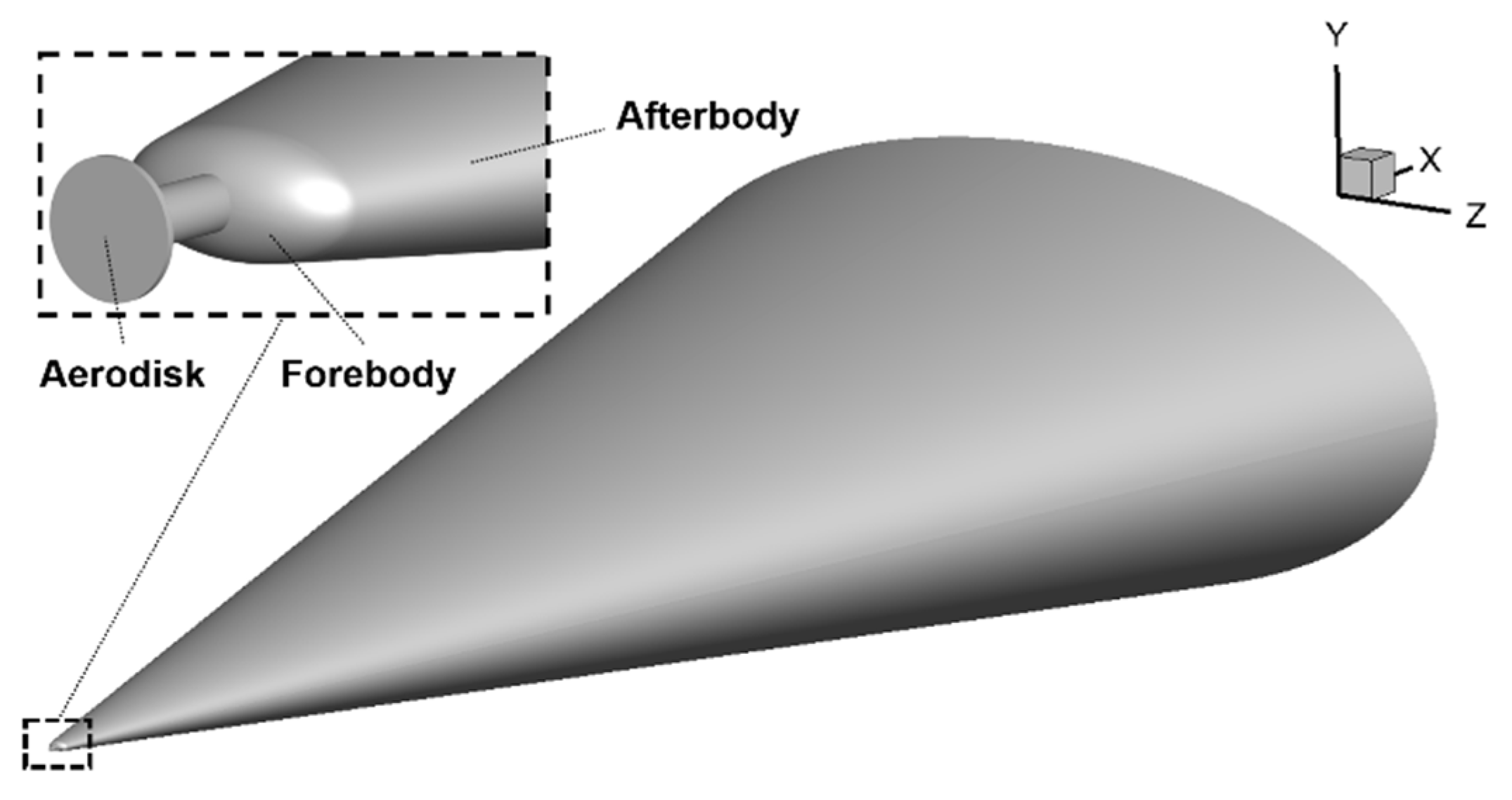
3.2. HIFiRE-5 Model with Aerodisk
3.3. Grid Sensitivity Analysis
4. Results and Discussion
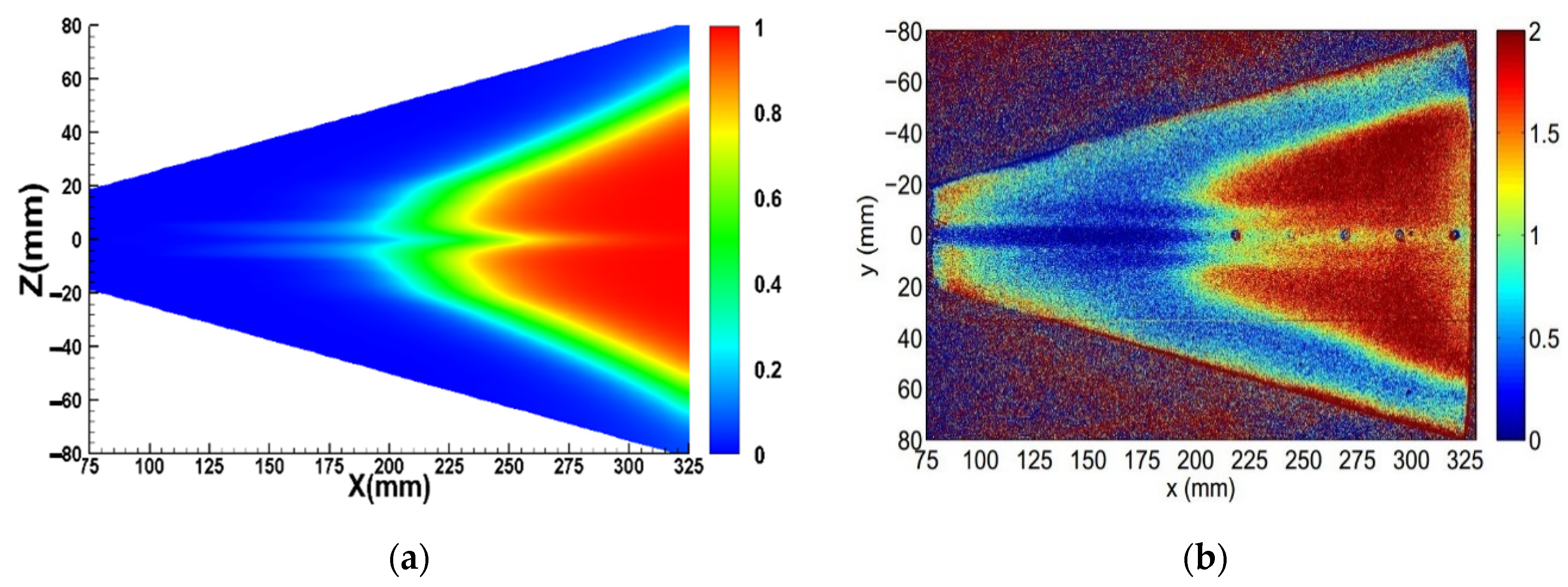
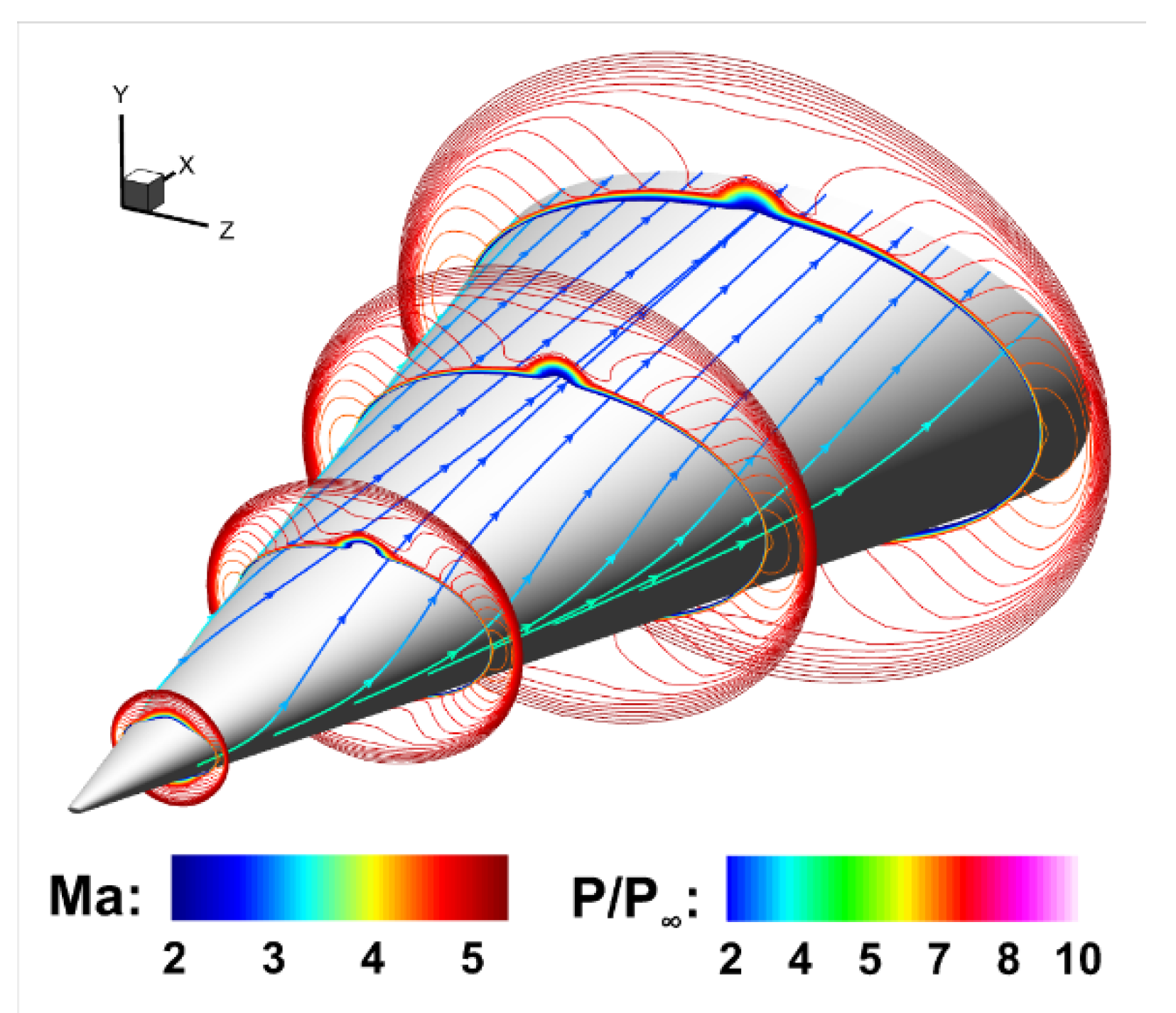
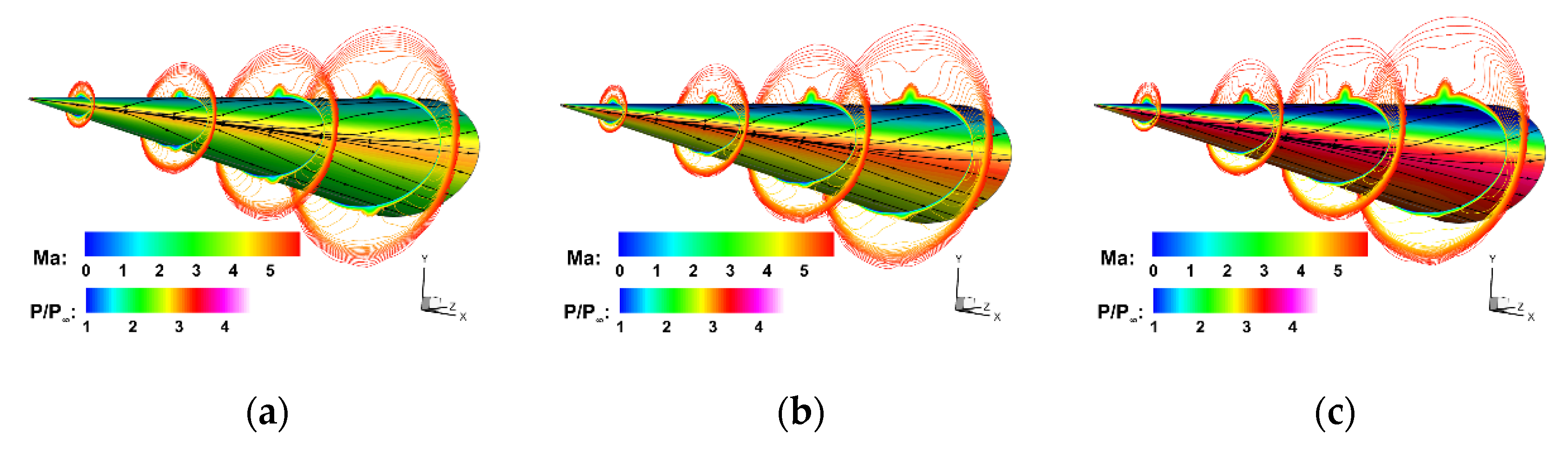
4.1. Analysis of Basic Flow Field
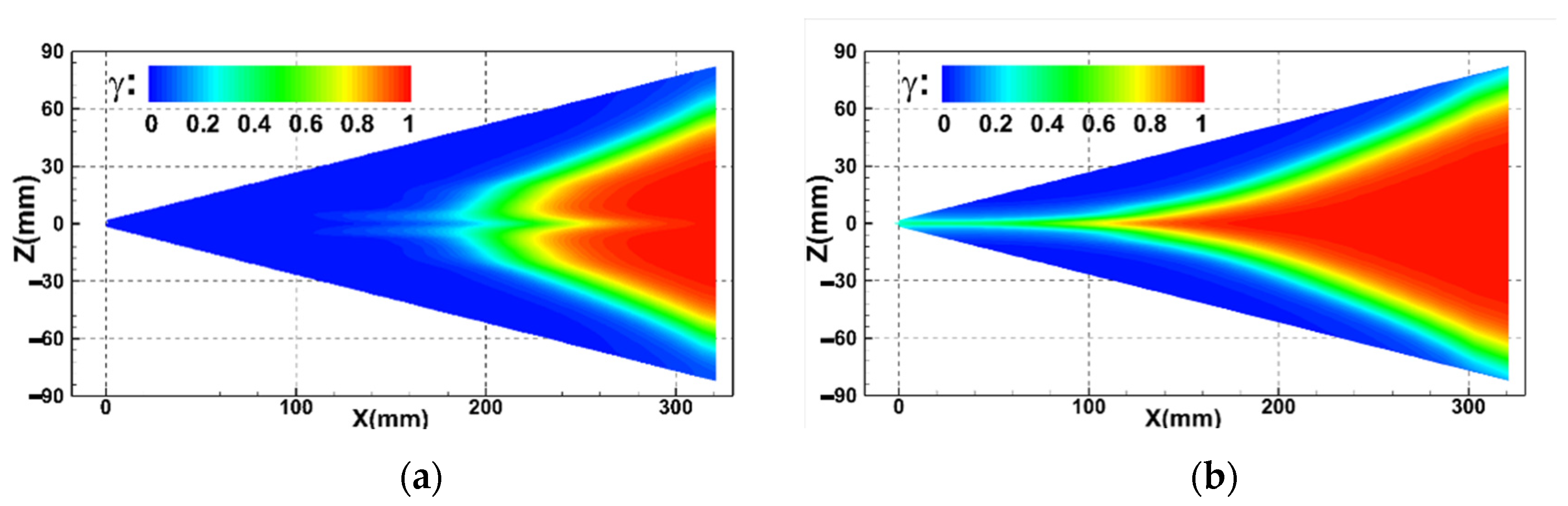
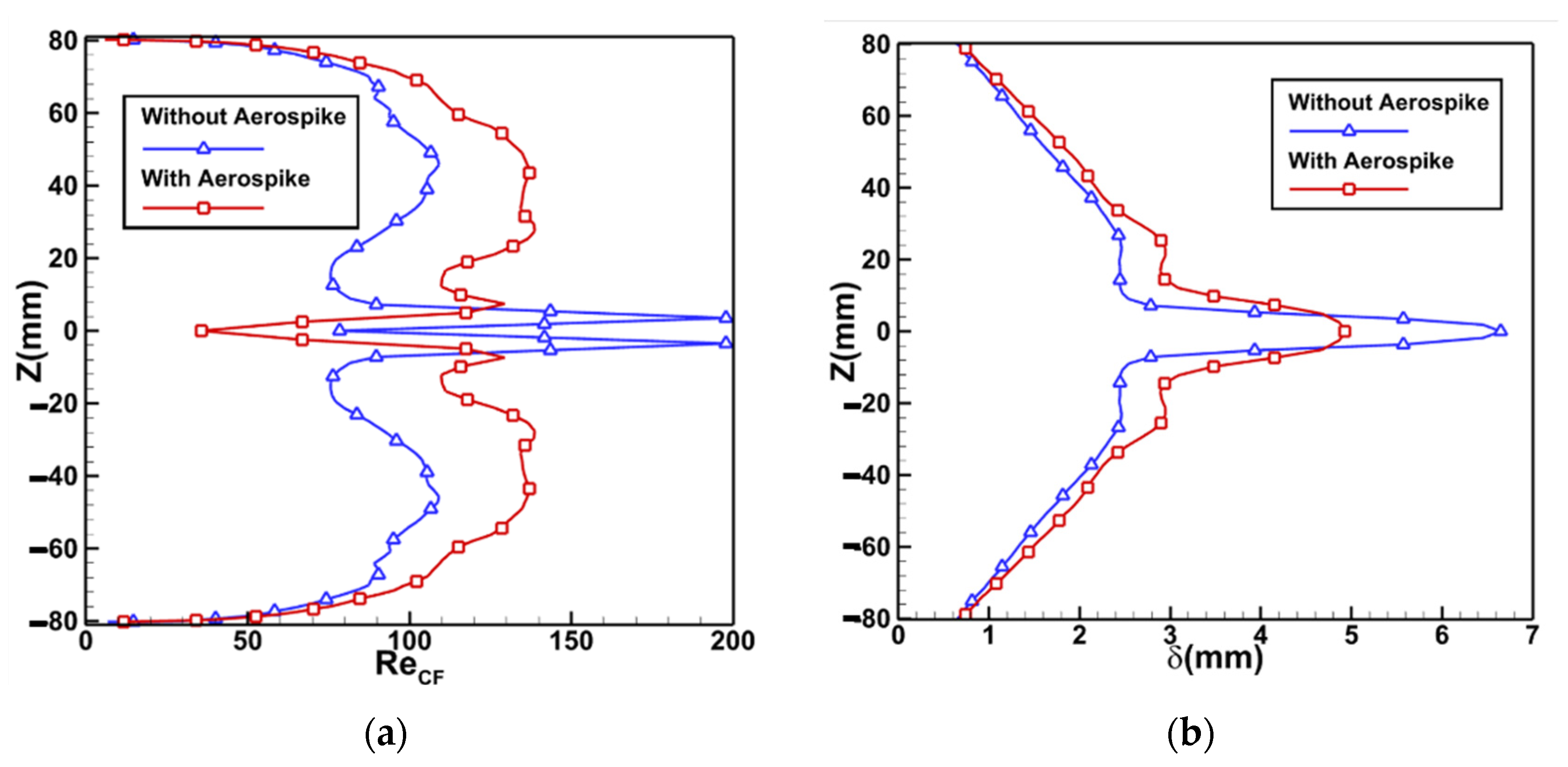
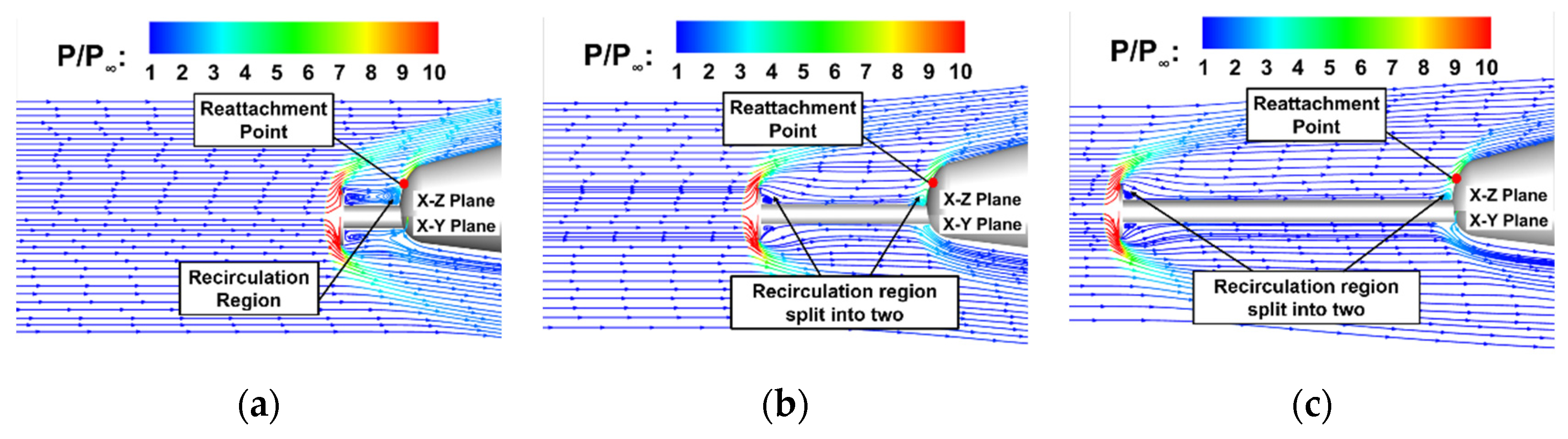
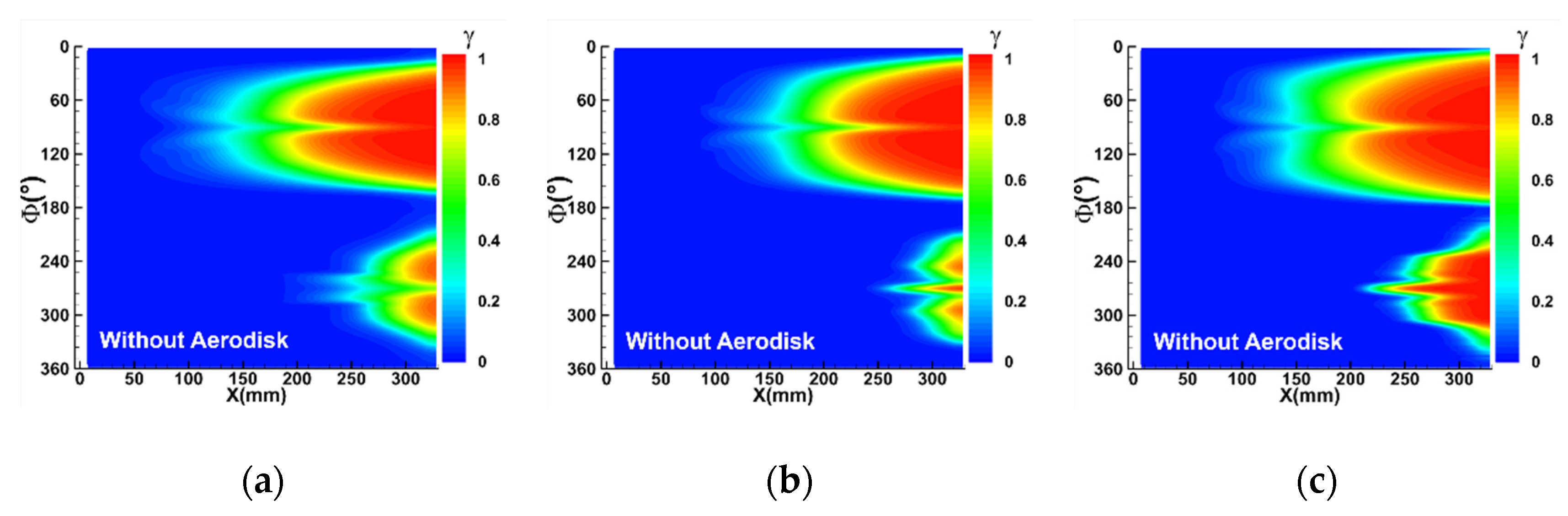
4.2. Influence of the Aerodisk
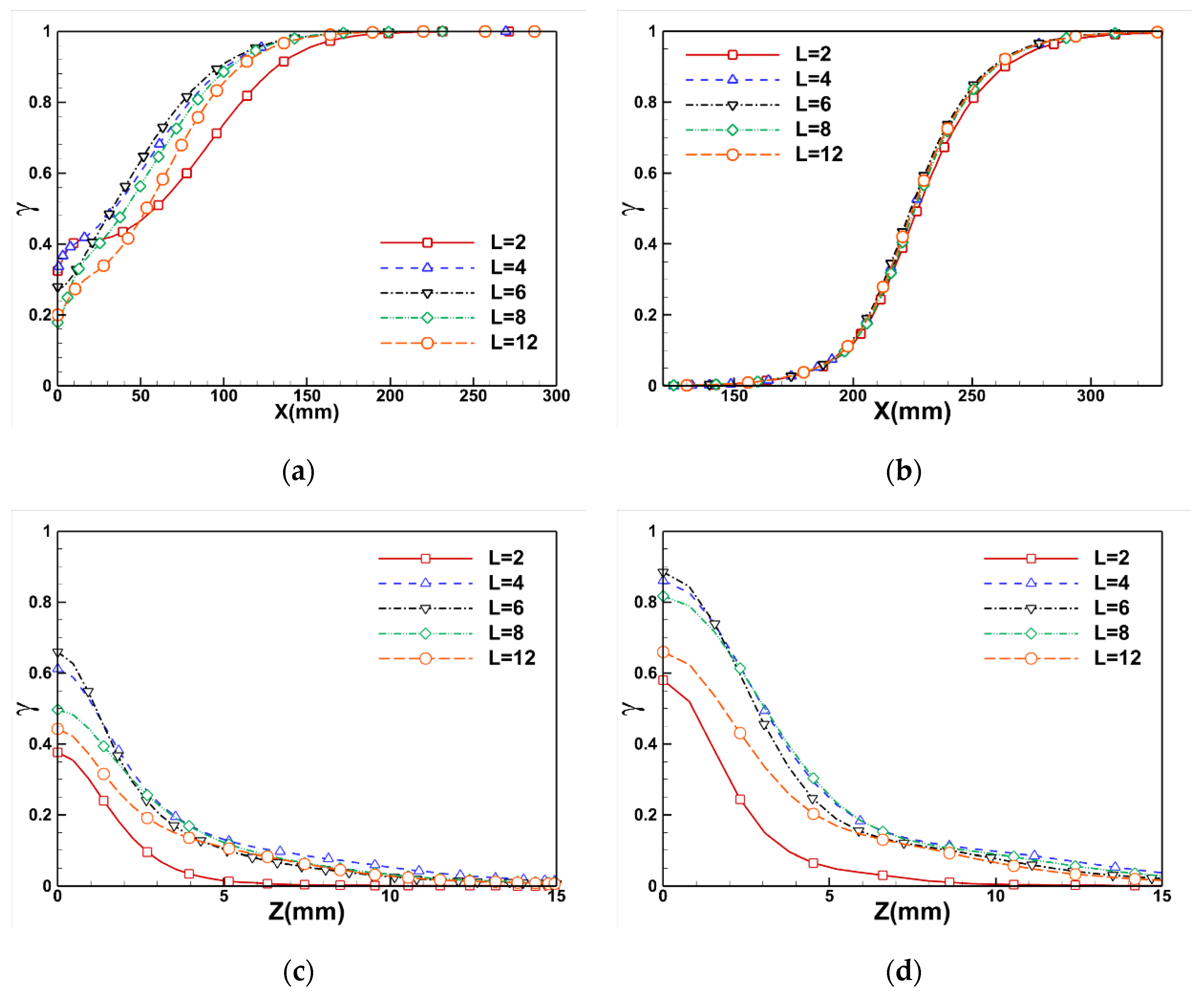
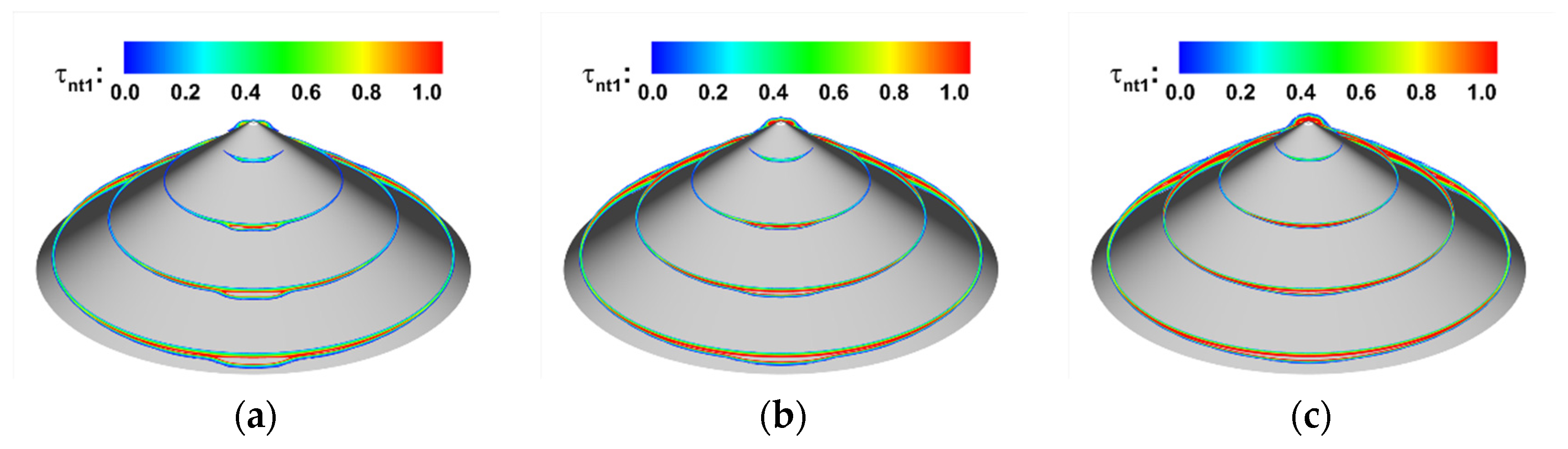
4.3. Influence of Aerodisk Length
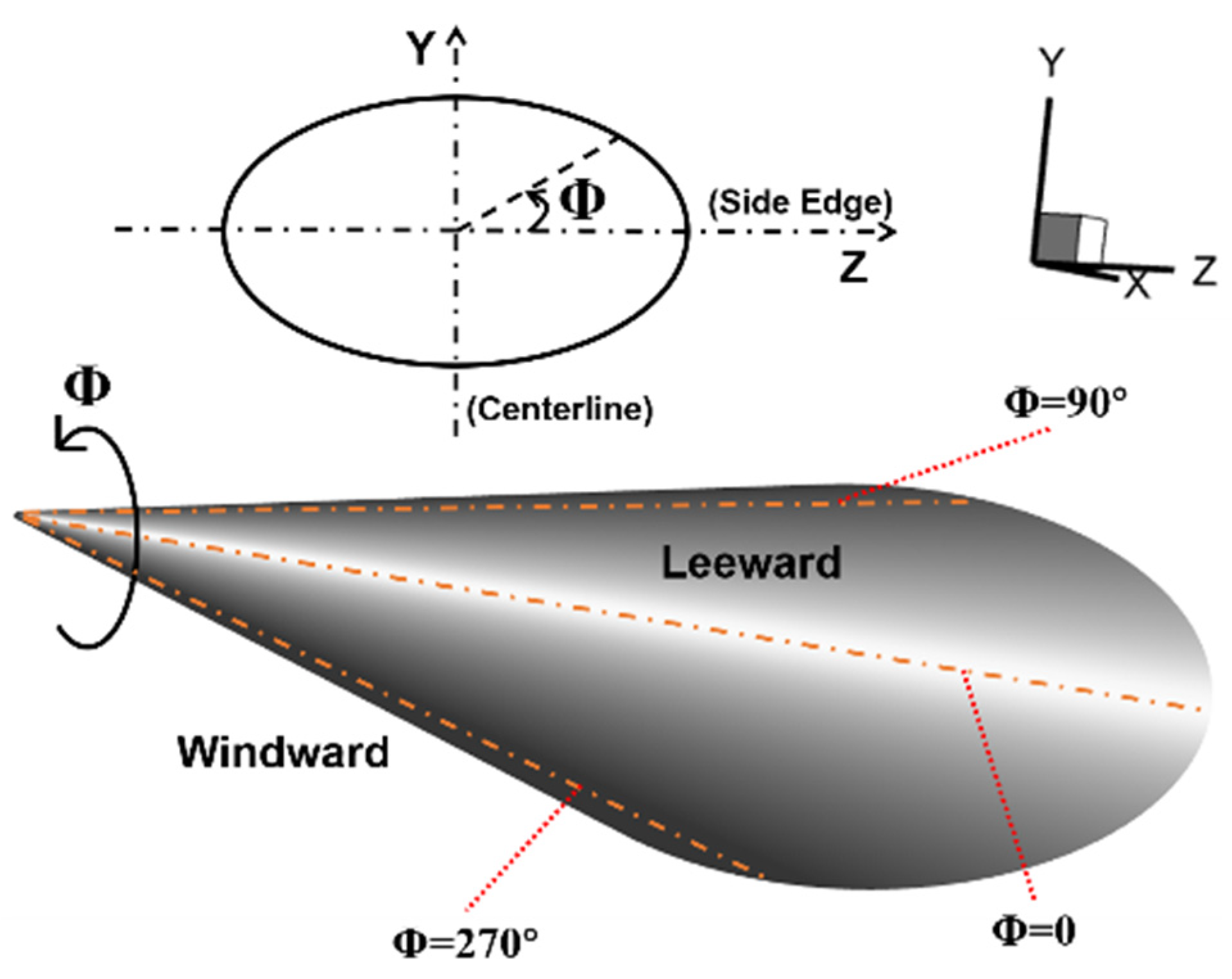
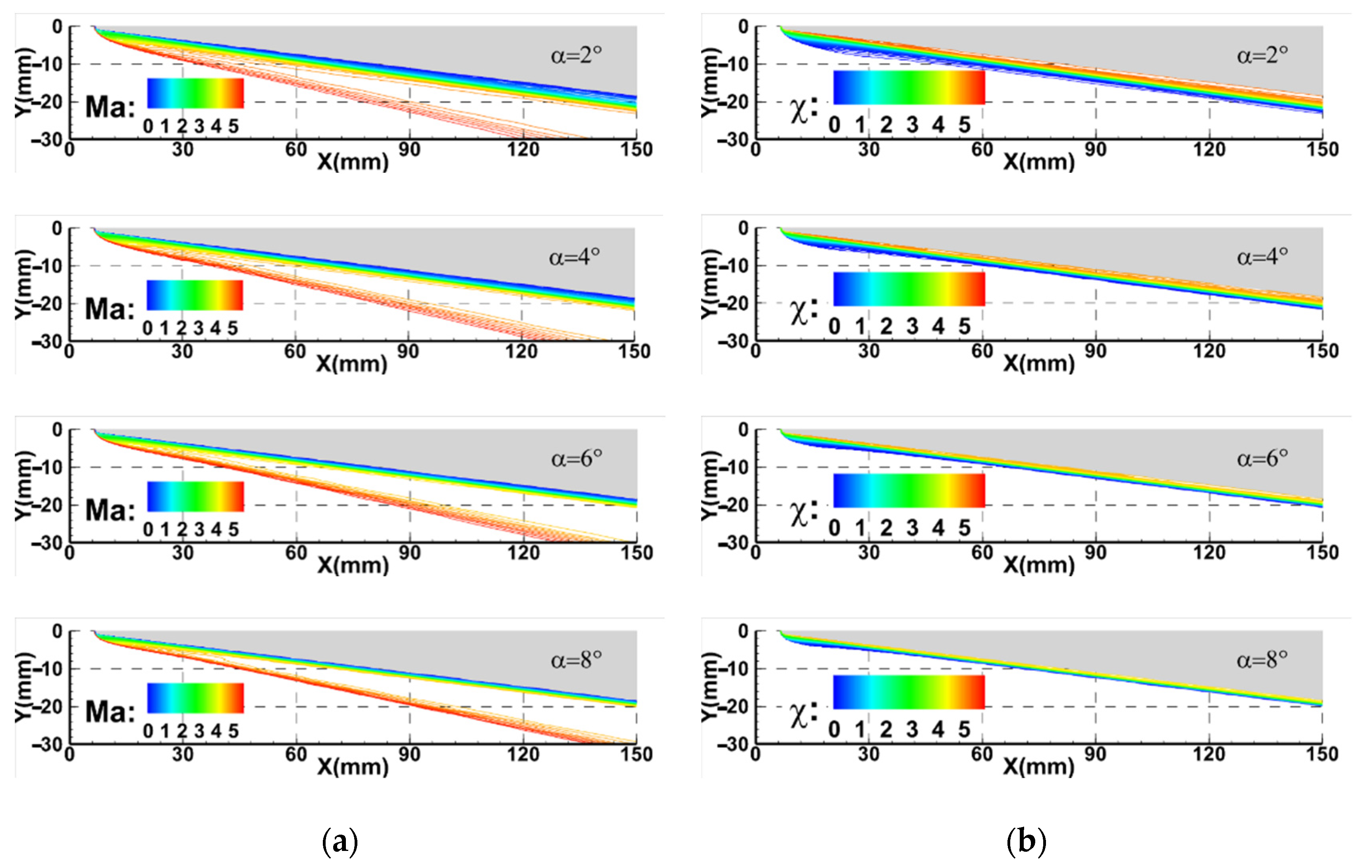
4.4. Influence of Angle of Attack
5. Conclusions
- (1)
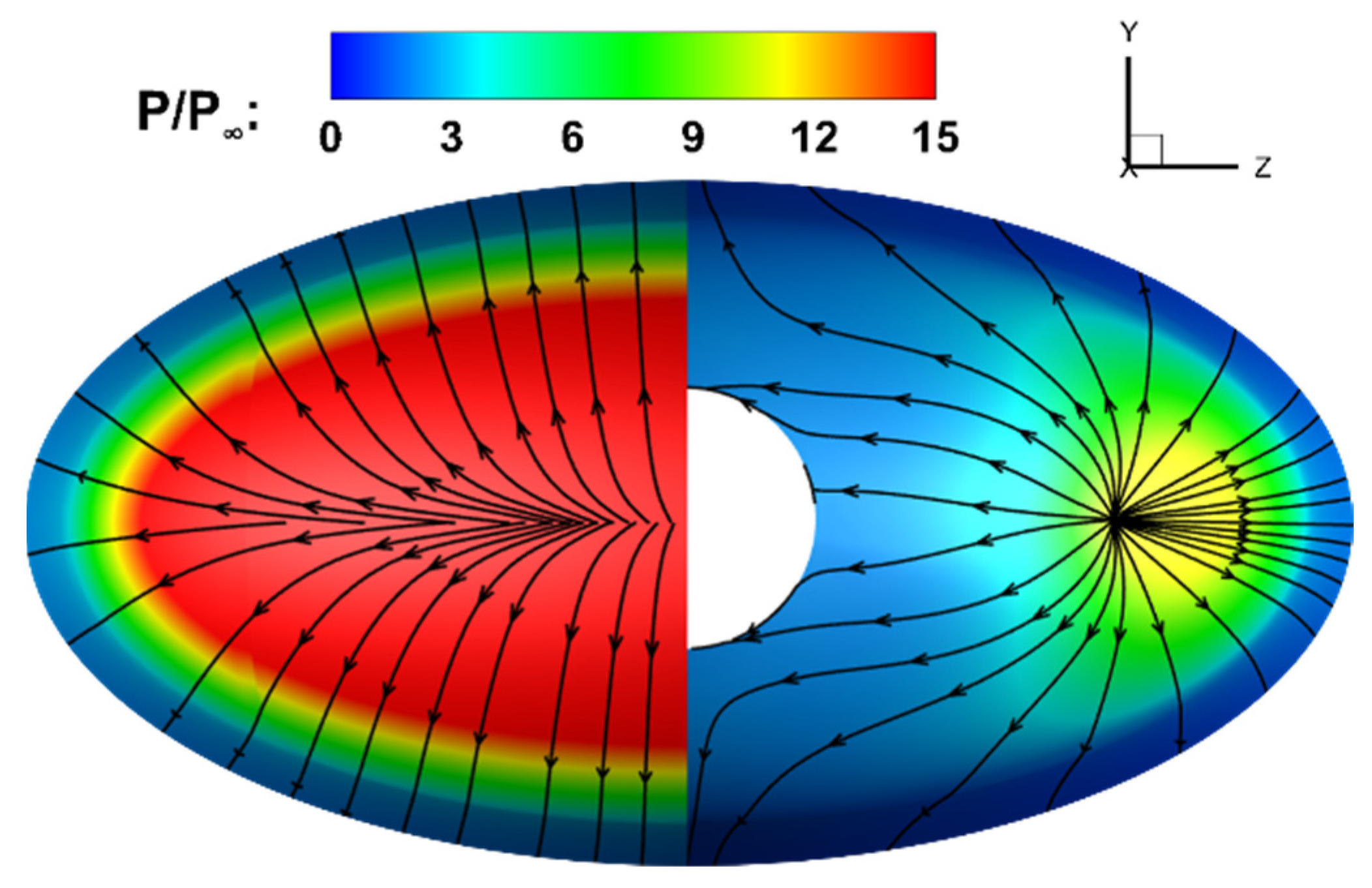
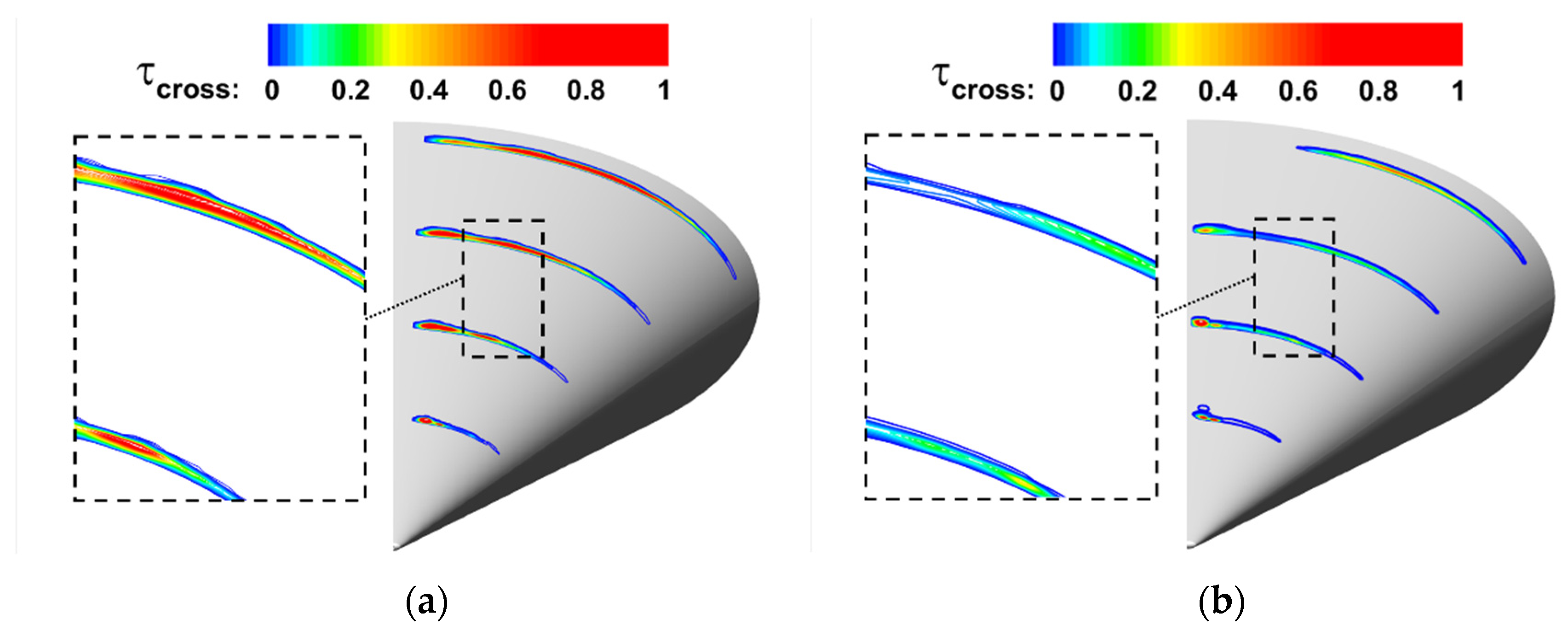
- Owing to the nonuniform distributed conical shock resulting from the elliptical cross section of HIFiRE-5 configuration, the crossflow initiates with streamlines travelling from the side edge to the centerline. Meanwhile, the mushroom-shaped longitudinal vortex is generated near the centerline, and the boundary layer transition near the centerline is dominated by the longitudinal vortex while other regions are dominated by the cross-mode unstable disturbance.
- (2)
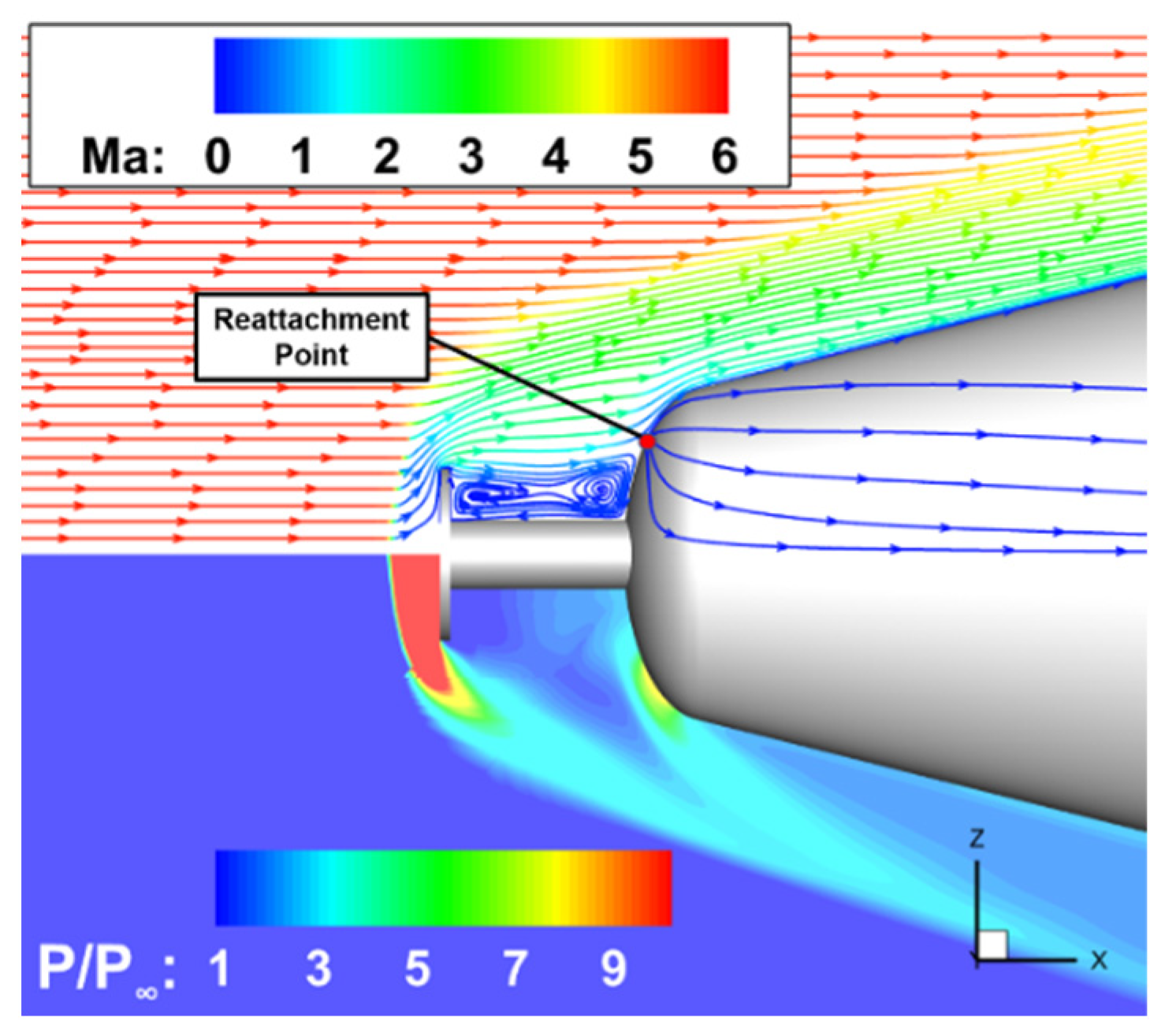
- The existence of an aerodisk transforms the flow field characteristic near the nose and creates recirculation regions with low pressure and reattachment shock, which results in an adverse pressure gradient. The separation-induced transition occurring in the shear layer of boundary layer separation position is triggered. Consequently, the transition region dilates and the transition onset near the centerline moves upstream compared to the case without an aerodisk.
- (3)
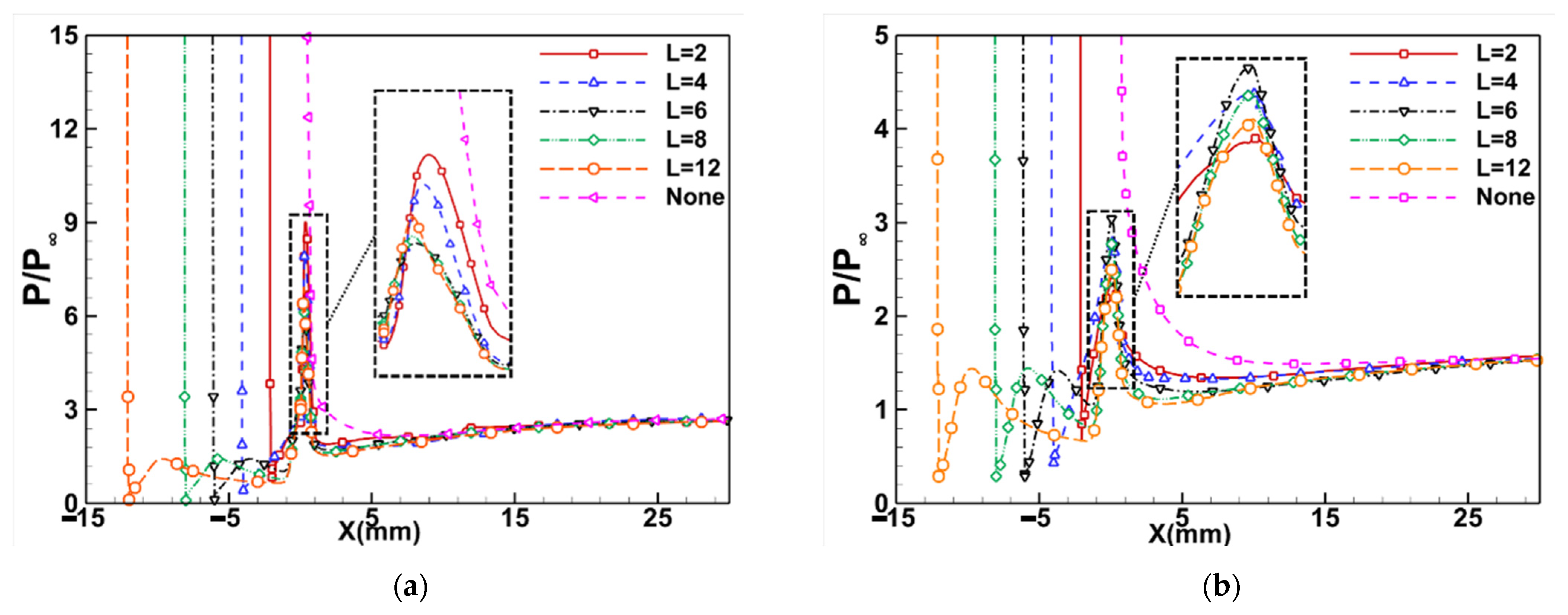
- By employing five lengths of an aerodisk, it is found that, with aerodisk length increasing, both varieties of maximum pressure (Pmax) and maximum heat flux (Qmax) are non-monotonous, which decrease first in the range of L = 2 mm to 6 mm and then increase. The aerodisk effects on drag and heat reduction are significant, whose aerodisk contributes to the reduction of Qmax by up to 52.0%, and Pmax without an aerodisk is even up to 5.1 times that with an aerodisk. The best drag and heat reduction efficiency is obtained when L = 6 mm. Nevertheless, the transition is triggered earlier by an aerodisk in the meantime, which dilates the region with high heat flux. In other words, the increase of boundary layer heat flux on afterbody is an inevitable compromise on reducing Pmax and Qmax on the forebody, which demands integration considerations during hypersonic vehicle and aerodisk design.
- (4)
- The influence of aerodisk length on boundary layer transition is largely concentrated near the centerline, while the effect on the transition shape in the area between centerline and side edge is nearly negligible. With an increase in the aerodisk length, the variety of γ growth rate along the centerline dominated by an adverse pressure gradient also obeys the non-monotonous trend and reaches its peak at a L = 6 mm aerodisk.
- (5)
- The effect of α is found to weaken the influence of an aerodisk on reducing wall heat flux and result in different shapes of the transition region on the windward and leeward surfaces. With increase in α, the transition onset on leeward side moves forward and crossflow becomes strong with a two-lobed shape. Regarding the windward side, as α increases, the crossflow weakens and the transition is dominated by the longitudinal vortex, which results in the transition front moving downstream first and then upstream.
Author Contributions
Funding
Conflicts of Interest
References
- Obinna, U.; Najafi, H. Thermal protection systems for space vehicles: A review on technology development, current challenges and future prospects. Acta Astronaut. 2020, 176, 341–356. [Google Scholar]
- Borg, M.P.; Schneider, S.P. Effect of freestream noise on roughness-induced transition for the X-51A forebody. J. Spacecr. Rocket. 2008, 45, 1106–1116. [Google Scholar] [CrossRef]
- Borg, M.P. Laminar Instability and Transition on the X-51A; Purdue University: West Lafayette, IN, USA, 2009. [Google Scholar]
- Borg, M.P.; Schneider, S.P. Effect of Freestream Noise on Instability and Transition for the X-51A Lee Side. AIAA Pap. 2009, 2009, 396. [Google Scholar]
- Yan, C.; Qu, F.; Zhao, Y.; Yu, J.; Wu, C.; Zhang, S. Review of development and challenges for physical modeling and numerical scheme of CFD in aeronautics and astronautics. Acta Aerodyn. Sin. 2020, 38, 829–857. [Google Scholar]
- Juniper Matthew, P. Triggering in the horizontal Rijke tube: Non-normality, transient growth and bypass transition. J. Fluid Mech. 2011, 667, 272–308. [Google Scholar] [CrossRef]
- Slotnick, J.P.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; NASA: Washington, DC, USA, 2014.
- Wang, L.; Fu, S. Modelling flow transition in a hypersonic boundary layer with Reynolds-averaged Navier-Stokes approach. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 768–774. [Google Scholar] [CrossRef]
- Wang, L.; Fu, S. Development of an intermittency equation for the modeling of the supersonic/hypersonic boundary layer flow transition. Flow Turbul. Combust. 2011, 87, 165–187. [Google Scholar] [CrossRef]
- Fu, S.; Wang, L. RANS modeling of high-speed aerodynamic flow transition with consideration of stability theory. Prog. Aerosp. Sci. 2013, 58, 36–59. [Google Scholar] [CrossRef]
- Zhou, L.; Li, R.; Hao, Z.; Zaripov, D.I.; Yan, C. Improved k-ω-γ model for crossflow-induced transition prediction in hypersonic flow. Int. J. Heat Mass Transf. 2017, 115, 115–130. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J.; Zhao, R.; Liu, X. Assessment and improvement of k-ω-γ model for separation-induced transition prediction. Chin. J. Aeronaut. 2022, 35, 219–234. [Google Scholar] [CrossRef]
- Vignesh, S.; Sundarraj, K.; Kulkarni, P.S. Thermo-fluid analysis of supersonic flow over ballistic shaped bodies with multiple aero-disk spike configurations. Acta Astronaut. 2021, 180, 292–304. [Google Scholar]
- Sebastian, J.J.; Suryan, A.; Kim, H.D. Numerical analysis of hypersonic flow past blunt bodies with aerodisks. J. Spacecr. Rocket. 2016, 53, 669–677. [Google Scholar] [CrossRef]
- Fan, D.; Xie, F.; Qin, N.; Huang, W.; Wang, L.; Chu, H. Drag reduction investigation for hypersonic lifting-body vehicles with aerodisk and long penetration mode counterflowing jet. Aerosp. Sci. Technol. 2018, 76, 361–373. [Google Scholar]
- Zhu, Y.; Peng, W.; Xu, R.; Jiang, P. Review on active thermal protection and its heat transfer for airbreathing hypersonic vehicles. Chin. J. Aeronaut. 2018, 31, 1929–1953. [Google Scholar] [CrossRef]
- Fan, D.; Xie, F.; Huang, W.; Dong, H.; Zhang, D. Numerical exploration on jet oscillation mechanism of counterflowing jet ahead of a hypersonic lifting-body vehicle. Sci. China Technol. Sci. 2018, 61, 1056–1071. [Google Scholar]
- Ou, M.; Yan, L.; Huang, W.; Li, S.-B.; Li, L.-Q. Detailed parametric investigations on drag and heat flux reduction induced by a combinational spike and opposing jet concept in hypersonic flows. Int. J. Heat Mass Transf. 2018, 126, 10–31. [Google Scholar] [CrossRef]
- David, R.; Nelson, H.F.; Johnson, E. Blunt-body wave drag reduction using focused energy deposition. AIAA J. 1999, 37, 460–467. [Google Scholar]
- Sajida, M.; Ahmed, Z.; Afzal, S. Numerical Study of Spike on Blunt Nose Configuration at Supersonic Speed. In Proceedings of the 2021 International Bhurban Conference on Applied Sciences and Technologies (IBCAST), Islamabad, Pakistan, 12–16 January 2021. [Google Scholar]
- Xie, Z.W. The Trident II head configuration. Missiles Space Veh. 1980, 6, 1–15. [Google Scholar]
- Zhang, R.-R.; Huang, W.; Yan, L.; Li, L.-Q.; Li, S.-B.; Moradi, R. Numerical investigation of drag and heat flux reduction mechanism of the pulsed counterflowing jet on a blunt body in supersonic flows. Acta Astronaut. 2018, 146, 123–133. [Google Scholar] [CrossRef]
- Ahmed, M.Y.M.; Qin, N. Recent advances in the aerothermodynamics of spiked hypersonic vehicles. Prog. Aerosp. Sci. 2011, 47, 425–449. [Google Scholar] [CrossRef]
- Sun, X.; Huang, W.; Ou, M.; Zhang, R.; Li, S. A survey on numerical simulations of drag and heat reduction mechanism in supersonic/hypersonic flows. Chin. J. Aeronaut. 2019, 32, 771–784. [Google Scholar] [CrossRef]
- Huang, W.; Chen, Z.; Yan, L.; Yan, B.B.; Du, Z.B. Drag and heat flux reduction mechanism induced by the spike and its combinations in supersonic flows: A review. Prog. Aerosp. Sci. 2019, 105, 31–39. [Google Scholar] [CrossRef]
- Sadegh, K.M.; Oboodi, M.J. Investigation and recent developments in aerodynamic heating and drag reduction for hypersonic flows. Heat Mass Transf. 2019, 55, 547–569. [Google Scholar]
- Qin, Q.; Xu, J.; Guo, S. Fluid-thermal analysis of aerodynamic heating over spiked blunt body configurations. Acta Astronaut. 2017, 132, 230–242. [Google Scholar] [CrossRef]
- Noboru, M.; Mihara, K.; Miyajima, R.; Watanuki, T.; Kubota, H. Thermal protection and drag reduction with use of spike in hypersonic flow. In Proceedings of the 10th AIAA/NAL-NASDA-ISAS International Space Planes and Hypersonic Systems and Technologies Conference, Kyoto, Japan, 24–27 April 2001. [Google Scholar]
- Xue, Y.; Wang, L.; Fu, S. Drag reduction and aerodynamic shape optimization for spike-tipped supersonic blunt nose. J. Spacecr. Rocket. 2018, 55, 552–560. [Google Scholar] [CrossRef]
- Zhong, K.; Yan, C.; Chen, S.-s.; Zhang, T.X.; Lou, S. Aerodisk effects on drag reduction for hypersonic blunt body with an ellipsoid nose. Aerosp. Sci. Technol. 2019, 86, 599–612. [Google Scholar] [CrossRef]
- Julio, S.; Gnemmi, P.; Runne, K.; Seiler, F. High-pressure shock tunnel experiments and CFD calculations on spike-tipped blunt bodies. In Proceedings of the 22nd AIAA Aerodynamic Measurement Technology and Ground Testing Conference, St. Louis, MO, USA, 24–26 June 2002. [Google Scholar]
- Crawford, D.H. Investigation of the Flow over Spiked-Nose Hemisphere-Cylinder at Mach Number of 6.8; National Aeronautics and Space Administration: Washington, DC, USA, 1959.
- Wei, H.; Li, L.; Yan, L.; Zhang, T.T. Drag and heat flux reduction mechanism of blunted cone with aerodisks. Acta Astronaut. 2017, 138, 168–175. [Google Scholar]
- Fan, B.; Huang, J. Coupled Fluid-Thermal Investigation on Drag and Heat Reduction of a Hypersonic Spiked Blunt Body with an Aerodisk. Aerospace 2021, 9, 19. [Google Scholar] [CrossRef]
- Kalimuthu, R.; Mehta, R.C.; Rathakrishnan, E. Experimental investigation on spiked body in hypersonic flow. Aeronaut. J. 2008, 112, 593–598. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J.; Liu, H. Application of improved k-ω-γ model to deformed hypersonic Inflatable Aerodynamic Decelerator aeroshell. Appl. Therm. Eng. 2022, 214, 118794. [Google Scholar] [CrossRef]
- Karen, B.; Rufer, S.; Kimmel, R.; Adamczak, D. Aerothermodynamic characteristics of boundary layer transition and trip effectiveness of the HIFiRE flight 5 vehicle. In Proceedings of the 39th AIAA Fluid Dynamics Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar]
- Juliano, T.J.; Matthew, P.B.; Steven, P.S. Quiet tunnel measurements of HIFiRE-5 boundary-layer transition. AIAA J. 2015, 53, 832–846. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, S.; Zou, Y.; Yuan, W.; Liu, T.; Zhao, Y. Uncertainty analysis of turbulence model in capturing flows involving laminarization and retransition. Chin. J. Aeronaut. 2022, 35, 148–164. [Google Scholar] [CrossRef]
- Smirnov, N.N.; Betelin, V.B.; Nikitin, V.F.; Stamov, L.I.; Altoukhov, D.I. Accumulation of errors in numerical simulations of chemically reacting gas dynamics. Acta Astronaut. 2015, 117, 338–355. [Google Scholar] [CrossRef]
- Smirnov, N.N.; Betelin, V.B.; Shagaliev, R.M.; Nikitin, V.F.; Belyakov, I.M.; Deryuguin, Y.N.; Aksenov, S.V.; Korchazhkin, D.A. Hydrogen fuel rocket engines simulation using LOGOS code. Int. J. Hydrogen Energy 2014, 39, 10748–10756. [Google Scholar] [CrossRef]
- Lyttle, I.; Reed, H. Use of Transition Correlations for Three-Dimensional Boundary Layers within Hypersonic Flows; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1995.
- Reed, H.L.; Haynes, T.S. Transition correlations in three-dimensional boundary layers. AIAA J. 1994, 32, 923–929. [Google Scholar] [CrossRef]
- Malik, M.R.; Balakumar, P. Instability and Transition in Three-Dimensional Supersonic Boundary Layers; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1992.
- Kara, K.; Balakumar, P.; Kandil, O.A. Effects of Nose Bluntness on Hypersonic Boundary-Layer Receptivity and Stability over Cones. AIAA J. 2011, 49, 2593–2606. [Google Scholar] [CrossRef]




| Ma∞ | Re∞ (/m) | T∞ (K) | ρ∞ (kg/m3) | Tw (K) | Tu∞ (%) |
|---|---|---|---|---|---|
| 5.8 | 6.1 × 106 | 51.4 | 0.024 | 300 | 0.1 |
| Grid Name | Grid Resolution | Wall Normal Distance of the First Grid Cell Δx (m) | Grid Reynolds Number ReΔx | ||
|---|---|---|---|---|---|
| Block 1 | Block 2 | Block 3 | |||
| G1 | 32 × 51 × 64 | 90 × 121 × 104 | 170 × 52 × 81 | 3.5 × 10−6 | 20 |
| G2 | 32 × 61 × 84 | 70 × 101 × 84 | 180 × 72 × 101 | 1.6 × 10−6 | 10 |
| G3 | 32 × 71 × 104 | 50 × 81 × 64 | 190 × 92 × 121 | 9.5 × 10−7 | 6 |
| Aerodisk Length (mm) | 0 (without Aerodisk) | 2 | 4 | 6 | 8 | 12 |
|---|---|---|---|---|---|---|
| Qmax (kW·m−2) | 121,850.82 | 93,976.25 | 87,560.46 | 58,497.42 | 71,650.69 | 86,419.36 |
| (P/P∞)max | 31.04 | 9.03 | 8.01 | 6.03 | 6.29 | 6.93 |
| Angle of Attack | 2° | 4° | 6° |
|---|---|---|---|
| Qmax (kW·m−2) without Aerodisk | 125,625.01 | 125,641.13 | 125,644.68 |
| Qmax (kW·m−2) with Aerodisk | 106,526.14 | 114,884.95 | 125,453.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Shao, Z.; Liu, H. Aerodisk Effect on Hypersonic Boundary Layer Transition and Heat Transfer of HIFiRE-5 Vehicle. Aerospace 2022, 9, 742. https://doi.org/10.3390/aerospace9120742
Zhao Y, Shao Z, Liu H. Aerodisk Effect on Hypersonic Boundary Layer Transition and Heat Transfer of HIFiRE-5 Vehicle. Aerospace. 2022; 9(12):742. https://doi.org/10.3390/aerospace9120742
Chicago/Turabian StyleZhao, Yatian, Zhiyuan Shao, and Hongkang Liu. 2022. "Aerodisk Effect on Hypersonic Boundary Layer Transition and Heat Transfer of HIFiRE-5 Vehicle" Aerospace 9, no. 12: 742. https://doi.org/10.3390/aerospace9120742
APA StyleZhao, Y., Shao, Z., & Liu, H. (2022). Aerodisk Effect on Hypersonic Boundary Layer Transition and Heat Transfer of HIFiRE-5 Vehicle. Aerospace, 9(12), 742. https://doi.org/10.3390/aerospace9120742








