Optimal Earth Gravity-Assist Maneuvers with an Electric Solar Wind Sail
Abstract
1. Introduction
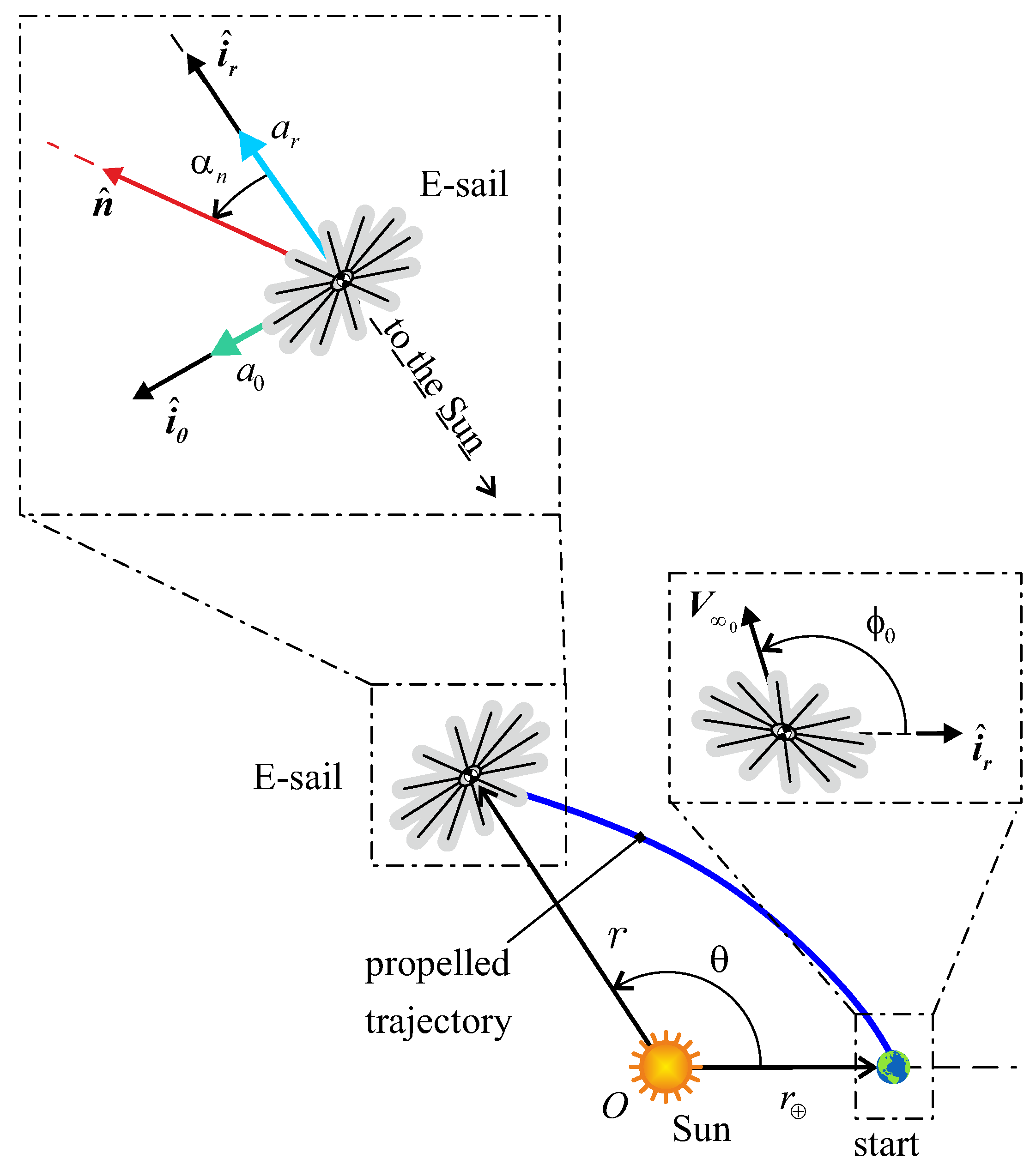
2. Mathematical Model
Spacecraft Trajectory Optimization
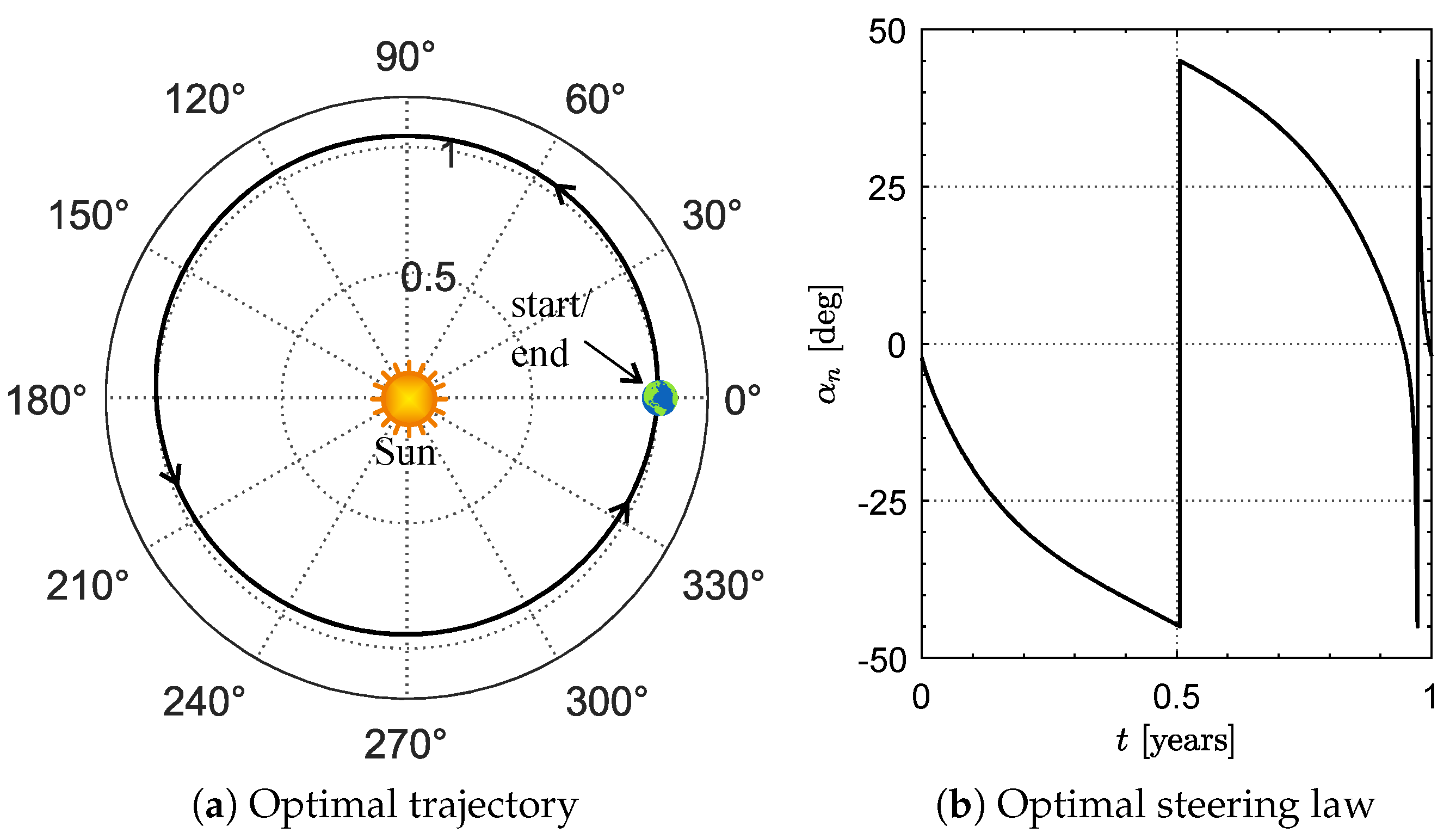
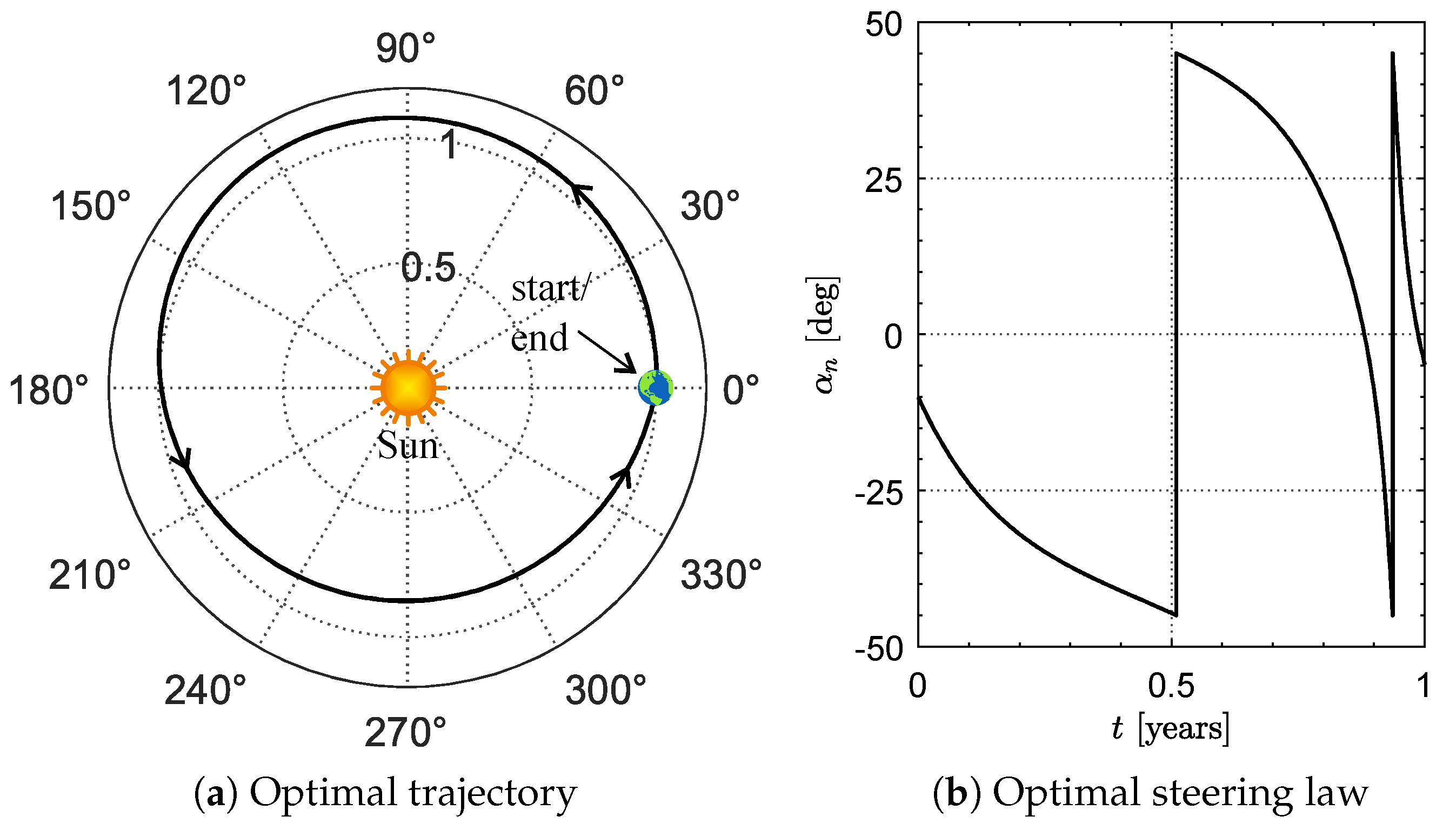
3. Case Study
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notation
| propulsive acceleration vector [mm/s] | |
| characteristic acceleration [mm/s] | |
| radial component of [mm/s] | |
| circumferential component of [mm/s] | |
| Hamiltonian function | |
| J | cost function; see Equation (13) [km/s] |
| radial unit vector | |
| circumferential unit vector | |
| P | dimensionless performance parameter, see Equation (27) |
| r | Sun–spacecraft distance [au] |
| Sun–Earth distance [au] | |
| t | time [days] |
| polar reference frame | |
| u | radial component of the spacecraft velocity [km/s] |
| spacecraft velocity vector relative to the Earth [km/s] (with ) | |
| v | circumferential component of the spacecraft velocity [km/s] |
| E-sail pitch angle [rad] | |
| auxiliary angle; see Equation (23) [rad] | |
| polar angle [rad] | |
| dimensionless costate variable adjoint to r | |
| dimensionless costate variable adjoint to u | |
| dimensionless costate variable adjoint to v | |
| dimensionless costate variable adjoint to | |
| Sun’s gravitational parameter [km/s] | |
| dimensionless switching parameter | |
| Subscripts | |
| 0 | initial value |
| f | final value |
| Superscripts | |
| ⋆ | optimal value |
References
- Janhunen, P. Electric sail for spacecraft propulsion. J. Propuls. Power 2004, 20, 763–764. [Google Scholar] [CrossRef]
- Bassetto, M.; Niccolai, L.; Quarta, A.A.; Mengali, G. A comprehensive review of Electric Solar Wind Sail concept and its applications. Prog. Aerosp. Sci. 2022, 128, 1–27. [Google Scholar] [CrossRef]
- Fu, B.; Sperber, E.; Eke, F. Solar sail technology—A state of the art review. Prog. Aerosp. Sci. 2016, 86, 1–19. [Google Scholar] [CrossRef]
- Gong, S.; Macdonald, M. Review on solar sail technology. Astrodynamics 2019, 3, 93–125. [Google Scholar] [CrossRef]
- Zhang, F.; Gong, S.; Baoyin, H. Three-axes attitude control of solar sail based on shape variation of booms. Aerospace 2021, 8, 198. [Google Scholar] [CrossRef]
- Zou, J.; Li, D.; Wang, J.; Yu, Y. Experimental study of measuring the wrinkle of solar sails. Aerospace 2022, 9, 289. [Google Scholar] [CrossRef]
- Bassetto, M.; Niccolai, L.; Quarta, A.A.; Mengali, G. Logarithmic spiral trajectories generated by solar sails. Celest. Mech. Dyn. Astron. 2018, 130, 18.1–18.24. [Google Scholar] [CrossRef]
- Andrews, D.G.; Zubrin, R.M. Magnetic sails and interstellar travel. J. Br. Interplanet. Soc. 1990, 43, 265–272. [Google Scholar]
- Zubrin, R.M. The use of magnetic sails to escape from low Earth orbit. J. Br. Interplanet. Soc. 1992, 46, 3–10. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Mengali, G. Magnetic sail-based displaced non-Keplerian orbits. Aerosp. Sci. Technol. 2019, 92, 363–372. [Google Scholar] [CrossRef]
- Niccolai, L.; Quarta, A.A.; Mengali, G. Electric sail elliptic displaced orbits with advanced thrust model. Acta Astronaut. 2017, 138, 503–511. [Google Scholar] [CrossRef]
- Niccolai, L.; Anderlini, A.; Mengali, G.; Quarta, A.A. Electric sail displaced orbit control with solar wind uncertainties. Acta Astronaut. 2019, 162, 563–573. [Google Scholar] [CrossRef]
- Aliasi, G.; Mengali, G.; Quarta, A.A. Artificial Equilibrium Points for an Electric Sail with Constant Attitude. J. Spacecr. Rocket. 2013, 50, 1295–1298. [Google Scholar] [CrossRef]
- Niccolai, L.; Caruso, A.; Quarta, A.A.; Mengali, G. Artificial collinear Lagrangian point maintenance with electric solar wind sail. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4467–4477. [Google Scholar] [CrossRef]
- Janhunen, P.; Quarta, A.A.; Mengali, G. Electric solar wind sail mass budget model. Geosci. Instrum. Methods Data Syst. 2013, 2, 85–95. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Janhunen, P. Electric sail option for cometary rendezvous. Acta Astronaut. 2016, 127, 684–692. [Google Scholar] [CrossRef]
- Janhunen, P.; Lebreton, J.P.; Merikallio, S.; Paton, M.; Mengali, G.; Quarta, A.A. Fast E-sail Uranus entry probe mission. Planet. Space Sci. 2014, 104, 141–146. [Google Scholar] [CrossRef]
- Sanchez-Torres, A. Propulsive force in electric solar sails for missions in the heliosphere. IEEE Trans. Plasma Sci. 2019, 47, 1657–1662. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Trajectory analysis and optimization of Hesperides mission. Universe 2022, 8, 364. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A.; Janhunen, P. Considerations of electric sailcraft trajectory design. J. Br. Interplanet. Soc. 2008, 61, 326–329. [Google Scholar]
- Huo, M.Y.; Mengali, G.; Quarta, A.A. Mission design for an interstellar probe with E-sail propulsion system. JBIS—J. Br. Interplanet. Soc. 2015, 68, 128–134. [Google Scholar]
- Quarta, A.A.; Mengali, G. Electric sail mission analysis for outer solar system exploration. J. Guid. Control Dyn. 2010, 33, 740–755. [Google Scholar] [CrossRef]
- Leipold, M.; Wagner, O. ‘Solar photonic assist’ trajectory design for solar sail missions to the outer solar system and beyond. In Proceedings of the AAS/GSFC International Symposium on Flight Dynamics, Greenbelt, MD, USA, 11–15 May 1998. [Google Scholar]
- Hollenbeck, G.R. New flight techniques for outer planet missions. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Nassau, Bahamas, 28–30 July 1975. [Google Scholar]
- Atkins, K.L.; Sauer, C.G., Jr.; Flandro, G.A. Solar electric propulsion combined with Earth gravity assist: A new potential for planetary exploration. In Proceedings of the AIAA/AAS Astrodynamics Conference, San Diego, CA, USA, 13–16 September 1976; 16 September 1976. [Google Scholar] [CrossRef]
- Kawaguchi, J. Solar electric propulsion leverage: Electric delta-VEGA (EDVEGA) scheme and its application. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Santa Barbara, CA, USA, 11–15 February 2001. [Google Scholar]
- Kawaguchi, J. Performance evaluation for the electric Delta-V Earth Gravity Assist (EDVEGA) scheme. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002. [Google Scholar] [CrossRef]
- O’Reilly, D.; Herdrich, G.; Kavanagh, D.F. Electric propulsion methods for small satellites: A review. Aerospace 2021, 8, 22. [Google Scholar] [CrossRef]
- Quarta, A.A.; Bianchi, C.; Niccolai, L.; Mengali, G. Optimal V∞ leveraging maneuvers using gray solar sail. Aerosp. Sci. Technol. 2022, 126, 1–9. [Google Scholar] [CrossRef]
- Quarta, A.A.; Bianchi, C.; Niccolai, L.; Mengali, G. Solar sail-based V-infinity leveraging missions from elliptic orbit. Aerosp. Sci. Technol. 2022, 130, 1–9. [Google Scholar] [CrossRef]
- Takao, Y.; Chujo, T. Delta-V Earth-gravity assist trajectories with hybrid solar electric-photonic propulsion. J. Guid. Control Dyn. 2022, 45, 162–170. [Google Scholar] [CrossRef]
- Sims, J.A.; Longuski, J.M. Analysis of V∞ leveraging for interplanetary missions. In Proceedings of the AIAA/AAS Astrodynamics Conference, Scottsdale, AZ, USA, 1–3 August 1994. [Google Scholar] [CrossRef]
- Sims, J.A.; Longuski, J.M.; Staugler, A.J. V∞ leveraging for interplanetary missions: Multiple-revolution orbit techniques. J. Guid. Control Dyn. 1997, 20, 409–415. [Google Scholar] [CrossRef]
- Brinckerhoff, A.T.; Russell, R.P. Pathfinding and V-Infinity leveraging for planetary moon tour missions. In Proceedings of the 19th AAS/AIAA Space Flight Mechanics Meeting, Savannah, GA, USA, 8–12 February 2009; Volume 134. [Google Scholar]
- Ozaki, N.; Chikazawa, T.; Kakihara, K.; Ishikawa, A.; Kawakatsu, Y. Extended robust planetary orbit insertion method under probabilistic uncertainties. J. Spacecr. Rocket. 2020, 57, 1153–1164. [Google Scholar] [CrossRef]
- Bianchi, C.; Niccolai, L.; Mengali, G. Solar sail-based deep space transfers using V-infinity leveraging maneuvers. In Proceedings of the 73rd International Astronautical Congress (IAC), Paris, France, 18–22 September 2022. [Google Scholar]
- Morante, D.; Sanjurjo Rivo, M.; Soler, M. A survey on low-thrust trajectory optimization approaches. Aerospace 2021, 8, 88. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Su, L.; Ma, Z.; Chen, H. A neural network warm-started indirect trajectory optimization method. Aerospace 2022, 9, 435. [Google Scholar] [CrossRef]
- Huo, M.Y.; Mengali, G.; Quarta, A.A. Electric sail thrust model from a geometrical perspective. J. Guid. Control Dyn. 2018, 41, 735–741. [Google Scholar] [CrossRef]
- Janhunen, P.; Toivanen, P.K.; Polkko, J.; Merikallio, S.; Salminen, P.; Haeggström, E.; Seppänen, H.; Kurppa, R.; Ukkonen, J.; Kiprich, S.; et al. Electric solar wind sail: Toward test missions. Rev. Sci. Instrum. 2010, 81, 111301. [Google Scholar] [CrossRef] [PubMed]
- Toivanen, P.K.; Janhunen, P. Thrust vectoring of an electric solar wind sail with a realistic sail shape. Acta Astronaut. 2017, 131, 145–151. [Google Scholar] [CrossRef]
- Liu, F.; Hu, Q.; Liu, Y. Attitude dynamics of electric sail from multibody perspective. J. Guid. Control Dyn. 2018, 41, 2633–2646. [Google Scholar] [CrossRef]
- Bassetto, M.; Mengali, G.; Quarta, A.A. Attitude dynamics of an electric sail model with a realistic shape. Acta Astronaut. 2019, 159, 250–257. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control: Optimization, Estimation and Control; Hemisphere Publishing Corporation: New York, NY, USA, 1975. [Google Scholar]
- Shampine, L.F.; Gordon, M.K. Computer Solution of Ordinary Differential Equations: The Initial Value Problem; W. H. Freeman & Co., Ltd.: San Francisco, CA, USA, 1975; Chapter 10; ISBN 0-716-70461-7. [Google Scholar]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Slavinskis, A.; Janhunen, P.; Toivanen, P.; Muinonen, K.; Penttilä, A.; Granvik, M.; Kohout, T.; Gritsevich, M.; Pajusalu, M.; Sunter, I.; et al. Nanospacecraft fleet for multi-asteroid touring with electric solar wind sails. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 3–10 March 2018; Volume 2018, pp. 1–20. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niccolai, L.; Bassetto, M.; Quarta, A.A.; Mengali, G. Optimal Earth Gravity-Assist Maneuvers with an Electric Solar Wind Sail. Aerospace 2022, 9, 717. https://doi.org/10.3390/aerospace9110717
Niccolai L, Bassetto M, Quarta AA, Mengali G. Optimal Earth Gravity-Assist Maneuvers with an Electric Solar Wind Sail. Aerospace. 2022; 9(11):717. https://doi.org/10.3390/aerospace9110717
Chicago/Turabian StyleNiccolai, Lorenzo, Marco Bassetto, Alessandro A. Quarta, and Giovanni Mengali. 2022. "Optimal Earth Gravity-Assist Maneuvers with an Electric Solar Wind Sail" Aerospace 9, no. 11: 717. https://doi.org/10.3390/aerospace9110717
APA StyleNiccolai, L., Bassetto, M., Quarta, A. A., & Mengali, G. (2022). Optimal Earth Gravity-Assist Maneuvers with an Electric Solar Wind Sail. Aerospace, 9(11), 717. https://doi.org/10.3390/aerospace9110717





