A Multifidelity Simulation Method for Internal and External Flow of a Hypersonic Airbreathing Propulsion System
Abstract
1. Introduction
2. Multifidelity Simulation Method
2.1. Computational Fluid Dynamics Solver
2.2. Quasi-One-Dimensional Flow Model
2.3. Coupling of the Quasi-One-Dimensional Model and CFD Codes
- (1)
- Solve 2D RANS equations and acquire the initial external flow fields;
- (2)
- Calculate the mass-weighted average quantities at the interfaces;
- (3)
- Solve the quasi-one-dimensional equation based on the upstream and downstream boundary conditions of the combustor;
- (4)
- Update the values at the interfaces and recompute the external flow fields; and
- (5)
- If the iteration converges, then stop; otherwise, return to step (1).
2.4. Validation
3. Results
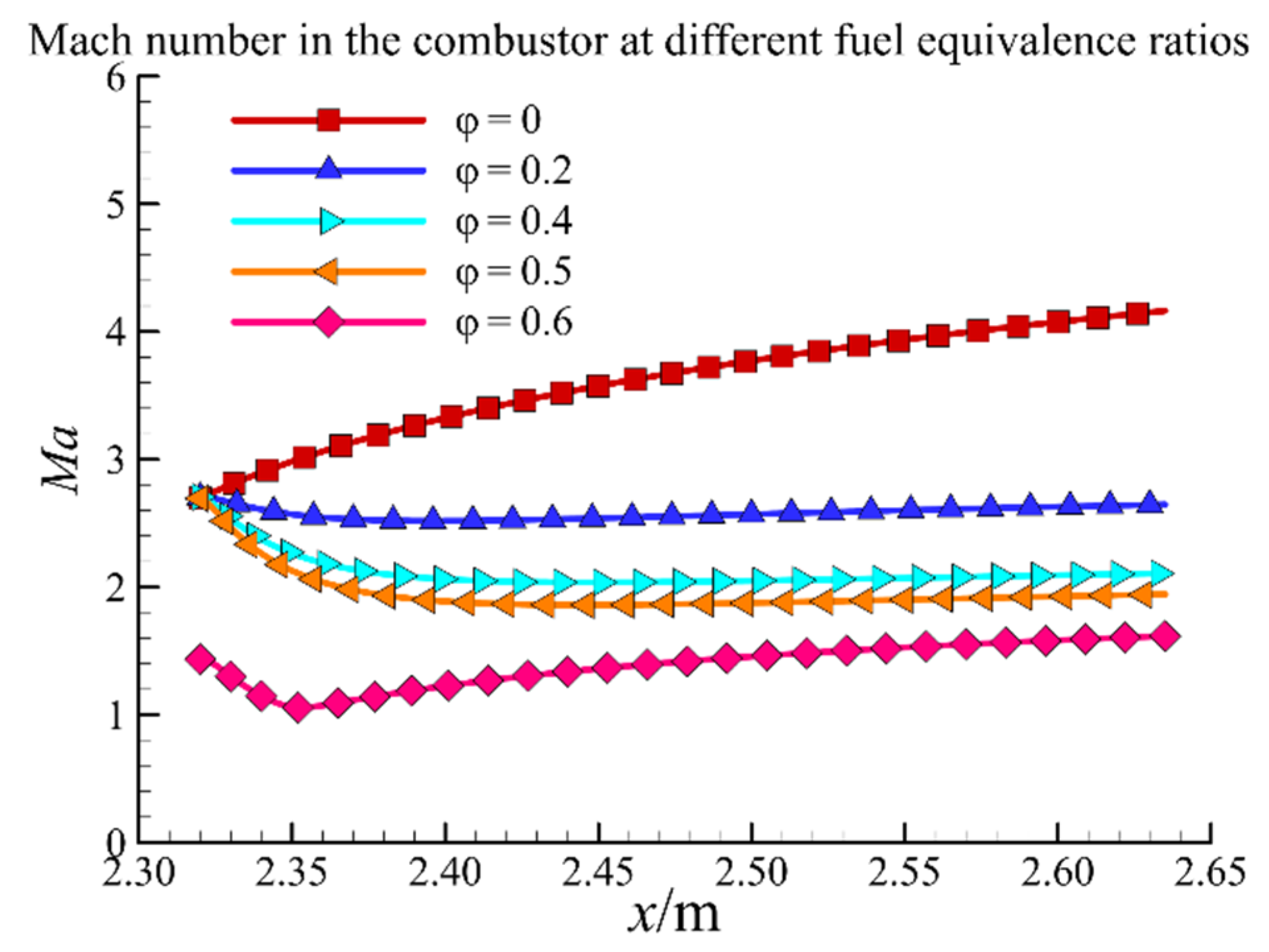
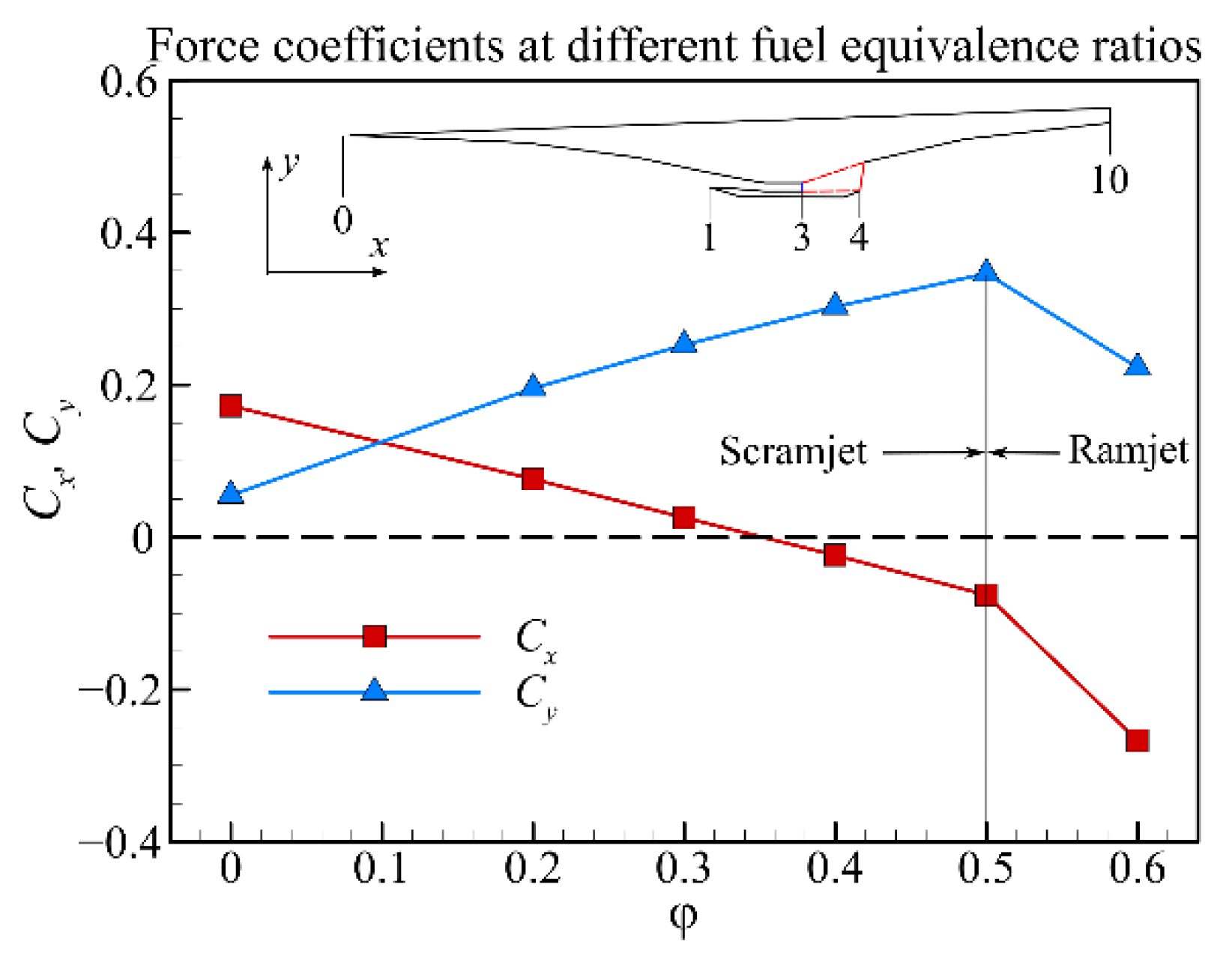
3.1. Design Point
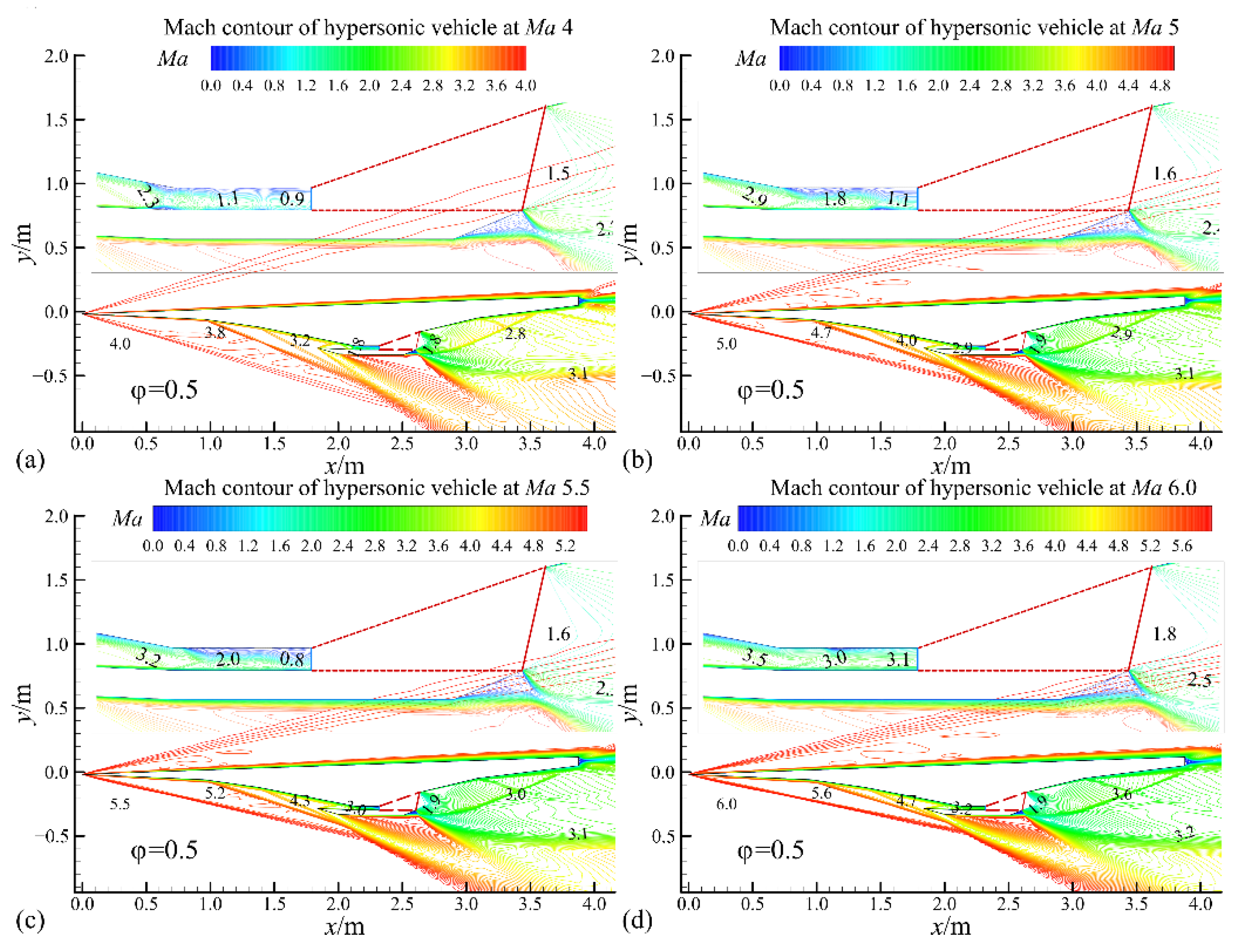
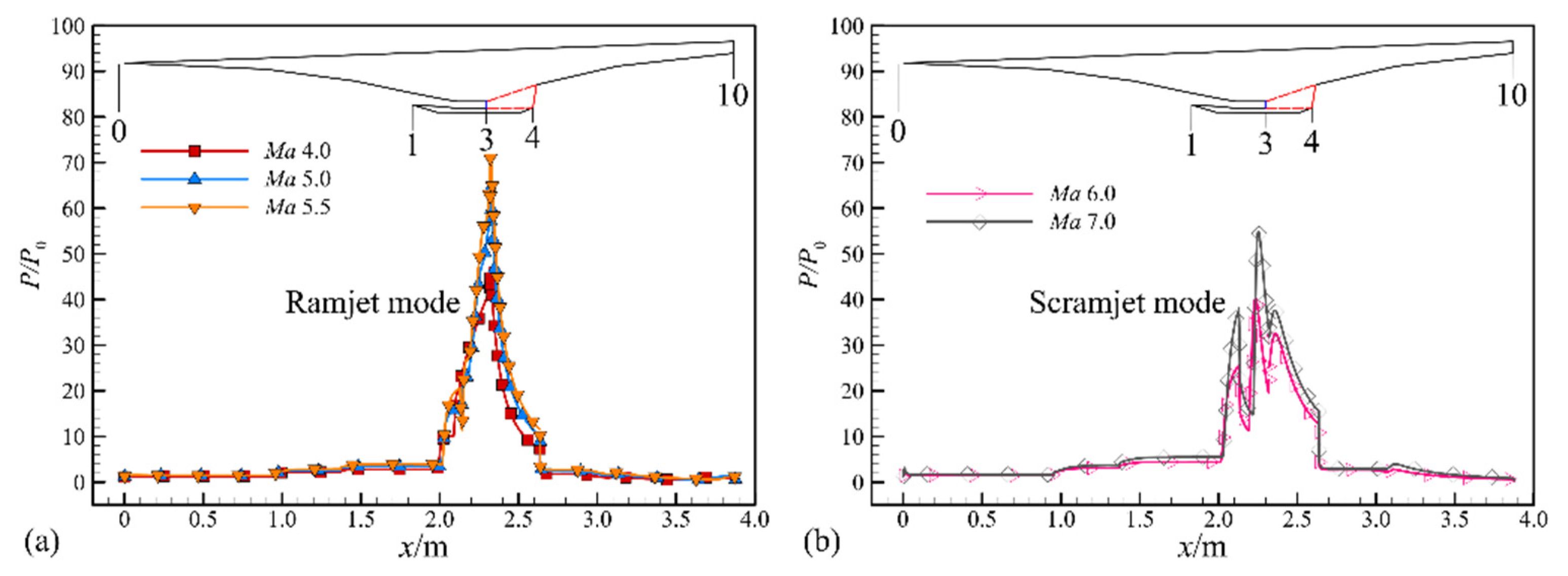
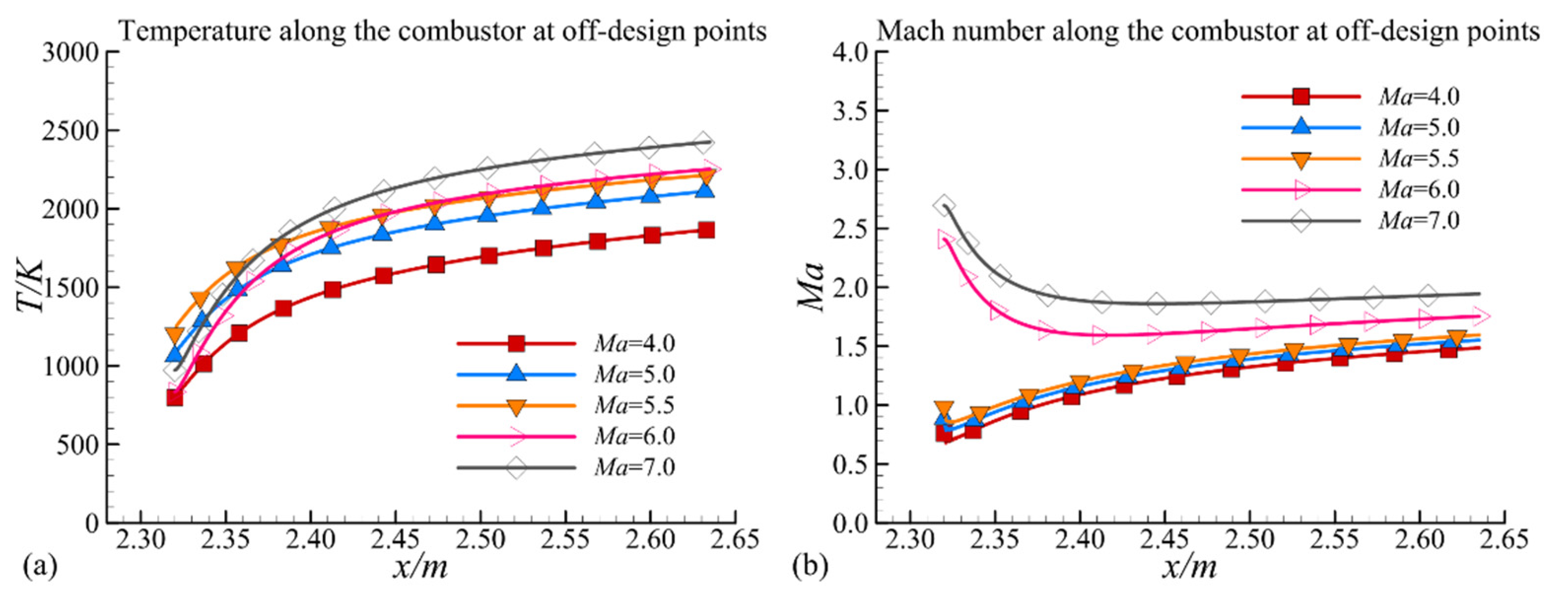
3.2. Off-Design Points
4. Conclusions
- (1)
- A multifidelity simulation method characterized by high-level fidelity numerical analysis of the inlet and nozzle components and low-level fidelity numerical analysis of the combustor was developed based on a user-defined function and a commercial solver. According to the validation with directed connect wind tunnel tests, the static pressure distribution along the flow path is in agreement with experimental data, indicating that this simulation method can be used to study the flow physics of hypersonic propulsion systems at a low cost.
- (2)
- The proposed multifidelity simulation method can be used for integration analysis of external and internal flow physics of hypersonic propulsion systems at design and off-design points. The design point results indicate that the combustor operation condition varies with the fuel equivalence ratio and operates in scramjet mode until φ = 0.60. The horizontal force increases with the fuel equivalence ratio, and thrust balance is achieved at φ = 0.35.
- (3)
- The off-design point results indicate that the combustor operates in ramjet mode from inflow Mach number 4.0 to 5.5 and then switches to scramjet mode. The static pressure, temperature and Mach number distributions along the combustor differ between ramjet and scramjet modes, resulting in net thrust produced by the propulsion system. The net thrust is positive during the whole flight regime between inflow Mach numbers 4 to 7, and the horizontal force coefficient is approximately 0.3 in ramjet mode, then decreasing to 0.1 in scramjet mode.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Walker, B.; Kennedy, K.; Mikkeison, C. US army hypersonic scramjet propelled missile technology program. In Proceedings of the 14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference, Canberra, Australia, 6–9 November 2006. AIAA Paper 2006-7927. [Google Scholar]
- Heiser, W.H.; Pratt, D.T.; Daley, D.; Mehta, U. Hypersonic Airbreathing Propulsion; AIAA Education Series; AIAA: Washington, DC, USA, 1994; pp. 346–370. [Google Scholar]
- Yuan, H.C.; Liu, J.; Zhang, J.S.; Wang, Y. The design and validation of over/under turbine-based combined cycle inlet. Aerosp. Sci. Technol. 2020, 105, 105960. [Google Scholar] [CrossRef]
- Wang, Y.H.; Song, W.Y. Experimental investigation of influence factors on flame holding in a supersonic combustor. Aerosp. Sci. Technol. 2019, 85, 180–186. [Google Scholar] [CrossRef]
- Yu, K.K.; Xu, J.L.; Lv, Z.; Song, G. Inverse design methodology on a single expansion ramp nozzle for scramjets. Aerosp. Sci. Technol. 2019, 92, 9–19. [Google Scholar] [CrossRef]
- Vu, L.N.; Wilson, D. Quasi-one-dimensional scramjet combustor flow solver using the numerical propulsion system simulation. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. AIAA paper 2018-4843. [Google Scholar]
- Cao, R.; Lu, Y.; Yu, D.; Chang, J. Study on influencing factors of combustion mode transition boundary for a scramjet engine based on one-dimensional model. Aerosp. Sci. Technol. 2020, 96, 105590. [Google Scholar] [CrossRef]
- Tian, L.; Chen, L.H.; Chen, Q.; Li, F.; Chang, X.Y. Quasi-one-dimensional multimodes analysis for dual-mode scramjet. J. Propul. Power 2014, 30, 1559–1567. [Google Scholar] [CrossRef]
- Lytle, J. Multi-fidelity simulations of air breathing propulsion systems. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. AIAA paper 2006-4967. [Google Scholar]
- Smart, M.K. Scramjets. Aeronaut. J. 2007, 111, 605–619. [Google Scholar] [CrossRef]
- Shapiro, A.H.; Shapiro, R.E. The Dynamics and Thermodynamics of Compressible Fluid Flow; Wiley: Hoboken, NJ, USA, 1953; Volume 1, pp. 219–238. [Google Scholar]
- Bussing, R.T.A.; Murman, E.M. A one-dimensional unsteady model of dual mode scramjet operation. In Proceedings of the 21st Aerospace Sciences Meeting, Reno, NV, USA, 10–13 January 1983. AIAA paper 83-0422. [Google Scholar]
- Liu, J.H.; Ling, W.H.; Liu, X.Z.; Liu, L.; Zhang, Z. A quasi-one dimensional unsteady numerical analysis of supersonic combustor performance. J. Propul. Technol. 1998, 19, 1–6. (In Chinese) [Google Scholar]
- Wang, L. The Numerical Simulation of the Combustor of Scramjet; Northwestern Polytechnical University: Xi’an, China, 2011. (In Chinese) [Google Scholar]
- Billig, F.S. Research on supersonic combustion. J. Propul. Power 1993, 9, 499–514. [Google Scholar] [CrossRef]
- Jiang, J.; Chu, M.; Xu, X. A quasi-one-dimensional method for prediction of dual mode scramjet combustor performance. J. Propul. Technol. 2013, 34, 802–808. (In Chinese) [Google Scholar]
- Kim, H.; Liou, M.S. Flow simulation of N2B hybrid wing body configuration. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. AIAA paper 2012-0838. [Google Scholar]
- Vijayakumar, N.; Wilson, D.R.; Lu, F.K. Multifidelity simulation of a dual mode scramjet compression system using coupled NPSS and FLUENT codes. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. AIAA paper 2014-3845. [Google Scholar]
- Connolly, B.J.; Krouse, C.; Musgrove, G.O. Implementing a dual-mode scramjet combustor model in NPSS. In Proceedings of the AIAA Propulsion and Energy Forum 2021, Virtual, 9–11 August 2021. AIAA paper 2021-3538. [Google Scholar]
- Riggins, D.; Tackett, R.; Taylor, T. Thermodynamic analysis of dual-mode scramjet engine operation and performance. In Proceedings of the 14th AIAA/AHI International Space Planes and Hypersonics Systems and Technologies Conference, Canberra, Australia, 6–9 November 2006. AIAA paper 2006-8059. [Google Scholar]
- Anderson, J.D. Computational Fluid Dynamics; McGraw-Hill Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 153–155. [Google Scholar]
- Baurle, R.A.; Gafney, R.L. Extraction of one-dimensional flow properties from multidimensional data sets. J. Propul. Power 2008, 24, 704–714. [Google Scholar] [CrossRef]
- Le, D.B.; Goyne, C.P.; Krauss, R.H.; McDaniel, J.C. Experimental study of a dual-mode scramjet isolator. J. Propul. Power 2008, 24, 1050–1057. [Google Scholar] [CrossRef]
- Shi, W.; Chang, J.; Zhang, J.; Ma, J.; Wang, Z.; Bao, W. Numerical investigation on the forced oscillation of shock train in hypersonic inlet with translating cowl. Aerosp. Sci. Technol. 2019, 87, 311–322. [Google Scholar] [CrossRef]
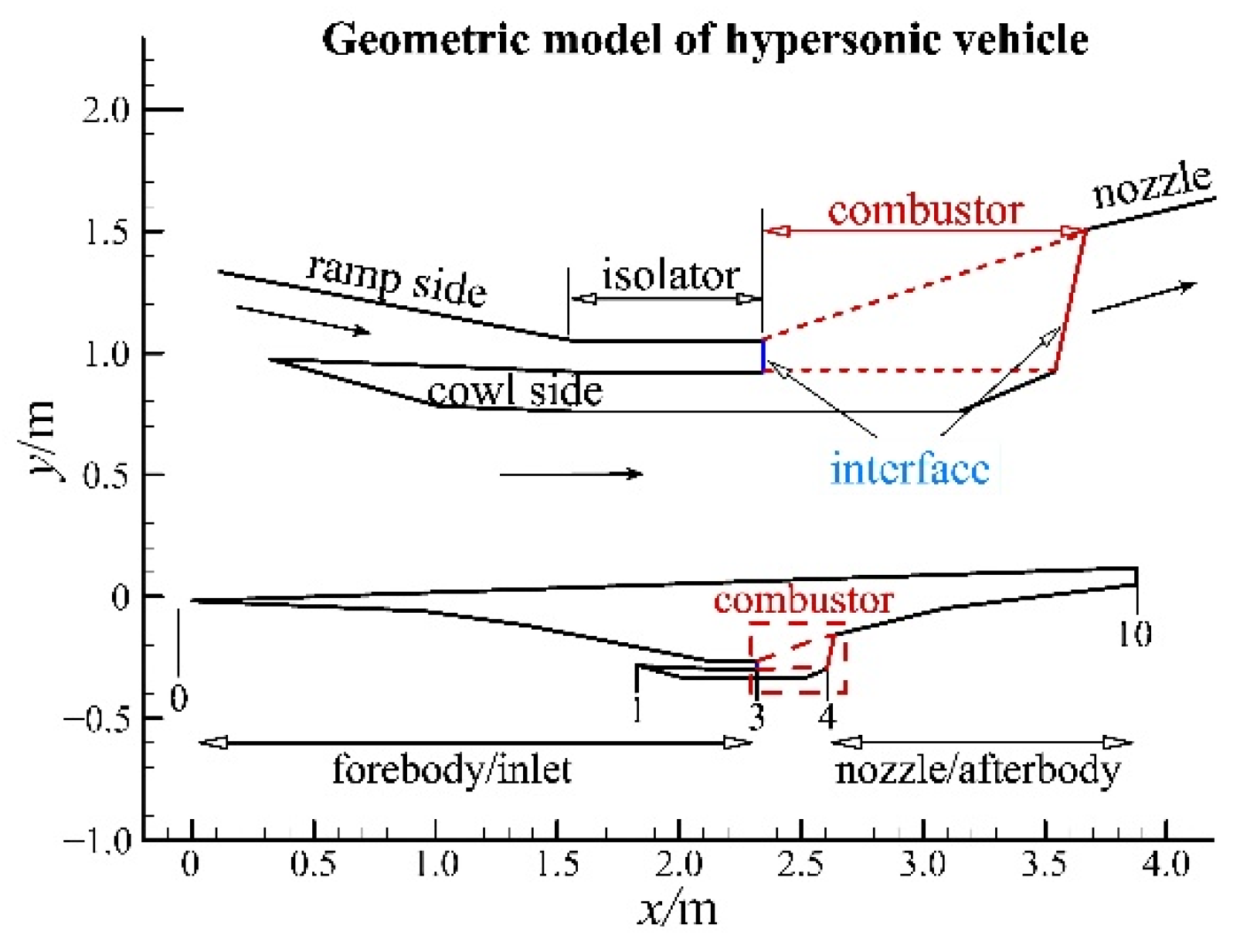

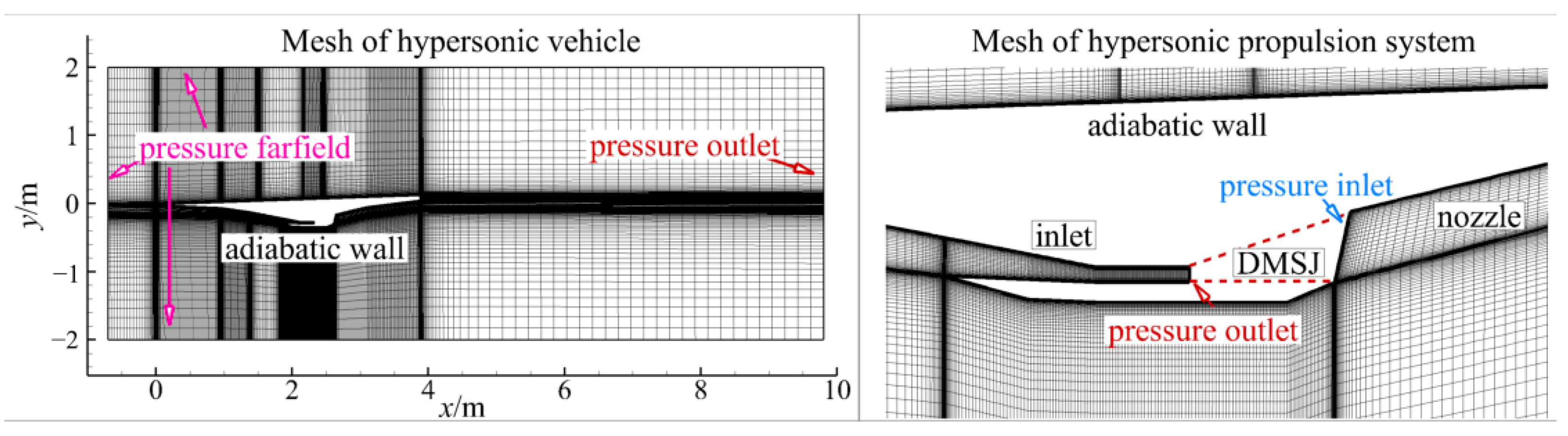
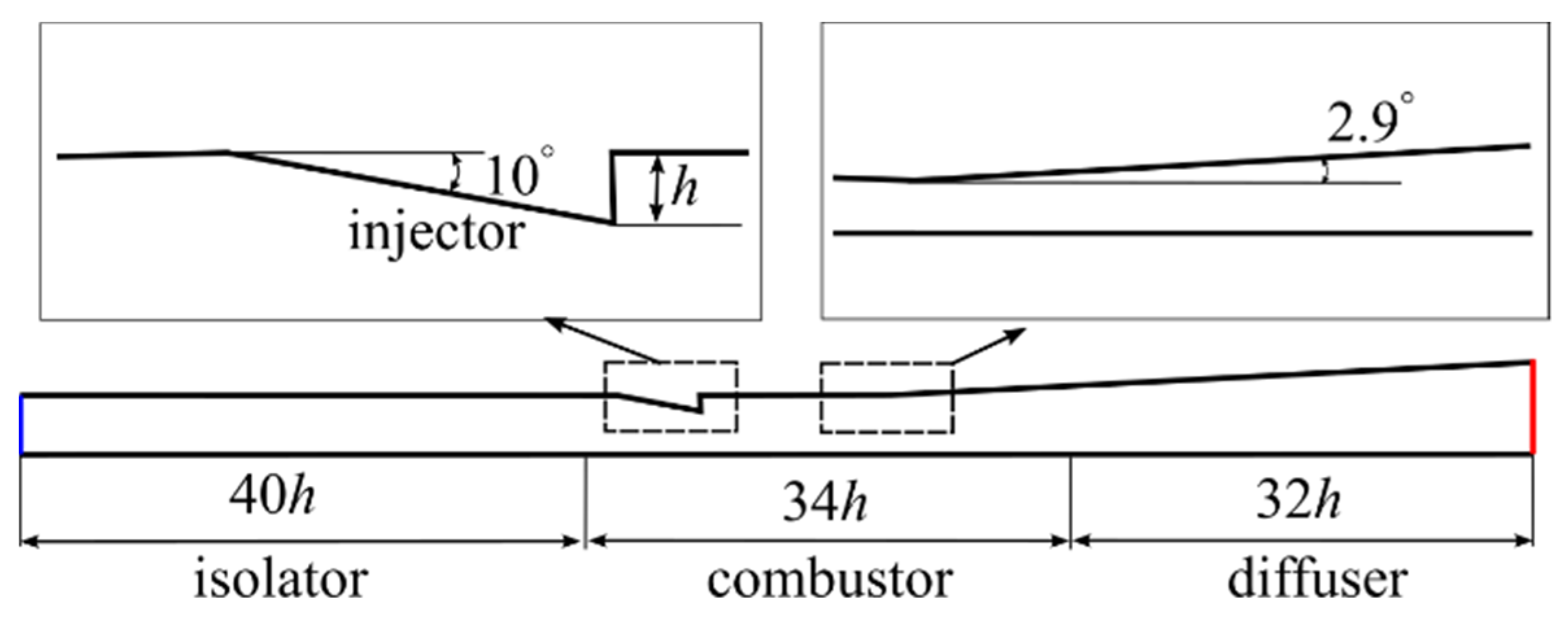
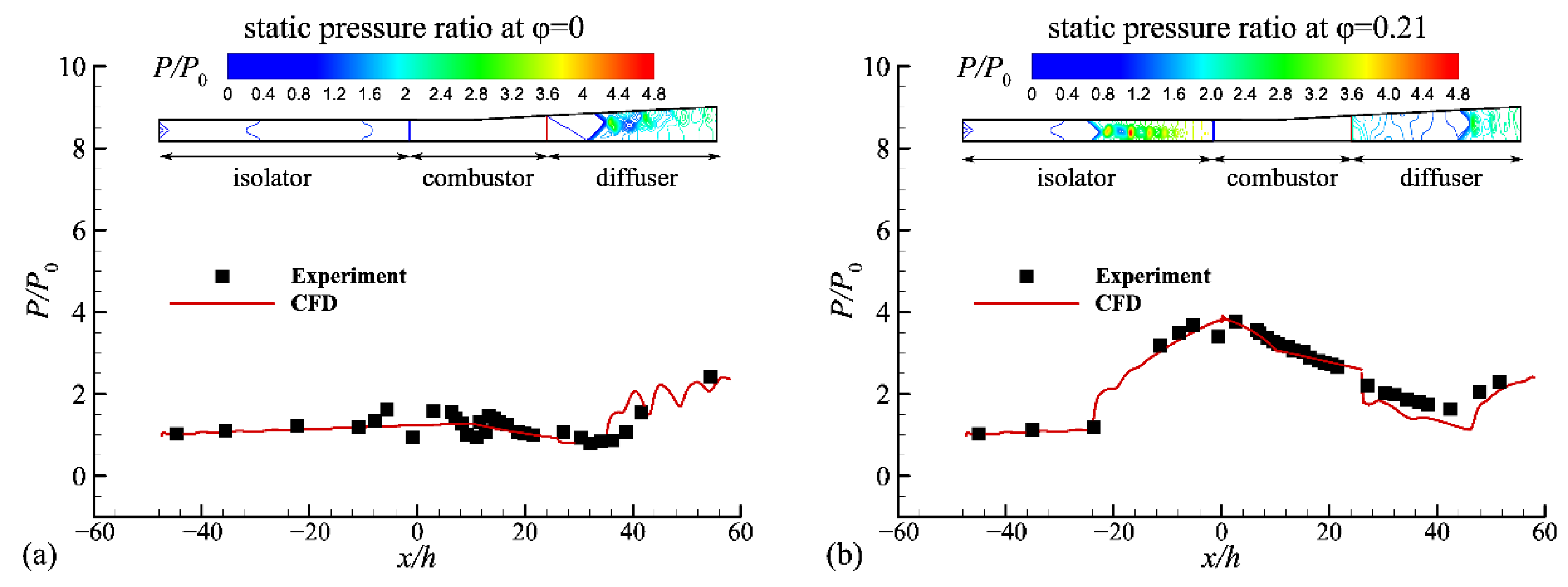




| Property | Value | Property | Value |
|---|---|---|---|
| Inlet length (m) | 2.13 | Capture height(m) | 0.27 |
| Isolator length (m) | 0.187 | Throat height(m) | 0.03 |
| Combustor length (m) | 0.32 | Total contraction ratio | 8.76 |
| Nozzle length (m) | 0.124 | Combustor area ratio | 4.63 |
| Ramp angles | 2.5°, 5.5° and 3° | Nozzle expansion ratio | 2.49 |
| φ | Ma | P (kPa) | T (K) | Pt (kPa) | Tt (K) |
|---|---|---|---|---|---|
| 0 | 1.81 | 49.09 | 617.1 | 298.93 | 1020.0 |
| 0.21 | 0.9871 | 129.75 | 848.75 | 257.62 | 1020.0 |
| φ | Station | Ma | P (kPa) | T (K) | Pt (kPa) | Tt (K) |
|---|---|---|---|---|---|---|
| 0 | 0 | 7.0 | 1.6 | 224.5 | 6736.4 | 2419.4 |
| 3 | 3.12 | 50.9 | 856.2 | 2908.5 | 2419.4 | |
| 4 | 4.16 | 5.40 | 534.2 | 1019.3 | 2382.1 | |
| 10 | 6.09 | 0.60 | 293.4 | 931.5 | 2382.1 | |
| 0.6 | 3 | 1.37 | 233.9 | 1548.9 | 872.5 | 2419.4 |
| 4 | 1.97 | 30.1 | 2022.9 | 223.2 | 3581.2 | |
| 10 | 3.47 | 2.8 | 1058.8 | 202.4 | 3578.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yuan, H.; Zhang, J.; Kuang, Z. A Multifidelity Simulation Method for Internal and External Flow of a Hypersonic Airbreathing Propulsion System. Aerospace 2022, 9, 685. https://doi.org/10.3390/aerospace9110685
Liu J, Yuan H, Zhang J, Kuang Z. A Multifidelity Simulation Method for Internal and External Flow of a Hypersonic Airbreathing Propulsion System. Aerospace. 2022; 9(11):685. https://doi.org/10.3390/aerospace9110685
Chicago/Turabian StyleLiu, Jun, Huacheng Yuan, Jinsheng Zhang, and Zheng Kuang. 2022. "A Multifidelity Simulation Method for Internal and External Flow of a Hypersonic Airbreathing Propulsion System" Aerospace 9, no. 11: 685. https://doi.org/10.3390/aerospace9110685
APA StyleLiu, J., Yuan, H., Zhang, J., & Kuang, Z. (2022). A Multifidelity Simulation Method for Internal and External Flow of a Hypersonic Airbreathing Propulsion System. Aerospace, 9(11), 685. https://doi.org/10.3390/aerospace9110685





