Experimental and Numerical Investigations on the Mixing Process of Supercritical Jet Injected into a Supersonic Crossflow
Abstract
1. Introduction
2. Experimental Setup and Method
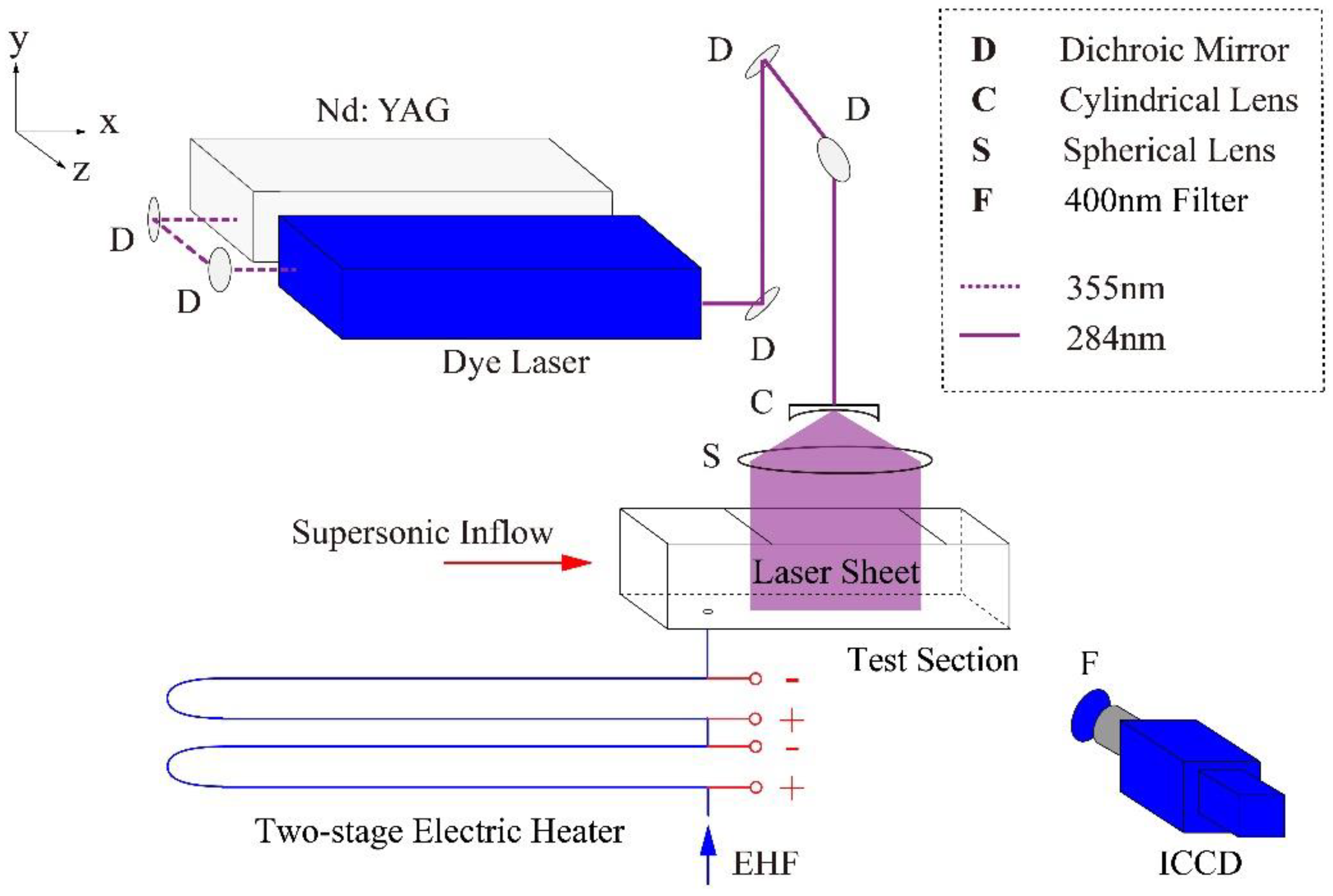
2.1. Experimental Facilities
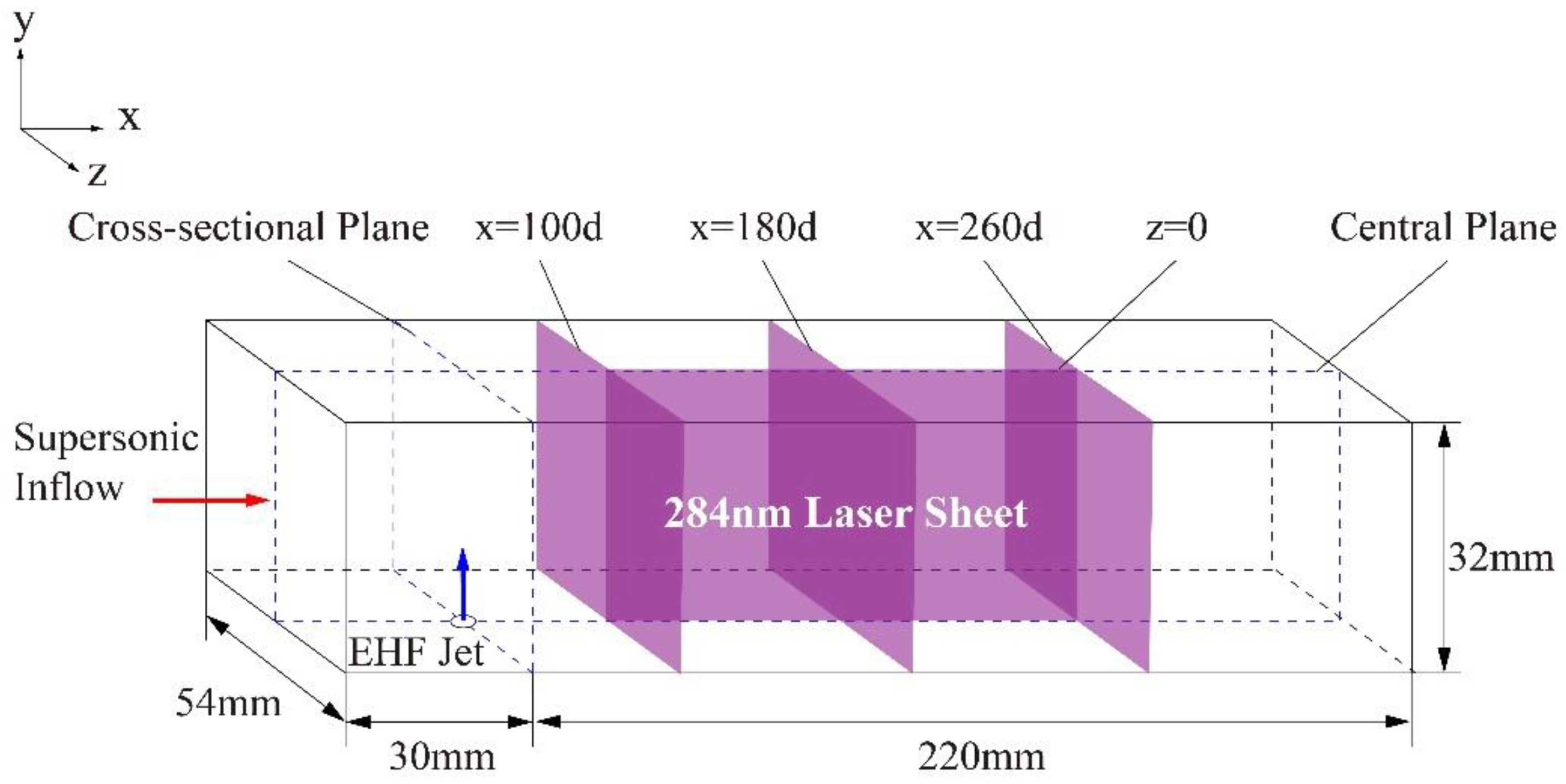
2.2. Optical Diagnostic System
2.3. Experimental Conditions
3. Numerical Methods
3.1. Mixture Model
3.2. Real Gas Model
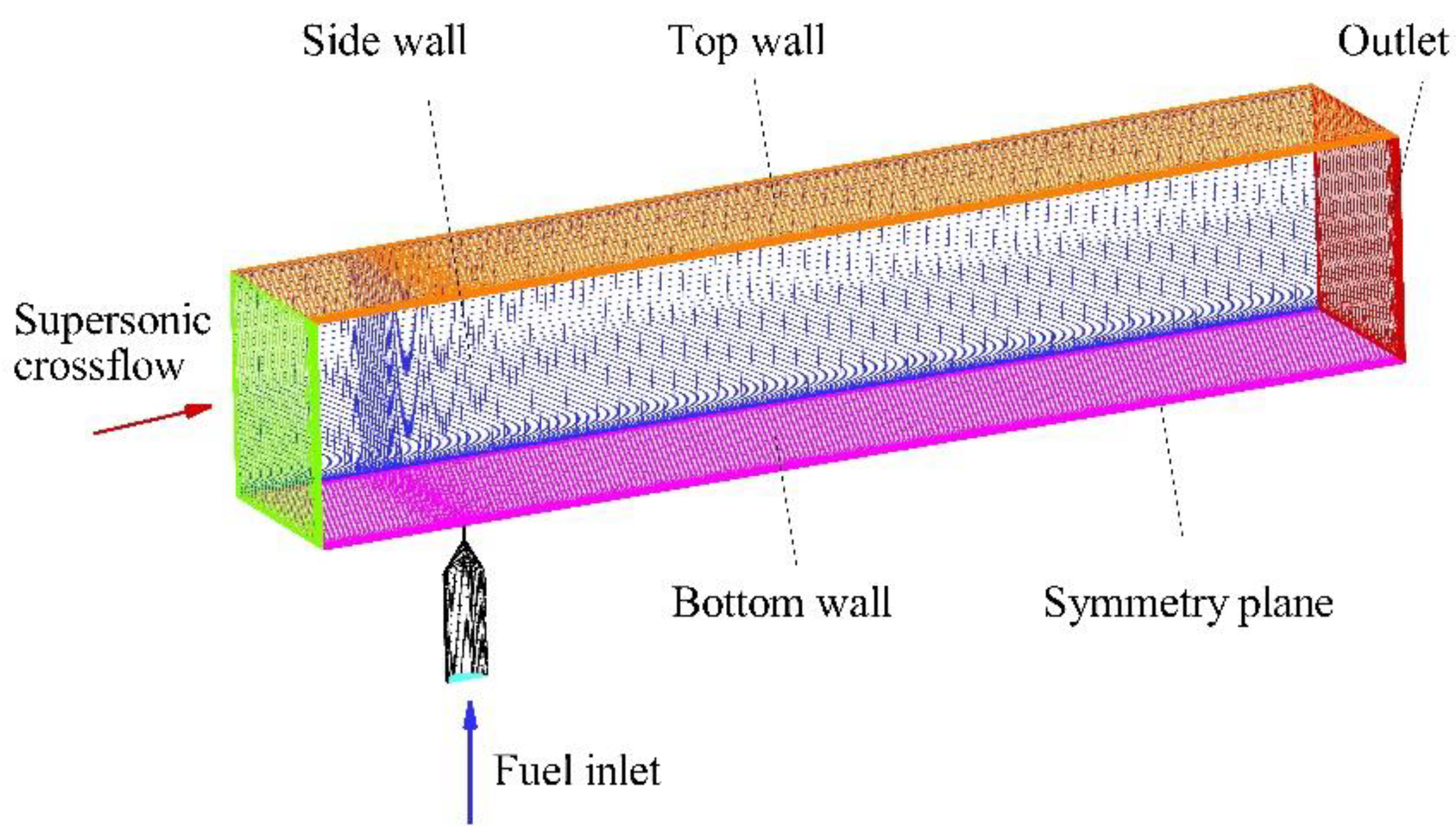
3.3. Simulation Settings
4. Results and Discussion
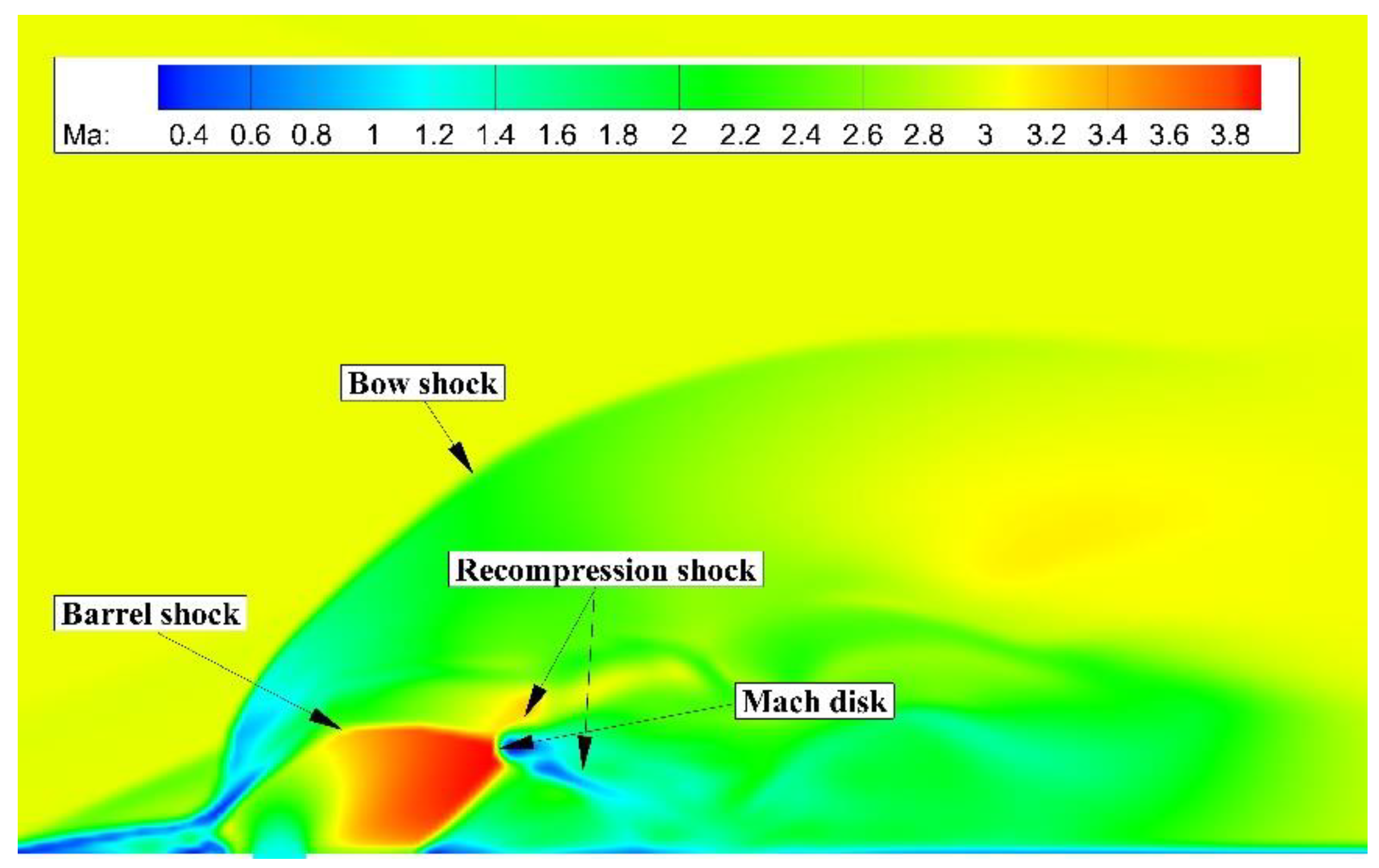
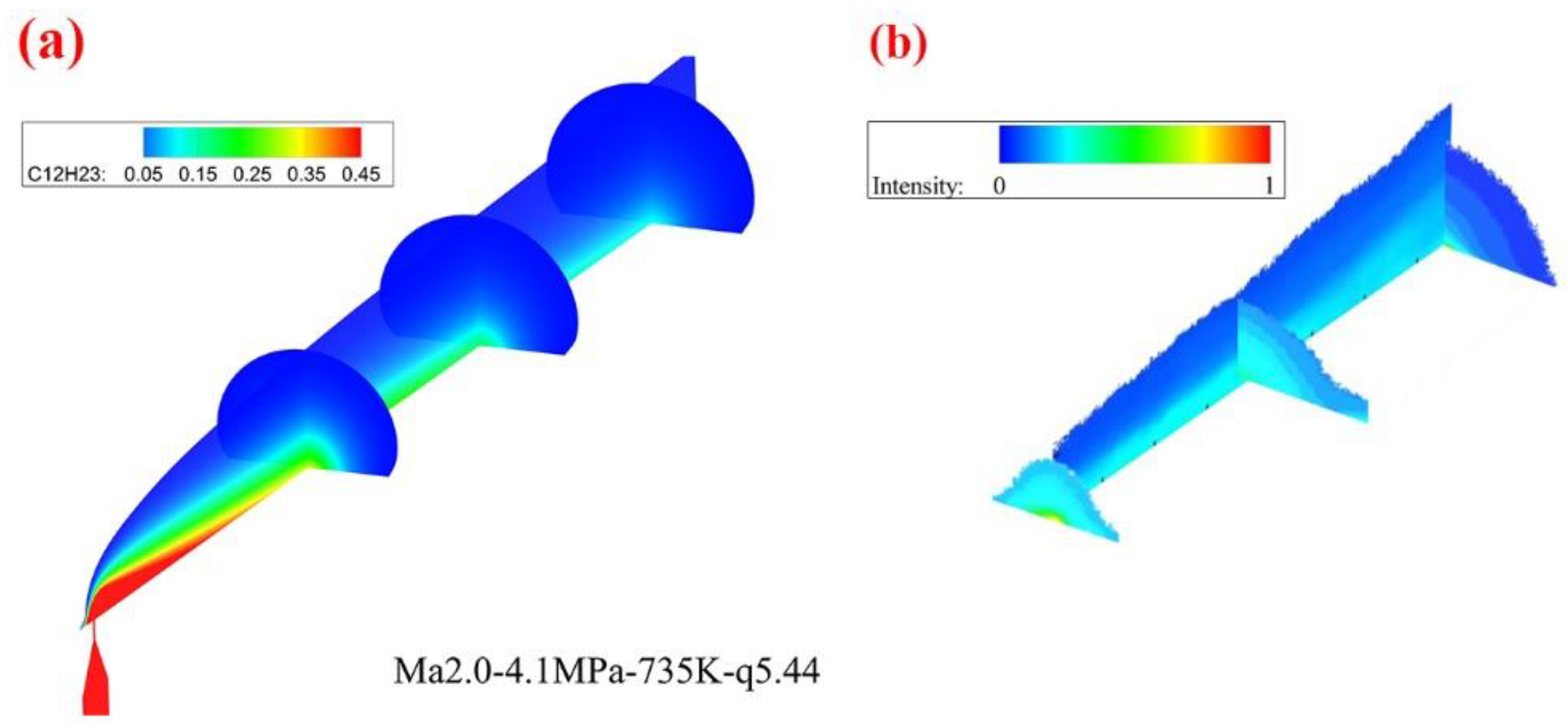
4.1. Flow Structure
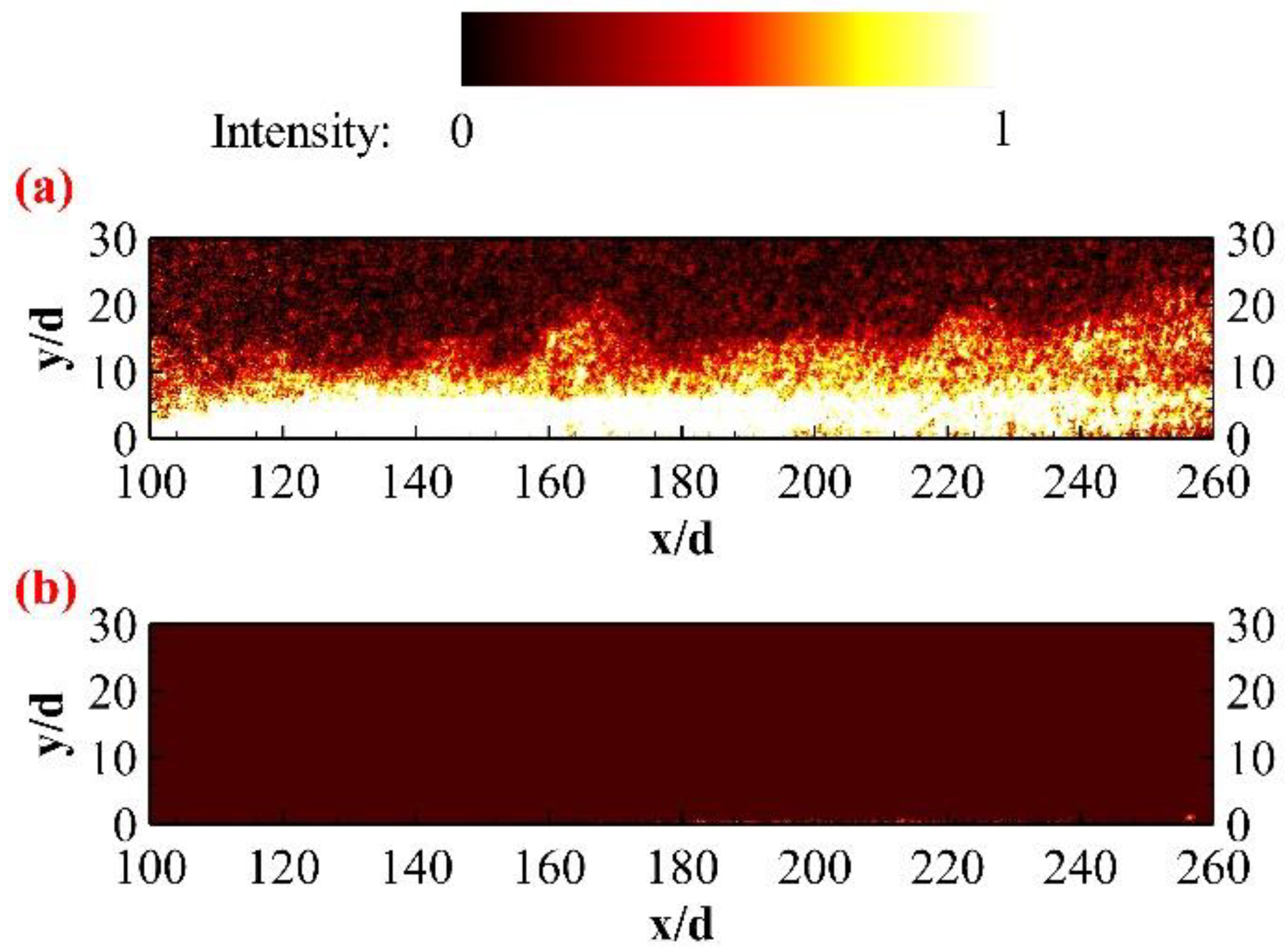
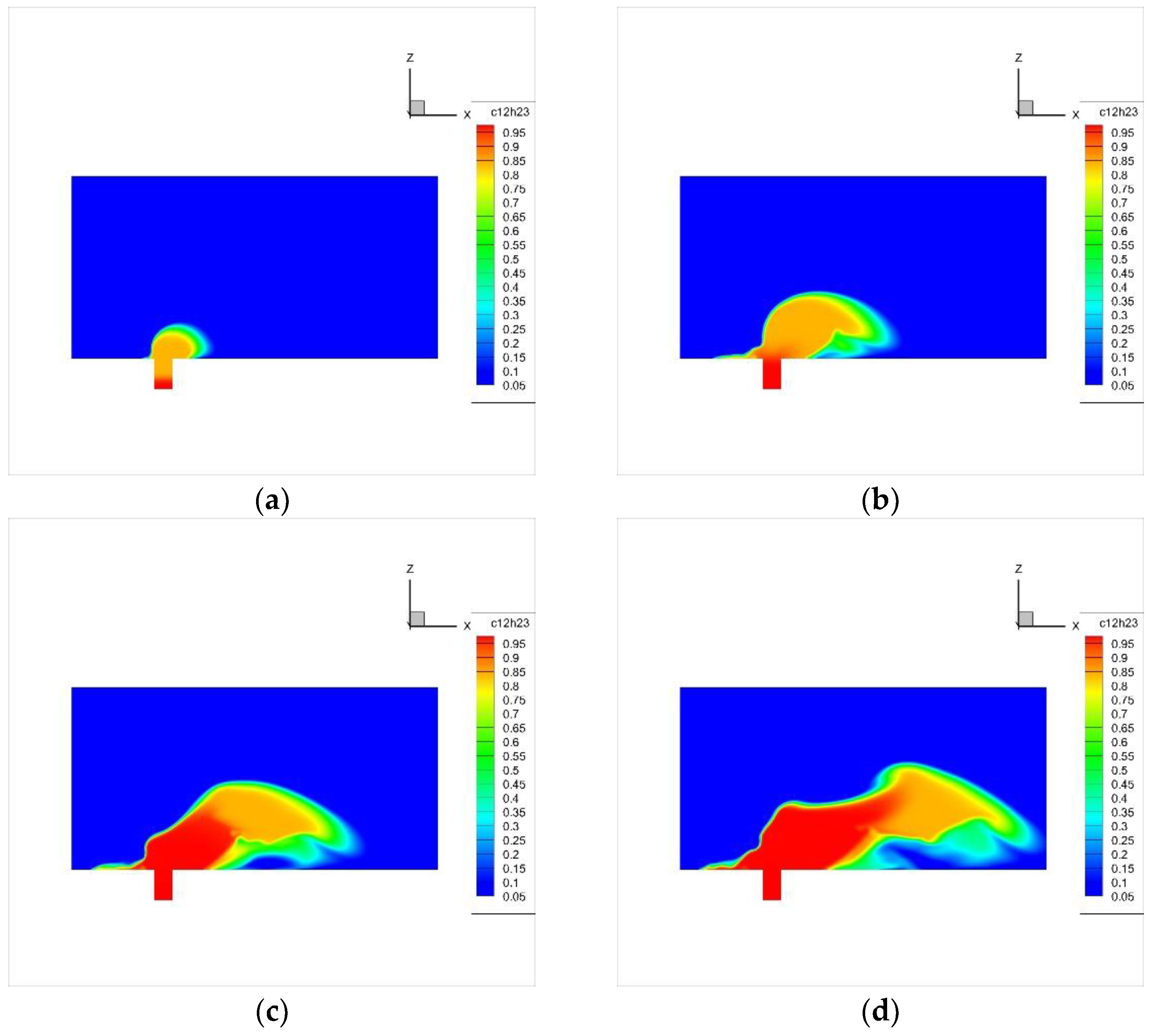
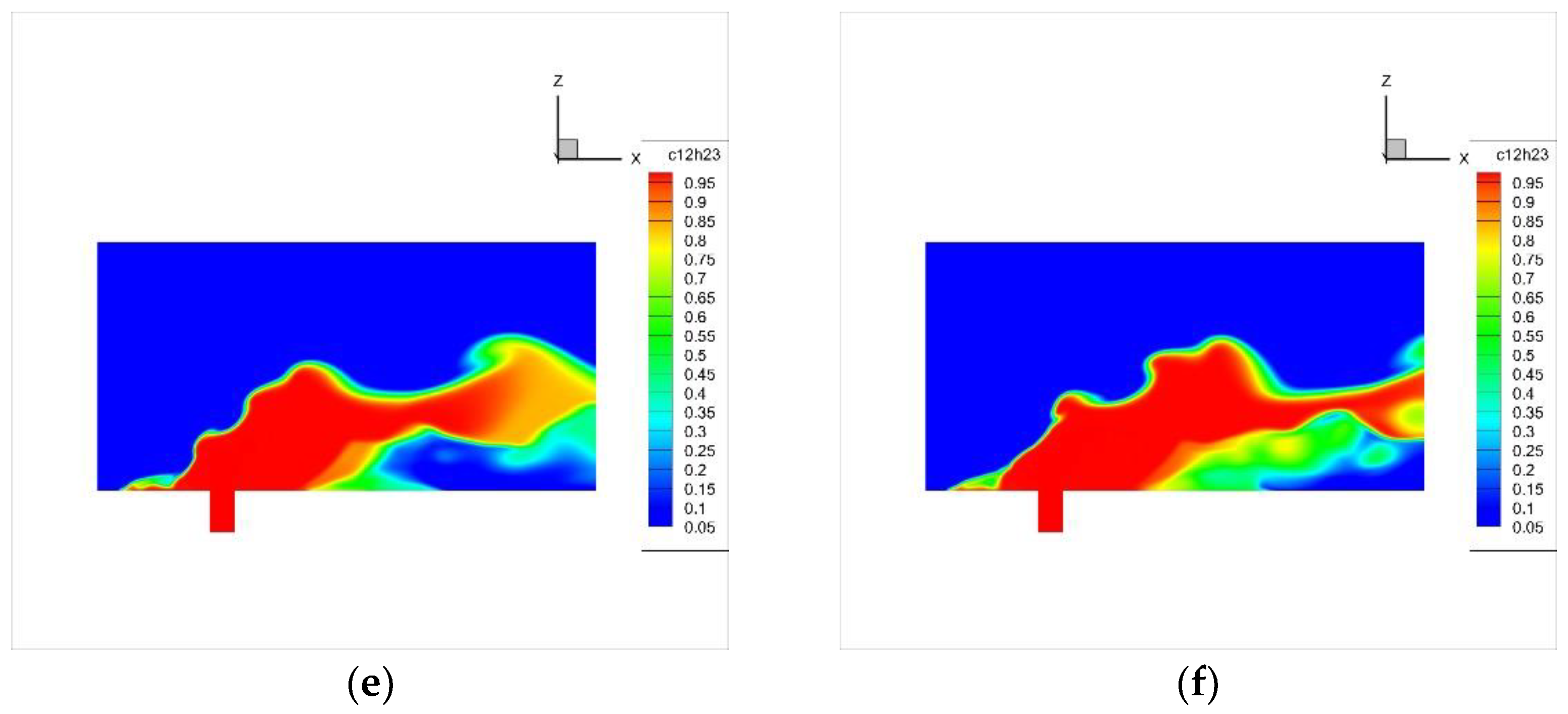
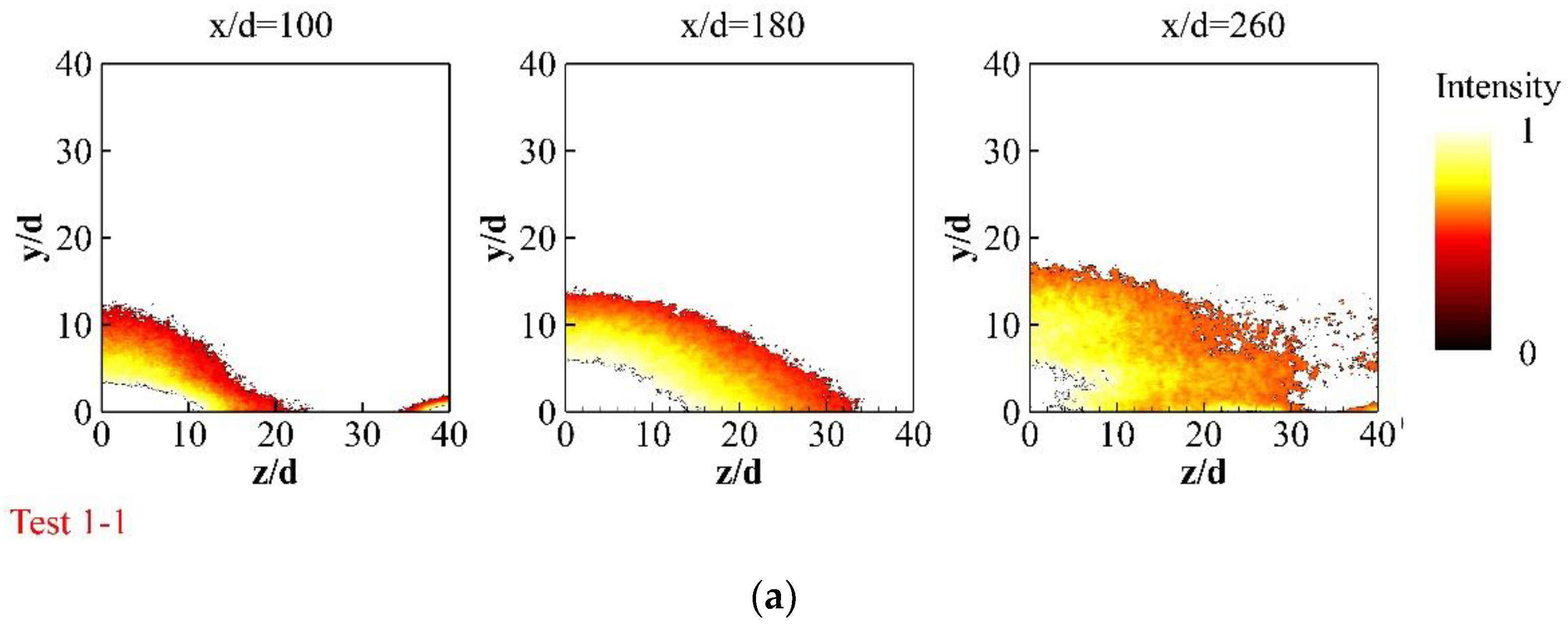
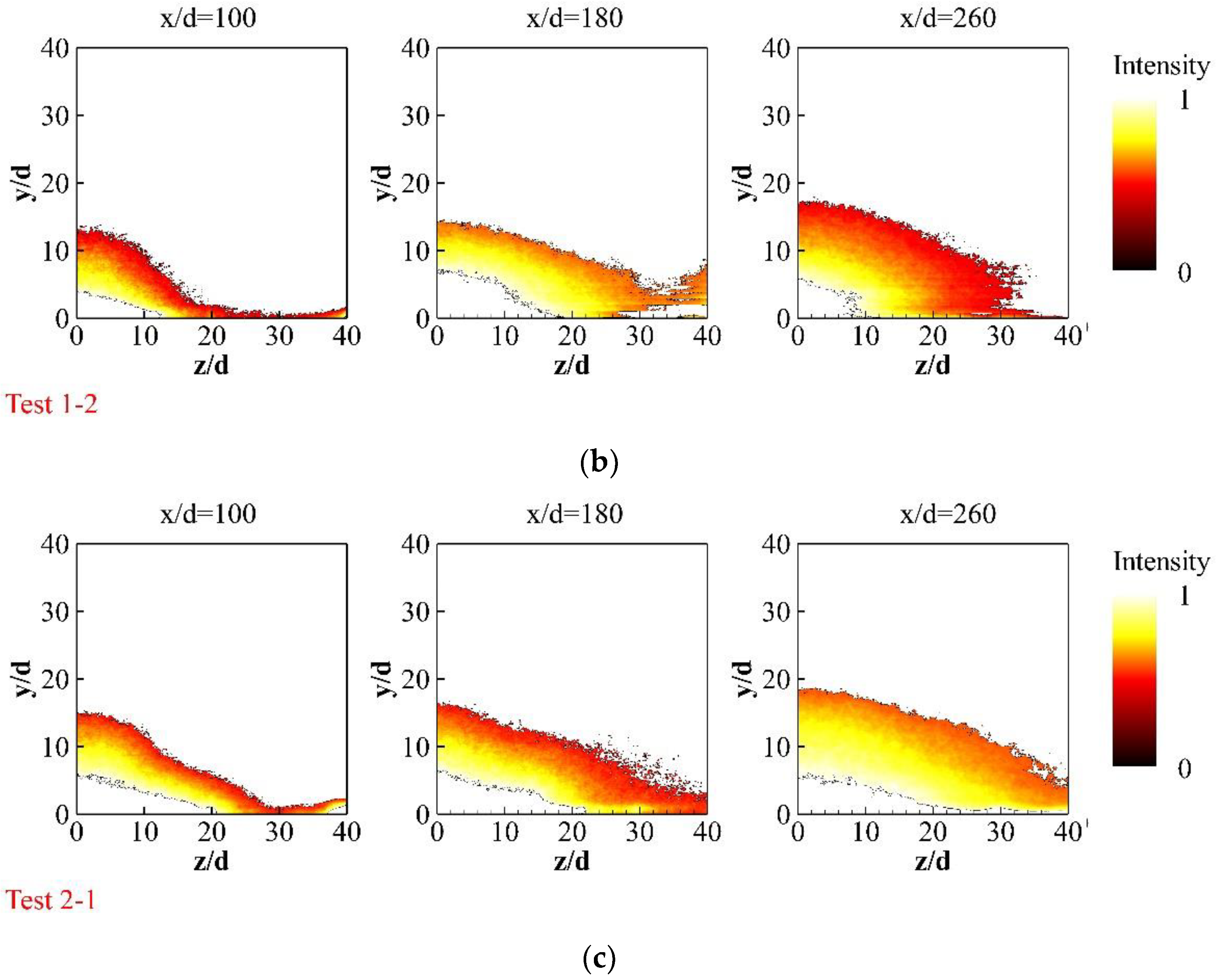
4.2. Spatial Distribution
4.3. Mixing Characteristics
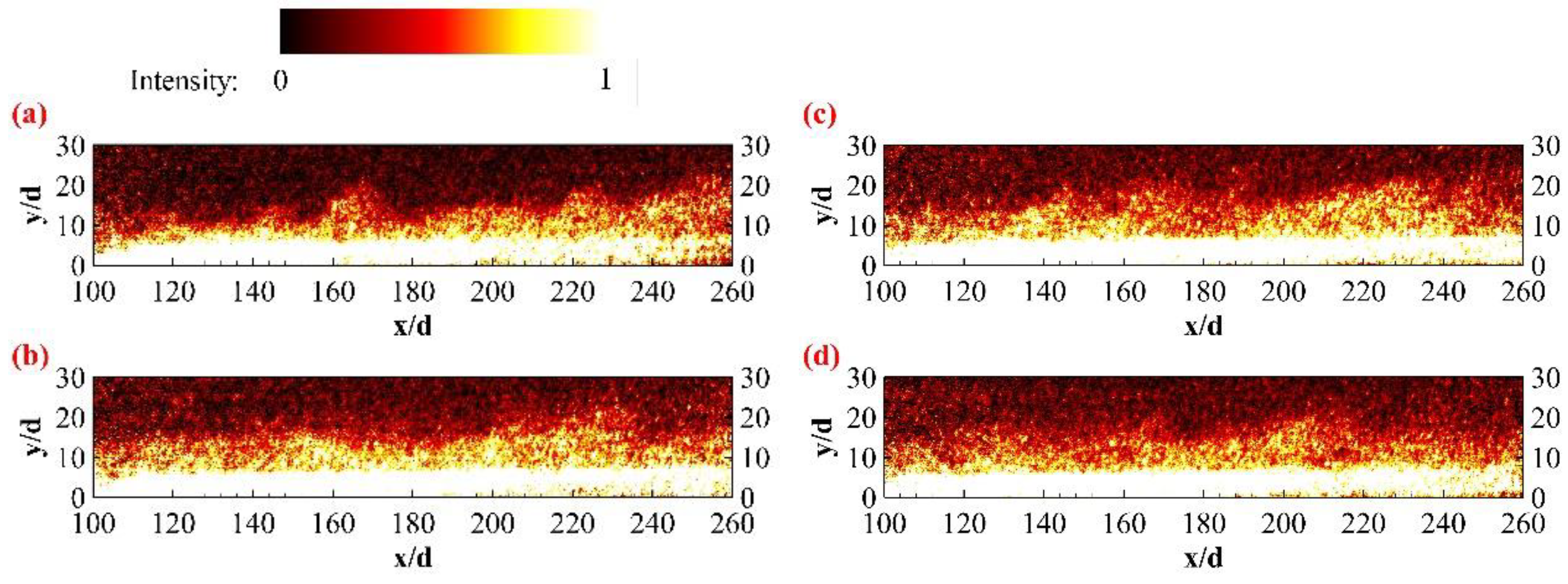
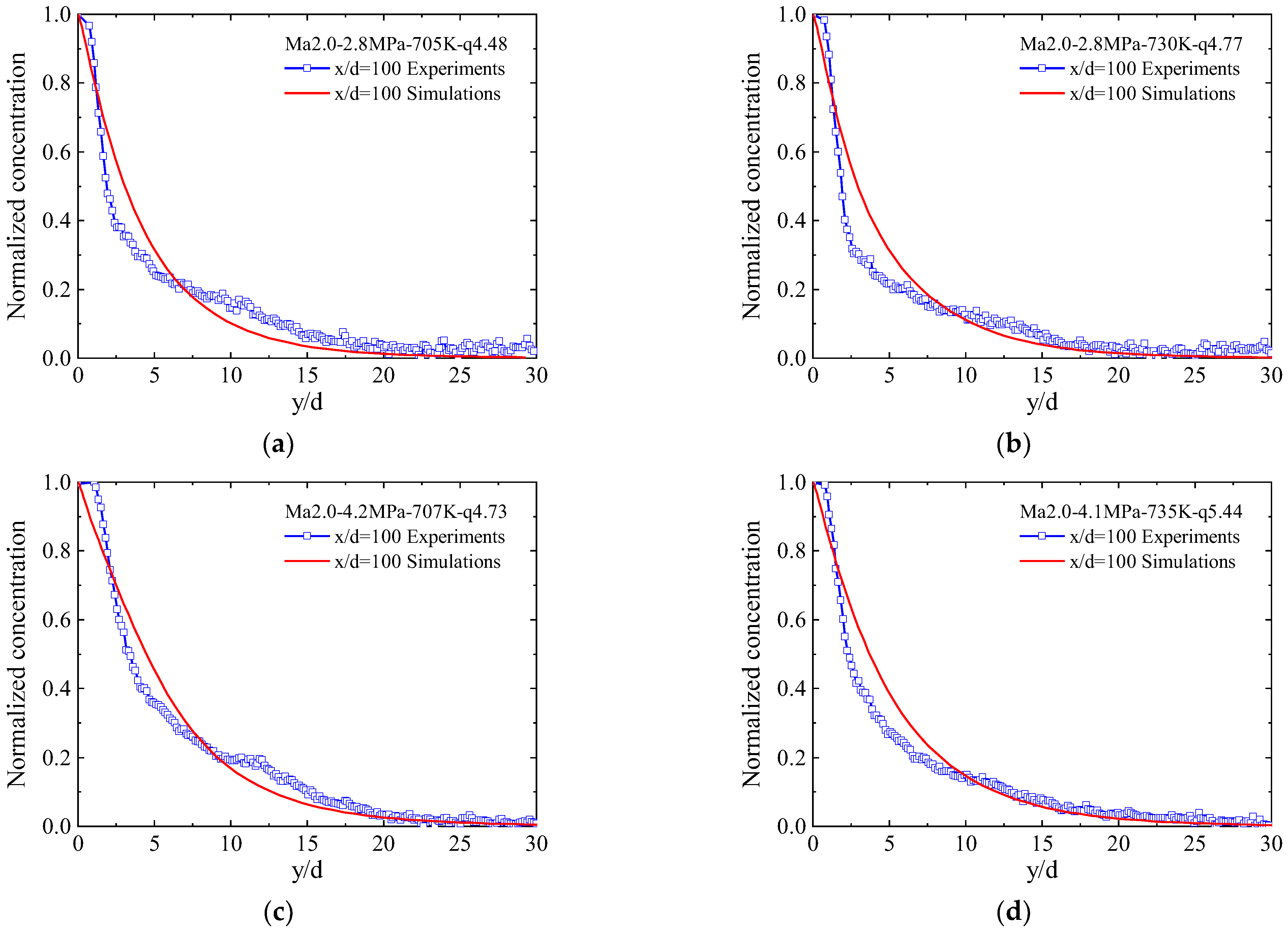
4.3.1. Concentration Distribution
4.3.2. Mixing Efficiency
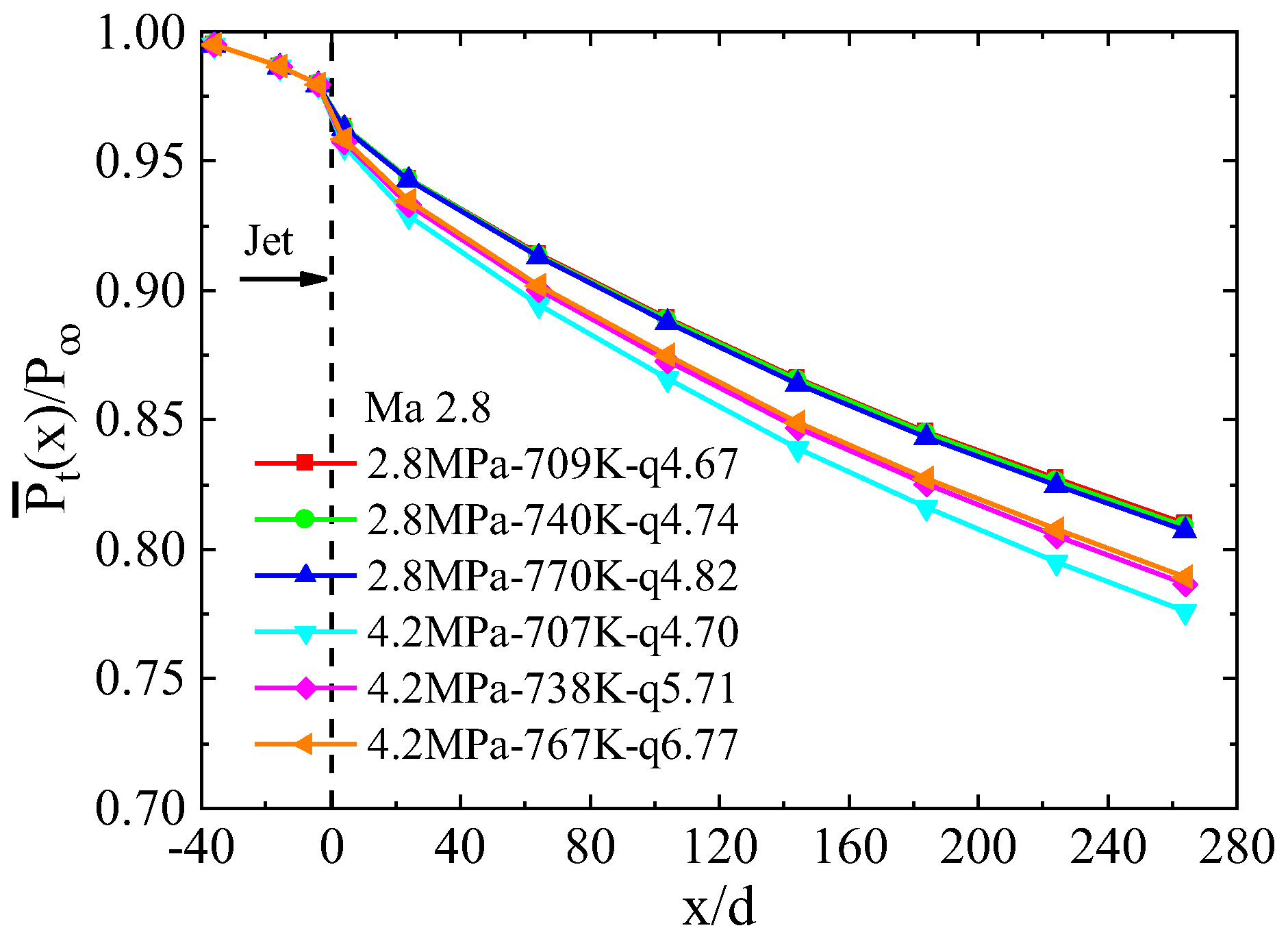
4.3.3. Total Pressure Loss
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | sound speed in the gas: m/s | u | velocity, m/s |
| d | injection orifice diameter, mm | volume fraction | |
| Ma | Mach number | x | mole fraction |
| P | pressure, Pa | ρ | density, kg/m3 |
| q | jet-to-air momentum flux ratio | μ | viscosity, mPa·s |
| T | temperature, K |
References
- Smart, M.K. Scramjets. Aeronaut. J. 2007, 111, 605–619. [Google Scholar] [CrossRef]
- Urzay, J. Supersonic combustion in air-breathing propulsion systems for hypersonic flight. Annu. Rev. Fluid Mech. 2018, 50, 593–627. [Google Scholar] [CrossRef]
- Edwards, T. Aviation fuel development-past highlights and future prospects. In Proceedings of the AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayton, OH, USA, 14–17 July 2003; p. 2611. [Google Scholar] [CrossRef]
- Li, Y.; Xie, G.; Sunden, B. Flow and thermal performance of supercritical n-decane in double-layer channels for regenerative cooling of a scramjet combustor. Appl. Therm. Eng. 2020, 180, 115695. [Google Scholar] [CrossRef]
- Feng, Y.; Qin, J.; Bao, W.; Yang, Q.; Huang, H.; Wang, Z. Numerical analysis of convective heat transfer characteristics of supercritical hydrocarbon fuel in cooling panel with local flow blockage structure. J. Supercrit. Fluids 2014, 88, 8–16. [Google Scholar] [CrossRef]
- Li, H.; Qin, J.; Bao, W.; Huang, H. Performance improvement of gaseous hydrocarbon fuel driven thermal power generation systems for hypersonic vehicles. Energy Convers. Manag. 2019, 199, 111949. [Google Scholar] [CrossRef]
- Wu, X.; Yang, J.; Zhang, H.; Shen, C. System design and analysis of hydrocarbon scramjet with regeneration cooling and expansion cycle. J. Therm. Sci. 2015, 24, 350–355. [Google Scholar] [CrossRef]
- Gascoin, N.; Abraham, G.; Gillard, P. Synthetic and jet fuels pyrolysis for cooling and combustion applications. J. Anal. Appl. Pyrol. 2010, 89, 294–306. [Google Scholar] [CrossRef]
- Vincent-Randonnier, A.; Rouxel, B.; Roux, P.; Poirot, M.; Sicard, M.; Raepsaet, B.; Ser, F. Experimental investigations on the self-ignition of a thermally decomposed endothermic fuel in hot supersonic air flow in the MPP-LAERTE combustion test bench. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008. [Google Scholar] [CrossRef]
- Li, X.; Liu, W.; Pan, Y.; Yang, L.; An, B.; Zhu, J. Characterization of ignition transient processes in kerosene-fueled model scramjet engine by dual-pulse laser-induced plasma. Acta Astronaut. 2018, 144, 23–29. [Google Scholar] [CrossRef]
- Zhang, J.; Chang, J.; Ma, J.; Wang, Y.; Bao, W. Investigations on flame liftoff characteristics in liquid-kerosene fueled supersonic combustor equipped with thin strut. Aero. Sci. Technol. 2019, 84, 686–697. [Google Scholar] [CrossRef]
- Tian, Y.; Yang, S.; Le, J. Study on flame stabilization of a hydrogen and kerosene fueled combustor. Aero. Sci. Technol. 2016, 59, 183–188. [Google Scholar] [CrossRef]
- Wu, L.Y.; Wang, Z.-G.; Li, Q.; Zhang, J. Investigations on the droplet distributions in the atomization of kerosene jets in supersonic crossflows. Appl. Phys. Lett. 2015, 107, 104103. [Google Scholar] [CrossRef]
- Thomas, R.H.; Schetz, J.A. Distributions across the plume of transverse liquid and slurry jets in supersonic airflow. AIAA J. 1985, 23, 1892–1901. [Google Scholar] [CrossRef][Green Version]
- Su, Y.-H.; Yuan, H.F.; Su, Y.-P. Liquid-fuel injection into supersonic cross flow. Combust. Sci. Technol. 2020, 192, 1436–1447. [Google Scholar] [CrossRef]
- Wei, X.; Li, L.; Zhao, Z.; Bo, T.; Bian, X.; Zuo, Y. The droplet size and penetration height of a kerosene jet in a crossflow. At. Sprays 2020, 30, 495–515. [Google Scholar] [CrossRef]
- Pan, Y.; Dai, J.; Bao, H. Effect of scramjet combustor configuration on the distribution of transverse injection kerosene. J. Mech. Sci. Technol. 2014, 28, 4997–5002. [Google Scholar] [CrossRef]
- Balasubramanyam, M.S.; Chen, C.P. Modeling liquid jet breakup in high speed cross-flow with finite-conductivity evaporation. Int. J. Heat Mass Transf. 2008, 51, 3896–3905. [Google Scholar] [CrossRef]
- Yuan, T.; Su, Y.H.; Lin, Y.T. The mixing of the spray in Mach 2 high enthalpy cross flow. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar] [CrossRef]
- Yang, K.; Li, C.-Y.; Pan, Y.; Wang, Z.-G.; Liu, C.-Y.; Wang, N. Investigation of the evaporation characteristics of a transverse vaporized kerosene jet in supersonic flow. Acta Astronaut. 2021, 185, 257–263. [Google Scholar] [CrossRef]
- Sun, M.-B.; Zhong, Z.; Liang, J.-H.; Wang, Z.-G. Experimental investigation of a supersonic model combustor with distributed injection of supercritical kerosene. J. Propuls. Power 2014, 30, 1537–1542. [Google Scholar] [CrossRef]
- Sun, M.-B.; Zhong, Z.; Liang, J.-H.; Wang, H.-B. Experimental investigation on combustion performance of cavity-strut injection of supercritical kerosene in supersonic model combustor. Acta Astronaut. 2016, 127, 112–119. [Google Scholar] [CrossRef]
- Fan, X.; Yu, G.; Li, J.; Zhang, X.; Sung, C.-J. Investigation of vaporized kerosene injection and combustion in a supersonic model combustor. J. Propul. Power 2006, 22, 103–110. [Google Scholar] [CrossRef]
- Lee, J.; Lin, K.-C.; Eklund, D. Challenges in fuel injection for high-speed propulsion systems. AIAA J. 2015, 53, 1405–1423. [Google Scholar] [CrossRef]
- Wegener, A.; Laser-Junga, H. Photography of the anterior eye segment according to Scheimpflug's principle: Options and limitations-a review. Clin. Exp. Ophthalmol. 2009, 37, 144–154. [Google Scholar] [CrossRef] [PubMed]
- Elbaz, A.M.; Roberts, W.L. Experimental study of the inverse diffusion flame using high repetition rate OH/acetone PLIF and PIV. Fuel 2016, 165, 447–461. [Google Scholar] [CrossRef]
- Thurber, M.C.; Hanson, R.K. Simultaneous imaging of temperature and mole fraction using acetone planar laser-induced fluorescence. Exp. Fluids 2001, 30, 93–101. [Google Scholar] [CrossRef]
- Koch, J.D.; Gronki, J.; Hanson, R.K. Measurements of near-UV Absorption Spectra of Acetone and 3-Pentanone at High Temperatures. J. Quant. Spectrosc. Rad. Trans. 2008, 109, 2037–2044. [Google Scholar] [CrossRef]
- Huber, M.L. NIST Standard Reference Database 4-NIST Thermophysical Properties of Hydrocarbon Mixtures Database; National Institute of Standards and Technology Standard Reference Data Program: Gaithersburg, MD, USA, 2007. [Google Scholar]
- Aungier, R.H. A Fast, Accurate Real Gas Equation of State for Fluid Dynamic Analysis Applications. J. Fluids Eng. 1995, 117, 277–281. [Google Scholar] [CrossRef]
- Gao, W.; Liang, H.-S.; Xu, Q.-H.; Lin, Y.-Z.; Sung, C.-J. Injection of supercritical aviation kerosene fuel into quiescent atmospheric environment. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009. [Google Scholar] [CrossRef]
- Gao, W.; Lin, Y.; Hui, X.; Zhang, C.; Xu, Q. Injection characteristics of near critical and supercritical kerosene into quiescent atmospheric environment. Fuel 2019, 235, 775–781. [Google Scholar] [CrossRef]
- Li, P.; Wang, Z.; Bai, X.-S.; Wang, H.; Sun, M.; Wu, L.; Liu, C. Three-dimensional flow structures and droplet-gas mixing process of a liquid jet in supersonic crossflow. Aero. Sci. Technol. 2019, 90, 140–156. [Google Scholar] [CrossRef]
- Mao, M.; Riggins, D.W.; Mcclinton, C.R. Numerical simulation of transverse fuel injection. In Proceedings of the Computational Fluid Dynamics Symposium on Aeropropulsion, Cleveland, OH, USA, 24–26 April 1990. [Google Scholar]
- Gao, Z.; Lee, C. Numerical research on mixing characteristics of different injection schemes for supersonic transverse jet. Sci. China Technol. Sci. 2011, 54, 883–893. [Google Scholar] [CrossRef]




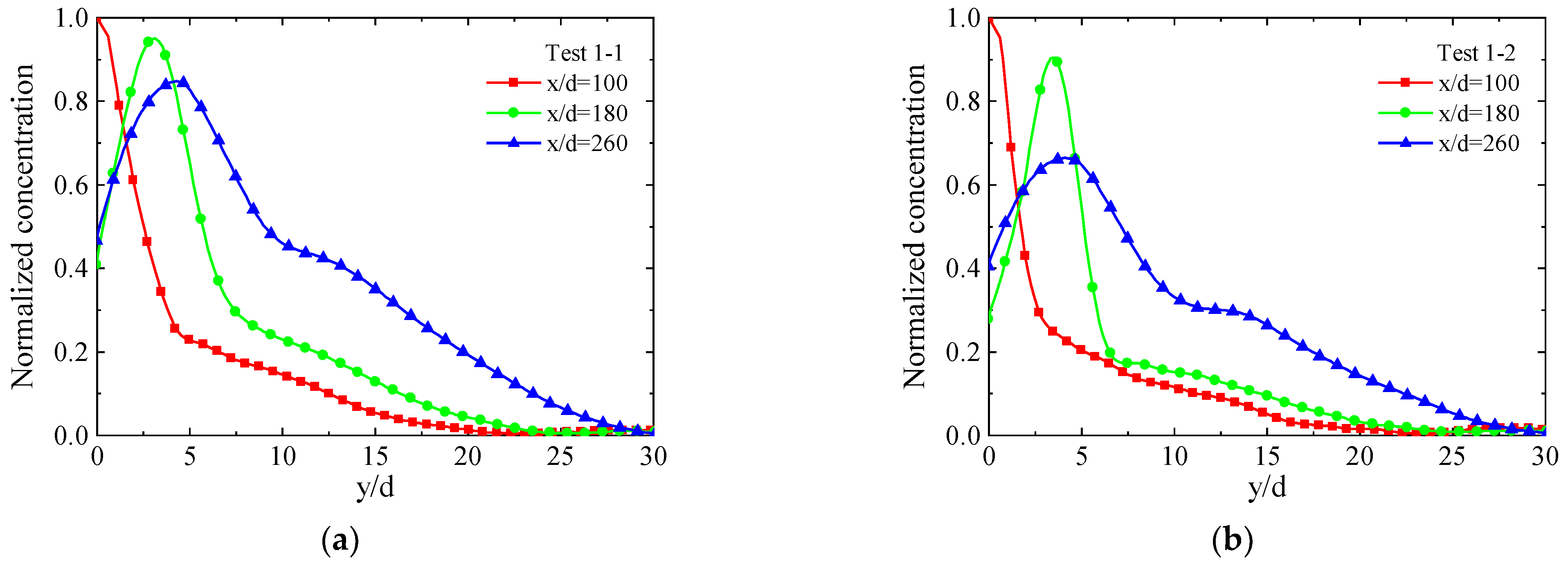
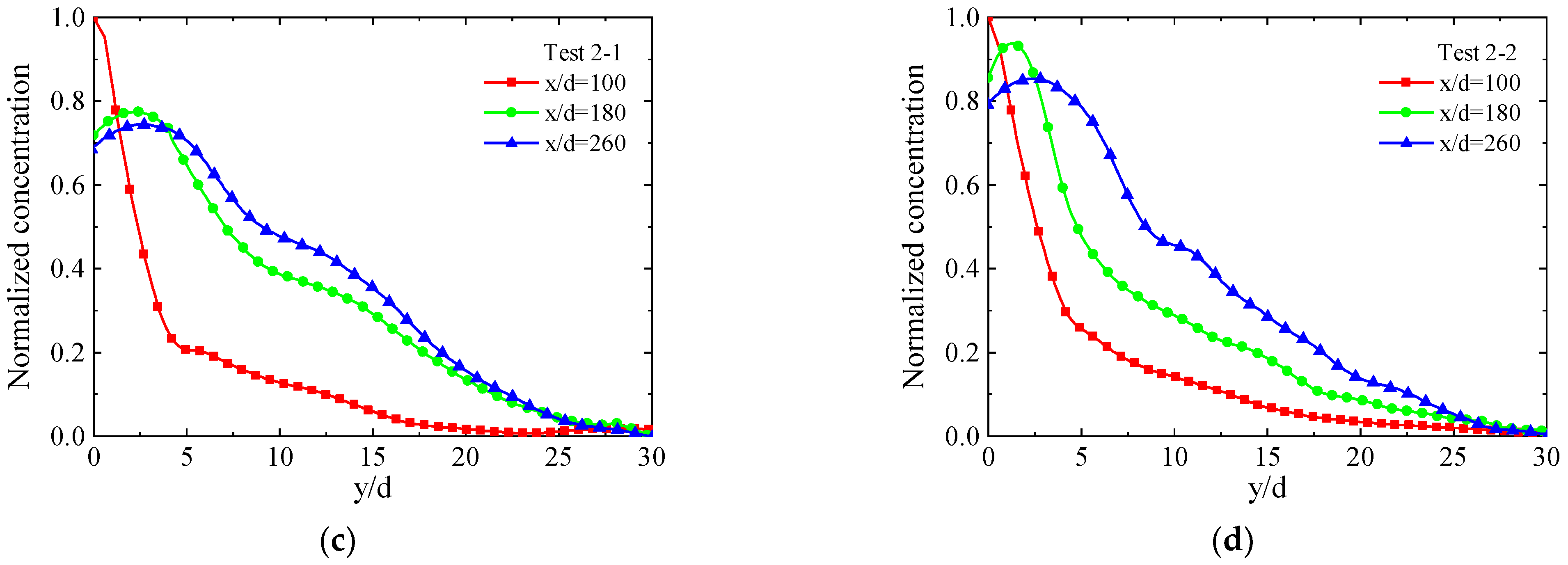
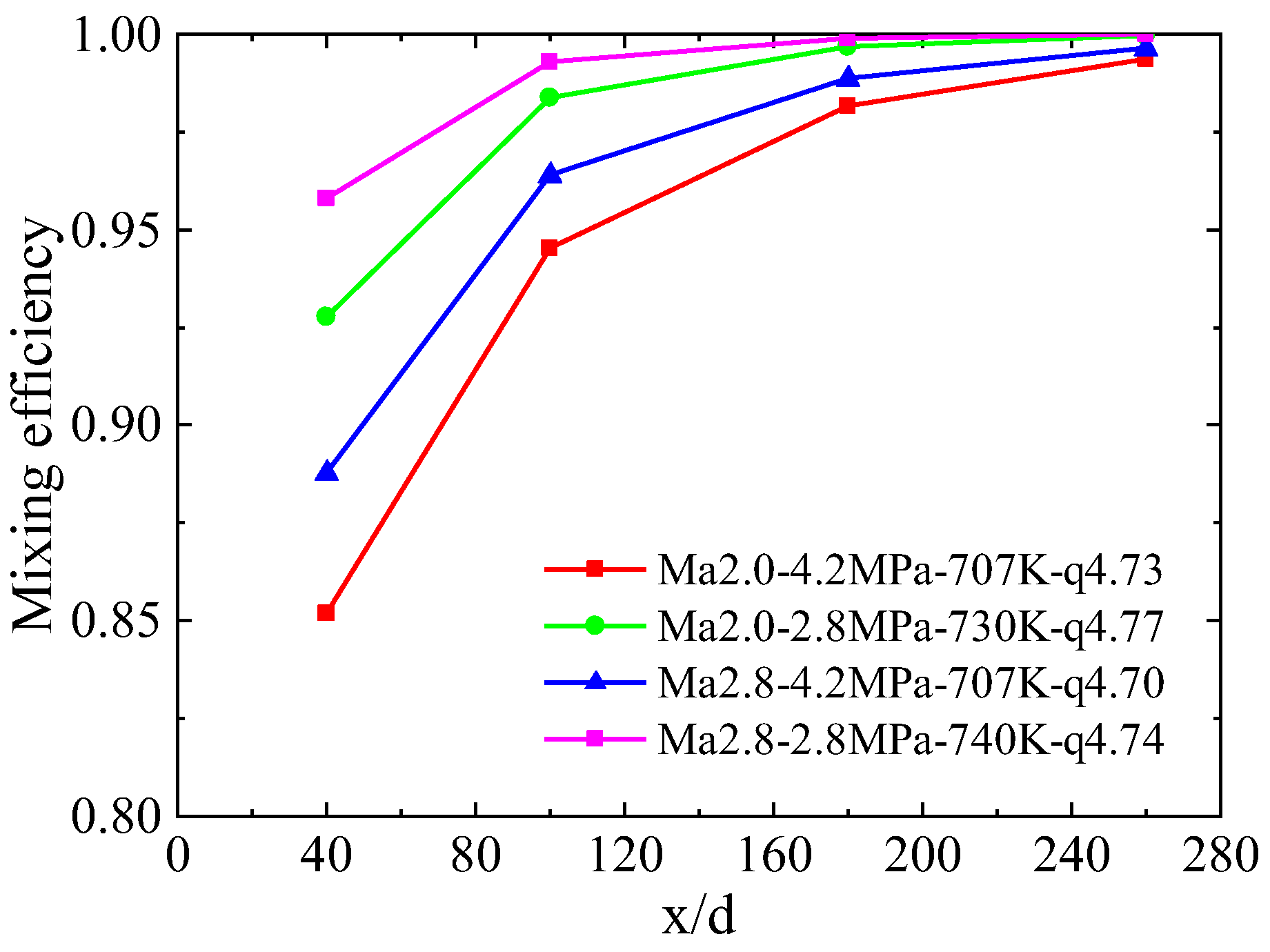
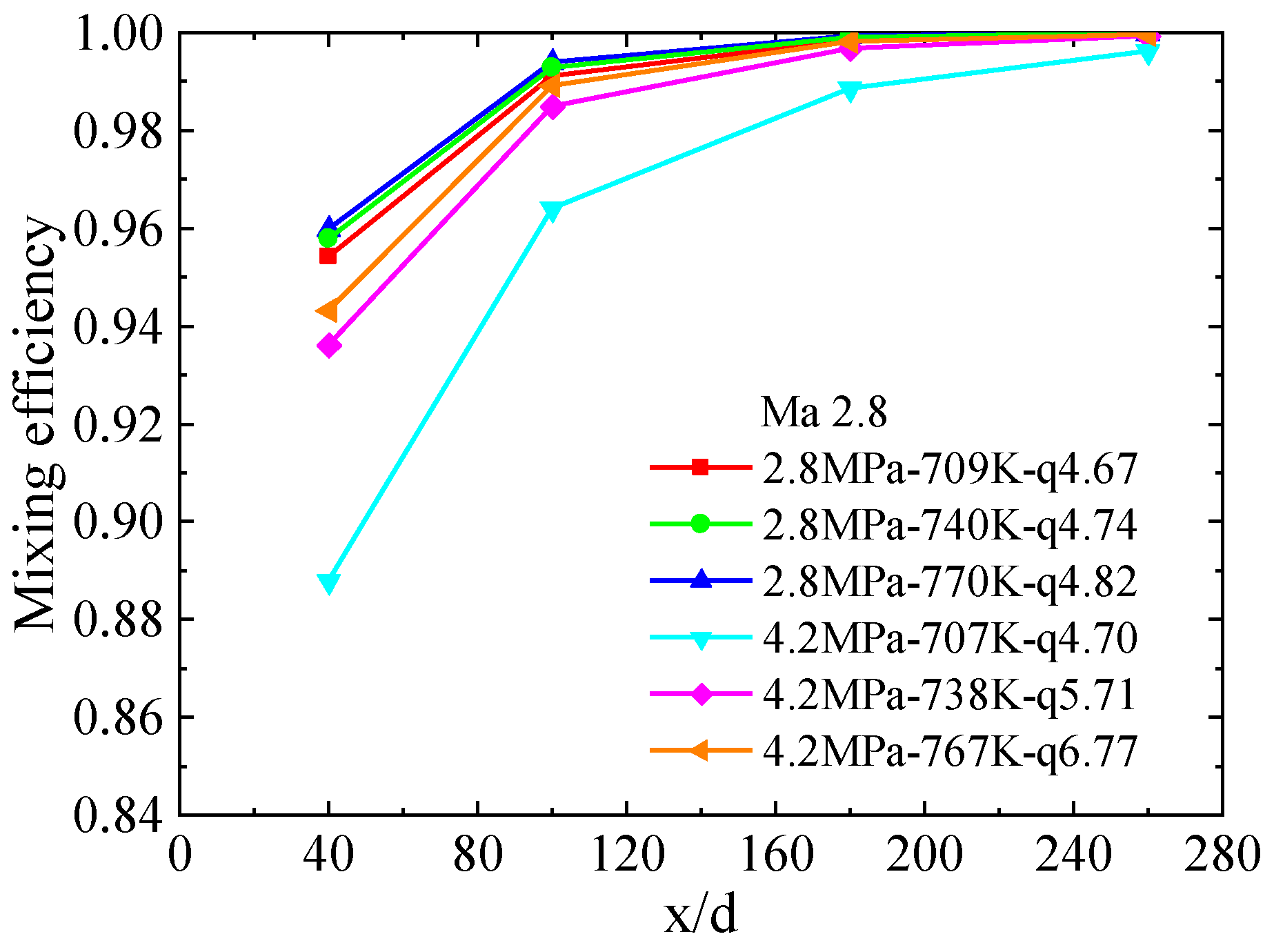

| Test | Mach Number, Ma | Total Pressure, P0/(MPa) | Injection Pressure, Pj/(MPa) | Injection Temperature, Tj/(K) | Momentum Flux Ratio, q |
|---|---|---|---|---|---|
| 1-1 | 2.0 | 0.44 | 2.8 | 705 | 4.48 |
| 1-2 | 2.0 | 0.43 | 2.8 | 730 | 4.77 |
| 1-3 | 2.0 | 0.44 | 2.8 | 780 | 4.96 |
| 2-1 | 2.0 | 0.43 | 4.2 | 707 | 4.73 |
| 2-2 | 2.0 | 0.46 | 4.1 | 735 | 5.44 |
| 2-3 | 2.0 | 0.44 | 4.1 | 776 | 6.58 |
| 3-1 | 2.8 | 0.75 | 2.8 | 709 | 4.67 |
| 3-2 | 2.8 | 0.72 | 2.8 | 740 | 4.74 |
| 3-3 | 2.8 | 0.79 | 2.8 | 770 | 4.82 |
| 4-1 | 2.8 | 0.77 | 4.2 | 707 | 4.70 |
| 4-2 | 2.8 | 0.79 | 4.2 | 738 | 5.71 |
| 4-3 | 2.8 | 0.76 | 4.2 | 767 | 6.77 |
| Case | Mach Number, Ma | Total Pressure, P0/(MPa) | Injection Pressure, Pj/(MPa) | Injection Temperature, Tj/(K) | Momentum Flux Ratio, q |
|---|---|---|---|---|---|
| S1-1 | 2.0 | 0.44 | 2.8 | 705 | 4.48 |
| S1-2 | 2.0 | 0.43 | 2.8 | 730 | 4.77 |
| S1-3 | 2.0 | 0.44 | 2.8 | 780 | 4.96 |
| S2-1 | 2.0 | 0.43 | 4.2 | 707 | 4.73 |
| S2-2 | 2.0 | 0.46 | 4.1 | 735 | 5.44 |
| S2-3 | 2.0 | 0.44 | 4.1 | 776 | 6.58 |
| S3-1 | 2.8 | 0.75 | 2.8 | 709 | 4.67 |
| S3-2 | 2.8 | 0.72 | 2.8 | 740 | 4.74 |
| S3-3 | 2.8 | 0.79 | 2.8 | 770 | 4.82 |
| S4-1 | 2.8 | 0.77 | 4.2 | 707 | 4.70 |
| S4-2 | 2.8 | 0.79 | 4.2 | 738 | 5.71 |
| S4-3 | 2.8 | 0.76 | 4.2 | 767 | 6.77 |
| U3-2 | 2.8 | 0.72 | 2.8 | 740 | 4.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Xing, K.; Dou, S.; Yang, Q.; Xu, X. Experimental and Numerical Investigations on the Mixing Process of Supercritical Jet Injected into a Supersonic Crossflow. Aerospace 2022, 9, 631. https://doi.org/10.3390/aerospace9110631
Zhou W, Xing K, Dou S, Yang Q, Xu X. Experimental and Numerical Investigations on the Mixing Process of Supercritical Jet Injected into a Supersonic Crossflow. Aerospace. 2022; 9(11):631. https://doi.org/10.3390/aerospace9110631
Chicago/Turabian StyleZhou, Wenyuan, Kai Xing, Suyi Dou, Qingchun Yang, and Xu Xu. 2022. "Experimental and Numerical Investigations on the Mixing Process of Supercritical Jet Injected into a Supersonic Crossflow" Aerospace 9, no. 11: 631. https://doi.org/10.3390/aerospace9110631
APA StyleZhou, W., Xing, K., Dou, S., Yang, Q., & Xu, X. (2022). Experimental and Numerical Investigations on the Mixing Process of Supercritical Jet Injected into a Supersonic Crossflow. Aerospace, 9(11), 631. https://doi.org/10.3390/aerospace9110631






