1. Introduction
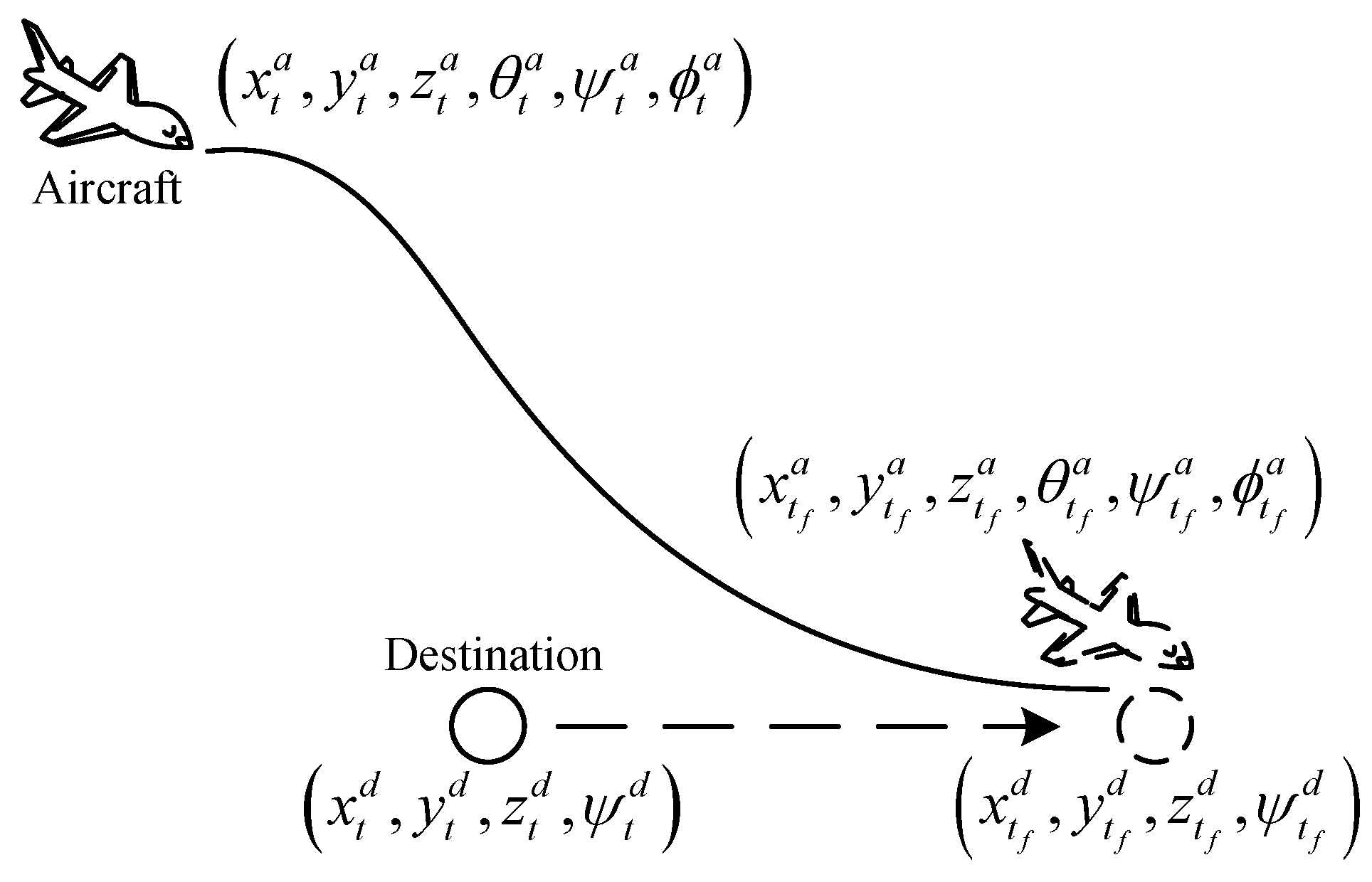
Aircraft guidance, especially in the scenario with a dynamic destination in three-dimensional space, is our research focus because it is widely used in reality. In air traffic control, aircraft can be guided to resolve conflicts or for follow-up flights. In aircraft carrier operations, aircraft need to be guided to land on the deck of a carrier moving at full speed. In air combat, fighters are guided to reach a position of advantage. The destinations have different movement patterns in different scenarios, so it is necessary to study a general method to solve the problem of aircraft guidance.
An aircraft guidance method is used to generate a trajectory or a set of instructions to guide an aircraft to a moving destination in a certain direction in three-dimensional continuous space. A series of advanced algorithms, such as optimal control techniques [
1], geometry methods [
2], model predictive control [
3] and knowledge/rule-based decisions [
4], have been investigated to guide and control aircraft. With the development of artificial intelligence, more and more scholars use intelligent algorithms for aircraft guidance.
Deep reinforcement learning (DRL) [
5] is a type of artificial intelligence with the advantages of high decision-making efficiency and model or data independence. It has been utilized in many fields and has obtained great achievements of human-level or superhuman performance [
6,
7,
8]. The theory of DRL is very suitable for solving sequential decision-making problems, including aircraft guidance.
Mainstream DRL algorithms, such as Deep Q Network (DQN) [
9], Deep Deterministic Policy Gradient (DDPG) [
10] and Proximal Policy Optimization (PPO) [
11], have been adopted to solve aircraft guidance problems. In [
12], an RL model is built to improve the autonomy of gliding guidance for complex flight missions. An analytical terminal velocity prediction method considering maneuvering flight is studied to adjust the maneuvering amplitude intelligently in velocity control. In [
13], a DQN algorithm is used to generate a trajectory to perform a perched landing on the ground. In this algorithm, the noise is added to the numerical model of airspeed in the training environment, which is more in line with the actual scenario. UAV autonomous landing on a moving platform is studied in [
14]. DDPG is used as the training algorithm, and a reward function including the position, velocity and acceleration of the UAV is designed. UAV landing can be completed in both simulation and real flight scenarios. However, the orientation of the landing platform is not considered, and vertical velocity control is not included in the action set. A DRL-based guidance law is proposed in [
15] to deal with maneuvering of high-speed targets. Based on the DQN algorithm, a relative-motion model is established and reward function is designed that can obtain continuous acceleration commands, make the LOS rate converge to zero rapidly, and hit the maneuvering target using only the LOS rate. In [
16], an actor–critic model with a reward-shaping algorithm is proposed for guiding an aircraft to 4D waypoints at a certain heading. The trained agent guides an aircraft to move along the waypoint in three-dimensional space by outputting a discrete heading angle, horizontal velocity and vertical velocity. In the research field of air traffic control, there are also many DRL-based methods for aircraft guidance to avoid conflicts [
17].
The authors of this article studied aircraft guidance based on the PPO algorithm [
18]. A shaped reward function including instruction continuity and relative position is presented that can significantly improve convergence efficiency and trajectory performance. However, the reward-shaping parameters are only given qualitatively and lack detailed design and sufficient theoretical support, and thus need further improvement. In addition, a pre-trained algorithm that directly reuses an agent is proposed for guidance tasks with different kinds of moving destinations. Using this algorithm, an agent that will be used in a new task can be trained quickly based on the existing agent. Pre-training is a method of direct policy reuse that can only be used between scenarios with high similarity. Though the study preliminarily verifies the feasibility of using policy reuse to study aircraft guidance, the scope of application needs to be expanded.
A policy-reuse approach based on destination position prediction is proposed based on our previous research to solve the above problems. The main contributions of this article are:
A meticulous design of reward-shaping parameters is done based on theoretical properties, and the consistency of optimal policy before and after reward shaping is proved.
By predicting the position of the destination at the possible termination time, the old policy/agent can be reused for efficiently training new agents in multiple scenarios. The application scope of the policy-reuse method is broadened, and it can be effectively used in scenarios with low similarity to the old scenario.
The rest of this paper is organized as follows.
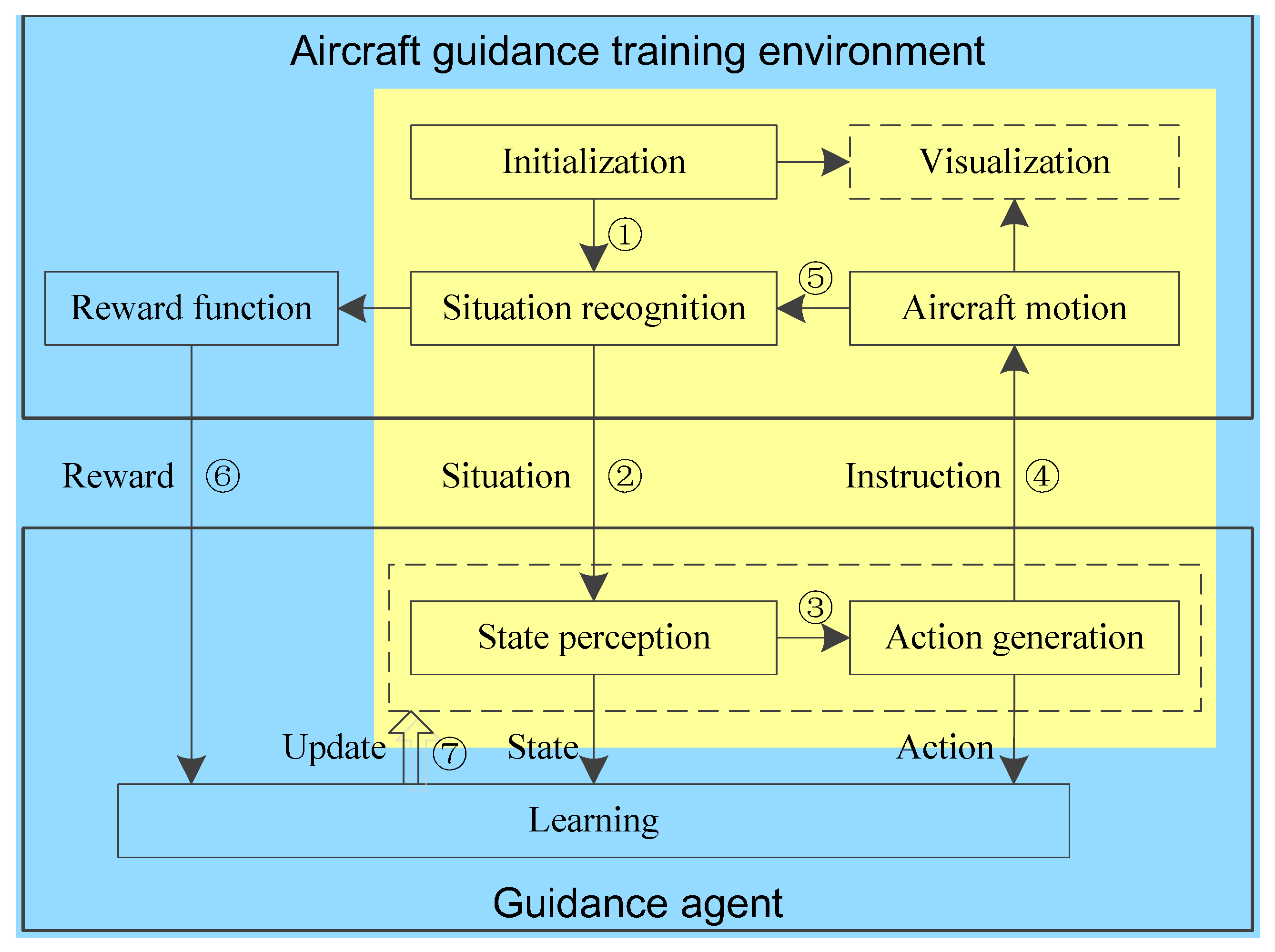
Section 2 describes the training framework and process of aircraft guidance using DRL.
Section 3 defines the DRL model for aircraft guidance.
Section 4 designs the policy-reuse approach based on destination position prediction using DRL.
Section 5 carries out simulations to demonstrate the effectiveness of the proposed algorithm.
Section 6 concludes this paper.
3. DRL Model for Aircraft Guidance
Establishing the DRL model for aircraft guidance entails establishing a Markov decision process (MDP) model including state space, action space and reward function.
3.1. State Space and Action Space
The equations of motion for the aircraft are given by [
21]:
where
is the axial load factor and
is the normal load factor. In this article, we assume that the aircraft has real-time perception of its and its destination’s correct position information. The state space of a guidance agent can be described with a vector:
where
is the last action, which is added to reflect the continuity of instructions.
Thrust, angle of attack and roll angle are used by an aircraft as control variables to change its flight path and are difficult for pilots to directly control. As an alternative, load factors can be utilized to control an aircraft. The maneuvering of an aircraft can be seen as a combination of some basic actions that can be used as the action space of the aircraft guidance agent to reduce the pressure on pilots. To build the action space, the continuous control variables are replaced with seven discrete control alternatives [
22], including steady flight, max load factor left turn, max load factor right turn, max long acceleration, max long deceleration, max load factor pull up, and max load factor push over. Using this action space, only one of the seven actions needs to be selected for each step. Complex maneuvering can be generated through the combination of basic actions.
3.2. Reward Function
The evaluation of agent performance should be reflected in the design of the reward function, including guidance success rate, flight trajectory quality, instruction generation time and agent training efficiency. In aircraft-guidance agent training, the reward function of each step is:
where
) is the termination reward and
is a potential-based shaping function [
23].
The termination reward is obtained at the end of each training episode, which is defined as:
The agent gets a positive reward when successfully guided, . The agent gets a negative reward when the guidance task fails. To encourage the agent to guide an aircraft to explore the airspace, the penalty for aircraft flying out of airspace should be greater than the penalty for reaching the maximum time step, that is, . In the non-terminating step, the reward obtained by the agent is 0.
The shaping function has the form:
where
is a real-valued function over states and actions. The greater its value, the more valuable the state and action of the aircraft at that time. It is defined as:
where
is the continuous action reward function and
is the position reward function.
The continuous action reward function is defined as:
To improve the smoothness of the trajectory, if the action is different from the previous one, a penalty is given. At each step, a smaller penalty is given to try to reduce the total time spent; that is, .
In different aircraft guidance tasks, evaluation of the relative position between the aircraft and the destination is different. In this paper, a general position reward function is used without considering the requirements of specific tasks for a relative position; it is given by:
where
is the horizontal distance reward function,
is the direction reward function and
is the altitude reward function. They are defined as:
The terms
,
and
are weights of
,
and
, respectively. They satisfy:
This makes the three functions of the same order so that the relative distance, relative direction and relative altitude have the same level of effect on training the agent.
If the sum of the shaping rewards of each step is greater than the positive termination reward value, the agent will guide the aircraft to seek a better trajectory and ignore the successful guidance. On the other hand, if the sum of the shaping rewards is less than the negative termination reward value, the agent will guide the aircraft to fail as soon as possible and get a relatively small penalty. Therefore, the design of each weight should satisfy:
The original MDP of aircraft guidance is , where . Using reward shaping, the MDP is transformed into , where . It needs to be proven that each optimal policy in will also be an optimal policy in M.
The action-state value function of
M is:
The action-state value function of
is:
In the initial step
, both the initial state
and the default action
are fixed values, so
is a constant. At the final step
,
has no effect on the training result and
does not need to be generated. Thus, we get:
By substituting Equations (14) and (16) into Equation (15), we can get:
For the optimal policy of
:
Thus, the optimal policy in is also an optimal policy in M.
4. Policy-Reuse Algorithm Based on Destination Position Prediction
For different guidance tasks, the destinations have different movement patterns and parameters. It still takes a lot of time if the guidance agent for a new task is trained from scratch. For two different aircraft guidance tasks, their MDPs are and . The state space, action space and reward function of the two MDPs are the same, but their transition functions are different due to different destination movement patterns. The policy-reuse algorithm, whether used to solve the problem of different state/action spaces or different reward functions, assumes that the transition function is unchanged, which makes it difficult to reuse policies in aircraft guidance tasks.
In the scenario studied in this paper, the destination moves according to its own dynamic model, which makes the position of the destination unaffected by the instructions generated by the agent. At any time
t, for the two different actions
and
performed by the aircraft in state
, the destination positions in
and
in tuple
and
are the same:
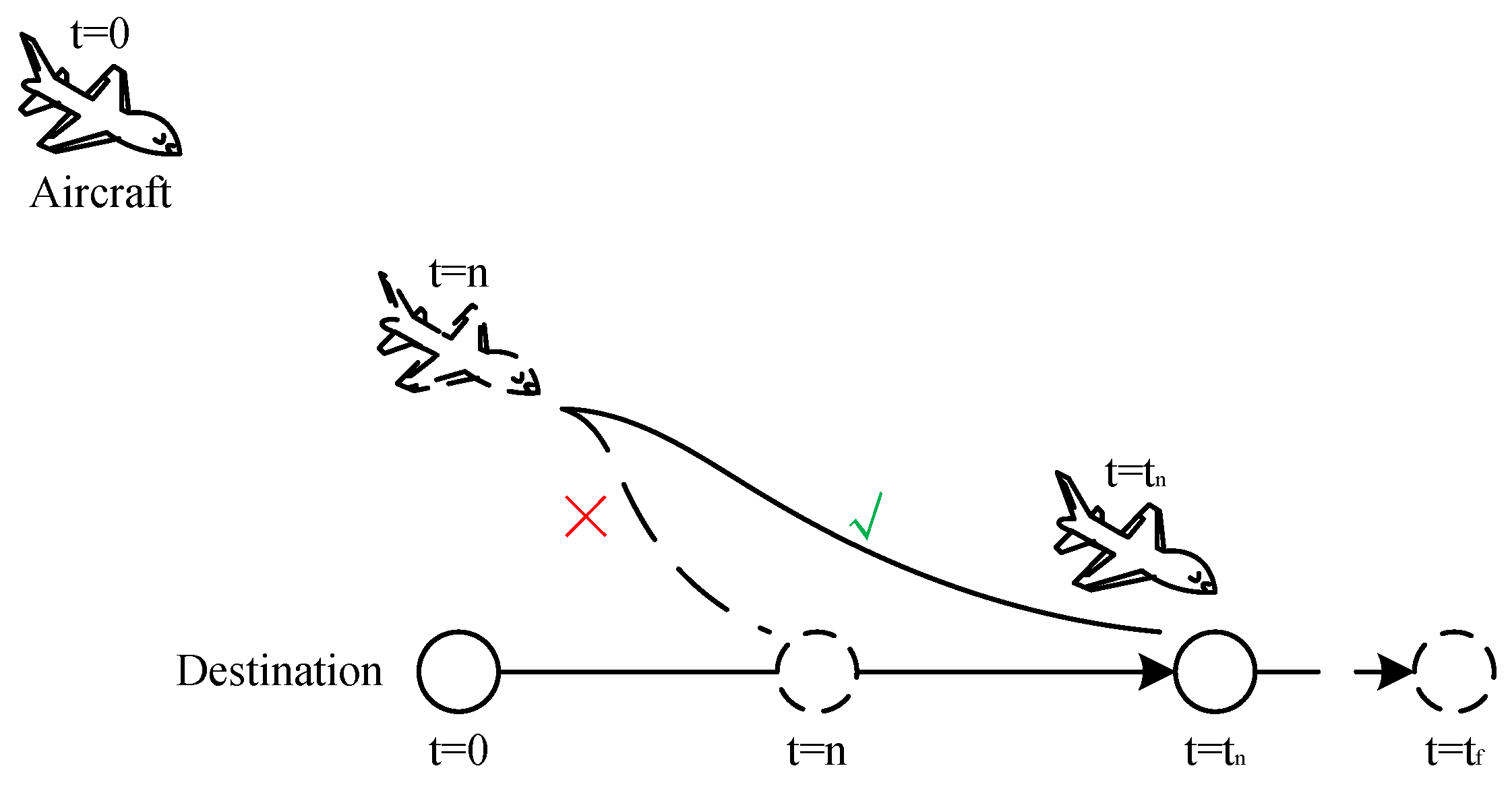
The sketch of destination position prediction is shown in
Figure 3. An episode from
to
is run in the moving destination scenario, and an action sequence is generated. Suppose there is an action sequence of the aircraft that is better than the current one and can make the aircraft arrive at the destination earlier at
,
. The destination position at the possible termination time step
can be predicted by running an episode in advance. For each step
n between 0 and
, if the destination position of
instead of
n is taken as the target, then the problem is equivalent to guiding an aircraft to a fixed-position destination. That is, the aircraft is guided to the predicted position of the destination at
.
A destination position prediction-based policy-reuse algorithm is proposed in this section. In a new guidance task, an existing policy/agent
B trained on a fixed-position destination scenario is used to reduce the exploration space of a new agent
Z. The destination positions in
and
in the state input of agent
B are fixed and are the same as the destination position in
. For agent
Z, the destination position in its state input
is constantly changing and cannot be directly used by agent
B. Thus, if the destination position in
is the same as that in the possible termination step
:
Then, the problem of aircraft guidance with a moving destination is transformed into the problem of aircraft guidance with a fixed-position destination. The prediction is realized by running an episode in the moving destination scenario in advance to obtain the destination position at each time in the future. In the training process, by predicting the future destination position, the current destination position can be replaced by the destination position at the possible termination time. In this way, agent B can be used to generate actions that improve the training efficiency on the new task.
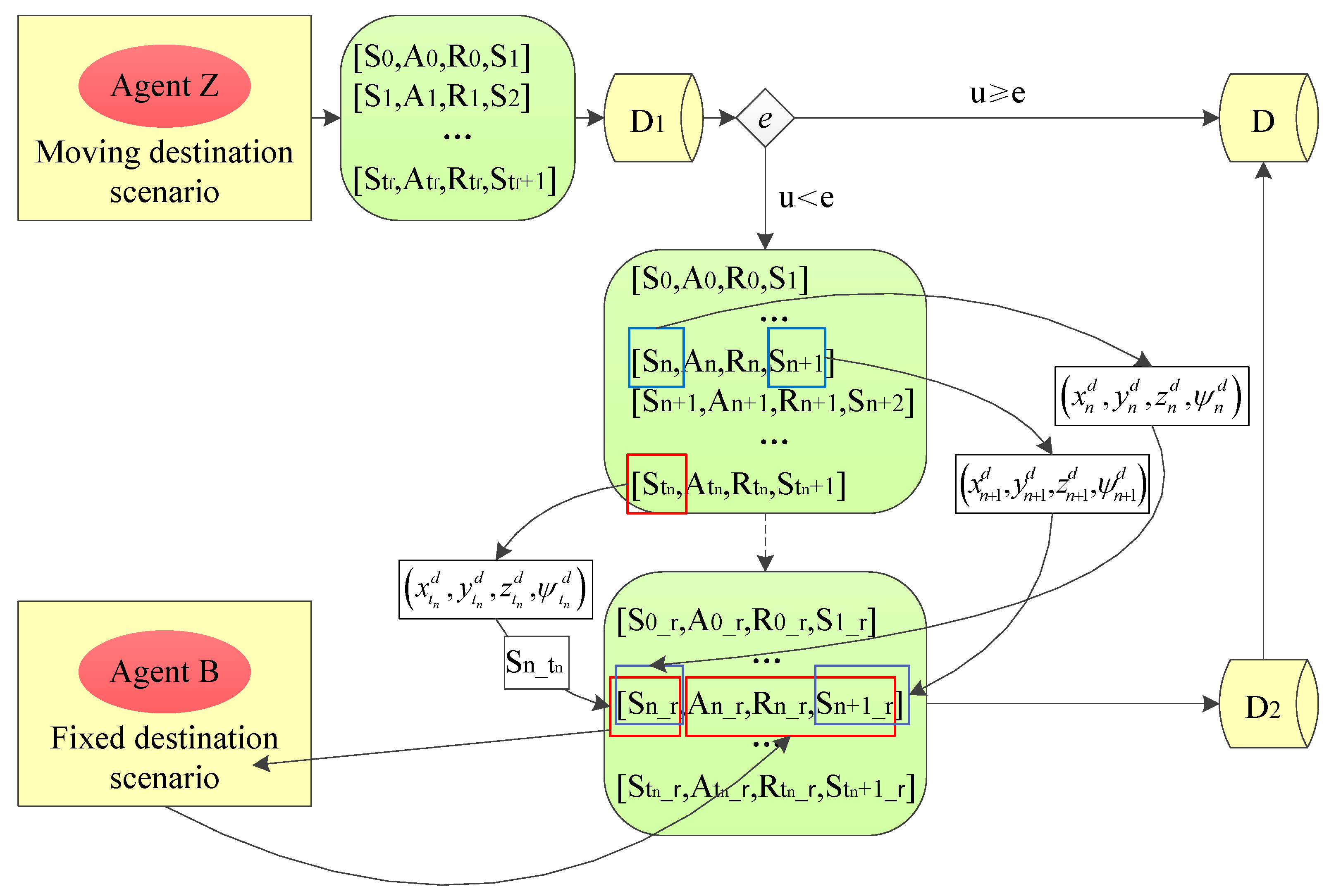
The policy-reuse algorithm based on destination position prediction is briefly illustrated in
Figure 4. The objective of an aircraft guidance task with a moving destination is to train a guidance agent
Z. The agent trained in the fixed-position destination scenario is taken as the baseline agent
B. At each training step
n, the destination position in
in the tuple is replaced by the destination position
in the possible termination state
of the episode. The term
is used to denote the state obtained by replacing the destination position at step
n with the predicted destination position at step
. Through this operation, the new guidance problem is transformed into a fixed-position destination guidance problem. A new action
can be generated by using the baseline agent
B, and then a tuple
is obtained. Since the destination position in the tuple is predicted rather than actually generated, it cannot be used to train an agent. The actual generated destination positions
and
in
and
are used to replace the destination positions in
and
and are saved as a new tuple
. The training efficiency is significantly improved by using this new tuple to train agent
Z.
The policy-reuse algorithm based on destination position prediction is shown in Algorithm 1. In the new guidance task, the input interface of agent Z includes aircraft position, destination position and the last action, and the output interface outputs one of the seven discrete actions, which are the same as those of agent B. At each time step t, the data generated in an episode using agent Z is stored in tuples. A random number u in [0, 1] is generated and compared with the current agent selection factor e. If u is greater than or equal to e, tuples are not updated; otherwise, agent B is used to update tuples.
As shown in
Figure 3, the aircraft has the possibility of reaching the destination at any step from 1 to
, so a loop from 1 to
is operated to search for a possible termination step
. For each step
in the loop, the destination position in each tuple from
to
is replaced with the destination position in
in step
, and it is saved as
. The purpose of this process is to change the tuple into the tuple in the fixed-position destination scenario by replacing the destination position in the state so as to meet the use conditions of baseline agent
B. With state
as input, a new tuple
is generated using baseline agent
B. In this tuple,
is the action performed by the aircraft, and
is the evaluation of this action, which can be used to train agent
Z. However, the destination positions in
and
are not the positions in the actual scenario, which need further transformation. Since the destination positions in
and
are generated by destination movement, a new tuple
is saved by replacing the destination positions in
and
with destination positions in
and
. In this tuple, the action is generated by the baseline agent
B, and the destination position in the state is the actual trajectory of the destination in the moving-destination scenario. At any time in the loop, the update of tuples finishes when the aircraft successfully arrives at the destination. Finally, the DRL algorithm is used to train agent
Z with the saved tuples. The agent selection factor
e needs to be updated. When it is less than or equal to 0, the algorithm stops updating and makes it equal to 0.
| Algorithm 1: Destination Position Prediction-Based Policy-Reuse Algorithm |
- 1:
Initialize agent Z to be trained - 2:
Select and load baseline agent B - 3:
Initialize agent selection factor - 4:
Initialize three memories , and D - 5:
for each episode do - 6:
Use agent Z to run a complete episode with steps - 7:
for every step t in do - 8:
Save tuple into - 9:
end for - 10:
Generate a random number u in [0,1] - 11:
if then - 12:
Transfer the data in to D and clear - 13:
else - 14:
for every step in do - 15:
Clear - 16:
Transfer in to and save it as - 17:
for every step n in do - 18:
Replace in with in and save it as - 19:
Select action in state using the baseline agent B - 20:
Execute action , receive reward , and transfer into the next state - 21:
- 22:
- 23:
Replace in with in and save it as - 24:
Replace in with in and save it as - 25:
Overwrite tuple into - 26:
if guide succeeded then - 27:
break - 28:
end if - 29:
end for - 30:
end for - 31:
Transfer the data in to D and clear - 32:
Update e by - 33:
end if - 34:
Use the data in D to train agent Z - 35:
end for
|
5. Simulation and Results Analysis
5.1. Simulation Setup
In this section, aircraft guidance simulation is carried out for fixed-position destination and different movement pattern destination scenarios to verify the reward shaping and policy-reuse methods proposed in this paper. The aircraft guidance simulation parameters are shown in
Table 1. The proposed algorithm does not limit the representation of position, and relative position or absolute position can be used. In this simulation, for the scenario with a fixed-position destination, the position of the destination is
. Therefore, in the moving destination scenario, for the predicted possible termination step
, its positional information
is transformed into
. For the guided aircraft, at each time step
n, its positional information
is transformed into
.
The PPO algorithm is used to train the agent in the simulation. The DRL parameters are shown in
Table 2.
5.2. Simulation of Aircraft Guidance in Fixed-Position Destination Scenario
The aircraft guidance simulation of a fixed-position destination is carried out to verify the effect of reward functions and to train a baseline agent. The training success rates using four kinds of reward functions are shown in
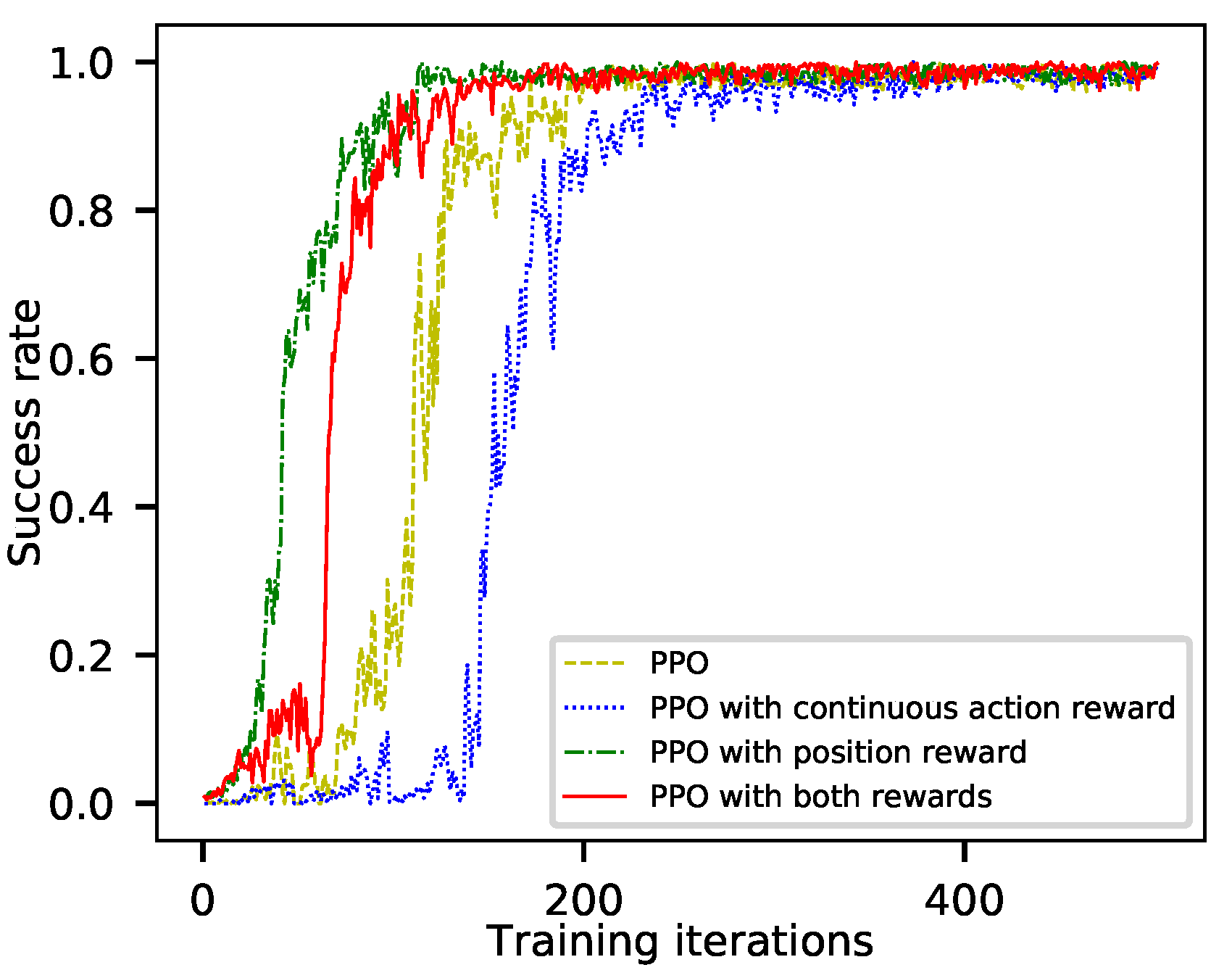
Figure 5.
The system converged after 200 training iterations using PPO only. The training speed of PPO with continuous-action reward function is the slowest, and the system converged after nearly 300 iterations. PPO with position reward function has the fastest training speed, and the system converged after about 100 training iterations. The system converged after 150 iterations using PPO with both reward functions. We found that during training, using different reward functions only makes a difference in training efficiency, and their success rates are stable at high levels after convergence.
Each well-trained agent is tested for 1000 simulations. The success rate, average number of control times and average computational time to generate an instruction are given in
Table 3.
The success rate of using the standard PPO algorithm is 98.6%, and the average number of control times is 11.31. The number of control times is an important index for evaluating the performance of an agent in aircraft guidance. The lower the number of control times, the less pressure the pilot and air traffic controller will have, and the smoother the flight trajectory will be. Although the training efficiency of PPO with continuous-action reward function is decreased, the average number of control times is reduced from more than 11 to less than 8. The training speed of using position reward function is significantly improved, but the average number of control times does not improved; it is still more than 11. The training efficiency and flight trajectory quality are significantly improved by using PPO with both reward functions. The agent trained by DRL takes less than 3 ms to generate an instruction, which has high computational efficiency.
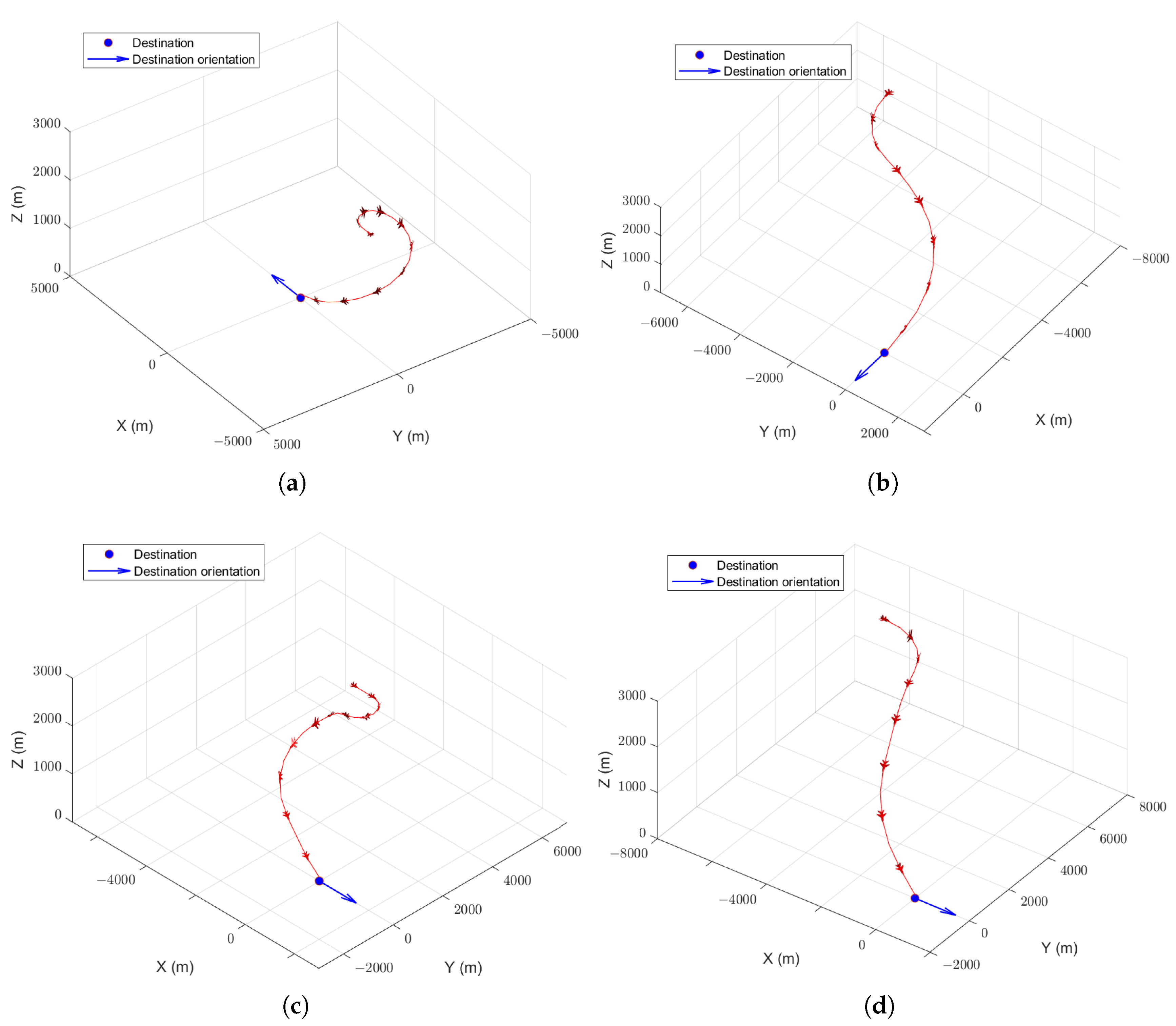
Typical trajectories are shown in
Figure 6. Using the standard PPO algorithm, the aircraft can reach the destination under the guidance of the agent in most scenarios. However, the agent may output unnecessary actions, resulting in the flight trajectory not being smooth enough, as shown in
Figure 6a. Using PPO with continuous-action reward function, although the training efficiency is decreased, the unnecessary instructions are fewer, and the flight trajectory is smoother, as shown in
Figure 6b. Using PPO with position reward function, the flight trajectory is still not smooth, as shown in
Figure 6c. Using PPO with both reward functions improves both training efficiency and flight trajectory quality, as shown in
Figure 6d.
In fixed-position destination scenarios, from the perspective of DRL, there are multiple optimal policies for aircraft guidance if reward shaping is not adopted. However, from the perspective of aircraft guidance, although using different optimal policies will lead to success, their guidance processes are different. Using reward shaping, an optimal guidance policy that is more suitable for pilots and air traffic controllers can be obtained by further optimization within the scope of DRL optimal policies.
5.3. Simulation of Aircraft Guidance in Moving-Destination Scenarios
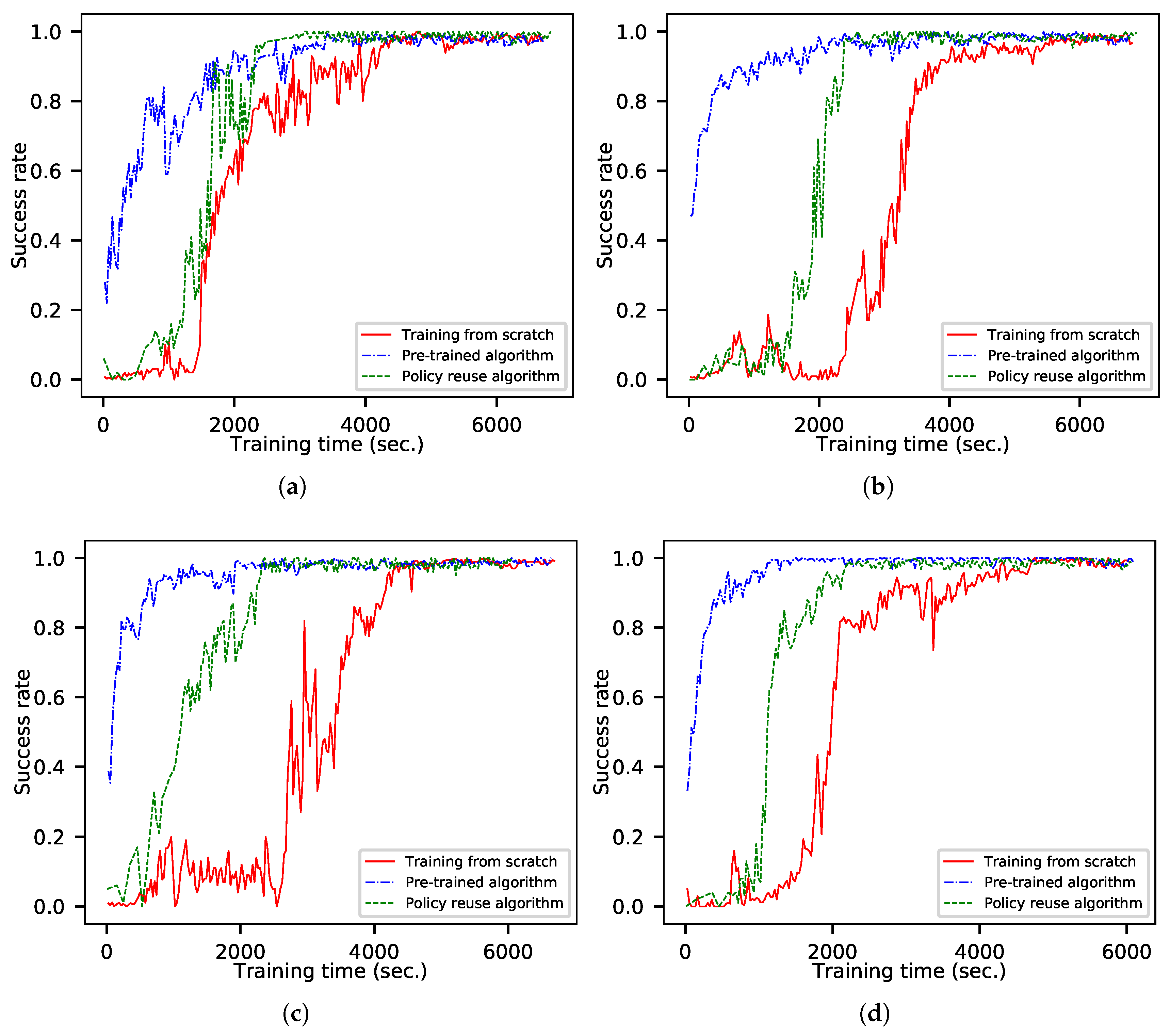
Scenarios with different moving destinations are set up for aircraft guidance agent training (1) from scratch, (2) with the pre-trained algorithm that reuses the baseline agent directly without any operations, and (3) with the proposed policy-reuse algorithm. In the uniform-motion destination scenario, the speed of the destination is set to 10 m/s, 20 m/s, 50 m/s and 100 m/s. In the curved-motion destination scenario, the speed is set to 20 m/s, and the turning radius is set to 500 m, 1000 m, 2000 m and 5000 m. The proposed policy-reuse algorithm needs to replace the stored data many times, which takes extra time. Therefore, the number of iterations for successful training cannot be used as an evaluation index. The training process chart in this section takes the training time as the abscissa and the success rate as the ordinate to compare the training efficiency of different algorithms.
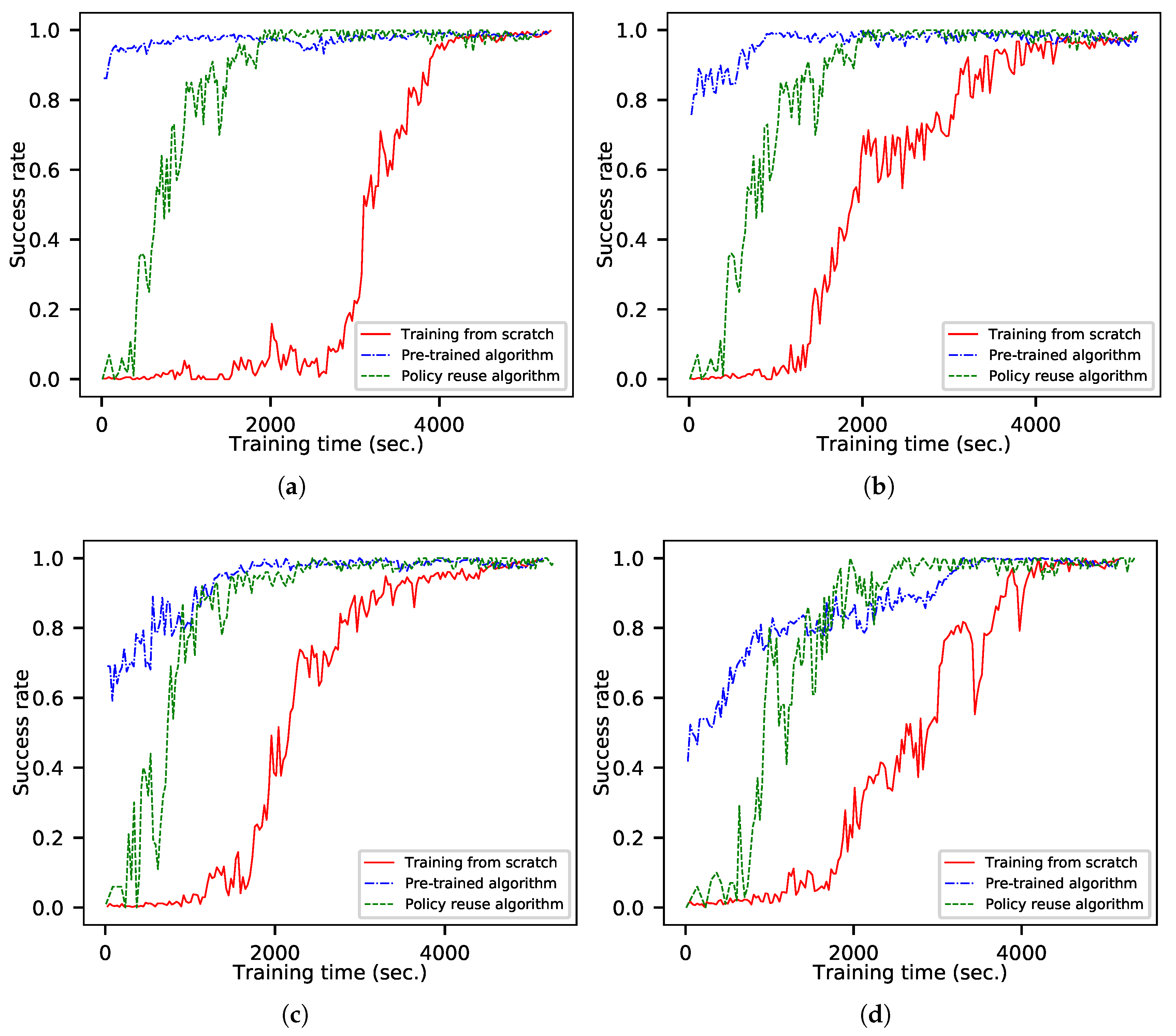
The success rates of the training processes in the uniform-motion destination scenario are shown in
Figure 7. Using the pre-trained algorithm, a new agent can be trained quickly when the speed of the destination is slow. The training efficiency is reduced when the destination is at high speed, but it is still better than the training method from scratch. This is because the baseline agent will guide the aircraft to maneuver to the current position of the destination. Although having a dynamic destination impacts the training process, the agent will still guide the aircraft to explore the area near the destination, which is better than the random exploration of the training method from scratch. The training efficiency of the policy-reuse algorithm based on the destination position prediction is lower than that of the pre-trained algorithm when the speed of the destination is slow. This is because it needs to replace the training data many times and takes more time. However, the algorithm has good stability, and its performance does not decrease significantly with increases in the destination speed. Its efficiency is better than that of the pre-trained algorithm when the destination speed is high.
Each well-trained agent is tested for 1000 simulations. The success rate is given in
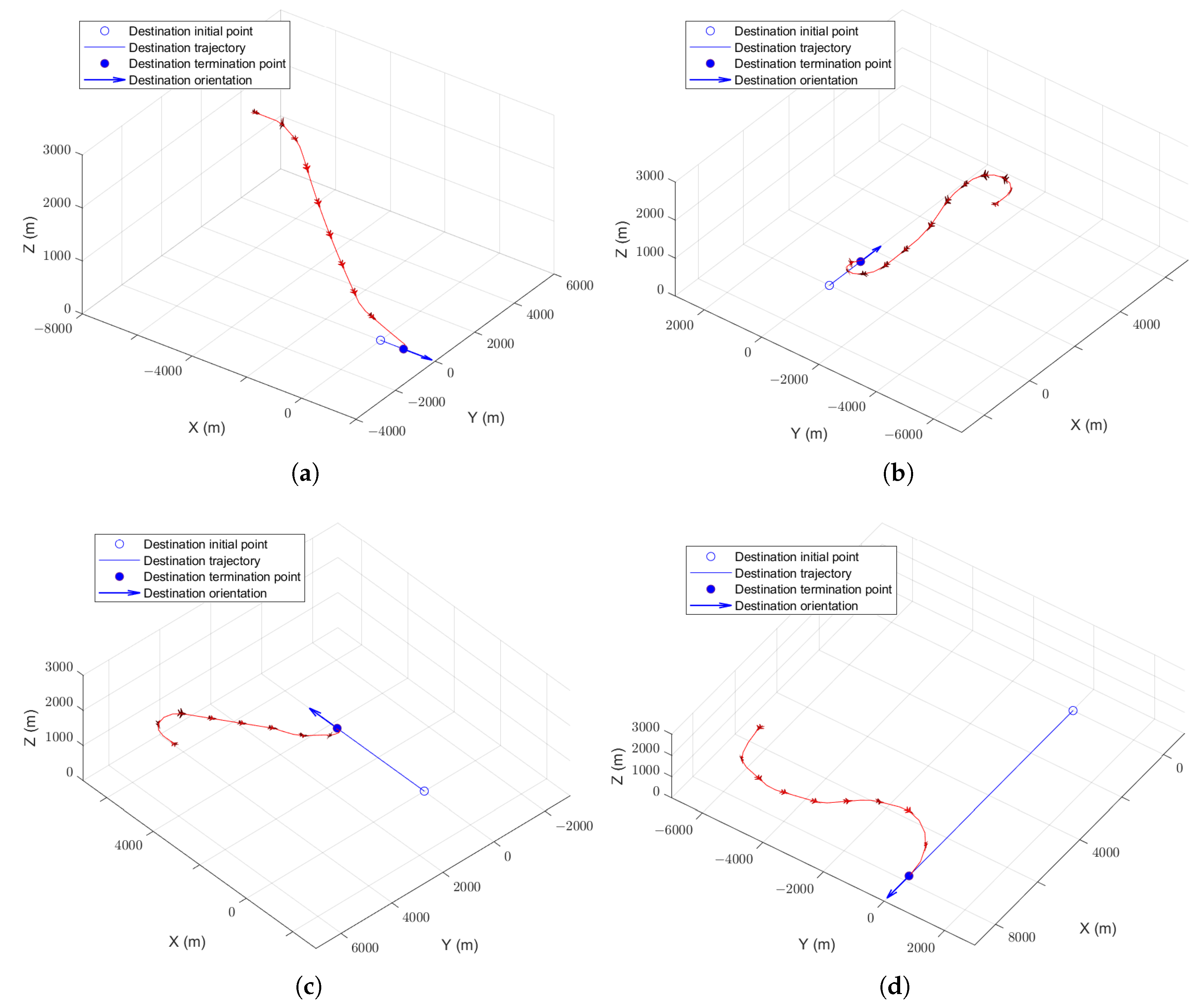
Table 4. The typical trajectories are shown in
Figure 8. It can been seen that there is almost no difference in the performance of agents among various training algorithms; only training efficiency is affected. The faster the speed of the destination, the lower the similarity with the fixed-position destination guidance task. The pre-trained algorithm is sensitive to task similarity, and the time required for convergence obviously increases with the decrease of similarity. The policy-reuse algorithm based on destination position prediction is less affected by task similarity, and the convergence time does not increase significantly with the decrease of the similarity. This makes the proposed algorithm applicable to a wider range, and the baseline agent can be used for a wider range of destination speeds.
The aircraft guidance simulation in the curved-motion destination scenario is carried out to further verify the applicability of the proposed algorithm. The success rates of the training processes are shown in
Figure 9. Under the premise that the destination speed is constant, a smaller turning radius, larger turning angle of the destination in unit time, and lower similarity with the baseline task resulted in more time required for training. Using the pre-trained algorithm, a new agent can be trained efficiently when the turning radius of the destination is large. When the turning radius is small, its performance is poor, but it is more efficient than training from scratch. The performance of the policy-reuse algorithm does not decrease significantly with the decrease of the turning radius of the destination, and it has stability with the change of similarity.
Each well-trained agent is tested for 1000 simulations. The success rate is given in
Table 5. The typical trajectories are shown in
Figure 10. It can been seen that the algorithm proposed in this paper can also be used if the destination moves in a curve. The smaller the turning radius of the destination, the better the performance of the algorithm compared to that of the pre-trained algorithm.
The simulation results of aircraft guidance in scenarios of different movement pattern destinations show that using the prior knowledge of the old policy/agent to guide the training of a new agent can effectively reduce the exploration space in the early stage of agent training, partially solve the problem of poor generalization of DRL, and improve the efficiency of agent training. Compared with the pre-trained algorithm using the old policy/agent directly, the proposed policy-reuse algorithm based on destination position prediction is not sensitive to the similarity between the old and new tasks, which expands the scope of policy reuse. The pre-trained algorithm has high efficiency when the similarity between the old and new tasks is high. On the contrary, the policy-reuse algorithm proposed in this paper is recommended when the similarity between the two tasks is low.