Simulation of Forced Convection Frost Formation in Microtubule Bundles at Ultra-Low Temperature
Abstract
:1. Introduction
2. Mathematical Modeling and Methods
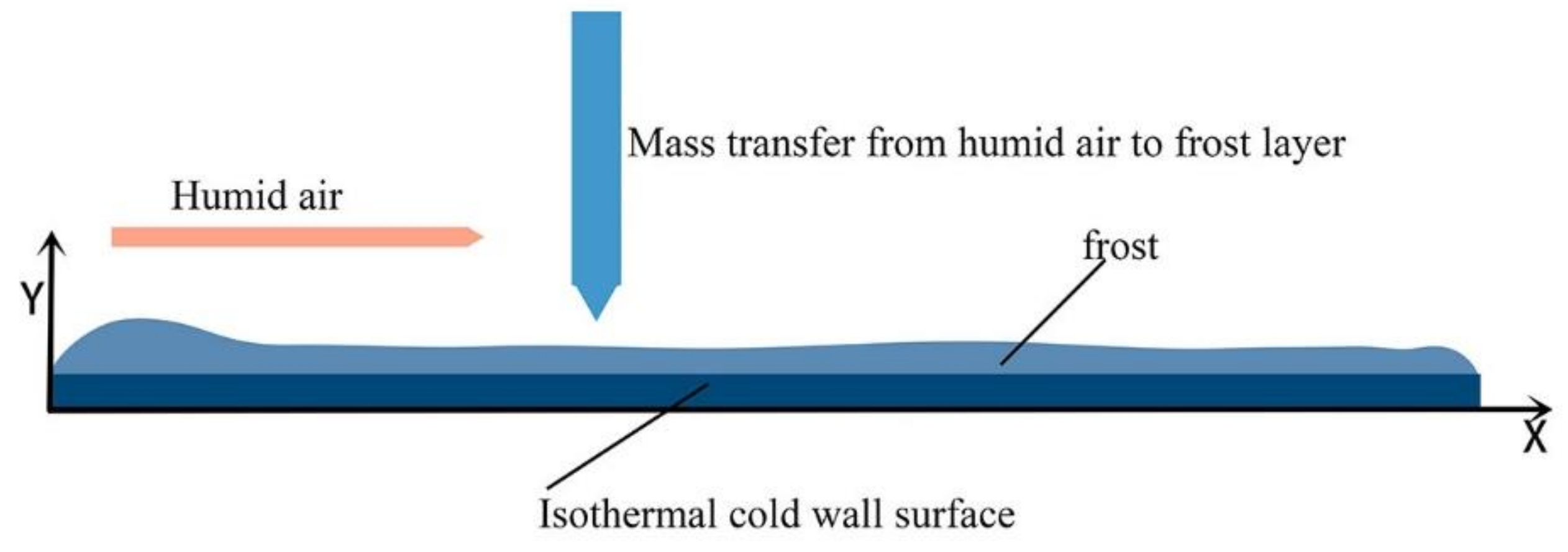
2.1. Frost Growth Mechanism
- The wet air is considered to be an incompressible Newtonian fluid with the airflow perpendicular to the inlet direction.
- The airflow and air pressure in the frost layer are uniform, and the airflow at the interface between the wet air and the frost layer is saturated.
- The amount of water vapor absorbed in the control volume during mass transfer in the frost layer is proportional to the density of water vapor in the control volume.
- The gas space in the frost layer is small enough that the natural convection in the frost layer can be neglected, and the heat radiation in the frost layer can be neglected considering the low frost temperature.
- The local humidity of the wet air phase in the control body of the frost layer is consistent with the saturation humidity at that temperature.
2.2. Mathematical Model
2.2.1. Governing Equations
2.2.2. Mass Transfer Rate
2.2.3. Conditions for Mass Transfer
2.2.4. Boundary conditions
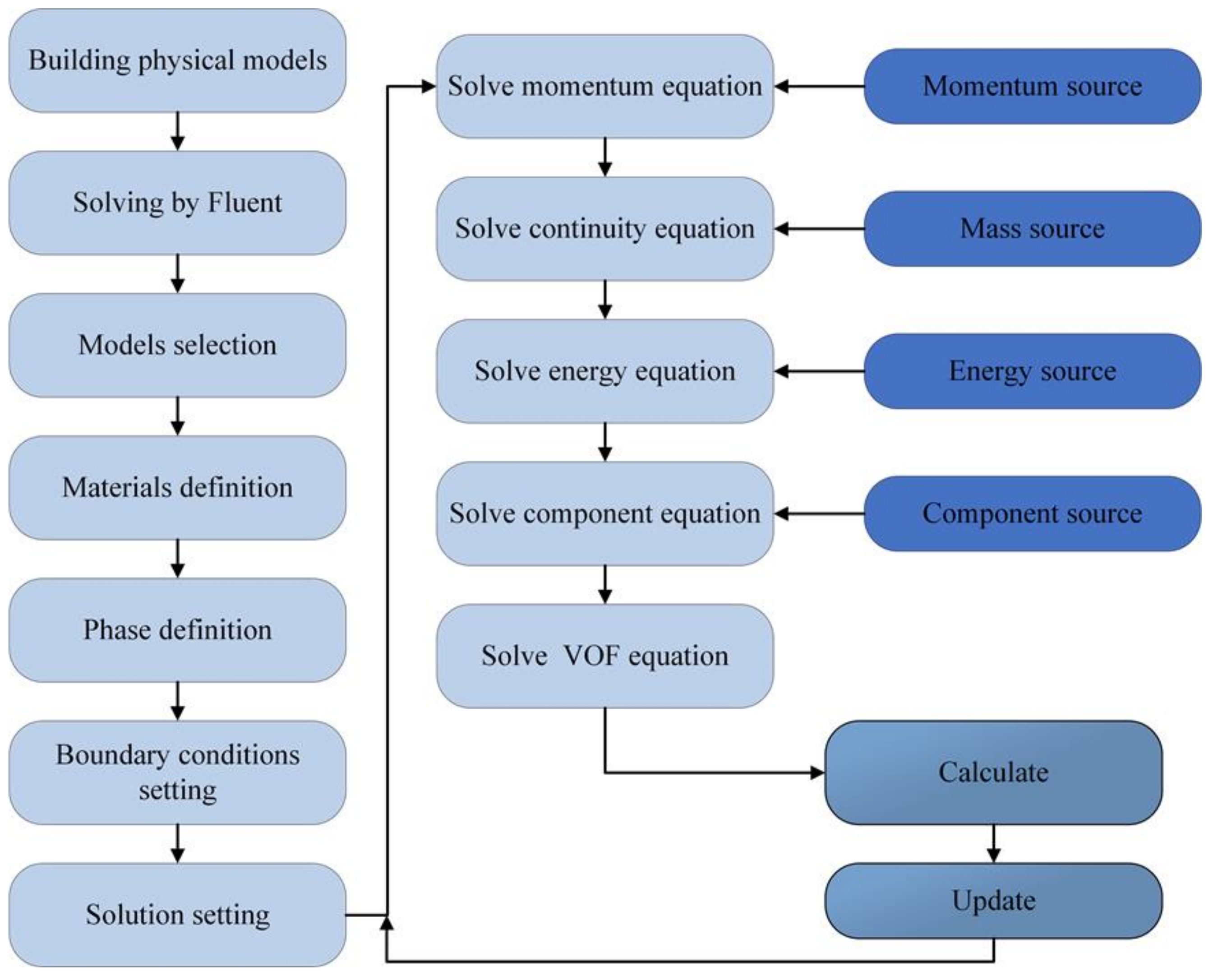
2.3. Solution Scheme
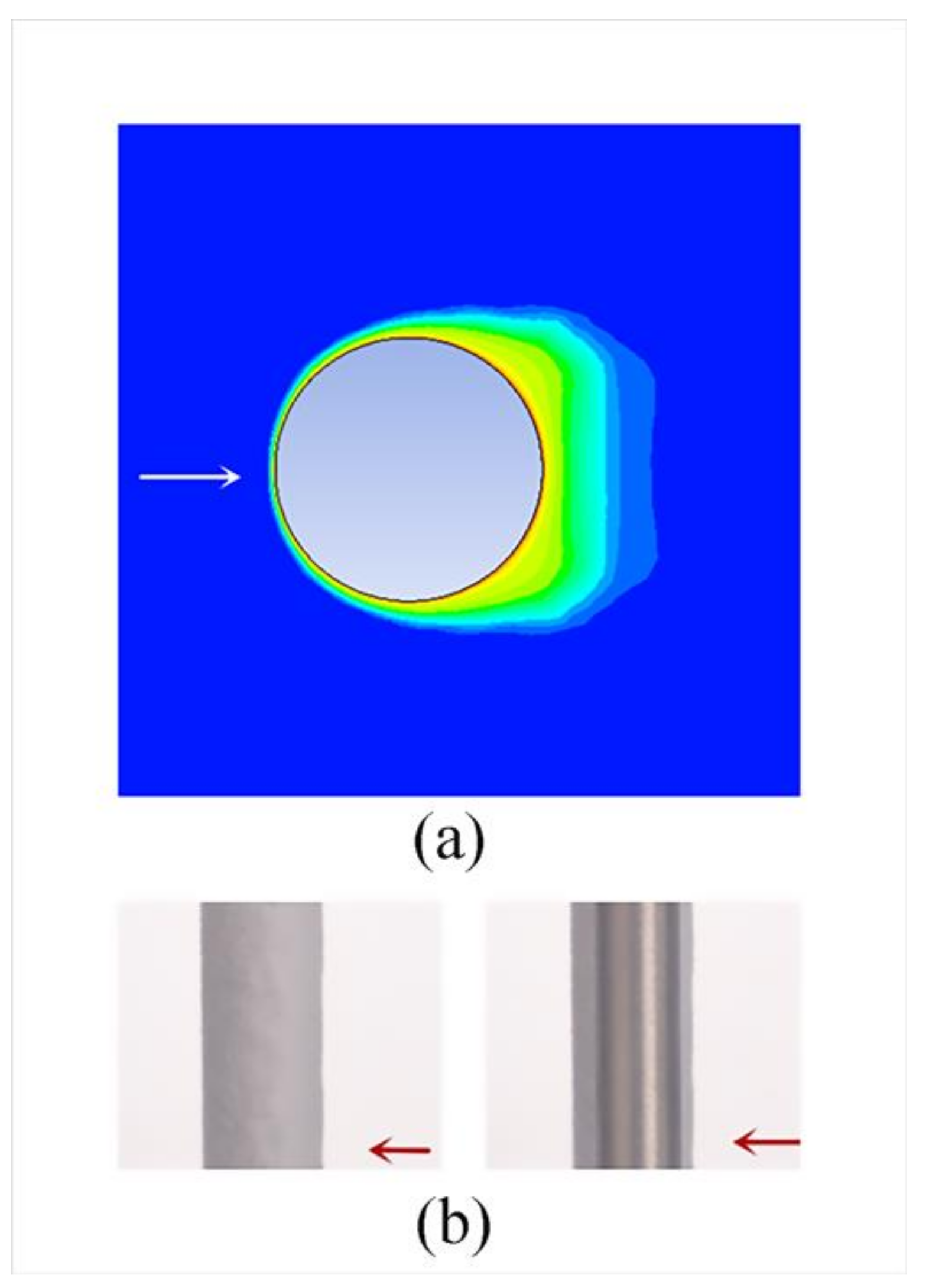
2.4. Model Verification
3. Simulation Experiment
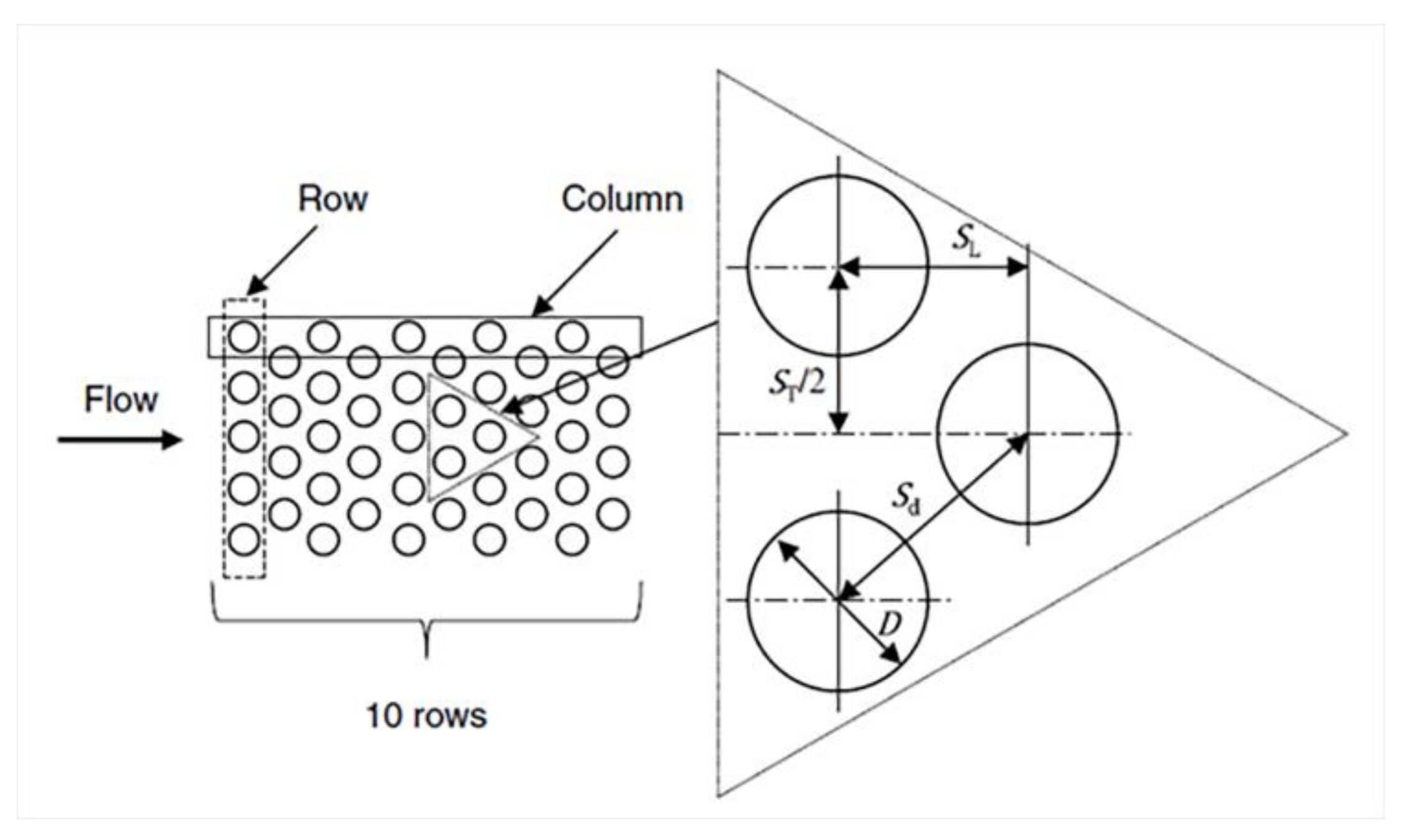
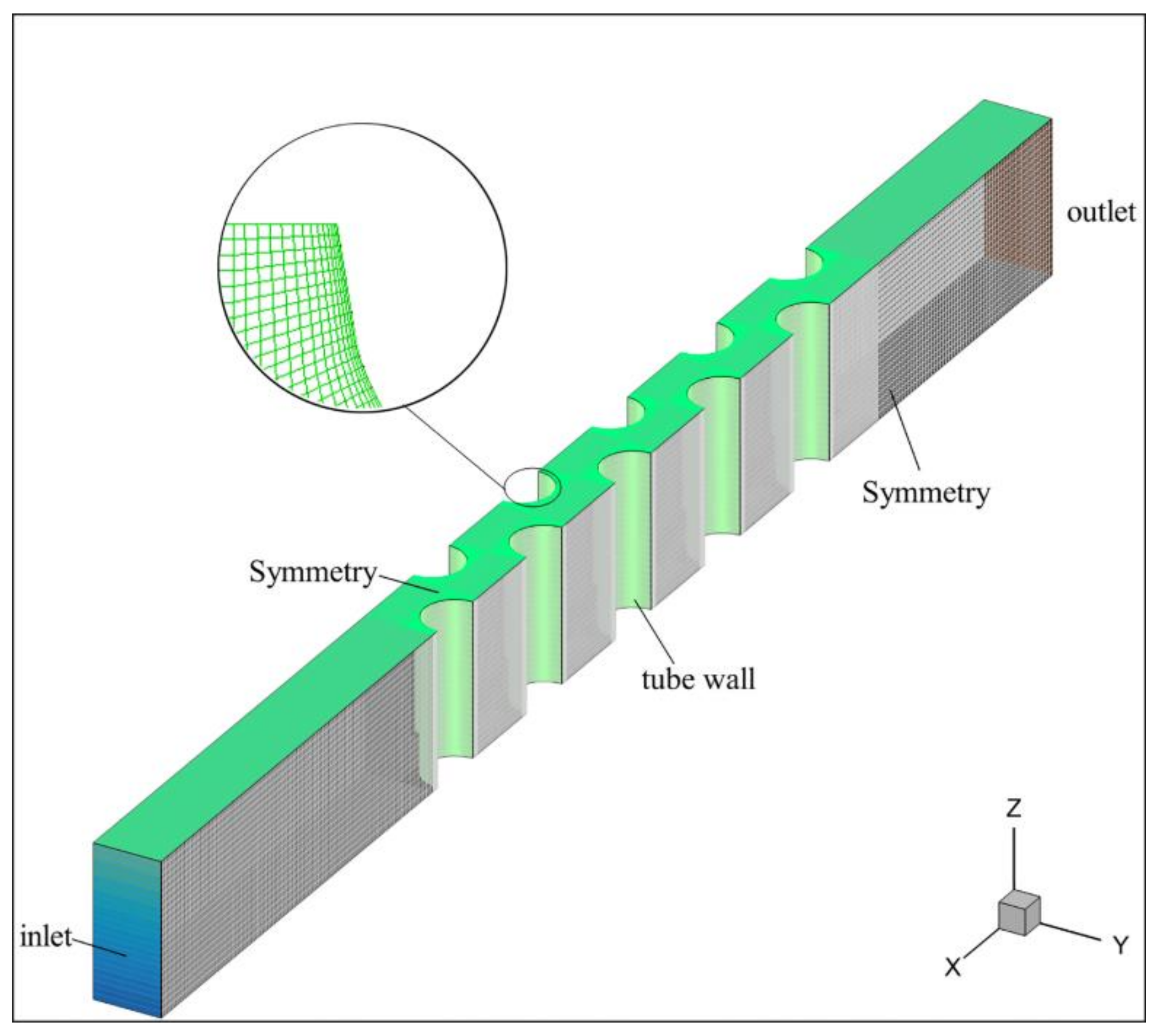
3.1. Physical Model
3.2. Grid-Independent Analysis
3.3. Numerical Calculation of Tube Bundle Frosting
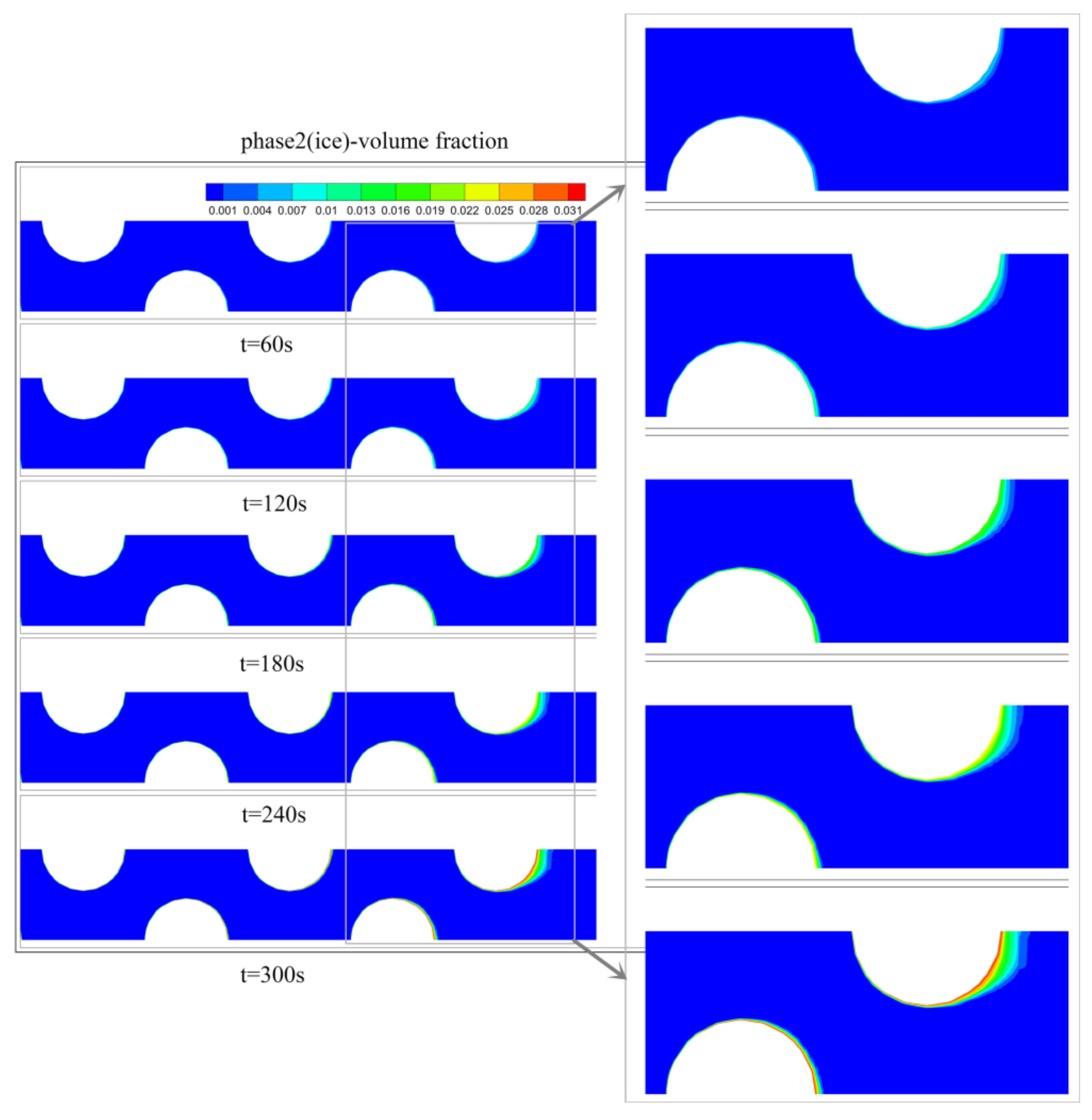
3.3.1. Distribution of Frost on Tube Bundle
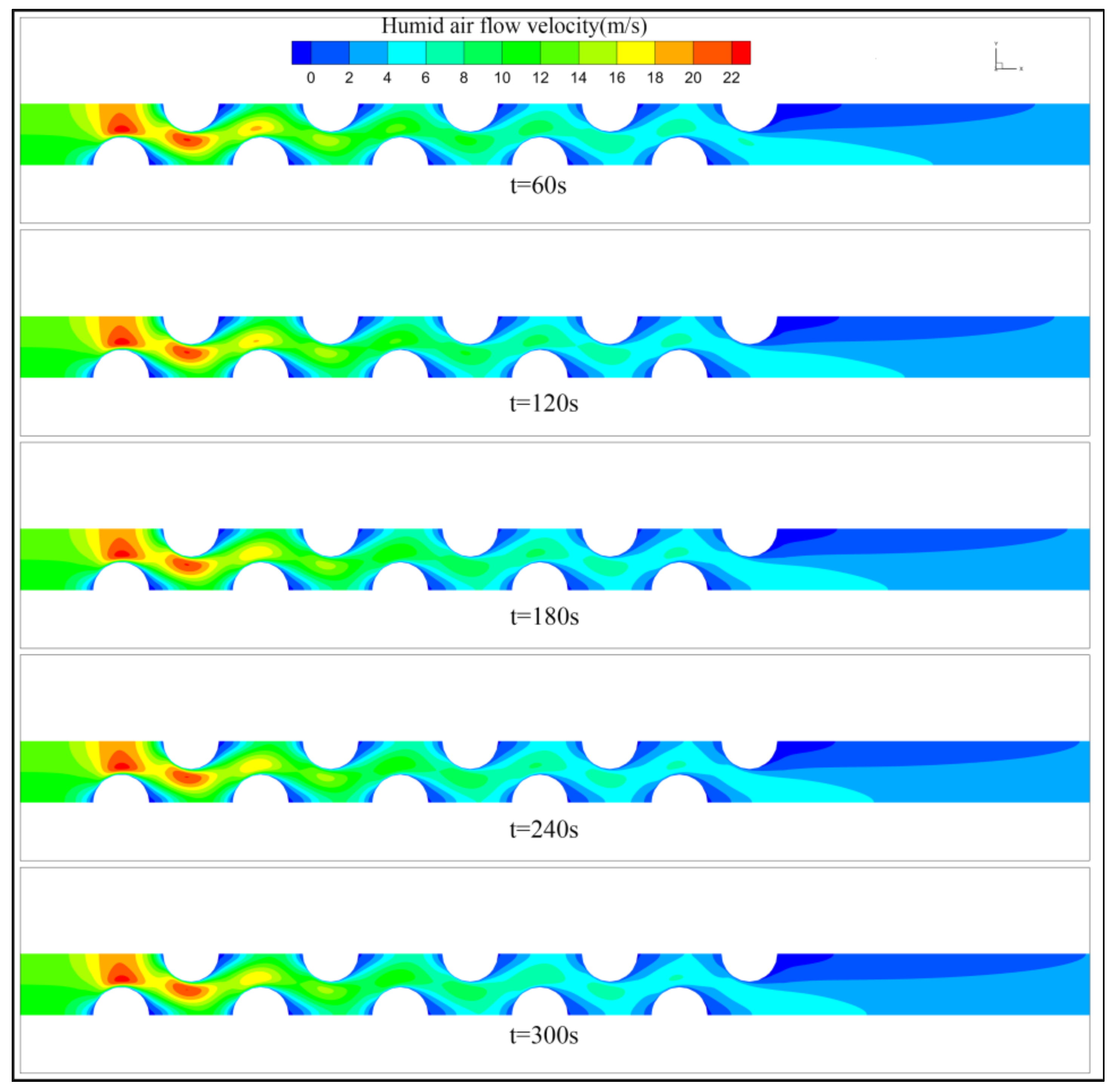
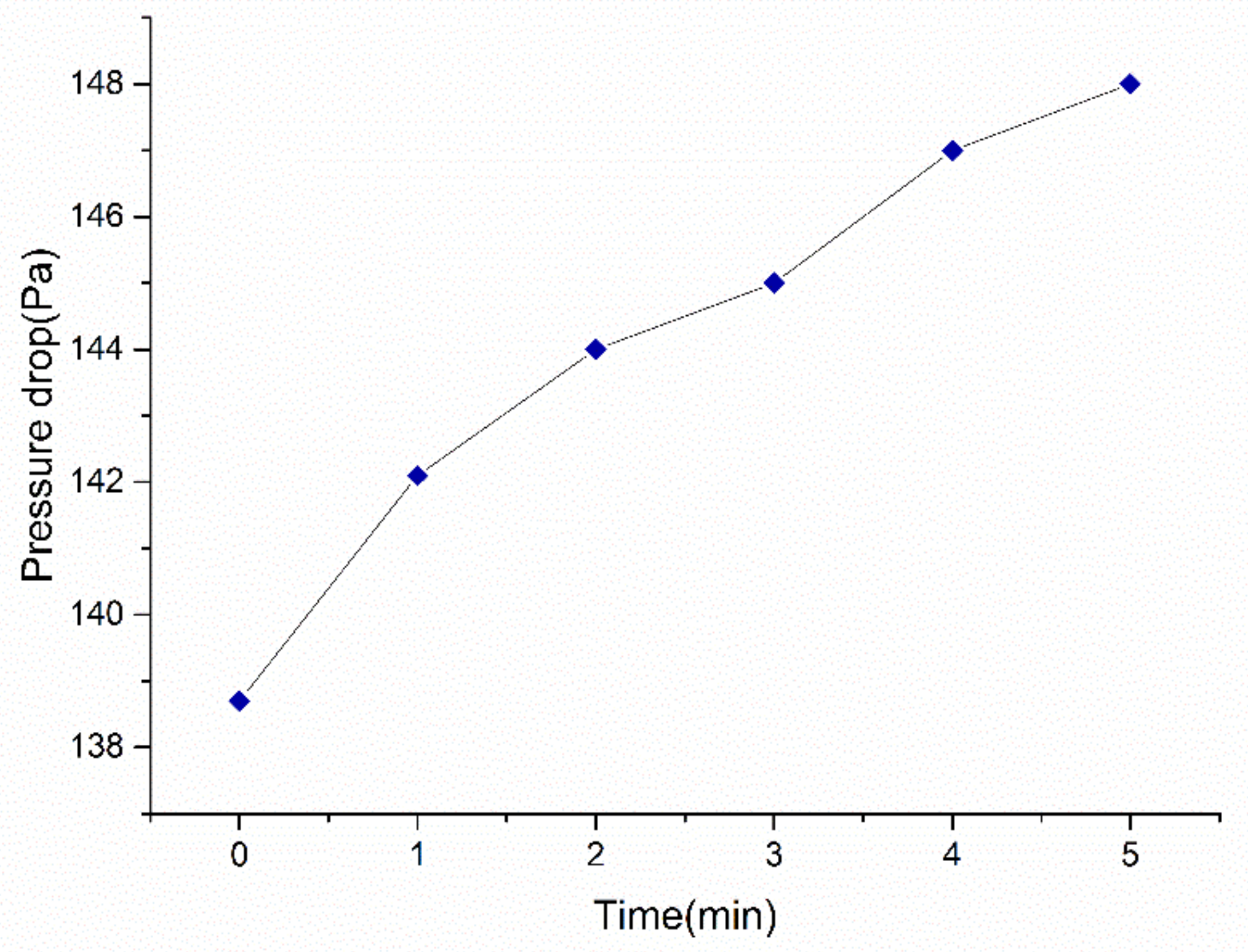
3.3.2. Humid Air Pressure Drop
4. Frosting under Different Influence Factors
4.1. Frosting at Different Refrigerant Temperatures
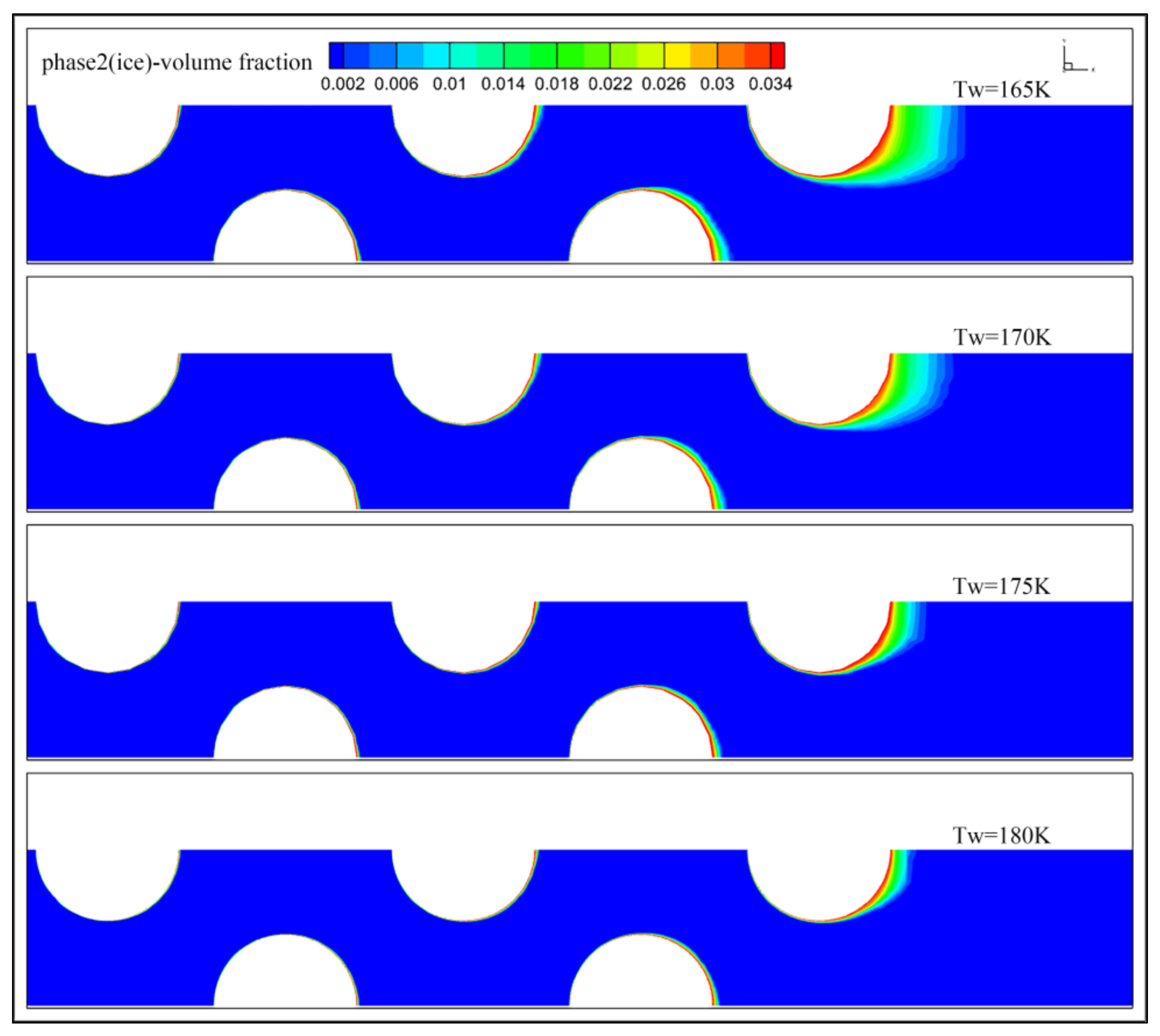
4.1.1. Frost Layer Morphology at Different Refrigerant Temperatures
- (1)
- The overall frost layer formed on each round tube at the beginning of frosting is very thin and the frost density is very low for different wall temperature conditions. At the beginning of frosting, the thickness of the frost layer formed on the wall of the back row (rows 8 to 10) is relatively thick compared to the front row (rows 1 to 7). At different wall temperatures, the thickness of the frost layer formed on rows 8 to 10 at the same time varied significantly. Additionally, the lower the wall temperature, the thicker the frost layer formed on the wall of the 10th row under the same conditions of other parameters. For example, the thickness of the frost layer formed at a wall temperature of 165 K in the 5th minute is about 3 times thicker than that at 180 K. It can be assumed that the frost layer growth is very sensitive to the change of the tube wall temperature. The maximum volume fraction of the second phase (ice phase) formed under the four wall temperature conditions is in the same order of magnitude, while the thickness of the frost layer is significantly different for the same calculation duration, indicating that the effect of the wall temperature on the frost layer growth rate is very obvious. Combined with the mass transfer rate equation:, it can be inferred that the lower the wall temperature the higher the frost driving force and the higher the mass transfer rate.
- (2)
- The growth morphology of the frost on the tube bundle is similar to the numerical calculation of the frost on a single tube. The volume fraction distribution of the second phase on the same tube wall can reflect the mass transfer capacity at different locations on the tube wall. As the high-temperature wet air flows through the tube bundle, the heat exchange between the wet air and the tube bundle is accompanied by a mass transfer from water vapor to frost. In the mass transfer process from water vapor to ice in the phase change process there is also the release of latent heat of phase change. The latent heat will affect the temperature distribution of wet air around the tube wall together with the wall temperature, resulting in differences in the thickness and density of the frost layer at different locations on the same tube wall. The wet air temperature gradually decreases along the flow direction, while the velocity of the wet air is constantly changing, and the heat transfer capacity of the wet air and the tube bundle at different locations is also changing. Therefore, it causes the difference in frost layer density on the circular tube at different locations.
- (3)
- The thickness of the frost layer formed on the wall of each tube increases with time. However, the increase in the thickness of the frost layer on the wall of the front row of tubes was not significant and the change in thickness was almost negligible. This is mainly due to the high inlet wet air temperature, which is taken as 1473 K. Although the wall temperature is ultra-low temperature, the temperature around the front wall is still high and the mass transfer coefficient is very low, and the frost layer can be formed very thin, and the frost layer has almost no effect on the surrounding temperature distribution. Therefore, no significant frost layer growth could be observed on the front row of round tubes.
- (4)
- The morphology of the frost layer formed on the tube bundle is slightly different from that calculated for single-tube frosting, as can be seen from the morphology of the frost layer in rows 9 and 10. One of the dominant factors affecting the formation of the frost layer is the temperature of the moist air. The wet air flowing in the tube bundle is jointly influenced by the adjacent circular tubes and the temperature field is different from that around the single circular tube, so the shape of the frost layer on the tube bundle is also different from that of the single tube.
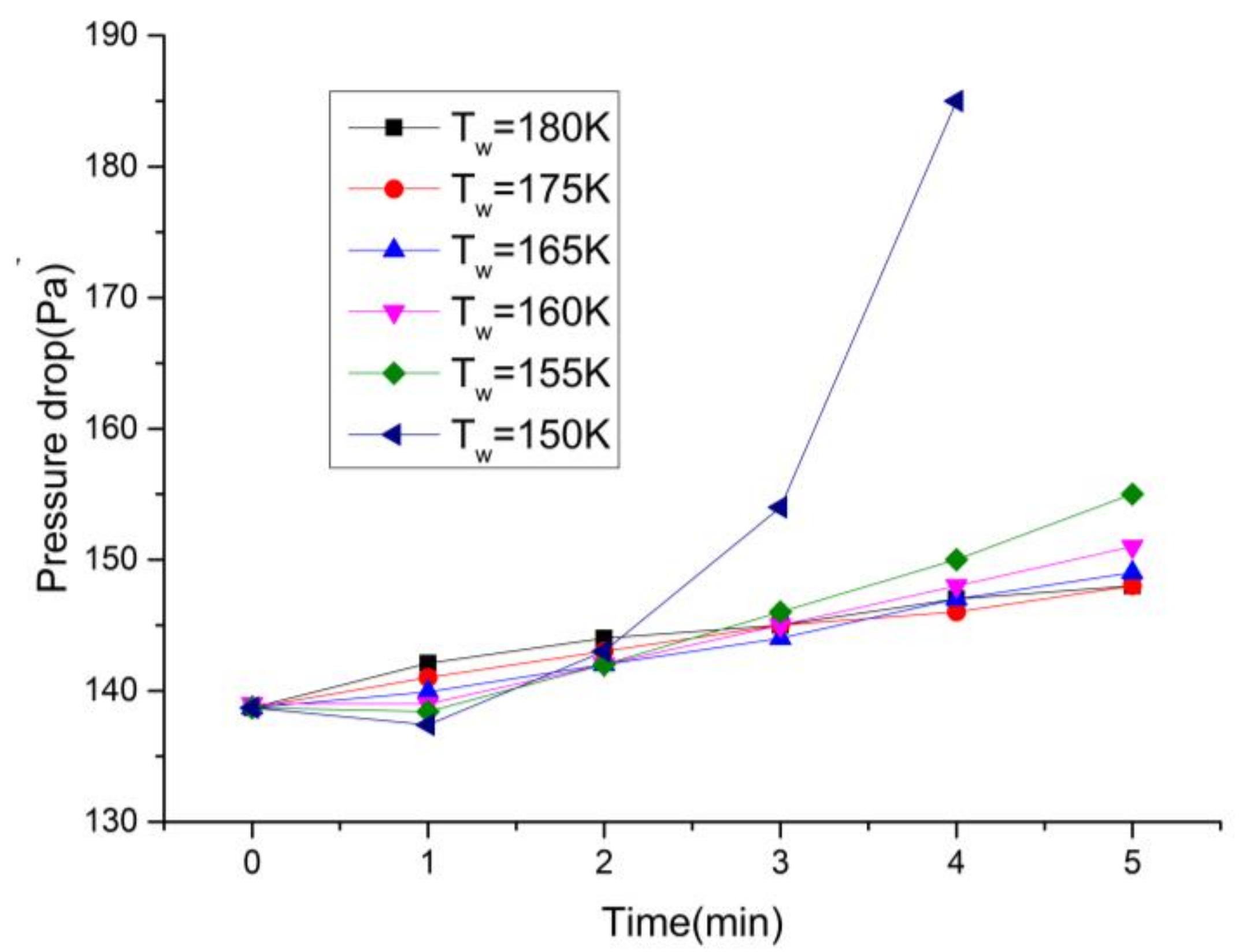
4.1.2. Pressure Drop at Different Refrigerant Temperatures
4.2. Frosting at Different Flow Velocity
4.2.1. Frost Layer Morphology at Different Flow Velocity
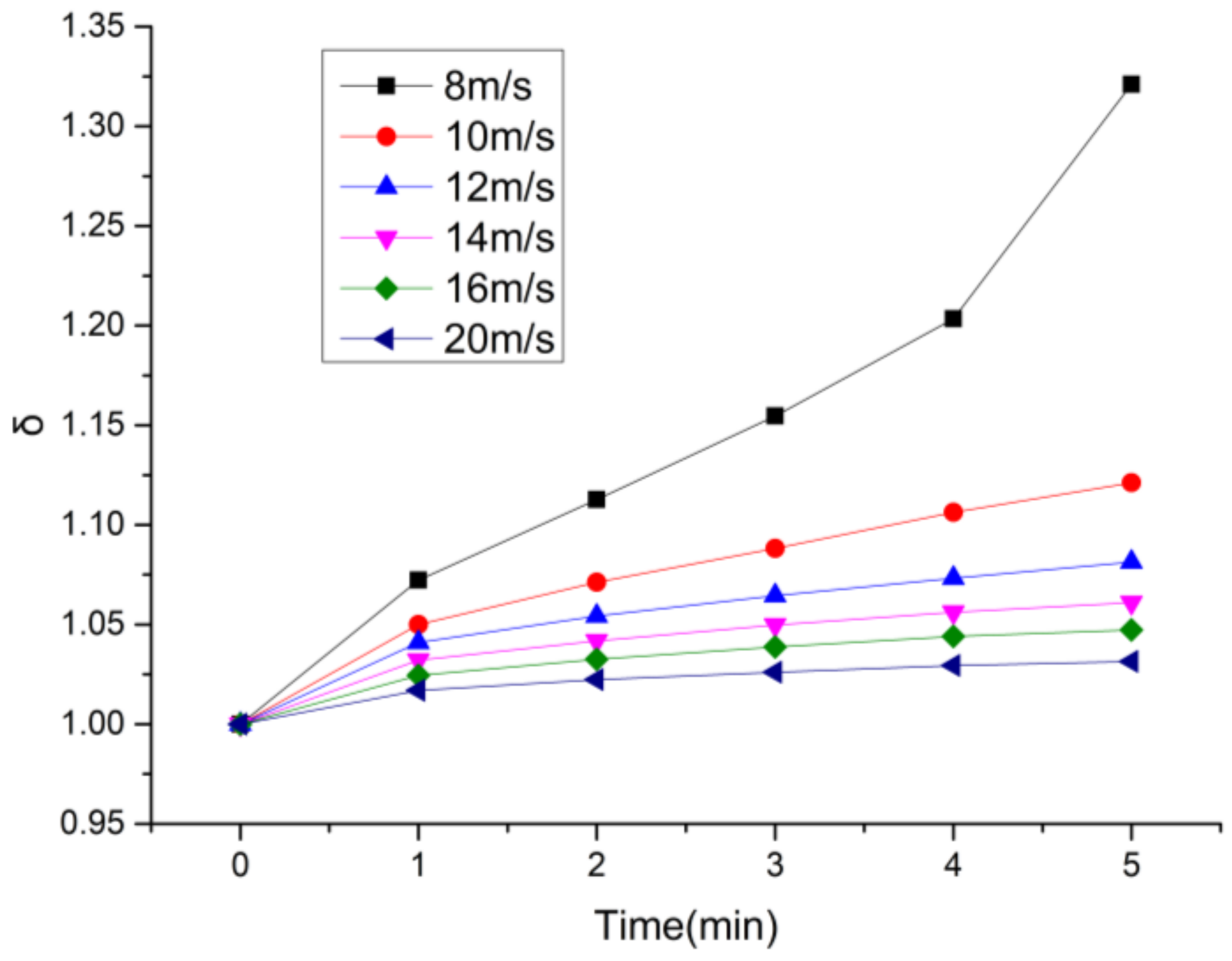
4.2.2. Pressure Drop at Different Flow Velocity
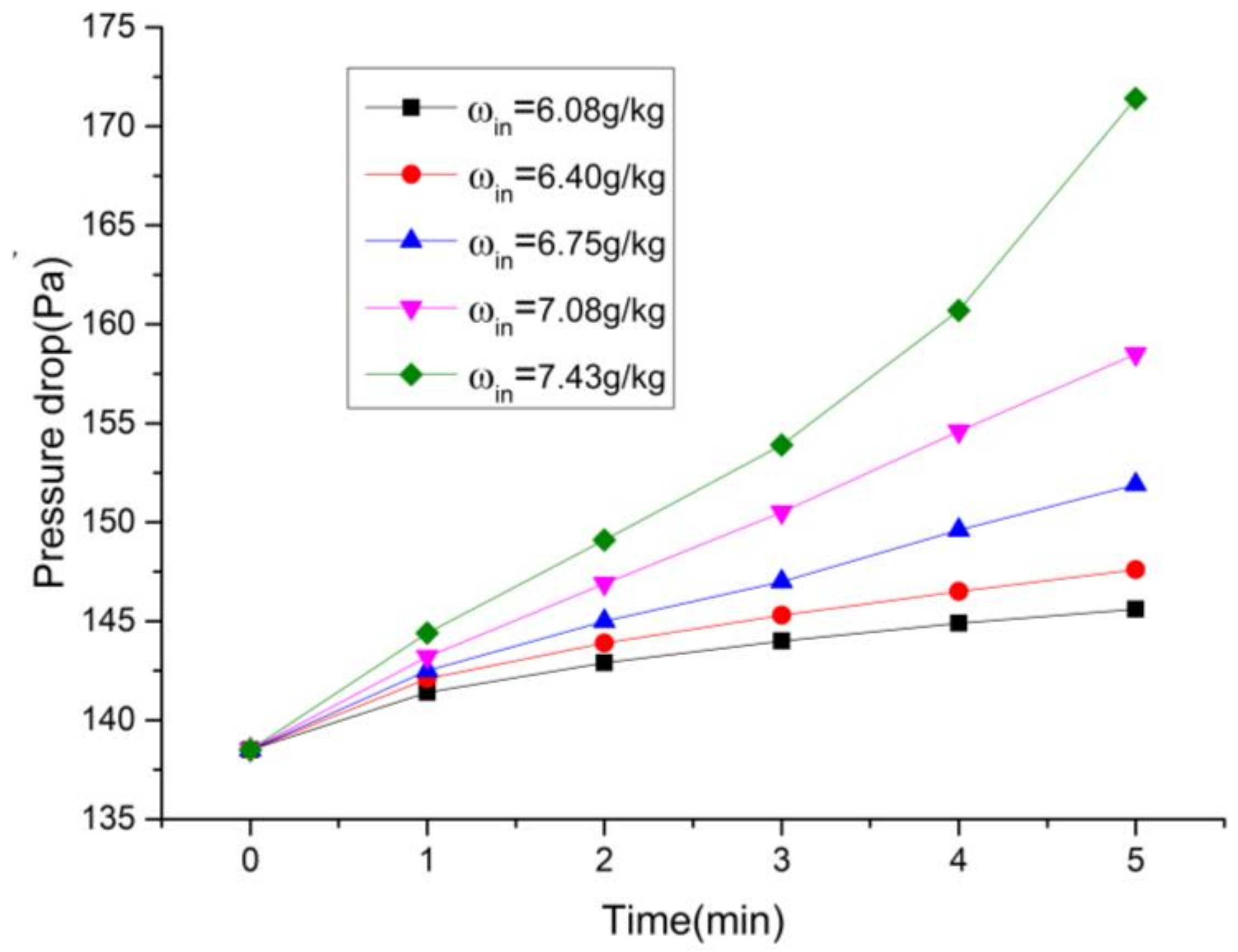
4.3. Frosting under Different Inlet Water Vapor Content
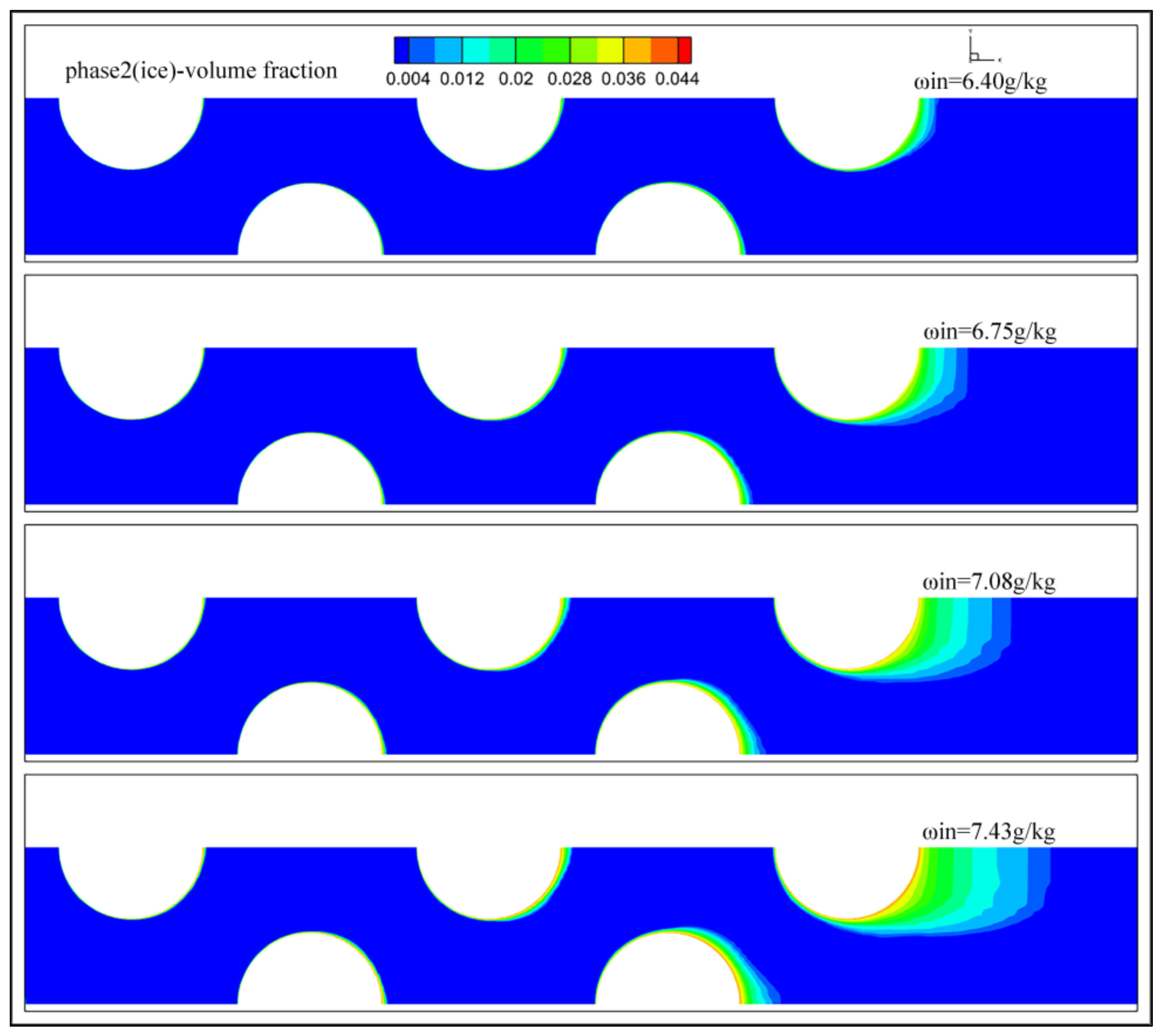
Frost Layer Morphology at Different Water Vapor Content
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mun, H.; Kim, H.; Park, J.; Lee, I. Novel boil-off gas reliquefaction system using liquid air for intercontinental liquefied natural gas transportation. Energy Convers. Manag. 2022, 269, 116078. [Google Scholar] [CrossRef]
- Brenk, A.; Kielar, J.; Malecha, Z.; Rogala, Z. The Effect of Geometrical Modifications to a Shell and Tube Heat Exchanger on Performance and Freezing Risk During Lng Regasification. Int. J. Heat Mass Transf. 2020, 161, 120247. [Google Scholar] [CrossRef]
- Liu, S.; Jiao, W.; Ren, L.; Tian, X. Thermal Resistance Analysis of Cryogenic Frosting and Its Effect on Performance of Lng Ambient Air Vaporizer. Renew. Energy 2020, 149, 917–927. [Google Scholar] [CrossRef]
- Kwon, J.; Yun, S.; Lee, S.; Cho, W.; Kim, Y. Air-Side Heat Transfer Characteristics of Ambient Air Vaporizers with Various Geometric Parameters under Cryogenic Frosting Conditions. Int. J. Heat Mass Transf. 2022, 184, 122245. [Google Scholar] [CrossRef]
- Liu, S.; Jiao, W.; Wang, H. Three-Dimensional Numerical Analysis of the Coupled Heat Transfer Performance of Lng Ambient Air Vaporizer. Renew. Energy 2016, 87, 1105–1112. [Google Scholar] [CrossRef]
- Lisowski, F.; Lisowski, E. Finite Element Analysis of Heat Flow through Longitudinal Finned Tubes in the Lng Ambient Air Vaporizer for a Total Frost Case. E3S Web Conf. 2021, 323, 00020. [Google Scholar] [CrossRef]
- Jadav, C.; Chowdhury, K. Design of Reverse Flow Ambient Air Heated Vaporizer under Different Ambient Temperatures and Optimization of the Fin Arrangement. Therm. Sci. Eng. Prog. 2022, 34, 101426. [Google Scholar] [CrossRef]
- Kim, K.H.; Ko, H.J.; Kim, K.; Kim, Y.W.; Cho, K.J. Analysis of Heat Transfer and Frost Layer Formation on a Cryogenic Tank Wall Exposed to the Humid Atmospheric Air. Appl. Therm. Eng. 2009, 29, 2072–2079. [Google Scholar] [CrossRef]
- Li, S.; Ma, T.; Liu, H.; Zhang, Z.; Xiang, Z.; Mo, Z.; Sun, L. Numerical Analysis of Effects of Pre-Cooler Structure Parameter on Its Performance in SABRE. J. Propuls. Technol. 2022, 43, 200818. [Google Scholar]
- Tanbay, T.; Uca, M.B.; Durmayaz, A. Assessment of Nox Emissions of the Scimitar Engine at Mach 5 Based on a Thermodynamic Cycle analysis. Int. J. Hydrog. Energy 2020, 45, 3632–3640. [Google Scholar] [CrossRef]
- Tanbay, T.; Durmayaz, A. Exergy and Nox Emission-Based Ecological Performance Analysis of the Scimitar Engine. J. Eng. Gas Turbines Power 2020, 142, 081008. [Google Scholar] [CrossRef]
- Harada, K.; Tanatsugu, N.; Sato, T. Development Study of a Precooler for the Air-Turboramjet Expander-Cycle Engine. J. Propuls. Power 2001, 17, 1233–1238. [Google Scholar] [CrossRef]
- Sato, T.; Tanatsugu, N.; Kobayashi, H.; Kimura, T.; Tomike, J.I. Countermeasures against the Icing Problem on the Atrex Precooler. Acta Astronaut. 2004, 54, 671–686. [Google Scholar] [CrossRef]
- Sato, T.; Tanatsugu, N.; Naruo, Y.; Omi, J.; Tomike, J.I.; Nishino, T. Development Study on Atrex Engine. In Proceedings of the 49th International Astronautical Congress, Melbourne, Australia, 28 September–2 October 1998. [Google Scholar]
- Hayashi, Y.; Aoki, A.; Adachi, S.; Hori, K. Study of frost properties correlating with frost formation types. J. Heat Transf. 1977, 99, 239. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, K.S.; Yook, S.J. Frost Behavior on a Fin Considering the Heat Conduction of Heat Exchanger Fins. Int. J. Heat Mass Transf. 2009, 52, 2581–2588. [Google Scholar] [CrossRef]
- Choi, S.; Kim, S.J. Effect of Initial Cooling on Heat and Mass Transfer at the Cryogenic Surface under Natural Convective Condition. Int. J. Heat Mass Transf. 2017, 112, 850–861. [Google Scholar] [CrossRef]
- Yang, D.K.; Lee, K.S. Dimensionless Correlations of Frost Properties on a Cold Plate. Int. J. Refrig. 2004, 27, 89–96. [Google Scholar] [CrossRef]
- Hermes, C.J. An Analytical Solution to the Problem of Frost Growth and Densification on Flat Surfaces. Int. J. Heat Mass Transf. 2012, 55, 7346–7651. [Google Scholar] [CrossRef]
- Le Gall, R.; Grillot, J.M.; Jallut, C. Modelling of frost growth and densification. Int. J. Heat Mass Transf. 1997, 40, 3177–3187. [Google Scholar] [CrossRef]
- Byun, S.; Jeong, H.; Kim, D.R.; Lee, K.S. Frost Modeling under Cryogenic Conditions. Int. J. Heat Mass Transf. 2020, 161, 120250. [Google Scholar] [CrossRef]
- Cui, J.; Li, W.Z.; Liu, Y.; Zhao, Y.S. A New Model for Predicting Performance of Fin-and-Tube Heat Exchanger under Frost Condition. Int. J. Heat Fluid Flow 2011, 32, 249–260. [Google Scholar] [CrossRef]
- Cui, J.; Li, W.Z.; Liu, Y.; Jiang, Z.Y. A New Time- and Space-Dependent Model for Predicting Frost Formation. Appl. Therm. Eng. 2011, 31, 447–457. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.; Kim, D.R.; Lee, K.S. Modeling of Frost Layer Growth Considering Frost Porosity. Int. J. Heat Mass Transf. 2018, 126, 980–988. [Google Scholar] [CrossRef]
- Kim, D.; Kim, C.; Lee, K.S. Frosting Model for Predicting Macroscopic and Local Frost Behaviors on a Cold Plate. Int. J. Heat Mass Transf. 2015, 82, 135–142. [Google Scholar] [CrossRef]
- Wu, X.; Ma, Q.; Chu, F. Numerical Simulation of Frosting on Fin-and-Tube Heat Exchanger Surfaces. J. Therm. Sci. Eng. Appl. 2017, 9, 031007. [Google Scholar] [CrossRef]
- Afrasiabian, E.; Iliev, O.; Lazzari, S.; Isetti, C. Numerical Simulation of Frost Formation on a Plate-Fin Evaporator. In Proceedings of the 3rd World Congress on Momentum, Heat and Mass Transfer, Budapest, Hungary, 12–14 April 2018. [Google Scholar]
- Kandula, M. Frost Growth and Densification in Laminar Flow over Flat Surfaces. Int. J. Heat Mass Transf. 2011, 54, 3719–3731. [Google Scholar] [CrossRef]
- Hermes, C.J.; Piucco, R.O.; Barbosa Jr, J.R.; Melo, C. A Study of Frost Growth and Densification on Flat Surfaces. Exp. Therm. Fluid Sci. 2009, 33, 371–379. [Google Scholar] [CrossRef]
- Wang, W.; Guo, Q.C.; Lu, W.P.; Feng, Y.C.; Na, W. A Generalized Simple Model for Predicting Frost Growth on Cold Flat Plate. Int. J. Refrig. 2012, 35, 475–486. [Google Scholar] [CrossRef]
- Jia, Y. Researches on the Flow, Heat Transfer and Frosting for Air Cooling by Mini Tube Bundle at Very Low Temperature. Ph.D. Thesis, Tsinghua University, Beijing, China.
- Fernandez Villace, V.; Paniagua, G. Simulation of a Variable-Combined-Cycle Engine for Dual Subsonic and Supersonic Cruise. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011. [Google Scholar]
- Zhukauskas, A. Convective Heat Transfer in Heat Exchangers; Science Publishing House: Beijing, China, 1986. [Google Scholar]
- Yu, S.; Jones, T.; Ogawa, H.; Karwa, N. Multi-Objective Design Optimization of Precoolers for Hypersonic Airbreathing Propulsion. J. Thermophys. Heat Transf. 2017, 31, 421–433. [Google Scholar] [CrossRef]









| Number | Relative Humidity | |||
|---|---|---|---|---|
| 1 | 10.5 | 80% | −8 | 5 |
| 2 | 22 | 80% | −15 | 0.7 |
| 3 | 15 | 68% | −130 | 2 |
| 4 | 15 | 48.7% | −130 | 1.5 |
| 5 | 10 | 29.2% | −160 | 1 |
| 6 | 20 | 67.8% | −100 | 2 |
| 7 | 10.5 | 80% | −10.5 | 5 |
| 8 | 16 | 80% | −16 | 0.7 |
| Wall Temperature (K) | Water Vapor Content (g/kg) | Inlet Flow Rate (m/s) |
|---|---|---|
| 120–180 | 6.08–7.43 | 8–20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, Y.; Liu, M.; Wu, H.; Wang, J.; Zhao, R. Simulation of Forced Convection Frost Formation in Microtubule Bundles at Ultra-Low Temperature. Aerospace 2022, 9, 630. https://doi.org/10.3390/aerospace9100630
Mi Y, Liu M, Wu H, Wang J, Zhao R. Simulation of Forced Convection Frost Formation in Microtubule Bundles at Ultra-Low Temperature. Aerospace. 2022; 9(10):630. https://doi.org/10.3390/aerospace9100630
Chicago/Turabian StyleMi, Youzhi, Meng Liu, Hao Wu, Jun Wang, and Ruikai Zhao. 2022. "Simulation of Forced Convection Frost Formation in Microtubule Bundles at Ultra-Low Temperature" Aerospace 9, no. 10: 630. https://doi.org/10.3390/aerospace9100630
APA StyleMi, Y., Liu, M., Wu, H., Wang, J., & Zhao, R. (2022). Simulation of Forced Convection Frost Formation in Microtubule Bundles at Ultra-Low Temperature. Aerospace, 9(10), 630. https://doi.org/10.3390/aerospace9100630





