Simplified Model for Forward-Flight Transitions of a Bio-Inspired Unmanned Aerial Vehicle
Abstract
1. Introduction
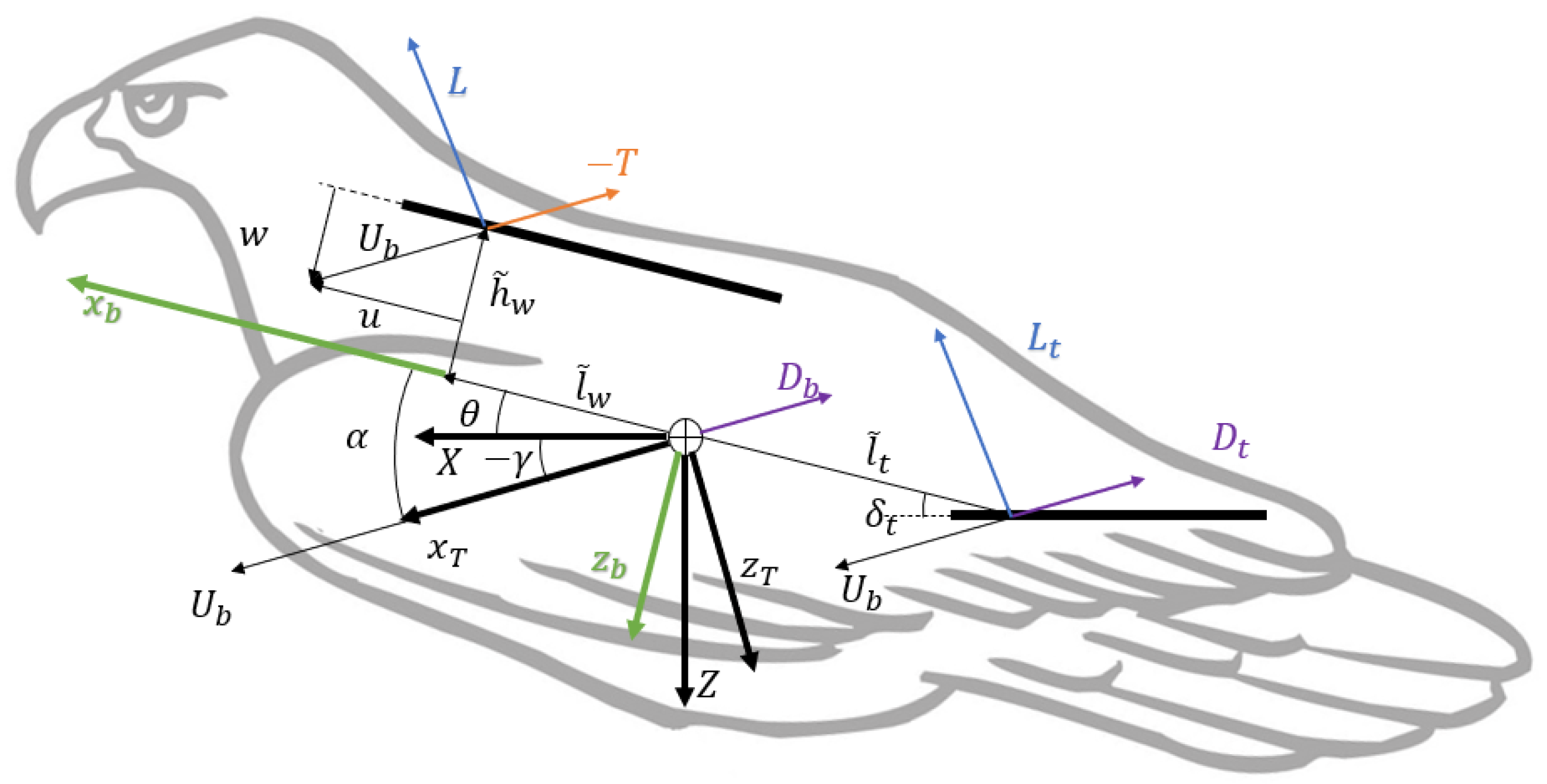
2. Flight Model
2.1. Non-Dimensional Newton–Euler Equations
2.2. Aerodynamic Characterization
 /(
/( + 2), where
+ 2), where  is the aspect ratio of the wing. On the other hand, Smits [16] proposes a discontinuous factor for the added mass terms, with
is the aspect ratio of the wing. On the other hand, Smits [16] proposes a discontinuous factor for the added mass terms, with  for
for  and just unity for
and just unity for  . This last factor is the appropriate one for the wings considered here. We can write the (modified) lift coefficient as a function of the state variables:
. This last factor is the appropriate one for the wings considered here. We can write the (modified) lift coefficient as a function of the state variables: 3. Numerical Results and Experimental Validation
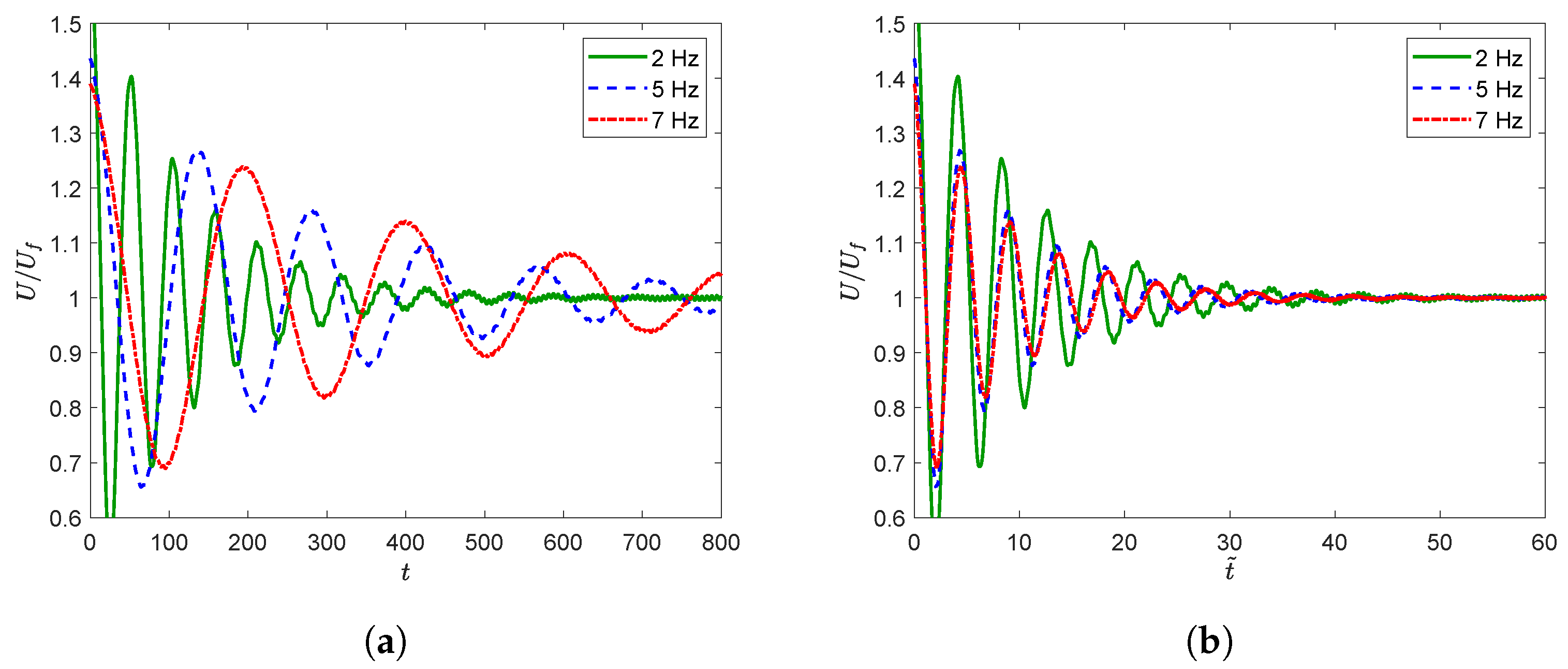
3.1. Numerical Results
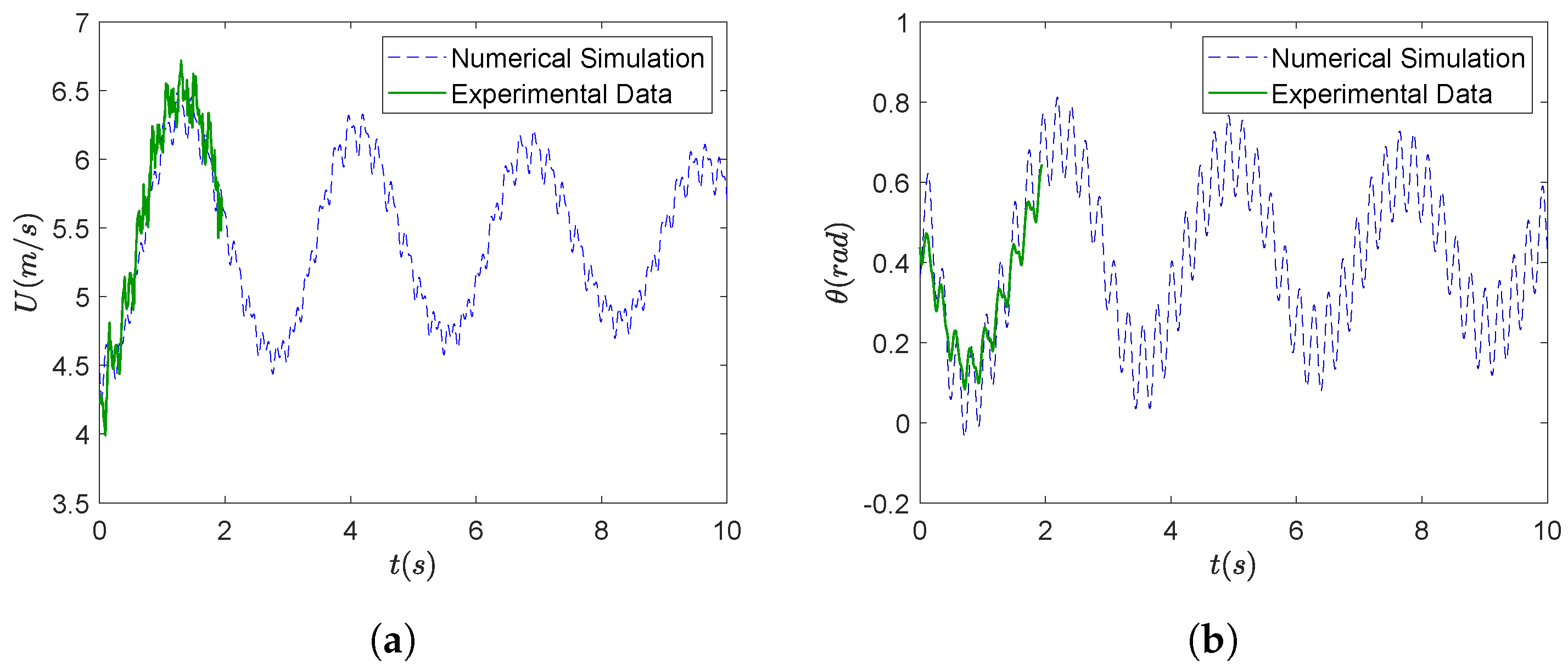
3.2. Experimental Validation
4. Analytical Perturbation Solution and Its Comparison with the Numerical Solution
4.1. Scales Analysis
- Small flight angles: . Reduced angles of attack are required by the present aerodynamic formulation, as well as small deflections of the tail. All of them are assumed to be in the same order of magnitude as the flapping amplitude . Small and mean that aggressive climbing trajectories are not considered. Moreover, small flapping amplitude implies a limited thrust, which is proportional to (see below), so reaching large flight path angles would be possible only with high reduced frequencies, which are difficult to obtain in bird-scale ornithopters.
- Thrust coefficient: . Clearly from the Formulation (9), with products of the aerodynamic angles and the flapping amplitude.
- Drag coefficients: . This is clear for the induced drag, as it is proportional to the square of the lift coefficient. On the other hand, friction drag cannot be larger than thrust to maintain flight.
- Non-dimensional inertia and reduced frequency: . Given in Table 1. Even though the frequency is a control variable, we can consider both terms of order unity in the typical range of bird-like ornithopters.
- All the remaining non-dimensional parameters either do not affect the structure of the solution or are order unity.
4.2. Perturbation Solution
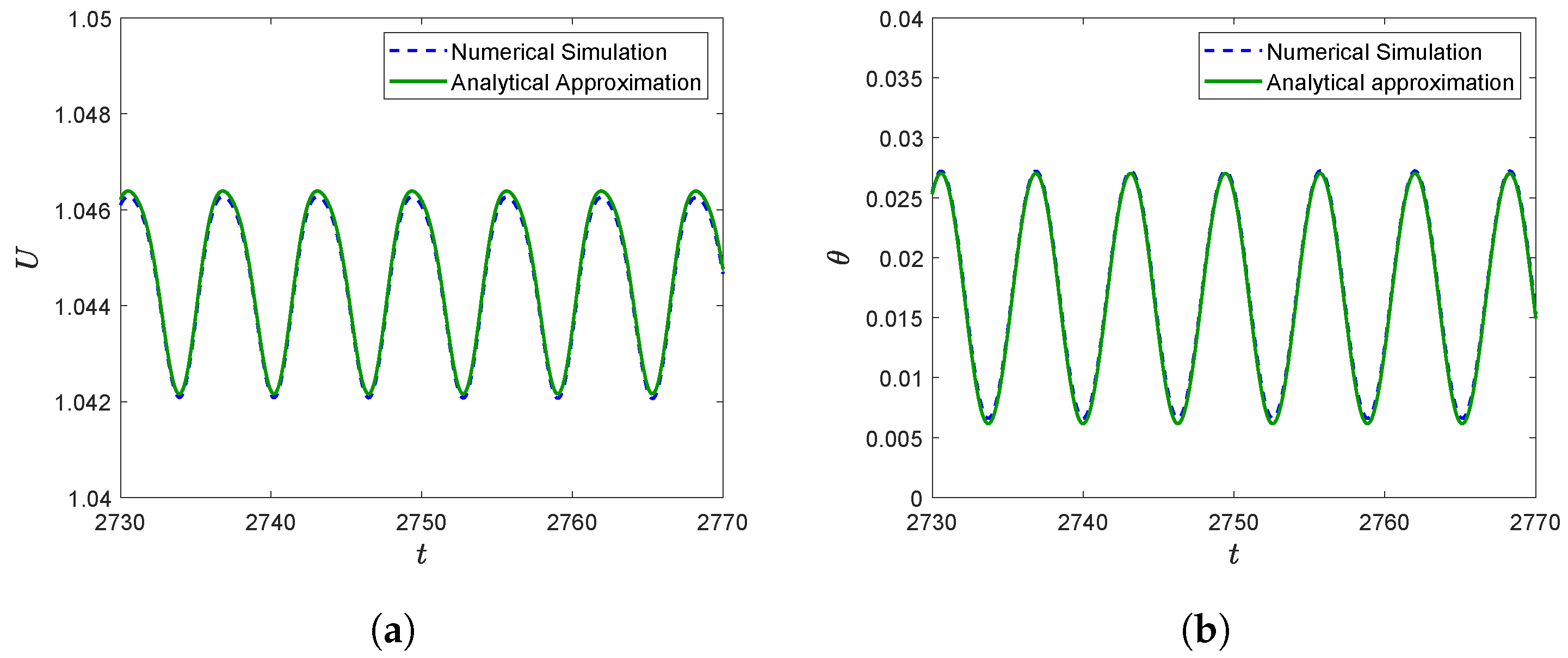
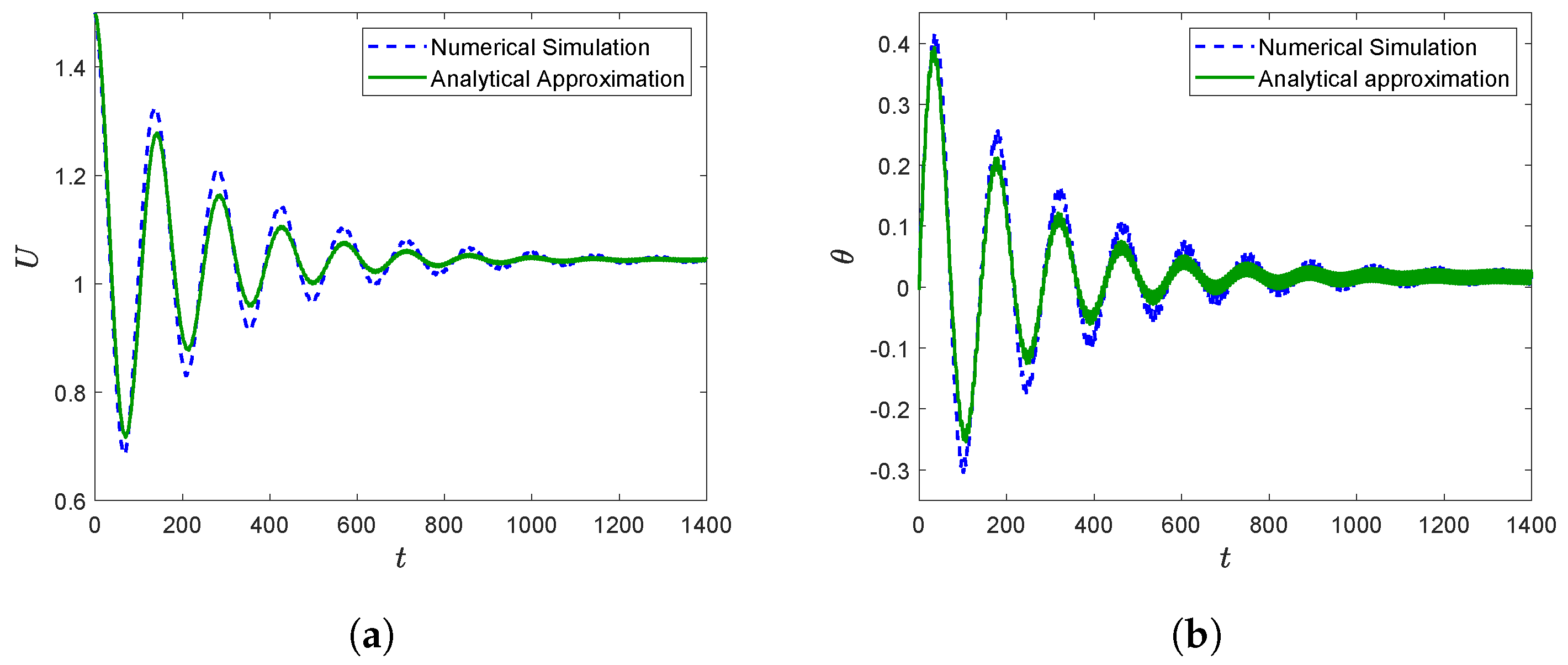
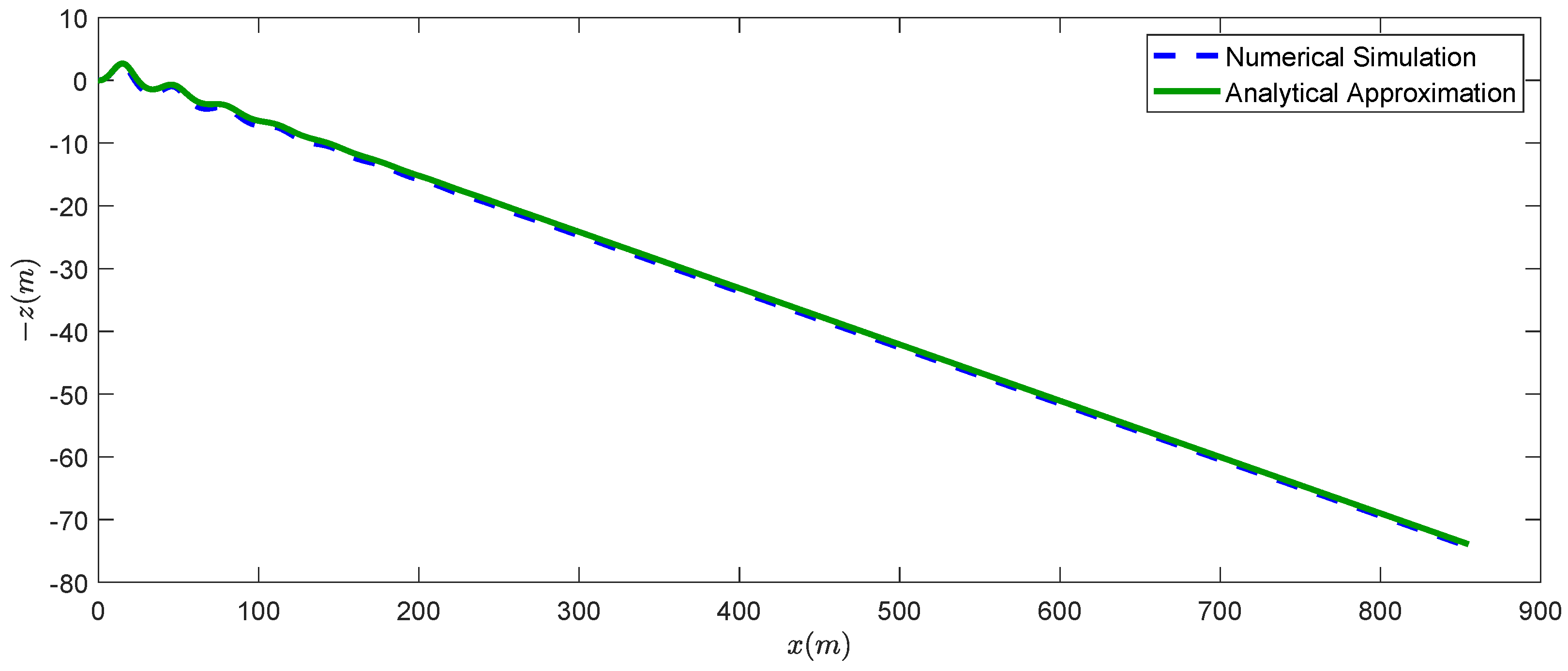
4.3. Comparison between Analytical and Numerical Results
- For the large-time asymptotic values of the velocity and the pitch angle, we consider terms up to order , while for the angle of attack, the approximation is even better, up to order .
- Transient terms are computed up to order for the velocity and the pitch angle, and to order for the angle of attack.
- Harmonic oscillations with the flapping frequencies are considered up to order for the three variables, including asymptotic and transient values.
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Aerodynamic Coefficients in Equations (9) and (10)
Appendix B. Higher Order Perturbation Terms
References
- Mueller, T.J. Fixed and Flapping Wing Aerodynamics for Micro Air Vehicle Applications; AIAA: Notre Dame, IN, USA, 2001. [Google Scholar]
- Gerdes, J.; Holness, A.; Perez-Rosado, A.; Roberts, L.; Greisinger, A.; Barnett, E.; Kempny, J.; Lingam, D.; Yeh, C.H.; Bruck, H.A.; et al. Robo Raven: A flapping-wing air vehicle with highly compliant and independently controlled wings. Soft Robot. 2014, 1, 275–288. [Google Scholar] [CrossRef]
- Srigrarom, S.; Chan, W.-L. Ornithopter Type Flapping Wings for Autonomous Micro Air Vehicles. Aerospace 2015, 2, 235–278. [Google Scholar] [CrossRef]
- Folkertsma, G.A.; Straatman, W.; Nijenhuis, N.; Venner, C.H.; Stramigioli, S. Robird: A robotic bird of prey. IEEE Robot. Autom. Mag. 2017, 24, 22–29. [Google Scholar] [CrossRef]
- Zufferey, R.; Tormo-Barbero, J.; Guzmán, M.M.; Maldonado, F.J.; Sanchez-Laulhe, E.; Grau, P.; Pérez, M.; Acosta, J.Á.; Ollero, A. Design of the High-Payload Flapping Wing Robot E-Flap. IEEE Robot. Autom. Lett. 2021, 6, 3097–3104. [Google Scholar] [CrossRef]
- Grauer, J.; Ulrich, E.; Hubbard, J., Jr.; Pines, D.; Humbert, J.S. Testing and system identification of an ornithopter in longitudinal flight. J. Aircr. 2011, 48, 660–667. [Google Scholar] [CrossRef]
- Taha, H.; Hajj, M.R.; Nayfeh, A. Flight dynamics and control of flapping-wing MAVs: A review. Nonlinear Dyn. 2012, 70, 907–939. [Google Scholar] [CrossRef]
- Wang, Z.J. Dissecting insect flight. Annu. Rev. Fluid Mech. 2005, 37, 183–210. [Google Scholar] [CrossRef]
- Hefler, C.; Kang, C.; Qiu, H.; Shyy, W. Distinct Aerodynamics of Insect-Scale Flight; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; NACA Technical Report TR 496; NACA: Washington, DC, USA, 1935. [Google Scholar]
- Garrick, I.E. Propulsion of a Flapping and Oscillating Airfoil; NACA Technical Report TR 567; NACA: Washington, DC, USA, 1936. [Google Scholar]
- DeLaurier, J.D. An aerodynamic model for flapping-wing flight. Aeronaut. J. 1993, 97, 125–130. [Google Scholar]
- Kim, D.K.; Lee, J.S.; Lee, J.Y.; Han, J.H. An aeroelastic analysis of a flexible flapping wing using modified strip theory. In Active and Passive Smart Structures and Integrated Systems 2008; International Society for Optics and Photonics: SPIE: Bellingham, WA, USA, 2008; Volume 6928, pp. 477–484. [Google Scholar]
- Fernandez-Feria, R. Linearized propulsion theory of flapping airfoils revisited. Phys. Rev. Fluids 2016, 1, 084502. [Google Scholar] [CrossRef]
- Ayancik, F.; Zhong, Q.; Quinn, D.B.; Brandes, A.; Bart-Smith, H.; Moored, K.W. Scaling laws for the propulsive performance of three-dimensional pitching propulsors. J. Fluid Mech. 2019, 871, 1117–1138. [Google Scholar] [CrossRef]
- Smits, A.J. Undulatory and oscillatory swimming. J. Fluid Mech. 2019, 874, 1–44. [Google Scholar] [CrossRef]
- Dietl, J.M.; Garcia, E. Stability in ornithopter longitudinal flight dynamics. J. Guid. Control. Dyn. 2008, 31, 1157–1163. [Google Scholar] [CrossRef]
- Dietl, J.M.; Garcia, E. Ornithopter optimal trajectory control. Aerosp. Sci. Technol. 2013, 26, 192–199. [Google Scholar] [CrossRef]
- Paranjape, A.A.; Dorothy, M.R.; Chung, S.J.; Lee, K.D. A flight mechanics-centric review of bird-scale flapping flight. Int. J. Aeronaut. Space Sci. 2012, 13, 267–281. [Google Scholar] [CrossRef][Green Version]
- Taylor, G.K.; Żbikowski, R. Nonlinear time-periodic models of the longitudinal flight dynamics of desert locusts Schistocerca gregaria. J. R. Soc. Interface 2005, 2, 197–221. [Google Scholar] [CrossRef] [PubMed]
- Gim, H.; Lee, B.; Huh, J.; Kim, S.; Suk, J. Longitudinal system identification of an avian-type UAV considering characteristics of actuator. Int. J. Aeronaut. Space Sci. 2018, 19, 1017–1026. [Google Scholar] [CrossRef]
- Grauer, J.A.; Hubbard, J.E., Jr. Multibody model of an ornithopter. J. Guid. Control. Dyn. 2009, 32, 1675–1679. [Google Scholar] [CrossRef]
- Amini, M.A.; Ayati, M.; Mahjoob, M. A Simplified Model, Dynamic Analysis and Force Estimation for a Large-scale Orinthopter in Forward Flight Based on Flight Data. J. Bionic Eng. 2020, 17, 989–1008. [Google Scholar] [CrossRef]
- Pfeiffer, A.T.; Lee, J.S.; Han, J.H.; Baier, H. Ornithopter flight simulation based on flexible multi-body dynamics. J. Bionic Eng. 2010, 7, 102–111. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, J.K.; Kim, D.K.; Han, J.H. Longitudinal flight dynamics of bioinspired ornithopter considering fluid-structure interaction. J. Guid. Control. Dyn. 2011, 34, 667–677. [Google Scholar] [CrossRef]
- Martín-Alcántara, A.; Grau, P.; Fernandez-Feria, R.; Ollero, A. A Simple Model for Gliding and Low-Amplitude Flapping Flight of a Bio-Inspired UAV. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 729–737. [Google Scholar] [CrossRef]
- Sanchez-Laulhe, E.; Fernandez-Feria, R.; Acosta, J.Á.; Ollero, A. Effects of Unsteady Aerodynamics on Gliding Stability of a Bio-Inspired UAV. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 1596–1604. [Google Scholar] [CrossRef]
- Ol, M.V.; Bernal, L.; Kang, C.-K.; Shyy, W. Shallow and deep dynamic stall for flapping low Reynolds number airfoils. Exp. Fluids 2009, 46, 883–901. [Google Scholar] [CrossRef]
- Baik, Y.S.; Bernal, L.P.; Granlund, K.; Ol, M.V. Unsteady force generation and vortex dynamics of pitching and plunging aerofoils. J. Fluid Mech. 2012, 709, 37–68. [Google Scholar] [CrossRef]
- Fernandez-Feria, R. Note on optimum propulsion of heaving and pitching airfoils from linear potential theory. J. Fluid Mech. 2017, 826, 781–796. [Google Scholar] [CrossRef]
- Alaminos-Quesada, J. Limit of the two-dimensional linear potential theories on the propulsion of a flapping airfoil in forward flight in terms of the Reynolds and Strouhal number. Phys. Rev. Fluids 2021, 6, 123101. [Google Scholar] [CrossRef]
- Sánchez-Rodríguez, J.; Raufaste, C.; Argentina, M. A minimal model of self propelled locomotion. J. Fluids Struct. 2020, 97, 103071. [Google Scholar] [CrossRef]
- Lopez-Lopez, R.; Perez-Sanchez, V.; Ramon-Soria, P.; Martin-Alcantara, A.; Fernandez-Feria, R.; Arrue, B.C.; Ollero, A. A Linearized Model for an Ornithopter in Gliding Flight: Experiments and Simulations. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France; 2020; pp. 7008–7014. [Google Scholar]
- Wang, Z.J.; Birch, J.M.; Dickinson, M.H. Unsteady forces and flows in low Reynolds number hovering flight: Two-dimensional computations vs robotic wing experiments. J. Exp. Biol. 2004, 207, 449–460. [Google Scholar] [CrossRef]
- Jones, R.T. Properties of Low-Aspect-Ratio Pointed Wings at Speeds below and above the Speed of Sound; NACA Technical Report TR 835; NACA: Washington, DC, USA, 1946. [Google Scholar]
- Thomas, A.L.R. On the aerodynamics of birds’ tails. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1993, 340, 361–380. [Google Scholar] [CrossRef]
- Evans, M.R. Birds’ tails do act like delta wings but delta-wing theory does not always predict the forces they generate. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2003, 270, 1379–1385. [Google Scholar] [CrossRef]
- Kevorkian, J.; Cole, J.D. Perturbation Methods in Applied Mathematics; Springer: New York, NY, USA, 1981. [Google Scholar]
- Ruiz, C.; Acosta, J.; Ollero, A. Aerodynamic reduced-order Volterra model of an ornithopter under high-amplitude flapping. Aerosp. Sci. Technol. 2022, 121, 107331. [Google Scholar] [CrossRef]


| f |  | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 Hz | |||||||||
| 5 Hz | |||||||||
| 7 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchez-Laulhe, E.; Fernandez-Feria, R.; Ollero, A. Simplified Model for Forward-Flight Transitions of a Bio-Inspired Unmanned Aerial Vehicle. Aerospace 2022, 9, 617. https://doi.org/10.3390/aerospace9100617
Sanchez-Laulhe E, Fernandez-Feria R, Ollero A. Simplified Model for Forward-Flight Transitions of a Bio-Inspired Unmanned Aerial Vehicle. Aerospace. 2022; 9(10):617. https://doi.org/10.3390/aerospace9100617
Chicago/Turabian StyleSanchez-Laulhe, Ernesto, Ramon Fernandez-Feria, and Anibal Ollero. 2022. "Simplified Model for Forward-Flight Transitions of a Bio-Inspired Unmanned Aerial Vehicle" Aerospace 9, no. 10: 617. https://doi.org/10.3390/aerospace9100617
APA StyleSanchez-Laulhe, E., Fernandez-Feria, R., & Ollero, A. (2022). Simplified Model for Forward-Flight Transitions of a Bio-Inspired Unmanned Aerial Vehicle. Aerospace, 9(10), 617. https://doi.org/10.3390/aerospace9100617






