A New Method for Analyzing the Aero-Optical Effects of Hypersonic Vehicles Based on a Microscopic Mechanism
Abstract
1. Introduction
2. Microscopic Mechanism of Aero-Optical Effects
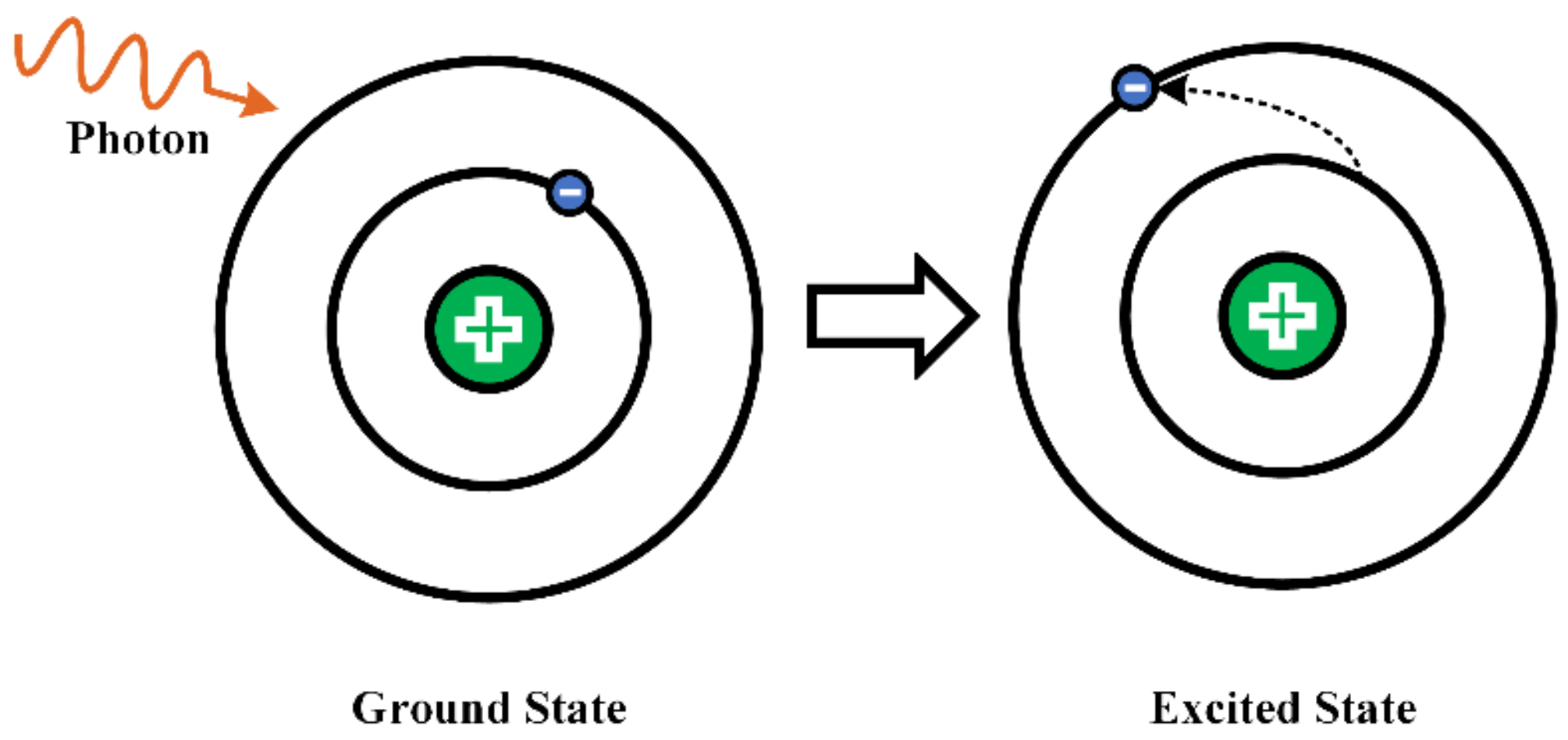
2.1. Absorption of Photons by Turbulent Molecules
2.2. Scattering of Photons by Turbulent Molecules
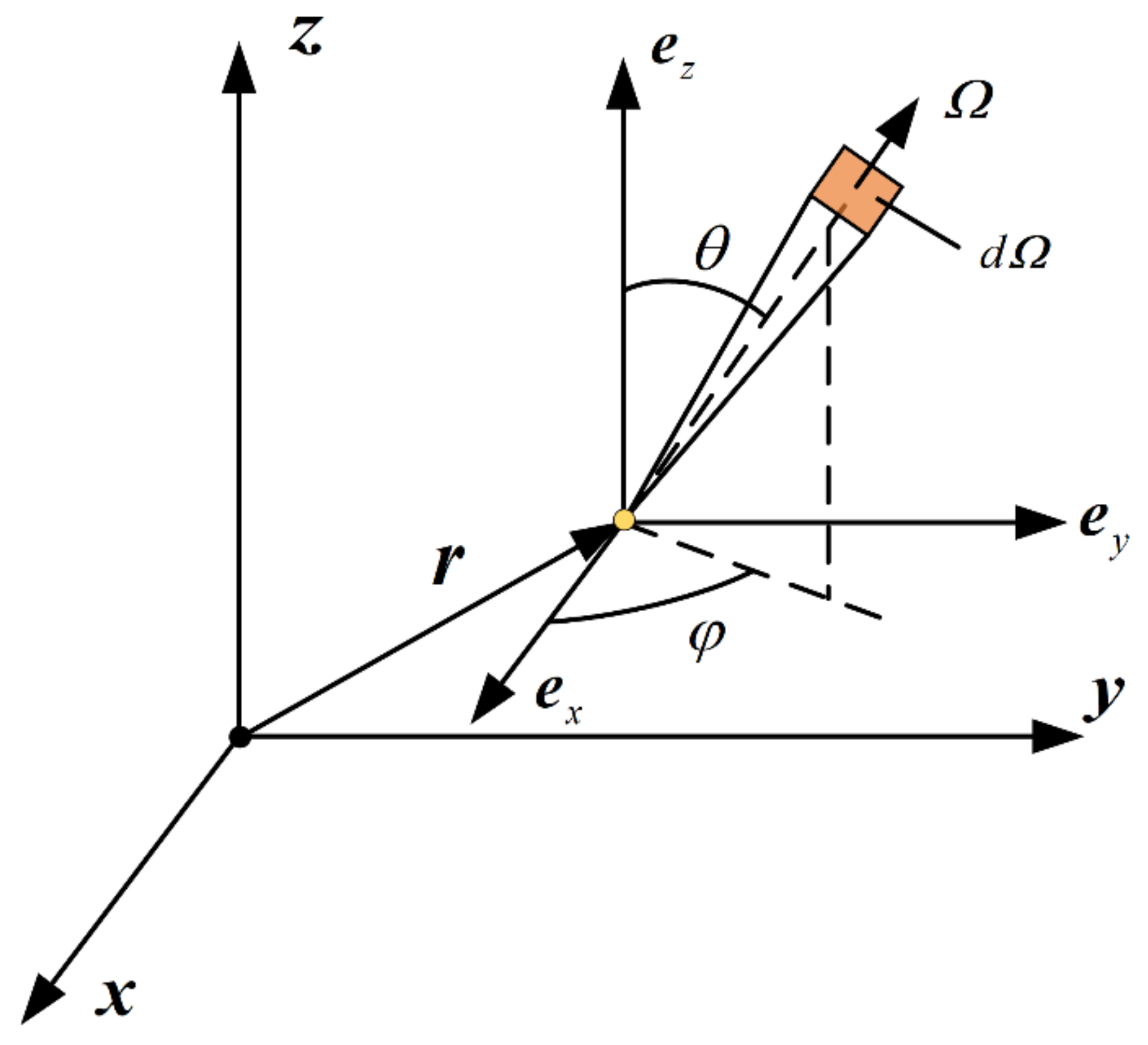
2.3. Transmission Equation of Photons in Turbulent Molecules
3. Design of a Simulation Method for Aero-Optical Effects Based on the Microscopic Mechanism
- Step 1:
- Determine the structure and flight conditions of the aircraft, conduct a large eddy simulation based on computational fluid dynamics, and obtain the turbulent flow field data under the corresponding simulation conditions;
- Step 2:
- Extract the density data from the flow field data and calculate the absorption and scattering coefficients according to the microscopic mechanism in Section 2;
- Step 3:
- Conduct a numerical simulation through the transmission equation of photons in turbulent molecules to obtain the transmission law of photons in turbulent molecules. The design flow chart is shown in Figure 5.
3.1. High-Speed Turbulence via LES
3.2. Numerical Simulation of Photon Transmission in Turbulence
- The photon transmission in turbulent molecules does not consider stimulated radiation;
- The interaction between light and turbulent molecules is described by the absorption coefficient and the scattering coefficient;
- The polarization and interference of photons are ignored.
3.3. Physical Description of Aero-Optical Effects Based on the MSAO
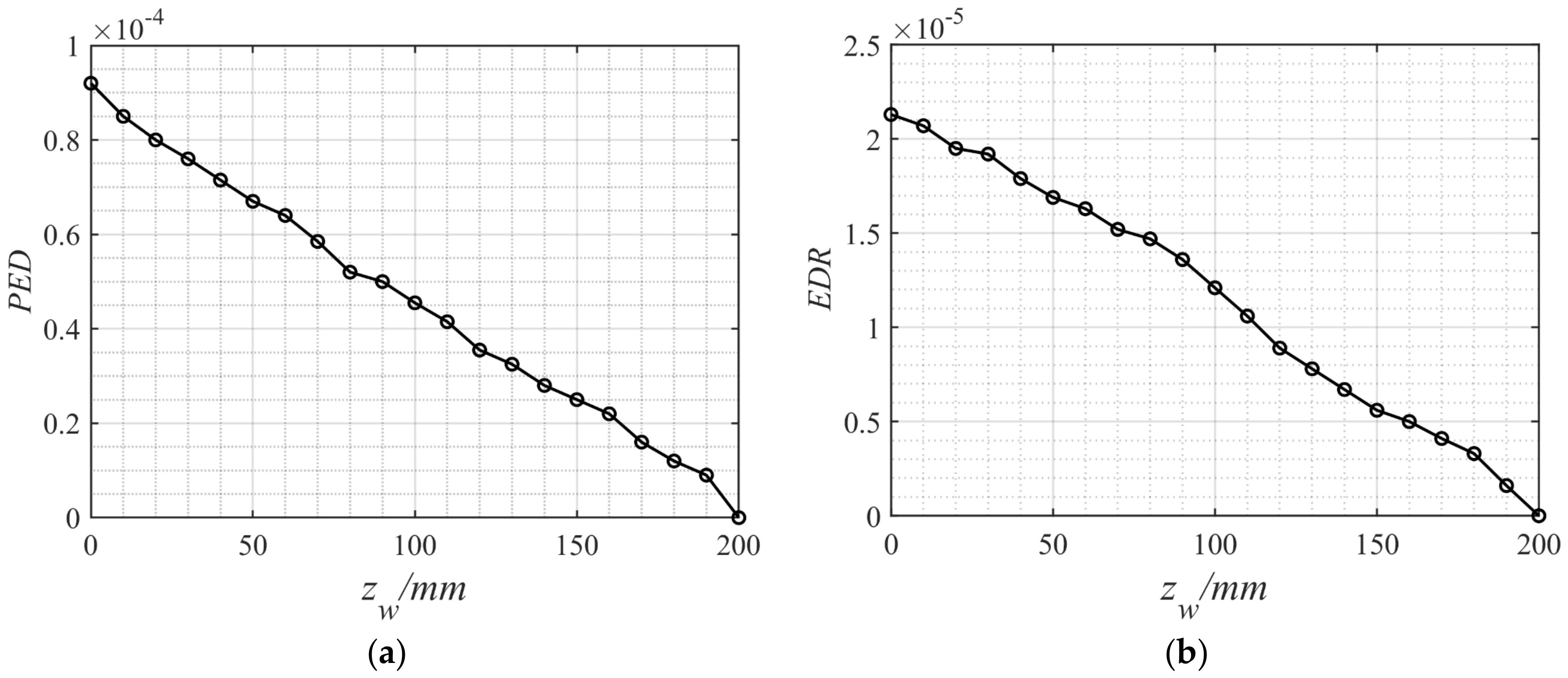
3.3.1. Photon Energy Divergence (PED)
3.3.2. Energy Dissipation Ratio (EDR)
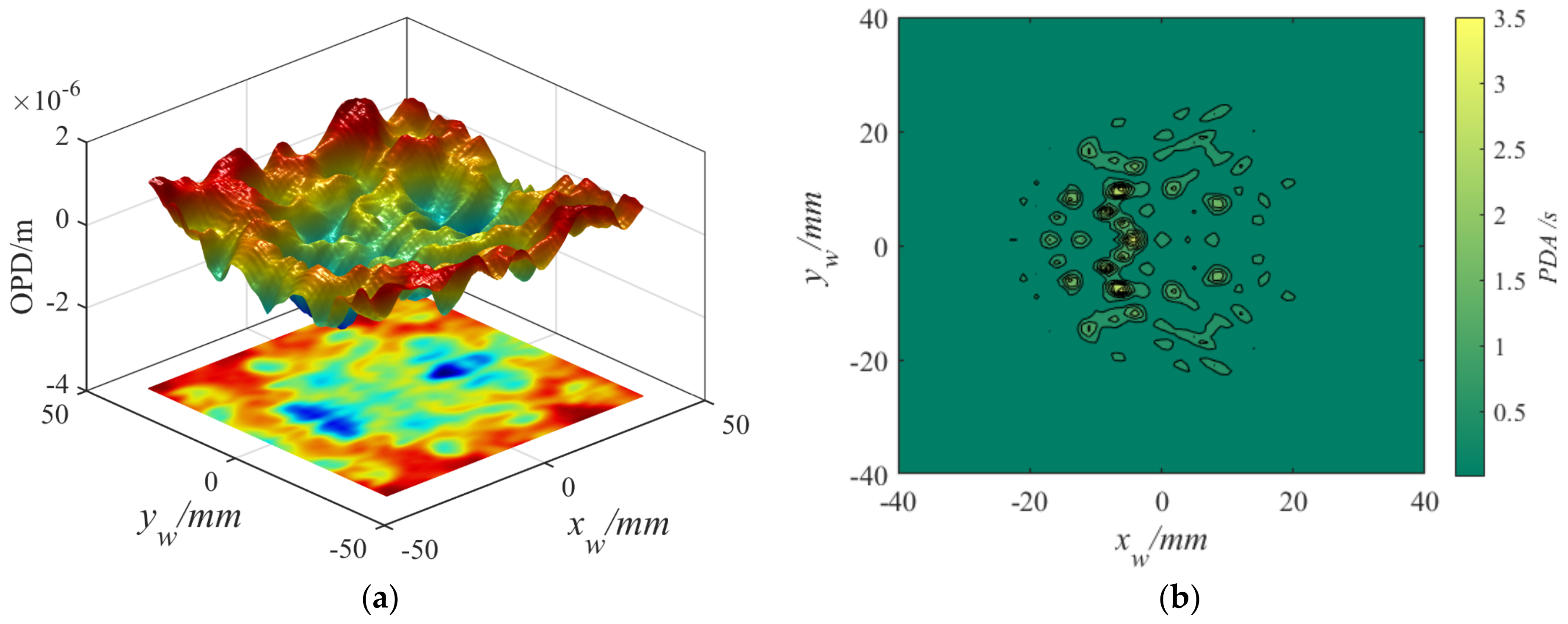
3.3.3. Photon Deflection Angle (PDA)
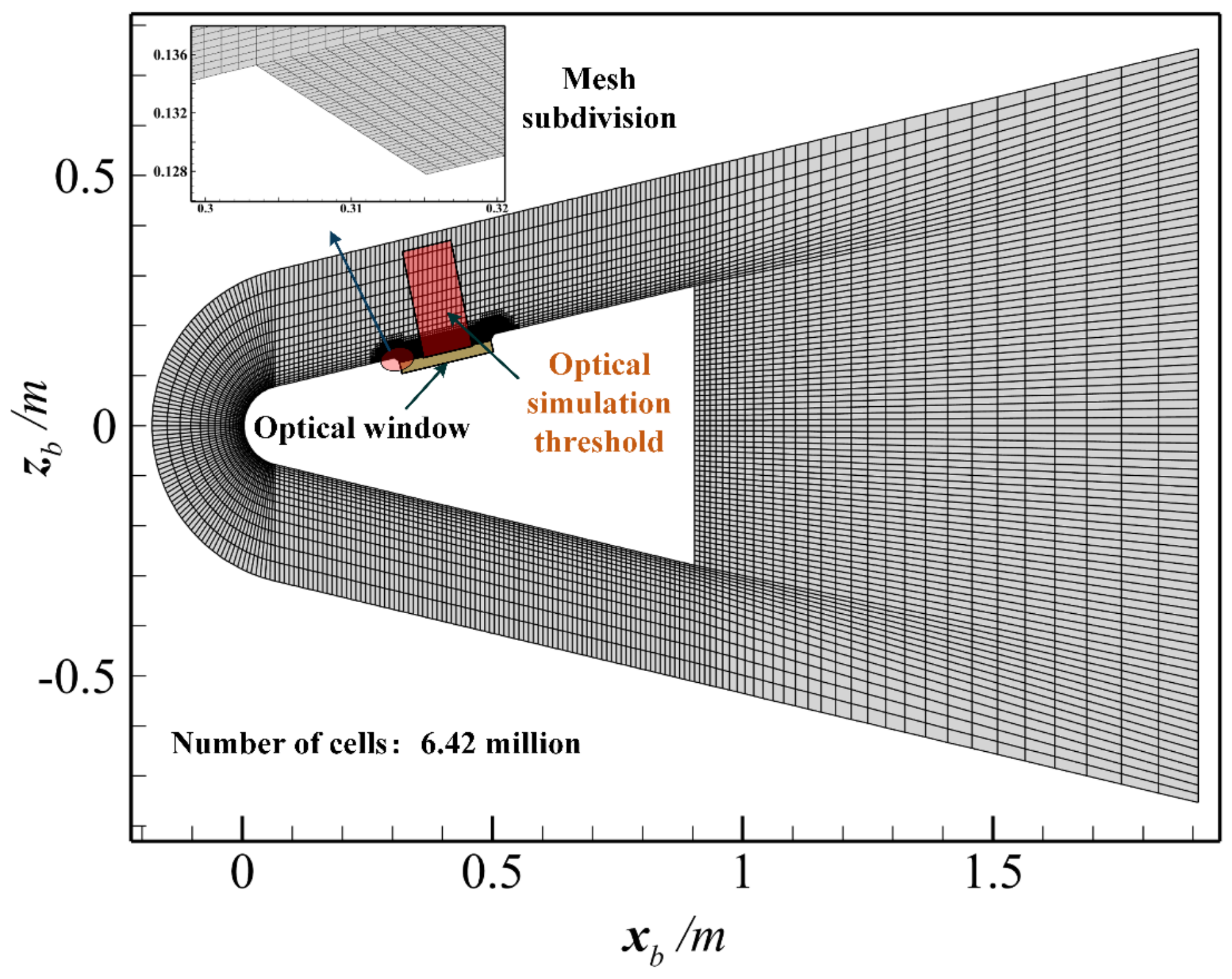
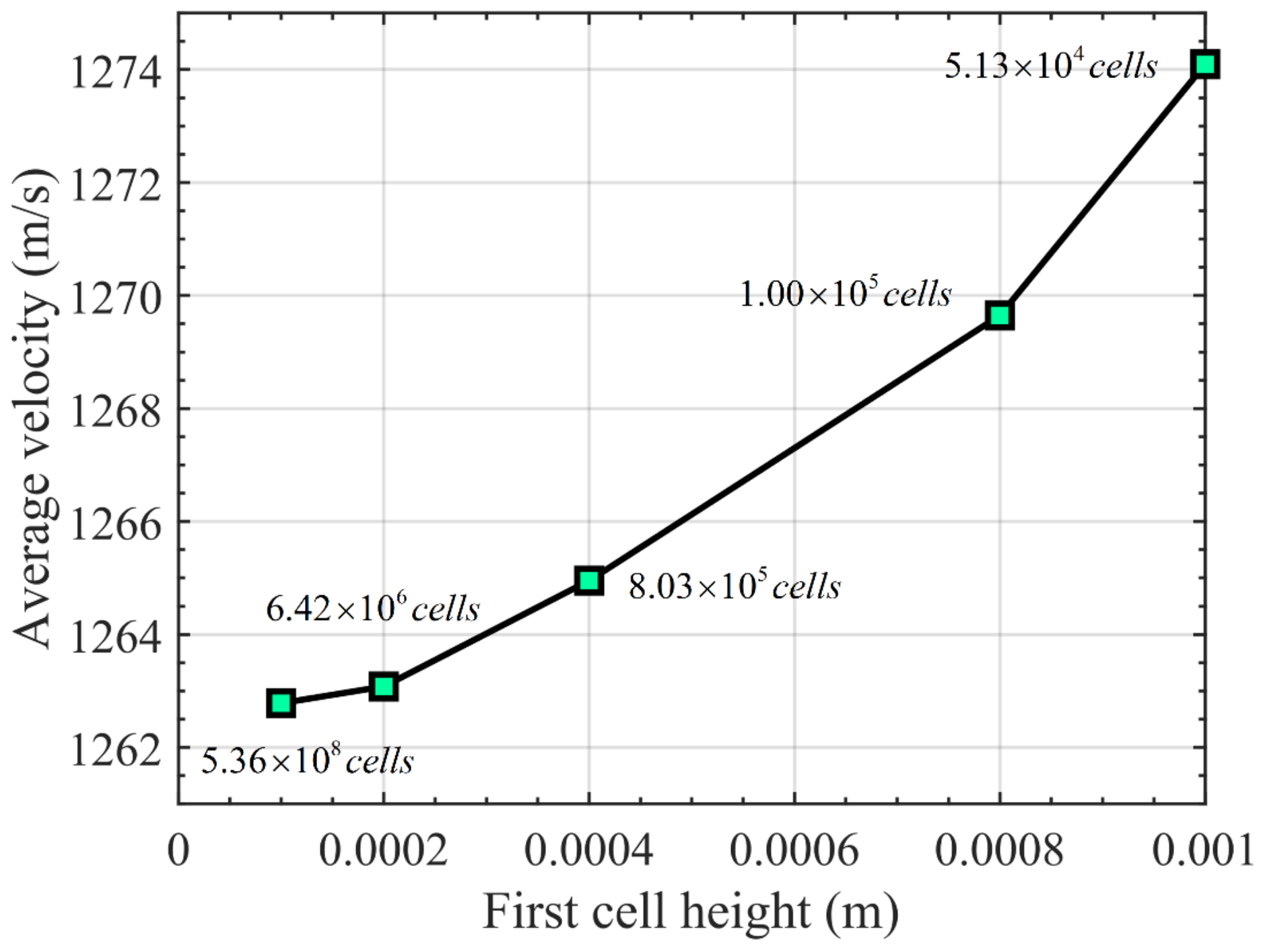
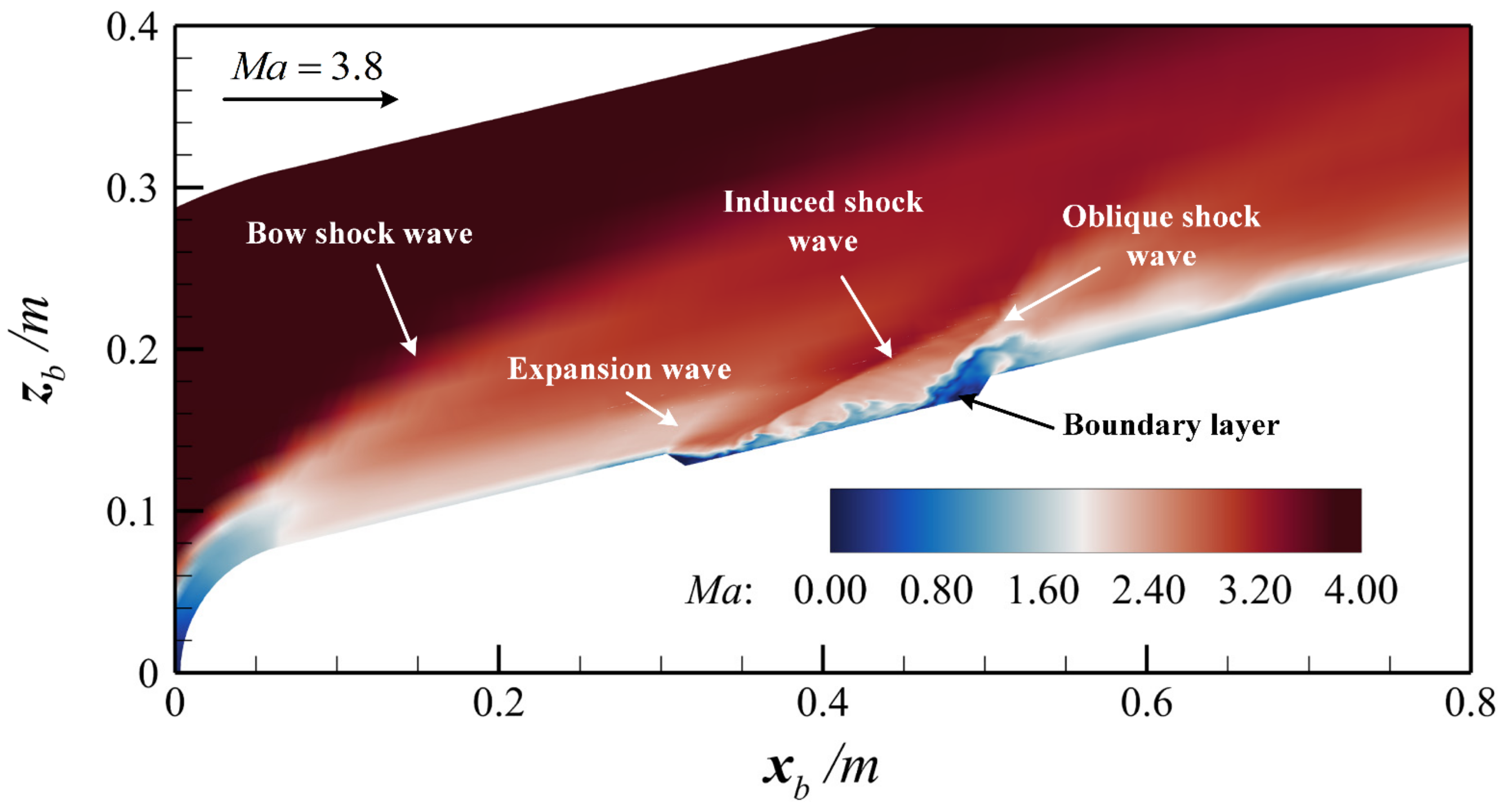
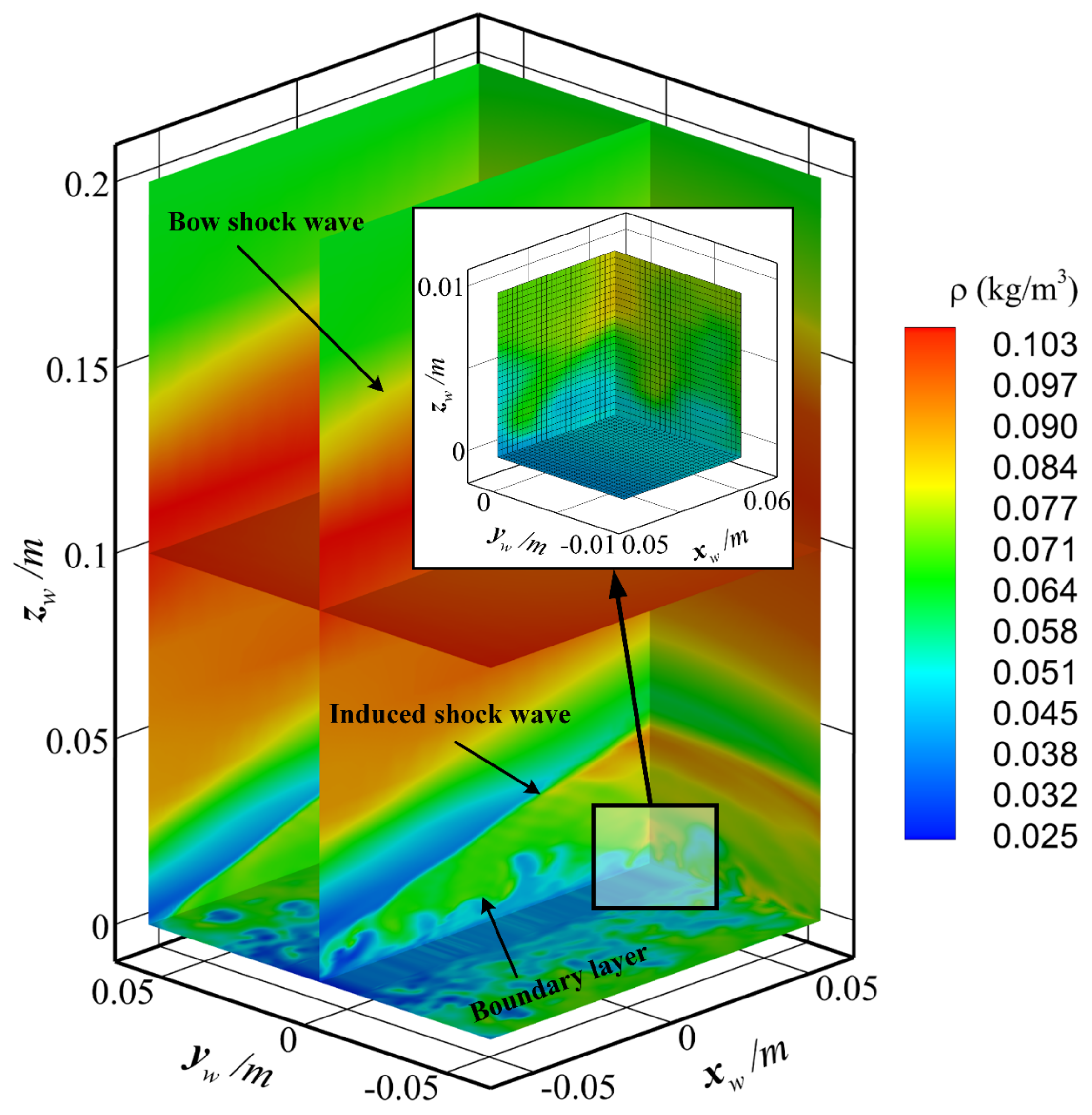
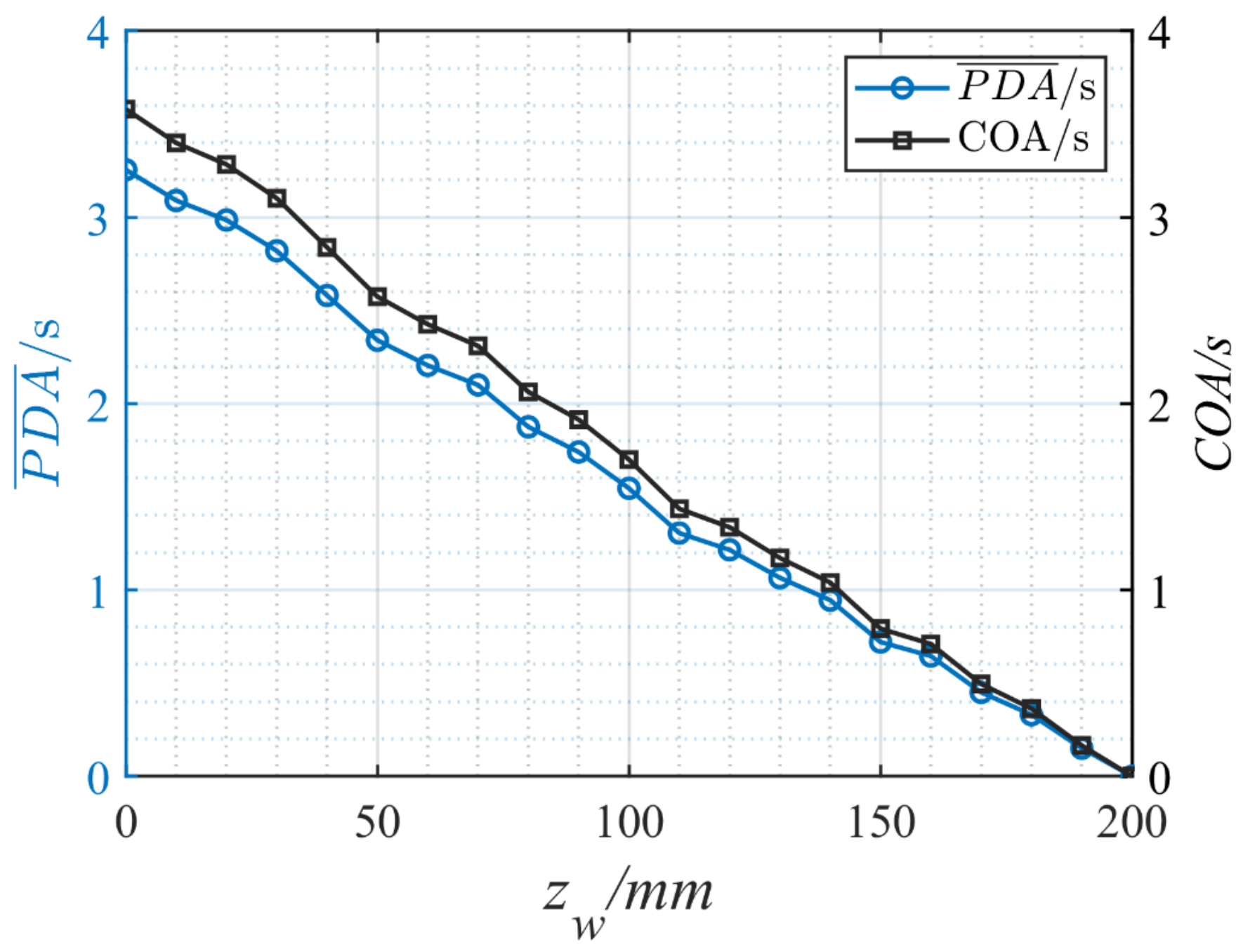
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fiorentini, L.; Serrani, A. Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model. Automatica 2012, 48, 1248–1261. [Google Scholar] [CrossRef]
- Viola, N.; Ferretto, D.; Fusaro, R.; Scigliano, R. Performance Assessment of an Integrated Environmental Control System of Civil Hypersonic Vehicles. Aerospace 2022, 9, 201. [Google Scholar] [CrossRef]
- Theil, S.; Steffes, S.; Samaan, M.; Conradt, M.; Vanschoenbeek, I.; Markgraf, M. Hybrid navigation system for spaceplanes, launch and re-entry vehicles. In Proceedings of the 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, Germany, 19–22 October 2009. [Google Scholar]
- Ning, X.; Gui, M.; Bai, X.; Fang, J. INS/VNS/CNS integrated navigation method for planetary rovers. Aerosp. Sci. Technol. 2016, 48, 102–114. [Google Scholar] [CrossRef]
- Tsou, M. Genetic algorithm for solving celestial navigation fix problems. Pol. Marit. Res. 2012, 19, 53–59. [Google Scholar] [CrossRef]
- Yang, B.; Hu, J.; Liu, X. A study on simulation method of starlight transmission in hypersonic conditions. Aerosp. Sci. Technol. 2013, 29, 155–164. [Google Scholar] [CrossRef]
- Jumper, E.; Gordeyev, S. Physics and measurement of aero-optical effects: Past and present. Annu. Rev. Fluid Mech. 2017, 49, 419–441. [Google Scholar] [CrossRef]
- Gordeyev, S.; Smith, A.; Cress, J.; Jumper, E. Experimental studies of aero-optical properties of subsonic turbulent boundary layers. J. Fluid Mech. 2014, 740, 214–253. [Google Scholar] [CrossRef]
- Ding, H.; Yi, S.; Zhu, Y.; He, L. Experimental investigation on aero-optics of supersonic turbulent boundary layers. Appl. Optics 2017, 56, 7604–7610. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Yi, S.; Zhao, X.; Xu, Y. Experimental investigation on aero-optical effects of a hypersonic optical dome under different exposure times. Appl. Optics. 2020, 59, 3842–3850. [Google Scholar] [CrossRef] [PubMed]
- Gordeyev, S.; Jumper, E. Fluid dynamics and aero-optics of turrets. Prog. Aeosp. Sci. 2010, 46, 388–400. [Google Scholar] [CrossRef]
- Wyckham, C.; Smits, A. Aero-optic distortion in transonic and hypersonic turbulent boundary layers. AIAA J. 2009, 47, 2158–2168. [Google Scholar] [CrossRef]
- Rennie, R.; Nguyen, M.; Gordeyev, S.; Jumper, E.; Cain, A.; Hayden, T. Wave-front measurements of a supersonic boundary layer using laser induced breakdown. AIAA J. 2017, 55, 2349–2357. [Google Scholar] [CrossRef]
- Gopal, V.; Maddalena, L. Review of Filtered Rayleigh Scattering technique for mixing studies in supersonic air flow. Prog. Aeosp. Sci. 2021, 120, 100679. [Google Scholar] [CrossRef]
- Ding, H.; Yi, S.; Ouyang, T.; Shi, Y.; He, L. Influence of turbulence structure with different scale on aero-optics induced by supersonic turbulent boundary layer. Optik 2020, 202, 163565. [Google Scholar] [CrossRef]
- Saxton-Fox, T.; McKeon, B.J.; Gordeyev, S. Effect of coherent structures on aero-optic distortion in a turbulent boundary layer. AIAA J. 2019, 57, 2828–2839. [Google Scholar] [CrossRef]
- Zhang, B.; He, L.; Yi, S.; Ding, H. Multi-resolution analysis of aero-optical effects in a supersonic turbulent boundary layer. Appl. Optics. 2021, 60, 2242–2251. [Google Scholar] [CrossRef] [PubMed]
- Mathews, E.; Wang, K.; Wang, M.; Jumper, E.J. Turbulence scale effects and resolution requirements in aero-optics. Appl. Optics 2021, 60, 4426–4433. [Google Scholar] [CrossRef] [PubMed]
- Guo, G.; Zhu, L.; Bian, Y. Numerical analysis on aero-optical wavefront distortion induced by vortices from the viewpoint of fluid density. Opt. Commun. 2020, 474, 126181. [Google Scholar] [CrossRef]
- Yang, B.; Fan, Z.; Yu, H.; Hu, H.; Yang, Z. A New Method for Analyzing Aero-Optical Effects with Transient Simulation. Sensors 2021, 21, 2199. [Google Scholar] [CrossRef] [PubMed]
- Vitkovicova, R.; Yokoi, Y.; Hyhlik, T. Identification of structures and mechanisms in a flow field by POD analysis for input data obtained from visualization and PIV. Exp. Fluids 2020, 61, 171. [Google Scholar] [CrossRef]
- Gordeyev, S.; Jumper, E.; Hayden, T. Aero-optical effects of supersonic boundary layers. AIAA J. 2012, 50, 682–690. [Google Scholar] [CrossRef]
- Ding, H.L.; Yi, S.H.; Xu, Y.; Zhao, X.H. Recent developments in the aero-optical effects of high-speed optical apertures: From transonic to high-supersonic flows. Prog. Aeosp. Sci. 2021, 127, 100763. [Google Scholar] [CrossRef]
- Sun, X.W.; Yang, X.L.; Liu, W. Numerical investigation on aero-optical reduction for supersonic turbulent mixing layer. Int. J. Aeronaut. Space Sci. 2021, 22, 239–254. [Google Scholar] [CrossRef]
- Yang, B.; Fan, Z.; Yu, H. Aero-optical effects simulation technique for starlight transmission in boundary layer under high-speed conditions. Chin. J. Aeronaut. 2020, 33, 1929–1941. [Google Scholar]
- Wang, K.; Wang, M. Aero-optics of subsonic turbulent boundary layers. J. Fluid Mech. 2012, 696, 122–151. [Google Scholar] [CrossRef]
- Xu, L.; Zhou, Z.; Ren, T. Study of a weak scattering model in aero-optic simulations and its computation. JOSA A 2017, 34, 594–601. [Google Scholar] [CrossRef] [PubMed]
- Lindel, F.; Bennett, R.; Buhmann, S.Y. Macroscopic quantum electrodynamics approach to nonlinear optics and application to polaritonic quantum-vacuum detection. Phys. Rev. A 2021, 103, 033705. [Google Scholar] [CrossRef]
- Oughstun, K.E.; Cartwright, N.A. On the Lorentz-Lorenz formula and the Lorentz model of dielectric dispersion. Opt. Express. 2003, 11, 1541–1546. [Google Scholar] [CrossRef]
- Richard, H.; Raffel, M.; Rein, M.; Kompenhans, J.; Meier, G. Demonstration of the applicability of a background oriented schlieren (BOS) method. In Laser Techniques for Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 145–156. [Google Scholar]
- Hossen, M.K.; MulayathVariyath, A.; Alam, J.M. Statistical Analysis of Dynamic Subgrid Modeling Approaches in Large Eddy Simulation. Aerospace 2021, 8, 375. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Yu, H.; Liu, C.; Wei, X.; Fan, Z.; Miao, J. A New Method for Analyzing the Aero-Optical Effects of Hypersonic Vehicles Based on a Microscopic Mechanism. Aerospace 2022, 9, 618. https://doi.org/10.3390/aerospace9100618
Yang B, Yu H, Liu C, Wei X, Fan Z, Miao J. A New Method for Analyzing the Aero-Optical Effects of Hypersonic Vehicles Based on a Microscopic Mechanism. Aerospace. 2022; 9(10):618. https://doi.org/10.3390/aerospace9100618
Chicago/Turabian StyleYang, Bo, He Yu, Chaofan Liu, Xiang Wei, Zichen Fan, and Jun Miao. 2022. "A New Method for Analyzing the Aero-Optical Effects of Hypersonic Vehicles Based on a Microscopic Mechanism" Aerospace 9, no. 10: 618. https://doi.org/10.3390/aerospace9100618
APA StyleYang, B., Yu, H., Liu, C., Wei, X., Fan, Z., & Miao, J. (2022). A New Method for Analyzing the Aero-Optical Effects of Hypersonic Vehicles Based on a Microscopic Mechanism. Aerospace, 9(10), 618. https://doi.org/10.3390/aerospace9100618




