A Novel Efficient Prediction Method for Microscopic Stresses of Periodic Beam-like Structures
Abstract
1. Introduction
2. The Homogenization Method for Periodic Timoshenko Beams
3. The Formulae for Calculating Microscopic Stresses
4. Numerical Examples
4.1. A Sandwich Beam with Square Cores
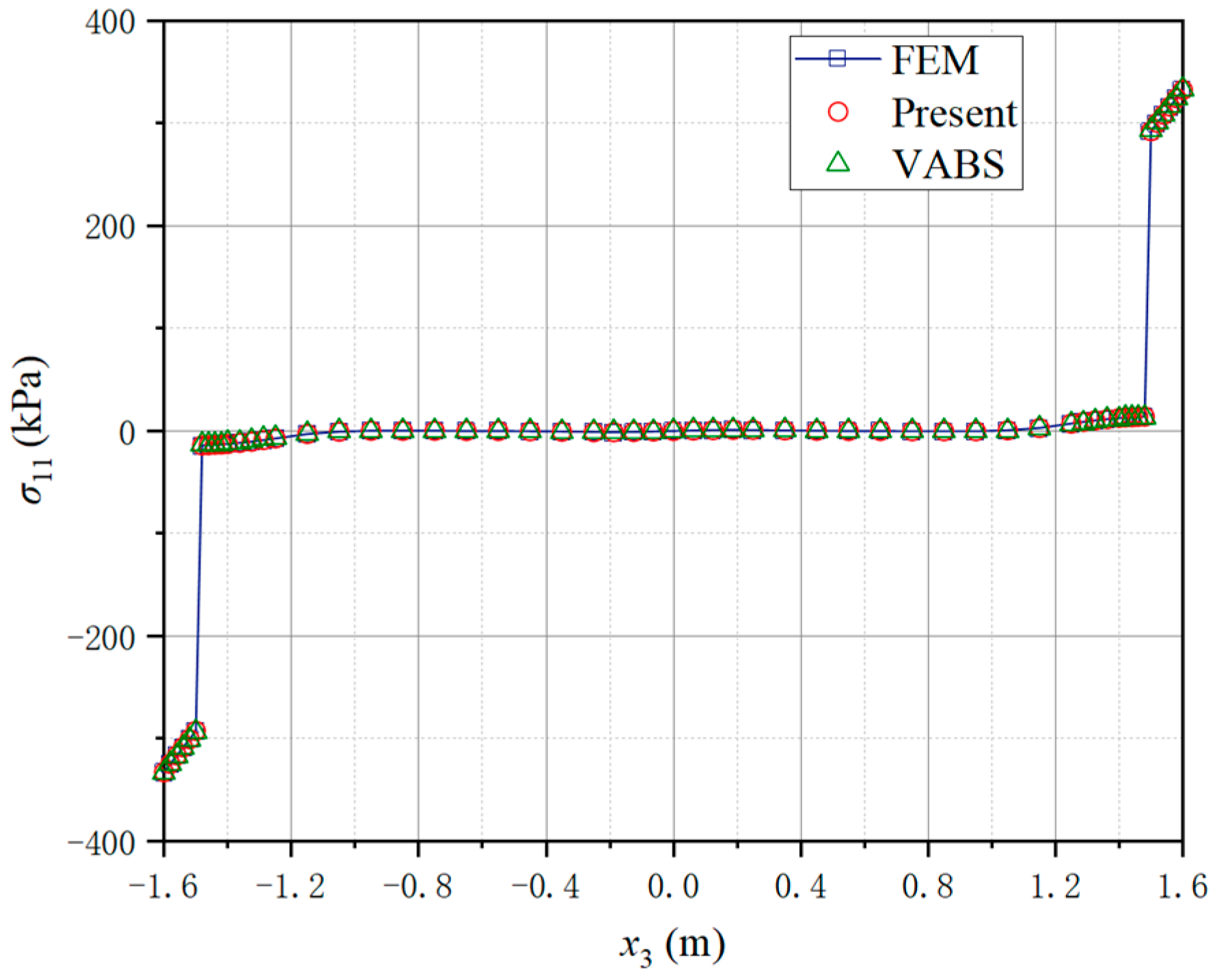
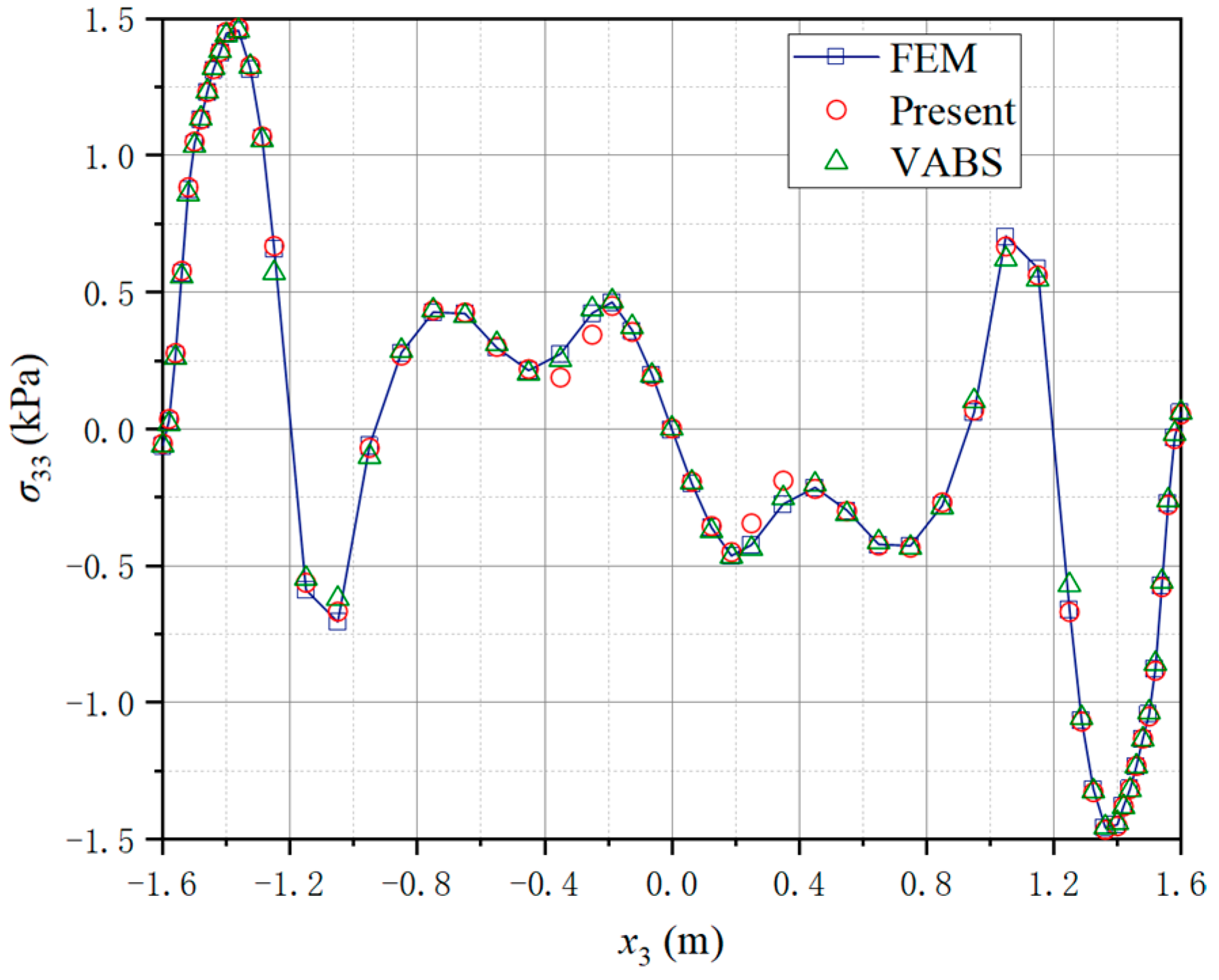
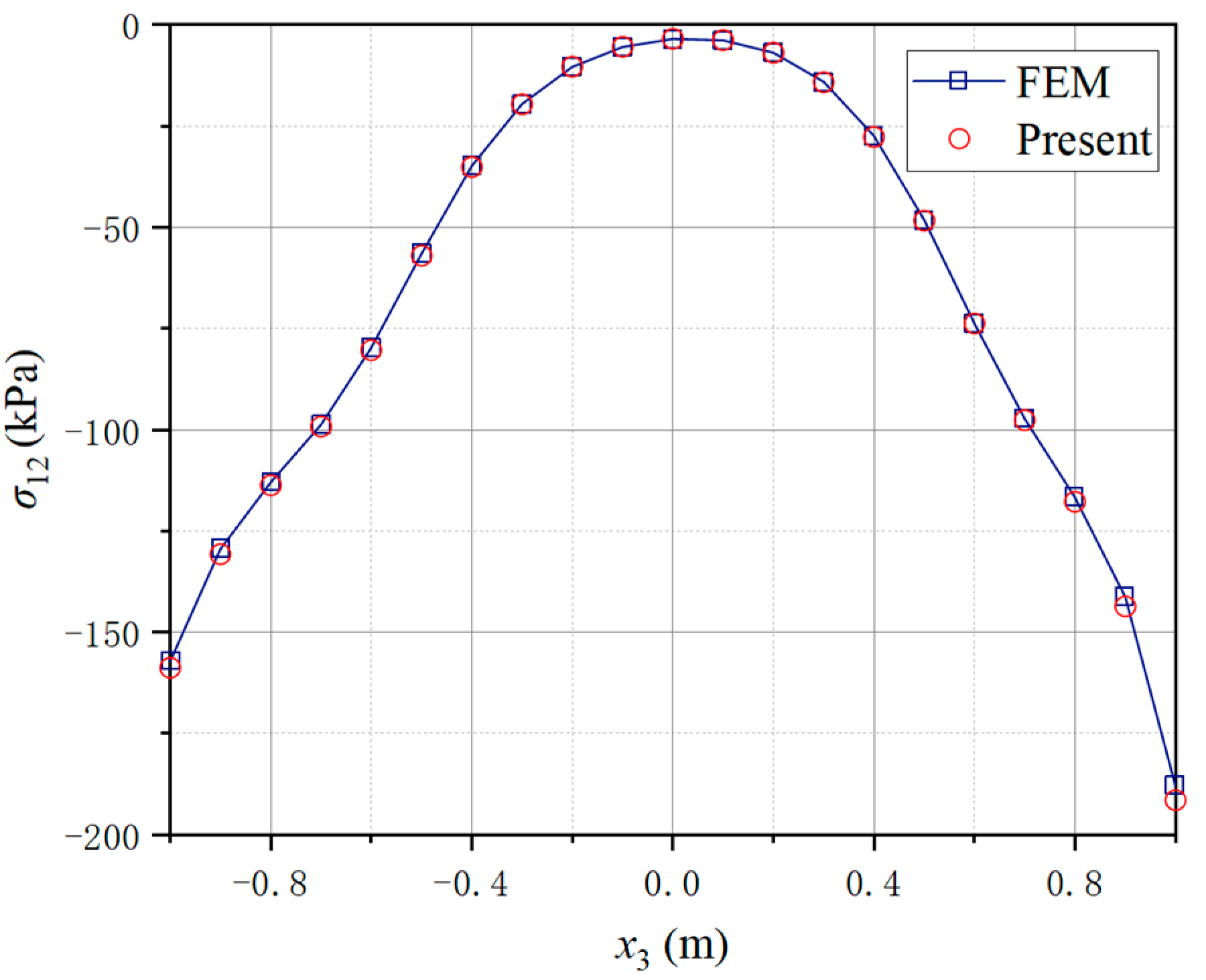
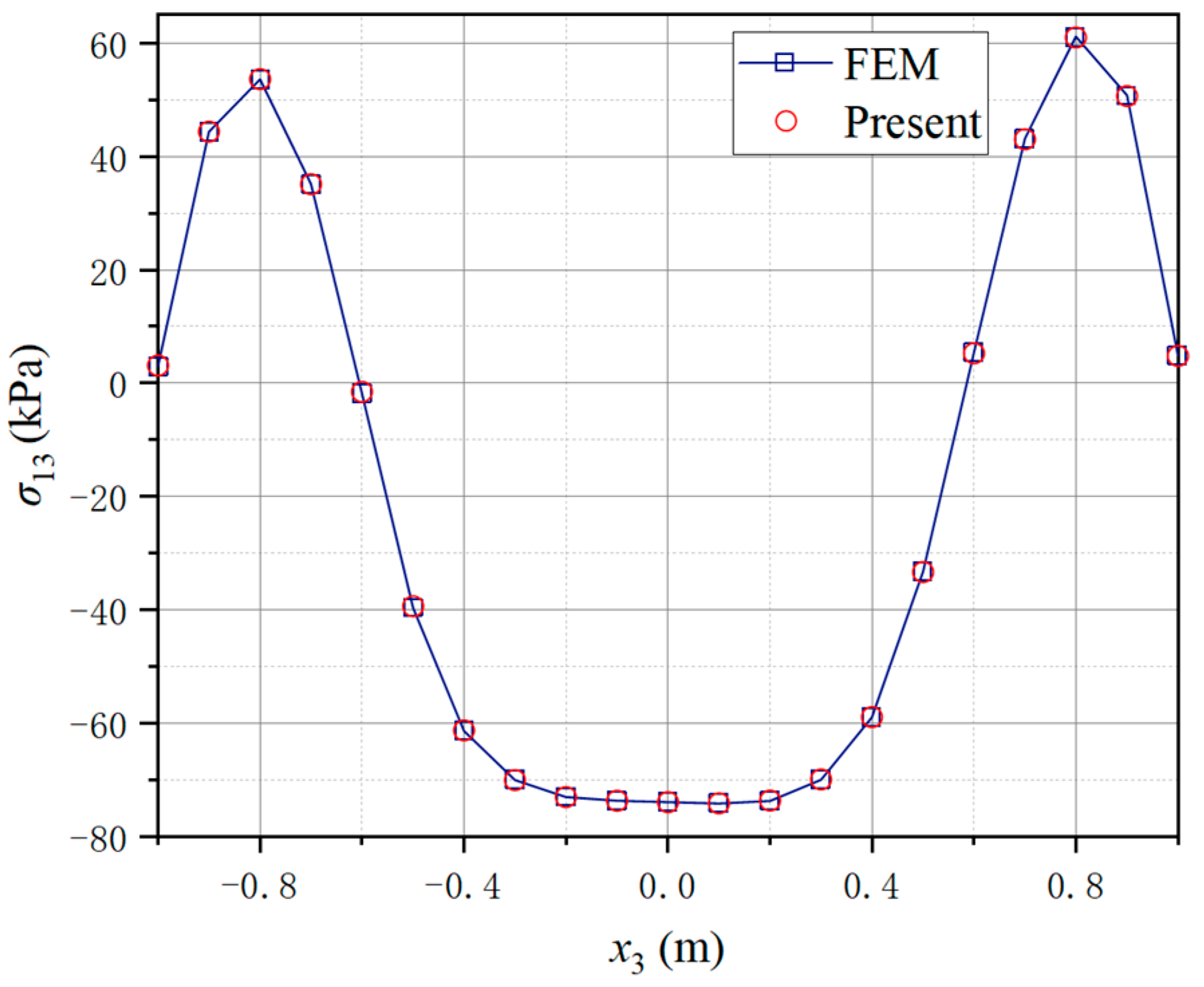
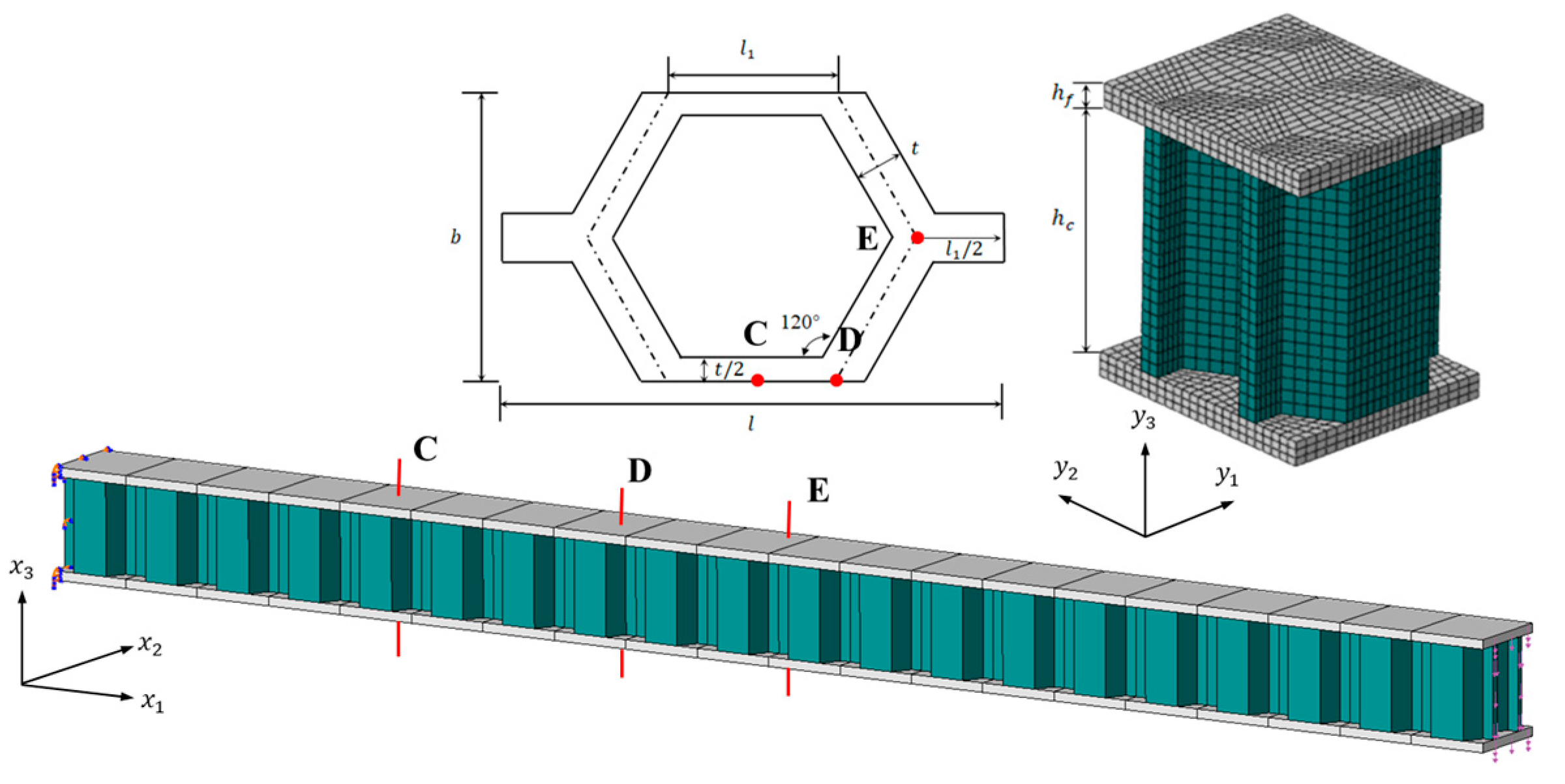
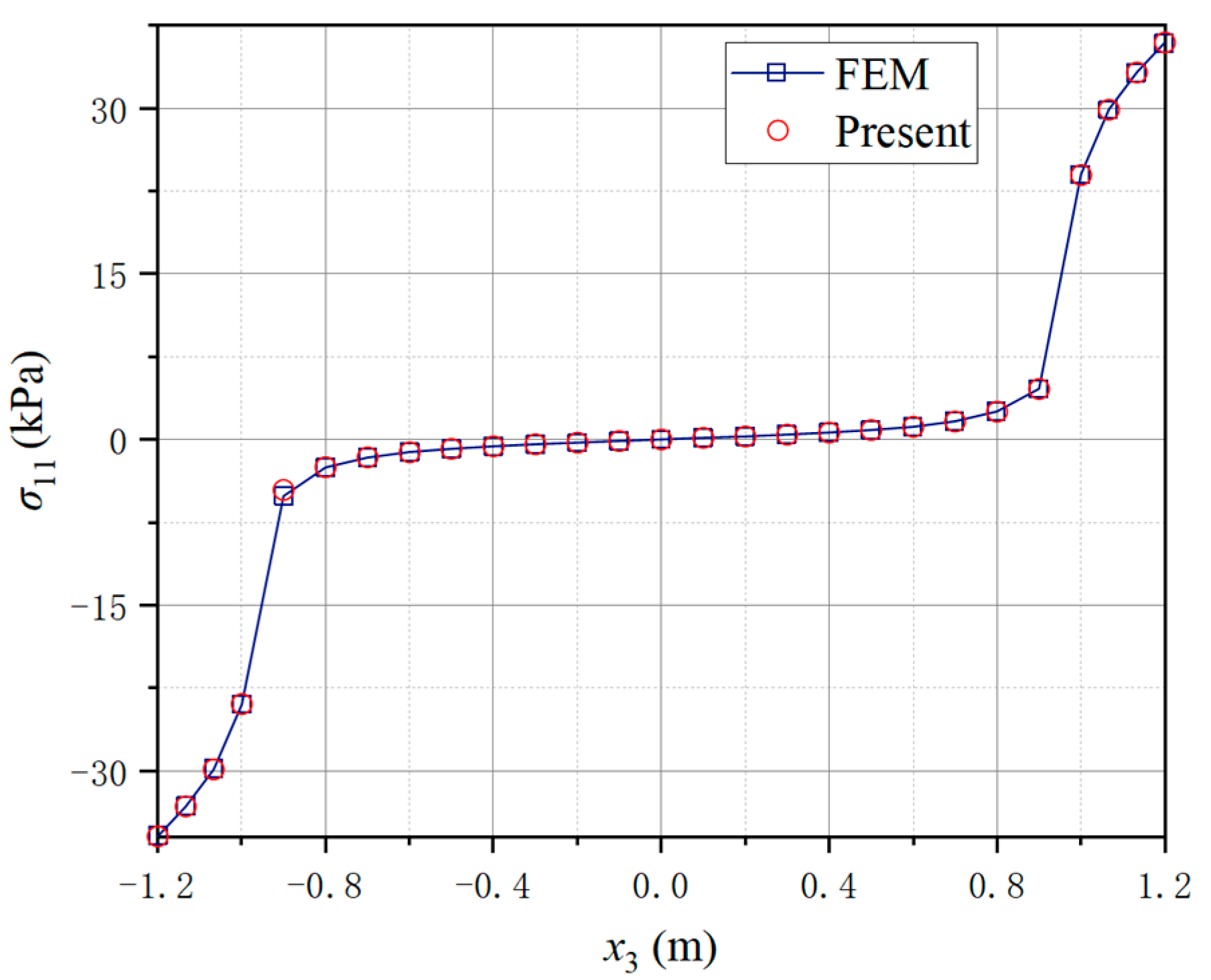
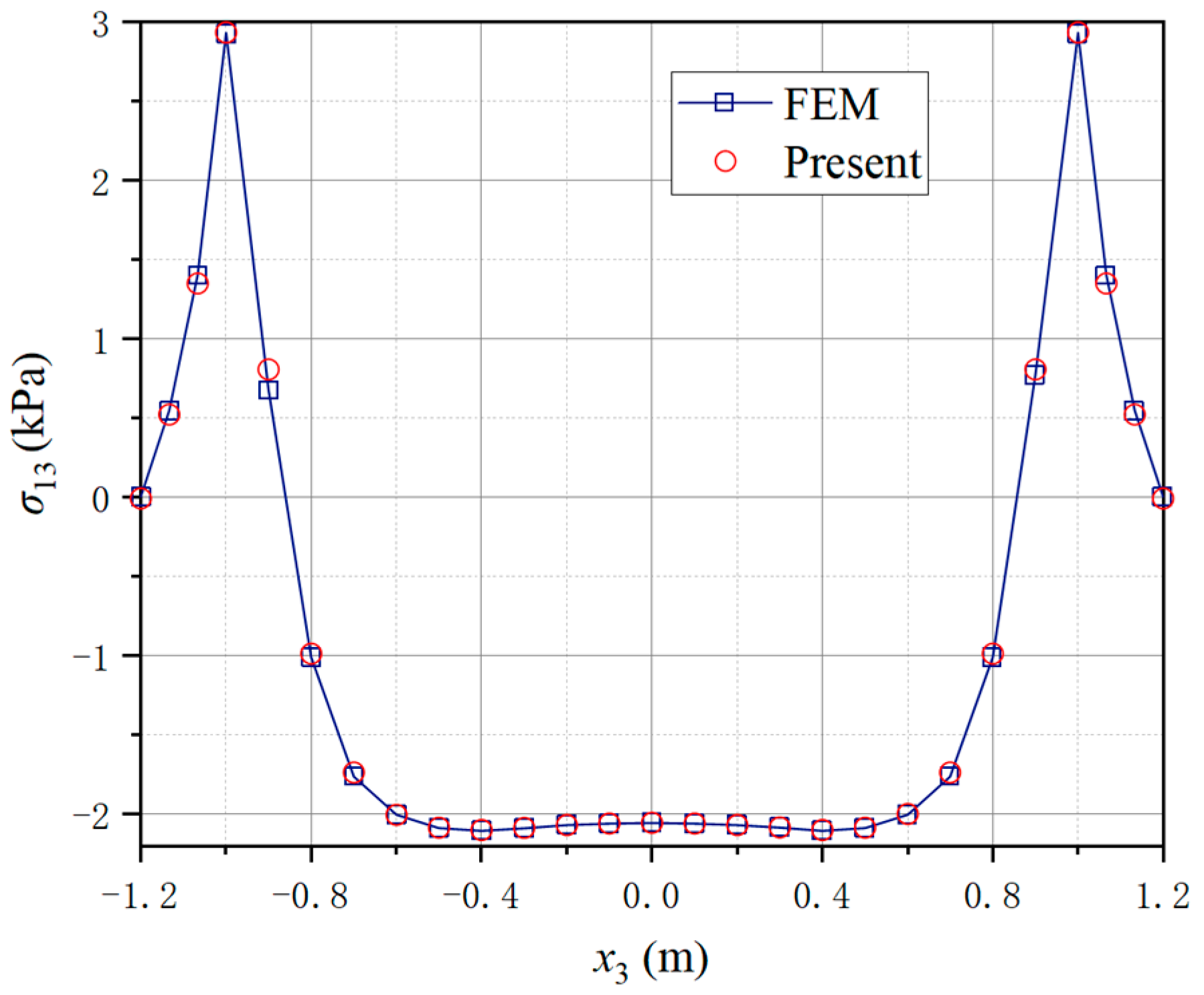
4.2. A Three-Way Perforated Beam
4.3. A Honeycomb-Core Sandwich Beam
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bensoussan, A.; Lions, J.L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; Elsevier: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Oleinik, O.A.; Shamaev, A.S.; Yosifian, G.A. Mathematical Problems in Elasticity and Homogenization; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Dai, G.M.; Zhang, W.H. Size effects of basic cell in static analysis of sandwich beams. Int. J. Solids Struct. 2008, 45, 2512–2533. [Google Scholar] [CrossRef]
- Dai, G.M.; Zhang, W.H. Cell size effects for vibration analysis and design of sandwich beams. Acta Mech. Sin. 2009, 25, 353–365. [Google Scholar] [CrossRef]
- Yi, S.A.; Xu, L.; Cheng, G.D.; Cai, Y.W. FEM formulation of homogenization method for effective properties of periodic heterogeneous beam and size effect of basic cell in thickness direction. Comput. Struct. 2015, 156, 1–11. [Google Scholar] [CrossRef]
- Kolpakov, A.G. Calculation of the characteristics of thin elastic rods with a periodic structure. J. Appl. Math. Mech. 1991, 55, 358–365. [Google Scholar] [CrossRef]
- Kolpakov, A.G. Variational principles for stiffnesses of a non-homogeneous beam. J. Mech. Phys. Solids 1998, 46, 1039–1053. [Google Scholar] [CrossRef]
- Kolpakov, A.G. Stressed Composite Structures: Homogenized Models for Thin-Walled Nonhomogeneous Structures with Initial Stresses; Springer: Berlin/Heidelberg, Germany; New York, USA, 2004. [Google Scholar]
- Cesnik, C.E.S.; Hodges, D.H.; Sutyrin, V.G. Cross-sectional analysis of composite beams including large initial twist and curvature effects. AIAA J. 1996, 34, 1913–1920. [Google Scholar] [CrossRef]
- Cesnik, C.E.S.; Sutyrin, V.G.; Hodges, D.H. Refined theory of twisted and curved composite beams: The role of short-wavelength extrapolation. Int. J. Solids Struct. 1996, 33, 1387–1408. [Google Scholar] [CrossRef]
- Cesnik, C.E.S.; Hodges, D.H. VABS: A New Concept for Composite Rotor Blade Cross-Sectional Modeling. J. Am. Helicopter Soc. 1997, 42, 27–38. [Google Scholar] [CrossRef]
- Popescu, B.; Hodges, D.H. On asymptotically correct Timoshenko-like anisotropic beam theory. Int. J. Solids Struct. 2000, 37, 535–558. [Google Scholar] [CrossRef]
- Yu, W.; Hodges, D.H.; Volovoi, V.; Cesnik, C.E.S. On Timoshenko-like modeling of initially curved and twisted composite beams. Int. J. Solids Struct. 2002, 39, 5101–5121. [Google Scholar] [CrossRef]
- Yu, W.; Hodges, D.H.; Ho, J.C. Variational asymptotic beam sectional analysis—An updated version. Int. J. Eng. Sci. 2012, 59, 40–64. [Google Scholar] [CrossRef]
- Lee, C.Y.; Yu, W.B. Variational asymptotic modeling of composite beams with spanwise heterogeneity. Comput. Struct. 2011, 89, 1503–1511. [Google Scholar] [CrossRef]
- Lee, C. Zeroth-Order Shear Deformation Micro-Mechanical Model for Periodic Heterogeneous Beam-like Structures. J. Korean Soc. Power Sys. Eng. 2015, 19, 55–62. [Google Scholar] [CrossRef]
- Huang, Z.W.; Xing, Y.F.; Gao, Y.H. A two-scale asymptotic expansion method for periodic composite Euler beams. Compos. Struct. 2020, 241, 112033. [Google Scholar] [CrossRef]
- Allaire, G. Two-scale convergence: A new method in periodic homogenization. In Nonlinear Partial Differential Equations and Their Applications: College de France Seminar; CRC Press: Boca Raton, FL, USA, 1994; pp. 1–14. [Google Scholar]
- Allaire, G.g. Homogenization and Two-Scale Convergence. SIAM J. Math. Anal. 1992, 23, 1482–1518. [Google Scholar] [CrossRef]
- Xu, L.; Cheng, G.D.; Yi, S.N. A new method of shear stiffness prediction of periodic Timoshenko beams. Mech. Adv. Mater. Struct. 2016, 23, 670–680. [Google Scholar] [CrossRef]
- Huang, Z.W.; Xing, Y.F.; Gao, Y.H. A new method of stiffness prediction for periodic beam-like structures. Compos. Struct. 2021, 267, 113892. [Google Scholar] [CrossRef]
- Gao, Y.H.; Huang, Z.W.; Li, G.; Xing, Y.F. A novel stiffness prediction method with constructed microscopic displacement field for periodic beam like structures. Acta Mech. Sin. 2022, 38, 421520. [Google Scholar] [CrossRef]
- Yu, W.B.; Volovoi, V.V.; Hodges, D.H.; Hong, X.Y. Validation of the Variational Asymptotic Beam Sectional Analysis. AIAA J. 2002, 40, 2105–2112. [Google Scholar] [CrossRef]
- Yu, W.B.; Hodges, D.H. Generalized Timoshenko theory of the variational asymptotic beam sectional analysis. J. Am. Helicopter Soc. 2005, 50, 46–55. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, W.B. Variational-asymptotic modeling of the thermoelastic behavior of composite beams. Compos. Struct. 2011, 93, 2330–2339. [Google Scholar] [CrossRef]
- Xiao, P.; Zhong, Y.F.; Dan, L.; Bing, D. Accurate recovery of 3D local field in FRP laminated beam based on asymptotic dimension reduction model. Constr. Build. Mater. 2019, 207, 357–372. [Google Scholar] [CrossRef]
- Liu, X.; Yu, W.B. A novel approach to analyze beam-like composite structures using mechanics of structure genome. Adv. Eng. Softw. 2016, 100, 238–251. [Google Scholar] [CrossRef]
- Kashefi, K.; Sheikh, A.H.; Ali, M.S.M.; Griffith, M.C. An efficient modelling approach based on a rigorous cross-sectional analysis for analysing box girder bridge superstructures. Adv. Struct. Eng. 2016, 19, 513–528. [Google Scholar] [CrossRef]
- Giavotto, V.; Borri, M.; Mantegazza, P.; Ghiringhelli, G.; Carmaschi, V.; Maffioli, G.C.; Mussi, F. Anisotropic beam theory and applications. Comput. Struct. 1983, 16, 403–413. [Google Scholar] [CrossRef]
- Dhadwal, M.K.; Jung, S.N. Multifield Variational Sectional Analysis for Accurate Stress Computation of Multilayered Composite Beams. AIAA J. 2019, 57, 1702–1714. [Google Scholar] [CrossRef]
- Xu, L.; Cheng, G.D. On the solutions to the Saint-Venant problem of heterogeneous beam-like structures with periodic microstructures. Int. J. Mech. Sci. 2019, 163, 105123. [Google Scholar] [CrossRef]
- Xu, L.; Qian, Z.H. On the Almansi-Michell solution and its numerical implementation for heterogeneous beams with periodic microstructures subject to periodically-varying loads. Compos. Struct. 2020, 250, 112540. [Google Scholar] [CrossRef]
- Treyssede, F.; Cartraud, P. A two-dimensional formulation for the homogenization of helical beam-like structures under bending loads. Int. J. Solids Struct. 2022, 234, 111270. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, Y.; Liang, H.P. Refined Beam Theory for Geometrically Nonlinear Pre-Twisted Structures. Aerospace 2022, 9, 360. [Google Scholar] [CrossRef]
- Sirimontree, S.; Thongchom, C.; Saffari, P.R.; Refahati, N.; Saffari, P.R. Jearsiripongkul, T.; Keawsawasvong, S. Effects of thermal environment and external mean flow on sound transmission loss of sandwich functionally graded magneto-electro-elastic cylindrical nanoshell. Eur. J. Mech. A Solids 2023, 97, 104774. [Google Scholar] [CrossRef]
- Huang, Z.W.; Xing, Y.F.; Gao, Y.H. A new method of stiffness prediction for composite plate structures with in-plane periodicity. Compos. Struct. 2022, 280, 114850. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Y.; Meng, L.; Huang, Z.; Gao, Y. A Novel Efficient Prediction Method for Microscopic Stresses of Periodic Beam-like Structures. Aerospace 2022, 9, 553. https://doi.org/10.3390/aerospace9100553
Xing Y, Meng L, Huang Z, Gao Y. A Novel Efficient Prediction Method for Microscopic Stresses of Periodic Beam-like Structures. Aerospace. 2022; 9(10):553. https://doi.org/10.3390/aerospace9100553
Chicago/Turabian StyleXing, Yufeng, Lingyu Meng, Zhiwei Huang, and Yahe Gao. 2022. "A Novel Efficient Prediction Method for Microscopic Stresses of Periodic Beam-like Structures" Aerospace 9, no. 10: 553. https://doi.org/10.3390/aerospace9100553
APA StyleXing, Y., Meng, L., Huang, Z., & Gao, Y. (2022). A Novel Efficient Prediction Method for Microscopic Stresses of Periodic Beam-like Structures. Aerospace, 9(10), 553. https://doi.org/10.3390/aerospace9100553






