Author Contributions
Conceptualization, E.O. and M.D.; methodology, E.O. and M.D.; software, E.O.; validation, E.O.; formal analysis, E.O. and M.D.; investigation, E.O.; resources, E.O.; data curation, E.O.; writing—original draft preparation, E.O. and M.D.; writing—review and editing, E.O. and M.D.; visualization, E.O.; supervision, E.O. and M.D.; project administration, M.D. All authors have read and agreed to the published version of the manuscript.
Figure 1.
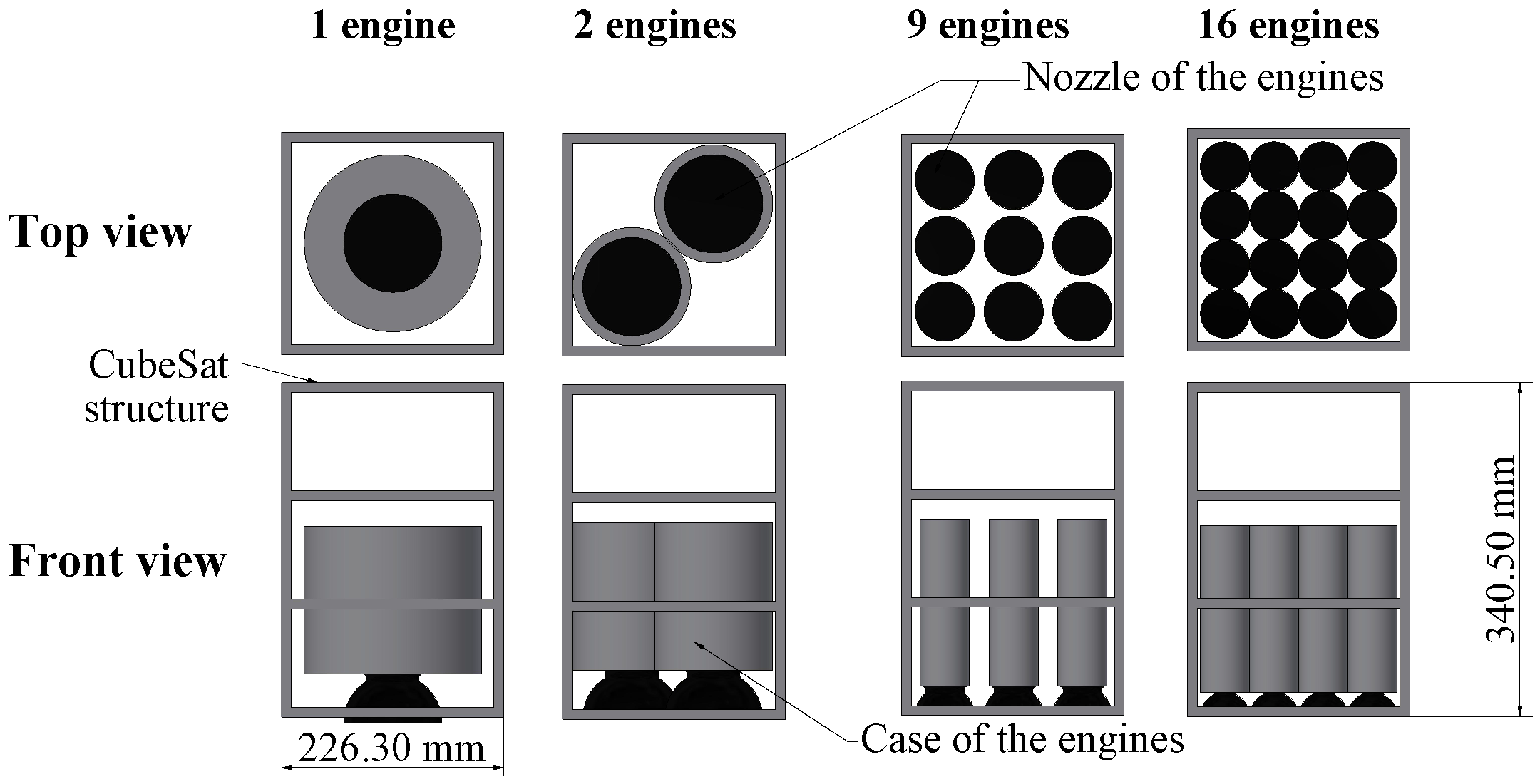
Example of 12U landers with engine arrangements. From left to right, 4 examples are shown: For a configuration of one, two, nine and sixteen engines.
Figure 1.
Example of 12U landers with engine arrangements. From left to right, 4 examples are shown: For a configuration of one, two, nine and sixteen engines.
Figure 2.
Example of a lander with 10 thrusters in the engine array in a one-dimensional dynamic model. The inertial reference frame is fixed on the lunar surface, and is perpendicular and positive to it. This configuration frees up space equivalent to 4U for electronic components.
Figure 2.
Example of a lander with 10 thrusters in the engine array in a one-dimensional dynamic model. The inertial reference frame is fixed on the lunar surface, and is perpendicular and positive to it. This configuration frees up space equivalent to 4U for electronic components.
Figure 3.
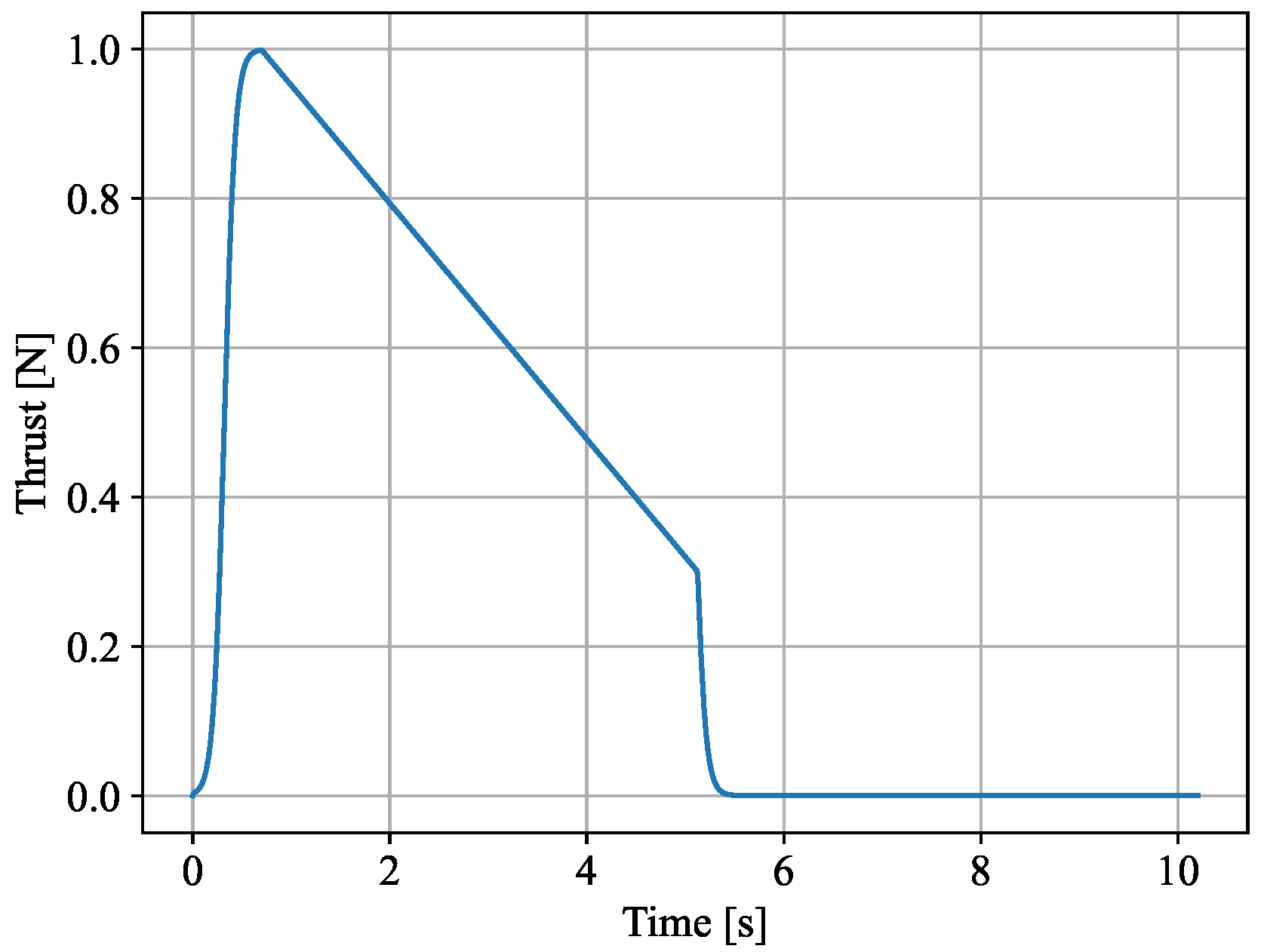
An example of regressive unitary thrust.
Figure 3.
An example of regressive unitary thrust.
Figure 4.
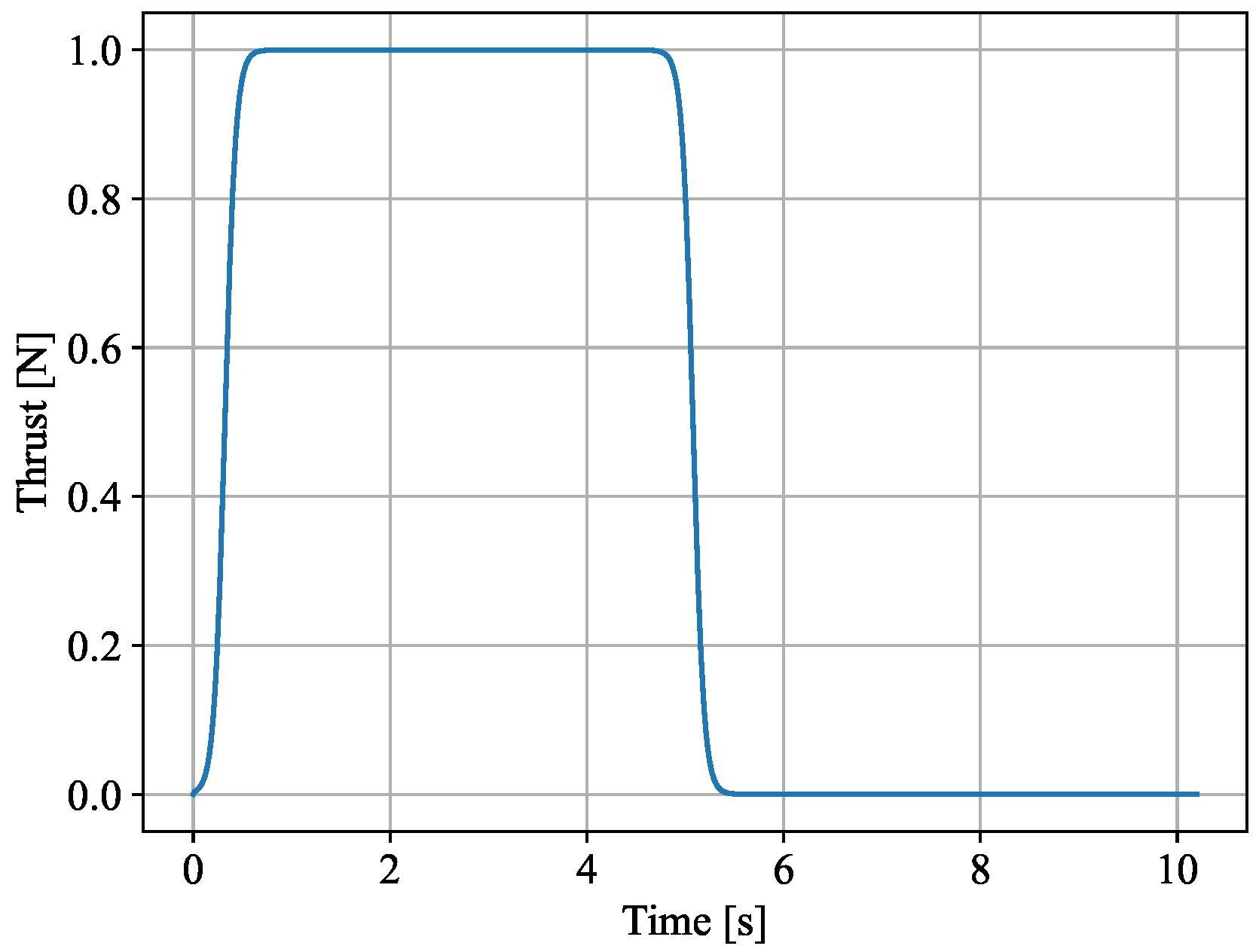
An example of neutral unitary thrust.
Figure 4.
An example of neutral unitary thrust.
Figure 5.
An example of progressive unitary thrust.
Figure 5.
An example of progressive unitary thrust.
Figure 6.
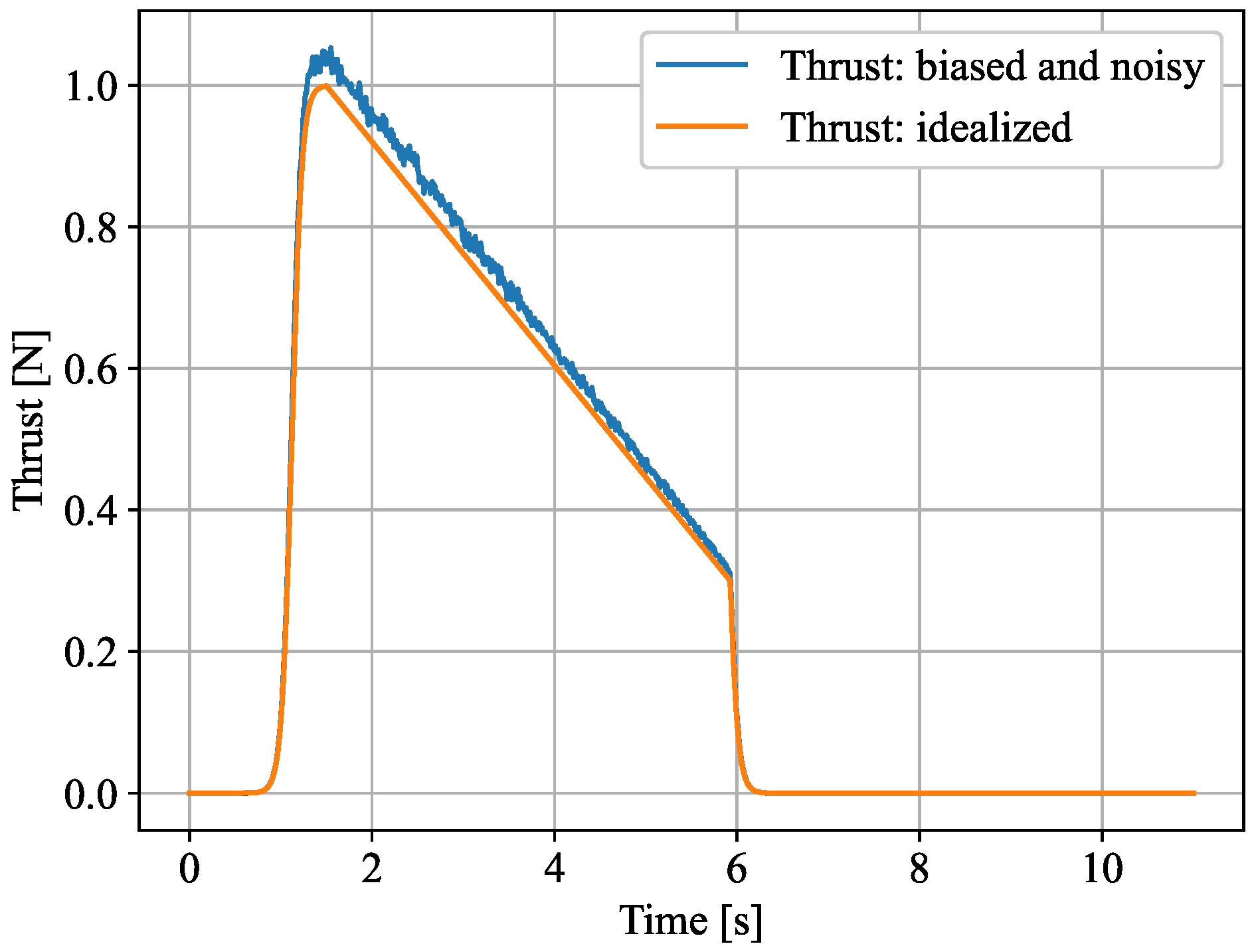
Example of regressive unitary thrust with bias and noise.
Figure 6.
Example of regressive unitary thrust with bias and noise.
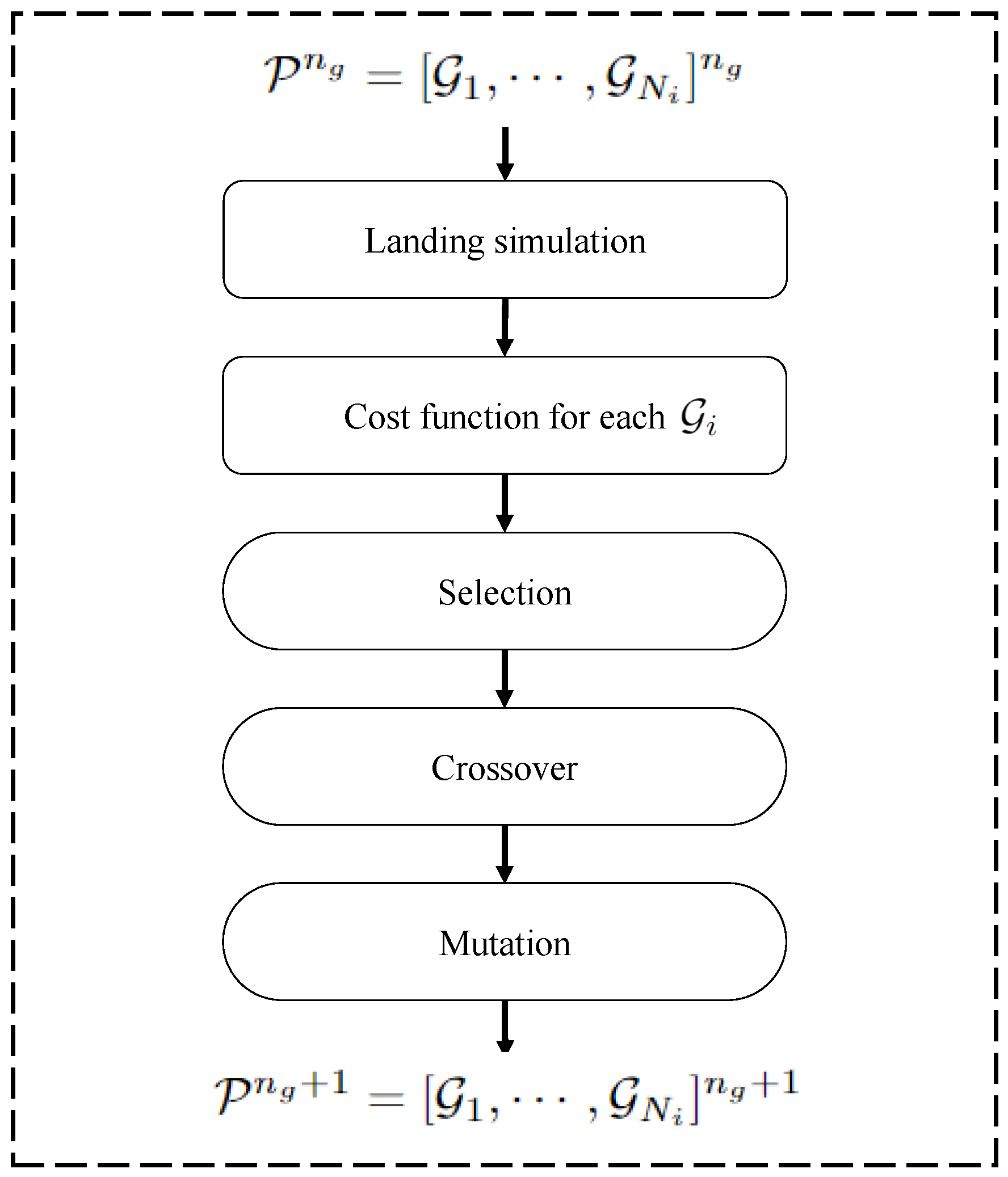
Figure 7.
Representation of the evolutionary process of the GA, where the landing simulation is used to create a new generation of population .
Figure 7.
Representation of the evolutionary process of the GA, where the landing simulation is used to create a new generation of population .
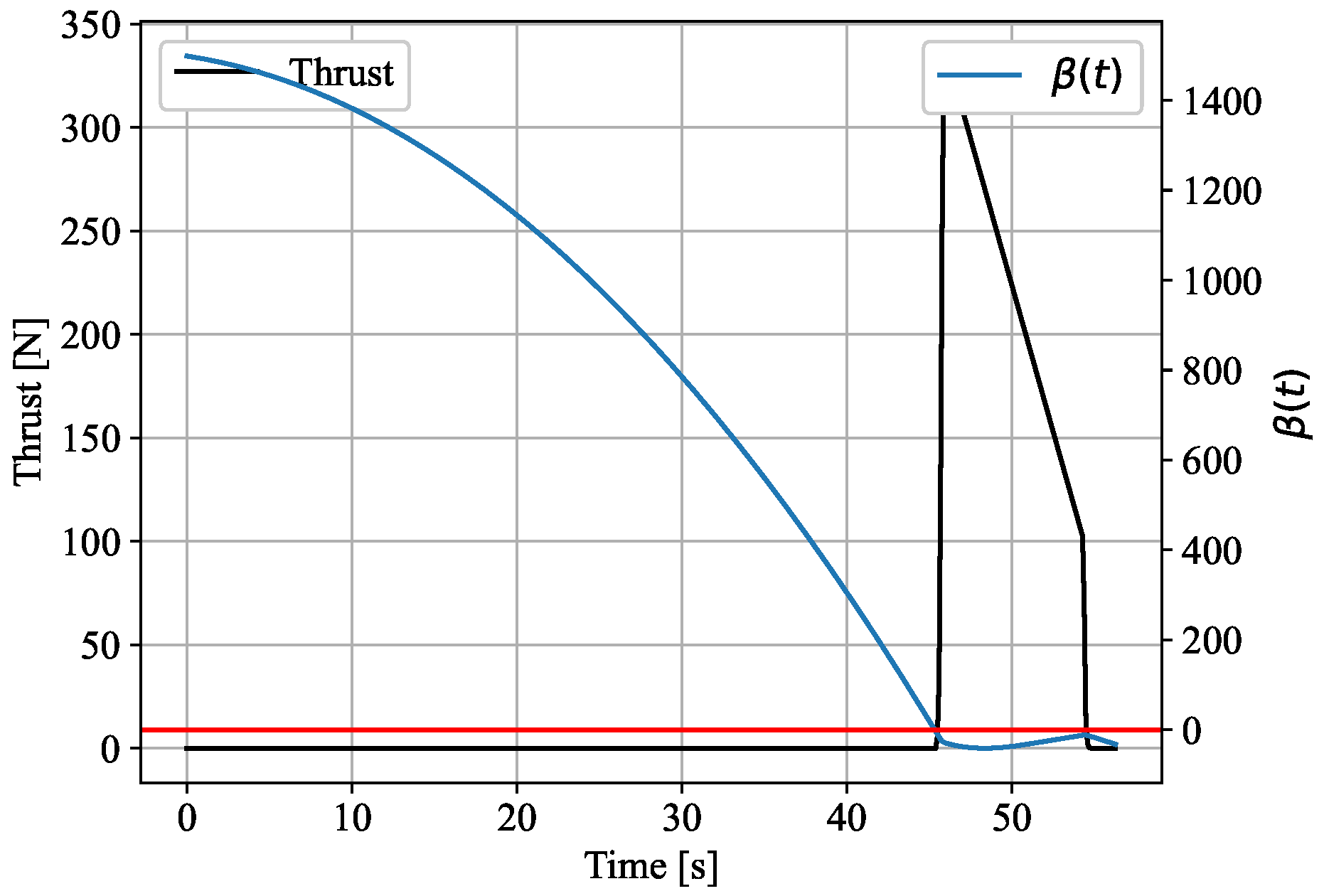
Figure 8.
Example of activation of each engine. When the control function is less than zero, crossing the red line, the engine turns on at the instant of the simulation. The ignition delay seen in the figure is due to the dead time of the propellant.
Figure 8.
Example of activation of each engine. When the control function is less than zero, crossing the red line, the engine turns on at the instant of the simulation. The ignition delay seen in the figure is due to the dead time of the propellant.
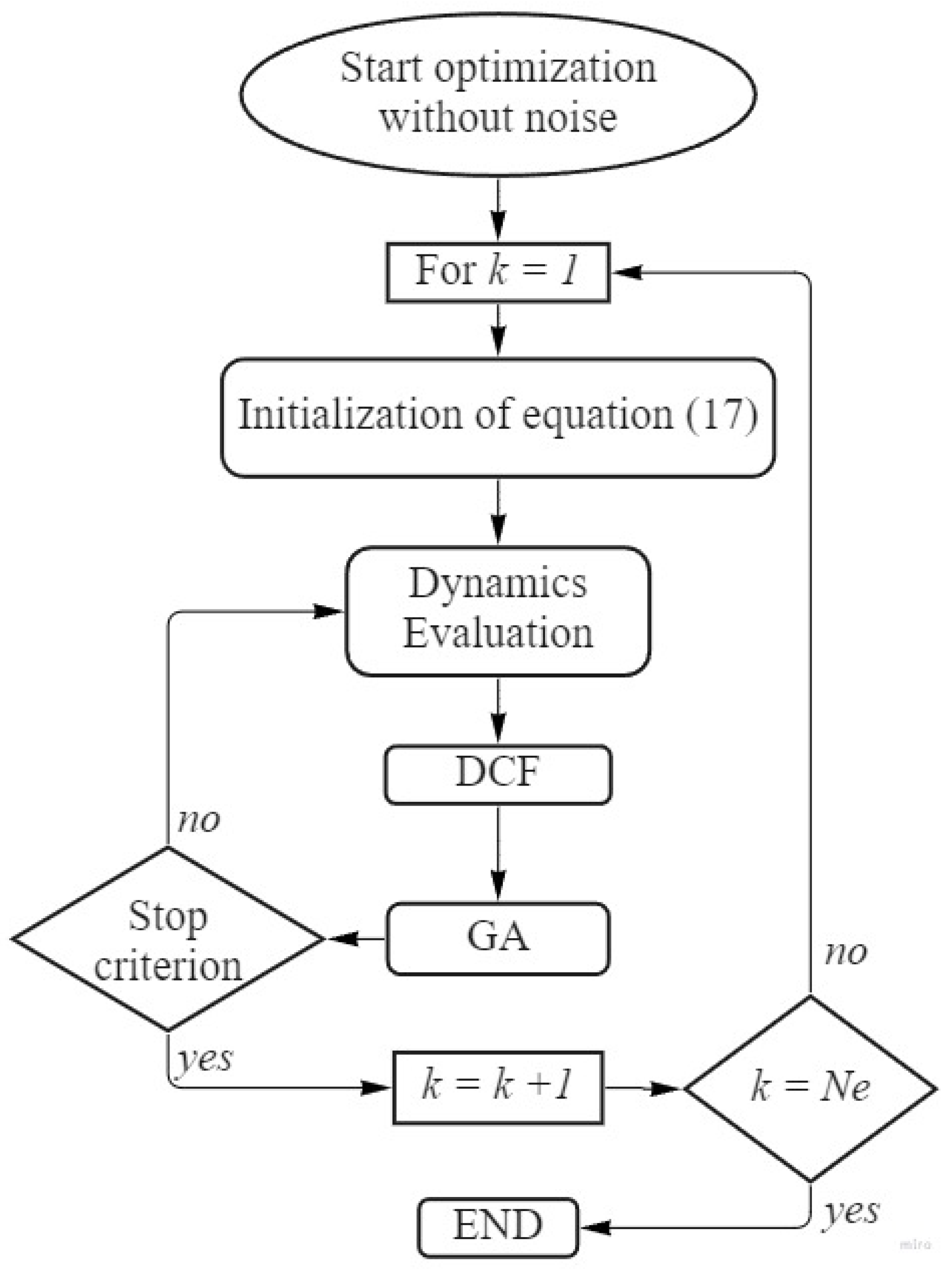
Figure 9.
First approach: Optimization for scenarios without uncertainties in the training process.
Figure 9.
First approach: Optimization for scenarios without uncertainties in the training process.
Figure 10.
Second approach: Optimization for scenarios with uncertainties in the training process.
Figure 10.
Second approach: Optimization for scenarios with uncertainties in the training process.
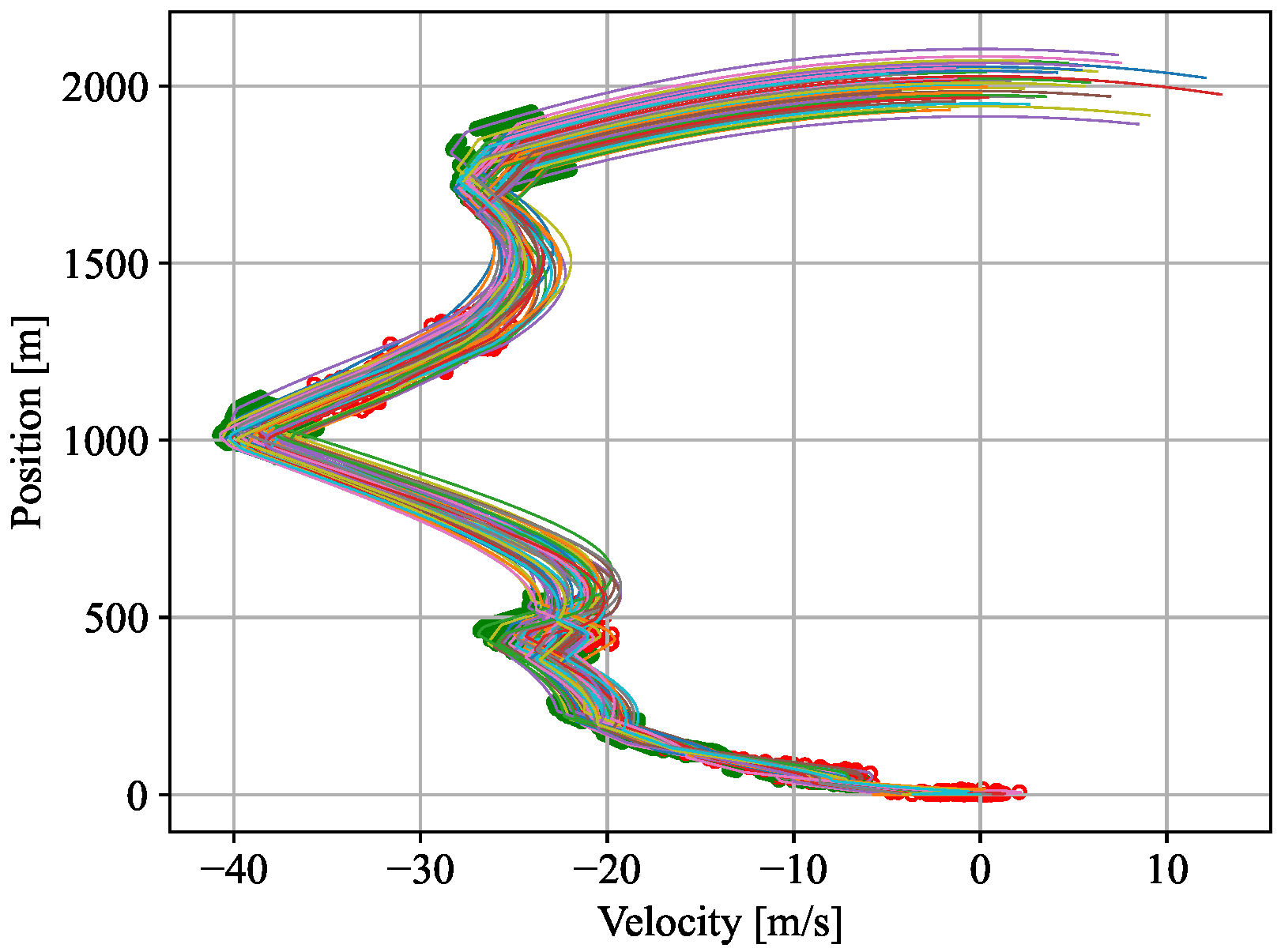
Figure 11.
Behavior of altitude and velocity in the evaluation of the best individual obtained from the optimization without uncertainties in training. The SPEs array has and Regressive PGCS. Color map is used to differentiate different random trajectories.
Figure 11.
Behavior of altitude and velocity in the evaluation of the best individual obtained from the optimization without uncertainties in training. The SPEs array has and Regressive PGCS. Color map is used to differentiate different random trajectories.
Figure 12.
Distribution of altitude and velocity landing in the evaluation of the best result obtained from the optimization without uncertainties in training. The SPEs array has and Regressive PGCS. The vertical axis shows the frequency of the values.
Figure 12.
Distribution of altitude and velocity landing in the evaluation of the best result obtained from the optimization without uncertainties in training. The SPEs array has and Regressive PGCS. The vertical axis shows the frequency of the values.
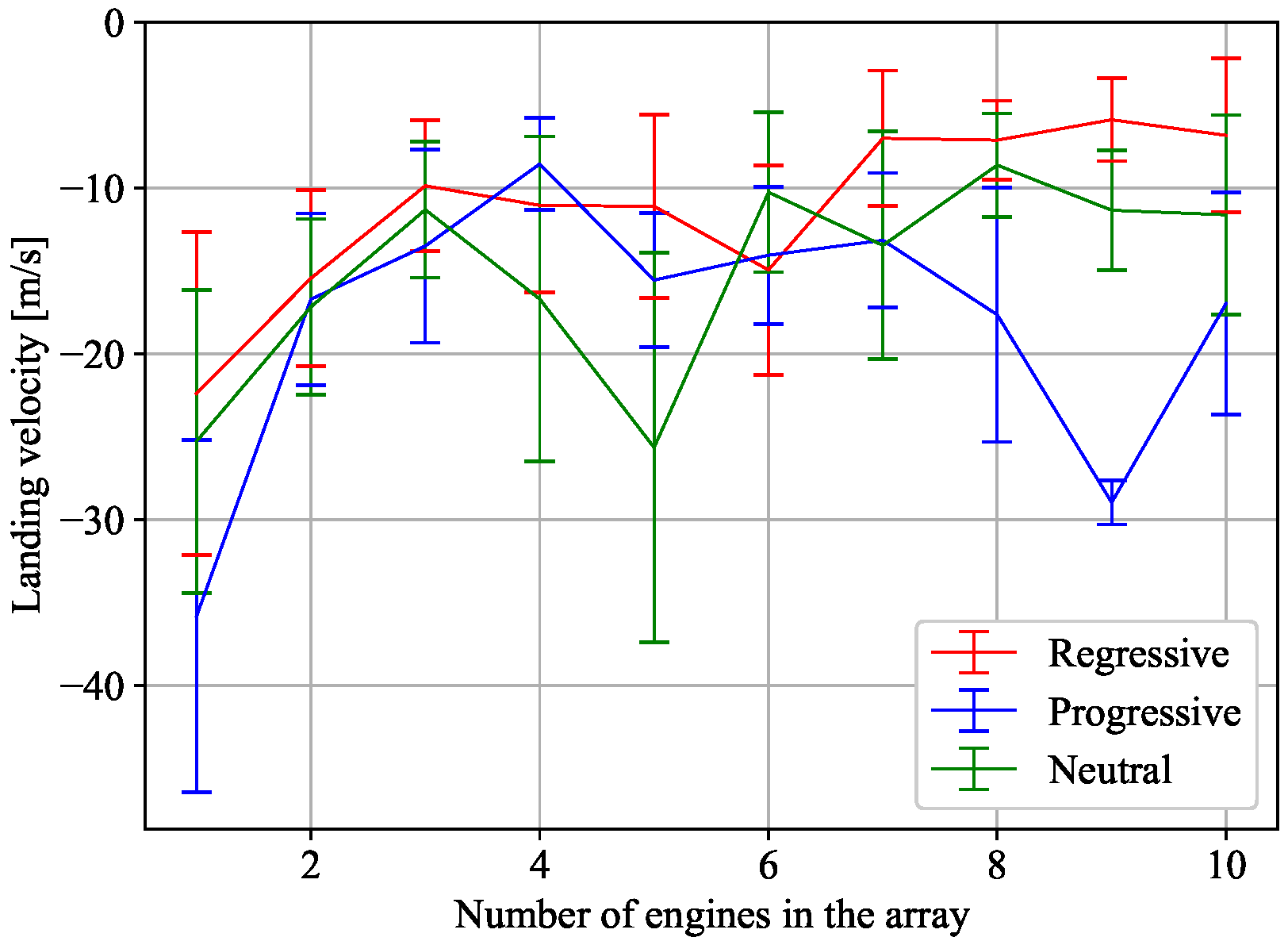
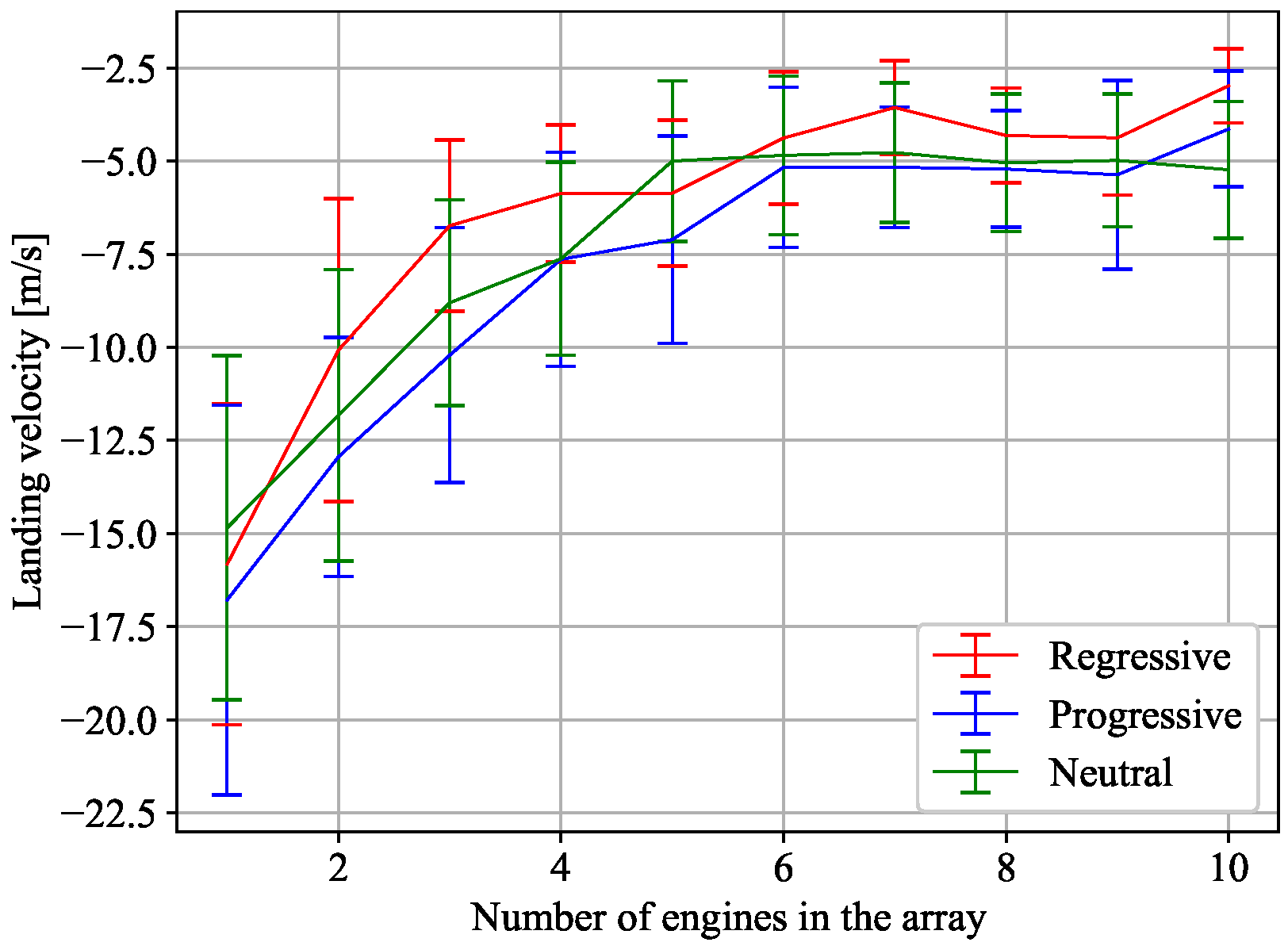
Figure 13.
First approach: performance comparison for an array between 1 and 10 configuration engines, and for the three types of PGCS: Regressive, Neutral and Progressive.
Figure 13.
First approach: performance comparison for an array between 1 and 10 configuration engines, and for the three types of PGCS: Regressive, Neutral and Progressive.
Figure 14.
Behavior of altitude and velocity in the evaluation of the best obtained from the optimization with uncertainties and . Color map is used to differentiate different random trajectories.
Figure 14.
Behavior of altitude and velocity in the evaluation of the best obtained from the optimization with uncertainties and . Color map is used to differentiate different random trajectories.
Figure 15.
Distribution of altitude and velocity landing in the evaluation of the best result obtained from the optimization with uncertainties and . The vertical axis shows the frequency of the values.
Figure 15.
Distribution of altitude and velocity landing in the evaluation of the best result obtained from the optimization with uncertainties and . The vertical axis shows the frequency of the values.
Figure 16.
Second approach: Performance comparison for an array between 1 and 10 configuration engines, and for the three types of PGCS: Regressive, Neutral and Progressive.
Figure 16.
Second approach: Performance comparison for an array between 1 and 10 configuration engines, and for the three types of PGCS: Regressive, Neutral and Progressive.
Figure 17.
Behavior of altitude and velocity in the evaluation of the best obtained from the optimization with uncertainties and . Color map is used to differentiate different random trajectories.
Figure 17.
Behavior of altitude and velocity in the evaluation of the best obtained from the optimization with uncertainties and . Color map is used to differentiate different random trajectories.
Figure 18.
Distribution of altitude and velocity landing in the evaluation of the best result obtained from the optimization with uncertainties and . The vertical axis shows the frequency of the values.
Figure 18.
Distribution of altitude and velocity landing in the evaluation of the best result obtained from the optimization with uncertainties and . The vertical axis shows the frequency of the values.
Table 1.
Advantages and disadvantages of different PGCS.
Table 1.
Advantages and disadvantages of different PGCS.
| Popular Types of PGCS | Advantages | Disadvantages |
|---|
| EndBurn (Neutral) | - Long action time | - Low thrust |
| | - Stable and neutral thrust | - The chamber wall must be thick (greater weight) due to direct and long exposure of high-pressure and high-temperature combustion gases |
| Star (Neutral, Progressive, and Regressive) | - The shape of the star can be modified depending on the thrust requirements | - Short action time |
| | | - The shape is more difficult to manufacture compared to the others |
| BATES (Progressive) | - High final thrust | - Very low thrust at the start of ignition |
| | - Low weight | - Short action time |
Table 2.
Percentage within the distribution concerning .
Table 2.
Percentage within the distribution concerning .
| gf | Confidence Interval | Percentage within the Distribution |
|---|
| 1 | +1 s | 68.27% |
| 2 | +2 s | 95.45% |
| 3 | +3 s | 99.73% |
Table 3.
Creation of each gene of the first generation of individuals.
Table 3.
Creation of each gene of the first generation of individuals.
| Genes | Random Method |
|---|
| |
| |
| |
| |
Table 6.
Design parameters of the best result obtained from the optimization scenario without uncertainties.
Table 6.
Design parameters of the best result obtained from the optimization scenario without uncertainties.
| Parameters | Value |
|---|
| PGCS | Regressive |
| 9 |
| 14.15 × 10 kg/s |
| s |
| m/s |
| Std Dev. of | m/s |
| Mass used | kg |
Table 7.
Control parameters from the best result obtained in the scenario without optimization uncertainties. The SPEs array has and Regressive PGCS.
Table 7.
Control parameters from the best result obtained in the scenario without optimization uncertainties. The SPEs array has and Regressive PGCS.
| k | | γk |
|---|
| 1 | 0.511 | 3.632 |
| 2 | 0.992 | 4.393 |
| 3 | 0.300 | 10.071 |
| 4 | 0.755 | 19.199 |
| 5 | 0.531 | 20.431 |
| 6 | 0.795 | 11.292 |
| 7 | 0.560 | 17.099 |
| 8 | 0.323 | 8.667 |
| 9 | 0.729 | 16.382 |
Table 8.
Design parameters of the best result obtained from the optimization scenario with uncertainties.
Table 8.
Design parameters of the best result obtained from the optimization scenario with uncertainties.
| Parameters | Value |
|---|
| PGCS | Regressive |
| 10 |
| 10.16 × 10 kg/s |
| s |
| m/s |
| Std Dev. of | m/s |
| Mass used | kg |
Table 9.
Control parameters from the best result obtained in the scenario with optimization uncertainties.
Table 9.
Control parameters from the best result obtained in the scenario with optimization uncertainties.
| k | | γk |
|---|
| 1 | 0.639 | 12.111 |
| 2 | 0.138 | 11.165 |
| 3 | 0.862 | 4.742 |
| 4 | 0.551 | 12.844 |
| 5 | 0.999 | 11.465 |
| 6 | 0.091 | 6.036 |
| 7 | 0.768 | 22.285 |
| 8 | 0.608 | 5.219 |
| 9 | 0.624 | 17.851 |
| 10 | 0.867 | 24.439 |