Abstract
Ice accretion on stratospheric airships, which affects the net buoyancy and reduces the ascent speed, thereby leading to component failure and further necessitating flight termination, has received considerable attention. In this study, the formation of ice occurred when the airship hit supercooled water droplets during the non-forming ascending process. Theoretical descriptions of an ice accretion model, a thermal model, and a dynamic model for airships were established to estimate the flight performance with ice mass. Then, validation of the simulation and the cloud chamber test was carried out, which indicated that the temperature, liquid water content (LWC), and pressure considerably influenced the ice mass. A lower temperature had a positive effect on ice accretion. The mass of ice accretion increased with the increase in LWC. Ice did not form easily under low pressure due to evaporation and sublimation. Finally, the effects of the ambient LWC and initial helium mass were analyzed. It was shown that an LWC of 0.5 g/m3 resulted in severe degradation of the ascent performance. When the initial helium mass was not sufficient, the airship landed due to ice accumulation. However, redundant inflation increased the ice mass and lowered the cruising altitude.
1. Introduction
Stratospheric airships, which are a new concept for an autonomous atmospheric flight platform, can operate at high altitudes to accomplish various military or commercial missions, such as monitoring, surveillance, and scientific exploration [1,2,3]. With the rapid development of airship technology, the popularization and application of these aircraft are imminent. In order to deal with emergencies, the stratospheric airship requires all-weather launch capabilities. However, on rainy or snowy days when the airship flies across ice clouds and encounters supercooled droplets during ascent, a risk of ice deposition exists in the windward part [4,5]. Research on aircraft icing can provide a reference for stratospheric airships [6,7,8,9].
It is reasonable and effective to launch the stratospheric airship in a non-forming launch mode [10,11]. The airship maintains a vertical upward attitude during the ascent process. Above the zero-pressure surface, the head of the envelope maintains a spherical inflatable shape under the action of positive pressure, which expands until the design volume is filled. However, the ice accretion will affect the net buoyancy, reduce the ascent speed of the airship, cause the failure of components, and further necessitate flight termination [12]. The High-Altitude Long Endurance Demonstrator (HALE-D) was launched at 6 am in July 2011, and its ascent height decreased due to ice accumulation after reaching an altitude of 9936 m. The post-flight analysis showed that the icing of the pressurization subsystem air valve restricted the emission of air inside the airship. The airship hovered in a high-LWC and high-humidity environment for about 80 min and could no longer resist the increasing weight of the ice.
Previous research on ice accumulation in the 1940s showed the effects on flight performance and mechanics, which was mainly based on experiments and flight testing. A series of icing tests for the ZPG-2 airship were conducted by the U.S. Navy. The results illustrated that ice formed only on the forward edges of protuberances and wires in supercooled clouds, and ice accretions occurred on the envelope in freezing drizzle conditions [13]. However, these tests were conducted below 5000 ft during the cruise and climb of low-altitude airships. In the non-forming ascending process of stratosphere airships, the expansion effect of the airbag was found to severely reduce the temperature of the helium and envelope, which exacerbated the icing of the airship envelope.
Compared with experimental research, the use of numerical simulations has significantly reduced resource consumption [14]. Messinger constructed a two-dimensional model based on the conservation of mass and energy to calculate icing performance [15]. On this foundation, the three-dimensional ice accretion model, a numerical method for computing ice shapes, and the mixed-phase icing thermodynamic model were then proposed to compute the performance characteristics of airfoils [16,17,18,19]. However, especially for non-formed launch airships, the temperature of the envelope was different from the ambient temperature. The supercooling effect of the helium enhanced the temperature difference between the inside and outside.
In this study, theoretical descriptions of a frosting model, an ice accretion model, and a thermal dynamic model for airships were firstly established, which estimated the icing performance of stratospheric airships in the non-formed ascent process. Then, a comparison between the simulation and the cloud chamber test was carried out to provide validation for the ice accretion model. Finally, the effects of the ambient environment and the initial helium mass were analyzed, and a further inspection of the ascent performance was conducted.
2. Methodology
2.1. Ice Accretion on Airship
The thermodynamic model of mixed-phase icing on the airship surface was based on the earlier Messinger theory [15]. Neglecting the heat transfer within the ice between the ice and the envelope, the mass transfer of the liquid water control body was analyzed using the control volume method [20,21,22]. The mass conservation equation can be calculated as follows:
where is the mass flow of water droplets hitting the envelope; , are the mass flow into and out of control body, respectively; , , and are the mass flow of evaporation, icing, and sublimation, respectively. Evaporative mass transfer occurs when there is a water layer on the ice, and sublimation occurs when there is only an ice layer [23]. The mass flow can be calculated as follows:
where is the adhesion coefficient of water droplets; is the far-field water droplet velocity; is the collection coefficient; A is the bottom area of the control body; is the liquid water content of supercooled water droplets; is the Lewis number, ; is the relative molecular mass; is the skin temperature; is the saturation vapor pressure at the equilibrium temperature of the skin; is the total pressure; is the total temperature; is the boundary layer outside air pressure; is the relative humidity; is the convective heat transfer coefficient; and is the specific heat capacity.
The energy conservation equation [24] can be calculated as follows:
where is the kinetic energy of the supercooled water droplets; is the latent heat of the inflow water from the previous control body and is the heat of outflow to the next control body; is the latent heat of icing; is the sensible heat transfer between the melting temperature and wall temperature; is the latent heat of evaporation when there is water on the surface and is the latent heat of sublimation when there is only ice on the surface; is the sensible heat of water droplets; and is the convective heat exchanger. Each type of energy in the above equation can be written as
In the ice accretion model, the finite element model was created. The water droplet collection coefficient, mass flow and heat flow of units were calculated as input parameters to calculate the final icing volume. For a three-dimensional ellipsoid airship, the surfaces are discretized into two-dimensional streamlines. Each control body element only considers the mass flow along the linear direction, without the circumferential diffusion. The mass flow into the control body at the stationary point is assumed to be zero, the outflow of which is divided equally into two parts to the upper and lower surfaces, respectively. There is a binding relationship in that the mass flow out of the former control body is equal to the mass flow into the latter control body. After the control body at the stationary point is calculated, all the elements in the streamline are sequentially solved.
2.2. Thermal and Dynamic Model of the Airship
The thermal and dynamical model is briefly summarized; further details not reported here can be found in [25,26,27,28], including the description of solar radiation, scattered radiation, infrared radiation, and convection heat transfer. The stratospheric airship thermal model uses a zero-dimensional model, treating the skin and the internal gas as masses. The thermal equilibrium equation can be calculated as follows:
where , , and are the mass, heat capacity, and temperature of the envelope element, respectively, and ,, and are the parameters of the helium. , , and are the solar energy received from direct radiation, atmospheric diffuse radiation, and ground reflected radiation per second, respectively. and are the infrared radiation received from the atmospheric environment and the ground per second, respectively. is the energy emitted from the envelope. and denotes the external and internal convection heat gain. , and are the pressure, volume, and Boltzmann constant of the helium gas, respectively. is the total system mass; is the added mass; is the buoyancy; is the aerodynamic drag; and is the ascent speed of the airship.
The direct solar radiation includes the absorption of the outer surface and the inner surface after multiple reflections. The reflectivity of the envelope , and the effective reflectivity can be expressed as . The expression for the energy exchange of the envelope is shown in Table 1.

Table 1.
Expressions for solar radiation, infrared radiation and thermal convection.
is the solar absorptivity of the envelope. is the illuminated projection area, is the surface area of the airship. is the solar radiation constant. is the atmospheric transmissivity. is the solar elevation angle. is albedo reflected factor. is the earth’s infrared emissivity. is the Stefan–Boltzmann constant. is the view factor. is the ground temperature, is the sky equivalent temperature, and is the envelope temperature. means the characteristic length, and are forced and natural convective heat transfer coefficients, respectively. The Knudsen number is related to the Grashof number, Prandtl number and Reynolds number. and are the thermal conductivities of air and helium.
2.3. Program Development Process
The numerical simulation program was developed in the VC2019 environment and the structure of the flow chart of the framework is shown in Figure 1. The calculation program consists of the main program, earth environment module, ice accretion module, thermal module, airship state module and dynamic module. The above models are discretized using the fourth-order Runge–Kutta (RK) numerical method. The steps of the framework are described below: The Earth Environment module calculates the density, temperature, pressure and LWC of the atmosphere at the current altitude and encapsulates them in a message to other modules; the ice accretion module uses the finite element method to calculate the cumulative ice mass; the thermal module calculates the skin and helium temperature from the differential equations [14,15]; the airship status module calculates the differential pressure, volume and buoyancy; the dynamics module accepts the above data and updates the current altitude, velocity and acceleration data, and stores the results of each iterative loops in a file. It should be noted that the time step of the RK method, which was usually set as 10–20 s, affected the numerical analysis in terms of the convergence and the calculation speed.
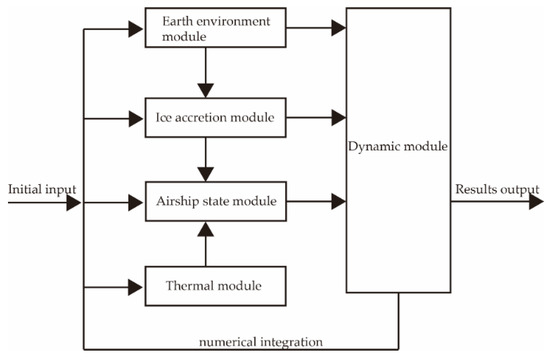
Figure 1.
Simulation program module interactions chart.
3. Experimental Validation
The cloud chamber tests with different conditions were selected to validate the accuracy of the model, respectively. Then, the influences of the liquid water contents, temperatures, and air pressures on the ice mass were analyzed.
There were great differences in the speed and direction in the airship ascent stage and aircraft cruise stage. The airship took off at a speed of no more than 10 m/s in the vertical direction in its ascent stage, while the aircraft flew even more than 300 m/s in the horizontal direction in its cruise stage. Therefore, the cloud chamber was chosen for experimental validation instead of a wind tunnel [29]. The expansion cloud chamber is an important piece of equipment for research on nucleation processes and the mechanism of aerosols. As shown in Figure 2, the cloud chamber system is mainly composed of a temperature control system, a cryogenic drying system, an air purification system, a pressure control system, a fogging system, a catalytic system, and a central control system [30].
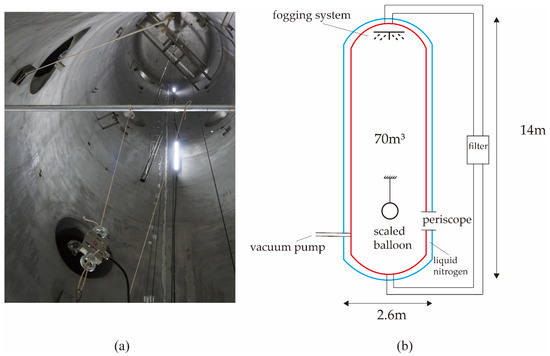
Figure 2.
(a) Practical setup (b) Diagram of experimental apparatus design.
During the ascent of the airship, the internal helium of the envelope above zero pressure gradually expanded as a spherical shape. Scaled balloons with a diameter of 55 cm, fabricated by the stratospheric airship envelope material, were used to validate the accuracy of the numerical model. The scaled balloon was firstly fixed at the bottom of the cloud chamber; the cloud chamber was then depressurized and cooled to the specified working condition, and the fogging system above the cloud chamber was sprayed according to the set liquid water content. In order to simulate a severe rain or snow weather environment that an airship may encounter during ascent, six different typical conditions, shown in Table 2, were set. During the tests, the data was recorded by the monitoring system. The temperature probe (HMP45, Vaisala Inc. (Vantaa, Finland)) with 100 Ω platinum resistance temperature detector (class AA, ±0.1 °C at 0 °C, −60–260 °C) was used to record the environment temperature. The air pressure was recorded using a sensor (PTB210, Vaisala Inc., ±0.1 hPa). The LWC was measured using a fog-monitor (FM-120, Droplet Measurement Technologies Inc. (Longmont, CO, USA), 2–50 μm). The tension sensor (DYLY-103, ±0.03%) was utilized to record the ice accretion mass.

Table 2.
The environment parameters and the ice mass of six conditions.
As shown in Figure 3, the parameter monitoring system recorded profiles for conditions 1-6 at one-second intervals. The liquid water ranged from 0 to 2.5 g/m3; the temperature of the environment was 255–270 K; and the pressure was 0.4–1.0 atm. These data were calculated using the ice accretion model, and then the obtained results were compared with the experimental results.
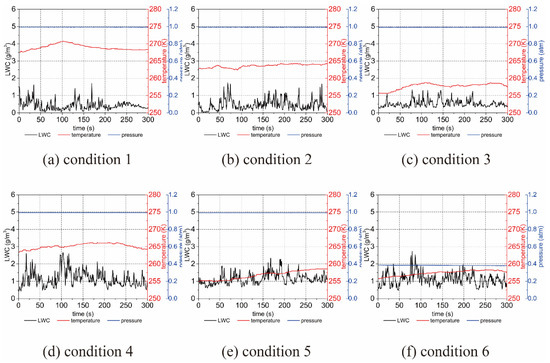
Figure 3.
The typical parameters of cloud chamber in (a) condition 1, (b) condition 2, (c) condition 3, (d) condition 4, (e) condition 5, and (f) condition 6.
The numerical simulation results of condition 1 are illustrated in Figure 4. Under the temperature of 268 K, the ice was mainly glazed ice. The thickness of mixed-phase icing was about 0.04 mm. The relatively high temperature caused the droplets to not freeze instantly after impact, but to flow backwards along the sphere’s surface for some distance. This process created an expansive shape of ice that extended below the waist of the sphere. In contrast, frost ice was mainly formed when the ambient temperature decreased. The droplets froze immediately after they impinged the balloon, and the ice gathered above the waist.
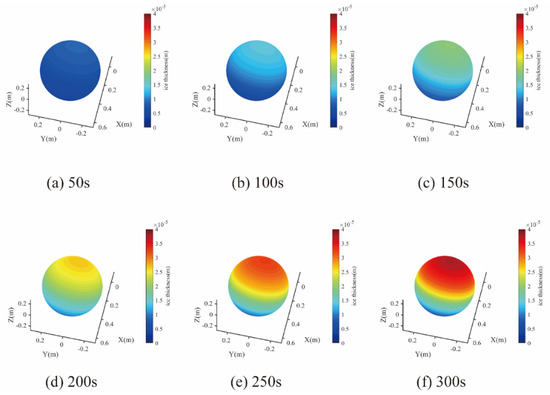
Figure 4.
Ice accretion of the scaled airship at (a) 50 s, (b) 100 s, (c) 150 s, (d) 200 s, (e) 250 s, and (f) 300 s during condition 1.
Figure 4 and Figure 5 represent the ice accretion of the scaled airship every 50 s during the simulation and experiment, respectively. It can be seen from the images that ice accretion first appeared on the top of the scaled airship; as time passed, ice accretion appeared on the windward parts of the scaled airship from top to bottom. The two sets of results matched well with each other in terms of trends. Compared with the simulation data, the experimental data had some fluctuations, which were caused by the unstable hit speed of the liquid water produced by the fogging system. The average liquid water velocity was used in the simulation, and the final ice accretion had a small discrepancy in comparison to that in the experiment. The comparisons between the simulation results and the experimental data showed fairly good agreement, which confirmed the validity and rationality of the model proposed in this paper.

Figure 5.
Ice accretion of the scaled airship at (a) 50 s, (b) 100 s, (c) 150 s, (d) 200 s, (e) 250 s, and (f) 300 s during condition 1.
Figure 6 shows the comparison of ice deposition during the whole process of the simulation and experiment. Comparing conditions 1–3, it can be concluded that when the air pressure and liquid water content remained unchanged, the mass of ice accretion increased with the decrease in temperature, which meant that a lower temperature had a positive effect on ice accretion. In comparison to conditions 2 and 4, in conditions 3 and 5, the mass of ice accretion increased with a higher liquid water content; therefore, we suggest avoiding releasing stratospheric airships on rainy days with high humidity. The comparison of conditions 5 and 6 led to the conclusion that it was more difficult to form ice under low pressure due to evaporation and sublimation. This indicated that as the altitude increased, the rate of ice deposition gradually decreased.
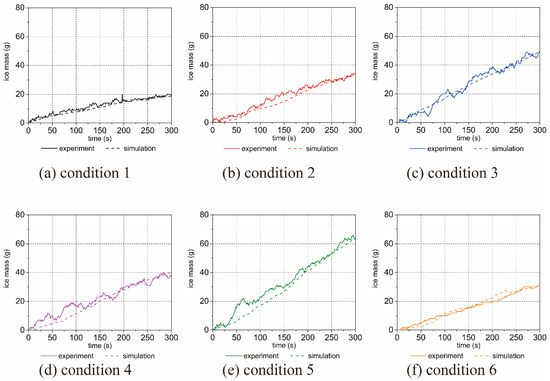
Figure 6.
Comparison of ice accumulation in the experiment and simulation in (a) condition 1, (b) condition 2, (c) condition 3, (d) condition 4, (e) condition 5, and (f) condition 6.
4. Results and Discussion
The results from the cloud chamber indicated that the liquid water content (LWC), temperature, and airspeed considerably influenced the ice mass. In this section, the ascent process with ice accretion of the stratospheric airship was simulated to determine the influence of ice mass. The formation of ice occurred when the airship hit supercooled water droplets in stratiform clouds where the temperature was below freezing point. Thus, the selection of the initial helium mass can ensure the consequent increase in speed and cruising height.
4.1. Model Establishment
The ascending model was implemented in a computer simulation, which was available for both non-formed ascending airships and balloons. A high-altitude balloon was used as the object of study to simulate its ascent process. The design parameters and radiation properties of the stratospheric balloon are illustrated in Table 3. Figure 7 shows the atmospheric parameters as a function of altitude, which are determined from historic soundings in Hainan, China. The LWC values were set as 0–0.5 g/m3 at an altitude of 2–7.5 km.

Table 3.
Stratospheric balloon parameters.
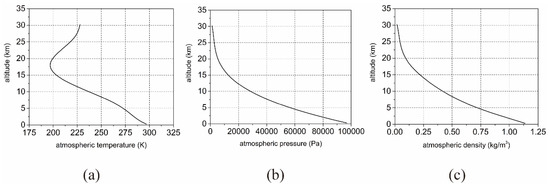
Figure 7.
The (a) temperature, (b) pressure and (c) density of atmospheric.
4.2. Effect of Liquid Water Content
Ice accumulation on the top of the balloon resulted in severe performance degradation, thus threatening flight safety. For example, the increased weight of the ice lowered the cruising altitude and climbing rate and extended the periods of helium supercooling. The results of the calculations for different LWCs at an altitude of 2–7.5 km were analyzed, as shown in Figure 8. The effects on the climbing height are clearly visible in Figure 8a. The balloon reached cruising height after 4381 s with 0 LWC. However, the climbing time increased to 5461 s and the cruising height was reduced by 200 m when the LWC was 0.5 g/m3. Figure 8b shows the velocity profile of the balloon during its ascent, showing a double “V”-shaped variation. The speed of the balloon increased rapidly to 6.5 m/s in the initial stage of the flight and then decreased due to the loss of buoyancy caused by the supercooling of the helium gas. However, as the air density and drag decreased, the speed increased slightly. Then, the velocity decreased significantly as the helium supercooling became more severe in the stratosphere. The velocity consequently increased gradually because the solar radiation heated the helium at a high altitude. The velocity decreased rapidly and equilibrated at the residence height after 1 h of oscillation. The oscillations decayed very slowly due to the high inertia and the low air density. When the LWC increased to 0.5 g/m3, the climbing rate was 2 m/s lower than in the dry climate.
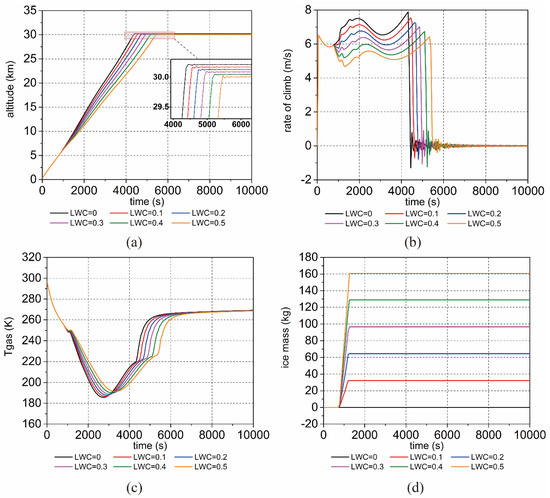
Figure 8.
Ascent performance of (a) altitude, (b) velocity, (c) helium temperature, and (d) ice mass at different LWCs.
Figure 8c shows the temperature of the helium during ascent, which gradually decreased due to the expansion of the helium and then rose rapidly due to solar radiation. When the LWC = 0, the helium temperature decreased to the minimum value of 185.7 K at an altitude of about 15 km. When the LWC increased to 0.5 g/m3, the supercooling helium temperature was 191.4 K due to the lower helium expansion rate and climbing velocity. However, the periods of helium supercooling and ice accumulation extended with the LWC. As shown in Figure 8d, the ice mass increased proportionally with the LWC. When the LWC = 0.5 g/m3, 160.8 kg of ice condensed at the top of the balloon, which can seriously affect ascent performance.
It should be noted that the most notable of input variables affect flight predictions such as altitude, velocity, gas temperatures, and ascent time. The simulation results were compared with the flight tests HASI2003 in the work in [31]. The velocity trends were consistent with each other, exhibiting a double “V”-shaped variation. The helium temperature profile was consistent with the flight test results, reaching a minimum of 190 K. However, the simulation demonstrated a greater maximum lift-off speed (8 m/s) and shorter lift-off time (5000 s) due to differences in envelope radiative properties, design parameters, and atmosphere parameters [32].
4.3. Effect of Helium Mass
There must be an accurate initial helium mass when the balloon flies in icing conditions. In this section, it was assumed that the LWC = 0.5 g/m3 with a different factor of the initial helium mass of Khe (0.9–1.4); the other parameter is shown in Table 3. Khe is defined as the ratio of the actual helium mass to the designed helium mass. The ascent performance obtained for these scenarios is illustrated in Figure 9. Figure 9a depicts the cruising altitude of the balloon. When Khe = 0.9, as a result of ice accumulation, the rising balloon began to descend at an altitude of 7335 m. Then, the balloon continued to freeze until it reached the landing. However, the cruising altitude slightly decreased with the increasing helium mass. In Figure 9b, the average climbing velocity was significantly higher and the period of ascent was shorter when the balloon was inflated with plenty of helium. However, as shown in Figure 9c, more Khe, from 1.0 to 1.4, led to a dramatic expansion, which cooled the helium temperature from 191.5 K to 173.9 K. Figure 9d illustrates that when the initial helium mass was not sufficient, the balloon landed due to the 479.5 kg of ice accumulation during ascent. When Khe varied from 1.0 to 1.4, the ice mass increased from 160.8 kg to 194.2 kg, and the balloon had a shorter freezing process with a faster freezing rate.
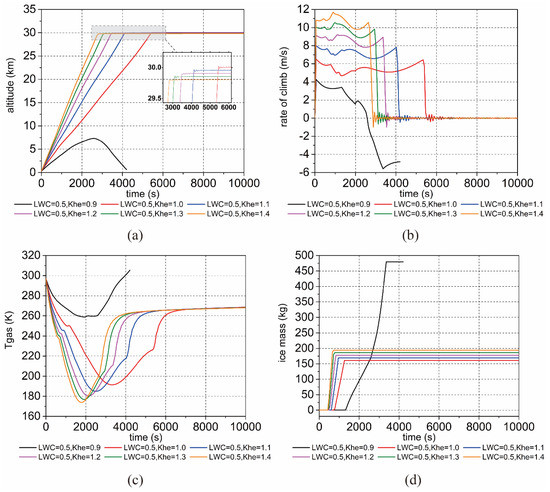
Figure 9.
Ascent performance of (a) altitude, (b) velocity, (c) helium temperature, and (d) ice mass with different helium masses.
It was indicated that excessive inflation also increased the amount of icing and thus lowered the cruising altitude. As depicted in Figure 9c,d, the slope of the ice mass curve was exacerbated by the redundant cold helium. The freezing rate of Khe = 1.4 was 0.821 kg/s, which is consistent with the result of 0.805 kg/s in [5] when the attack angle of the airship was 4°.
5. Conclusions
This study set out to model the airship ascent process on rainy or snowy days. In this study, we established an ice accretion model, a thermal model, and a dynamic model for airships. The validation study indicated that the simulation agreed well with the experimental results for a wide range of ambient temperatures, pressures, and liquid water contents. The cloud chamber test showed that lower temperatures had a positive effect on ice accretion. The mass of ice accretion increased with the increase in liquid water content. Additionally, the ice did not form as easily under low pressure due to the effect of evaporation and sublimation.
The non-forming launch process of a high-altitude balloon was simulated. The LWC of 0.5 g/m3 caused an icing mass of 160.8 kg and resulted in severe degradation of the ascent performance. When Khe = 0.9, the balloon landed due to the 479.5 kg ice mass. However, excessive inflation increased the amount of icing and lowered the cruising altitude. When Khe varied from 1.0 to 1.4, the ice mass increased from 160.8 kg to 194.2 kg, and the balloon had a shorter freezing process with a faster freezing rate. The freezing rate of Khe = 1.4 was 0.821 kg/s.
These findings improved the ascent predictions in cloudy and rainy conditions, which can calculate accurate initial helium mass (Khe) and ensure the launch feasibility of stratospheric airship.
Author Contributions
Conceptualization, D.L. and D.Z.; Data curation, C.F.; Formal analysis, C.F. and D.L.; Funding acquisition, M.Z.; Methodology, D.L.; Project administration, M.Z.; Resources, M.H.; Validation, Y.D. and P.T.; Writing—original draft, C.F.; Writing—review & editing, Y.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Fundamental Research Funds for the Central Universities (Grant No. YWF-22-JC-01,02,03), and the National Natural Science Foundation of China (Grant No. 61827901).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zuo, Z.; Song, J.; Zheng, Z.; Han, Q.-L. A survey on modelling, control and challenges of stratospheric airships. Control Eng. Pract. 2021, 119, 104979. [Google Scholar]
- Li, J.; Lv, M.; Sun, K.; Zhu, W. Thermal insulation performance of lightweight substrate for solar array on stratospheric airships. Appl. Therm. Eng. 2016, 107, 1158–1165. [Google Scholar] [CrossRef]
- Li, J.; Lv, M.; Tan, D.; Zhu, W.; Sun, K.; Zhang, Y. Output performance analyses of solar array on stratospheric airship with thermal effect. Appl. Therm. Eng. 2016, 104, 743–750. [Google Scholar] [CrossRef]
- Liu, Q.; Cui, Y.; Yang, Y.; Cai, J.; Xu, G. Three dimensional simulation of stratospheric airship ice accretion in ascending process. In Proceedings of the AIAA SPACE 2016, Long Beach, CA, USA, 13–16 September 2016. [Google Scholar]
- Liu, Q.; Yang, Y.; Wang, Q.; Cui, Y.; Cai, J. Icing performance of stratospheric airship in ascending process. Adv. Space Res. 2019, 64, 2405–2416. [Google Scholar]
- Tran, P.; Brahimi, M.T.; Paraschivoiu, I.; Pueyo, A.; Tezok, F. Ice accretion on aircraft wings with thermodynamic effects. J. Aircr. 1995, 32, 444–446. [Google Scholar]
- Saeed, F.; Selig, M.S.; Bragg, M.B. Design of Subscale Airfoils with Full-Scale Leading Edges for Ice Accretion Testing. J. Aircr. 1997, 34, 94–100. [Google Scholar]
- Mingione, G.; Brandi, V. Ice Accretion Prediction on Multielement Airfoils. J. Aircr. 1998, 35, 240–246. [Google Scholar] [CrossRef]
- Cebeci, T.; Chen, H.H.; Alemdaroglu, N. Fortified LEWICE with viscous effects. J. Aircr. 1991, 28, 564–571. [Google Scholar]
- Zhao, S.; Liu, D.; Zhao, D.; Wu, G.; Yin, S.; Zhou, P. Change rules of a stratospheric airship’s envelope shape during ascent process. Chin. J. Aeronaut. 2017, 30, 752–758. [Google Scholar] [CrossRef]
- Smith, I.; Lee, M. The HiSentinel Airship. In Proceedings of the 7th AIAA ATIO Conf, 2nd CEIAT Int’l Conf on Innov and Integr in Aero Sciences, 17th LTA Systems Tech Conf; Followed by 2nd TEOS Forum, Belfast, UK, 18–20 September 2007. [Google Scholar]
- Androulakakis, S.P.; Judy, R. Status and Plans of High Altitude Airship (HAATM) program. In Proceedings of the AIAA Lighter-Than-Air Systems Technology (LTA) Conference, Daytona Beach, FL, USA, 25–28 March 2013. [Google Scholar]
- Lewis, W.; Perkins, P.J. A Flight Evaluation and Analysis of the Effect of Icing Conditions on the ZPG-2 Airship; technical report archive & image library; Lewis Flight Propulsion Laboratory: Cleveland, OH, USA, 1958. [Google Scholar]
- Bragg, M.; Hutchison, T.; Merret, J. Effect of ice accretion on aircraft flight dynamics. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000. [Google Scholar]
- Messinger, B.L. Equilibrium Temperature of an Unheated Icing Surface as a Function of Air Speed. J. Aeronaut. Sci. 1953, 20, 29–42. [Google Scholar] [CrossRef]
- Shen, X.; Lin, G.; Yu, J.; Bu, X.; Du, C. Three-Dimensional Numerical Simulation of Ice Accretion at the Engine Inlet. J. Aircr. 2013, 50, 635–642. [Google Scholar] [CrossRef]
- Cao, Y.; Huang, J.; Yin, J. Numerical simulation of three-dimensional ice accretion on an aircraft wing. Int. J. Heat Mass Transf. 2016, 92, 34–54. [Google Scholar] [CrossRef]
- Fortin, G.; Laforte, J.-L.; Ilinca, A. Heat and mass transfer during ice accretion on aircraft wings with an improved roughness model. Int. J. Therm. Sci. 2006, 45, 595–606. [Google Scholar] [CrossRef]
- Özgen, S.; Canıbek, M. Ice accretion simulation on multi-element airfoils using extended Messinger model. Heat Mass Transf. 2008, 45, 305–322. [Google Scholar] [CrossRef]
- Beaugendre, H.; Morency, F.; Habashi, W.G. FENSAP-ICE’s Three-Dimensional In-Flight Ice Accretion Module: ICE3D. J. Aircr. 2003, 40, 239–247. [Google Scholar] [CrossRef]
- Bu, X.; Huang, P.; Lin, G. Numerical simulation of mixed phase icing on two-dimensional airfoil. Acta Astronautica et Astronautica Sinica 2020, 41, 124085. [Google Scholar]
- Bu, X.; Lin, G.; Yu, J.; Shen, X.; Hou, P. Numerical analysis of a swept wing hot air ice protection system. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2013, 228, 1507–1518. [Google Scholar] [CrossRef]
- Incropera, F.P. Fundamentals of Heat and Mass Transfer, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Bu, X.; Lin, G.; Shen, X.; Hu, Z.; Wen, D. Numerical simulation of aircraft thermal anti-icing system based on a tight-coupling method. Int. J. Heat Mass Transf. 2020, 148, 119061. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, D.; Zhu, M. A surrogate model for thermal characteristics of stratospheric airship. Adv. Space Res. 2018, 61, 2989–3001. [Google Scholar] [CrossRef]
- Lv, M.; Yao, Z.; Zhang, L.; Du, H.; Meng, J.; Li, J. Effects of solar array on the thermal performance of stratospheric airship. Appl. Therm. Eng. 2017, 124, 22–33. [Google Scholar] [CrossRef]
- Farley, R. BalloonAscent: 3-D Simulation Tool for the Ascent and Float of High-Altitude Balloons. In Proceedings of the AIAA 16th Lighter-Than-Air and Balloon Systems Conference, Arlington, VA, USA, 26–28 September 2005. [Google Scholar]
- Morris, A. (Ed.) Scientific Ballooning Handbook—NCAR TN/1A-99; National Center for Atmospheric Research: Boulder CO, USA, 1975. [Google Scholar]
- Busch, G.T.; Broeren, A.P.; Bragg, M.B. Aerodynamic Simulation of a Horn-Ice Accretion on a Subscale Model. J. Aircr. 2008, 45, 604–613. [Google Scholar] [CrossRef]
- Su, Z.; Guo, X.; Zhuge, J.; Wang, P. Developing and Testing of an Expansion Cloud Chamber for Cloud Physics Research. J. Appl. Meteorol. Sci. 2019, 30, 722–730. [Google Scholar]
- Palumbo, R.; Russo, M.; Filippone, E.; Corraro, F. ACHAB: Analysis code for high-altitude balloons. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2013; p. 6642. [Google Scholar]
- Garde, G. Comparison of Two Balloon Flight Simulation Programs. In Proceedings of the AIAA Atio & Lighter-Than-Air Sys Tech & Balloon Systems Conferences, Arlington, VA, USA, 26–28 September 2005. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).