Nonlinear Robust Control on Yaw Motion of a Variable-Speed Unmanned Aerial Helicopter under Multi-Source Disturbances
Abstract
:1. Introduction
- A fourth-order yaw error dynamic model considering actuator output fault, matched and unmatched disturbances is constructed. Based on the adaptive command filtered method, we built a simple control framework with no need for using DOB and solving complex HJI inequality to attenuate system multi-source perturbation.
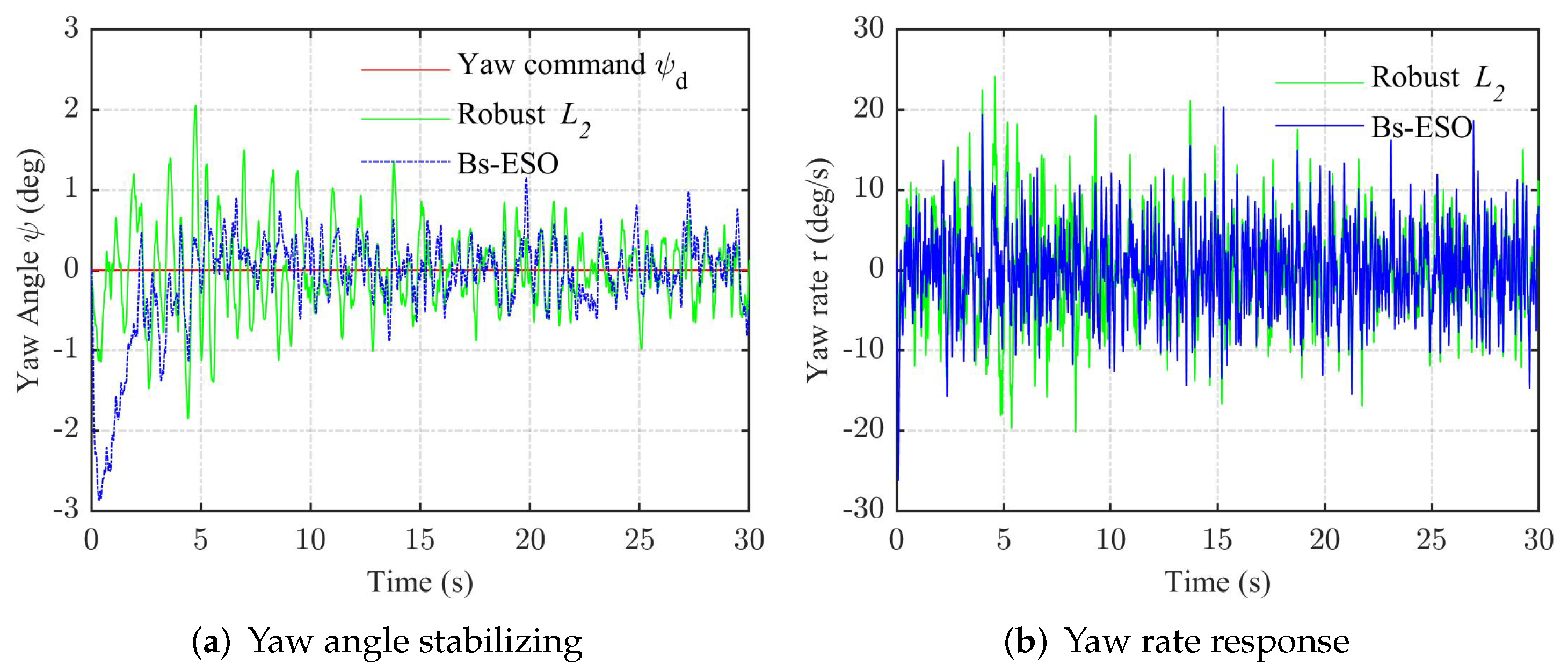
- A rigorous stability analysis of the closed-loop yaw system was completed, which achieved the predefined performance of -gain disturbance suppression. Four groups of comparative simulation results show the effectiveness and superiority of this control law.
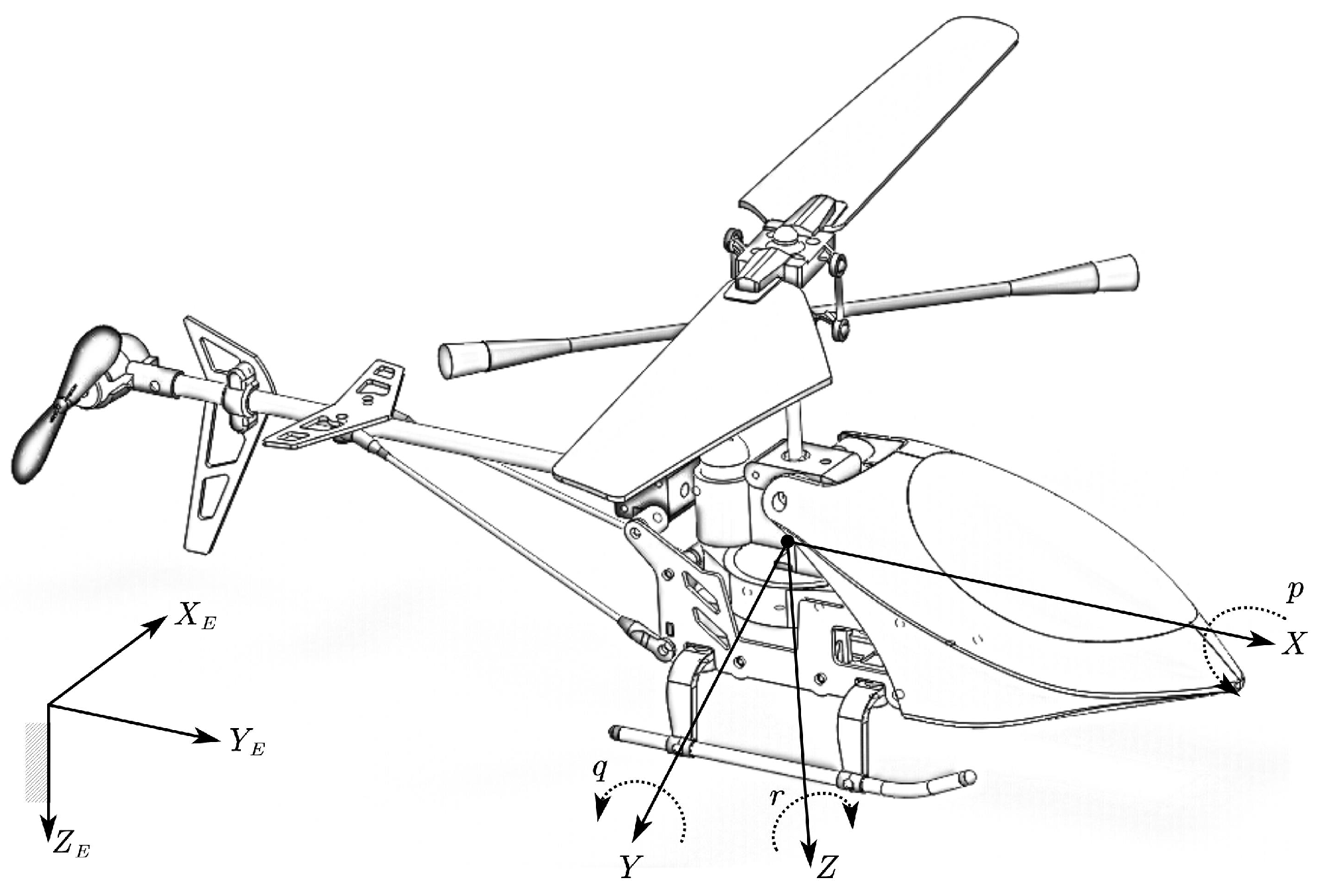
2. Yaw Error Dynamic Model
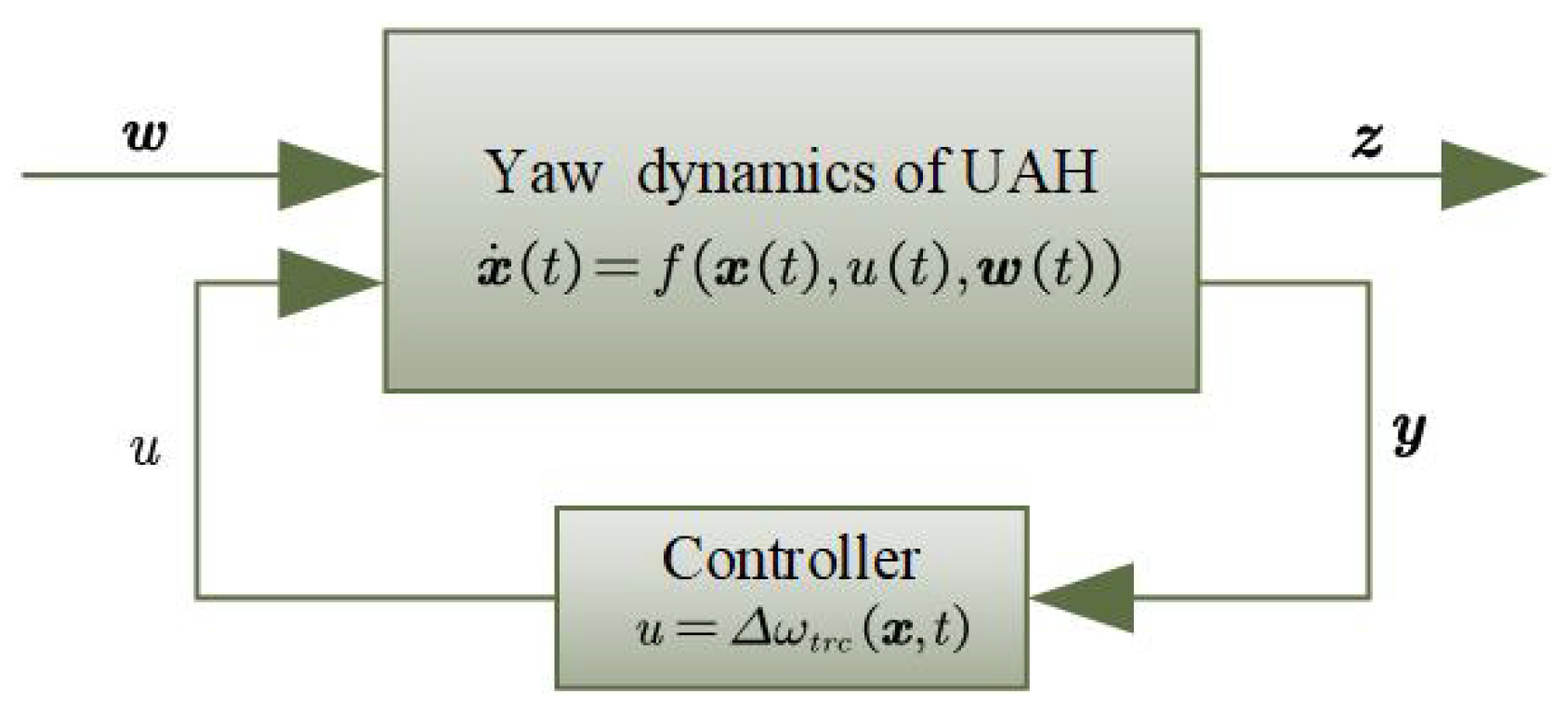
3. Controller Design
- (1)
- When , all signals are uniform-ultimately bounded stable.
- (2)
- When , the evaluation signal vector for initial state , satisfiesε is a sufficiently small constant [27], the is a state-dependent vector and is designed later.
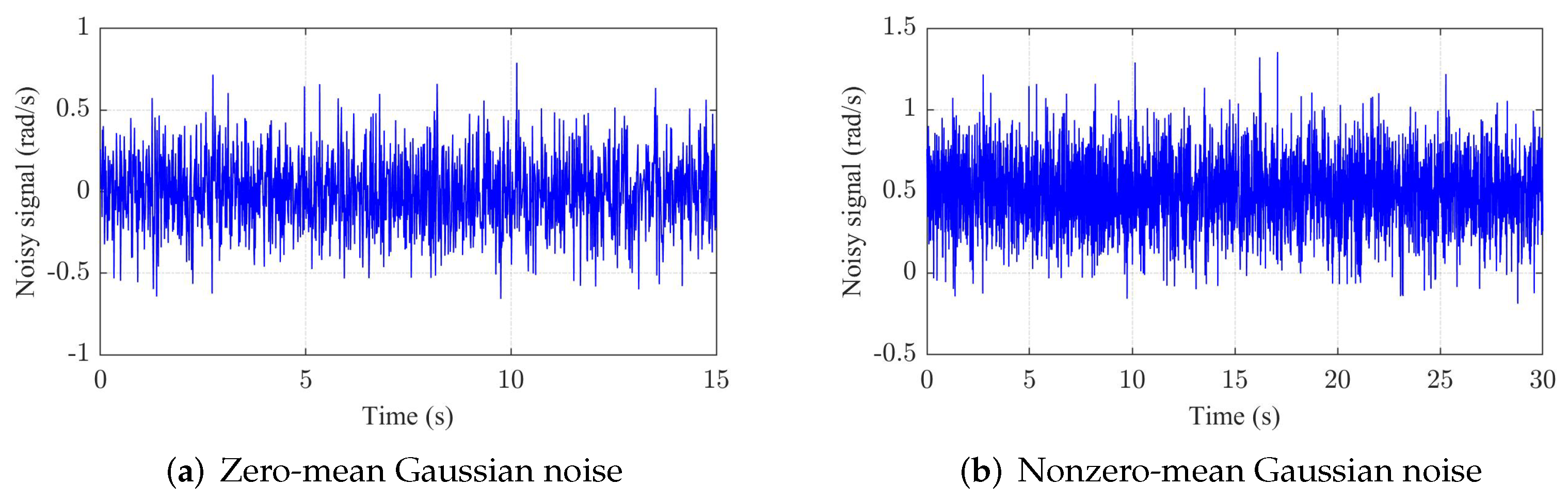
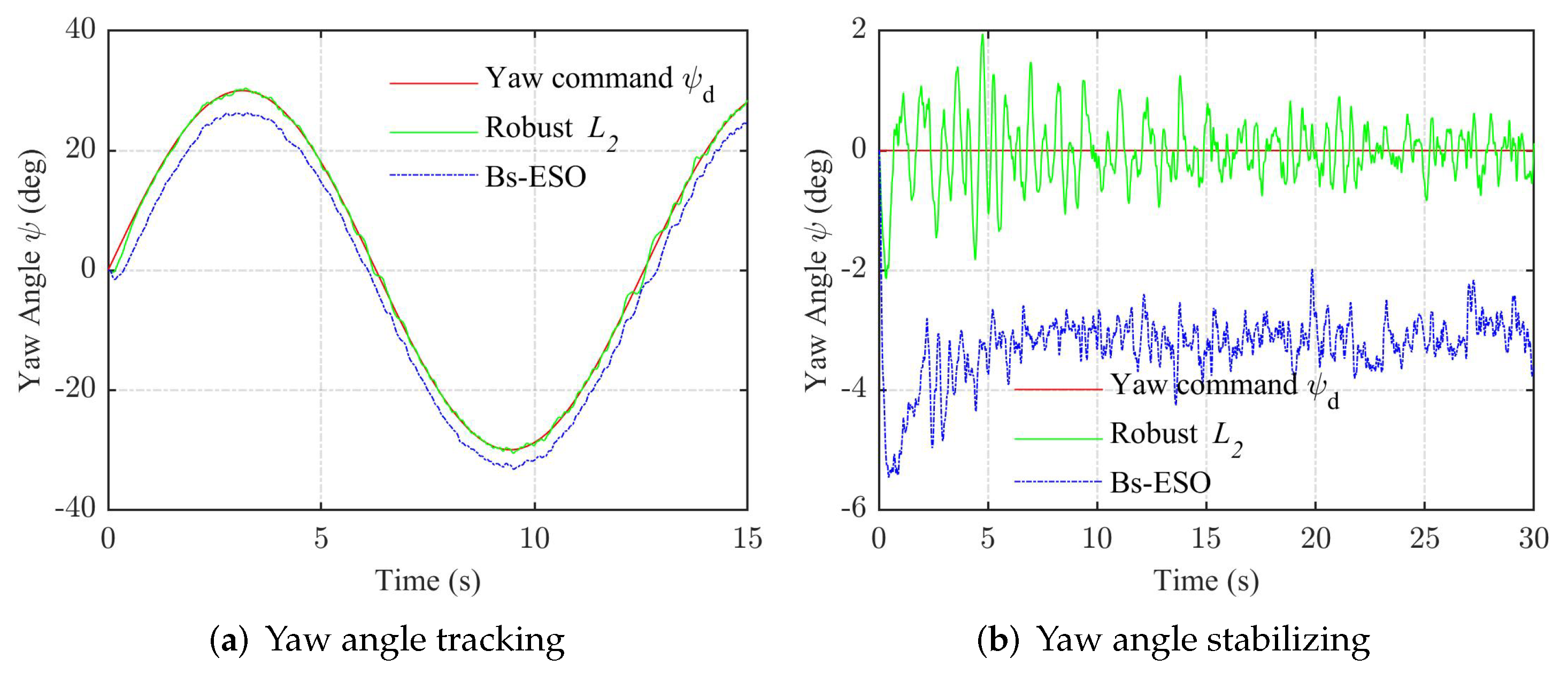
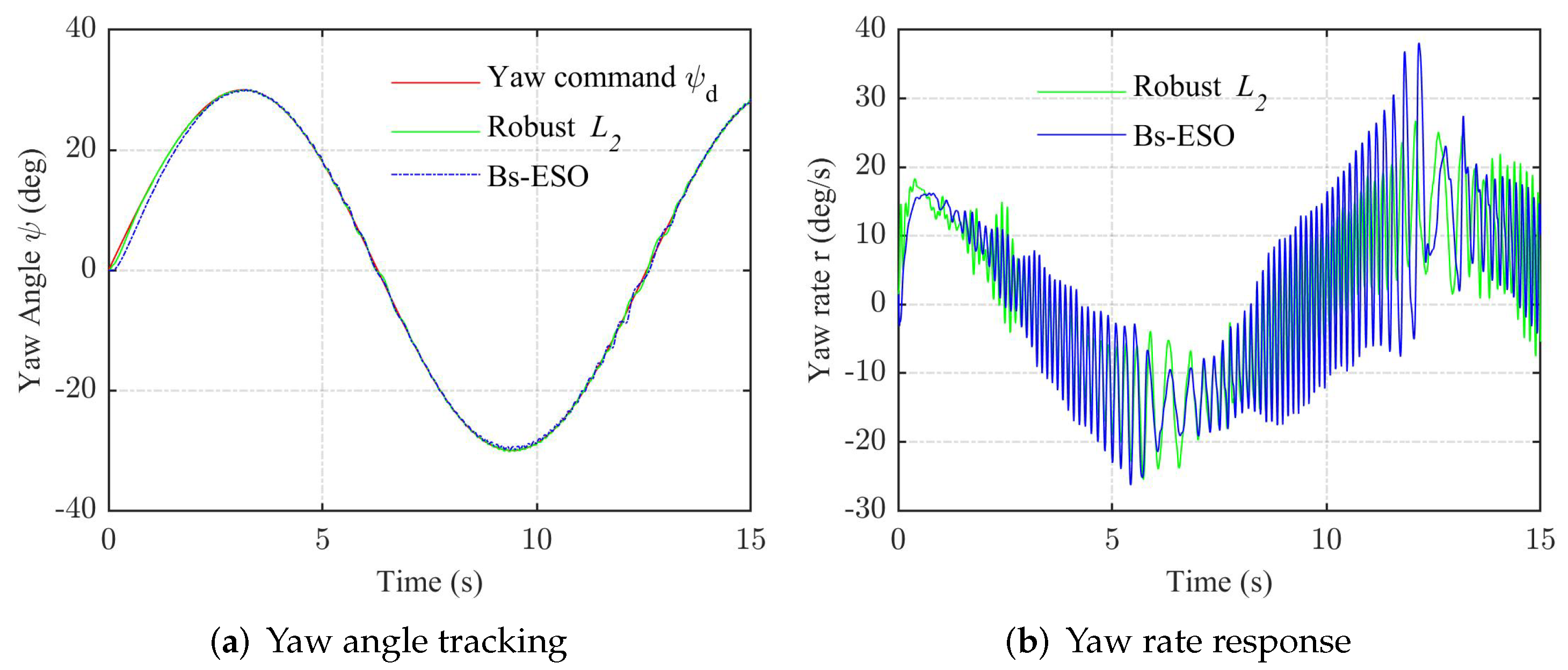
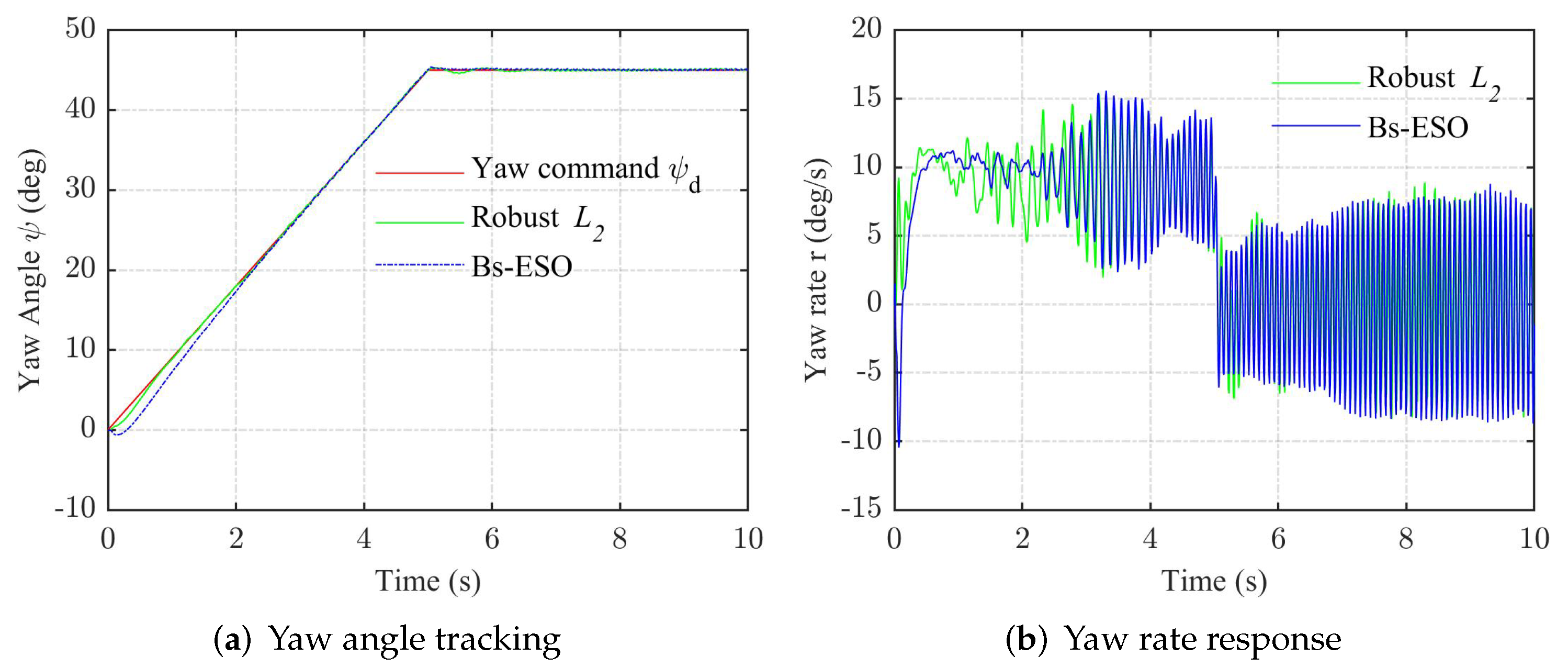
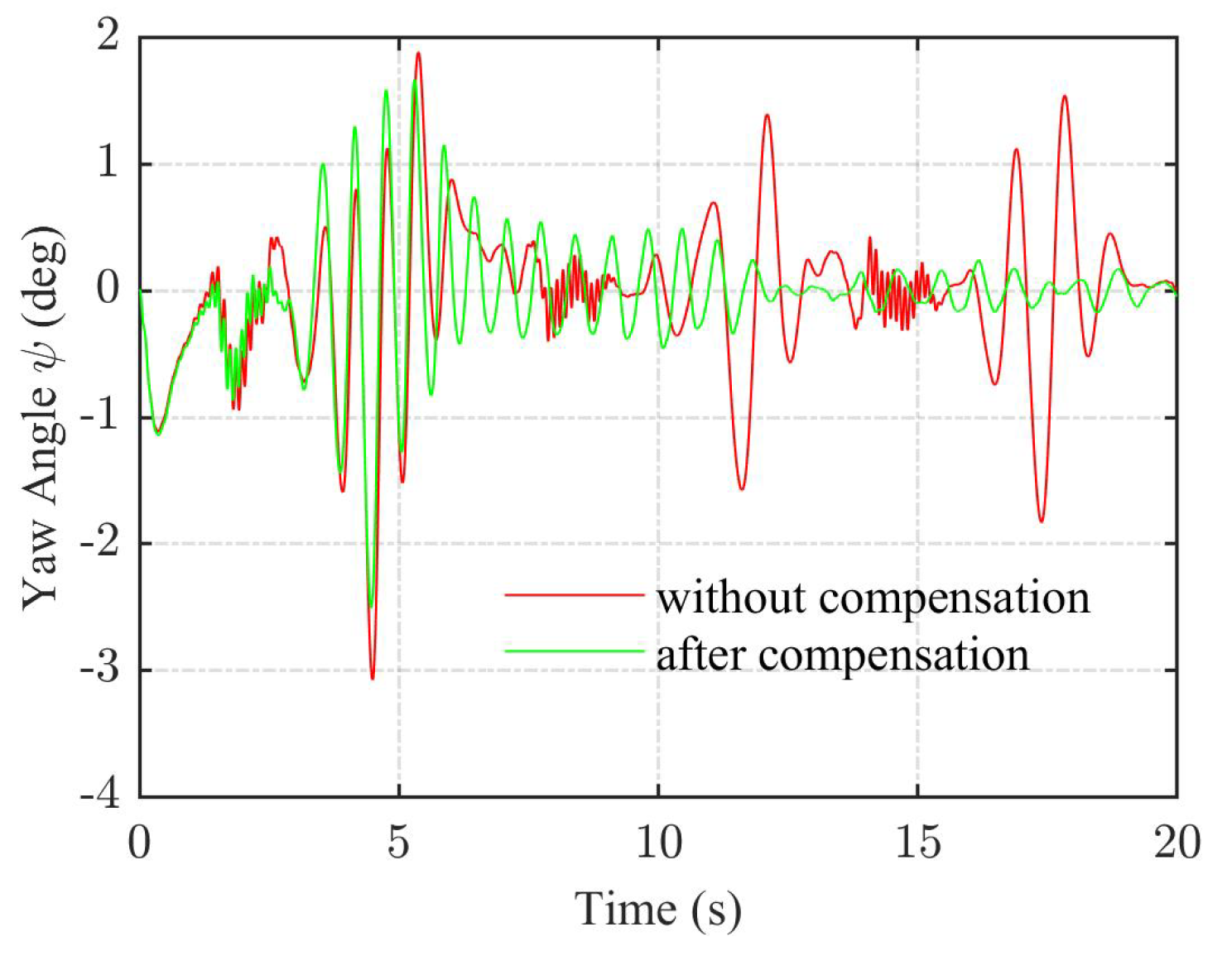
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAH | Unmanned Aerial Helicopter |
| AYDS | Artificial Yaw Damping System |
| ADRC | Active Disturbance Rejection Control |
| SMC | Sliding Mode Control |
| DOB | Disturbance-Observer-Based |
| UUB | Uniform-Ultimately bounded |
| HJI | Hamilton–Jacobi-Issacs |
| Bs | Backstepping |
| ESO | Extended State Observer |
| RBF | Radial Basis Function |
References
- La Civita, M.; Papaueorgiou, G.; Messner, W.C.; Kanade, T. Design and flight testing of an H(infinity) controller for a robotic helicopter. J. Guid. Control Dyn. 2006, 29, 485–494. [Google Scholar] [CrossRef]
- Nedjati, A.; Vizvari, B.; Izbirak, G. Post-earthquake response by small UAV helicopters. Nat. Hazards 2016, 80, 1669–1688. [Google Scholar] [CrossRef]
- Ding, L.; Ma, R.; Wu, H.; Feng, C.; Li, Q. Yaw control of an unmanned aerial vehicle helicopter using linear active disturbance rejection control. Proc. Inst. Mech. Eng. Part I-J. Syst. Control Eng. 2017, 231, 427–435. [Google Scholar] [CrossRef]
- Ding, L.; He, Q.; Wang, C.; Qi, R. Disturbance Rejection Attitude Control for a Quadrotor: Theory and Experiment. Int. J. Aerosp. Eng. 2021, 2021, 8850071. [Google Scholar] [CrossRef]
- Xu, D.Z.; Jiang, B.; Shi, P. Global Robust Tracking Control of Non-affine Nonlinear Systems with Application to Yaw Control of UAV Helicopter. Int. J. Control Autom. Syst. 2013, 11, 957–965. [Google Scholar] [CrossRef]
- Jiang, T.; Lin, D.; Song, T. Novel integral sliding mode control for small-scale unmanned helicopters. J. Frankl. Inst. 2019, 356, 2668–2689. [Google Scholar] [CrossRef]
- Krishna, A.B.; Sen, A.; Kothari, M. Super Twisting Algorithm for Robust Geometric Control of a Helicopter. J. Intell. Robot. Syst. Theory Appl. 2021, 102, 61. [Google Scholar] [CrossRef]
- Ullah, I.; Pei, H.L. Fixed Time Disturbance Observer Based Sliding Mode Control for a Miniature Unmanned Helicopter Hover Operations in Presence of External Disturbances. IEEE Access 2020, 8, 73173–73181. [Google Scholar] [CrossRef]
- Liu, L.; Chen, M.; Li, T.; Wang, H. Composite Anti-Disturbance Reference Model L2–L∞ Control for Helicopter Slung Load System. J. Intell. Robot. Syst. Theory Appl. 2021, 102, 15. [Google Scholar] [CrossRef]
- Tang, S.; Mao, L.; Liu, G.; Wang, W. Active Disturbance Rejection Control Design of the Yaw Channel for a Small-scale Helicopter based on Backstepping. In Proceedings of the 38th 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 8073–8078. [Google Scholar]
- Zhao, W.; Meng, Z.; Wang, K.; Zhang, H. Backstepping Control of an Unmanned Helicopter Subjected to External Disturbance and Model Uncertainty. Appl. Sci. 2021, 11, 5331. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Q.; Duan, Y. Finite-Time Backstepping Sliding Mode Control Applied to the Yaw Control of UAV Helicopters with Actuator Faults. In Proceedings of the 39th Chinese Control Conference, Shenyang, China, 27–29 July 2020; pp. 6911–6916. [Google Scholar] [CrossRef]
- Li, Y.; Chen, M.; Ge, S.S. Anti-disturbance control for attitude and altitude systems of the helicopter under random disturbances. Aerosp. Sci. Technol. 2020, 96, 105561. [Google Scholar] [CrossRef]
- Sheng, S.; Sun, C. Yaw Control of an Unmanned Helicopter Using Adaptive Model Feedback and Error Compensation. J. Aerosp. Eng. 2016, 29, 06015002. [Google Scholar] [CrossRef]
- Soltanpour, M.R.; Hasanvand, F.; Hooshmand, R. Robust linear parameter varying attitude control of a quadrotor unmanned aerial vehicle with state constraints and input saturation subject to wind disturbance. Trans. Inst. Meas. Control 2020, 42, 1083–1096. [Google Scholar] [CrossRef]
- Fan, X.; Yi, Y.; Zhang, T. Disturbance rejection control of yaw channel of a small-scale unmanned helicopter via Takagi-Sugeno disturbance modeling approach. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416671113. [Google Scholar] [CrossRef]
- Yan, W.X.; Huang, J.; Xu, D.Z. Adaptive fuzzy tracking control for non-affine nonlinear yaw channel of unmanned aerial vehicle helicopter. Int. J. Adv. Robot. Syst. 2017, 14, 1729881416678137. [Google Scholar] [CrossRef] [Green Version]
- Le, T.Q.; Lai, Y.C.; Yeh, C.L. Adaptive tracking control based on neural approximation for the yaw motion of a small-scale unmanned helicopter. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419828277. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.C.; Le, T.Q. Adaptive Learning-Based Observer With Dynamic Inversion for the Autonomous Flight of an Unmanned Helicopter. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1803–1814. [Google Scholar] [CrossRef]
- Shen, S.; Xu, J. Adaptive neural network-based active disturbance rejection flight control of an unmanned helicopter. Aerosp. Sci. Technol. 2021, 119, 107062. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, X.; Xu, D. Adaptive Neural Fault-Tolerant Control for the Yaw Control of UAV Helicopters with Input Saturation and Full-State Constraints. Appl. Sci. 2020, 10, 1404. [Google Scholar] [CrossRef] [Green Version]
- Ezekiel, D.M.; Samikannu, R.; Matsebe, O. Pitch and Yaw Angular Motions (Rotations) Control of the 1-DOF and 2-DOF TRMS: A Survey. Arch. Comput. Methods Eng. 2021, 28, 1449–1458. [Google Scholar] [CrossRef]
- Singh, R.; Bhushan, B. Data-Driven Technique-Based Fault-Tolerant Control for Pitch and Yaw Motion in Unmanned Helicopters. IEEE Trans. Instrum. Meas. 2021, 70, 3502711. [Google Scholar] [CrossRef]
- Dong, W.; Farrell, J.A.; Polycarpou, M.M.; Djapic, V.; Sharma, M. Command filtered adaptive backstepping. IEEE Trans. Control Syst. Technol. 2011, 20, 566–580. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Yun, M.M.; Li, T. A new approach to fast global finite-time stabilization of high-order nonlinear system. Automatica 2017, 81, 455–463. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Zhao, L. Finite-time command filtered backstepping control for a class of nonlinear systems. Automatica 2018, 92, 173–180. [Google Scholar] [CrossRef]
- Ishii, C.; Shen, T.; Qu, Z. Lyapunov recursive design of robust adaptive tracking control with L2-gain performance for electrically-driven robot manipulators. Int. J. Control 2001, 74, 811–828. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, P.; Dai, Y.; Chen, J. Nonlinear Robust Control on Yaw Motion of a Variable-Speed Unmanned Aerial Helicopter under Multi-Source Disturbances. Aerospace 2022, 9, 42. https://doi.org/10.3390/aerospace9010042
Tang P, Dai Y, Chen J. Nonlinear Robust Control on Yaw Motion of a Variable-Speed Unmanned Aerial Helicopter under Multi-Source Disturbances. Aerospace. 2022; 9(1):42. https://doi.org/10.3390/aerospace9010042
Chicago/Turabian StyleTang, Peng, Yuehong Dai, and Junfeng Chen. 2022. "Nonlinear Robust Control on Yaw Motion of a Variable-Speed Unmanned Aerial Helicopter under Multi-Source Disturbances" Aerospace 9, no. 1: 42. https://doi.org/10.3390/aerospace9010042
APA StyleTang, P., Dai, Y., & Chen, J. (2022). Nonlinear Robust Control on Yaw Motion of a Variable-Speed Unmanned Aerial Helicopter under Multi-Source Disturbances. Aerospace, 9(1), 42. https://doi.org/10.3390/aerospace9010042





