Analysis of Aircraft Operation System Regarding Readiness—Case Study
Abstract
:1. Introduction
1.1. Operation Process
1.2. Reliability of Aircraft
2. Case Study
2.1. TS-11 “Iskra”
- initial training;
- aerobatic training;
- instrument flying;
- training in shooting and bombing;
- recognition and photography of objects.
2.2. Process of Aircraft Operation
- preliminary maintenance- conducted every 7(+3) flight hours, every two flight shifts or 10(+/−2) days of downtime;
- Pre-flight services, carried out before each first flight shift departure;
- Pre-flight services, carried out before each first flight shift departure—take-off services, carried out before each departure;
- Flight services, conducted after the last flight of the day;
- monthly services.
3. Methods
3.1. Markov Processes
3.2. Operating State Model
- pre-flight service—carrying out a thorough check of the aircraft’s systems together with an extended engine test performed before each flight day (according to the provisions of the “time standards for performing current maintenance” the duration of the service is 45 min);
- Starting service—refueling and replacing operating fluids and checking the airplane by technicians carried out each time before the flight (in accordance with the provisions of the “time standards for current service” the duration of the service is 15 min.);
- Flight—time from starting the engine with the intention of performing the flight task until its shutdown after taxing;
- post-flight maintenance—refueling, fueling and securing of the aircraft, carried out after the last flight of each day (according to the provisions of the “time standards for current maintenance” the duration of the service is 30 min);
- taking over the aircraft by the pilot—checking the efficiency of the aircraft by the pilot each time before performing the flight (the duration of the take-over was determined to be 10 min based on the observation of the pilots’ behavior);
- aircraft malfunction or work carried out at WZL No. 1 in Dęblin;
- waiting time—time when no activities are performed on the aircraft but it is ready to perform flight tasks.
- pre-flight services;
- take-off services;
- in-flight services;
- waiting time.
3.3. Readiness of Analysed Objects to Perform an Aviation Task
- P1(t)—the probability of the aircraft being in a ‘pre-flight maintenance’ state;
- P2(t)—the probability of the aircraft being in a “star-up” state;
- P3(t)—the probability of the aircraft being in the ‘flight’ state;
- P4(t)—the probability of the aircraft being in a state of “ after flight service”;
- P5(t)—the probability of the aircraft being in the ‘pilot take-over’ state;
- P6(t)—the probability of the aircraft being in a state of WZL or failure;
- P7(t)—the probability of the aircraft being in the ‘waiting’ state;
4. Results
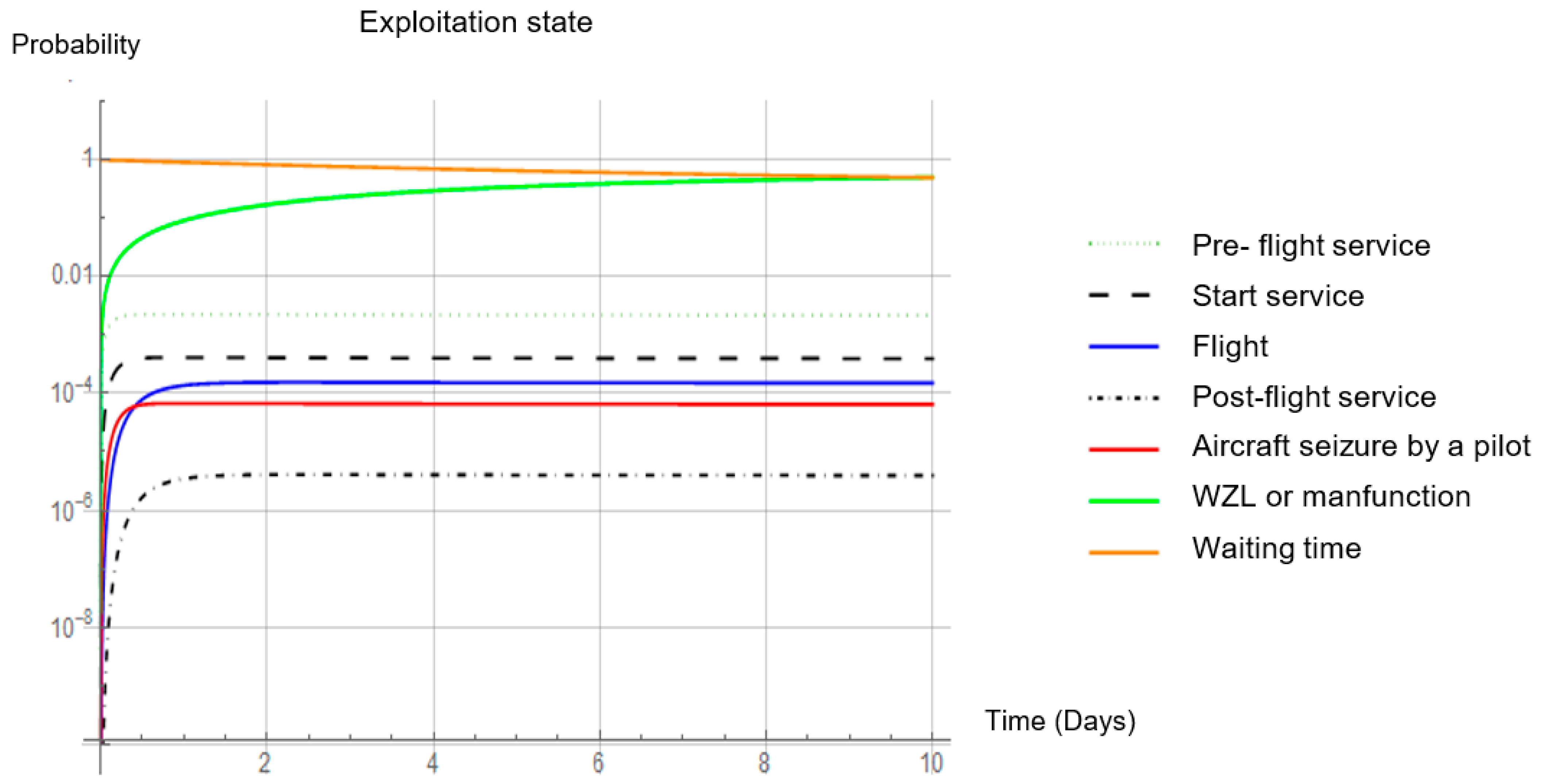
4.1. Analysis of the Probability of Occurrence Limits in the Different States
4.2. Analysis of the Probability of Limit Values in the Different States
- the probability of the analysed objects being in a state of full readiness to perform an aviation task:
- the probability of analysed objects being in a state of incomplete readiness for a flight task:
- the probability of analysed objects being in a state of unpreparedness for an aerial task:
- task readiness is: 0.021%;
- not ready to perform the task is: 37.032%;
- ready to perform the task is: 62.946%.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Basora, L.; Bry, P.; Olive, X.; Freeman, F. Aircraft Fleet Health Monitoring with Anomaly Detection Techniques. Aerospace 2021, 8, 103. [Google Scholar] [CrossRef]
- Zurek, J.; Jankowski, A.; Rajchel, J. Analysis of the Aircraft Operation in the Context of Safety and Effectiveness; Gomes, J.F.S., Meguid, S.A., Eds.; Inegi-Feup: Porto, Portugal, 2015; pp. 193–202. ISBN 978-989-98832-3-9. [Google Scholar]
- Zurek, J.; Zieja, M.; Ziolkowski, J. The Analysis of the Helicopter Technical Readiness by Means of the Markov Processes; Gomes, J.F.S., Meguid, S.A., Eds.; Inegi-Inst Engenharia Mecanica E Gestao Industrial: Porto, Portugal, 2018; pp. 1387–1400. ISBN 978-989-20-8313-1. [Google Scholar]
- Tomaszewska, J.; Zurek, J. Analysis of the Equipment Operation System in Terms of Availability. J. KONBiN 2017, 40, 5–20. [Google Scholar] [CrossRef] [Green Version]
- McPherson, J.W. Reliability Physics and Engineering: Time-to-Failure Modeling, 3rd ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-319-93682-6. [Google Scholar]
- Żurek, J. Review of the safety evaluation methods in aviation. Probl. Eksploat. 2009, nr 4, 61–70. [Google Scholar]
- Ntantis, E.L.; Botsaris, P. Diagnostic Methods for an Aircraft Engine Performance. J. Eng. Sci. Technol. Rev. 2015, 8, 64–72. [Google Scholar] [CrossRef]
- Liao, B.; Sun, B.; Li, Y.; Yan, M.; Ren, Y.; Feng, Q.; Yang, D.; Zhou, K. Sealing Reliability Modeling of Aviation Seal Based on Interval Uncertainty Method and Multidimensional Response Surface. Chin. J. Aeronaut. 2019, 32, 2188–2198. [Google Scholar] [CrossRef]
- Yadav, C.S.; Singh, R. Reliability of Object Oriented Systems with Markov Transfer of Control. In Proceedings of the 2011 International Conference on Computer and Management (CAMAN), Wuhan, China, 19–21 May 2011; pp. 1–3. [Google Scholar]
- Zhou, C.; Chang, Q.; Zhou, C.; Zhao, H.; Shi, Z. Fault Tree Analysis of an Aircraft Flap System Based on a Non-Probability Model. Qinghua Daxue Xuebao/J. Tsinghua Univ. 2021, 61, 636–642. [Google Scholar] [CrossRef]
- Diamoutene, A.; Noureddine, F.; Kamsu-Foguem, B.; Barro, D. Reliability Analysis with Proportional Hazard Model in Aeronautics. Int. J. Aeronaut. Space Sci. 2021, 22, 1222–1234. [Google Scholar] [CrossRef]
- Zieja, M.; Ważny, M.; Stępień, S. Outline of a Method for Estimating the Durability of Components or Device Assemblies While Maintaining the Required Reliability Level. EiN 2018, 20, 260–266. [Google Scholar] [CrossRef]
- Rudnicki, J. Comparative Analysis of Results of Application of Markov and Semi-Markov Processes to Reliability Models of Multi-State Technical Objects. J. Pol. CIMEEAC 2016, 1, 169–181. [Google Scholar]
- Grabski, F. Markov and Semi-Markov Processes as a Failure Rate. AIP Conf. Proc. 2016, 1738, 480012. [Google Scholar] [CrossRef]

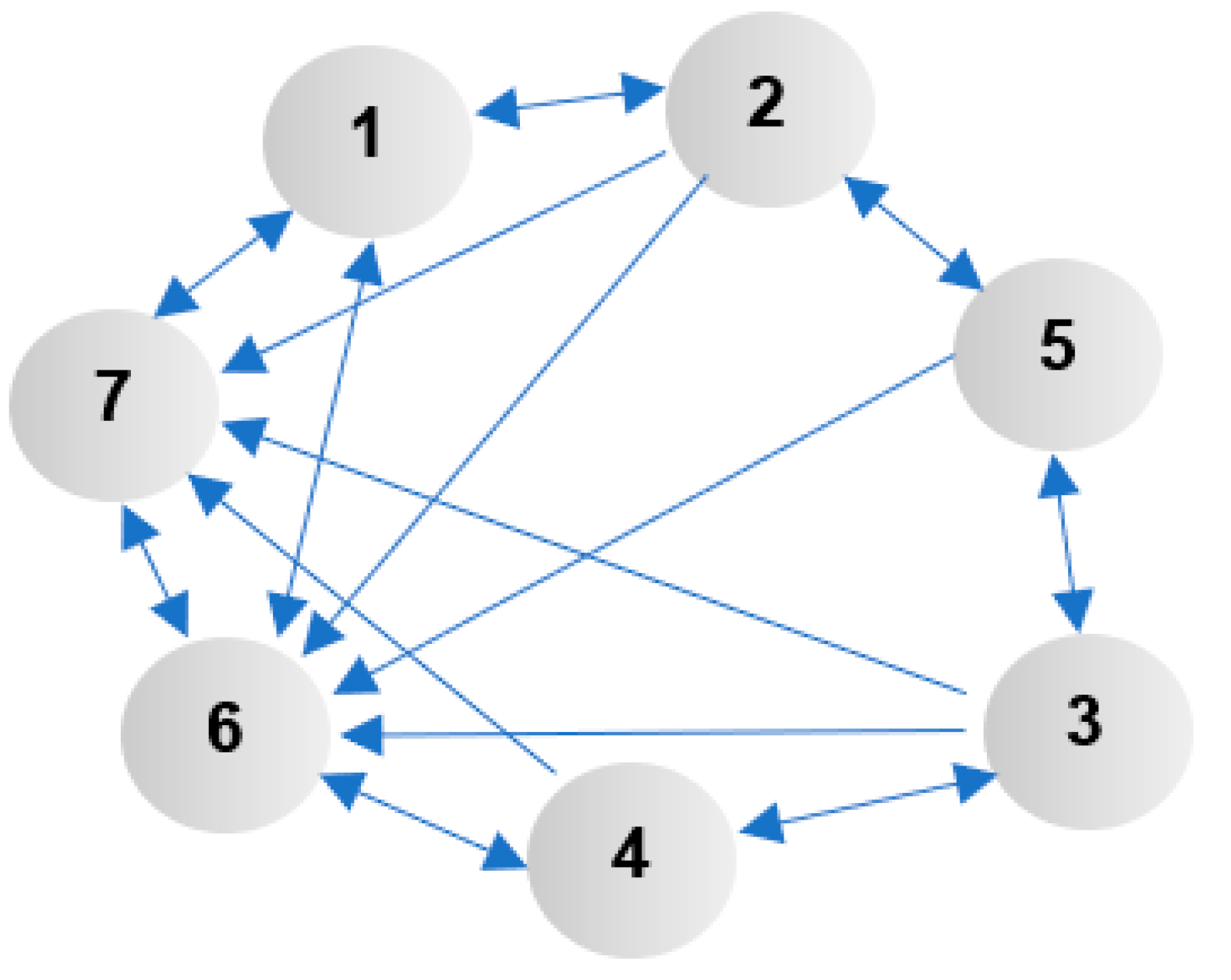
| λij | S1 | S2 | S3 | S4 | S5 | S6 | S7 | |
|---|---|---|---|---|---|---|---|---|
| S1—pre-flight service | S1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| S2—start-up service | S2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| S3—flight | S3 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| S4—post-flight service | S4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| S5—taking over of the aircraft by the pilot | S5 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| S6—WZL or failure | S6 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| S7—waiting | S7 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| Average Annual Time of Occurrence Duration [min] | Average Duration of One Single Occurrence [h] | Average Number of Occurrences within a Year | Average Annual Time of Occurrence Duration [h] | Average Daily Time of Occurrence Duration [h] | |
|---|---|---|---|---|---|
| S1—pre-flight service | 2351.25 | 0.75 | 52.25 | 39.1875 | 0.107363 |
| S2—start service | 1740 | 0.25 | 116 | 29 | 0.079452 |
| S3—flight | 7653 | 1.099569 | 116 | 127.55 | 0.349452 |
| S4—post-flight service | 1567.5 | 0.5 | 52.25 | 26.125 | 0.071575 |
| S5—taking over of the aircraft by the pilot | 1160 | 0.166667 | 116 | 19.33333 | 0.052968 |
| S6—WZL or malfunction | 309,600 | 24 | 215 | 5160 | 14.13699 |
| S7—waiting time | 201,528.25 | 24 | 139.95 | 3358.804 | 9.202203 |
| Altogether | 525,600 | 8760 | 24 |
| pij | S1 | S2 | S3 | S4 | S5 | S6 | S7 |
|---|---|---|---|---|---|---|---|
| S1 | 0 | 0.24631 | 0.0000 | 0 | 0 | 0.45652 | 0.29717 |
| S2 | 0 | 0 | 0 | 0 | 0.246311 | 0.45652 | 0.29717 |
| S3 | 0 | 0 | 0 | 0.12832 | 0 | 0.528 | 0.34369 |
| S4 | 0 | 0 | 0 | 0 | 0 | 0.60572 | 0.39428 |
| S5 | 0 | 0 | 0.35045 | 0 | 0 | 0.64955 | 0 |
| S6 | 0.27185 | 0 | 0 | 0 | 0 | 0 | 0.72815 |
| S7 | 0.19551 | 0 | 0 | 0 | 0 | 0.80449 | 0 |
| λij | S1 | S2 | S3 | S4 | S5 | S6 | S7 |
|---|---|---|---|---|---|---|---|
| S1 | −9.314 | 2.294 | 0 | 0 | 0 | 4.252 | 2.768 |
| S2 | 0 | −12.586 | 0 | 0 | 3.1 | 5.746 | 3.74 |
| S3 | 0 | 0 | −2.862 | 0.367 | 0 | 1.511 | 0.984 |
| S4 | 0 | 0 | 0 | −13.971 | 0 | 8.463 | 5.509 |
| S5 | 0 | 0 | 6.616 | 0 | −18.879 | 12.263 | 0 |
| S6 | 0.019 | 0 | 0 | 0 | 0 | −0.071 | 0.052 |
| S7 | 0.021 | 0 | 0 | 0 | 0 | 0.087 | −0.109 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żyluk, A.; Cur, K.; Tomaszewska, J.; Czerwiński, T. Analysis of Aircraft Operation System Regarding Readiness—Case Study. Aerospace 2022, 9, 14. https://doi.org/10.3390/aerospace9010014
Żyluk A, Cur K, Tomaszewska J, Czerwiński T. Analysis of Aircraft Operation System Regarding Readiness—Case Study. Aerospace. 2022; 9(1):14. https://doi.org/10.3390/aerospace9010014
Chicago/Turabian StyleŻyluk, Andrzej, Krzysztof Cur, Justyna Tomaszewska, and Tomasz Czerwiński. 2022. "Analysis of Aircraft Operation System Regarding Readiness—Case Study" Aerospace 9, no. 1: 14. https://doi.org/10.3390/aerospace9010014
APA StyleŻyluk, A., Cur, K., Tomaszewska, J., & Czerwiński, T. (2022). Analysis of Aircraft Operation System Regarding Readiness—Case Study. Aerospace, 9(1), 14. https://doi.org/10.3390/aerospace9010014





