Abstract
In this paper, the design and optimization method of rocket parameters based on the surrogate model and the trajectory simulation system of the 3-DOF air-launched rockets were established. The Gaussian kernel width determination method based on the relationship between local density and width is used to ensure the efficiency and reliability of the optimization method, and at the same time greatly reduces the amount of calculation. An adaptive sampling point updating method was established, which includes three stages: location sampling, exploration sampling, and potential optimal sampling of the potential feasible region. The adaptive sampling is realized by the distance constraint. Based on the precision of the surrogate model, the convergence end criterion was established, which can achieve efficient and reliable probabilistic global optimization. The objective function of the optimization problem was deduced to determine the maximum load mass and reasonable constraints were set to ensure that the rocket could successfully enter orbit. For solid engine rockets with the same take-off mass as Launcherone, the launch altitude and target orbit were optimized and analyzed, and verified by 3-DOF trajectory simulation. The surrogate-based optimization algorithm solved the problem of the overall parameter design optimization of the air-launched rocket and it provides support for the design of air-launched solid rockets.
1. Introduction
Air-launched rocket refers to relying on large aircraft (large transport aircraft, cargo aircraft, strategic bombers, aircraft, etc.) as an air-launch platform, which carries the rocket to high altitude to release and launch, after a certain attitude adjustment, the rocket engine ignites and transports the load to the preset space orbit [1]. According to the way the rocket is loaded on the aircraft, it can be divided into four kinds: hanging type, back support type, built-in type, and towed type [2]. Compared with the land launched rocket, the high-altitude launched rocket has the following advantages: (1) low dependence on ground equipment, there is no need to consider the limitation of the ground launch site and the huge infrastructure on the ground; (2) shortened launch preparation time, there is no need to consider the launch site and no need to rely on large ground facilities, so the preparation time for all launches is greatly reduced; (3) flexible launch conditions, high-altitude launch greatly reduces the impact of meteorological conditions on the launch, so it can be launched at any time on demand; (4) reduce launch consumption, the consumption of manpower and material resources for high-altitude launch is far less than that of ground launch. In particular, fuel consumption can be reduced, which can reduce launch costs [3].
In this paper, we mainly consider using large transport aircraft to launch rockets, which are launched under the condition of certain altitude and initial velocity. In 1990, America’s Orbital Sciences Corporation had successfully launched its “Pegasus” rocket for the first time, this was the world’s first air-launched rocket to launch a satellite. Russian aerospace company is also developing the “Flying” air-launched rocket and Boeing from the United States is also planning to develop an air-launched rocket [4]. According to relevant research data, the total mass of airborne rockets can be reduced by 20∼30% [5] compared with that of ground-launched rockets under the same load capacity. Recently, Virgin Orbit launched the Launcherone rocket with a Boeing 747, which had 300 kg of sun-synchronous orbit carrying capacity and the capacity of 500 kg of low earth orbit. Given the present research status of air-launched rockets, the research on the design and optimization of the overall parameters of air-launched rockets is still lacking. To solve this problem, this paper established the reliable air-launched rocket launch system and trajectory simulation model [6], the surrogate-based optimization method was adopted, the design and optimization of the overall parameters (engine mass, flight time, trajectory) of the solid rocket were carried out with reference to the LauncherOne rocket with a launch altitude of 10,668 m and a takeoff mass of 25.85 t. The target orbit is a 500 km Sun-synchronous orbit (SSO). The objective function is the maximum capacity of the rocket, which is analyzed by the results of algorithm optimization and three-degree-of-freedom(3-DOF) trajectory simulation.
In the development of optimization algorithms in recent years, simulated annealing algorithm, genetic algorithm, ant colony algorithm, and intelligent optimization algorithm have developed more mature [7,8,9,10,11]. However, in general, this kind of optimization algorithm will appear a lot of repeated calculation of the objective function and calculation constraints, which greatly affects the optimization efficiency. So the reduction of the number of calls from the original mode is very important for the efficiency of the optimization method. For this kind of problem, response surface methods and sequence approximate optimization methods have been developed gradually. To a large extent, these methods provide a reference for optimization methods that call the original model less frequently [12,13]. More commonly in the sequence, the approximate optimization method is based on the surrogate-based optimization method, which is the common way to solve the problem of multidisciplinary optimization.
The overall design of aircraft is a typical multidisciplinary coupled problem. The complex coupling relationship among disciplines makes it difficult for traditional single-disciplinary design optimization methods to find the optimal solution. The Multidisciplinary Design Optimization (MDO) method is a methodology that fully explores and utilizes the synergistic mechanism of interaction in the system to design complex engineering systems and subsystems, it is the process of finding the optimal multidisciplinary design through optimization and compromise under each disciplinary model [14,15,16].
Cheng et al. [17] proposed a cooperative coevolution MDO algorithm based on the combination of cooperative coevolution and MDO algorithm and applied it to the design and optimization process of the overall parameters of the missile. The minimum take-off mass of the missile was taken as an indicator to optimize the parameters satisfying the aerodynamic, engine, and control requirements of the missile. Zhang et al. [18] proposed a multidisciplinary optimization method with an improved hybrid genetic algorithm. By establishing a multidisciplinary model integrating the aerodynamic, propulsion, and trajectory of the missile for analysis, and taking the range as the optimization index, the overall parameters of the missile satisfying the constraints were obtained. Although the MDO method used in the above literature considers the correlation between various disciplines in the overall design of the missile, it does not apply to the initial stage of the conceptual design of the missile due to the variety of disciplines involved and the difficulty and complexity of model establishment. To solve the above problems, Zhou et al. [19] proposed a multi-attribute comprehensive optimization design method based on variable weight TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) evaluation and particle swarm optimization algorithm fusion and took Euclidean distance as the optimization evaluation index to optimize the overall parameters of the missile. This method can effectively solve the problem of multi-disciplinary, multi-attribute, and multi-objective parameter optimization in the process of missile overall parameter design. With the innovation of approximation technology and parallel computing technology, the traditional MDO method exposes problems such as complex discipline model, large information exchange capacity, high computing cost, complex organization form, nonlinear design space, and rigid interactive environment, and so on [20]. To improve the efficiency of MDO for complex design problems, it is necessary to establish a clear discipline variable relationship network, an accurate discipline analysis model, an efficient MDO solution strategy, and a coherent discipline interface. Due to the high computational cost of some disciplines, it is necessary to replace the discipline model with advanced surrogate model technology to save optimization time and cost.
The traditional surrogate models mainly include polynomial model, Kriging model and neural network model. Polynomial model is suitable for low order nonlinear problems modeling; Kriging model is suitable for high-dimensional and low-order nonlinear problem modeling; Neural network model is suitable for high-order nonlinear problems modeling [21,22,23]. In recent years, new surrogate models suitable for actual objects have been gradually developed. By simplifying and forming low-precision calculation samples, a low-precision surrogate model can be obtained, and then a high-precision surrogate model can be obtained through high-precision calculation by updating the samples [24,25]. This can not only reduce the amount of calculation, but also make the surrogate model more accurate by using high-precision samples.
2. Multi-Stage Adaptive Sampling Point Updating Method
2.1. Analysis of Sampling Point Updating Method
The exploration and development ability of the surrogate-based optimization method depends on the updating method of sampling points. A more reasonable updating method of sampling points is the key to ensuring the convergence speed of the optimization method under the premise of global optimization. At present, the commonly used sampling point updating methods include EI criterion [26] (Maximum expectation improvement infill criterion), potential optimal infill criterion, maximum distance infill criterion, maximum curvature criterion, and adaptive distance constrained sampling strategy, etc.
Firstly, based on the optimal Latin Hypercube (OLH), an efficient Design of Experiment (DoE) approach for constrained regions is used to form the initial sampling points from the design variable interval. Secondly, the surrogate model is established based on RPF. Finally, the multi-stage sampling point criteria and convergence criteria are used to update the sampling points.
In terms of the exploration and development ability of the optimization method, the maximum distance infill criterion, and the potential optimal infill criterion have shown superior performance, while the adaptive distance constraint strategy can balance the exploration and development ability of the surrogate-based optimization method to a certain extent. The mathematical models and performance characteristics of these three updating methods are as follows.
Optimization problems can generally be expressed in the following form:
where, is an real column vector, is the original objective function, is inequality constraint, is equality constraint, and represent the number of inequality constraints and equality constraints respectively. If they are zero, then there are no inequality constraints or equality constraints.
The sampling point of the potential optimal infilling criterion is the solution of the following optimization problem:
where, , and are the approximate models of the original objective function , inequality constraint , and equality constraint . This method can accelerate the convergence of the optimization method, but it is difficult to ensure that it is the global optimal solution.
The sampling point of the maximum distance criterion is the solution of the following optimization problem:
where, is the minimum Euclidean distance between the new sample point and the original sample point, and is the number of existing sample points. This method can modify the surrogate-based optimization method to a strong ability of exploration, but it is difficult to converge globally.
The adaptive sample updating strategy [27,28] generally adds the optimal solution as a new sampling point to the sample by solving the specific optimization problem, and the principle is as follows:
New sampling points are obtained by solving the above equation, where, is the minimum distance constraint among sampling points. It can be obtained by
is the number of sample points, and , are the coordinates of sampling points.
2.2. Multi-Stage Adaptive Sampling Point Updating Method Model
The multi-stage adaptive sampling points updating method proposed in this paper is based on the surrogate model and the sequence approximate optimization method, which can greatly improve the optimization efficiency of the optimization method under the premise of ensuring the probabilistic global optimum. The main steps are as follows:
- (1)
- The optimization problem of the multi-stage adaptive sampling points updating method is established. The known optimization problems are as follows:
When transforming constrained optimization problems into unconstrained optimization problems, the multiplier method or penalty function method is generally considered [29], as shown below:
where, and are penalty factors, , and are continuous functions satisfying the following conditions:
where, represents equality constraint or inequality constraint or distance constraint. and mean that the constraints are satisfied, and mean that these constraints are not satisfied.
The optimization method proposed in this paper is to add new sampling points to the original sample, which are the optimal solutions of the unconstrained optimization problem corresponding to Equation (7). The unconstrained optimization problem also includes the penalty function term of constraints , and, and also the penalty function term of adaptive distance constraint corresponding to the original optimization problem. The ability to explore and develop the surrogate-based optimization can be changed by adjusting the penalty factor and .
- (2)
- Establish the accuracy evaluation model of the surrogate model of the objective function and the constraint value relative to the original model
Suppose is the sampling point obtained by updating the sampling points. The approximate models based on the first N sample points are respectively , and , then the accuracy evaluation model of the approximate model of the objective function and the constraint value relative to the original model is as follows:
In the Formula (9), when the independent variable is greater than or equal to zero, , and are non-negative functions, and , ,.
- (3)
- First sampling stage—Location sampling of potential feasible region
The value of penalty factor and are set to make greater than 103 to 105 times, greater than 103 to 105 times, when sampling is conducted in the potential feasible region.
The main steps for updating the sampling point in the potentially feasible region are as follows: (a) firstly, an approximate surrogate model based on the objective function and constraint values of the existing sample points is constructed; (b) according to Equation (7), the optimal solution is obtained, namely, the coordinates of the new sampling point are obtained; (c) calculate the objective function and constraint value according to the coordinates of the new sampling points, the surrogate model and the original model. The constraint value can be expressed as . The sampling updating process is repeated until the new sampling point satisfies any of the following criteria, and then the localization sampling phase of the potentially feasible region is completed.
In the above criteria, is calculated according to Equation (9), , , and are preset parameters in the location sampling stage and related to the criteria at the end. Criterion I means that value of the nearest sample points are less than or equal to ; Criterion II means that the number of sampling points in the potential feasible region is more than or equal to .
In the sampling stage of the potential feasible region, the sampling points first need to satisfy the adaptive distance constraints . On the premise of satisfying the distance constraints, the sampling points will tend to the approximate model satisfying the inequality constraints and the equality constraints , which indicates that the sampling points will be distributed in the sparse region and tend to the potential feasible region. The sampling stage of the potential feasible region is to explore the whole solution domain in the sampling process, and gradually tends to the potential feasible region. In this way, the approximate accuracy of the entire surrogate model in the design space can be gradually improved, and the positioning of the potential feasible region can be well realized. The end criterions of sampling stage based on the objective function and the constraint value of the approximate model accuracy have the characteristics of strong maneuverability and can use a reasonable number of sampling points to end the sampling stage of the potential feasible region, which greatly improves the optimization efficiency of the surrogate-based optimization method.
- (4)
- Second sampling stage—potential feasible region exploration sampling
The second sampling stage is the exploratory sampling under the potential feasible region. In this process, the value of penalty factor is set to constant value. The value of and have the same order of magnitude through adjusting .
The judgment basis for the end of sampling at the sampling point in the exploration sampling stage of potential feasible region is similar to that in the first stage. The main sampling and updating process is as follows: (a) firstly, an approximate surrogate model of objective function and constraint values is constructed based on the existing sample points; (b) according to Equation (7), the optimal solution is obtained, which means the coordinates of the new sampling points are obtained; (c) calculate the objective function and constraint value according to the coordinates of the new sampling points, the approximate model and the original model. The constraint value can be expressed as: . The sampling updating process is repeated until the new sampling point satisfies any of the following criteria, and the exploratory sampling phase of the potential feasible region is ended.
where, is calculated according to Equation (9), , , are preset parameters in the exploratory sampling stage and related to the criteria at the end.
The sampling points in the exploration and sampling stage of the potential feasible region are mainly distributed in the potential feasible region, and the new sampling points will keep a certain distance from the original sample points. The main sampling mode is to explore and sample the whole feasible region, which can greatly improve the approximate accuracy of the approximate surrogate model in the feasible region.
- (5)
- Third sampling stage—potentially optimal sampling
In the potentially optimal sampling stage, the penalty factors in Equation (7) are adjusted as remains unchanged, .
The sampling process in this stage is the same as the main steps in the previous two stages. When the sampling points are updated for the time, the following steps are mainly carried out: (a) firstly, an approximate surrogate model of the objective function and constraint values is constructed based on the existing sample points. (b) According to Equation (7), the optimal solution is obtained, which means the coordinates of the new sampling points are obtained. (c) Calculate the objective function and constraint values according to the coordinates of the new sampling points, the approximate model, and the original model, and the constraint value can be expressed as . The process of sampling updating is repeated until the new sampling point satisfies any of the following criteria, and sampling stage of potential optimal sampling can be completed. In this algorithm, the end of convergence in the potential optimal sampling stage is the end of convergence of the whole algorithm. The criteria are as follows:
where, , and are the preset parameters required by the convergence criterion. The meaning of criterion I is that the current feasible solution is , which satisfies the inequality and equality constraints. Criterion II means the Euclidean distance between the current feasible solution and the recent sampling points is less than or equal to . Criterion III means the absolute value of error between the current sample points surrogate approximation model and its original function is less than or equal to .
The potential optimal sampling points are in the complete development mode, and the update of sampling points will converge quickly to the optimal point, which ensures the optimization convergence efficiency to a great extent.
2.3. The Proof of Global Optimal
Since the penalty function method has been used to transform the constrained optimization problem into an unconstrained optimization problem, the unconstrained optimization problem is considered in the proof of global convergence.
Define function: ,
where is an independent variable. Then the objective function can be defined as:
Construct an auxiliary objective function as follows:
where, when is in the feasible area, . When is not in the feasible area, .
Then there is the following theorem: Let increase and tend to infinity, then the unconstrained problem can be described as
Define the global optimal solution of the above optimization problem be . If , then is the global optimal solution of the unconstrained problem.
Proof.
Because is the global optimal solution of unconstrained problem , there is
That is
Replace with at the right end of Equation (15) to obtain:
Adding Equations (15) and (16) and a transfer merge can get
Because :
Combining Equations (15) and (19) gives:
Then take any point (Attention: )
Equations (17) and (20) illustrate and are incremental. In Equation (21), it is shown that they are upper bounded, so the limit and the limit exist. Further notes that:
So the limit exist, thus . Then due to the continuance of , we can get
This can illustrate . Pay more attention to both ends of Equation (21), (Due to the continuance of )
So is the global optimal solution of the unconstrained problem. □
Note 1: Although the global convergence of this method has been proved in this section, considering the influence of interval selection of optimization variables, number of iteration steps, and accuracy of the approximate model, the optimization method based on surrogate model can only ensure the global optimization of probability.
2.4. Features of Method
- This method realizes the adaptive adjustment of the distance between the new sampling points and the existing sample points, which can ensure that the distance constraint value is always within a reasonable range in the process of updating the sampling points.
- This method makes each stage of sampling have a unified form and adjusts the exploration and development ability of the surrogate-based optimization method by changing the penalty factor, which can realize the sampling purpose of different stages.
- Based on the approximate model of the objective function and the constraint value, the convergence end criterion of each sampling stage is established, which is conducive to terminating the sampling update after a reasonable number of samples and achieving the purpose of improving the optimization efficiency.
- Decision science, convenient operation, clearly defined objective and process controllability are the salient characteristics of this method, which ensures the reliability and global optimality of the surrogate-based optimization method, with good convergence efficiency.
3. Improve Surrogate-Based Optimization Method
The flow chart of the surrogate-based optimization method proposed in this paper is as follows:
The blue lines in Figure 1 mean that adaptive sampling will be carried out in each stage. The difference is that the values of penalty factors and in Formula (7) are different in different stages of adaptive sampling, which can make the exploration and development capabilities of different stages different.
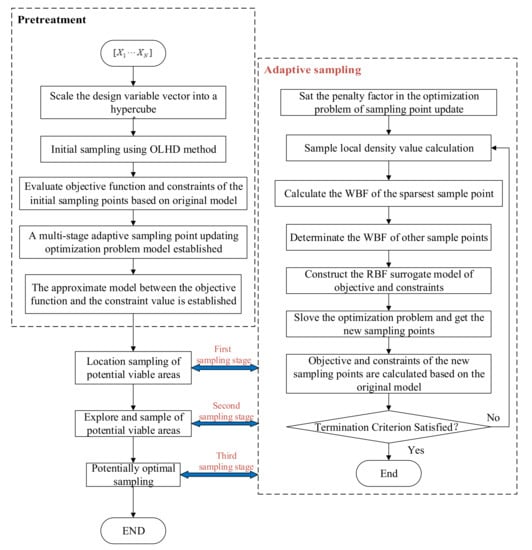
Figure 1.
Flow Chart of Improved surrogate-based optimization method.
The improved surrogate-based optimization method is mainly divided into the initialization stage, the approximation stage, the convergence judgment stage, and the adaptive sampling stage:
- (1)
- Initialization stage
The design space is mapped to the unit hypercube space, and the optimized Latin hypercube method is used to determine the initial sample. The sample number is determined by the following equation:
where, is the dimension of the design space, and in this paper = 9. The original model is used to calculate the objective function and constraint value of the sample, and the initial sample set can be obtained:
where, represents the coordinate of the sampling points, represents the output response of the original model. Generally, it is a vector composed of the objective function and all constraints.
- (2)
- The approximate stage
The improved radial basis function is used to establish the approximate model, and the particle swarm optimization algorithm is used to solve the optimal solution of the approximate model.
- (3)
- The convergence criterion
The convergence criterion is consistent with the above in the three stages of location sampling, exploration sampling, and potential optimal sampling in the potential feasible region.
- (4)
- The updating stage of sampling points
The adaptive infill strategy proposed [30] in this paper is as follows:
The information of new sampling points can be obtained by solving the optimization problem of the above equation.
4. Mathematical Modeling and Verification of Overall Parameters
The LauncherOne air-launched rocket referred to in this paper adopts the hanging loading mode, and its carrier is a modified Boeing 747-400 large passenger aircraft. Considering the flight capability of the carrier aircraft, the initial launch altitude of the rocket is 10.67 km, the initial launch velocity is 262 m/s, and the initial launch velocity inclination is 25 degrees.
In this paper, according to the launching conditions and overall parameter of LauncherOne, the rocket (original proposal) is designed with a three-stage solid engine and a four-stage solid engine, and its main overall parameters are shown in the Table 1.

Table 1.
Overall parameter design of the solid rocket.
Table 1 mainly shows the relevant overall parameters of the original scheme, which provides support for the overall parameters optimal design below.
Rocket trajectory simulation is an important module to judge whether the optimization results meet the requirements. For the trajectory simulation of the air-launched rocket, the dynamic equation is the basis of trajectory simulation. As the mass of the rocket will change with the consumption of propellant and the falling off of the engine during flight, it is necessary to establish a mass and thrust model. As the falling off of the engine changes the aerodynamic reference area of the rocket and the change in air density, which will affect the aerodynamic force of the rocket, it is necessary to establish its aerodynamic model. Different flight timing affects the integration results of the rocket trajectory dynamic equation, so the flight timing model is also established. Various models are shown in the following sections:
4.1. 3-DOF Trajectory Simulation Model
In the launch coordinate, the 3-DOF trajectory equation of the rocket [31] are as follows:
where, are angle of attack and angle of sideslip; are flight path angle, heading angle and bank angle; is motor thrust; are drag, lift force, and yawing force; are the coordinate in the launching coordinate system; is the speed of the rocket; is the mass of the rocket; is the gravitational acceleration; is the derivative of time.
4.2. Mass Calculation Model
The mass model of the rocket mainly includes load mass, equipment mass, structure mass, and propellant mass. The calculation of the take-off weight of the rocket is the basis of the trajectory simulation and the optimization of the overall parameter design. The derived calculation equation [32] of the takeoff mass of the rocket can be expressed as:
In the above formula, is the takeoff mass of the rocket; is the mass of the rocket fairing; is the quality of instruments and equipment on the rocket; is the mass of stage motor propellant; is the structural mass of stage engine; is the mass of stage motor interstate section (connecting mechanism, missile wing, tail fin, etc.).
The relation between the take-off mass of the sub-stage rocket and the take-off mass of the sub-stage rocket is
The mass coefficient of the stage rocket motor structure is denoted by (refers to the ratio of structural mass and charge quantity, ), and it can be concluded that
4.3. Thrust Calculation Model
As the overall scheme in this paper belongs to the demonstration stage of the rocket carrying capacity, the thrust model of the motor can be simplified to the average thrust. Set the average thrust of the i stage-level rocket motor as , the working time of thrust as , and specific impulse is defined as , then the following relation can be obtained:
That is, the thrust multiplied by the working time is equal to the total impulse. In the design scheme of this paper, considering the height of the motor ignition moment of each level, the average thrust of the primary motor is set as the ground average thrust, and the average thrust of the secondary and higher engines is the vacuum average thrust.
4.4. Aerodynamic Calculation Model
Like other objects, when the rocket moves relative to the atmosphere, the atmosphere will form forces on the surface of the rocket, among which the main forces are lift force and drag force, which are expressed as follows [31]:
In the above formula, and are drag and lift coefficients respectively; is atmospheric density; is the pneumatic reference area. The relationship between lift coefficient and drag coefficient is expressed as follows:
In the above formula, , and are constants, and their values are as follows:
is the zero-lift drag coefficient, and its value changes with the change of Mach number. The specific value can be referred to in the literature [33].
The first stage of the LauncherOne rocket is known to have a diameter of 1.6 m and the second stage is 1.3 m. Therefore, the reference area of the solid rocket designed in this paper is: = 2.01 m2, = 1.32 m2.
4.5. Flight Program Design
LauncherOne is an air-launched two-stage rocket. Its flight process is mainly divided into five stages, namely, the first powered flight stage, the first unpowered glide stage, the second powered flight stage, the second unpowered glide stage, and the second re-ignition (final boost) stage. The flight procedure is as follows:
- (1)
- The take-off stage of the carrier aircraft.
- (2)
- Separation and launch stage of rocket and carrier aircraft: When the carrier aircraft flew to an altitude of nearly 11 km and the speed reached 262 m/s, it was pulled up at an angle of more than 25 degrees to release the rocket suspended under the aircraft.
- (3)
- Primary power stage: After the rocket was separated from the carrier aircraft for 5 s, the first-stage motor was ignited, and the working time was about 3 min.
- (4)
- Primary glide stage: After gliding for a certain period, the first stage motor was separated.
- (5)
- Secondary power stage: After the separation of the primary engine, the secondary motor ignited, the operation time was about 6 min and after 20 s of operation, the rocket cowling separated.
- (6)
- Secondary sliding stage: After the second stage motor was shut down, the rocket will run for about 22 min without power.
- (7)
- The final push stage: The second stage motor was ignited again for about 15 s.
After the final push stage was shut down, the load was sent to the preset orbit.
According to the basic timing sequence and overall parameters of LauncherOne, the simulation of 500 km solar synchronous orbit entry was realized by adjusting the relevant parameters, and the carrying capacity was at least 300 kg. The simulation results are as shown in Figure 2.
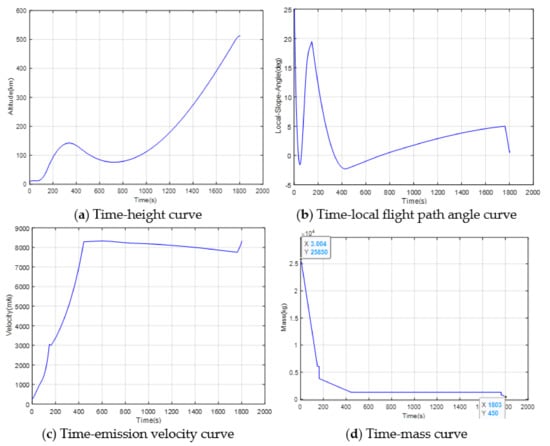
Figure 2.
The trajectory of the LauncherOne rocket.
It can be seen from the above Figure 2 that the LauncherOne rocket designed can send an object with a total mass of 450 kg into a solar synchronous orbit of 500 km, which proved that the 3-DOF trajectory simulation module in this paper had certain reliability and provided support for the design optimization of the next step of solid rocket
Based on the flight time sequence of LauncherOne, this paper designed the flight time sequence of an air-launched rocket based on a solid rocket engine, which adopted the way of direct entry into orbit. It was mainly divided into five stages, such as aircraft and rocket separation stage, first-stage flight, second-stage flight, third-stage flight, and final boost stage. The details are as follows [31]:
- (1)
- Aircraft and rocket separation stage
Referring to the parameters information of Virgin air-launched rocket and carrier aircraft when separating, the launch parameters of the designed air-launched rocket in the 3-DOF trajectory simulation were consistent with the LauncherOne, that was, the launch altitude was 10.67 km, the speed was 262 m/s, and the launch inclination was 25 degrees.
- (2)
- First stage flight
After separation, the rocket flew at an altitude of nearly 11 km, fired at an inclination of 25 degrees, and then ignited the first stage motor and performed a programmed angle-of-attack pull-up flight after transonic velocity, and maintained zero-angle-of-attack flight after reaching a certain altitude and velocity inclination. The flight procedure is as follows:
Among them
In the above formula, is the time to start the pull-up of the angle of attack. Since the initial velocity of the rocket after separation had reached 0.9 Ma, it can be set as a few seconds. is The moment to pull up the end for the angle of attack; is the end time of the first gliding stage; is the end time of separation between the first and second stages. Write the gliding time of first stage as: , then there is . is the maximum absolute value of attack angle; is the time corresponding to the maximum angle of attack.
- (3)
- Secondary and tertiary flight stage
The rocket is already flying in the rarefied atmosphere during the second stage, then the aerodynamic for pitch Angle program choice is negligible. In general, the simplified form of the secondary flight procedure is adopted in engineering applications. In this case, the linear expression of the pitch angle program in terms of time is
where is the pitching angle program of the starting point of the stage, which is equal to the pitching program angle of the termination point of the previous stage, is the change rate of the pitching program angle of this stage, and the initial value of the optimal pitching program angle and other trajectory parameters can be provided for the next flight stage by designing and of the gliding stage according to .
In the optimization theory, the optimal solution obtained by the numerical method is very close to the linear relationship. Equation (27) applies not only to the second flight stage in the vacuum section but also to all flight stages above the second flight stage in the vacuum section.
The flight procedure [28] at this stage is designed as follows:
In the above equation, is the program pitch angle at the end of the first stage flight. The separation between the first stage and the second stage is zero angle of attack, is mainly determined by the flight path angle . The optimal initial pitching angle of the second stage program can be obtained by designing the first stage gliding time . is the shutdown time of the second-stage engine; and are respectively the change rate of pitch angle in the second-stage power flight stage and the change rate of pitch angle in the second-stage glide stage. Set the second-stage gliding time as , then, is the end moment of the second-stage gliding; is the end time of fairing separation.
- (4)
- Final boost stage
The program pitch angle of the final boost stage is designed as follows:
In the above formula, is the shutdown time of the final stage engine, and is the change rate of the pitch angle of the final boost stage. The final stage motor shutdown time should make the rocket reach the conditions of orbit.
Take the three-stage rocket as an example, the flight process is as shown in Figure 3.
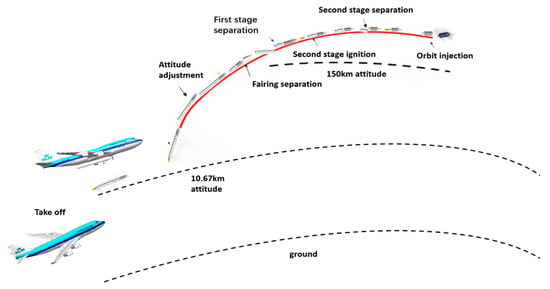
Figure 3.
The flight process of the three-stage rocket.
5. Establish the Overall Optimization Problem Model
5.1. Design Variables
Based on the rocket flight procedure described above, the design variables selected for rocket optimization are shown below [34]:
where, and are respectively thrust and working time of each motor; is the launch azimuth; , and are respectively the sliding time of the working clearance between the first and second motors, the second and third motors, the third and fourth motors; is the variable of the load mass, that is, the separation mass at the time of take-off; and are respectively the duration of the attack angle and the value of attack angle. The range of optimization design variables are shown in the following Table 2.

Table 2.
Upper and lower limits of optimal design variables.
5.2. Objective Function
The objective of the optimization algorithm for trajectory optimization is to seek the maximum payload mass whereas the takeoff mass remains constant. Therefore, this paper selects the maximum payload mass as the optimization objective function [28]. In the optimization process, the change of load mass at ground take-off time is taken as the objective function, that is, the minimum separation mass is taken as the optimization objective.
5.3. Constraint Conditions
In this paper, the optimization problem needs to meet inequality constraints and equality constraints. To ensure the safety of the rocket body and the launching requirements during the flight, the constraints of normal overload , dynamic pressure during the separation of the first and second engines and Mach number before the attack angle pulling up are constrained. The inequality constraints are as follows:
where is the upper limit of normal overload, is the maximum dynamic pressure at the time of separation, is the minimum Mach number. Considering that the angle of attack should keep zero at transonic velocity, in this paper, , and .
According to a sun-synchronous circular orbit with a target orbit of 500km, the following equality constraints can be obtained:
where, are respectively orbital altitude, orbital velocity, orbital eccentricity, and orbital inclination; the target orbit parameter are .
Since the orbital inclination is mainly affected by the launch azimuth , it is easy to satisfy in the optimization process and take . The constraints for height, velocity, and orbital eccentricity are complex, which are sensitive to more variables, and difficult to obtain the global optimal solution under the three constraints. To simplify the optimization problem, , , and are transformed to some other inequality constraints. Consider calculating the perigee height at the shutdown point of the final boost stage, the perigee height is taken as the constraint. Since the objective function is the maximum load mass, the global optimal solution must be a circular orbit of 500 km. Thus, the constraint conditions of the air-launched rocket in this paper can be obtained as follows:
6. Optimization Results and Analysis
The trajectory of the air-launched rocket was optimized by using the surrogate-based optimization method. Firstly, the overall parameters of the solid rocket were designed and adjusted to meet the constraint indexes (defined as the original scheme), and the 3-DOF trajectory model was applied for simulation analysis. The overall parameters were optimized to maximize the carrying capacity, and 100 initial samples were selected. The results of the optimization for the three-stage air-launched and four-stage air-launched rockets are shown in the following Table 3. Its trajectory simulation is shown in the following Figure 4.

Table 3.
Optimal values of design variables of the air-launched solid base rocket.
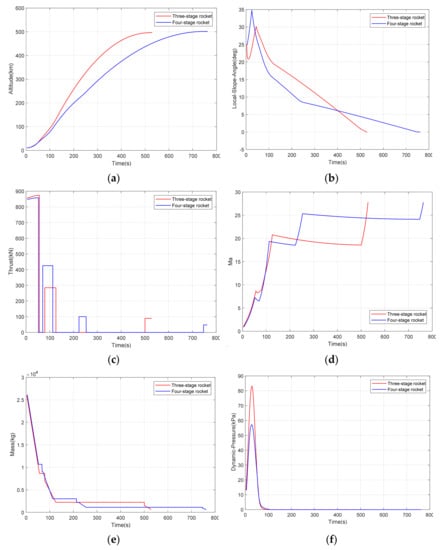
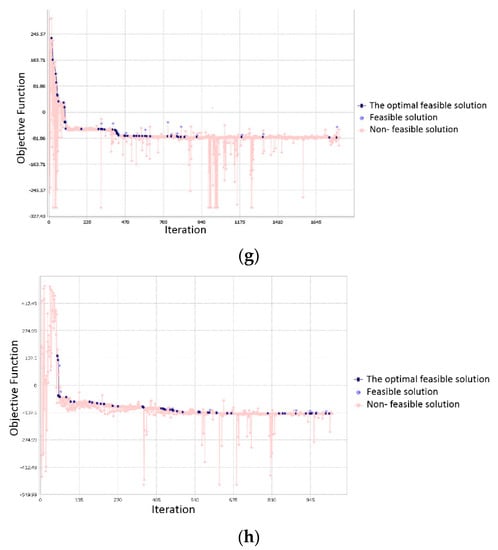
Figure 4.
Optimization results for air-launched rockets. (a) Time–height curve, (b) Time–local flight path angle curve, (c) Time–thrust curve, (d) Time–Mach number curve, (e) Time–mass curve, (f) Time–dynamic pressure curve, (g) Three-stage rocket objective function convergence curve, (h) Four-stage rocket objective function convergence curve.
The optimized convergence curves are as follows:
The results show that the objective function of the three-stage rocket converges at 1750 iterations, and the optimal feasible solution is –79.35 kg at the 1730th time, (the separation mass at launch is –79.35 kg) which is equivalent to the payload mass of the rocket can be increased by 79.35 kg. Compared with the original scheme, the carrying capacity is increased by 26.45%, and all the indicators met the constraints. The objective function of the four-stage rocket converges at 1020 iterations, and the optimal feasible solution is -141.48 kg at 1012th iteration, which means the load capacity is improved by 141.48 kg. The load capacity is improved by 47.16% compared with the original scheme and all the indexes also meet the constraints.
From the above comparative results of air-launched three-stage and four-stage solid rockets, it is clear that the four-stage rocket has stronger launch capability, but generally has a longer flight time and a more complex structure. To further compare the air-launched rocket for the improvement of the launch capacity, the four-stage rocket is selected for the optimization of the maximum launch capacity for ground vertical launch, and the results are as shown in Table 4 and Figure 5.

Table 4.
Optimal values of design variables of ground-based vertical launch.
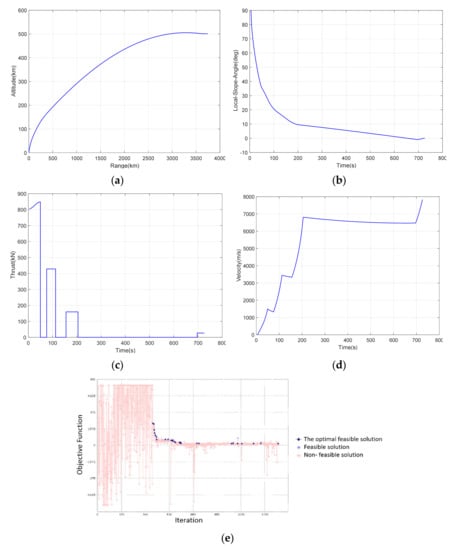
Figure 5.
Optimization results for ground-launched rockets. (a) Range–height curve, (b) Time–local flight path angle curve, (c) Time–thrust curve, (d) Time–velocity number curve, (e) Convergence curve of the objective function.
The optimized convergence curves and the height, velocity, local flight path angle, and thrust curves are as follows:
Figure 5 show that the objective function converges after 1279 iterations, and the optimal solution is 13.71 kg after the 1028 iteration, which is equivalent to a 13.71 kg reduction in carrying capacity. Compared with the original scheme, the carrying capacity is 4.57% lower. According to the four-stage rocket model proposed in this paper, the carrying capacity of the air-launched rocket is about 51.49% higher than that of the ground-launched rocket. It further explained the superiority of an air-launched rocket.
7. Conclusions
The surrogate-based optimization algorithm proposed in this paper has the characteristics of high global optimization efficiency and high precision. The precision of the surrogate model is significantly improved by the adaptive sampling point updating strategy and the kernel width estimation of the radial basis function, which balances the sampling exploration and development ability of the optimization method. Through the establishment of the 3-DOF trajectory simulation model, mass calculation model, thrust calculation model, aerodynamic calculation model, and flight program design to determine the overall parameter design simulation model, and through the replication of LauncherOne rocket to verify the correctness of the design model, lay a foundation for the next design optimization.
Based on the proposed method, the overall parameter design and optimization problem of the air-launched rocket is illustrated, and the load capacity is optimized with the amount of change in payload mass (separation mass) as the objective function and analyzed by 3-DOF trajectory simulations. Based on the overall parameters and basic flight time sequence of the LauncherOne air-launched rocket, the overall parameters of the air-launched solid rocket in this paper were designed, and the original scheme was formed through 3-DOF trajectory simulation. Then the optimization calculation was carried out based on the original scheme by designing the optimization variables, determining the optimization objective function, and defining the constraint conditions.
Compared with the traditional optimization algorithm, which calls the original model thousands of times, this method greatly improves the optimization efficiency and optimization precision. From the optimization results, the optimal feasible solution of the air-launched rocket increases the capacity respectively by 26.45% and 47.16%, compared with the original solution, which demonstrates the reliability of the optimization method in this paper. For the four-stage rocket, compared with the ground launch, the carrying capacity of the optimal solution is improved by 51.49%. This further illustrates the advantages of air-launched rockets.
In summary, the surrogate-based model optimization algorithm proposed in this paper solves the main difficulties of multidisciplinary optimization algorithms. The method was applied to the conceptual design and parameter optimization of the air-launched rocket system. The results show that the method is effective and reliable for the optimal design of the launch vehicle, which can improve the launch capacity and reduce the amount of calculation under the same take-off mass. In addition, the calculation results of the four-stage rocket are compared. The results show that the air-launched rocket can significantly improve the carrying capacity and indirectly reduce the economic cost of the launch mission. Therefore, combined with the financial cost and reliability model, this research work can find the ideal overall parameters for the air-launched rocket system, and provide support for the development of low financial cost, fast response, and high-reliability satellite launching device. In general, it has a certain reference significance for the development of the overall parameter optimization of air-launched rockets.
Author Contributions
S.C. is responsible for model construction and simulation verification, J.L. is responsible for learning and developing optimization theory, S.Z. and X.B. are responsible for grasping the structure and content of the article and providing technical support, and D.S. is responsible for the final typesetting and revision of the article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data, models, and code generated or used during the study appear in the submitted article.
Acknowledgments
Thanks to the reviewers and editors for manuscript improvements.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sarigul-Klijn, N.; Sarigul-Klijn, M. A comparative analysis of methods for air-launching vehicles from earth to sub-orbit or orbit. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2006, 220, 439–452. [Google Scholar] [CrossRef]
- Song, W.; Ai, B.; Zhao, X. Prediction and evaluation of the stage-separation compatibility of an internally carried air-launch vehicle. Aerosp. Sci. Technol. 2020, 105, 106001. [Google Scholar] [CrossRef]
- Donahue, B.B. Beating the Rocket Equation: Air Launch with Advanced Chemical Propulsion. J. Spacecr. Rocket. 2004, 41, 302–309. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y. Multidisciplinary design and optimization of an innovative nano air launch vehicle with a twin-fuselage UAV as carrier aircraft. Acta Astronaut. 2020, 170, 397–411. [Google Scholar] [CrossRef]
- Jiu Xing, Z.; Haojun, X.; Dengcheng, Z.; Yanhua, Z. Study on conditions of internally carried air-launched launch vehicles based on the virtual prototype technology. High Tech. Commun. 2014, 20, 166–172. [Google Scholar]
- Changjun, P.; Yingqing, G. Design and simulation of ex-range gliding wing of high altitude air-launched autonomous underwater vehicles based on SIMULINK. J. Aeronaut. China 2013, 26, 319–325. [Google Scholar]
- Ryan, J. Genetic Algorithms in Search, Optimization and Machine Learning (Book Review). ORSA J. Comput. 1991, 3, 176. [Google Scholar] [CrossRef]
- Wang, D.; Wu, Z.; Fei, Y.; Zhang, W. Structural design employing a sequential approximation optimization approach. Comput. Struct. 2014, 134, 75–87. [Google Scholar] [CrossRef]
- Hayward, K.; Urdiales, J.M.L. Small Satellite Launch Vehicle from a Balloon Platform. In Proceedings of the 13th Reinventing Space Conference; Springer: Berlin/Heidelberg, Germany, 2018; pp. 177–192. [Google Scholar]
- Linshu, H.; Rafique, A.F.; Rahman, T. (Eds.) Small launch vehicle trajectory profile optimization using hybrid algorithm. In Proceedings of the 2013 10th International Bhurban Conference on Applied Sciences & Technology (IBCAST), Islamabad, Islamabad, Pakistan, 15–19 January 2013. [Google Scholar]
- Bayley, D.J.; Hartfield, R.J., Jr.; Burkhalter, J.E.; Jenkins, R.M. Design Optimization of a Space Launch Vehicle Using a Genetic Algorithm. J. Spacecr. Rocket. 2008, 45, 733–740. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. (Eds.) Particle swarm optimization. In IEEE International Conference on Neural Networks; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 1995. [Google Scholar]
- Yıldız, A.R. An effective hybrid immune-hill climbing optimization approach for solving design and manufacturing optimization problems in industry. J. Mater. Process. Technol. 2009, 209, 2773–2780. [Google Scholar] [CrossRef]
- Rafique, A.F.; He, L.S.; Zeeshan, Q.; Kamran, A.; Nisar, K. Multidisciplinary design and optimization of an air launched satellite launch vehicle using a hybrid heuristic search algorithm. Eng. Optim. 2011, 43, 305–328. [Google Scholar] [CrossRef]
- Rafique, A.; He, L.; Kamran, A.; Zeeshan, Q. Multidisciplinary design of air launched satellite launch vehicle: Performance comparison of heuristic optimization methods. Acta Astronautica. 2010, 67, 826–844. [Google Scholar] [CrossRef]
- Qifeng, C.; Xiaobin, L.; Jinhai, D. Cooperative coevolutionary multidisciplinary design optimization of missile system. J. Natl. Univ. Def. Technol. 2001, 23, 9–12. [Google Scholar]
- Fei, Z.; Quanbin, R.; Jun, Y. Air-to-ground missile conceptual design based on multidisciplinary design optimization. J. Solid Rocket. Technol. 2013, 36, 149–154. [Google Scholar]
- Wei, Z.; Jianjun, L.; Hongfu, Q.; Fei, X. Variable weight TOPSIS evaluation combined with particle swarm method for missile overall parameters optimization design. J. Solid Rocket. Technol. 2018, 41, 388–394. [Google Scholar]
- Jiao, X.; Chang, J.; Wang, Z.; Yu, D. Hysteresis phenomenon of hypersonic inlet at high Mach number. Acta Astronautica. 2016, 128, 657–668. [Google Scholar] [CrossRef]
- Luo, J.; Lu, W. Comparison of surrogate models with different methods in groundwater remediation process. J. Earth Syst. Sci. 2014, 123, 1579–1589. [Google Scholar] [CrossRef]
- Feng, F.; Jin, J.; Liu, W.; Yan, S. Recent Advances in Multi-Feature Assisted Neuro-Transfer Function Surrogate Based EM Optimization for Microwave Filter Design. In Proceedings of the 13th UK-Europe-China Workshop on Millimetre-Waves and Terahertz Technologies (UCMMT), Tianjin, China, 29 August–1 September 2020. [Google Scholar]
- Namura, N.; Shimoyama, K.; Obayashi, S. Kriging Surrogate Model Enhanced by Coordinate Transformation of Design Space Based on Eigenvalue Decomposition. In Evolutionary Multi-Criterion Optimization; Springer Natural: Guimarães, Portugal, 2015; Volume 9018, pp. 321–335. [Google Scholar]
- Mifsud, M.; MacManus, D.; Shaw, S. A variable-fidelity aerodynamic model using proper orthogonal decomposition. Int. J. Numer. Methods Fluids 2016, 82, 646–663. [Google Scholar] [CrossRef] [Green Version]
- Masters, D.A.; Taylor, N.J.; Rendall, T.C.S.; Allen, C.B.; Poole, D.J. Geometric Comparison of Aerofoil Shape Parameterization Methods. AIAA J. 2017, 55, 1575–1589. [Google Scholar] [CrossRef] [Green Version]
- Farias Filho, U.P.; Antunes, A.R.; Bastos, S.M.; Lyra, P.R. Minimization of vortex induced vibrations using Surrogate Based Optimization. Struct. Multidiscip. Optim. 2015, 52, 717–735. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, D.; Jiang, Z.; Zhang, W. Unified estimate of Gaussian kernel width for surrogate models. Neurocomputing 2016, 203, 41–51. [Google Scholar] [CrossRef]
- Wu, Z.; Donghui, W.; Weihua, Z.; Yang, F. Modeling design framework for sold-rocketmotor performance. J. Spacecr. Rocket. 2017, 54, 1–10. [Google Scholar]
- Yeh, I.C.; Chen, C.C.; Zhang, X.; Wu, C.; Huang, K.C. Adaptive radial basis function networks with kernel shape parameters(Article). Neural Comput. Appl. 2012, 21, 469–480. [Google Scholar] [CrossRef]
- Xu, P.; Jayawardena, A.W.; Li, W.K. Model selection for RBF network via generalized degree of freedom. Neurocomputing 2013, 99, 163–171. [Google Scholar] [CrossRef]
- Kejun, C.; Luhua, L.; Yunhe, M. Launch Vehicle Flight Dynamics and Guidance; National Defense Industry Press: Beijing, China, 2014. [Google Scholar]
- Xingjian, L. Introduction to Missile Overall Design; National Defense Industry Press: Beijing, China, 2017. [Google Scholar]
- Yao, Z.; Yongzhi, S.; Xiangdong, L. Sliding mode control based guidance law with impact angle constraint. J. Aeronaut. China 2014, 27, 145–152. [Google Scholar]
- Rhee, I.; Lee, C.; Lee, J.-W. Optimal design for hybrid rocket engine for air launch vehicle. J. Mech. Sci. Technol. 2008, 22, 1576–1585. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).