Development of a Numerical Model to Simulate Laser-Shock Paint Stripping on Aluminum Substrates
Abstract
:1. Introduction
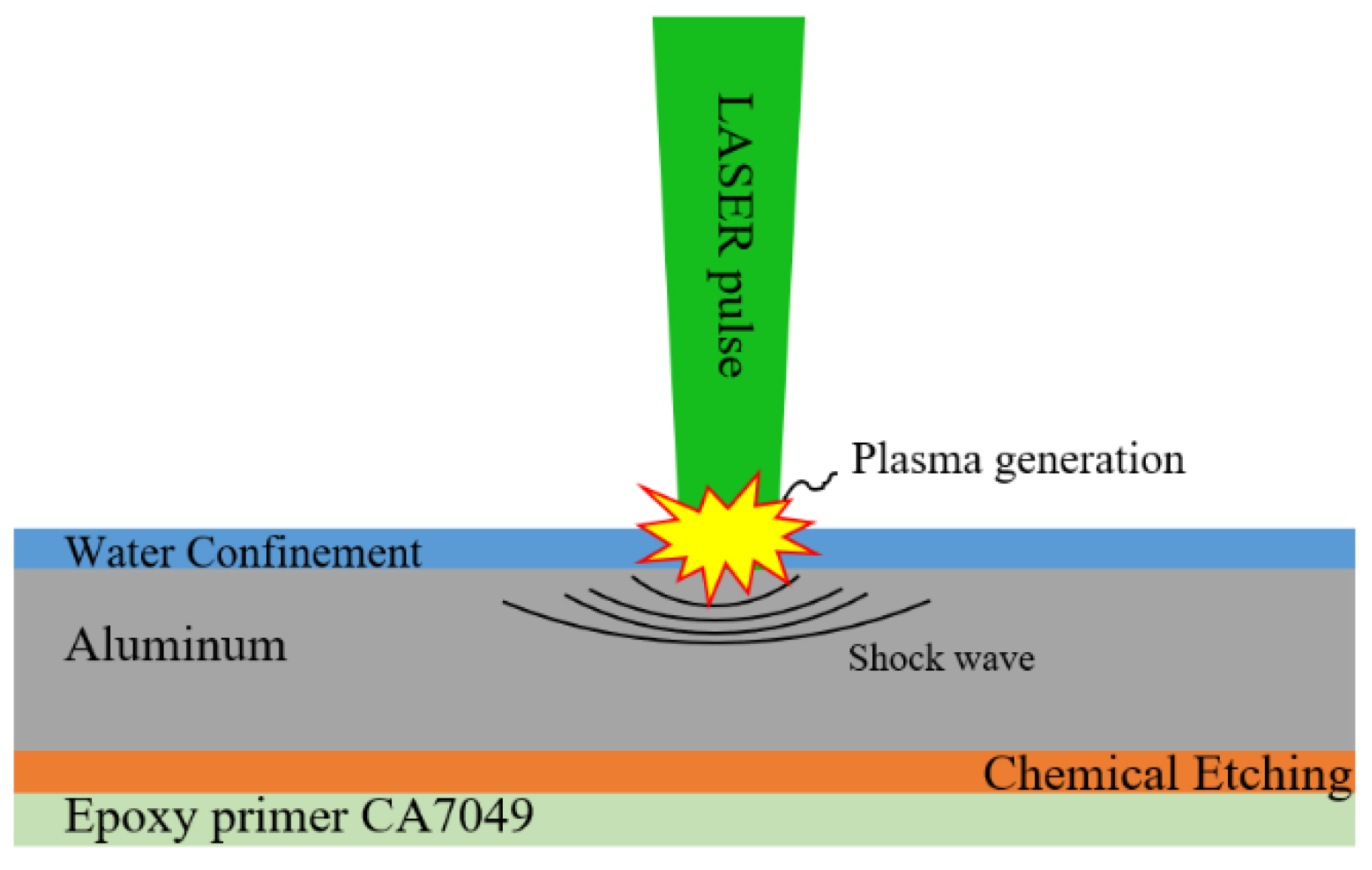
2. The Laser Shock Stripping Process
3. Specimen and Materials
4. Theoretical Models and Numerical Modeling
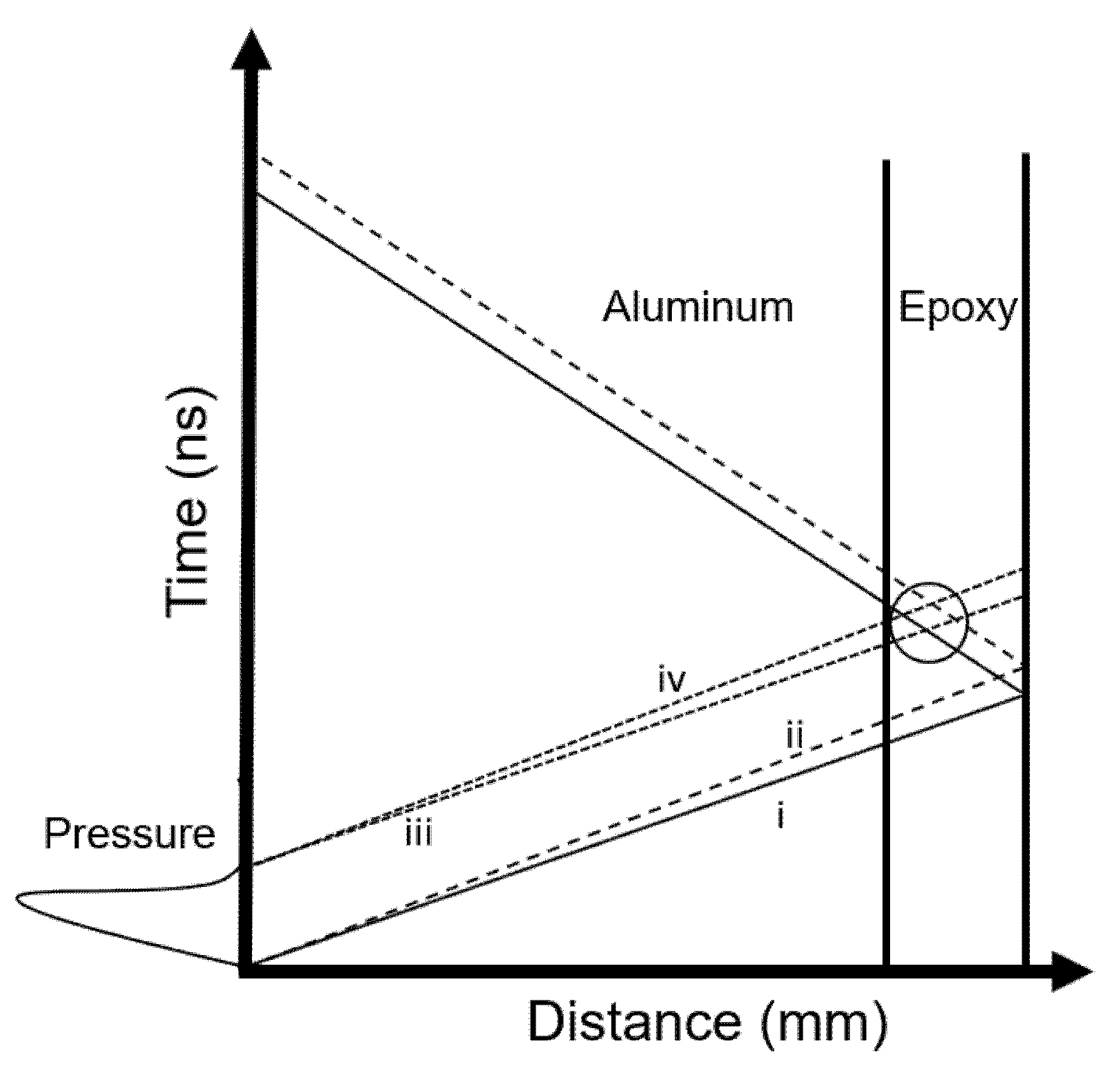
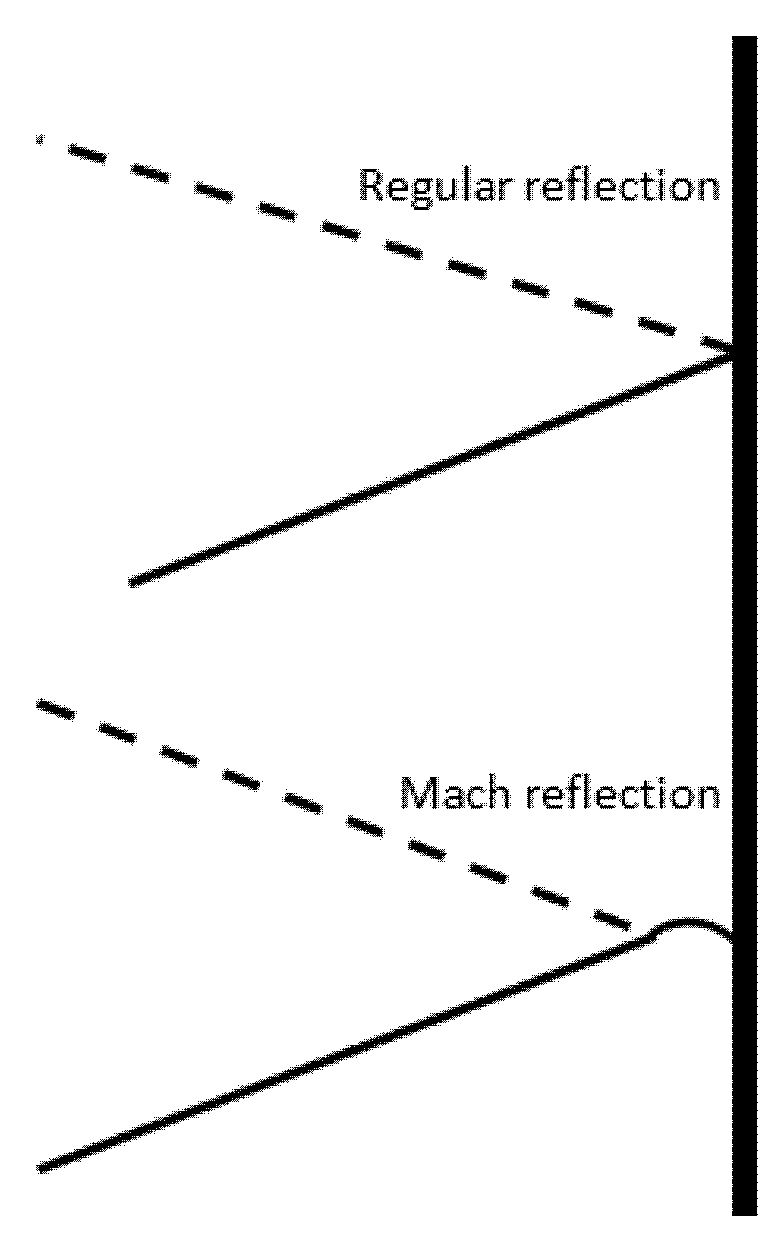
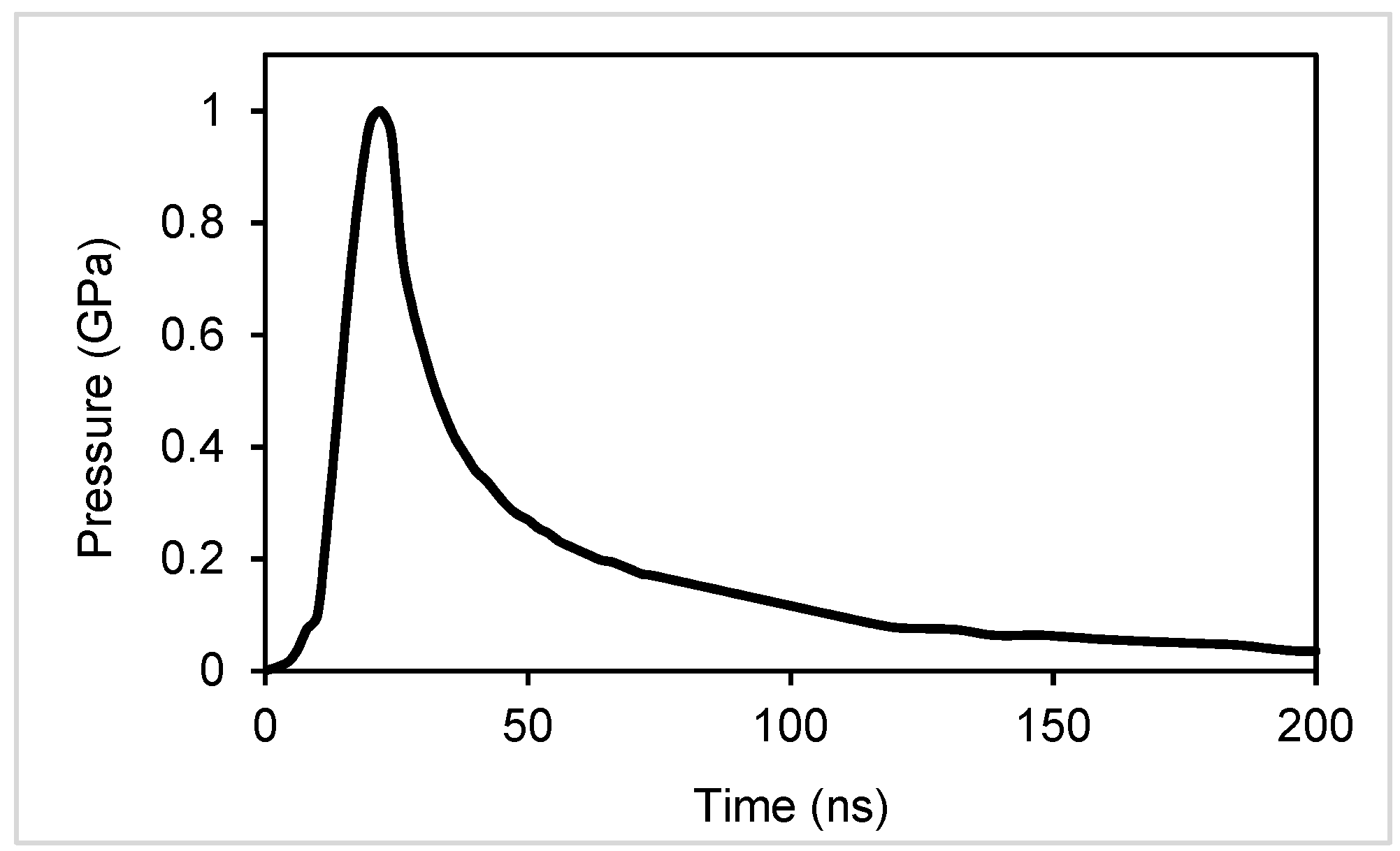
4.1. Calculation of Pressure’s Profile
4.2. Constitutive Material Models
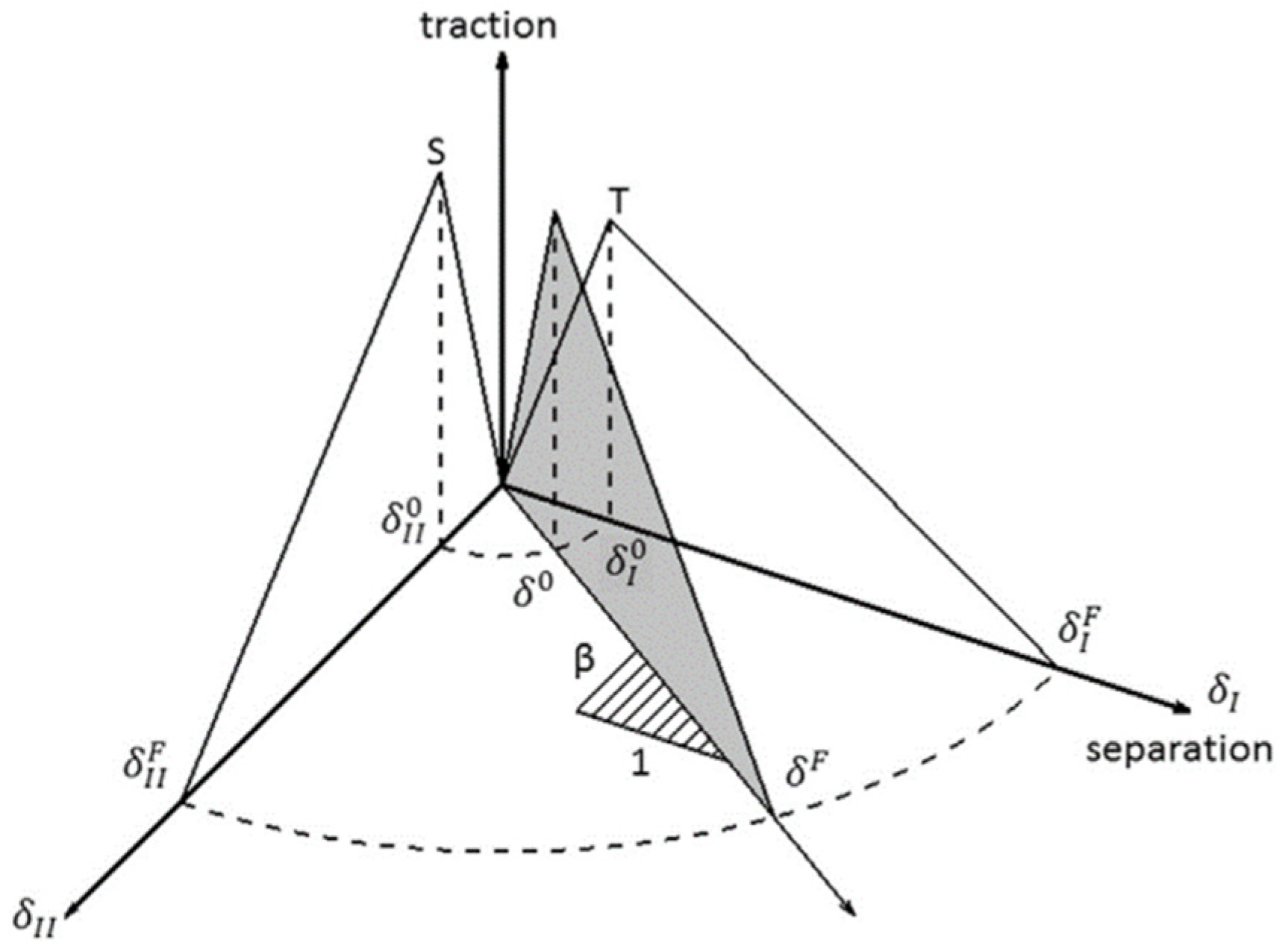
4.3. Stripping Simulation by Cohesive Zone Modeling
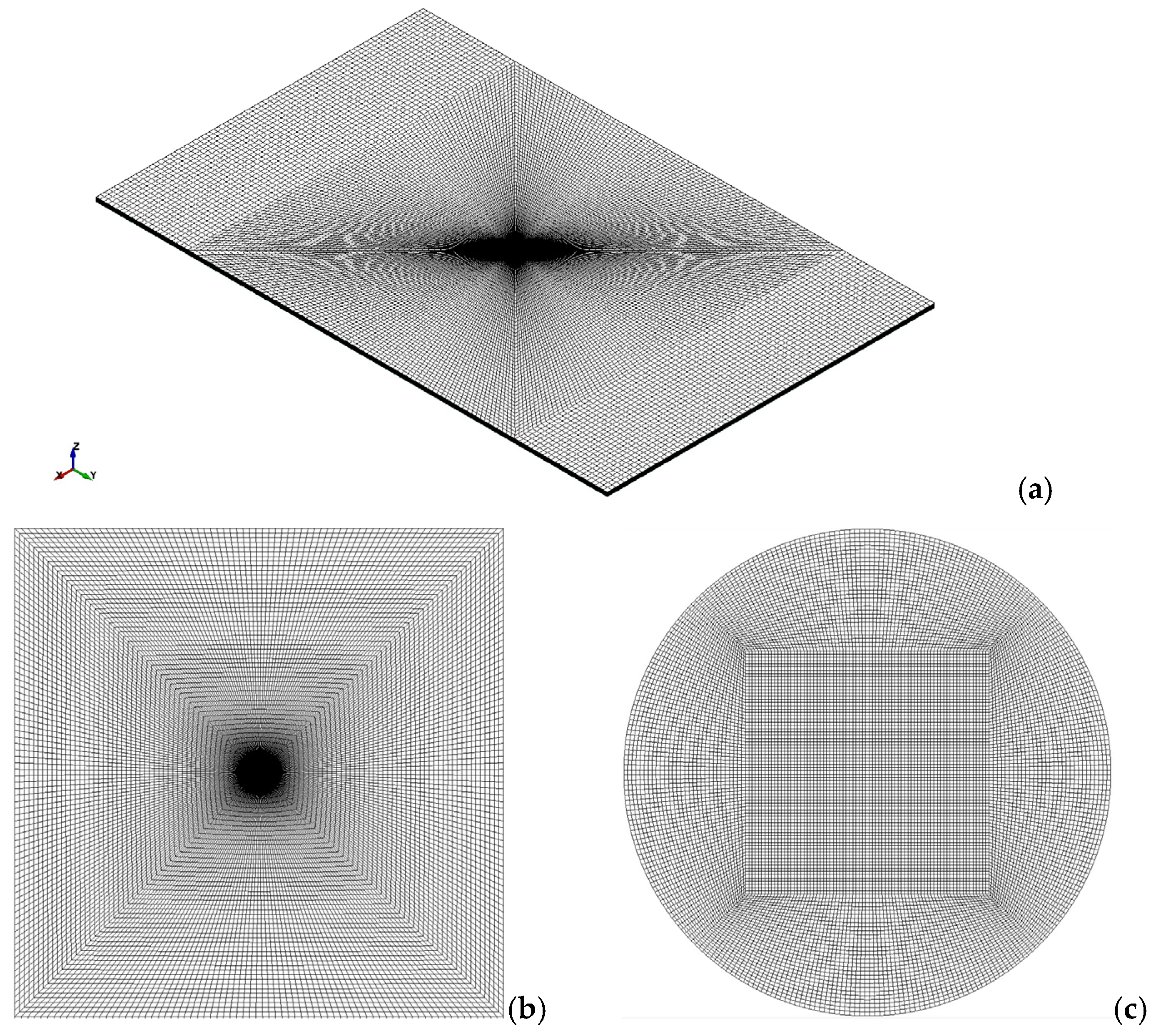
5. Finite Element Modeling
6. Parametric Study
7. Numerical Results
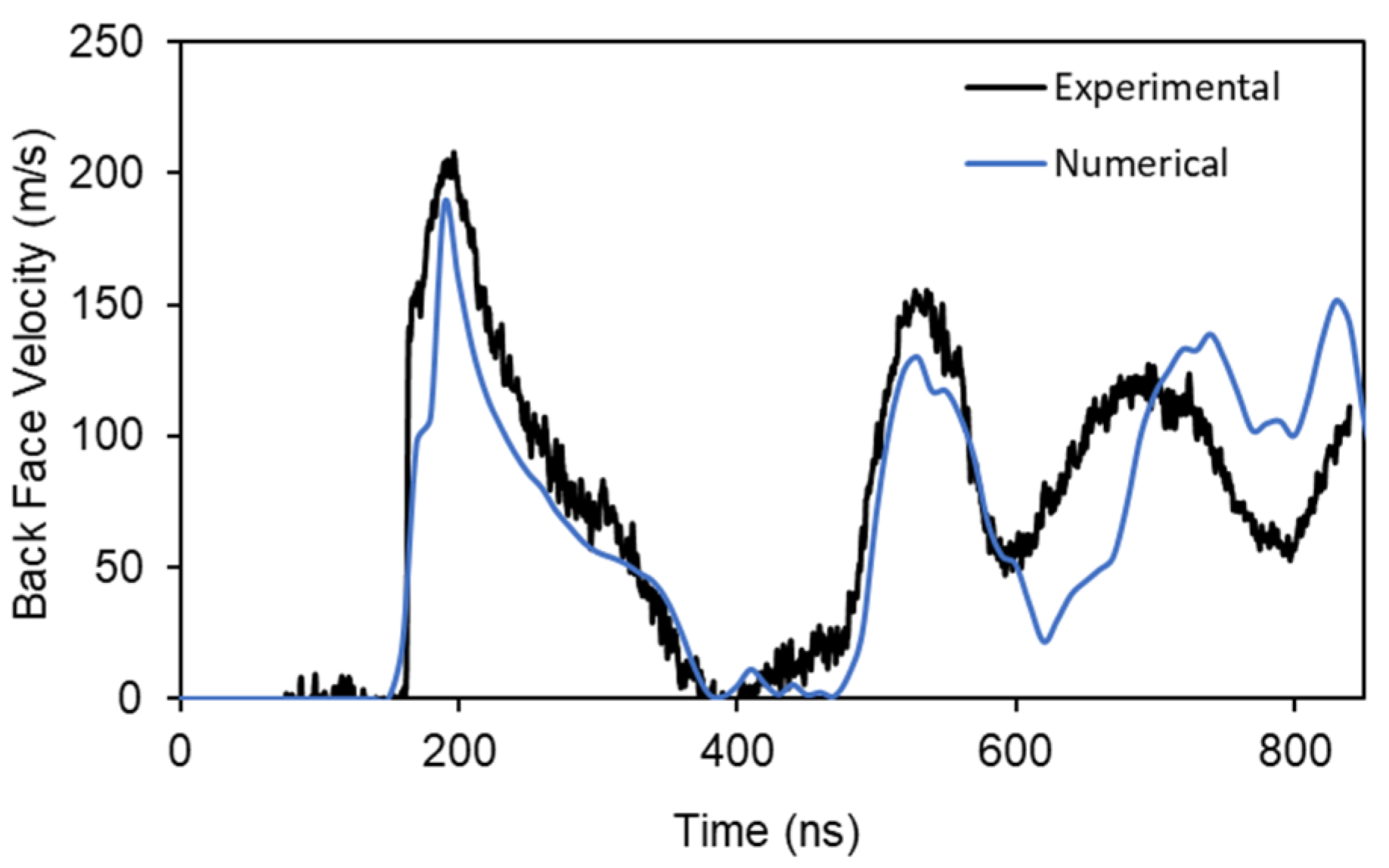
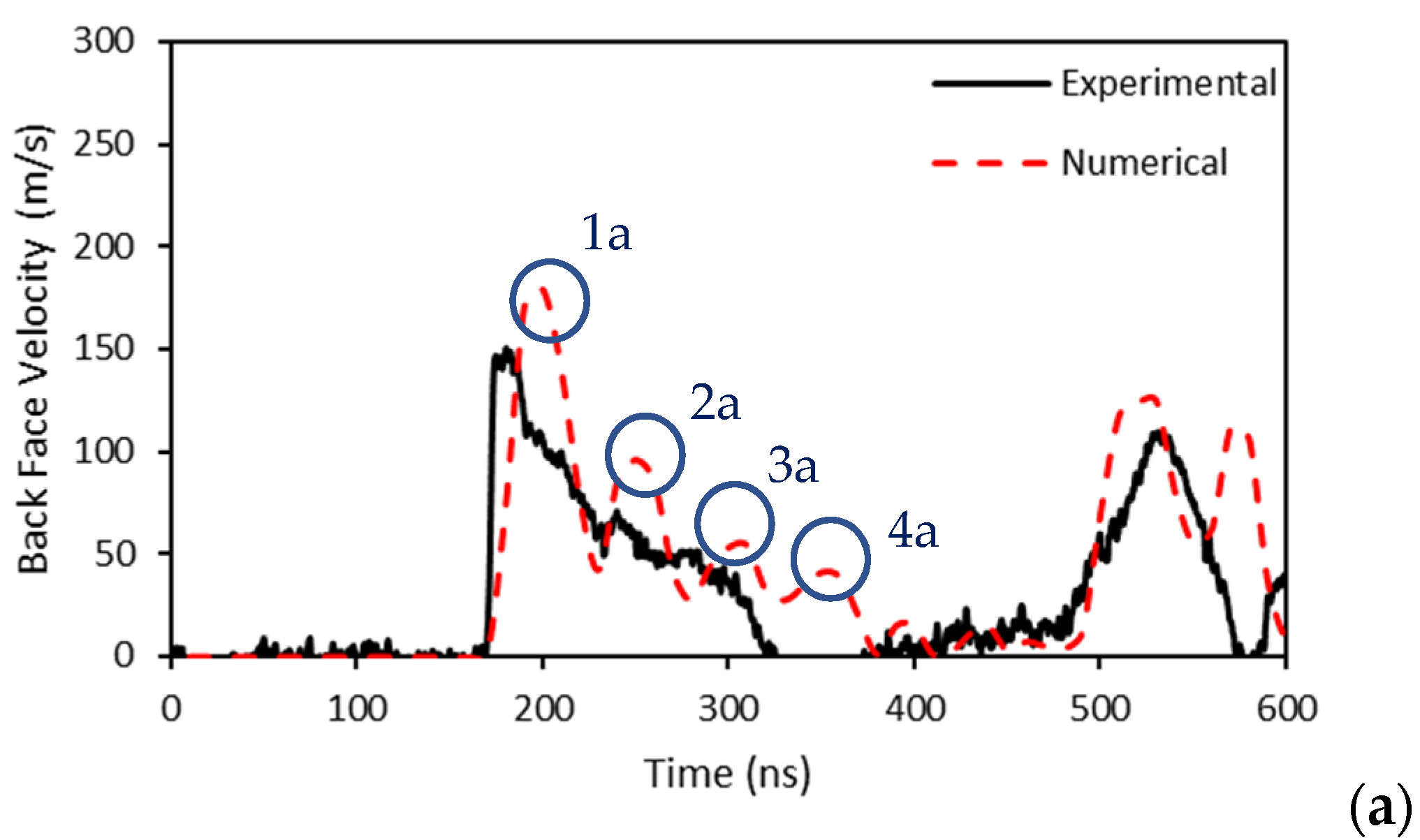
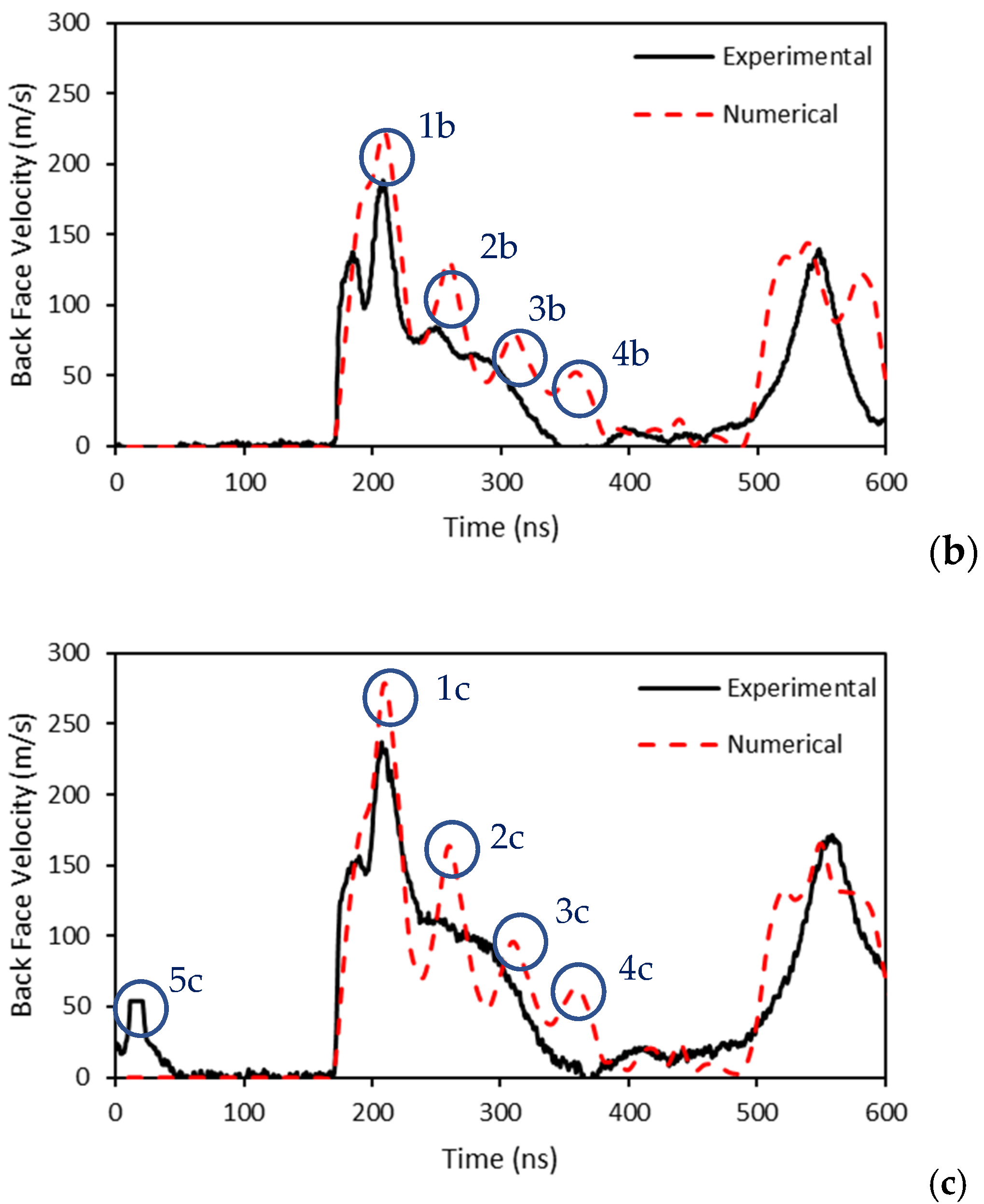
7.1. Model Validation
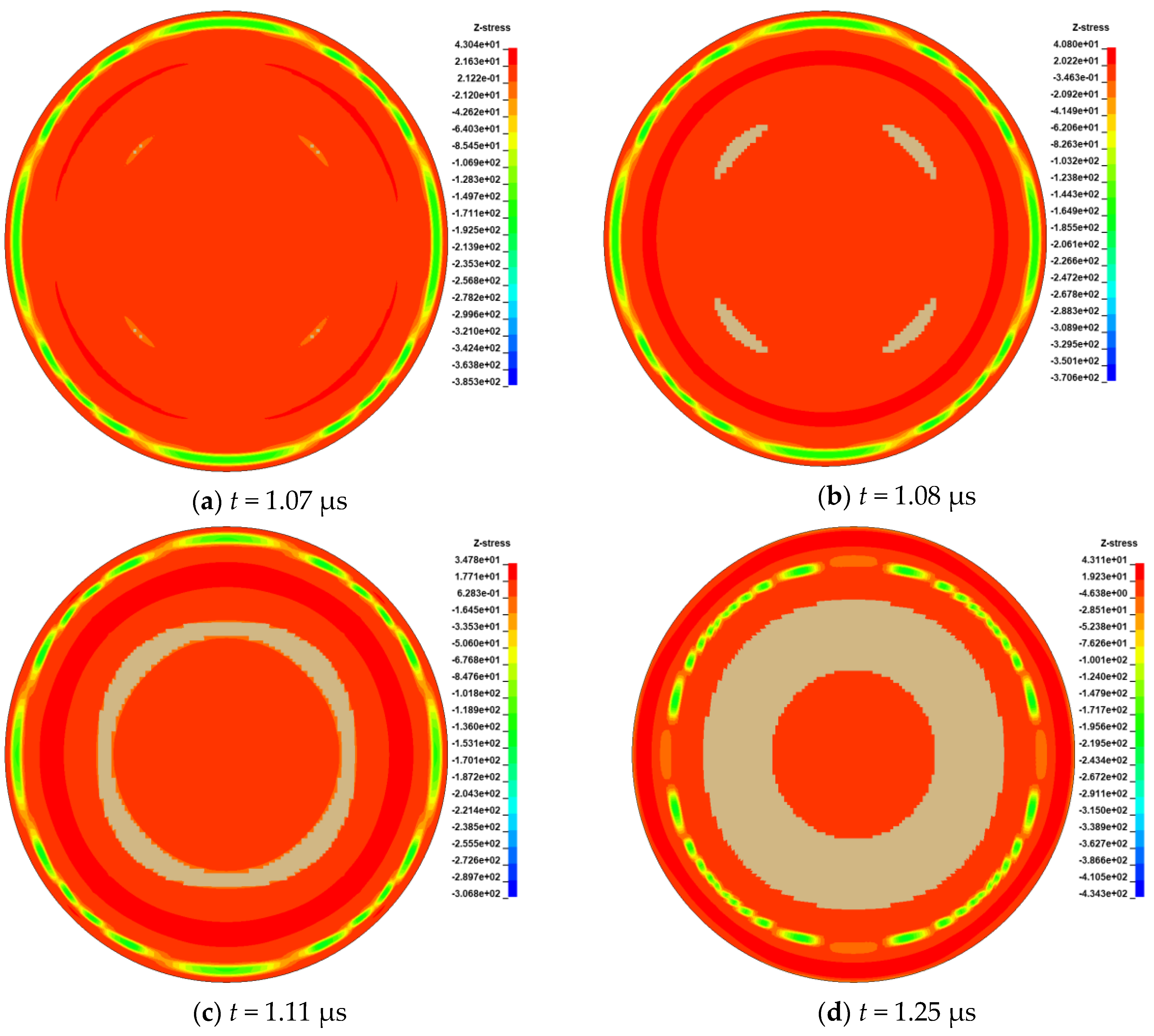
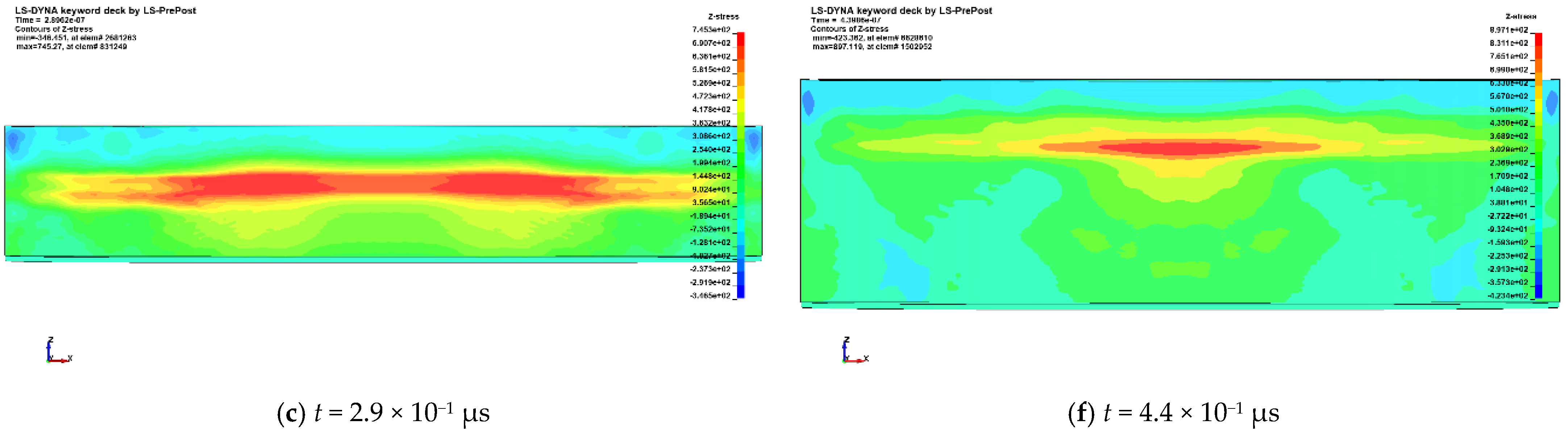
7.2. Stripping Simulation
7.3. Parametric Study
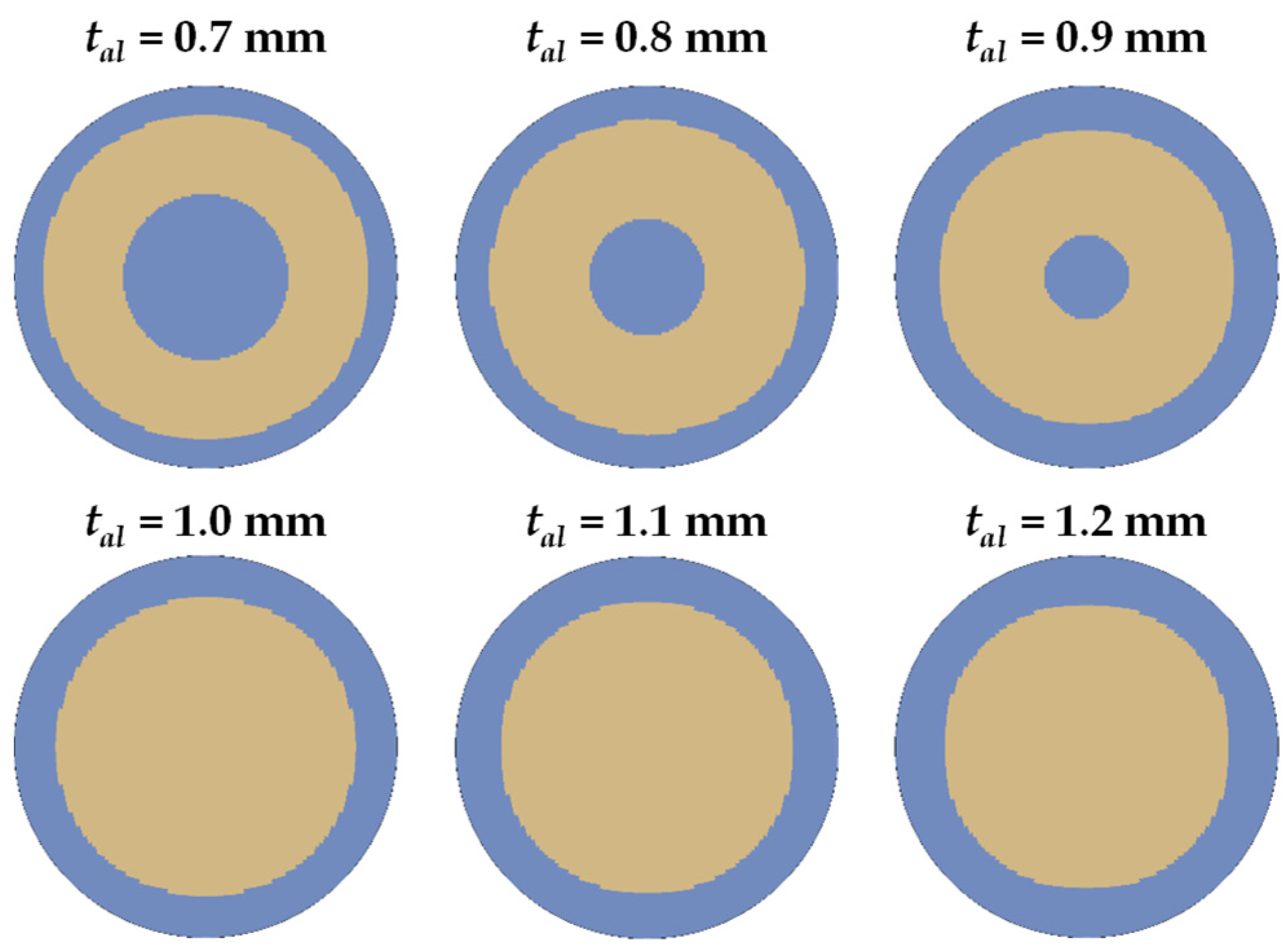
7.3.1. Effect of Aluminum Thickness
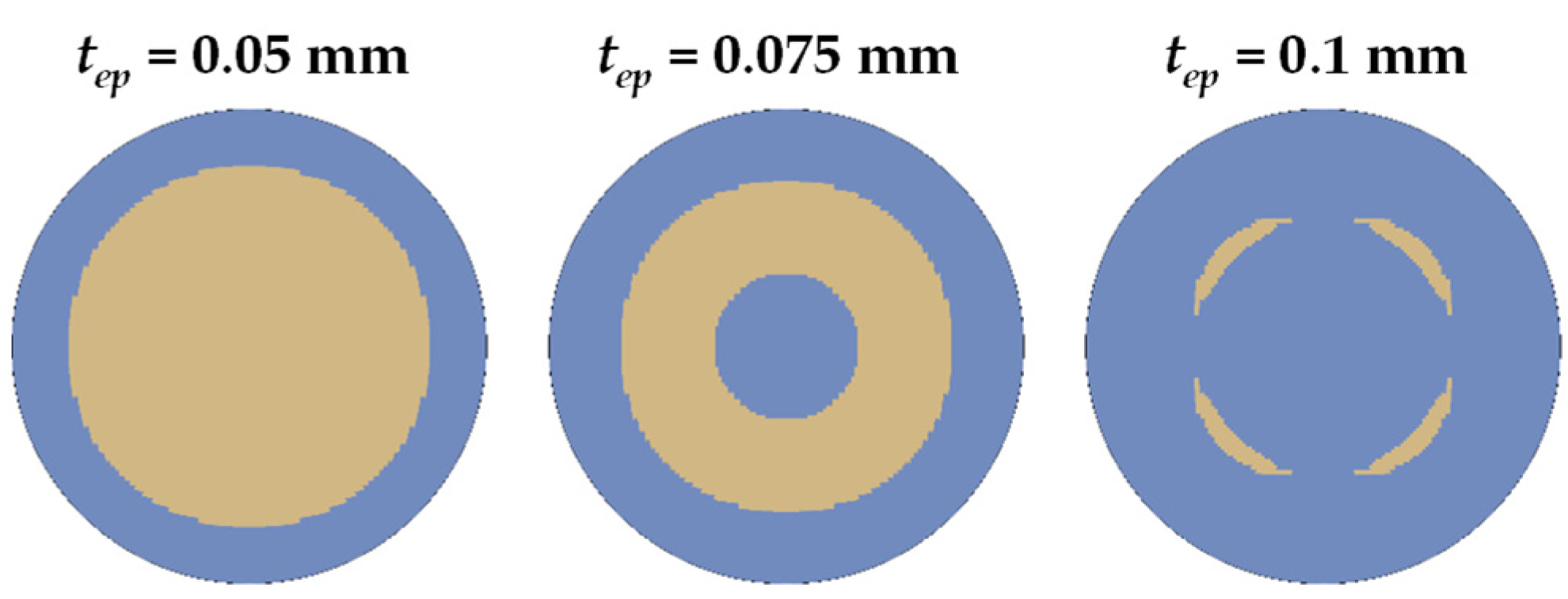
7.3.2. Effect of Epoxy Thickness
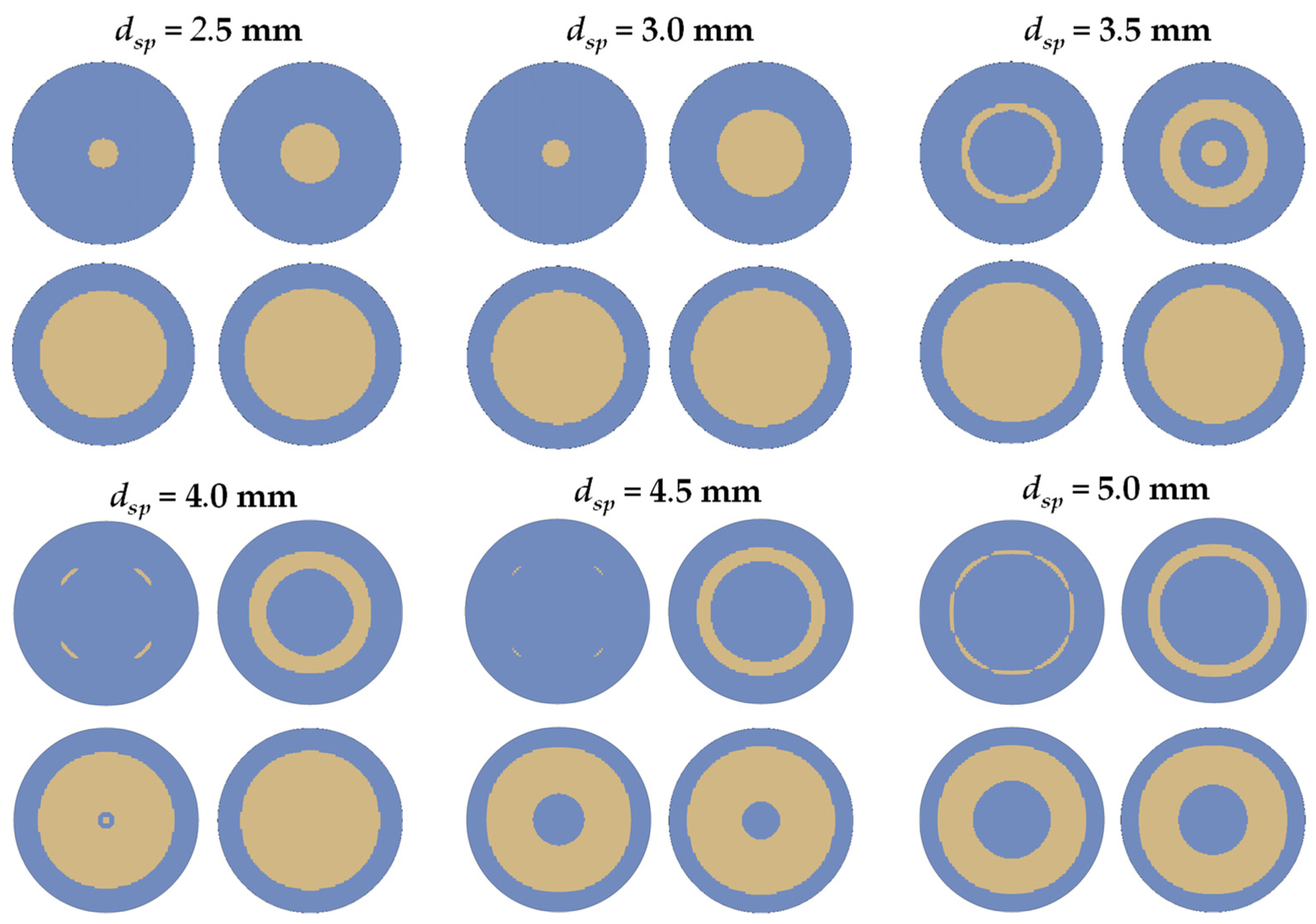
7.3.3. Effect of Spot’s Diameter
7.3.4. Effect of G1C
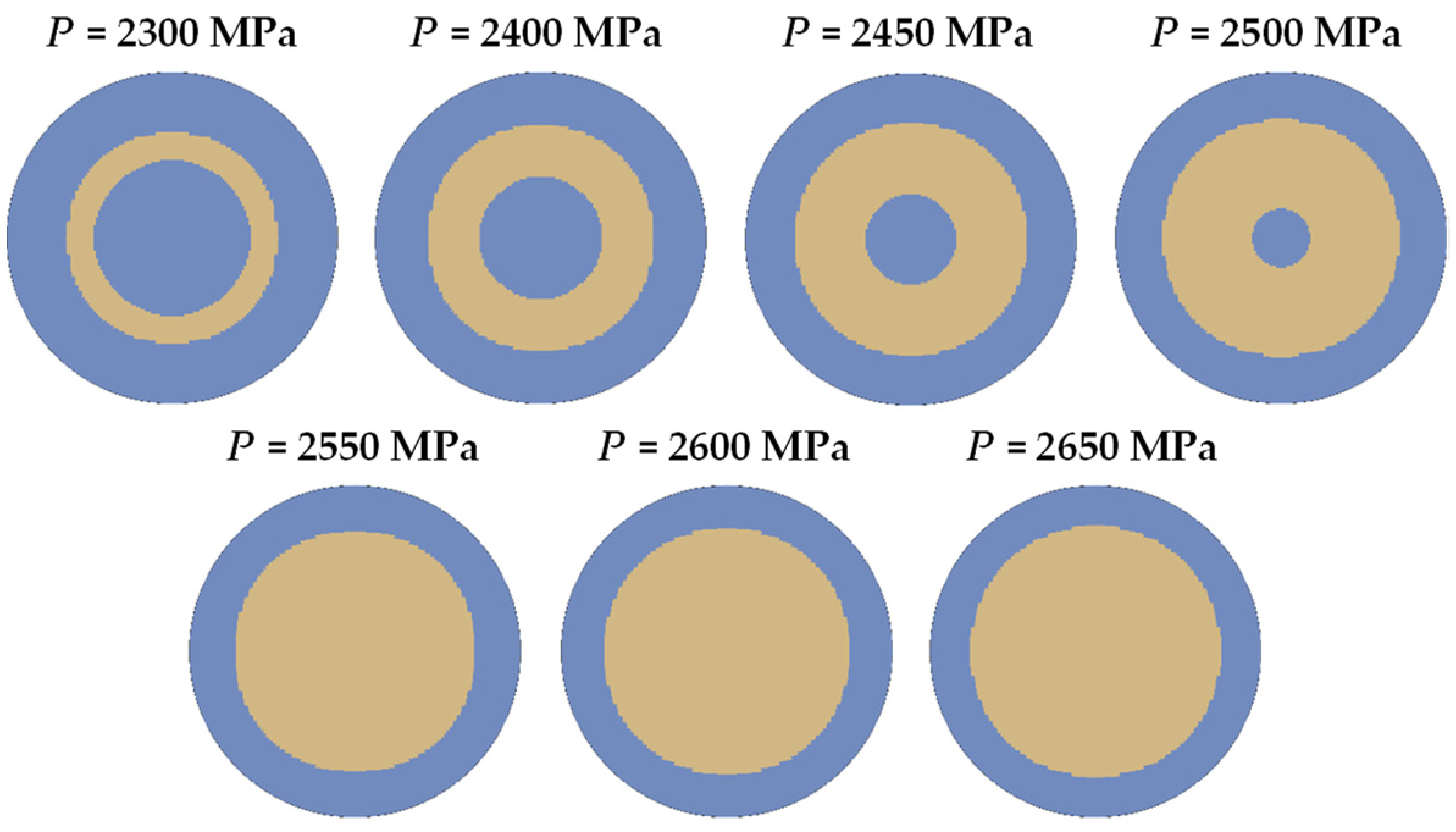
7.3.5. Effect of Maximum Applied Pressure
8. Conclusions
- The model is capable of efficiently simulating the laser shock stripping process as indicated by the comparison of numerical and experimental results.
- By increasing the aluminum thickness, a transition from the annular to the solid stripping pattern takes place. For values of aluminum thickness smaller than 1 mm, an incomplete stripping is predicted.
- By increasing the epoxy thickness, a transition from a solid circular to an annular stripping pattern takes place. For 0.075 mm and 0.1 mm epoxy thickness, an incomplete stripping is predicted.
- The laser spot’s diameter significantly affects the stripping propagation and the final stripping pattern. For values of dsp larger than 4.0 mm, an incomplete stripping is predicted.
- GIC affects the first stages of stripping evolution, while GIIC does not affect stripping evolution.
- With increasing the maximum applied pressure, a transition from the annular to the solid stripping pattern takes place. For values smaller than 2500 MPa, an incomplete stripping (annular) is predicted.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peyre, P.; Fabbro, R.; Merrien, P.; Lieurade, H.P. Laser shock processing of aluminium alloys. Application to high cycle fatigue behaviour. Mater. Sci. Eng. A 1996, 210, 102–113. [Google Scholar] [CrossRef]
- Ivetic, G. Three-dimensional FEM analysis of laser shock peening of aluminium alloy 2024-T351 thin sheets. Surf. Eng. 2011, 27, 445–453. [Google Scholar] [CrossRef]
- Le Bras, C.; Rondepierre, A.; Seddik, R.; Scius-Bertrand, M.; Rouchausse, Y.; Videau, L.; Fayolle, B.; Gervais, M.; Morin, L.; Valadon, S.; et al. Laser Shock Peening: Toward the Use of Pliable Solid Polymers for Confinement. Metals 2019, 9, 793. [Google Scholar] [CrossRef] [Green Version]
- Peyre, P.; Berthe, L.; Vignal, V.; Popa, I.; Baudin, T. Analysis of laser shock waves and resulting surface deformations in an Al-Cu-Li aluminum alloy. J. Phys. D Appl. Phys. 2012, 45, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ocana, J.L.; Correa, C.; García-Beltrán, A.; Porro, J.A.; Díaz, M.; Ruiz-de-Lara, L.; Peral, D. Laser Shock Processing of thin Al2024-T351 plates for induction of through-thickness compressive residual stresses fields. J. Mater. Process. Technol. 2015, 223, 8–15. [Google Scholar] [CrossRef]
- Ecault, R.; Touchard, F.; Boustie, M.; Berthe, L.; Dominguez, N. Numerical modeling of laser-induced shock experiments for the development of the adhesion test for bonded composite materials. Compos. Struct. 2016, 152, 382–394. [Google Scholar] [CrossRef] [Green Version]
- Ecault, R.; Touchard, F.; Berthe, L.; Boustie, M. Laser shock adhesion test numerical optimization for composite bonding assessment. Compos. Struct. 2020, 247, 112441. [Google Scholar] [CrossRef]
- Courapied, D.; Berthe, L.; Peyre, P.; Coste, F.; Zou, J.-P.; Sautivet, A.-M. Laser-delayed double shock-wave generation in water-confinement regime. J. Laser Appl. 2015, 27, S29101. [Google Scholar] [CrossRef]
- Unaldi, S.; Papadopoulos, K.; Rondepierre, A.; Rouchausse, Y.; Karanika, A.; Deliane, F.; Tserpes, K.; Floros, G.; Richaud, E.; Berthe, L. Towards selective Laser paint stripping using shock waves produced by Laser—Plasma interaction for aeronautical applications on AA 2024 Based Substrates. Opt. Laser Technol. 2021, 141, 107095. [Google Scholar] [CrossRef]
- Morales, M.; Porro, J.A.; Blasco, M.; Molpeceres, C.; Ocana, J.L. Numerical simulation of plasma dynamics in laser shock processing experiments. J. Appl. Surf. Sci. 2009, 255, 5181–5185. [Google Scholar] [CrossRef]
- Bardy, S.; Aubert, B.; Bergarac, T.; Berthe, L.; Combis, P.; Hébertb, D.; Lescoute, E.; Rouchausse, Y.; Videau, L. Development of a numerical code for laser-induced shock waves applications. J. Opt. Laser Technol. 2020, 124, 105983. [Google Scholar] [CrossRef]
- Scius-Bertrand, M.; Videau, L.; Rondepierre, A.; Lescoute, E.; Rouchausse, Y.; Kaufman, J.; Rostohar, D.; Brajer, J.; Berthe, L. Laser induced plasma characterization in direct and water confined regimes: New advances in experimental studies and numerical modelling. J. Phys. D Appl. Phys. 2021, 54, 14. [Google Scholar] [CrossRef]
- Ecault, R.; Berthe, L.; Touchard, F.; Boustié, M.; Lescoute, E. Experimental and numerical investigations of shock and shear wave propagation induced by femtosecond laser irradiation in epoxy resins. J. Phys. D Appl. Phys. 2015, 48, 9. [Google Scholar] [CrossRef]
- Bolis, C.; Berthe, L.; Boustie, M.; Arrigoni, M.; Barradas, S.; Jeandin, M. Physical approach to adhesion testing using laser-driven shock waves. J. Phys. D Appl. Phys. 2007, 40, 3155–3163. [Google Scholar] [CrossRef]
- Fox, J.A. Effect of water and paint coatings on laser irradiated targets. Appl. Phys. Lett. 1974, 24, 461–464. [Google Scholar] [CrossRef]
- Sagnard, M.; Berthe, L.; Ecault, R.; Touchard, F.; Boustie, M. Development of the symmetrical laser shock test for weak bond inspection. Opt. Laser Technol. 2019, 111, 644–652. [Google Scholar] [CrossRef] [Green Version]
- Davison, L. Fundamentals of Shock Wave Propagation in Solids; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ben-Dor, G. Shock Wave Reflection Phenomena, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Fabbro, R.; Peyre, P.; Berthe, L.; Scherpereel, X. Physics and applications of laser-shock processing. J. Laser Appl. 1998, 10, 265–279. [Google Scholar] [CrossRef]
- Berthe, L.; Fabbro, R.; Peyre, P.; Tollier, L.; Bartnicki, E. Shock waves from a water-confined laser-generated plasma. J. Appl. Phys. 1997, 82, 2826–2832. [Google Scholar] [CrossRef]
- LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2018; Volumes I–III.
- Buyuk, M.; Kan, S.; Loikkanen, M. Explicit Finite-Element Analysis of 2024-T3/T351 Aluminum Material under 459 Impact Loading for Airplane Engine Containment and Fragment Shielding. J. Aerosp. Eng. 2009, 22, 287–295. [Google Scholar] [CrossRef]
- Floros, I.; Tserpes, K.; Lobel, T. Mode-I, mode-II and mixed-mode I-II fracture behavior of composite bonded joints: Experimental characterization and numerical simulation. Compos. Part B 2015, 78, 459–468. [Google Scholar] [CrossRef]
- Ecault, R. Etude Expérimentale et Numérique du Comportement Dynamique de Composites Aéronautiques Sous Choc Laser. Optimisation du Test D’adhérence par ondes de Choc sur les Assemblages Composites Collés; Ecole Nationale Supérieure de Mécanique et d’Aérotechique-Poitiers: Paris, France, 2013. [Google Scholar]
- Barker, L.; Hollenbach, R. Laser interferometer for measuring high velocities of any reflecting surface. J. Appl. Phys. 1972, 43, 4669–4675. [Google Scholar] [CrossRef]



| Input Parameter | Value |
|---|---|
| Johnson–Cook—Gruneisen | |
| Young’s modulus, Ε | 73,084 MPa |
| Poisson’s ration, ν | 0.33 |
| Strain yield limit, A | 352 MPa |
| Strain hardening modulus, Β | 440 MPa |
| Strain hardening exponent, n | 0.42 |
| Strain rate coefficient, C | 0.0083 |
| Density, ρ | 2770 kg/m3 |
| Speed of the wave, C0 | 5328 m/s |
| Linear Hugoniot slope coefficient, S | 1.338 |
| Gruneisen constant, Γ | 2 |
| Input Damage Parameters | |
| D1 | 0.13 |
| D2 | 0.13 |
| D3 | −1.5 |
| D4 | 0.011 |
| D5 | 0 |
| Elastic Plastic Hydrodynamic—Gruneisen | |
|---|---|
| Density | 1700 kg/m3 |
| Shear modulus | 1600 MPa |
| Speed of the wave | 2000 m/s |
| Linear Hugoniot slope coefficient | 1.493 |
| Gruneisen constant | 1.13 |
| Parameter | Range | Reference |
|---|---|---|
| Aluminum thickness | 0.7–1.2 mm | 0.97 mm |
| Epoxy thickness | 25–150 μm | 25 μm |
| Laser spot diameter | 2.5–5 mm | 4 mm |
| GIC and GIIC | Division factor: 1.25, 1.50, 1.75, 2.0 | 1018.52 J/m2 and 783.41 J/m2 |
| Pmax for 1.75 GW/cm2 | 2300–2650 MPa | 2639 MPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tserpes, K.; Papadopoulos, K.; Unaldi, S.; Berthe, L. Development of a Numerical Model to Simulate Laser-Shock Paint Stripping on Aluminum Substrates. Aerospace 2021, 8, 233. https://doi.org/10.3390/aerospace8090233
Tserpes K, Papadopoulos K, Unaldi S, Berthe L. Development of a Numerical Model to Simulate Laser-Shock Paint Stripping on Aluminum Substrates. Aerospace. 2021; 8(9):233. https://doi.org/10.3390/aerospace8090233
Chicago/Turabian StyleTserpes, Konstantinos, Kosmas Papadopoulos, Selen Unaldi, and Laurent Berthe. 2021. "Development of a Numerical Model to Simulate Laser-Shock Paint Stripping on Aluminum Substrates" Aerospace 8, no. 9: 233. https://doi.org/10.3390/aerospace8090233
APA StyleTserpes, K., Papadopoulos, K., Unaldi, S., & Berthe, L. (2021). Development of a Numerical Model to Simulate Laser-Shock Paint Stripping on Aluminum Substrates. Aerospace, 8(9), 233. https://doi.org/10.3390/aerospace8090233







