The Lunar Radiation Environment: Comparisons between PHITS, HETC-HEDS, and the CRaTER Instrument
Abstract
:1. Introduction
A NASA-established LRO Objectives/Requirements Definition Team (ORDT) identifies the following high-priority objective for this initial robotic mission in the Lunar Exploration Program (LEP): “Characterization of the global lunar radiation environment and its biological impacts and potential mitigation, as well as investigation of shielding capabilities and validation of other deep space radiation mitigation strategies involving materials.”
2. Methodology
2.1. The CRaTER Instrument
2.2. PHITS
In the transport process, PHITS can simulate a motion under external fields such as magnetic and gravity. Without the external fields, neutral particles move along a straight trajectory with constant energy up to the next collision point. However, charged particles and heavy ions interact many times with electrons in the material losing energy and changing direction. PHITS treats ionization processes not as collision but as a transport process under an external field. The average dE/dx is given by the charge density of the material and the momentum of the particle taking into account the fluctuations of the energy loss and the angular deviation. The second category of the physical processes is the collision with the nucleus in the material. In addition to the collision, we consider the decay of the particle as a process in this category. The total reaction cross section, or the lifetime of the particle, is an essential quantity in the determination of the mean free path of the transport particle. According to the mean free path, PHITS chooses the next collision point using the Monte Carlo method. To generate the secondary particles of the collision, we need the information on the final states of the collision. For neutron induced reactions in the low energy region, PHITS employs the cross sections from Evaluated Nuclear Data libraries. For high energy neutrons and other particles, we have incorporated two models, JAM [18] and JQMD [19], to simulate the particle induced reactions up to 200 GeV and the nucleus–nucleus collisions, respectively.
2.3. HETC-HEDS
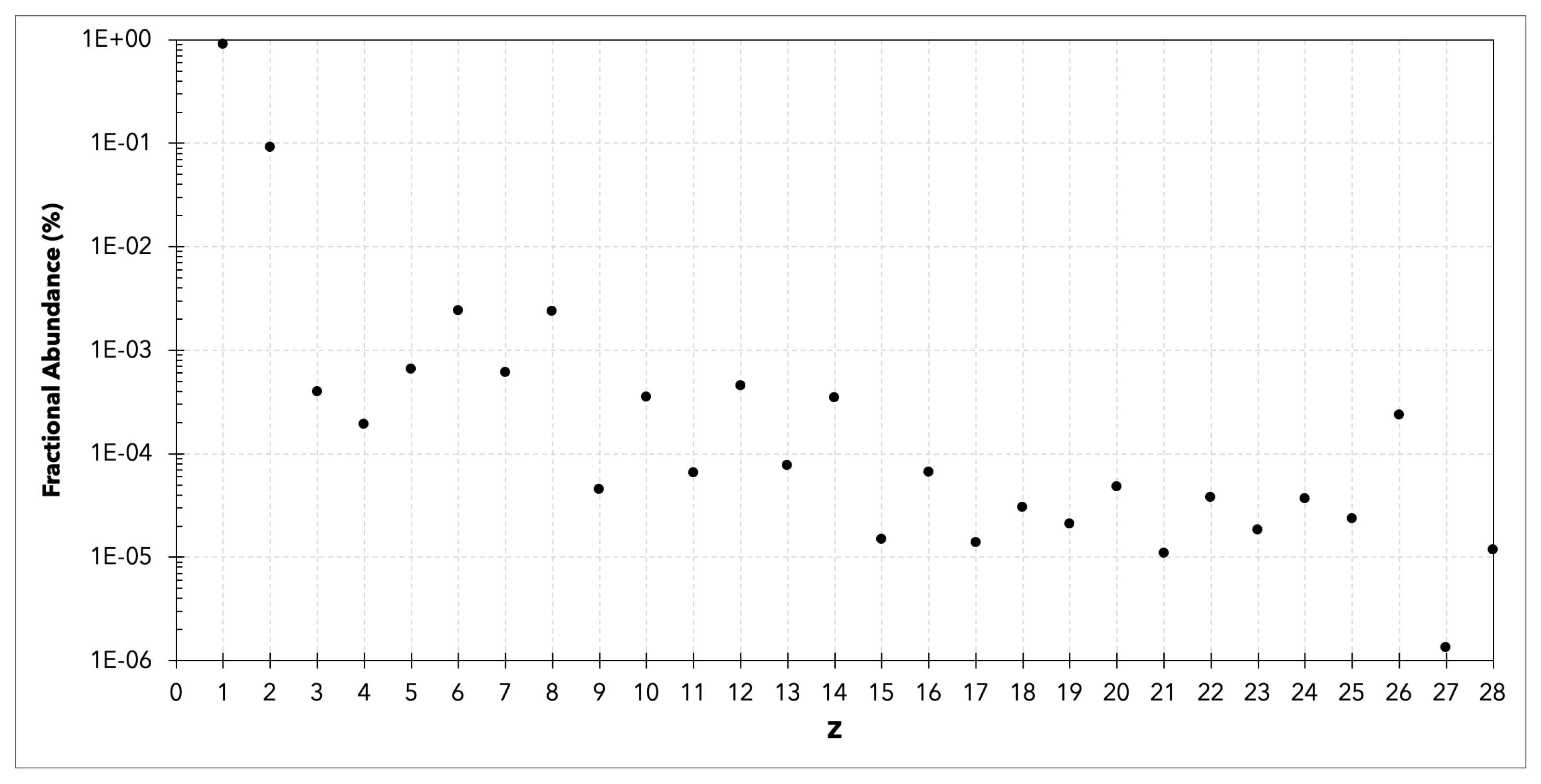
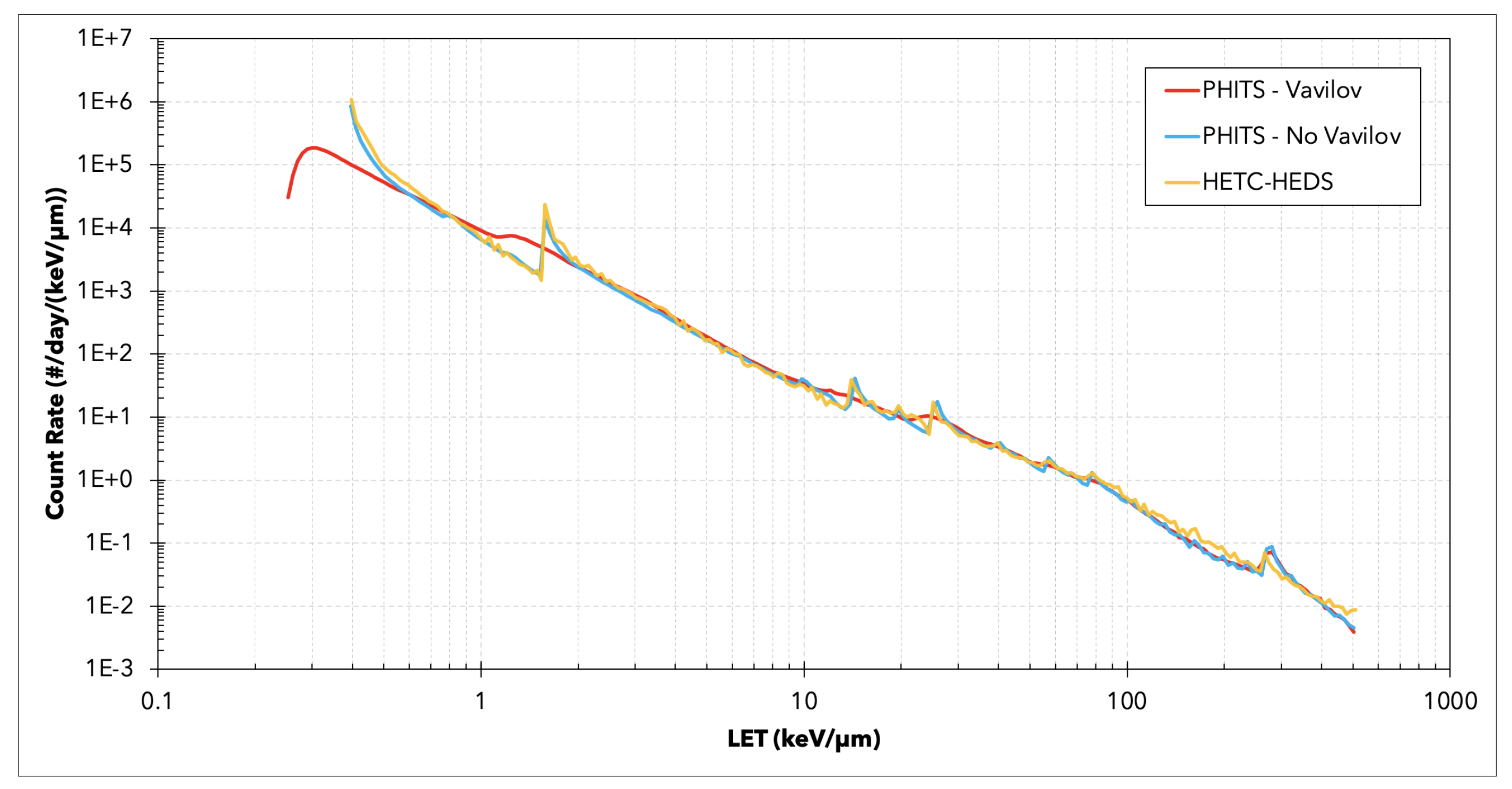
3. Results and Discussion
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Spence, H.E.; Case, A.W.; Golightly, M.J.; Heine, T.; Larsen, B.A.; Blake, J.B.; Caranza, P.; Crain, W.R.; George, J.; Lalic, M.; et al. CRaTER: The cosmic ray telescope for the effects of radiation experiment on the lunar reconnaissance orbiter mission. J. Space Sci. Rev. 2010, 150, 243–284. [Google Scholar] [CrossRef] [Green Version]
- Townsend, L.W.; Moussa, H.M.; Charara, Y.M. Monte Carlo simulations of energy losses by space protons in the CRaTER detector. J. Acta Astronaut. 2009, 66, 643–647. [Google Scholar] [CrossRef]
- Porter, J.A.; Townsend, L.W.; Spence, H.; Golightly, M.; Schwadron, N.; Kasper, J.; Case, A.W.; Blake, J.B.; Zeitlin, C. Radiation environment at the Moon: Comparisons of transport code modeling and measurements from the CRaTER instrument. J. Space Weather 2014, 12, 329–336. [Google Scholar] [CrossRef] [Green Version]
- Looper, M.D.; Mazur, J.E.; Blake, J.B.; Spence, H.E.; Schwadron, N.A.; Golightly, M.J.; Case, A.W.; Kasper, J.C.; Townsend, L.W. The radiation environment near the lunar surface: CRaTER observations and Geant4 simulations. J. Space Weather 2013, 11, 142–152. [Google Scholar] [CrossRef] [Green Version]
- Spence, H.E.; Golightly, M.J.; Joyce, C.J.; Looper, M.D.; Schwadron, N.A.; Smith, S.S.; Townsend, L.W.; Wilson, J.; Zeitlin, C. Relative contributions of galactic cosmic rays and lunar proton “albedo” to dose and dose rates near the Moon. J. Space Weather 2013, 11, 643–650. [Google Scholar] [CrossRef]
- Zaman, F.; Townsend, L.W.; Wouter, C.; Schwadron, N.A.; Spence, H.E.; Wilson, J.K.; Jordan, A.P.; Smith, S.S.; Looper, M.D. Absorbed doses from GCR and albedo particles emitted by the lunar surface. Acta Astronaut. 2020, 175, 185–189. [Google Scholar] [CrossRef]
- Farmer, C.; Charara, Y.M.; Townsend, L.W. LET spectra of iron particles on A-150: Model predictions for the CRaTER detector. In Proceedings of the 37th International Conference on Environmental Systems, Chicago, IL, USA, July 2007. [Google Scholar]
- Charara, Y.M. Characterization of the cosmic ray telescope for the effects. Ph.D. Dissertation, Department of Nuclear Engineering, University of Tennessee, Knoxville, TN, USA, 2008. [Google Scholar]
- Anderson, J.A.; Townsend, L.W. LET comparisons for the CRaTER instrument on LRO and HETC-HEDS. In Proceedings of the 2011 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011. [Google Scholar]
- Anderson, J.A.; Townsend, L.W. Dose estimates for the CRaTER instrument on LRO using HETC-HEDS. In Proceedings of the 56th Annual Meeting of Health Physics Society, West Palm Beach, FL, USA, 26–30 June 2011. [Google Scholar]
- Slaba, T.C.; Blattnig, S.R.; Badavi, F.F. Faster and more accurate transport procedures for HZETRN. J. Comput. Phys. 2010, 229, 9397–9417. [Google Scholar] [CrossRef] [Green Version]
- Sato, T.; Iwamoto, Y.; Hashimoto, S.; Ogawa, T.; Furuta, T.; Abe, S.; Kai, T.; Tsai, P.; Ratliff, H.; Matsuda, N.; et al. Features of Particle and Heavy Ion Transport code System (PHITS) version 3.02. J. Nucl. Sci. Technol. 2018, 55, 684–690. [Google Scholar] [CrossRef] [Green Version]
- Sihver, L.; Sato, T.; Puchalska, M.; Reitz, G. Simulations of the MATROSHKA experiment at the international space station using PHITS. Radiat. Environ. Biophys. 2010, 49, 351–357. [Google Scholar] [CrossRef] [PubMed]
- Bahadori, A.A.; Sato, T.; Slaba, T.C.; Shavers, M.R.; Semones, E.J.; Van Baalen, M.; Bolch, W.E. A comparative study of space radiation organ doses and associated cancer risks using PHITS and HZETRN. Phys. Med. Biol. 2013, 58, 7183–7207. [Google Scholar] [CrossRef]
- Heilbronn, L.H.; Borak, T.B.; Townsend, L.W.; Tsai, P.E.; Burnham, C.A.; McBeth, R.A. Neutron yields and effective doses produced by Galactic Cosmic Ray interactions in shielded environments in space. Phys. Med. Biol. 2015, 7, 90–99. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.W. Transport Methods and Interactions for Space Radiations; NASA RP 1257; NASA: Washington, DC, USA, 1991. [Google Scholar]
- Slaba, T.C.; Whitman, K. The Badhwar-O’Neill 2020 GCR Model. Space Weather 2020, 18, e2020SW002456. [Google Scholar] [CrossRef]
- Nara, Y.; Otuka, N.; Ohnishi, A.; Niita, K.; Chiba, S. Relativistic nuclear collisions at 10A GeV energies from p + Be to Au + Au with the hadronic cascade model. Phys. Rev. 1999, 61, 024901. [Google Scholar]
- Niita, K.; Chiba, S.; Maruyama, T.; Maruyama, T.; Takada, H.; Fukahori, T.; Nakahara, Y.; Iwamoto, A. Analysis of the (N,xN’) reactions by quantum molecular dynamics plus statistical decay model. Phys. Rev. 1995, 52, 2620. [Google Scholar] [CrossRef] [Green Version]
- Case, A.W.; Kasper, J.C.; Spence, H.E.; Zeitlin, C.J.; Looper, M.D.; Golightly, M.J.; Schwadron, N.A.; Townsend, L.W.; Mazur, J.E.; Blake, J.B.; et al. The deep-space galactic cosmic ray lineal energy spectrum at solar minimum. Space Weather 2013, 11, 361–368. [Google Scholar] [CrossRef] [Green Version]
- Turner, J.T. Atoms, Radiation, and Radiation Protection; Wiley-VCH: Weinheim, Germany, 2004; ISBN 0–471-59581-0. [Google Scholar]
- Townsend, L.W.; Miller, T.M.; Gabriel, T.A. HETC radiation transport code development for cosmic ray shielding applications in space. Radiat. Prot. Dosim. 2005, 116, 135–139. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.W.; Shinn, J.L.; Townsend, L.W.; Tripathi, R.K.; Badavi, F.F.; Chun, S.Y. NUCFRG2: A semiempirical nuclear fragmentation model. Nucl. Instrum. Methods Phys. Res. 1994, 94B, 95–102. [Google Scholar] [CrossRef]
- Miller, T.M.; Townsend, L.W. Double differential heavy ion production cross sections. Radiat. Prot. Dosim. 2004, 110, 53–60. [Google Scholar] [CrossRef]
- Charara, Y.M.; Townsend, L.W.; Gabriel, T.A.; Zeitlin, C.J.; Heilbronn, L.H.; Miller, J. HETC-HEDS code validation using laboratory beam energy loss spectra data. IEEE Trans. Nucl. Sci. 2008, 55, 3164–3168. [Google Scholar] [CrossRef]
- Heinbockel, J.H.; Slaba, T.C.; Blattnig, S.R.; Tripathi, R.K.; Townsend, L.W.; Handler, T.; Gabriel, T.A.; Pinsky, L.S.; Reddell, B.; Clowdsley, M.S.; et al. Comparison of the transport codes HZETRN, HETC, and FLUKA for a solar particle event. Adv. Space Res. 2011, 47, 1079–1088. [Google Scholar] [CrossRef]
- Heinbockel, J.H.; Slaba, T.C.; Tripathi, R.K.; Blattnig, S.R.; Norbury, J.W.; Badavi, F.F.; Townsend, L.W.; Handler, T.; Gabriel, T.A.; Pinsky, L.S.; et al. Comparison of the transport codes HZETRN, HETC, and FLUKA for galactic cosmic rays. Adv. Space Res. 2011, 47, 1089–1105. [Google Scholar] [CrossRef]


| Component | Material | Thickness (mm) |
|---|---|---|
| S1 | Aluminum | 0.813 |
| V1 | Void | 2.363 |
| D1 | Silicon | 0.148 |
| V2 | Void | 3.360 |
| D2 | Silicon | 1.000 |
| V3 | Void | 3.943 |
| A1 | A-150 | 53.97 |
| V4 | Void | 3.554 |
| D3 | Silicon | 0.149 |
| V5 | Void | 3.568 |
| D4 | Silicon | 1.000 |
| V6 | Void | 11.90 |
| A2 | A-150 | 26.98 |
| V7 | Void | 11.90 |
| D5 | Silicon | 0.149 |
| V8 | Void | 3.060 |
| D6 | Silicon | 1.000 |
| V9 | Void | 2.362 |
| S2 | Aluminum | 0.811 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaman, F.A.; Townsend, L.W.; de Wet, W.C.; Burahmah, N.T. The Lunar Radiation Environment: Comparisons between PHITS, HETC-HEDS, and the CRaTER Instrument. Aerospace 2021, 8, 182. https://doi.org/10.3390/aerospace8070182
Zaman FA, Townsend LW, de Wet WC, Burahmah NT. The Lunar Radiation Environment: Comparisons between PHITS, HETC-HEDS, and the CRaTER Instrument. Aerospace. 2021; 8(7):182. https://doi.org/10.3390/aerospace8070182
Chicago/Turabian StyleZaman, Fahad A., Lawrence W. Townsend, Wouter C. de Wet, and Naser T. Burahmah. 2021. "The Lunar Radiation Environment: Comparisons between PHITS, HETC-HEDS, and the CRaTER Instrument" Aerospace 8, no. 7: 182. https://doi.org/10.3390/aerospace8070182
APA StyleZaman, F. A., Townsend, L. W., de Wet, W. C., & Burahmah, N. T. (2021). The Lunar Radiation Environment: Comparisons between PHITS, HETC-HEDS, and the CRaTER Instrument. Aerospace, 8(7), 182. https://doi.org/10.3390/aerospace8070182






