Abstract
The optimal design of the propulsion system for a potential Mars Ascent Vehicle is analyzed, in the context of the Mars Sample Return Mission. The Mars Ascent Vehicle has to perform an initial ascent phase from the surface and then circularize into a 170 km orbit. A two-stage launcher is taken into account: the same hybrid rocket engine is considered for both stages in order to limit the development costs. A cluster of two, three or four engines is employed in the first stage, whereas a single engine is always used in the second stage. Concerning the feeding system, three alternatives are taken into consideration, namely a blow down, a regulated and an electric turbo-pump feed system. The latter employs an electric motor to drive the oxidizer turbopump, whereas the power is supplied to the motor by lithium batteries. All the design options resulted in viable Mars Ascent Vehicle configurations (payloads are in the range of 70–100 kg), making the hybrid alternative worth considering for the sample return mission. The use of an electric turbo-pump feed system determines the highest vehicle performance with an estimated 10–25% payload gain with respect to gas-pressure feed systems.
1. Introduction
Hybrid Rocket Engines (HREs) are suitable for the replacement of both Solid Rocket Motors (SRMs) and Liquid Rocket Engines (LREs) in many applications [1,2,3] due to their high performance, which is close to that of storable liquid propellants. In addition, the physical separation of the solid fuel and the liquid oxidizer until ignition results in intriguing features, such as high safety and reliability, low costs of manufacturing and operation, throttle ability and shut-down/restart capabilities. In the present work, the feasibility of a hybrid powered Mars Ascent Vehicle (MAV) for the return of samples from Mars’s surface is considered and analyzed.
The use of HREs has already been proposed for sample return missions [4,5,6,7,8,9,10,11], but at the moment, the baseline plan for the human exploration of Mars provides for only traditional liquid rocket propulsion [12]. The liquid propellant concept envisages the production in situ of the Liquid OXygen (LOX), employed as oxidizer, from carbon dioxide in Mars’ atmosphere, whereas the liquid methane, used as fuel, is carried from Earth. An analogous concept can be used for an HRE employing in situ-produced LOX and paraffin-based wax as propellants [13,14].
On the other hand, the peculiar combustion process of hybrids bounds the solid fuel grain design and the oxidizer flow control strategy during operation. Given the propellant combination, the delivered specific impulse depends on the choice of chamber pressure and mixture ratio. The latter varies during operation because the fuel flow coming from the solid grain is a function of both grain port area and burning surface, which evolve even if a constant oxidizer mass flow is used. This phenomenon is the so-called mixture ratio shifting typical of HREs. The characteristics of the propellants combination (density, thermo-chemical properties as a function of the mixture ratio and regression rate) are also of concern in the search for the optimal design, making the optimization process quite tricky. Moreover, a strict relationship exists between design trajectory and operation optimization in HREs due to their peculiar one-lever control mechanism. Therefore, a coupled optimization of the engine design and ascent trajectory is required and performed here by means of a hybrid optimization procedure that combines an indirect trajectory optimization method with a direct approach for the optimization of the engine design parameters [15].
In previous works, similar approaches have been applied aiming at the upgrade of existing launchers, and/or those under development, that use SRMs and/or storable LREs in the upper stages [2,3,16,17,18]. In Reference [19], different HRE design options (number of engines per stage, feed system, etc.) for MAV have been compared. In particular a simple blow-down type and a partially regulated system have been taken into account as feed system options. The use of electrically driven turbo-pump feed systems was beneficial, in terms of payload, when compared to simpler gas pressurized systems in previous hybrid applications [20,21]. In the proposed feed system, a battery-powered electric motor is used to drive a turbo-pump. Despite the relatively limited power and energy density of today’s batteries, this solution has already been applied to bipropellant LREs, solving the small-scale turbine issues of gas cycles (e.g., see the Rutherford engine used to power the Rocket Lab’s Electron launch vehicle [22,23]). Moreover, the use of electric pump is even more appealing for HREs, since the presence of just one liquid propellant makes it difficult to produce a working fluid for the turbine [24]. Thus, in the present work, the viability of a two-stage MAV for sample return mission is discussed, in which electric turbo-pumps are employed in the feed system. Benefits of electric turbo-pump feed systems with respect to gas-pressure feed systems are evaluated. Results are presented in Section 4 after presenting the needed modeling and optimization procedures in Section 2 and Section 3.
2. Engine Design and Optimization
The chosen propellants combination is LOX/paraffin-based wax. This choice is driven by the large regression rate value and promising performance shown when employed in sounding rockets and upper stages [25,26]. Moreover, oxygen can be extracted from Mars’ atmosphere, making in situ exploitation of resources a viable option.
A chamber pressure is assumed in the evaluation of the performance of the propellants as the mixture ratio varies [27]. Even though the actual chamber pressure can span over a wide range during engine operations, the error due to the constant-pressure assumption is small for the value of chamber pressures and mixture ratios considered in this work. The characteristic velocity is evaluated assuming an ideal frozen equilibrium expansion, i.e., an isentropic expansion without changes in the chemical composition of the gas mixture throughout the nozzle. Moreover, a -efficiency equal to 0.96 is introduced, taking into account the low overall combustion efficiency typical of HREs [28]. The dependence of the characteristic velocity and the specific heat ratio on mixture ratio is modeled by means of third-degree polynomial curves fitting, which are directly embedded in the code. Once the nozzle area expansion ratio and the ambient pressure are given, the thrust coefficient can be computed assuming constant specific heat ratio, isentropic expansion and a 0.98 -efficiency. The latter is introduced in order to take losses into account [28]. The relatively high regression rate of the chosen propellants combination allows for a cylindrical grain with a single circular port. A uniform regression rate along the port axis is considered, and its value is given by the time derivative of the port radius as reported in Equation (1).
where the coefficient and exponent when SI units are used [29,30]. The pyrolisis of the lateral ends of the grain is neglected. The presence of pressure losses inside the combustion chamber is taken into account by relating the chamber head-end pressure to the chamber/nozzle stagnation pressure by means of an approximate relation similar to that proposed by Barrere et al. for side-burning grains (see Equation (2)) [31].
Equation (3) provides the oxidizer flow rate during operation, under the assumption of constant hydraulic resistance Z in the oxidizer flow path from the tank and incompressible turbulent flow.
On the other hand, the fuel mass flow and the propellant mixture ratio are given by Equations (4) and (5).
The chamber stagnation pressure at nozzle entrance is determined assuming an isentropic expansion as reported in Equation (6).
Three options for the feed systems are considered: blow down, partially regulated and electric turbo-pump. In the partially regulated case, the burn starts with a constant tank pressure phase, followed by blow-down operation. Five parameters define the design of the HRE in the proposed ballistic model, namely initial thrust (evaluated on Mars’s surface), initial mixture ratio , nozzle expansion ratio , initial value of feed system pressure and initial gas volume in the oxidizer tank (ullage volume) . For the regulated feed system and the turbo-pump feed system, the initial ullage volume is fixed at 3% of the oxidizer volume in order to grant a regular response at engine ignition. The initial value of feed system pressure is equal to for the gas pressurized feed systems, whereas the initial discharge pressure provided by the pump has to be considered for the turbo-pump operation. In the partially regulated case, is replaced as optimization variable by , which stands for the amount of oxidizer that has been exhausted when the blow down phase starts (that is, the oxidizer exhausted during the regulated phase).
The initial value of the chamber pressure is fixed and such that . During operation, the actual ratio is not constant, but the assumed initial ratio is able to grant for the whole engine burn, avoiding the coupling between the engine and the oxidizer feed system. In order to avoid excessive pressure losses and nonuniform grain regression, a fixed value of the initial port area to throat area is assumed, although a larger value could result in better performance. The optimized initial thrust was shown to be very large in preliminary calculations. Therefore, was dropped from the optimization parameters and its value was imposed.
Given the aforementioned set of design parameters, the engine and grain initial characteristics and performance are determined. The initial values of and at engine ignition are given by , and can be computed from . Knowing the ambient pressure , the thrust coefficient and can then be calculated. The initial thrust fixes the propellants mass flow rates at ignition as reported by Equation (7).
The throat area can be determined from the aforementioned Equation (6). In this context, throat erosion effects are neglected, and thus . This assumption is adopted due to the preliminary nature of the present analysis, albeit easily managed by the proposed optimization procedure [25,26]. The initial port area and radius are calculated as and the initial burning area is determined from Equation (4). The grain length is obtained as reported in Equation (8), completely specifying the initial grain geometry.
The feed system pressure rules engine operation. During blow down operation, it is calculated assuming an isentropic expansion of the pressurizing gas in the tank, as described by Equation (9).
where is the auxiliary gas volume in the propellant tank at the start of the blow-down phase, and is its value at the generic time t. In the simpler blow-down feed system, one has and , whereas when the regulated feed system is considered.
In the turbo-pump feed system, an electric motor drives the pump that feeds the oxidizer into the combustion chamber. The power available is assumed as constant during operation and thus determined by Equation (10), considering the initial values of discharge pressure and oxidizer flow rate .
In this context, the authors assume during operation and neglect the small amount of pressurizing gas mass required to keep constant during engine burn. The pump power is held as fixed during operation, and Equation (10) provides the feed pressure as a function of the oxidizer flow rate. Thus, in the electric turbo-pump case, the number of the optimization variable is equal to four, because is fixed and no additional parameters are required to determine the oxidizer flow rate during operation. In the conversion process of electrical energy into flow head rise, the authors assume an overall efficiency [32].
Solid fuel geometry and oxidizer-exhausted mass can be computed by the numerical integration of Equations (1) and (3) during engine operation, also providing the tank pressure in the gas-pressurized cases. The regression rate, the propellant flow rates (and their ratio ), and are determined numerically by solving Equations (1)–(6) and using the fitting for as a function of . The thrust level is calculated once is known at the actual altitude, allowing for trajectory integration. One can then compute the grain outer radius and the grain web thickness w at engine burnout. At this point, the overall propellant mass is known and structural masses can be estimated in order to compute the launcher payload, which is the optimization merit function to be maximized.
The engine and stage length is given by the sum of the lengths of oxidizer tank, grain and nozzle. In addition, the helium tank comprises the regulated feed system. A 1-mm-thick cylindrical aluminum casing encapsulates each stage, and the case diameter is fixed by the oxidizer tank diameter, which is assumed as equal to the combustion chamber diameter in the blow down case or to the auxiliary gas tank diameter in the regulated case. A 6 mm insulating liner (with density equal to that of the solid fuel) is taken into account in the combustion chamber, together with an aluminum alloy cylindrical wall. Aluminum is also employed for the cylindrical oxidizer tank. The walls’ thicknesses are determined to withstand the internal pressure in the oxidizer tank and combustion chamber, assuming a safety factor equal to 1.25. In addition, a lower limit of 0.5 mm is imposed. A 45 deg convergent and a 20 deg divergent nozzle are taken into account, assuming a phenolic silica ablative layer. The thickness is considered as uniform and evaluated according to Reference [33]. The ablative layer mass estimation is conservative, and thus the small nozzle structural mass is negligible. In the end, the authors neglect the mass of interstage adapters and separation mechanism. It is worth noting that different architectures could be considered for the engine (e.g., multiple oxidizer tanks surrounding the combustion chamber, instead of a single tank stacked on top of it) characterized by different values of the dry mass. The optimization of the system architecture is assumed to be a possible growth margin whose evaluation is beyond the scope of the present article, which only aims at demonstrating the feasibility of a hybrid MAV and evaluating benefits derived from the use of electric turbo-pumps.
In the electric turbo-pump feed system, the power required by the electric motor that drives the pump is provided by batteries. The masses of the pump, electric motor and batteries are calculated by means of typical power density (power to mass ratio) values, which are provided by existing literature. The electric motor and pump mass are evaluated as reported in Equation (11), where is the maximum electrical power required, which is given by the initial discharge pressure (which is an optimization variable) and oxidizer flow rate at ignition.
has been assumed for the evaluation of the electric drive system plus the pump mass [32]. The batteries’ mass is constrained by the most stringent between two requirements: the maximum electrical power required and the total electrical energy needed to drive the pump for the whole engine burning time , which is given by Equation (12).
The batteries’ mass can thus be evaluated by means of Equation (13), where a power density , an energy density (energy-to-mass ratio) and a safety factor of 1.2 are considered [32].
The reader can notice that the power-constrained mass is known before the actual trajectory is optimized, depending only on the pump power level, which in turn is a function of the initial discharge pressure (i.e., of a design variable). On the contrary, the energy-constrained mass has to be computed “a posteriori” because the actual burning time is not know before trajectory optimization. For this reason, a characteristic burn time is defined, which represents the simultaneous fulfillment of both constraints. The battery mass is given by the power constraint when (i.e., shorter missions), whereas the energy constraint is binding when (i.e., longer missions). In the latter case, the batteries’ mass has to be checked “a posteriori” to take into account the energy surplus required.
A direct method optimizes the engine design parameters once initial tentative values for the design parameters are provided [34]. Then, given the engine design, the fast and accurate indirect procedure computes the optimal trajectory, and the corresponding payload is known. The computation of engine design and optimal trajectory for a given set of design parameters requires only few seconds on a modern personal computer. The initial values of the design parameters are then varied by small quantities in order to numerically evaluate the derivatives of the performance index (i.e., launcher payload) with respect to the design parameters. A procedure based on Newton–Raphson’s method is employed in the determination of the set of design parameters that simultaneously nullify every index partial derivatives. Only a few minutes are required to obtain the optimal design and the corresponding optimized trajectory.
3. Rocket Configurations and Trajectory Optimization
In this work, a two-stage MAV is considered, and the same HRE is employed in both the stages. engines are used in the first stage, where , whereas a single HRE is present in the second stage (i.e., ). This strategy allows for a reduction in the development cost of the hybrid engines when compared to the use of different engines in each stage.
The ascent trajectory is split into several phases: (1) vertical ascent (followed by an instantaneous velocity rotation) and (2) zero-lift gravity-turn ascent until the first stage is exhausted and jettisoned (3) coast arc and (4) second-stage burn with optimal thrust direction until insertion into the desired orbit. Phases (2) and (4) are further divided into two sub-phases when the regulated feed system is employed, corresponding to constant tank pressure, i.e., (2a) and (4a), and then blow down engine operation, i.e., (2b) and (4b). The optimization aims at the maximization of the launcher payload mass , which is equal to the second-stage final mass minus its inert mass. The j-th phase starts at time and ends at . The launcher is modeled as a point-mass rocket, and the state equations in an inertial Mars-centered reference frame, coded in non-dimensional form to improve the integration numerical accuracy, are: improve the integration’s numerical accuracy, are
where an inverse-square gravity field is assumed and is the aerodynamic drag, which is regarded as independent from the value of the payload mass in the present approach. For each sub-rocket, the reference cross section is a function of the rocket diameter d and the number of hybrid engines N, i.e., . The aerodynamic drag coefficient of both stages is calculated as a function of the Mach number by means of the typical law for rockets reported in Figure 1.
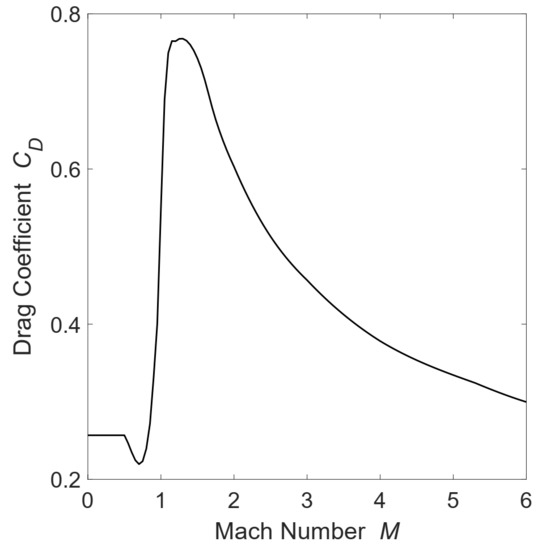
Figure 1.
Drag coefficient.
It is worth noting that, due to the thinness of Mars’s atmosphere, the drag influence on rocket performance is practically negligible. The relative velocity can be computed as , where stands for Mars’s angular velocity. The thrust F is written as a function of the vacuum thrust as reported in Equation (15), where, once the engine design has been specified, is a given function of time.
The computation of aerodynamic drag D and thrust F require the knowledge of ambient density and pressure , respectively, as functions of rocket altitude h. Thus, the authors employ numerical fits of pressure and temperature of Mars’s atmosphere according to a simplified model. These fits are reported as Equations (16) and (17), where SI units (K, Pa and m) are employed. The atmospheric density is then computed by means of the perfect gas equation.
The initial values (i.e., at ) of the problem state variables (position, velocity and rocket mass) and the altitude at the end of the first phase (vertical ascent) are prescribed by the problem boundary conditions, whereas at the final time , a circular orbit of assigned altitude is imposed. The use of the same engine in both stages introduces the additional condition because the burning time of the first and second stage must be equal. In addition, is added, to the boundary conditions when the regulated feed system is employed.
Given the engine performance, the optimal trajectory is found applying the theory of optimal control. Adjoint variables are associated to the state equations and the Hamiltonian, whose formal expression depends on the phase of flight, can be written as reported in Equation (18).
Euler–Lagrange equations are then provided by the Optimal Control Theory (OCT) for the adjoint variables, as shown in Equation (19).
In this work, the thrust is vertical during phase (1), parallel to the relative velocity during phase (2), zero during phase (3) (coasting) and free and optimized during phase (4). The thrust direction during phase (4) is provided by the OCT, which is shown to be parallel to the velocity adjoint vector, also named the primer vector. Boundary conditions for optimality, at the initial and final point and at the boundaries of each phase, are given by the OCT [35]. The velocity adjoint vector must be parallel to the velocity vector just after the velocity turn. Moreover, the transversality conditions are provided by the OCT and allow for the determination of the relevant times. The latter are somewhat complex because thrust and specific impulse are time-dependent in HREs. Thus, their derivation is detailed in the following. The time dependencies of vacuum thrust and specific impulse make the Hamiltonian not constant, and additional virtual equations for , c, and port radius R are introduced (see Equations (20)–(23)),
where the functions in the RHS of Equations (20)–(23) are given, albeit implicit, functions of R and . Then, the augmented Hamiltonian can be defined as , and the related transversality conditions are reported as Equation (24).
This formulation makes the augmented Hamiltonian explicitly independent from time and therefore piecewise constant. One has and and the transversality conditions become and . , c, , and R do not appear in the boundary conditions at and ; thus, the corresponding adjoint variables are null and . Hence, the aforementioned transversality conditions are equivalent to (i.e., the Hamiltonian is zero during the coast arc) and (i.e., the Hamiltonian has the same magnitude but different sign at the end of the burns). In the end, it is worth noting that the evaluations of the augmented Hamiltonian and of the additional adjoint variables are actually not necessary. The application of the OCT generates a multipoint boundary value problem, which is solved by a procedure based on Newton’s method [36].
4. Results
Concerning the roadmap for Mars exploration, the return of a sample from the surface of Mars would be a milestone and a very important scientific achievement. The use of HREs has been already proposed in the past [4,5,6,7,8,9,10,11], and the comparison of several design options is the main focus of the present work. The initial mass of the MAV is here fixed and equal to 500 kg, whereas the expected payload is expected to be in the 75–100 kg range. Motion on the Mars equatorial plane and ascent to a 170 km circular orbit are considered. The best value of has been discussed in a previous work on the same topic and was shown to fall between 2 and 3 for the sample return mission [19]. In addition, is investigated in the present work. The three feed systems, described in the previous sections, are analyzed, and their performance is compared. Table 1 and Table 2 report the launcher mass budget and performance. The length-to-diameter ratio of each stage is below 10 for every feed system and first-stage option, allowing for vertically stacked stages.

Table 1.
Overall MAV mass budget and performance. BD, R and TP stand for blow down, regulated and turbo pump feed system, respectively.

Table 2.
Hybrid engine design. BD, R and TP stand for blow down, regulated and turbo pump feed system, respectively. The sixth column () reports the sum of electrical components masses (motor, pump and batteries) when the turbo pump feed system is employed.
Concerning the gas-pressurized systems, the highest payload masses are obtained for and 3, when the blow-down and regulated feed systems are, respectively, used. solutions exhibit for both cases reduced velocity losses and smaller dry mass for the single HRE used in the stage. However, the most relevant effect is related to the non-uniform acceleration distribution, thus resulting in lower performance in terms of payload for . The use of a regulated feed system improves the performance with respect to the blow down case due to the lower dry mass. This improvement is mainly due to the lower initial tank pressures, which allows for lighter oxidizer tanks. Moreover, the use of the regulated system results in a less-steep ascent trajectory during the constant pressure operation with respect to the blow down cases, which is more efficient in terms of velocity losses. The mixture ratio shifting is present in both blow-down and regulated solutions, albeit being more severe in the regulated case, as reported in Figure 2.
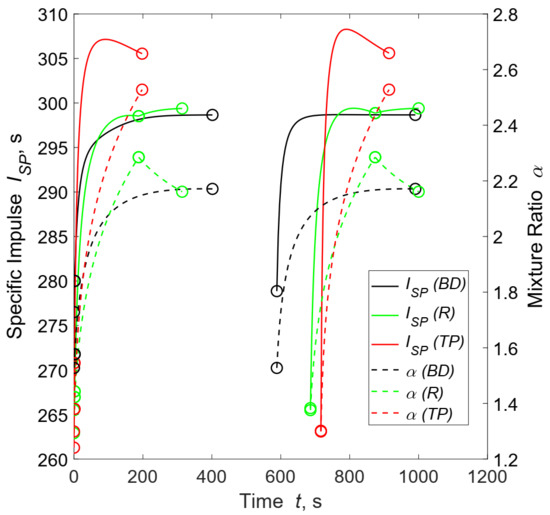
Figure 2.
Specific impulse and mixture ratio histories for the best solution of each feed system. The BD solution was obtained with and R and TP solutions with .
The electric turbo-pump feed system further reduces the system dry mass and improves the payload due to the absence of pressurization in the oxidizer tanks, despite the additional masses of the electric components required. The highest payload is obtained for , as in the regulated case. The initial thrust of this solution is far greater than blow-down or regulated ones, as reported in Figure 3. This optimization strategy seems to be caused by the relatively small increase in electric components masses resulting from high thrust levels, whereas an analogous strategy would be extremely penalizing in terms of engine dry mass in the gas-pressurized cases. As a consequence, the engine burn is shorter and the trajectory steeper, as shown in Figure 4, resulting in relevant decreases in gravitational and aerodynamic losses (see the last column of Table 1).
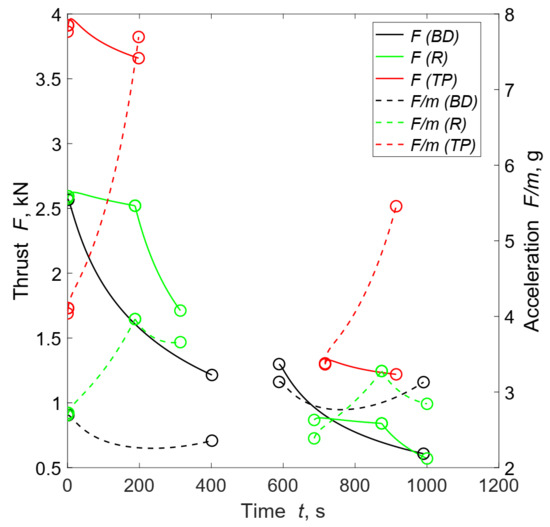
Figure 3.
Thrust F and longitudinal acceleration histories for the best solution of each feed system. The BD solution was obtained with and R and TP solutions with .
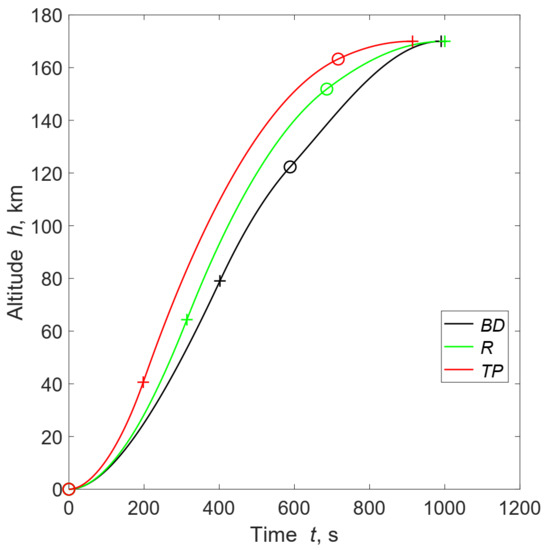
Figure 4.
Trajectory for the best solution of each feed system. The BD solution was been obtained with and R and TP solutions with . The dots and crosses represent the stages ignition and burnout, respectively.
5. Conclusions
In this work, the design and optimization of a HRE suitable for a MAV have been analyzed in the context of a sample return mission. A multi-disciplinary approach has been employed: an indirect method optimizes the ascent trajectory given the engine design, which is in turn optimized by a direct optimization method. Several feed system options and first-stage configurations have been taken into account and the resulting performance compared. The results demonstrated the feasibility of a hybrid MAV concept, being the payload masses comparable to those provided by heritage LREs envisaged for such mission. Hence, hybrids are an option worth considering, also taking into account their intrinsic simplicity and low cost. The results also show that the use of an electric turbo-pump feed system is able to grant a remarkable increase in payload, although issues related to the lower technological readiness level, with respect to more consolidated feed systems, should be considered. The proposed procedure represents a powerful and efficient means for a preliminary but accurate design and estimation of performance of the hybrid propulsion system. The time required by the whole computation is relatively short even on an everyday personal computer, making the procedure suitable for fast evaluation of trade-offs. In order to increase the accuracy of this approach, future developments will include more precise aerodynamic modeling of the subrockets and structural weights estimation alongside a throat erosion model.
Author Contributions
Conceptualization, L.C., F.M. and D.P.; Formal analysis, L.C., F.M. and D.P.; Methodology, L.C., F.M. and D.P.; Supervision, L.C. and D.P.; Writing—original draft, F.M.; Writing—review and editing, L.C., F.M. and D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BD | Blow Down |
| LRE(s) | Liquid Rocket Engine(s) |
| LOX | Liquid OXygen |
| MAV | Mars Ascent Vehicle |
| R | Regulated |
| RHS | Right-Hand Side |
| SRM(s) | Solid Rocket Motor(s) |
| TP | Turbo Pump |
| Nomenclature | |
| burning surface area, m | |
| port area, m | |
| nozzle throat area, m | |
| a | regression constant, m kg s |
| thrust coefficient | |
| characteristic velocity, m/s | |
| drag vector, N | |
| d | rocket outer diameter, m |
| thrust vector, N | |
| F | thrust, N |
| G | gravitational constant, Nm/kg |
| gravity acceleration, m/s | |
| H | Hamiltonian |
| h | altitude, km |
| mean specific impulse, s | |
| J | throat area to initial port area ratio |
| L | overall engine length, m |
| fuel grain length, m | |
| M | rocket mass, kg |
| m | mass, kg |
| engines number in the first stage | |
| n | mass-flux exponent |
| electric power, kW | |
| p | pressure, bar |
| position vector, m | |
| t | time, s |
| T | temperature, K |
| V | volume, m |
| velocity vector, m/s | |
| w | web thickness, m |
| y | burning distance, m |
| Z | hydraulic resistance, 1/(kg m) |
| mixture ratio | |
| specific heat ratio | |
| electric motor and pump power density, kW/kg | |
| batteries energy density, Wh/kg | |
| batteries power density, kW/kg | |
| nozzle area ratio | |
| electric motor and pump efficiency | |
| adjoint variable | |
| payload, kg | |
| density, kg/m | |
| Superscripts | |
| time derivative | |
| * | characteristic |
| Subscripts | |
| 1 | combustion chamber at head-end |
| atmospheric | |
| average | |
| combustion chamber | |
| d | discharge |
| dry | |
| e | nozzle exit |
| electric motor and pump | |
| F | fuel |
| f | final |
| feed system | |
| i | initial value |
| maximum | |
| minimum | |
| n | nozzle |
| O | oxidizer |
| p | overall propellant (oxidizer + fuel) |
| relative | |
| residual | |
| t | oxidizer propellant tank |
| throat | |
| total | |
References
- Casalino, L.; Pastrone, D. Optimal Design of Hybrid Rocket Motors for Microgravity Platform. J. Propuls. Power 2008, 24, 491–498. [Google Scholar] [CrossRef]
- Casalino, L.; Pastrone, D. Optimal Design of Hybrid Rocket Motors for Launchers Upper Stages. J. Propuls. Power 2010, 26, 421–427. [Google Scholar] [CrossRef]
- Casalino, L.; Pastrone, D. Optimization of Hybrid Sounding Rockets for Hypersonic Testing. J. Propuls. Power 2012, 28, 405–411. [Google Scholar] [CrossRef]
- Chandler, A.; Cantwell, B.; Hubbard, G.S.; Karabeyoglu, A. A Two-Stage, Single Port Hybrid Propulsion System for a Mars Ascent Vehicle. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010. [Google Scholar] [CrossRef]
- Chandler, A.A.; Cantwell, B.J.; Hubbard, G.S.; Karabeyoglu, A. Feasibility of a Single Port Hybrid Propulsion System for a Mars Ascent Vehicle. Acta Astronaut. 2011, 69, 1066–1072. [Google Scholar] [CrossRef]
- Sopegno, L.; Valavanis, K.P.; Rutherford, M.J.; Casalino, L. Mars Sample Return Mission: Mars Ascent Vehicle Propulsion Design. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–9. [Google Scholar] [CrossRef]
- McCollum, L.T.; Schnell, A.; Yaghoubi, D.; Bean, Q.; McCauley, R.; Prince, A. Development Concepts for Mars Ascent Vehicle (MAV) Solid and Hybrid Vehicle Systems. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Karp, A. Hybrid Rocket Propulsion for a Low Temperature Mars Ascent Vehicle. In Proceedings of the Lecture Held at Jet Propulsion Laboratory, National Aeronautics and Space, Pasadena, CA, USA, 13 March 2017. [Google Scholar]
- Oglesby, B.; Prince, A.; Story, G.; Kam, A. Qualification of a Hybrid Propulsion System for a Mars Ascent Vehicle. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–7. [Google Scholar]
- Evans, B.; Cantwell, B. Development and testing of SP7 fuel for mars ascent vehicle application. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–11. [Google Scholar]
- Muirhead, B.K.; Karp, A. Mars Sample Return Lander Mission Concepts. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–9. [Google Scholar]
- Drake, B.G. (Ed.) Human Exploration of Mars Design Reference Architecture 5.0; NASA-SP-2009-566; NASA: Washington, DC, USA, 2009. [Google Scholar]
- Boiron, A.J.; Cantwell, B. Hybrid Rocket Propulsion and in situ Propellant Production for Future Mars Missions. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013; p. 3899. [Google Scholar] [CrossRef] [Green Version]
- Shotwell, R.; Benito, J.; Karp, A.; Dankanich, J. Drivers, developments and options under consideration for a Mars ascent vehicle. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–14. [Google Scholar]
- Casalino, L.; Pastrone, D. Optimal Design and Control of Hybrid Rockets for Access to Space. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Tucson, AZ, USA, 10–13 July 2005. [Google Scholar] [CrossRef]
- Pastrone, D.; Casalino, L. Optimal Robust Design of Hybrid Rocket Engines. In Space Engineering; Springer: Berlin/Heidelberg, Germany, 2016; Volume 114, pp. 269–285. [Google Scholar] [CrossRef]
- Casalino, L.; Masseni, F.; Pastrone, D. Robust Design Approaches for Hybrid Rocket Upper Stage. J. Aerosp. Eng. 2019, 32. [Google Scholar] [CrossRef]
- Casalino, L.; Masseni, F.; Pastrone, D. Uncertainty Analysis and Robust Design for a Hybrid Rocket Upper Stage. J. Spacecr. Rockets 2019, 56, 1424–1431. [Google Scholar] [CrossRef]
- Casalino, L.; Pastrone, D. Optimization of Hybrid Propellant Mars Ascent Vehicle. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar] [CrossRef]
- Casalino, L.; Pastrone, D. Optimization of a Hybrid Rocket Upper Stage with Electric Pump Feed System. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010. [Google Scholar] [CrossRef]
- Casalino, L.; Masseni, F.; Pastrone, D. Viability of an Electrically Driven Pump-fed Hybrid Rocket for Small Launcher Upper Stages. Aerospace 2019, 6, 36. [Google Scholar] [CrossRef] [Green Version]
- Morring, F.J.; Norris, G. Rocket Lab Unveils Battery-Powered Turbomachinery. Available online: http://aviationweek.com/space/rocket-lab-unveils-battery-powered-turbomachinery (accessed on 21 June 2021).
- Bailey, M. Frequent and Reliable Launch for Small Satellites: Rocket Lab’s Electron Launch Vehicle and Photon Spacecraft. In Handbook of Small Satellites: Technology, Design, Manufacture, Applications, Economics and Regulation; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–17. [Google Scholar]
- Gegeoglu, K.; Kahraman, M.; Ucler, C.; Karabeyoglu, A. Assessment of using electric pumps on hybrid rockets. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar] [CrossRef]
- Casalino, L.; Letizia, F.; Pastrone, D. Design Trade-offs for Hybrid Rocket Motors. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Atlanta, GA, USA, 30 July–1 August 2012. [Google Scholar] [CrossRef]
- Casalino, L.; Letizia, F.; Pastrone, D. Optimization of Hybrid Upper-Stage Motor with Coupled Evolutionary/Indirect Procedure. J. Propuls. Power 2014, 30. [Google Scholar] [CrossRef]
- McBride, B.J.; Reno, M.A.; Gordon, S. CET93 and CETPC: An Interim Updated Version of the NASA Lewis Computer Program for Calculating Complex Chemical Equilibria with Applications; NASA TM-4557; NASA: Washington, DC, USA, 1994. [Google Scholar]
- Sutton, G.P.; Biblarz, O. Rocket Propulsion Elements; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Maisonneuve, V.; Godon, J.; Lecourt, R.; Lengelle, G.; Pillet, N. Hybrid Propulsion for Small Satellites Design Logic and Tests. Int. J. Energ. Mater. Chem. Propuls. 2002, 5. [Google Scholar] [CrossRef]
- Schoonover, P.; Crossley, W.A.; Heister, S. Application of a Genetic Algorithm to the Optimization of Hybrid Rockets. J. Spacecr. Rockets 2000, 37, 622–629. [Google Scholar] [CrossRef]
- Barrere, M.; Jaumotte, A.; Fraeijs de Veubeke, B.; Vandenkerckhove, J. Rocket Propulsion; Elsevier: Amsterdam, The Netherlands, 1960. [Google Scholar]
- Kwak, H.D.; Kwon, S.; Choi, C.H. Performance Assessment of Electrically Driven Pump-fed LOX/Kerosene Cycle Rocket Engine: Comparison with Gas Generator Cycle. Aerosp. Sci. Technol. 2018, 77, 67–82. [Google Scholar] [CrossRef]
- Barker, D.; Belnap, R.; Hall, A.; Kordig, J. A Simplified Method of Predicting Char Formation in Ablating Rocket Exit Cones. In Chemical Engineering Progress, Symposium Series; American Institute of Chemical Engineers: New York, NY, USA, 1965; Volume 61, pp. 108–114. [Google Scholar]
- Casalino, L.; Pastrone, D. Oxidizer Control and Optimal Design of Hybrid Rockets for Small Satellites. J. Propuls. Power 2005, 21, 230–238. [Google Scholar] [CrossRef]
- Casalino, L.; Colasurdo, G.; Pastrone, D. Optimal Low-Thrust Escape Trajectories Using Gravity Assist. J. Guid. Control Dyn. 1999, 22, 637–642. [Google Scholar] [CrossRef]
- Colasurdo, G.; Pastrone, D. Indirect Optimization Method for Impulsive Transfers. In Proceedings of the Astrodynamics Conference, Scottsdale, AZ, USA, 1–3 August 1994; pp. 441–448. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).