Abstract
One of the crucial issues affecting the structural safety of propeller vehicles is the propeller tonal excitation and related vibrations. Propeller rotation during flight generates vibrating sources depending upon its rotational angular velocity, number of blades, power at shaft generating aircraft thrust, and blade geometry. Generally, the higher energy levels generated are confined to 1st blade passing frequency (BPF) and its harmonics, while additional broadband components, mainly linked with the blade shape, the developed engine power, and the turbulent boundary layer (TBL), also contribute to the excitation levels. The vibrations problem takes on particular relevance in the case of composite structures. The laminates in fact could exert damping levels generally lower than metallic structures, where the greater amount of bolted joints allow for dissipating more vibration energy. The prediction and reduction of aircraft vibration levels are therefore significant considerations for conventional propeller aircrafts now entering the commercial market as well as for models currently being developed. In the Clean Sky 2 framework, the present study focuses on a practical case inherent to the AIRBUS-Racer program aiming to design and develop a multi-tasking fast rotorcraft. This paper defines a finite elements (FE)-based procedure for the characterization of the vibration levels of a main landing gear (MLG) composite door with respect to the expected operating tonal loads. A parametric assessment was carried out to evaluate the principal modal parameters (transfer functions and respective resonance frequencies, mode shapes, and damping coefficients) of the landing gear-door assembly in order to achieve reduced vibration levels. Based on the FE analysis results, the influence of the extra-damping, location, and number of ballast elements, the boundary conditions were investigated with respect to failure scenarios of the kinematic line opening the study towards aeroelastic evaluations. Further experimental ground test results serve as a validation database for the prediction numerical methods representative of the composite door dynamic response.
1. Introduction
1.1. Industrial Advance Scenario
Nowadays, composite structures are established more prominently in the aerospace sector thanks mostly to the manufacturing and integration technology advances. About 40 years ago, Zweben outlined the forward-thinking status of composite material technology with an outlook to future challenges [1]. Particularly in the aviation sector, composite laminates have found a great use in fixed wing and rotary wing aircrafts [2]. Fuselages, wing structures, aerodynamic appendages, tanks, internal and external panels, propellers, rotor blades, and many other details are being made with composite materials. Pioneering outcomes were provided by Lockheed, Boeing, and NASA that attested the service experience on civil flight programs such as L-1011 TriStar and Boeing 737 and military ones too such as C-130 Hercules and F-14 Tomcat [3,4,5]. The composites revealed durability at least equal to that of metals as well as suggested that maintenance costs could be lower [6,7]. Furthermore, the fiber composite configuration could provide significant improvements in specific strength and stiffness over conventional metal alloys [8]. Vosteen and Hadcock performed a study of composite aircraft structure programs by recognizing some lessons learned and best practices relative to materials, processes, and manufacturing [9]. Automated manufacturing was simplified by the development of high-speed fiber placement and stitching equipment. Different manufacturing methods have the potential to yield low-cost, high-performance structures by fabricating composite structures to net shape out-of-autoclave [10]. Due to their level of damping being lower than metallic materials, the problem of vibrations assumes particular importance in composite structures. Special focus must be given to propeller vehicles, typically stressed by two main types of vibrating sources: one coming from the engine and one from the turbulent boundary layer (TBL). Consequently, this issue of dynamic nature is receiving attention even in the first stages of the aircraft design process. The study in [11] focused on the details of ground vibration testing (GVT) of an all carbon-fiber-reinforced polymer (CFRP) composite unmanned aerial vehicle (UAV). Modal parameters including natural frequencies, mode shapes, and damping coefficients were numerically estimated for the full aircraft in a free-free condition and then compared to the experimental vibration characteristics measured by means of a shaker-table approach. Previous studies were performed on finite element (FE) simulations, and static and vibration testing of the wing assembly [12,13] and fuselage [14]. Current research programs are addressing the development of design, analysis, and manufacturing methodologies for complex composite components in order to achieve improved primary structures in terms of weight and cost, thus enabling immediate decisions for next generation vehicles. The design and technological demonstration of a novel main landing gear (MLG) bay architecture were addressed in the Clean Sky 2—ITEMB project. Numerical-experimental activities corroborated the feasibility of a “more integrated” concept fulfilling next AIRBUS A320 class targets comprising low weight and production streamlining [15]. Within the EU funded Project AFLoNext [16], flow-induced vibrations of the MLG door due to downstream vorticity coming from nose landing gear (NLG) was the object of deep investigation by DLR (German Aerospace Center) on research aircraft A320 ATRA (advanced technology research aircraft). Unsteady flow simulations and flight test have been precious in obtaining detailed knowledge of the fluid–structure interaction on the NLG and MLG doors [17]. In the framework of the Clean Sky 2 scenario [18], the ANGELA consortium aimed to develop the landing gear system of the Airbus Helicopters Racer flight prototype (sketched in Figure 1) [19,20,21]. The development team comprising Magnaghi Aeronautica S.p.A. and the Italian Research Aerospace Centre (CIRA) has the ambitious objective of achieving a high TRL (technology readiness level). TRL is a scale from 1 to 9 used by NASA to quantify the maturity level of a technology. The ANGELA team targets its technology development challenge to achieve at least TRL 6, aiming for a transition from research levels to the industrial scale. Research activities were carried out to substantiate the feasibility of an innovative landing gear system with a fully composite trap door in compliance with the demanding safety requirements applicable to next generation helicopters. Significant dynamic loads generally affect MLG doors during flight, primarily due to the aerodynamic excitation [22,23]. A surrogate modeling methodology was applied to the wind tunnel data obtained for the MLG Doors of AIRBUS A350 deriving the unsteady aerodynamic effects at different flight and aircraft conditions previously untested [24]. Such an approach could improve the wind tunnel test management, leading to a selection of new experimental scenarios prior to a detailed and exhaustive measurement campaigns. Thus, an accurate forecast since the design stage represents a fundamental purpose for assessing the optimal aerodynamic configuration. An innovative assembly method for making NLG sandwich-type doors was qualified for use on F-22A. The baseline configuration of composite doors consisted of a sandwich of glass honeycomb cores with carbon epoxy skins and constrained to the frame by aluminum hinges. In the process, new analytical tools were validated with more traditional methods [25].
1.2. Scope of the Research
This technical paper discusses these specific aspects referring to the MLG composite door assembly conceived for a Racer fast rotorcraft. More in detail, the fundamental topics will focus on the modeling strategies, spectral analysis, and further laboratory testing planning. The design, static, and buckling aspects were already investigated by the same research team [26]. The authors proposed a detailed nonlinear FEM (Finite Element Model) approach to assess the MLG door functioning and flushness targets as well under flight loads. Relying upon a ready advanced numerical model, a parametric assessment allowed for investigating the dynamic performance of the MLG door system: the influence of the composite material damping, the stiffening effect of static aerodynamic loads, and the location and number of ballast elements to mitigate the vibration response levels were analyzed with respect to operative BPFs (blade passing frequencies). The evaluation of the dynamic response is a crucial aspect as a composite structure can exhibit less damping than an equivalent metal, where the number of connections is certainly larger [27,28,29,30,31,32]. The trap door should be considered a lift surface, especially due to the high-speed regimes, in which the helicopter can operate. In particular, its dynamic response can also vary considerably according to different possible combinations of in-flight operations. For these reasons, the analyzes took into account the actual boundary conditions of the door too: this aspect made it possible to evaluate the deviation of the modal parameters as a function of the kinematic attitude of the door when it is completely closed and fully open. In this perspective, the work is novel as a technical case study within the aeronautical industrial scenario. Furthermore, a sensitivity investigation was carried out to assess the dynamic stability of the component in the presence of critical scenarios related to malfunctions of the kinematic system in order to build a rational database for future safety studies and experimental campaigns looking at potential certification and industrialization issues.
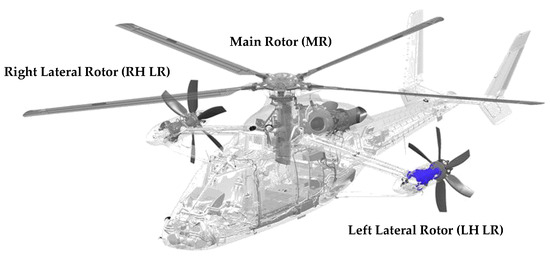
Figure 1.
Racer rotorcraft view: details of the vibration sources [33].
2. Material and Methods
2.1. Architecture Overview
The Racer LGs (Landing Gears) system comprises a tricycle wheeled type and oleo-pneumatic shock absorber for dissipation of the energy during landing. In particular, MLG is a direct cantilever type, equipped with carbon fiber epoxy sandwich LG doors hinged to the H/C frame by means of two metallic fittings. The actuation system consists of a dedicated hydraulic side-brace actuator (SBA) attached on landing gear leg; thus, the door is connected to landing gear by means of a rod link. The MLG system including the main door components are shown and detailed in Figure 2. In the hypothesis of an infinitely rigid pushrod and the absence of large deformations, the door opening is kinematically linked to the MLG leg according to a linear gear ratio (Figure 3). Following a rotation θLEG of one degree of the leg around the pintle pins axis, the door will rotate (θDOOR) by approximately 1.3 degrees around the goosenecks axis (gear ratio, Kgear = θDOOR/θLEG ≈ 1.3); see Figure 3b. When the MLG leg is stowed into the bay, the door is in contact by means of the gaskets on the border of bay cutoff. The static properties of the seal were experimentally estimated to take into account its actual stiffness in the numerical simulations. A hybrid arrangement of composite sandwich panels including carbon fiber/epoxy face sheets and honeycomb core materials with various thicknesses were conceptualized for the door design (Figure 4). Both the HRH-10 Aramid Fiber Reinforced Honeycomb (Nomex, I.MA.TEC, Milan, Italy) and Aluminum 5052 Corrugate Honeycomb (HexWeb® Aluminum Flex-Core®, Hexcel Corporation, Stamford, CT, USA) were downselected.

Figure 2.
Main landing gear (MLG) system architecture: (a) door and fairing with the actuation system; (b) MLG door with a focus on the metallic gooseneck connecting the door to the airframe and the pushrod linking the door to the LG (Landing Gear) leg.

Figure 3.
Kinematic deployment of the MLG system: (a) details of the relative angles and rotation points; (b) gear ratio relationship.

Figure 4.
MLG door architecture.
2.2. FE Model Description
The three-dimensional (3D) FE models were conceived to be fully representative of the detailed MLG door assembly (widely detailed in [26]; Figure 5). The models include several solid components, i.e., ctet4 and chex4 [34], such as goosenecks, joints, and rod links, as summarized in Table 1. The CFRP laminates were modelled by two-dimensional (2D) shell linear elements (Figure 6). The lay-up sequences are reported in Table 2. To connect metallic parts to the composite substrate, 3/16″ size bolts (cbeam and cbush 1D elements) were implemented; their stiffness were properly evaluated according to the design Huth formula [35,36].
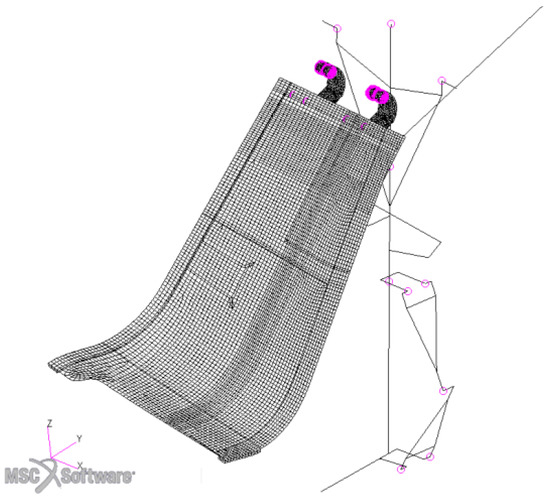
Figure 5.
Global finite element (FE) model for dynamic analysis.

Table 1.
FE model data.

Figure 6.
Laminate FE model: mapping of plies distribution.

Table 2.
Stacking sequences.
2.3. Boundary Conditions
A stick-equivalent schematization was adopted to discretize the LG leg and the hydraulic actuator, generally used to preliminary explore the load distribution on subcomponents (local modeling technique) for complex configurations [37]. Elastic elements represent the gasket stiffness when the door is closed (panel pinned on two longer sides), whilst in the deployment conditions, the pushrod is the only element to guarantee internally the door static equilibrium, constraining the rotational dof (degree-of-freedom) around the axis of the goosenecks (i.e., Rx); see Figure 7.

Figure 7.
Boundary conditions details: MLG leg, H/C, and additional elastic constraints to be considered when the door is closed.
2.4. Damping Characterization of Metallic Fittings and Composite Parts
The MLG door vibration characteristics were investigated, including structural damping coefficients. The damping performance of materials represent a key aspect of vibration characterization. The experimental activities were carried out to quantify the dissipative properties of the samples representative of the final composite arrangement and metallic interfaces (Table 3). In a conservative way, for the honeycomb part, the lowest value was used. Qualification tests were compliant with the ESDU (Engineering Sciences Data Unit) technical procedure [38]. The ESDU “Vibration and Acoustic Fatigue Series” provided methodologic approaches as well as technical flowcharts for assessing the dynamic response and fatigue life of typical aerospace structures, including fiber-reinforced composites, when subjected to vibration loading. The damping estimation requires analysis both in the transient and spectral domains [39,40]. The two methods consist in the evaluation of response decay at the first resonant frequency of the structure: they should return almost similar values. The measurement accuracy of the damping ratio could be affected by boundary conditions and transducer weights. The tested specimens are in general of small size (slender beam for metals and shells for laminates) and therefore sensible to small variations in mass too; for this reason, noncontact measurement (i.e., by laser vibrometry) is preferred as well as a free-free constraint arrangement. The time response is measured following an impact test on the specimen: the amplitude decays proportionally to the structural damping factor ξ, which can be calculated according to relationship (1):

Table 3.
Damping evaluation (ESDU values) [38].
The term δ is the logarithmic decrement (LD) calculated between two consecutive peaks, ai and ai+1, of the acceleration time history (2):
Filtering of the signal is a step often necessary to clean the response from the participation of secondary modes. The half-power bandwidth method (HPB) is then applied to assess the modal damping factor ζ corresponding to the fundamental vibration mode: two points (with frequency f1 and f2, f2 > f1) matching a drop of 3 dB down from the resonance peak (with frequency f0) are used for the calculation of ratio (3).
Figure 8 represents a schematic of the experimental characterization of damping values. These coefficients are then implemented in the numerical simulations for a more accurate representation of structural dynamic response. The GE coefficient on the MAT card was used to specify structural damping for the elements that reference this material entry within all numerical analyses in Nastran® [34].

Figure 8.
Experimental setup schematic to measure the damping material in free-free conditions.
2.5. Gasket Stiffness Characterization
The optimal sealing component is highly compressible in order to be able to adapt to all flange surface unevenness when it is fitted; it is at the same time recovered by 100%. This property determines the adaptability of the gasket to the sealing surface. Characterization of the compression properties of a gasket specimen by measuring deflection with respect to an increasing compressive load was performed as per ASTM F3270/F3270M-17 [41]. Equivalent stiffness was chosen considering the linear region of the load–displacement curve due to the smaller amount of preload expected in the service (K = 50 N/mm); see Figure 9. The first flat area of the curve is due to a rigid slip of the gasket before deforming: after about 7 mm of deflection, a behavior almost linear is measured.

Figure 9.
Stiffness characterization of leap seal: (a) compression test; (b) linear (Kseal = 50 N/mm) and nonlinear loading curves.
3. Results
3.1. Dynamic Constraints
In this section, the main results of the vibration FE analysis on an MLG door are outlined: the purpose is to characterize its dynamic response with respect to the H/C harmonics of MR (main rotor) and LR (lateral rotor) provided by AIRBUS Helicopters as per Table 4. The basic principle in designing the MLG door is to minimize vibration levels, avoiding possible coupling mechanisms among structural resonance and exciting forces. The tonal amplitude is confidential.

Table 4.
Racer H/C dynamic constraints: operating blade passing frequency (BPF) (peak amplitude confidential).
3.2. MLG Door Baseline Configuration: Normal Modes Analysis
The first rational steps were mainly addressed to identify normal modes of the MLG door assembly—in its former configuration—and integrated on the primary LG stick. Firstly, the case with the door completely closed is considered. Subsequently, the configuration with maximum deployment of the LG leg-door assembly is taken into account to simulate an approach maneuver of the helicopter. In such a way, an evaluation of the deviation from the mechanical tones (Table 4) can be carried out. Figure 10 reports the numerical mode shapes in the bandwidth of interest [0; 60 Hz], achieved by implementing Lanczos’ method in solution 103 [34].

Figure 10.
Normal modes of an MLG door baseline configuration: closed door (a) main flexural mode f = 200 Hz; open door (b) harmonic mode, f = 20.6 Hz; (c) fore and aft mode, f = 36 Hz; and (d) torsional mode, f = 52.4 Hz.
When the door is closed, the door behaves as a panel pinned on the two longer sides: the first vibrating mode shape is the typical flexural deformation with maximum modal shift in the center of the structure (Figure 10a). The natural frequency (about 200 Hz) is well above the analysis threshold for which the following modes are not reported. The system dynamics changes dramatically when the door is open. The free oscillation analysis highlighted the stiffening of the first mode shape, as the door is fully open, mainly due to the “constraining” action of the mechanical linkages behind it, i.e., pushrod, SBA, and so on. This effect significantly modifies this first eigenvector, as shown in Figure 10b. Theoretically, in the assumption of rod link system full failure and, hence, in total absence of dry friction in the spherical hinges, this motion is representative of a rigid mode (f = 0 Hz), evolving as free rotation around the goosenecks axis. In nominal conditions, this “quasi-rigid” motion involves a partial flexural of the door due to the pushrod link, which augments the local stiffness, moving the deformability to other regions of the structure. The modal deformation is in fact asymmetrical with maximum generalized displacement next to the forward corner. The dynamic test allows for characterizing the deviation of joints elasticity from a standard modelling strategy based on perfectly rigid elements. The third and fourth modes represent two elastic properties of the door itself: respectively, a bending mode (cantilevered-like mode, Figure 10c) and a torsional mode (Figure 10d).
3.3. Spectral Analysis
The frequency response was useful for estimating the amplitude of structural oscillation too: in the present case, the mode shape association in the [0; 60 Hz] bandwidth was analyzed according to that performed in Section 3.2. Numerical analysis was performed within MSC Nastran® (MSC Software, Newport Beach, US) environment implementing solution 111 (modal frequency response) [34]. For the spectral response identification, 25 points were chosen from the MLG door mesh for the acquisition of linear accelerations. Moreover, the MLG door system was excited by a white noise load applied on the door forward corner: the point corresponded to the area with maximum modal displacement, as per Figure 10. The transfer functions (g/N) were extracted calculating the g-forces (1 g = 9806.65 mm/s2) with respect to the reference load in the driving point (Figure 11a). The graphs outlined later were given by the sum of the spectra of each acquisition point. The acceleration reference value a0 = 0.001 mm/s2 was adopted for conversion to the decibel scale. The frequency response function (FRF) was independent of the excitation amplitude: it expresses a relationship between the vibrational response and the applied load, clearly in conditions of linearity. Additionally, the influence of a ballast mass effect on vibration reduction of natural frequencies was investigated (Figure 11b). The choice of extra-mass position was mainly driven by two reasons: the first one was of an energetic nature, while the second one was linked to a technical-practical issue. The point of maximum modal deformation was also the one with the lowest mechanical impedance: every inertial action, even if of small entity, was transmitted with maximum energy level to the whole host structure [42,43,44]. Relying upon this criterion, the amount of ballast could be assessed. The arrangement was symmetrical in order to guarantee a balanced configuration of the door without affecting the LG system deploying/retracting operating performance. Moreover, such a mass distribution allows for achieving a less invasive modification in the manufacturing phase and a good compatibility with the design clearance requirements as well.
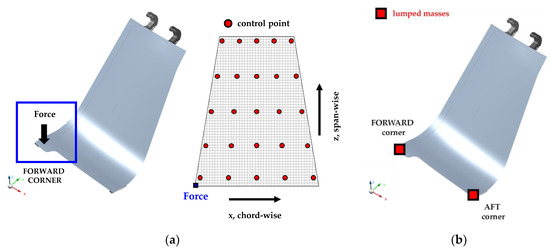
Figure 11.
MLG door analysis setup: (a) dynamic load application and virtual acquisition points on MLG door; (b) ballast mass position.
3.3.1. Nominal Case: Ballast Mass and Effect of Aerodynamic Action
Two possible positions for the lumped mass (schematized as conm2 [34]) were assumed at the free-end of door, in particular at the forward and aft corners. A trial value of 1 kg was initially supposed to evaluate the impact on dynamic response: both asymmetrical (1 kg on forward or on aft corner only) and symmetrical (0.5 kg on both of them) distributions were analyzed. With reference to the transfer function in Figure 12, it seems that the baseline spectrum would be preferable to those with extra-mass: it emerges that just two of three natural frequencies are present in the analyzed range, as already observed by the eigenvectors preceding extrapolation. The addition of a ballast causes in fact a shift of the former third resonance (torsional mode) towards lower values, making the overall response more complex. Due to its close proximity to 5/rev MR in the baseline configuration, the first natural frequency made the use of nonstructural masses necessary. The final design choice should be therefore a rational compromise. The compared results imply that positioning the ballast in forward position allows for achieving maximum shift of the first resonance: about 6 Hz less than the baseline case as well as an amplitude reduction of about 4 dB. However, the antisymmetric distribution denotes an imbalance configuration to emphasize the torsional deformation. The third natural frequency, in addition to the move itself very next to the 10/rev MR harmonic, exhibits significant oscillation amplitude too due precisely to the mass imbalance with respect to the span-wise symmetry axis (z-axis, Figure 11a) of the door. The configuration with symmetrical inertial arrangement would seem the most suitable to mitigate the first frequency as well as to guarantee a much more balanced condition, limiting the impact on the right opening/closing operation of the door. Based on this last configuration, the influence of a “tuning” mass effect on whole spectrum was investigated (Figure 13). Considering a pair of 0.3 kg masses seems to provide an acceptable design compromise: in addition to ensuring a good distance from the critical frequencies, it is the one with a smaller generalized displacement, especially in the case of the first mode shape.

Figure 12.
Extra-mass addition on an MLG door.

Figure 13.
Tuning mass sensitivity on an MLG door.
For the sake of clarity, natural frequencies for each configuration including the external H/C BPFs are summarized in Table 5. The influence of preload on the door dynamic performances due to the aerodynamic pressure in operative conditions was examined. The two worst limit-loading conditions were considered in the case of maximum deployment of the trap door: blowing (opens the door, P = 7255 Pa) and pushing (closes the door, P = −7040 Pa).

Table 5.
Matrix of nominal cases with deployed door: natural frequencies trend.
The FE results in Table 5 show a peculiar behavior of the baseline door that static preload acts upon. The resonance frequencies increase when the aerodynamic pressure blows (pulling aero-load), i.e., leading to opening the door; this stiffening action may be explained by observing the geometric configuration of the door. The stiffness distribution as well as the curvature profile are such that a blowing pressure field counteracts deformation of the panel. The door works in a pre-tensioned state and is therefore more rigid: both a slight increase in vibrational frequencies and a consequent reduction in generalized displacements (Figure 14) are the most noticeable effects.

Figure 14.
Aerodynamic preload effect on the dynamic transfer function.
When the door is sucked on instead (pushing aero-load which closes the door), the structure exhibits a lower generalized stiffness that leads to a larger displacement field too. This behavior is almost uniform overall in the investigated range. In other words, changes in the geometry curvature affect the modal characteristics, even not significantly, with respect to external aerodynamic loads. Moreover, except for a slight percentage variation with respect to the “clean” configuration of a door, a remarkable eigenvalues stability is observed even in the presence of a combined static load.
3.3.2. Failure Case
Landing gear door is not generally classified as a “safety critical” structure. This means that any loss of the system function could not potentially result in “catastrophic” events for the aircraft [45]. Potential fault conditions should be considered from the design phase:
- Hazard description: door uncontrolled dynamic motion;
- Potential impact: door moving undamped in airflow, which may cause structural damages to the H/C frame;
- Recovery action: Immediate speed reduction.
The spectral analyzes were also extended to possible malfunction cases: a failure condition was simulated considering the functionality loss of a pushrod link between the MLG leg and door system. This component was surely more susceptible to potential failure risks than other connection elements as the two goosenecks have a double-shear configuration too (fail safe design). Based on the spectrum of Figure 15, the baseline configuration appears to be the safest one, where instead, the additional masses move the first resonance peak almost in correspondence with the 1/rev LR tone. A couple of 0.3 kg or at least 0.2 kg masses represent a suitable design choice not only in the nominal condition. Looking still at Figure 15, such arrangements generate on the one hand lower amplitude vibrations than the clean configuration as well as have the first peak quite distant from the 1/rev LR critical frequency. The deviation form nominal condition are reported in Table 6.
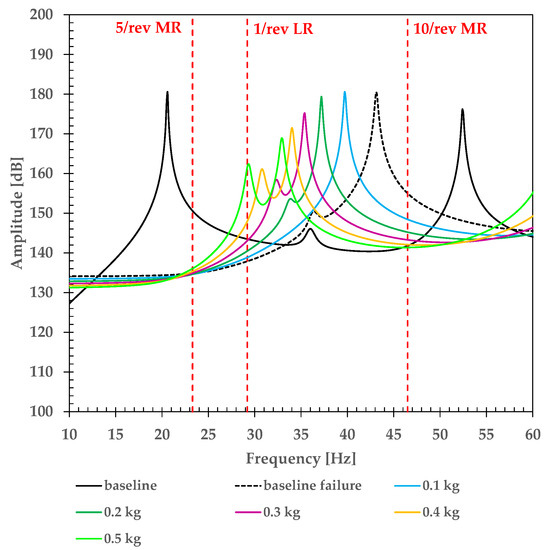
Figure 15.
Extra-mass addition on the MLG door: rod link failure.

Table 6.
Matrix of failure cases with a deployed door: natural frequencies trend.
3.4. Mode Shapes Cross-Correlation
The eigenvectors of the main analyzed configurations were compared with respect to the baseline database. The mode shapes cross matching in terms of MAC (modal assurance criterion) are summarized in Figure 16. The cross-MAC method allows for proving how much the modal shapes deviate from their reference configuration and therefore how the dynamics of the structure changes. Values of this parameter close to one show good agreement between the reference (baseline) and correlation (configurations with extra-mass, aerodynamic preload, and failure event) data. An alteration of the first mode shape (harmonic mode) is observed in the case of a ballast mass placed on the rear corner (cross MAC = 0.77) and in the event of failure (cross MAC = 0.86). Both conditions are actually representative of two stiffness distributions really far from the former properties. A mass on the aft corner constitutes a strongly antisymmetric condition, which contributes together with the pushrod (acting on the rear side) to stiffening the whole rear sector of the panel, thus modifying the vibrating shape. The failure of the pushrod results in a lack of local stiffness leading to a rigid body motion of the entire door without elastic deformations. This effect is even more evident for the fore and aft bending deformation (second mode) but, above all, for the torsional one (third mode). This analysis shows more clearly that a symmetrical distribution of ballast masses is preferable. The action of the aerodynamic preload does not greatly influence the modal shapes: the assumed pressure field is uniform and acts on the entire surface so only the frequency response amplitude is modified and not the eigenvectors.

Figure 16.
Mode shape orthogonalization verification with respect to the baseline configuration: (a) 0.5 kg on each side; (b) 1 kg on the forward corner; (c) 1 kg on the aft corner; (d) pushrod link failure; (e) pulling down aero pressure; and (f) pushing up aero pressure.
4. Conclusions and Next Developments
Significant dynamic loads generally affect MLG doors during flight, primarily due to aerodynamic excitation. Thus, an accurate forecast from the design stage represents a fundamental purpose for assessing the optimal aerodynamic configuration. This paper addresses the dynamic numerical analysis of an MLG door conceived for a high-speed regime compound rotorcraft. Focus was given to characterization of the modal parameters and spectral response of the assembly in the force of the relevant excitation sources. Studies revealed that, during the design phase of a trap door, its different operating regimes should be taken into account for a broad overview of the dynamic response. In the first place, the boundary conditions must be appropriately schematized: the door drastically changes its behavior from when it is closed to when it is completely deployed. Lab test characterizations were carried out to implement the stiffness properties of sealing materials and the structural damping of each subcomponent as well. The additional action of the aerodynamic loads expected in flight was considered in the simulations: the modal parameters and the amplitude of the frequency response are affected, for example, if the pressure field pulls down or pushes up the door. The influence of a tuning mass effect on vibration reduction of the spectrum peaks was investigated by studying several possible mass arrangements considering possible malfunction scenarios too of the mechanical subcomponents. The ANGELA team targets this technology development challenge to achieve at least TRL, 6 aiming for a transition from research levels to the industrial scale. The adequacy of the adopted approach with respect to design requirements and system specifications will be proven by means of next functionality and vibration tests on a ground demonstrator. In the framework of the Racer program, Ground Resonance Test (GRT) will be carried out in order to validate the dynamic FE model of the MLG door assembly. In such a manner, a proven FE model will generate reliable results for the upcoming FHA (Fault and Hazard) assessment. The structural dynamic response and excitation loads will be detected respectively by means of a tri-axial piezoelectric accelerometer or laser vibrometry, and a load cell connected to the electro-dynamic shaker or instrumented hammer. The MLG door assembly will be installed on the real MLG prototype or on a strong-back dummy frame representing the actual constraining interfaces. The modal parameters achieved within the FRF analysis will be measured by a dedicated DAQ (data acquisition) system allowing for identification of the following test article information: its resonance frequencies, mode shapes, and modal damping. The well-correlated modal base of the MLG trap door could represent a proof of compliance of the whole system with airworthiness requirements on safety.
Author Contributions
All authors (M.A., A.C., M.C., and L.D.P.) have equally contributed to this research paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Clean Sky 2 Joint Undertaking under the European Union’s Horizon 2020 research and innovation program under grant agreement No. CS2-GAM-FRC-2014-2015 and the following extensions. More in detail, the activities were funded in the framework of the CS2 project ANGELA part of CS2-GAM-FRC.

Data Availability Statement
Data sharing not applicable.
Acknowledgments
The authors are grateful to all three reviewers for their critical and constructive comments on this paper. The authors thanks Pierre Pardoux and Jaroslaw Zakrzewski of AIRBUS Helicopter for providing the loads, the requirements, and the follow-up during the development.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zweben, C. Advanced composites for aerospace applications: A review of current status and future prospects. Composites 1981, 12, 235–240. [Google Scholar] [CrossRef]
- Harris, C.E.; Starnes, J.H.; Shuart, M.J. Design and Manufacturing of Aerospace Composite Structures, State-of-the-Art Assessment. J. Aircr. 2002, 39, 545–560. [Google Scholar] [CrossRef]
- Stone, R.H.; Harvill, W.E. Service experience of composite parts on the L-1011 and C-130. In Proceedings of the 9th National SAMPE Technical Conference, Atlanta, GA, USA, 4–6 October 1977. [Google Scholar]
- Hoffman, D.J.; Stoecklin, R.L. The 737 Graphite Composite Flight Spoiler Flight Service Evaluation; NASA Langley Technical Report Server; NASA Langley Research Center: Hampton, VA, USA, 1980. [Google Scholar]
- Cowles, A.; Forsch, H. Design, fabrication and test of an F-14 composite overwing fairing. In Proceedings of the Annual Conference SPI Reinforced Plastics/Composites Institute, Society of the Plastics Industry, SPI 30th Annual Conference, Washington, DC, USA, 4–7 February 1975. [Google Scholar]
- Dastin, S.J. Design and concepts of composite structures. In Proceedings of the Third International Conference on Composite Materials, Paris, France, 26–29 August 1980; pp. 46–68. [Google Scholar]
- Hadcock, R.N.; Dastin, S.J.; Erbacher, H.A. Design and fabrication of a mixed composite wing box. In Proceedings of the 5th SAMPE National Technical Conference, Kiamesha Lake, NY, USA, 9–11 October 1973. [Google Scholar]
- Baker, A.; Scott, M.L. (Eds.) Composite Materials for Aircraft Structures, 3th ed.; AIAA Education Series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar]
- Vosteen, L.F.; Hadcock, R.N. Composite Chronicles: A Study in the Lessons Learned in the Development, Production, and Service of Composite Structures; NASA Contractor Report 4620; NASA Langley Research Center: Hampton, VA, USA, 1994; p. 23. [Google Scholar]
- Shuart, M.J.; Johnston, N.J.; Dexter, H.B.; Marchello, J.M.; Grenoble, R.W. Automated Fabrication Technologies for High Performance Polymer Composites Composite Fabrication; NASA Langley Technical Report Server; NASA Langley Research Center: Hampton, VA, USA, 1998. [Google Scholar]
- Simsiriwong, J.; Warsi Sullivan, R. Experimental Vibration Analysis of a Composite UAV Wing. Mech. Adv. Mater. Struct. 2012, 19, 196–206. [Google Scholar] [CrossRef]
- Sullivan, R.; Rais-Rohani, M.; Lacy, T.; Alday, N. Structural testing of an ultralight UAV composite wing. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006. [Google Scholar]
- Sullivan, R.W.; Hwang, Y.; Rais-Rohani, M.; Lacy, T. Structure analysis and testing of an ultralight UAV carbon composite wing. J. Aircr. 2009, 46, 814–820. [Google Scholar] [CrossRef]
- Simsiriwong, J.; Sullivan, R. Vibration testing of a carbon composite fuselage. In Proceedings of the 23rd American Society for Composites Conference, Memphis, TN, USA, 9–11 September 2008. [Google Scholar]
- Viscardi, M.; Arena, M.; Ciminello, M.; Guida, M.; Meola, C.; Cerreta, P. Experimental Technologies Comparison for Strain Measurement of a Composite Main Landing Gear Bay Specimen. In Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, Civil Infrastructure, and Transportation XII, Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Denver, CO, USA, 4–8 March 2018; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; p. 105990N. [Google Scholar]
- Official AFLoNext. Available online: http://www.aflonext.eu (accessed on 8 December 2020).
- Schwochow, J.; Sinske, J.; Buchbach, R. Inflight-Measurements of Aircraft Undercarriage Vibration during Deployment. In ettc2018-Proceedings, Proceedings of the ettc2018—European Test and Telemetry Conference 2018, Nürnberg, Germany, 26–28 June 2018; AMA Service GmbH: Wunstorf, Germany, 2018; p. 54. [Google Scholar]
- Official Clean Sky. Available online: http://cleansky.eu (accessed on 8 December 2020).
- Lienard, C.; Salah el Din, I.; Renaud, T.; Fukari, R. RACER high-speed demonstrator: Rotor and rotor-head wake interactions with tail unit. In Proceedings of the AHS International 74th Annual Forum & Technology Display, Phoenix, AZ, USA, 14–17 May 2018; Vertical Flight Society (VFS): Fairfax, VA, USA, 2018. [Google Scholar]
- Stokkermans, T.; Veldhuis, L.; Soemarwoto, B.; Fukari, R.; Eglin, P. Breakdown of aerodynamic interactions for the lateral rotors on a compound helicopter. Aerosp. Sci. Technol. 2020, 101, 105845. [Google Scholar] [CrossRef]
- Thiemeier, J.; Öhrle, C.; Frey, F.; Keßler, M.; Krämer, E. Aerodynamics and flight mechanics analysis of airbus helicopters’ compound helicopter RACER in hover under crosswind conditions. CEAS Aeronaut. J. 2019, 11, 49–66. [Google Scholar] [CrossRef]
- Belardo, M.; Paletta, N.; Di Palma, L.; Pecora, M. Structural and aeroelastic design of a joined-wing UAV. J. Aerosp. Eng. 2014, 27, 93–111. [Google Scholar] [CrossRef]
- Paletta, N.; Belardo, M.; Di Palma, L.; Pecora, M. Evaluation of wing loads during the flight drop test of the Italian Unmanned Space Vehicle. In Proceedings of the 5th International Operational Modal Analysis Conference, IOMAC 2013, Guimarães, Portugal, 13–15 May 2013; pp. 1–12. [Google Scholar]
- Viúdez-Moreiras, D.; Martín, M.; Abarca, R.; Andrés, E.; Ponsín, J.; Monge, F. Surrogate modeling for the main landing gear doors of an airbus passenger aircraft. Aerosp. Sci. Technol. 2017, 68, 135–148. [Google Scholar] [CrossRef]
- Barnes, J.; McMichael, J.; Walker, J.; Olliffee, R.; Baker, B. Nose Landing Gear Door Re-design. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, AIAA Meeting Paper, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar]
- Chiariello, A.; Orlando, S.; Vitale, P.; Linari, M.; Longobardi, R.; Di Palma, L. Development of a Morphing Landing Gear Composite Door for High Speed Compound Rotorcraft. Aerospace 2020, 7, 88. [Google Scholar] [CrossRef]
- Berger, E.J. Friction modelling for dynamic system simulation. Appl. Mech. Rev. 2002, 55, 430–453. [Google Scholar] [CrossRef]
- Ferri, A.A. Friction damping and isolation systems. J. Mech. Des. 1995, 117, 196–206. [Google Scholar] [CrossRef]
- Gaul, L.; Nitsche, R. The role of friction in mechanical joints. Appl. Mech. Rev. 2001, 52, 93–106. [Google Scholar] [CrossRef]
- Tleilia, A.; Nasri, R.; Chakhari, J. Damping in Bolted Structures. In Condition Monitoring of Machinery in Non-Stationary Operations; Springer: Berlin/Heidelberg, Germany, 2012; pp. 617–626. [Google Scholar]
- Gaul, L.; Becker, J. Damping prediction of structures with bolted joints. Shock Vib. 2010, 17, 359–371. [Google Scholar] [CrossRef]
- Goyder, H.; Lancereau, D.; Ind, P.; Brown, D. Friction and damping associated with bolted joints: Results and signal processing. In Proceedings of the 27th International Conference on Noise and Vibration Engineering (ISMA2016) and 5th International Conference on Uncertainty in Structural Dynamics (USD2016), Leuven, Belgium, 19–21 September 2016. [Google Scholar]
- Helicopter History Site (HELIS). Available online: https://www.helis.com/database/model/Airbus-Racer (accessed on 8 December 2020).
- MSC Nastran®, Quick Reference Guide 2019; MSC Software: Newport Beach, CA, USA, 2019.
- Huth, H. Zum Einfluβ der Nietnachgiebigkeit Mehrreihiger Nietverbindungen auf die Lastübertragungs und Lebensddauervorhersage; Bericht Nr. FB-172; LBF-Bericht: Darmstadt, Germany, 1984. [Google Scholar]
- Huth, H. Influence on Fastener Flexibility on the Prediction of Load Transfer and Fatigue Life for Multiple-Row Joints; ASTM STP 927; ASTM International: West Conshohocken, PA, USA, 1986. [Google Scholar]
- Caputo, F.; De Luca, A.; Greco, A.; Marro, A.; Apicella, A.; Sepe, R.; Armentani, E. Established Numerical Techniques for the Structural Analysis of a Regional Aircraft Landing Gear. Adv. Mater. Sci. Eng. 2018, 2018, 8536581. [Google Scholar] [CrossRef]
- ESDU online engineering manual: ESDU Vibration and Acoustic Fatigue Series, Featured Product from IHS ESDU. Available online: https://www.esdu.com/cgi-bin/ps.pl?sess=unlicensed_1210222080433dxf&t=ser&p=ser_vacf (accessed on 20 December 2020).
- North Atlantic Treaty Organization; Advisory Group for Aerospace Research and Development; Structures and Materials Panel. Damping Effects in Aerospace Structures: Papers. In Proceedings of the 48th Meeting of the AGARD Structures and Materials Panel, AGARD, Williamsburg, VA, USA,, 2–3 April 1979. [Google Scholar]
- Casiano, M.J. Extracting Damping Ratio from Dynamic Data and Numerical Solutions; Technical Memorandum; NASA/TM—2016–218227; NASA Marshall Space Flight Center: Huntsville, AL, USA, 2016. [Google Scholar]
- ASTM F3270/F3270M-17, Standard Practice for Compression versus Load Properties of Gasket Materials; ASTM International: West Conshohocken, PA, USA, 2017. Available online: www.astm.org (accessed on 8 December 2020).
- Sun, J.Q.; Jolly, M.R.; Norris, M.A. Passive, Adaptive and Active Tuned Vibration Absorbers-A Survey. Trans. Am. Soc. Mech. Eng. (ASME) 1995, 117, 234–242. [Google Scholar]
- Wright, R.I.; Kidner, M.R.F. Vibration Absorbers: A Review of Applications in Interior Noise Control of Propeller Aircraft. J. Vib. Control 2004, 10, 1221–1237. [Google Scholar] [CrossRef]
- Marano, G.C.; Greco, R.; Chiaia, B. A comparison between different optimization criteria for tuned mass dampers design. J. Sound Vib. 2010, 329, 4880–4890. [Google Scholar] [CrossRef]
- EASA. Certification Specifications and Acceptable Means of Compliance for Large Rotorcrafts; CS-29; Amendment 8; EASA: Cologne, Germany, 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).